Performance enhancement for crystallization unit of a sugar plant using genetic algorithm technique

Abstract

This paper deals with the performance enhancement for crystallization unit of a sugar plant using genetic algorithm. The crystallization unit of a sugar industry has three main subsystems arranged in series. Considering exponential distribution for the probable failures and repairs, the mathematical formulation of the problem is done using probabilistic approach, and differential equations are developed on the basis of Markov birth-death process. These equations are then solved using normalizing conditions so as to determine the steady-state availability of the crystallization unit. The performance of each subsystem of crystallization unit in a sugar plant has also been optimized using genetic algorithm. Thus, the findings of the present paper will be highly useful to the plant management for the timely execution of proper maintenance decisions and, hence, to enhance the system performance.

Background

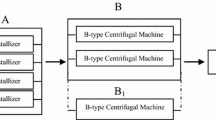
The sugar industry comprises of large complex engineering systems arranged in series, parallel, or a combination of both. Some of these systems are feeding, crushing, refining, steam generation, evaporation, crystallization, etc. The crystallization unit is one of the most important functionary units of a sugar plant where the sugar crystals are formed. The concentrated juice available in the form of thick syrup from refining unit is heated slowly for long time at low temperature condition resulting into the formation of crystals called crystallization process. The semi-solid juice from the cooking pans of refining unit is first fed to the crystallizers arranged in parallel. Now, the juice mixture consisting of yellowish sugar crystals is suspended in a semi solid mass (molasses or magma). This mixture is processed in centrifuges to separate the sugar crystals from magma. These yellowish sugar crystals are treated chemically to yield white crystals, whereas crystal-free magma is recycled through sulphitors for more recovery. The sugar crystals are then sent to the grading unit, which comprises of a hopper, elevator, cooler, and grader, arranged in series. It grades the sugar crystals according to their shape and size.

Literature review

The available literature reflects that several approaches have been used to analyze the system performance in terms of reliability and availability. These include reliability block diagram, Monte Carlo simulation, Markov modeling, failure mode and effect analysis, fault tree analysis, and Petri nets (Misra and Weber [1989]; Singer [1990]; Bradley and Dawson [1998]; Modarres et al. [1999]; Gandhi et al. [2003]; Adamyan and Dravid [2004]; Panja and Ray [2007]; Bhamare et al. [2008]). Dhillon and Singh ([1981]) have frequently used the Markovian approach for the availability analysis, using exponential distribution for failure and repair times. Kumar et al. ([1988, 1989, 1993]) used the Markov modeling in the analysis and evaluation of the performances of sugar and urea fertilizer plants. Srinath ([1994]) has explained a Markov model to determine the availability expression for a simple system consisting of only one component. Gupta et al. ([2005]) have evaluated the reliability parameters of butter manufacturing system in a dairy plant considering exponentially distributed failure rates of various components. The reliability of the system is determined by forming the differential equations with the help of transition diagram using Markovian approach and then solving these differential equations with the help of fourth-order Runge–Kutta method. They applied the recursive method for calculating long-run availability and mean time between failure (MTBF) using numerical technique. Kumar et al. ([2007]) dealt with the simulated availability of CO₂ cooling system in a fertilizer plant.

Gupta et al. ([2008]) developed the performance models and decision support system for a feed water unit of thermal power plant with the help of mathematical formulation based on Markov birth-death process using probabilistic approach. In this way, the decision matrices are developed which provide the various performance levels for different combinations of failure and repair rates for all subsystems. The model developed helps in to decide about correct and orderly execution of proper maintenance in order to enhance the performance of the feed water unit of the thermal power plant. Khanduja et al. ([2008a, b]) have discussed availability analysis of bleaching unit of a paper plant. They also developed the performance evaluation system of screening unit in a paper plant. For long-run failure-free operation of the bleaching and screening units, the expression of steady-state availability has been developed, and behavior of each sub-system has also been analyzed.

Deb ([1995]) has explained the optimization techniques and how they can be used in the engineering problems. Tewari et al. ([2000, 2005]) dealt with the development of decision support system of refining system of sugar plant. They determined the availability for the refining system with elements exhibiting independent failures and repairs or the operation with standby elements for sugar industry. They also dealt with mathematical modeling and behavioral analysis for a refining system of a sugar industry using genetic algorithm. Ying-Shen et al. ([2008]) proposed a genetic algorithm-based optimization model to optimize the availability for a series–parallel system. The objective is to determine the most economical policy of component’s MTBF and mean time to repair.

In this paper, the mathematical (availability) model has been developed to evaluate the performance of crystallization unit of a sugar plant on the basis of certain assumptions. After that, the performance optimization using genetic algorithm technique (GAT) is done, which gives the optimum unit availability levels for different combinations of failure and repair rates of the subsystems of crystallization unit for improving the performance of the sugar plant. Thus, the findings of the present paper will be highly useful to the plant management in futuristic maintenance planning and control to enhance the unit performance.

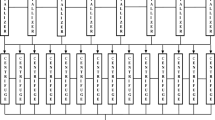
The crystallization unit

Crystallization unit consists of three subsystems in series configuration with the following description:

· Subsystem A _i (i = 1 to 6): It consists of six crystallizer units connected in parallel. The failure of any one reduces the capacity of the system and, hence, loss in production. Complete failure occurs when more than one unit fail at a time.

· Subsystem A _j (j = 1 to 19): It consists of nineteen centrifuge units connected in parallel. Complete failure occurs when more than two units fail at a time.

· Subsystem A _k (k = 1 to 4): It consists of four sugar grader units connected in series. The failure of any one causes the complete failure of the system.

Assumptions

The assumptions used in the probabilistic model are the following:

• 1. Failure/repair rates are constant over time and statistically independent.

• 2. A repaired unit is as good as new and performance wise for a specified duration.

• 3. Sufficient repair facilities are provided, i.e., no waiting time to start the repairs.

• 4. Standby units (if any) are of the same nature and capacity as the active units.

• 5. System failure/repair follows exponential distribution.

• 6. Service includes repair and/or replacement.

• 7. System may work at a reduced capacity/efficiency.

• 8. There is no simultaneous failure among the system. However, simultaneous failure may occur among various subsystems in a system/unit.

Notations

The following notations are associated with the crystallization unit:

• α _i , β _i

i = 22, 23, 24

Respective failure and repair rates of various subsystems

• P _i (t)

Probability function that the unit is in a particular state at time ‘t’

• P _i ′(t)

Derivative of probability functionP _i (t)

Performance modeling

The mathematical modeling is carried out and done using simple probabilistic considerations and differential equations which are developed on the basis of Markov birth-death process. These equations are further solved for determining the steady-state availability of crystallization unit. Various probability considerations give the following differential equations associated with the crystallization unit:

• State 0 - full capacity working with no standby

• State 1 to 5 - reduced capacity working

• State 6 to 16- represents the system in failed state

$$P_0\prime \left(t\right)+{\sum \alpha }_r{P}_0\left(t\right)=\sum {\beta }_j{P}_k\left(t\right)$$

(1)

$$P_1\prime \left(t\right)+{\sum \alpha }_r{P}_1\left(t\right)=\sum {\beta }_j{P}_k\left(t\right)$$

(2)

$$P_2\prime \left(t\right)+{\sum (\alpha }_r{\beta }_{23}\left)P_2\right(t)=\sum {\beta }_j{P}_5(t)+{\alpha }_{23}{P}_0(t)$$

(3)

$$P_3\prime \left(t\right)+{\sum (\alpha }_r+{\beta }_m\left)P_3\right(t)=\sum {\beta }_j{P}_k(t)+{\alpha }_{23}{P}_1(t)+{\alpha }_{22}{P}_2(t)$$

(4)

$$P_4\prime \left(t\right)+{\sum (\alpha }_r{\beta }_{23}\left)P_4\right(t)=\sum {\beta }_j{P}_k(t)+{\alpha }_{23}{P}_2(t)$$

(5)

$$P_5\prime \left(t\right)+{\sum (\alpha }_r{\beta }_m\left)P_5\right(t)=\sum {\beta }_j{P}_k(t)+{\alpha }_{22}{P}_4(t)+{\alpha }_{23}{P}_3(t)$$

(6)

$$P_i\prime \left(t\right)+{\beta }_m{P}_i\left(t\right)={\alpha }_m{P}_1\left(t\right)$$

(7)

By putting d/dt = 0 as t → ∞ in Equations 1 to 7, the steady-state probabilities are given as follows:

$$\sum {\alpha }_r{P}_0=\sum {\beta }_i{P}_k$$

$$\sum {\alpha }_r{P}_1=\sum {\beta }_i{P}_k$$

$$\sum ({\alpha }_r+{\beta }_m)P_3=\sum {\beta }_i{P}_k+{\alpha }_{23}{P}_1+{\alpha }_{22}{P}_2$$

$$\sum ({\alpha }_r+{\beta }_m)P_5=\sum {\beta }_i{P}_k+{\alpha }_{22}{P}_4+{\alpha }_{23}{P}_3$$

$$P_i=({\alpha }_m/{\beta }_m)P_1$$

The probability of full capacity working viz. P₀ is determined by normalizing condition, i.e.,

$$\sum _{i=0}^{16}{P}_i=1$$

Substituting the values of P₁ to P₁₆ in terms of P₀ into normalizing condition, we get

$$P_{0}N=1$$

Let

$$A={\alpha }_{22}/{\beta }_{22},B={\alpha }_{23}/{\beta }_{23},C={\alpha }_{24}/{\beta }_{24}$$

$$X_1={\alpha }_{22}+{\alpha }_{23}–\left({\alpha }_{22*}{\beta }_{23}/\left({\alpha }_{22}{}_{+}{\beta }_{23}\right)\right)$$

$$X_2={\beta }_{22}+\left({\alpha }_{23*}{\beta }_{22}/\left({\alpha }_{22}+{\beta }_{23}\right)\right)$$

$$X_3=X_1/X_2$$

$$X_4=({\alpha }_{22}+{\alpha }_{23}{}_{-}{\beta }_{22}*{\text{X}}_3)/{\beta }_{23}$$

$$X_5={\left({\alpha }_{23}/{\beta }_{23}\right)}^2*{\beta }_{23}+{\alpha }_{23}*X_4\text{.}$$

Then,

$$\begin{array}{l}N=1+X_3+X_4+B*X_3+X_5+B^2*X_3+B*X_5+B^3*X_3+C*B^2*X_3+A*B^2*\\ X_3+A*B*X_3+C*B*X_3+A*X_3+C*X_3+C+C*X_4+C*X_5\end{array}$$

Now, the steady-state availability of the crystallization unit may be obtained as the summation of all the working state probabilities, i.e.,

$$\text{Availability}=\sum _{i=0}^5{P}_i$$

or

$$\text{Availability}\left(\text{Av}.\right)=\left(1/N\right)[1+X_3+X_4+X_5+B{}_{*}{X}_3+B^2*X_3]$$

Performance analysis

From the maintenance history sheet of crystallization unit of sugar plant and the detailed discussions with the plant personnel, appropriate failure and repair rates of all the subsystems are taken, and availability matrices (performance values) are prepared accordingly by putting these failure and repair rate values in expression of availability for P₀. This deals with the quantitative analysis of all the factors viz. courses of action and states of nature, which influence the maintenance decisions associated with the crystallization unit. These availability models are developed under the real decision-making environment, i.e., decision making under risk (probabilistic model) and used to implement the proper maintenance decisions for the crystallization unit of sugar plant.

Table 1 represents the availability matrices for various subsystems of the crystallization unit. These matrices simply reveal the various performance levels for different combinations of failure and repair rates/priorities. It also depicts the effect of failure/repair rate of all the subsystems on crystallization unit performance. On the basis of analysis, one may select the best possible combinations (α _i , β _i ) to increase the unit availability. Table 1 shows optimal availability level for all the subsystems (for crystallizer is 0.9403; for centrifuge, 0.6615; for sugar grader, 0.6059) which can be optimized using genetic algorithm technique.

Table 1 Availability matrices of the subsystems for crystallization unit

Genetic algorithm technique

Genetic algorithms (GA) are computerized search and optimization algorithms based on the mechanics of natural genetics and natural selection (Figure 1). Genetic algorithms have become important because they are found to be potential search and optimization techniques for complex engineering optimization problems. The action of GAT for parameter optimization in the present problem can be stated as follows:

• 1. Initialize the parameters of the genetic algorithm.

• 2. Randomly generate the initial population and prepare the coded strings.

• 3. Compute the fitness of each individual in the old population.

• 4. Form the mating pool from the old population.

• 5. Select two parents from the mating pool randomly.

• 6. Perform the crossover of the parents to produce two off springs.

• 7. Mutate if required.

• 8. Place the child strings to new population.

• 9. Compute the fitness of each individual in new population.

• 10. Create best-fit population from the previous and new population.

• 11. Repeat the steps 4 to 10 until the best individuals in new population represent the optimum value of the performance function (unit availability).

The performance behavior of the crystallization unit is highly influenced by the failure and repair parameters of each subsystem. These parameters ensure high performance of the crystallization unit. GAT is hereby proposed to coordinate the failure and repair parameters of each subsystem for stable system performance, i.e., high availability. Here, the number of parameters is six (three failure parameters and three repair parameters). The design procedure is described as follows: To use GAT for solving the given problem, the chromosomes are to be coded in real structures. Here, concatenated, multi-parameter, mapped, fixed-point coding is used. Unlike, unsigned fixed-point integer coding parameters are mapped to a specified interval [X_min, X_max], where X_min and X_max are the maximum and minimum values of system parameters. The maximum value of the availability function corresponds to the optimum values of system parameters. These parameters are optimized according to the performance index, i.e., desired availability level. To test the proposed method, failure and repair rates are determined simultaneously for optimal value of unit availability. Effects of population size and number of generations on the availability of crystallization unit are shown in Tables 2 and 3. To specify the computed simulation more precisely, trial sets are also chosen for GA and system parameters. The performance (availability) of the crystallization unit is determined by the designed values of the unit parameters.

Figure 1

Flow chart for typical genetic algorithm technique.

Table 2 Effect of population size on availability of the crystallization unit using genetic algorithm

Table 3 Effect of number of generation on availability of the crystallization unit using genetic algorithm

Failure and repair rate parameter constraints

$$\begin{array}{l}\left({\alpha }_{22},{\beta }_{22},{\alpha }_{23},{\beta }_{23},{\alpha }_{24},{\beta }_{24}\right)\\ \begin{array}{ccc}\hfill {\alpha }_{22},\left[\text{A}1\right]\epsilon \left(0.01\text{,}0.05\right)\hfill & \hfill {\alpha }_{\mathbf{2}\mathbf{3}},\epsilon \left(0.04\text{,}0.12\right)\hfill & \hfill {\alpha }_{\mathbf{2}\mathbf{4}},\epsilon \left(0.02\text{,}0.10\right)\hfill \\ \hfill {\beta }_{\mathbf{2}\mathbf{2}},\epsilon \left(0.01\text{,}0.05\right)\hfill & \hfill {\beta }_{\mathbf{2}\mathbf{3}},\epsilon \left(0.01\text{,}0.05\right)\hfill & \hfill {\beta }_{\mathbf{2}\mathbf{4}},\epsilon \left(0.01\text{,}0.05\right)\hfill \end{array}\end{array}$$

Here, real-coded structures are used. The simulation is done to a maximum number of population size, which is varying from 20 to 120. The effect of population size on availability of the crystallization unit is shown in Figure 2.The optimum value of unit’s performance is 94.91%, for which the best possible combination of failure and repair rates is α₂₂ = 0.0205, β₂₂ = 0.2823, α₂₃ = 0.0207, β₂₃ = 0.4406, α₂₄ = 0.0203, and β₂₄ = 0.4905 at population size 100 as given in Table 2.

Figure 2

Effect of population size on crystallization unit availability.

Now, the simulation is done to a maximum number of generations, which is varying from 100 to 350. The effect of number of generations on availability of the crystallization unit is shown in Figure 3. The optimum value of unit’s performance 90.39%, for which the best possible combination of failure and repair rates is α₂₂ = 0.01001, β₂₂ = 0.04978, α₂₃ = 0.04033, β₂₃ = 0.46868, α₂₄ = 0.02049, and β₂₄ =0.47530 at generation size 300 as given in Table 3.

Figure 3

Effect of number of generations on crystallization unit availability.

Conclusions

The performance optimization of crystallization unit of a sugar plant is discussed in this paper. Genetic algorithm technique is hereby proposed to select the various feasible values of the unit failure and repair parameters. Then, GAT is successfully applied to coordinate simultaneously these parameters for an optimum level of unit performance. Besides, the effect of GA parameters such as population size and number of generations on unit performance, i.e., availability, has also been discussed. The findings of this paper are discussed with the concerned sugar plant management. Such results are found highly beneficial for the purpose of performance enhancement of a crystallization unit in the sugar plant concerned.