Abstract
Distribution network design as a strategic decision has long-term effect on tactical and operational supply chain management. In this research, the location-allocation problem is studied under demand uncertainty. The purposes of this study were to specify the optimal number and location of distribution centers and to determine the allocation of customer demands to distribution centers. The main feature of this research is solving the model with unknown demand function which is suitable with the real-world problems. To consider the uncertainty, a set of possible scenarios for customer demands is created based on the Monte Carlo simulation. The coefficient of variation of costs is mentioned as a measure of risk and the most stable structure for firm's distribution network is defined based on the concept of robust optimization. The best structure is identified using genetic algorithms and 14% reduction in total supply chain costs is the outcome. Moreover, it imposes the least cost variation created by fluctuation in customer demands (such as epidemic diseases outbreak in some areas of the country) to the logistical system. It is noteworthy that this research is done in one of the largest pharmaceutical distribution firms in Iran.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A supply chain is a set of facilities, suppliers, customers, products, and methods of purchasing, monitoring inventory, and distribution. In a supply chain, the flow of goods between suppliers and customers goes across several stages and each stage may include some facilities (Sabri and Beamon 2000). Supply chain design is the most fundamental decision that will impact the entire supply chain, and it has been obtaining much importance recently due to increasing competitiveness in markets (Simchi-Levi and Kaminsky 2004; Thomas and Griffin 1996). Firms are forced to keep high customer service levels while they are obliged to reduce costs and maintain profit margins simultaneously.
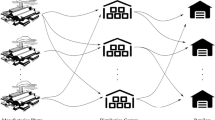
Distribution networks are considered as the main profitability key because they directly affect both the cost of supply chains and satisfaction of the customers (Chopra 2003). The high cost of buying assets and building facilities has made locating or relocating the facilities a long-term investment, and the deployed facilities are expected to carry out their activities for a long period of time. Therefore, it seems essential to design a supply chain network which performs well with some parameters variation across time (Santosa 2003). General structure of the supply chain is shown in Figure 1.
Typical supply chain structure (Melo et al. 2009 ).
Supply chain design includes strategic decisions such as determining the number and location and capacity of facilities in each echelon of the supply chain. The location of facilities and the allocation of demands to them have been a substantial research area. The typical location-allocation problem involves selecting p facilities among n potential locations and allocating demand to the open facilities to minimize the total cost (Hakimi 1965). In addition, distances, times, or costs among customers and facilities can be considered (Drezner and Hamacher 2004; ReVelle and Eiselt 2005). This is p-median problem which has attracted much attention in the literature (Daskin 1995; Mladenovic et al. 2007).
Different techniques have been employed to solve problems relating to facility location. The p-median problem is typically formulated as an integer program (IP). Enumeration and heuristics methods were the primary techniques which are proposed to solve this problem. Also, several methods have been used to solve LP relaxations of the IP formulation problems including branch-and-bound, dual ascent, sub-gradient optimization, and Lagrangian relaxation.
Metaheuristics and approximation algorithms are the prominent techniques in the literature over the last few years. The most common metaheuristics are genetic algorithms, simulated annealing, variable neighborhood search, tabu search, and neural networks. Moreover, some approximation algorithms have been created which attain different bounds on the favorable solution quality.
In fact, the configuration stability of a supply chain network is highly desirable because of great investments normally dedicated with this type of decisions. In this paper, the goal is to obtain a distribution network design that can cope with the future demand variations and achieve a 'robust’ network design. In this case study, actual data is used from a company which is one of the largest pharmaceutical distribution firms in Iran. Because drug and medicine are considered as strategic commodity in all around the world, minimizing the total cost of pharmaceutical supply chain is not the entire objective and achieving a robust supply chain design is more important than having the least cost network.
In this paper, the goal is to determine the optimal number and location of distribution centers. Moreover, the allocation of customer demands to distribution centers under demand uncertainty is defined in order to minimize the total annual cost including warehouse fixed costs, inventory costs, and transportation costs while maintaining the required service level.
This paper is organized as follows: In the 'Problem statement’ section, the mathematical model and background on methodology is stated. The proposed genetic algorithm is given in the third section, and the approach to deal with uncertainty is discussed in the fourth section. Numerical results are presented in the 'Results and analysis’ section, and finally, the paper is concluded in the 'Conclusion’ section.
Problem statement
The problem considered in this paper is designing the distribution network for pharmaceutical distribution companies in Iran. Existing in the pharmaceutical industry entails accepting a series of requirements and commitments related to the Department of Health. For example, manufacturers and importers in this industry do not have the permission to distribute their own products and they are obliged to distribute their products through distribution companies. Actually, the pharmaceutical distribution firms are the connecting chain between suppliers and retailers.
Based on the scope of activity, pharmaceutical distribution companies are divided into provincial and national firms. Provincial distribution companies are licensed to operate in particular region bounds whereas national distribution companies are forced by the Ministry of Health to distribute drugs in all provinces of the country. This company is one of the national distribution firms in Iran which should cover the demands of all cities in country with its own products.
According to the latest published statistics, the market share of this company is 15% of the medicines and medical equipment market in Iran. The suppliers of this company include 32 manufactures and 46 importers of medicine and medical equipment which are the main suppliers of the country. These infrastructures make this company as the second pharmaceutical distribution company in Iran.
The customers of this company include pharmacies, hospitals, and medical centers in most of the cities in Iran whose numbers roughly equate 10,000. It is obvious that this optimization problem needs a very large amount of data. Therefore, data aggregation is the first essential step that should be done. The efficient approach which is used for this purpose is classifying the pharmacies, hospitals, and medical centers in each city in one cluster.
Then, all customers located in each group are replaced by a single demand point in the center of cluster. Even if suitable technology exists to solve the problem with large initial data, data aggregation would be useful. Aggregation causes reduce the data variability and forecasting with aggregated data is significantly more precise compared with non-aggregated data (Simchi-Levi and Kaminsky 2004).
This company approximately owns 1,900 different drugs and medical equipment in its product portfolio, and the composition of them has been determined based on market demands. Due to the relatively large number and small size of the products, these are integrated to one product. Moreover, what is significant matter for the company is how much space each customer demands occupies the content of vehicles in the transportation process. So, according to the length, width, and height of product packages, the total volume of demand products is calculated, and it is used as the measure of customer demands. So, this problem is considered as a single product and multi-level supply chain design problem (Sousa et al. 2011).
The current logistical structure of the company includes a warehouse in Tehran and 18 distribution centers in different provinces. The company wants to redesign its distribution network to satisfy all customer demands and tolerate the minimum total costs caused by demand fluctuations.
Location-allocation model
The design of the distribution network for this company is modeled in the form of a mixed integer linear programming problem in both location and allocation phases. In the location phase, the objective is to determine the optimal number of distribution centers and define which customers are supplied with each distribution center. In the allocation phase, the objective is to specify the amount of inventory which is transferred from the warehouse to distribution centers and from distribution centers to the customers (Amiri 2006; Gebennini et al. 2009; Jayaraman and Ross 2008; Jayaraman and Pirkul 2001). The assumptions considered in this model are
-
The delivery time of transferring goods from warehouses to distribution centers and from distribution centers to customers is considered constant.
-
The cost of transportation is calculated based on the distance between two points and the shipping cost of a product unit in each path.
-
The total demand of each customer must be provided by a distribution center.
-
The number of customers and their demands are known.
-
The numbers and capacities of potential distribution centers and warehouses are known.
Set I represents the set of customer zones, J is the set of potential distribution centers, K is the set of potential warehouse locations, and L is the set of products. The location model intends to minimize three types of costs. The first type of costs is fixed costs associated with open warehouses (V K ) and distribution centers (F J ).
Second, external transportation cost to transfer products from the warehouses to distribution centers (C jkl ). The third type is internal transportation costs to transfer products from distribution centers to customer zones (C ijl ). The customer demands for products (a il ), the capacity of distribution centers (b j ), and warehouses (d k ) are all given as input parameter to the model.
The decision variables track the set of customer zones that are dedicated to distribution centers for products (X ijl ), the set of open distribution centers that are dedicated to open warehouses (Y jkl ), and the set of distribution centers (Z j ) and warehouses (P K ) which are open or closed.
M1: Location model
Subject to:
In allocation model, (S ijl ) shows the cost to supply one unit of product L from distribution center J which would be used by customer I, (S jkl ) is transportation cost for one unit of product L from warehouse K to distribution center J, (TC kl ) is the transportation cost to deliver one unit of product L to warehouse K and a il is the demand from customer I for product L. The decision variables are represented by B kl which is the quantity of product L sent to warehouse k, Q jkl is the quantity of product L sent from warehouse k to distribution center J, and V ijl is the quantity of product L sent from distribution center J to customer I (Jang et al. 2002; Shu et al. 2010; Tragantalerngsak et al. 2000).
M2: Allocation model
Subject to:
Backgrounds on methodology
Over the past 40 years, a great number of combinatorial problems have emerged from computer science and engineering (such as the location-allocation problem studied here). It has been proved that these combinatorial problems belong to the class of NP-complete problems (Garey and Johnson 1979) and with increase in number of variables, the time required to find the optimal solution are enhanced exponentially (Garey and Johnson 1979). Thus, solving large scale of these problems to achieve optimality in a reasonable amount of computational time is not possible.
To solve these problems, heuristic algorithms were developed which provide acceptable solutions in proper computational time. One of the major defects of heuristic algorithms is the high risk of being trapped in local optimal solutions. To improve these algorithms, new approaches were presented in 1970s. They were meta-heuristic algorithms which explore the solution area to find optimality with diversification and intensification search (Talbi 2009).
These algorithms are very efficient and successful in solving complex optimization problems which classical methods are unable to solve. As a meta-heuristic algorithm, genetic algorithms have been used widely as a tool in simulation and exploring the solution area in various contexts. The high applicability and simplicity usage are the main reasons for the widespread use of this algorithm.
Proposed genetic algorithm
Genetic algorithms (GA) are based on Darwin's theory, and two main ideas are considered in this theory. First, next generations are created from the evolution of the previous generations. Second, members who are stronger in the struggle for survival have greater living chance. So, GA is an algorithm which utilizes initial population, and each member of the population is considered as a solution (Arostegui et al. 2006; Melo et al. 2012).
Representation
The first step to solve a problem by genetic algorithm is defining the structure of representation and the way to convert a chromosome to a solution. Representation is one of the most important subjects that influence the performance of genetic algorithms. The first application of GAs in distribution problems was carried out by Michalewicz et al. (1991). One known way to represent network problems is tree-based representation. Basically, there are three ways for representing a tree: edge-based encoding, vertex-based encoding, and edge-and-vertex-based encoding (Gen and Cheng 2000). In this paper, matrix-based representation which belongs to edge-based encoding category is used to represent the solutions (Altiparmak et al. 2009; Drezner and Wesolowsky 2003; Syarif et al. 2002).
For this purpose, the (n × m) binary matrix is used which n indicates the number of distribution centers and m indicates the number of demand points. There are two constraints in the representation of solutions which associate with assumptions. First, the summation of the columns of the representation matrix should certainly be one which means that the demand of each city should be covered only by a distribution center. Second, the summation of each row of this matrix must not be zero which means each distribution center should cover the demand of at least one customer. It is noticeable that the number of initial population size be considered 250 with regards to the problem largeness.
Fitness function
Fitness function indicates the quality of the solutions with a numerical value and guides the Searching process to better solutions. The fitness function in this problem consists of three costs. The first cost is external transportation which is defined as the cost of transportation from warehouses to distribution centers. The second is internal transportation cost which is defined as the cost of transportation from distribution centers to customers and the third cost is the inventory holding costs in distribution centers (Talbi 2009).
-
External transportation cost
-
The location of each distribution center (DC) is identified based on logistical structure and the latitude and longitude of each demand point. After the calculation of distances between each DC to the warehouse, the required vehicles for transportation of products are determined with regard to the demand of the cities. Then, the external transportation cost is calculated based on the unit cost of transportation in each path.
-
Internal transportation cost
-
According to the specific location of each DC, the distance between DCs and cities are calculated and with regard to the demand of each city, the required vehicles and the internal transportation cost are determined.
-
Inventory holding costs
-
The number of distribution centers to cover all demand points is determined by logistical structure of each solution. Based on the financial department documents related to the costs of DCs, a strong linear relationship between the amount of inventory in storage facilities and the available labors in DCs and annual cost of DCs are found. Thus, the required labor and annual cost of each DC is estimated, and accordingly, the inventory holding cost is calculated.
Genetic operators
In each generation, the chromosomes are evaluated by measuring their related fitness functions. The chromosomes of next generation which are produced through two ways mentioned below are called offspring.
-
1.
Merging two chromosomes using crossover operator
-
2.
Changing chromosomes using mutation operator
Crossover is an operator used to explore new solutions in search space, and it is responsible to exchange parts of chromosomes among selected parents. In this study, two-point crossover operator is employed which these two points is randomly selected among the corresponding parts of parents. It is noteworthy that crossover probability has been considered 0.8 in this operator.
Mutation is another operator that is responsible for modifying genes within a chromosome at low rates and creates random variations in some chromosomes. The main role of mutation is identifying some areas of the search space whose possibility of being explored is low. Also, this operator reduces the probability of trapping populations in local optimal and prevents the premature convergence (Jaramillo et al. 2002). In the proposed algorithm, uniform mutation is employed and mutation probability is considered 0.1 in this operator.
Selection strategy
The most important question that should be answered to determine the selection strategy is which parents should be selected for creating the next generation to move toward a better fitness function. In this paper, roulette wheel method is used to determine the parents. In this method, the selection probability of each chromosome is proportional to the degree they deserve. The reason for using this method is to maintain diversification in the population and provide even low chance of being selected for parents which have low fitness function (Talbi 2009).
Control parameters
This parameter impacts on the stopping criteria of algorithms and can be decreased when the convergence in solution occur. Also, this parameter can be increased when significant improvement was not observed after a certain number of iterations in order to enhance the diversification in the population. It is noticeable that the optimal solution is not known in advance in this problem and the stopping criteria are set to achieve a certain number of iterations (Talbi 2009). In this paper, the number of generations is set to 1,000 and the algorithm stops if it has not any improvement over 400 generations.
Regarding to the proposed mathematical model and being in the NP-hard category, there is no rational computational time for solving medium and large scale of this problem. To validate the proposed algorithm, some small scale problems are solved by exact solutions and the answers are compared with the answers of the proposed genetic algorithm. It is noticeable that 'Gams 21.7’ is the software which is used to solve the mathematical model with exact approach.
The results of solving small scale problems with exact algorithms demonstrate that they are identical with the answers resulting from the proposed genetic algorithm. Exact algorithms find the optimal solution with exploring all the search space of the problems. This equality indicates that the proposed genetic algorithm can achieve optimality in problems with small size and this demonstrates the validation of the algorithm. Therefore, it can be concluded that the proposed algorithm is appropriate for solving large and medium problems.
The approach to deal with uncertainty
With studying the data of customer demands in the past 40 months, it becomes clear that the demands' behavior do not follow any specific probability distribution function. This uncertainty occurs due to the strong bullwhip effect which exists in most of the industries, but it is very impressive in pharmaceutical industry in Iran. Figure 2 illustrates the behavior of the demands quantity in an instance city in the last 40 months.
The main reason for the demand fluctuations and the bullwhip effect exacerbation is false orders in periods of drug shortages. Such orders are so common because the customers think that the future supply of drugs and medicines will encounter by reduction. Also, the fluctuation in the price of medicines is a cause to intensify this phenomenon (Simchi-Levi and Kaminsky 2004).
An important step in the process of decision making is risk analysis. If there is a lot of uncertainty in a parameter or there is not enough availability or accessibility to the previous information, the future cannot be predicted accurately. Monte Carlo simulation provides the possibility to distinguish all the consequences of decisions and evaluate the related risk of each factor and helps to make better decisions under uncertain conditions. This technique is used in a wide variety of fields such as insurance, financial management, project management, manufacturing, research development, and transportation (Deleris and Erhun 2005; Flores et al. 2006).
Monte Carlo simulation conducts risk analysis based on the outputs with replacing the values of uncertain variables. In this technique, a random set of values between the upper and lower bound for each variable is obtained from its probability distribution function. Monte Carlo simulation can contain even several thousands of calculations with regard to the number of uncertain variables and their variation ranges. Thus, a set of patterns are generated in each scenario which represent one of the possible conditions. The output of the Monte Carlo simulation illustrates the frequency of objective function values which is associated with occurrence of different scenarios (Kalos and Whitlock 2008; Klibi et al. 2010). It is obvious that the higher numbers of scenarios, the more likely conditions are examined in the available space.
Results and analysis
As was mentioned, to consider the uncertainty in customer demands, some scenarios are created based on Monte Carlo simulation. For each scenario, the optimal number and location of distribution centers and the allocation of customers demand to distribution centers is determined. Figure 3 shows the location of 209 demand points which are the integration of pharmacies, hospitals, and health centers in the intended cities with their geographical specifications (longitude and latitude).
Figure 4 demonstrates the histogram of the optimal number of distribution centers based on the 400 scenarios of customer demands. In each scenario, the best number of distribution centers is calculated using the proposed genetic algorithm. This figure illustrates that the logistical structures with 9, 10, and 11 distribution centers gain the most frequencies among the structures. In the next step, the optimal logistical structures for candidate solutions are determined. This time, a great number of scenarios (10,000 scenarios) for customer demands are created, and the average and standard deviation of costs for these three structures are compared and shown in Table 1.
The results show that logistical structure with nine distribution centers has the least coefficient of variation among others. In this paper, the coefficient of variation is mentioned as an index of risk, so it can be concluded that this structure is more stable against uncertainty in customer demands. Figure 5 illustrates the logistical structure with nine distribution centers which is selected as the best distribution network for this company. It is remarkable that the total cost in current distribution network is 9.97 × 108 monthly and the proposed distribution network leads to 14% reduction in total cost compared with the current distribution network.
To prove the significance of the difference between the costs of the structures, ANOVA test is used in SPSS 20.0 software. This test is done to compare the mean cost of these three groups and to study the influence of independent variables on dependent variable.
In this problem, the independent variables include the number of distribution centers in each candidate logistical structure, and the dependent variable is the logistical costs associated with the structures. The result of this test is shown in Table 2. As it can be shown, Sig is smaller than 0.05 which means H0 is rejected and there are significant differences between the average costs of these structures.
Conclusion
In this study, a model of location-allocation problem in a three echelon supply chain with the aim of locating an unknown number of distribution centers to distribute pharmaceutical products from a specific warehouse to customers (pharmacies, hospitals, and medical centers in specific cities) is provided. The objective function of this model was minimizing the external and internal transportation costs and holding costs of inventory in distribution centers.
On the one hand, increasing the number of distribution centers is a cause to enhance the service levels and reducing the transportation costs from the distribution centers to the customers. On the other hand, decreasing the number of distribution centers leads to inventory integration and take advantage of risk pooling and reduce the inventory holding cost. Thus, the questions which are raised in this paper are how the optimal number of distribution centers should be determined, where distribution centers should be established and which customers must be assigned to each distribution center.
We are witnessing the customer demand uncertainty in pharmaceutical industry, and it cannot be considered in any specific probability distribution function. This uncertainty is due to the intense bullwhip effect created by retailers and other factors. To consider the uncertainty in this study, a set of possible scenarios is created based on the Monte Carlo simulation method, and for each scenario, the distribution network has been optimized using genetic algorithm.
According to the frequency of optimal distribution center numbers specified from scenarios, three structures with 9, 10, and 11 distribution centers which have the highest frequency are introduced as candidate solutions. The mean and standard deviation of the costs of structures are compared, and the significant difference between them was proved. The results show that logistical structure with nine distribution centers leads to 14% reduction in total distribution network cost compared to current network. Moreover, it has fewer coefficient of variation than two others. In this paper, the coefficient of variation is mentioned as an index of risk, and with considering the risk of solutions, it can be concluded that this structure is more robust than other structures and in case of happening turbulence in customer demands such as epidemic diseases outbreak in some areas of the country, fewer costs will be imposed to this company distribution network.
References
Altiparmak F, Gen M, Lin L, Karaoglan I: A steady-state genetic algorithm for multi-product supply chain network design. Comput Ind Eng 2009, 56: 521–537. 10.1016/j.cie.2007.05.012
Amiri A: Designing a distribution network in a supply chain system: formulation and efficient solution procedure. Eur J Oper Res 2006, 171: 567–576. 10.1016/j.ejor.2004.09.018
Arostegui MA Jr, Kadipasaoglub SN, Khumawala BM: An empirical comparison of tabu search, simulated annealing, and genetic algorithms for facilities location problem. Int J Prod Econ 2006, 103: 742–754. 10.1016/j.ijpe.2005.08.010
Chopra S: Designing the distribution network in a supply chain. Transp Res E 2003, 39: 123–140. 10.1016/S1366-5545(02)00044-3
Daskin MS: Network and Discrete Location: Models, Algorithms, and Applications. New York: John Wiley & Sons; 1995.
Deleris LA, Erhun F: Risk management in supply networks using Monte-Carlo simulation. Simulation Conference, Proceedings of the Winter, Orlando, FL, 4–7 Dec. 2005 2005.
Drezner Z, Hamacher HW: Facility Location: Applications and Theory. New York: Springer; 2004.
Drezner Z, Wesolowsky GO: Network design: selection and design of links and facility location. Transp Res A 2003, 37: 241–256.
Flores C, Makiyama F, Nassar S, Freitas P, Jacinto C: Risk Analysis using Monte Carlo Simulation and Bayesian Networks. Simulation Conference, WSC 06. Proceedings of the Winter, Monterey, 3–6 Dec. 2006 2006.
Garey M, Johnson D: Computers and intractability: A guide to the theory of NP-completeness. San Francisco: W. H Freeman & Co; 1979.
Gebennini E, Gamberini R, Manzini R: An integrated production–distribution model for the dynamic location and allocation problem with safety stock optimization. Int J Prod Econ 2009, 122: 286–304. 10.1016/j.ijpe.2009.06.027
Gen M, Cheng R: Genetic algorithms and engineering optimization. New York: John Wiley & Sons; 2000.
Hakimi SL: Optimum distribution of switching centers in a communication network and some related graph theoretic problems. Oper Res 1965, 13: 462–475. 10.1287/opre.13.3.462
Jang YJ, Jang SY, Chang BM, Park J: A combined model of network design and production/distribution planning for a supply network. Comput Ind Eng 2002, 43: 263–281. 10.1016/S0360-8352(02)00074-8
Jaramillo JH, Bhadury J, Batta R: On the use of genetic algorithms to solve location problems. Comput Oper Res 2002, 29: 761–779. 10.1016/S0305-0548(01)00021-1
Jayaraman V, Pirkul H: Planning and coordination of production and distribution facilities for multiple commodities. Eur J Oper Res 2001, 133: 394–408. 10.1016/S0377-2217(00)00033-3
Jayaraman V, Ross A: An evaluation of new heuristics for the location of cross-docks distribution centers in supply chain network design. Comput Ind Eng 2008, 55: 64–79. 10.1016/j.cie.2007.12.001
Kalos MH, Whitlock PA: Monte Carlo methods. New York: John Wiley & Sons; 2008.
Klibi W, Martel A, Guitouni A: The design of robust value-creating supply chain networks: a critical review. Eur J Oper Res 2010,203(2):283–293. 10.1016/j.ejor.2009.06.011
Melo MT, Nickel S, Saldanha-Da-Gama F: Facility location and supply chain management - a review. Eur J Oper Res 2009, 196: 401–412. 10.1016/j.ejor.2008.05.007
Melo MT, Nickel S, Saldanha-da-Gama F: A Tabu search heuristic for redesigning a multi-echelon supply chain network over a planning horizon. Int J Prod Econ 2012, 136: 218–230. 10.1016/j.ijpe.2011.11.022
Michalewicz Z, Vignaux GA, Hobbs M: A non-standard genetic algorithm for the nonlinear transportation problem. ORSA J Comput 1991, 3: 307–316. 10.1287/ijoc.3.4.307
Mladenovic N, Brimberg J, Hansen P, Moreno-perez JA: The p-median problem: a survey of meta-heuristic approaches. Eur J Oper Res 2007,179(3):927–939. 10.1016/j.ejor.2005.05.034
ReVelle CS, Eiselt HA: Location analysis: a synthesis and survey. Eur J Oper Res 2005, 165: 1–19. 10.1016/j.ejor.2003.11.032
Sabri EH, Beamon BM: A multi-objective approach to simultaneous strategic and operational planning in supply chain. Omega 2000,28(5):581–598. 10.1016/S0305-0483(99)00080-8
Santosa T: A comprehensive model and efficient solution algorithm for the design of global supply chains under uncertainty. Dissertation, Georgia Institute of Technology; 2003:22–44.
Shu J, Ma Q, Li S: Integrated location and two-echelon inventory network design under uncertainty. Ann Oper Res 2010, 181: 233–247. 10.1007/s10479-010-0732-z
Simchi-Levi D, Kaminsky P: Managing the supply chain: The definitive guide for the business professional. Boston: Irwin McGraw-Hill; 2004.
Sousa RT, Liu S, Papageorgiou LG, Shaha N: Global supply chain planning for pharmaceuticals. Chem Eng Res Des 2011, 89: 2396–2409. 10.1016/j.cherd.2011.04.005
Syarif A, Yun YS, Gen M: Study on multi-stage logistic chain network: a spanning tree-based genetic algorithm approach. Comput Ind Eng 2002, 43: 299–314. 10.1016/S0360-8352(02)00076-1
Talbi EG: METAHEURISTICS, from design to Implementation. Hoboken, New Jersey: John Wiley & Sons; 2009:190–221.
Thomas DJ, Griffin PM: Coordinated supply chain management. Eur J Oper Res 1996, 94: 1–115. 10.1016/0377-2217(96)00098-7
Tragantalerngsak S, Holt J, Ronnqvist M: An exact method for the two-echelon, single-source, capacitated facility location problem. Eur J Oper Res 2000, 13: 473–489.
Acknowledgements
I would like to express my deep gratitude to Dr. Ali Mohammad Kimiagari, the research supervisor, for his patient guidance and enthusiastic encouragement of this research work. I would also like to extend my thanks to the technicians of the laboratory of the Industrial engineering department in Amirkabir university of technology for their help in offering me the resources in running the program. Finally, I wish to thank my parents for their support and encouragement throughout my study.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AI, AmK The main contribution of this paper is the simulation based optimization approach which is mentioned in solving the distribution network design problem. It is noticeable that the uncertainty in pharmaceutical product demands is high duo to available intense bullwhip effect in Iran. Thus, in this paper, customer demand uncertainty is considered through creating scenarios with Monte Carlo simulation method and Genetic algorithm is employed to find the optimal solution. In addition, the concept of robust optimization is regarded to obtain the most stable logistical structure for one of the greatest pharmaceutical distribution companies in Iran. It is remarkable that the related holding company (TPICO) has decided to implement this research in other Subordinate distribution companies. Both authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Izadi, A., Kimiagari, A.m. Distribution network design under demand uncertainty using genetic algorithm and Monte Carlo simulation approach: a case study in pharmaceutical industry. J Ind Eng Int 10, 1 (2014). https://doi.org/10.1186/2251-712X-10-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-10-1