Combination of nanophotocatalysis with electro-Fenton-like process in the removal of phenol from aqueous solution: GC analysis and response surface approach

Abstract

Background

This study focuses on the application of photoelectro-Fenton (PEF) with Mn²⁺ as catalyst combined with a photocatalytic process using supported TiO₂ nanoparticles for the removal of phenol from aqueous solutions. TiO₂ nanoparticles (Degussa P-25) immobilized on glass plates were used as photocatalyst, and carbon nanotube-polytetrafluoroethylene electrode was employed as cathode. Response surface methodology (RSM) was performed to evaluate the effects of the four key factors (initial amount of Mn²⁺, initial concentration of phenol, reaction time, and applied current) on the PEF/TiO₂ process.

Results

The application of RSM after analysis of variance showed a high coefficient of determination value (R² = 0.918) and thus indicated a high correlation between the observed and predicted values. The optimum operation conditions were located by graphical response surface and contour plots. The optimum initial amount of Mn²⁺, initial phenol concentration, applied current, and reaction time were found to be 0.3 mM, 15 mg/L, 300 mA, and 150 min, respectively. The observed experimental response for removal efficiency was 69.36 in optimum conditions of variables. The total organic carbon measurements showed 95% mineralization of 20 mg/L phenol at 15 h using the PEF/TiO₂ process. The degradation product evolution was verified by gas chromatography analysis.

Conclusions

An empirical relationship between the response and independent variables was attained and expressed by the second-order polynomial equation. Effect of experimental parameters on the removal efficiency of phenol was established by the response surface and contour plots of the model-predicted responses.

Background

Nowadays, one of the major problems facing industrialized nations is contamination of the environment by hazardous chemicals. Among the various wastes, phenol is a characteristic pollutant found in wastewaters and industrial effluents. This pollutant has been a typical molecule present in most aromatic products, highlighting its relevance. Phenol is lethal to most aquatic organisms exposed to concentrations of 10 to 100 ppm [1], being considered toxic to fish at a 1- to 2-ppm concentration level [2], and presents acute toxicity to man [3]. Due to its toxic properties, the efficient removal of this compound from wastewater is an environmental concern. In recent years, various technologies have been developed for environmental pollutant remediation [4–9]. The advanced oxidation processes (AOPs), which can produce oxidizing hydroxyl radicals (OH^·), have been proven to be an efficient method for the degradation of organic pollutants [8, 10, 11]. Among AOPs, Fenton-based processes (reaction (1)) have been encountering a notable development due to their favorable results in combination with easy handling [12]:

$$F{e^2}^{+}+H_2{O}_2+H^{+}\to F{e}^{3+}+O{H}^{·}+H_{2}O$$

(1)

Ferrous ions and hydrogen peroxide are simultaneously produced in an aqueous medium by ferric ions, initially introduced at a catalytic concentration, (reaction (2)) and a bi-electronic reduction of the dissolved molecular oxygen (reaction (3)) [13, 14]:

$$F{e}^{3+}+e^{-}\to F{e}^{2+}$$

(2)

$$O_2+2H^{+}+2e^{-}\to H_2{O}_2$$

(3)

A Pt or a boron-doped diamond anode in an undivided cell is utilized in the electro-Fenton (EF) technique, while Fe²⁺ or Fe³⁺ is added to the solution to permit the degradation of pollutants by OH^· generated from reaction (1) in the medium. In the photoelectro-Fenton (PEF) method, the solution is treated under EF conditions, and ultraviolet light is simultaneously irradiated to accelerate the mineralization rate of organics. Main effects of the photocatalytic action of this irradiation can be related to (a) the photolysis of Fe(OH)²⁺, which is the predominant Fe³⁺ species at pH 3.0, regenerating a greater amount of Fe²⁺ and producing more quantity of OH^· via reaction (4) [8, 15, 16]:

$${\left[Fe\left(OH\right)\right]}^{2+}+h\text{υ}\to F{e}^{2+}+O{H}^{·}$$

(4)

and (b) the photodecomposition of Fe³⁺ complexes with generated carboxylic acids, e.g., oxalic acid. Oxalic acids behave as photo-active complexes in the presence of ferric ions at acidic pH, which undergo photo-decarboxylation reaction (Equation 5) [17, 18]:

$$\text{Fe}\left(\text{III}\right){\left({\text{RCO}}_2\right)}^{2+}+\text{hυ}\to {\text{Fe}}^{2+}+{\text{CO}}_2+{\text{R}}^{·}$$

(5)

One of the forms of the Fe³⁺/Fe²⁺ redox couple (E₀ = 0.77 V/NHE) is utilized in the classical electro-Fenton process. Some homogeneous redox couple M(n+1)⁺/Mn⁺ can also undergo Fenton-type reaction and lead to the formation of hydroxyl radical according to reaction (6) [19].

$$M^{n+}+H_2{O}_2\to M^{\left(n+1\right)+}+O{H}^{-}+O{H}^{·}$$

(6)

This process can be called as ‘electro-Fenton-like’ process. Several metal cations such as Mn(II), Fe(III), Ag(I), Cu(II), or Co(II) have been tested in common Fenton or photo-Fenton reactions [19, 20]. The electro-Fenton-like process efficiency is affected by the standard potential of the M(n+1)⁺/Mn⁺ redox couple used and by the scavenging catalyst effect. Therefore, it is very important to gain insight in this electro-Fenton-like process activated by transition metals, which would certainly help widen the application of this promising technology for wastewater treatment.

On the other hand, heterogeneous photocatalysis through UV illumination on semiconductor surface is an attractive advanced oxidation process. TiO₂ is a wide bandgap semiconductor, and when it is illuminated with the light of λ < 390 nm, electrons are promoted from the valence band to the conduction band to give electron–hole pairs through reaction (7) [6, 21, 22]:

$$Ti{O}_2+h\text{υ}\left(\lambda <390nm\right)\to e^{-}+h^{+}$$

(7)

The valence band (h⁺) potential is positive enough to generate hydroxyl radicals at the surface of TiO₂, and the conduction band (e⁻) potential is negative enough to reduce molecular oxygen, as shown in Equations 8 to 12:

$${\text{e}}^{-}+{\text{O}}_{2\left(\text{ads}\right)}\to {\text{O}}^{·}{2\left(\text{ads}\right)}^{–}$$

(8)

$$e^{-}+{H_{\left(ads\right)}}^{+}\to {H^{·}}_{\left(ads\right)}$$

(9)

$${\text{O}}^{·}{2\left(\text{ads}\right)}^{–}+{\text{H}}^{+}\to {\text{HOO}}^{·}$$

(10)

$$2HO{O}^{·}\to H_2{O}_2+O_2$$

(11)

$${\text{H}}_2{\text{O}}_2+{\text{O}}^{·}{2\left(\text{ads}\right)}^{–}\to {\text{OH}}^{·}+{\text{OH}}^{–}+{\text{O}}_2$$

(12)

Moreover, the hydroxyl radicals formed are strong oxidants and attack organic pollutants present at or near the surface of TiO₂ (Equation 13). It causes photodegradation of organic matters (OM) [6, 23].

$$O{H^{·}}_{\left(ads\right)}+OM\to degradationoftheOM$$

(13)

A serious inconvenience appears when treating iron-chelating organic compounds because an iron catalyst needed to carry out Fenton's reaction (Equation 1) is no longer available, and the process becomes ineffective. Phenol is able to form stable complexes with ferric ions [24]. So, in this work, we have studied the removal of phenol as a model pollutant from aqueous solutions using the process of PEF/supported TiO₂ nanoparticles with carbon nanotube-polytetrafluoroethylene (CNT-PTFE) electrode as the cathode and Mn²⁺ as the catalyst. The reaction of Mn²⁺ with H₂O₂ and the regeneration of Mn²⁺ are shown in Equations 14 and 15, respectively [25]:

$$M{n}^{2+}+H_2{O}_2+H^{+}\to M{n}^{3+}+H_{2}O+O{H}^{·}$$

(14)

$$M{n}^{3+}+e^{-}\to M{n^2}^{+}$$

(15)

As it has been reported previously [4–9], the efficiency of phenol removal by PEF is dependent on various parameters such as the initial amount of catalyst, initial concentration of phenol, reaction time, and applied current. To determine the influence of these parameters, experiments were carried out, varying systematically one of the parameters and keeping constant the others in conventional methods. This should be repeated for all of the influencing parameters which results in an unreliable number of experiments. Central composite design (CCD) was employed to optimize the effective parameters with the minimum number of experiments. In this case, it would be possible to estimate linear interaction and quadratic effects of the factors and to provide a prediction model for the response. So in this work, we have used response surface methodology (RSM) to study the influence of experimental parameters on the phenol removal efficiency of the PEF/TiO₂ process. Phenol removal efficiency was selected as the response for optimization, and the functional relationship between the response and the most significant independent variables (factors) was established by means of an experimental design. All the parameters are simultaneously applied in order to calculate their relative effect [26, 27].

Methods

Chemicals

Phenol (λ_max = 270 nm, M_w = 94.11 g/mol) was purchased from Merck Co. (Dramstadt, Germany). Sulfuric acid, sodium sulfate, and manganese (II) sulfate were obtained from Merck Co. The other chemicals used in this study such as methanol, methyltrimethoxysilane, and HCl were obtained from Merck Co. and were used as received. Multi-walled carbon nanotubes were produced from Cheap Tubes Inc. (Brattleboro, VT, USA). Their specific surface area, inside diameters, and outer diameters were 233 m²/g, 3 to 5 nm, and 8 to 15 nm, respectively. TiO₂ nanoparticles (Degussa P-25, Düsseldorf, Germany) having 80% anatase and 20% rutile were immobilized on glass plates. Their specific surface area (BET) and mean crystalline size were 49.7 m²/g and 21 nm, respectively. The scanning electron microscopy image of used TiO₂ was reported previously [18].

Instruments

The solution pH was measured with a Metrohm 654 pH-meter (Herisau, Switzerland). The experiments were performed using a DC power supply (ADAK PS 808, Tehran, Iran). The removal of phenol from the aqueous solution was followed by using a UV-visible (UV–vis) spectrophotometer (Light wave S2000, Nottingham, England). Irradiation was carried out with a 6-W UV-C lamp (T5 fluorescent cool light, Guangdong, China), which was placed in a quartz tube inside a 2,000-mL batch cell. Total organic carbon (TOC) measurements were carried out using a Shimadzu TOC–VCSH (Columbia, MD, USA) TOC analyzer. Nitrogen sorption analyses were obtained with a Micromeritics Tristar sorptometer (Norcross, GA, USA) using standard continuous procedures at 77.15 K on calcined samples that had been degassed at 363 K for 1 h and then at 403 K under high vacuum for at least 10 h. The surface area was calculated according to the Brunauer-Emmett-Teller (BET) model [28] over a relative pressure range of 0.05 to 0.30. Pore diameter distribution was calculated according to the Barret-Joyne-Halenda method [28], modified by the Halsey thickness curve correction [29] on the desorption branch. The BET surface area, total pore volume, and pore size of TiO₂ nanoparticles were 49.7 m²/g, 0.26 cm³/g, and 24 nm, respectively. For gas chromatography (GC) analysis, a Shimadzu GC-2010 gas chromatograph (North America) with a 25-m to 0.22-mm CBP 1 capillary column was used.

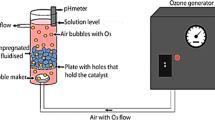
Combined photoelectro-Fenton and photocatalytic system

The treatment of phenol was performed at constant current and room temperature (25°C) in an undivided, cubic tank with a capacity of about 2,000 mL. The CNT-PTFE electrode was selected as the cathode, and Pt sheets of 11.5 cm² area were used as the anode. The distance between electrodes was about 1 cm. The fabrication and schematic diagram of the CNT-PTFE electrode was explained previously [30]. The cathode, anode, and UV lamp (placed in a quartz tube) were centered in the cell, surrounded by the TiO₂ nanoparticles immobilized on glass plates, which covered the four sides of the inner wall of the cell. The schematic diagram of the used electrolytic-photocatalytic system was reported previously [18]. In all experiments, the solutions were vigorously stirred with a magnetic bar to ensure suitable transport of reactants towards/from the electrodes. Pure O₂ gas at 140 mL/min was fed into the diffusion cathode for the production of H₂O₂ from reaction (3). Solutions of phenol (2,000 mL) containing 0.05M Na₂SO₄ as background electrolyte were degraded in all cases at pH 4.0. The removal efficiency (R (%)) was defined by the following expression:

$$\text{Removal efficiency}\left(R\left(\%\right)\right)=\left(1-\frac{A}{A_0}\right)\times 100$$

(16)

where A₀ and A are the phenol aqueous solution absorbance at time 0 and t at λ_max = 270 nm, respectively.

Results and discussion

Comparative removal and mineralization of phenol

Phenol degradation was carried out by using EF, PEF, UV/TiO₂, and PEF/TiO₂ processes. In order to compare the above processes, 20-mg/L phenol solutions at pH 4 have been used as the sample in all experiments. Figure 1 shows the removal efficiency for the 20-mg/L phenol solution under electrolysis at 300 mA and an initial Mn²⁺ concentration of 0.3 mM after 180 min at room temperature (25°C). It can be observed that the highest removal efficiency was obtained using the PEF/TiO₂ process. The results also showed that phenol removal after 180 min of reaction time follows a decreasing order: PEF/TiO₂ > PEF > EF > UV/TiO₂. Furthermore, the pollutant was destroyed during 180 min of PEF/TiO₂ process, yielding 78% of removal efficiency, whereas at the same reaction time, PEF, EF, and UV/TiO₂ processes led to 28%, 23%, and 13% removal efficiency, respectively. These results indicate that combining the PEF method with the photocatalytic process can effectively accelerate the removal efficiency. Figure 2 shows representative UV–vis spectral changes of the phenol solution as a function of reaction time through the PEF/TiO₂ process. The absorption peak at λ = 270 nm diminished and finally disappeared under 180 min of PEF/TiO₂ process. The efficiency of the PEF/TiO₂ process to mineralize the phenol solution was evaluated by TOC decay. This study was carried out with a solution of pH 4.0 containing 20 mg/L of phenol by applying 300-mA current for 15 h. A TOC abatement was observed attaining 95% of mineralization after 15 h of PEF/TiO₂ process. TOC decay shows that the PEF/TiO₂ process can effectively degrade the pollutant solution containing phenol.

Figure 1

Removal efficiency ( R (%)) for a 20-mg/L phenol solution at room temperature. I = 300 mA, pH = 4.0, [Na₂SO₄] = 0.05M, [Mn²⁺]_o = 0.3 mM, reaction time = 180 min.

Figure 2

UV–vis spectral changes with electrolysis time for 20 mg/L phenol solution by PEF/TiO ₂ process. pH = 4.0, I = 300 mA, [Na₂SO₄] = 0.05 M.

Central composite design model

The four-factor CCD matrix and experimental results obtained in the PEF/TiO₂ process are presented in Table 1. The second-order polynomial response equation (Equation 17) was employed to attain the interaction between the dependent and independent variables.

$$Y=b_0+{\displaystyle \sum }{b}_{\text{i}}{x}_{\text{i}}+{\displaystyle \sum }{b}_{\text{ii}}{x}_{\text{i}}^2+{\displaystyle \sum }{b}_{\text{ik}}{x}_{\text{i}}{x}_{\text{k}}$$

(17)

where Y is a response variable of removal efficiency. The b_i is the regression coefficients for linear effects; b_ii is the regression coefficients for squared effects; b_ik is the regression coefficients for interaction effects, and x_i is the coded experimental levels of the variables.

Table 1 The four-factor central composite design matrix and the value of response function ( R (%))

Based on these results, an empirical relationship between the response Y and the four significant independent variables (x₁, x₂, x₃, and x₄) was attained as shown below:

$$\begin{array}{l}Y=25.0000-9.{8964\text{x}}_1-6.{8971\text{x}}_2-0.00{11\text{x}}_3+8.{8131\text{x}}_4+1.0{521\text{x}}_1{\text{x}}_2+3.{6771\text{x}}_1{\text{x}}_3+1.{9271\text{x}}_2{\text{x}}_3+\\ 1.0{625\text{x}}_2{\text{x}}_4-0.000{2\text{x}}_3{\text{x}}_4-4.5625x_1^2-0.0004x_2^2-1.0625x_3^2+0.0002x_4^2\end{array}$$

(18)

From Equation 18, it can be seen that the initial Mn²⁺ concentration, initial phenol concentration, and applied current have negative effect on the response compared to the reaction time, which has a positive effect on the removal of phenol. The phenol removal efficiencies (R (%)) have been predicted by Equation 18 and presented in Table 1. These results indicated good agreements between the experimental and predicted values of removal efficiency. The square of determination coefficient (R²) quantitatively evaluates the correlation between the experimental data and the predicted responses. The experimental results and the predicted values obtained from the model (Equation 18) were compared. It was found that the predicted values matched the experimental values reasonably well with R² = 0.918. This implies that 91.8% of the variations for percent removal is explained by the independent variables, and this also means that the model does not explain only about 8.2% of variation.

Adjusted R² (Adj-R²) is also a measure of the goodness of a fit, but it is a useful tool for comparing the explanatory power of models with different numbers of independent variables. The adjusted R² will increase only if the new term improves the model more than would be expected by chance, and it will decrease when a predictor improves the model less than expected by chance. It corrects the R² value for the sample size and the number of terms in the model by using degrees of freedom in its computations. If there are many terms in a model and the sample size is not very large, Adj-R² may be visibly smaller than R²[31]. Here, the Adj-R² value (0.847) was very close to the corresponding R² value (see Table 2).

Table 2 Analysis of variance for the fit of removal efficiency from the central composite design

Table 2 summarizes the results of the quadratic response surface model fitting in the form of analysis of variance (ANOVA). ANOVA confirms the adequacy of the quadratic model [30, 32]. ANOVA divides the sum of squares of each of the two sources of variation, the model and the experimental error, showing whether the variation from the model is significant or not when compared with the ones associated with residual error [30, 31, 33]. This comparison is performed by degrees of freedom (F value). If the model predicts the experimental results well, the F value should be greater than the tabulated value of F distribution for a certain number of degrees of freedom in the model at a level of significance α. The F value obtained, 12.82, is clearly greater than the tabulated F (2.352 at 95% significance), confirming the adequacy of the model fits.

Table 3 gives the Student's t distribution and the corresponding values, together with the parameter estimate. The P values show the significance of each of the coefficients. The larger the magnitude of the Student's t test and the smaller the P value, the more significant is the corresponding coefficient [30, 32].

Table 3 Estimated regression coefficients and corresponding t and P values from the data of central composite design experiments

The Pareto analysis calculates the percentage effect of each factor on the response and gives more significant information to interpret the results. The following relation was used to perform this analysis [26, 34]:

$$P_{\text{i}}=\left(\frac{b_{\text{i}}^2}{{\displaystyle \sum }{b}_{\text{i}}^2}\right)\times 100\left(i\ne 0\right)$$

(19)

Figure 3 shows the Pareto graphic analysis. As can be seen in this figure, among the variables, the initial Mn²⁺ concentration (b₁, 37.01%), reaction time (b₄, 29.35%), and initial phenol concentration (b₂, 17.98%) produce the main effect on the removal efficiency.

Figure 3

Pareto graphic analysis.

Effect of variables as response surface and contour plots

The response surface and contour plots of the model-predicted responses were obtained by the Minitab software while two variables were kept constant and the others were varied within the experimental ranges. These plots were utilized to assess the interactive relationships between the process variables and treatment outputs for the removal of phenol.

In Figure 4, the response surface and contour plots were developed as a function of the initial Mn²⁺ concentration and applied current while the initial phenol concentration and reaction time were kept constant at 15 mg/L and 90 min, respectively, being the central levels. As can be seen in Figure 4, phenol removal efficiency decreased with increasing initial Mn²⁺ concentration. The catalyst concentration (e.g., Fe²⁺, Fe³⁺, Mn²⁺, …) is a key factor in EF processes and is a function of the cathode employed. For example, concentrations of 0.5 to 1.0 mM Fe²⁺ are optimum for carbon-PTFE GDE cathodes because of their lower ability for Fe²⁺ regeneration [8, 35]. At high Mn²⁺ concentrations, the phenol removal rate decreased, which can be explained by metal deposition that leads to decreasing hydroxyl radical production according to reaction (21). Anodic deposition observed during the experiments has been reported by several studies [19, 36, 37] on acidic solutions according to reaction (20):

$$M{n}^{2+}+2H_{2}O\to Mn{O}_{2\left(S\right)}+4H^{+}+2e^{-}$$

(20)

Figure 4

Removal efficiency as a function of initial Mn²⁺concentration and applied current. The response surface plot and contour plot of the removal efficiency (R (%)) as a function of initial Mn²⁺ concentration (mM) and applied current (mA).

On the other hand, the phenol removal efficiency increased with increasing applied current values from 100 to 500 mA. The enhancement in phenol removal efficiency with the applied current can be related to a high production of H₂O₂ through reaction (3).

The response surface and contour plots of the removal efficiency as a function of initial phenol concentration and applied current have been shown in Figure 5. As can be seen, an increase in initial phenol concentration from 5 to 25 mg/L decreases removal efficiency. This behavior is one of the properties of AOPs. In the constant conditions of the system (e.g., constant current, pH, etc.), a certain amount of hydroxyl radicals is produced while the phenol concentration is increased. Therefore, the amount of hydroxyl radicals is not enough to remove the high concentrations of the pollutant; removal efficiency then decreases [38].

Figure 5

Removal efficiency as a function of initial phenol concentration and applied current. The response surface plot and contour plot of the removal efficiency (R (%)) as a function of initial phenol concentration (mg/L) and applied current (mA).

Figure 6 displays the 2D and 3D plots of phenol removal efficiency as a function of applied current and reaction time at fixed initial Mn²⁺ and phenol concentrations of 0.5 mM and 15 mg/L, respectively. As can be seen, increasing reaction time increased the phenol removal efficiency at all applied currents.

Figure 6

Removal efficiency ( R (%)) as a function of applied current and reaction time. The response surface plot and contour plot of the removal efficiency (R (%)) as a function of applied current (mA) and reaction time (min).

Determination of optimal conditions and evolution of degradation

The model obtained using experimental data was used to verify the optimum values of PEF/TiO₂ process variables. The optimum values of the PEF/TiO₂ process variables to reach the maximum removal efficiency are shown in Table 4. The predicted values were verified by further experimental test, and the result indicated that the maximal removal efficiency was obtained when the values of each operational parameter were justified at the optimum values. It implies that the strategy to optimize the removal conditions and to obtain the maximal removal efficiency by CCD for phenol removal by electrochemical and photocatalytic processes is successful. The theoretical response proposed by Minitab software for the removal of phenol was 70.35%. To confirm the used model adequacy and the validity of the resulted optimization conditions, additional experiment was performed under optimal operating conditions. The value of the experimental response was 69.36% and was found to be very close to the value proposed by the model (70.35%).

Table 4 Optimum operating conditions of the process variables

GC was used to follow the time evolution of stable aromatic intermediates generated during phenol mineralization. The samples were analyzed by GC with the following temperature program: 70°C for 3 min, 10°C/min up to 90°C and hold time 2 min, 10°C/min up to 200°C and hold time 5 min. The temperatures of the inlet and detector were 200 and 250°C, respectively. The GC chromatographs (Figure 7) of the samples collected at various time points throughout the PEF/TiO₂ process of a 20-mg/L phenol solution at pH 4, electrolyzed at 300 mA showed the disappearance of phenol peak and the formation of a new peak which elutes after the parent compound. This observed new peak disappeared after approximately 3 h. This behavior is consistent with the fast destruction of phenol and proves that the generated oxidation products can further react with OH^· to form various breakdown products and eventually mineralize.

Figure 7

Gas chromatography analysis. Evolution of GC chromatographs during the PEF/TiO₂ process treatment of a 20-mg/L phenol aqueous solution at pH 4.0, I = 300 mA, [Na₂SO₄] = 0.05M. (a) Reaction time = 0 h; (b) reaction time = 6 h; (c) reaction time = 9 h.

Electrical energy consumption during the PEF/TiO₂ process

The removal of aqueous organic pollutants by photoelectrolytic processes is an electric energy-intensive process. So, the electric energy can represent a major fraction of the operating costs, and simple figures of merit based on electric energy consumption can be very useful and informative. In the case of low concentrations of a pollutant, which applies here, the appropriate figure of merit is the electrical energy per order (E_EO). E_EO is defined as the number of kilowatt hour of electrical energy required to reduce the concentration of a pollutant by one order of magnitude (90%) in 1 m³ of contaminated water. The E_EO can be calculated according to the proposal of the Photochemistry Commission of the International Union of Pure and Applied Chemistry (see Equation 21) [18].

$$E_{\mathit{EO}}=\frac{P\times t\times 1,000}{V_{\text{s}}\times 60\times \text{log}\left(C_{\text{i}}/C_{\text{f}}\right)}$$

(21)

where P is the lamp power (kW) of the photochemical system, V_s is the solution volume (L), C_i and C_f are the initial and final pollutant concentrations, and t is the reaction time (min). So, the electrical energy (kWh/m³) required to photochemically remove 20 mg/L of phenol from 2,000 mL of phenol solution in the optimized conditions (I = 0.3 A, pH = 4, [Mn²⁺₀ = 0.3 mM) is 15 kWh/m³. The electrical energy consumption in the electrochemical process was calculated using the commonly used Equation 22 [18]:

$$E=\frac{U\times {\rm I}\times t}{V_{\text{s}}\times 3.6\times {10}^3}$$

(22)

where E is the electrical energy (kWh/m³), U is the cell voltage in volt (V), I is the current in ampere (A), t is the time of process per second, and V_s is the solution volume (L). Using Equation 22, the electrical energy (kWh/m³) required to electrochemically remove 20 mg/L of phenol from 2,000 mL of its solution in the optimized conditions is 9 kWh/m³. In this preliminary economic study, energy costs in the electrochemical and photochemical processes are taken into account as major cost items in the calculation of the operating cost as kilowatt hour per volume (m³) of the water in the reactor (Equation 23).

$$\text{Operating cost}=a\left(E_{\text{Photochemical process}}+E_{\text{Electrochemical process}}\right)$$

(23)

where E_{Photochemical process} (E_EO) and E_{Electrochemical process} (E) are 15 and 9 kWh/m³, respectively. ‘a’ is the electrical energy price in Iranian market in September 2012, which is equal US$ 0.036/kWh. So, the operating cost is equal to US$ 0.8640/m³, which is very low in comparison with different AOP processes in different papers [39–41]. As an example, Brillas et al. [42] reported the results obtained from the different treatments of a 1,000-mg/L aniline solution at selected electrolysis times where most TOC removal was achieved. It was reported that anodic oxidation in the presence of electro-generated H₂O₂ at 20 A has very low oxidizing power and very high energy cost (18% and 502 kWh/m³ at 6 h, respectively) that it is not useful in practice. According to their reports, the EF process presented much more degradation ability with moderate consumption, lower than 45 kWh/m³. For both processes, the increase in current leads to higher energy cost. On the other hand, higher degradations and energy costs were always obtained when the solution volume was reduced from 30 to 10 L.

Hanafi et al. [43] reported the treatment of olive mill wastewater containing polyphenols, considering modifying chemical oxygen demand (COD), dark color removal, and pH. Through an optimum time of 15 min, 2 mg/L of Cl₂ concentration, pH of 4.2, and density of 250 A/m², polyphenols were reduced by 70%, and energy consumption was 2.63 kWh/kg COD removed. Agladze et al. [39] reported that 87% to 90% of the initial COD of solution containing phenol was removed in 1 h with a 5-A current in the membrane cell and 40 kWh/m³ of energy consumption, whereas the same process took 30 min of electro-Fenton treatment in an undivided cell with 22 kWh/m³ of energy consumption. On the other hand, only 10 min of electrolysis with a 5-kWh/m³ power cost was needed when the electrolyzed solution was treated with Fe(II)/H₂O₂ in a 1:1 molar ratio addition outside. They reported that the significant economy of specific energy consumption (29.4 kWh/m³ for 92.6% COD removal against 39 kWh/m³ for 91% TOC removed) was achieved in the present study for the ex-cell treatment.

Experimental

In this study, to find the optimum conditions for phenol degradation by photoelectro-Fenton combined with photocatalytic process, CCD was employed. CCD is a widely used form of RSM. A five-level CCD consisting of 31 experiments was employed in this work, including 16 cube points, seven replications at the center point, and eight axial points. Initial Mn²⁺ concentration (X₁), initial phenol concentration (X₂), applied current (X₃), and reaction time (X₄) were chosen as the main factors in order to evaluate the influence of operating parameters on phenol removal efficiency. Experimental data were analyzed using the Minitab 15 software (State College, PA, USA). For statistical calculations, the variables X_i were coded as x_i according to the following relationship:

$$x_{\text{i}}=\frac{X_{\text{i}}-X_{\text{o}}}{\delta X}$$

(24)

where X_o is the value of X_i at the center point and δX presents the step change [30, 44, 45]. The experimental ranges and the levels of the independent variables for phenol removal are given in Table 5.

Table 5 Experimental ranges and levels of the independent test variables

Conclusions

The removal of phenol from aqueous solutions by a photocatalytic process using immobilized TiO₂ nanoparticles combined with photoelectro-Fenton process with CNT-PTFE electrode as cathode and Mn²⁺ ions as catalyst has been studied. A comparison of EF, PEF, UV/TiO₂, and PEF/TiO₂ processes for the removal of phenol solution was performed. The pollutant was destroyed during 180 min of the PEF/TiO₂ process, yielding 78% of removal efficiency, whereas at the same time, the PEF, EF, and UV/TiO₂ processes led to 28%, 23%, and 13% removal efficiency, respectively. Based on experimental results, an empirical relationship between the response and independent variables was attained and expressed by the second-order polynomial equation. Effect of experimental parameters on the removal efficiency of phenol was established by the response surface and contour plots of the model-predicted responses. Analysis of variance showed a high coefficient of determination value (R² = 0.918), thus ensuring a satisfactory adjustment of the second-order regression model with the experimental data. To follow the time evolution of stable aromatic intermediates generated during phenol mineralization, samples were analyzed by means of GC.