Structural phase transformation and hysteresis behavior of Cu-Zn ferrites

Abstract

A series of Cu_1-xZn _x Fe₂O₄ ferrite (with x = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6) compositions were synthesized using the standard solid-state reaction technique. X-ray diffraction was used to study the structure of the above investigated samples. The theoretical and experimental lattice parameters (a_th and a_exp) were calculated for each composition. A significant decrease in density and subsequent increase in porosity were observed with increasing Zn content. Curie temperature, T_C, has been determined from the temperature dependence of permeability and found to decrease with increasing Zn content. The anomaly observed in the temperature dependence of permeability was attributed to the existence of two structural phases: cubic phase and tetragonal phase. Low-field hysteresis measurements have been performed using a B-H loop trace from which hysteresis parameters have been determined. Coercivity and hysteresis loss were estimated with different Zn contents.

Background

Soft ferrites are the most widely used magnetic materials for low-cost, high-performance, and high-frequency applications. Ferrites are stable and easily manufactured and possess environmental stability. The usefulness of ferrite is influenced by the physical and chemical properties of the materials and depends on many factors including the preparation conditions, such as sintering temperature, sintering time, rates of heating and cooling, and grinding time [1–3]. The magnetic and electric properties of ferrite materials strongly depend on their chemical compositions and additives/substitutions. A small amount of foreign ions in the ferrite can dramatically change the properties of ferrites. The magnetic properties of Zn-substituted ferrites have attracted considerable attention because of the importance of these materials for high-frequency applications. Zinc ferrite (ZnFe₂O₄) possesses a normal spinel structure, i.e., ${\left({\mathrm{Zn}}^{2+}\right)}_{\mathrm{A}}\left[{\mathrm{Fe}}^{3+}2\right]{}_{\mathrm{B}}{\mathrm{O}}^{2-}4$, where all Zn²⁺ ions reside on A sites and Fe³⁺ ions on B sites. Therefore, substitution of Cu by Zn in Cu_1-xZn _x Fe₂O₄ is expected to modify the magnetic properties. The magnetization behavior and magnetic ordering of Zn-substituted Co-Zn [4], Cu-Zn [5], Ni-Zn [6], and Mg-Zn [7] ferrites have been studied by many authors. However, no detail works have been found in the literature regarding structural and hysteresis behavior of mixed Cu-Zn ferrite. In this paper, we study the structural and hysteresis parameters of Cu-Zn ferrites.

Methods

The ferrite system Cu_1-xZn _x Fe₂O₄ (x = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6) has been prepared by the standard double sintering technique using high-purity oxides of CuO, ZnO, and Fe₂O₃.

The reagent powders were weighed precisely according to their molecular weight. Intimate mixing of the materials was carried out using agate mortar for 4 h, and then, the materials were ball-milled in a planetary ball mill in ethyl alcohol media for 4 h with stainless steel balls of different diameters. The samples were dried, and the dried powder was pressed into a disk shape. The disk-shaped samples were pre-sintered at 800°C for 3 h in air to form ferrite through solid-state reaction. The pre-sintered material was again crushed and wet-milled for another 4 h in distilled water to reduce it to small crystallites of uniform size. The mixture was dried, and a small amount of saturated solution of polyvinyl alcohol was added as a binder. Then, the resulting powders were pressed into the desired shape using metal dies. The pressed products were finally sintered at 1,000°C in air for 6 h and at 1,050°C, 1,100°C, 1,150°C, and 1,200°C for 3 h. The surfaces of all the samples were polished in order to remove any oxide layer which formed during the process of sintering. Formation of ferrite was confirmed by a Philips Analytical X-ray diffractometer using CuKα radiation (PANalytical B.V., Almelo, The Netherlands). Crystal structure was determined from X-ray diffraction (XRD) data. Curie temperature measurements were performed by using an impedance analyzer with a laboratory-built oven and a thermocouple-based thermometer. Frequency dependence of complex initial permeability of the toroid-shaped samples was measured with the impedance analyzer. B-H loops were measured by using a B-H loop tracer.

Results and discussions

XRD analysis

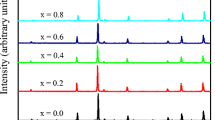
Figure 1 shows the XRD pattern indicating (hkl) values of each peak of all the samples of Cu_1-xZn _x Fe₂O₄. The XRD pattern of the sample, showing well-defined reflections without any ambiguity, exhibits the formation of a single-phase cubic spinel structure except pure CuFe₂O₄ (x = 0.0). Optimum magnetic and transport properties of the ferrites necessitate having a single-phase cubic structure. The peaks (220), (311), (222), (400), (422), (511), and (440) are either odd or even, indicating the spinel phase. Pure CuFe₂O₄ showed an ideal tetragonal structure which has been manifested by twin peaks in the XRD pattern. CuFe₂O₄ is distorted inverse spinel, and its tetragonal distortion has been explained by the Jahn-Teller effect [8]. The authors have demonstrated that tetragonal deformation has been found with the higher concentration of Cu (x = 0.0 to 0.3). However, in our case, tetragonality occurs only for pure copper ferrite possibly due to the insignificant amount of tetragonal phase with higher Cu content concomitant with the study of Manjura et al. [9]. It is noteworthy that the existence of tetragonal deformation has been found from temperature dependence of initial permeability for x = 0.1 to 0.3 possibly due to high sensitivity of initial permeability measurement technique.

Figure 1

XRD patterns of Cu _{1- x} Zn _x Fe ₂ O ₄ ferrites.

Cation distribution and theoretical lattice parameter

Using standard XRD data, the lattice constant and hence X-ray density were determined. The lattice parameter was determined by the Nelson-Riley extrapolation method. The values of the experimental lattice parameter obtained from each reflected plane were plotted against the Nelson-Riley function [10]:

$$F\left(\theta \right)=\frac{1}{2}\left[\frac{{cos}^2\theta }{sin\theta }+\frac{{cos}^2\theta }{\theta }\right],$$

(1)

where θ is the Bragg angle. The accurate values of the experimental lattice parameter were estimated from the extrapolation of these straight lines to F(θ) = 0 or θ = 90. It shows that the lattice parameter increases with increasing Zn content. To obtain more information about this behavior, the theoretical values of the lattice parameter were calculated.

It is known that there is a correlation between the ionic radii of both A and B sublattices and the lattice parameter. Then, the lattice parameter can be calculated theoretically using the following equation [11]:

$$a_{\mathrm{th}}=\frac{8}{3\sqrt{3}}\left[\left(r_{\mathrm{A}}+R_O\right)+\sqrt{3}\left(r_{\mathrm{B}}+R_O\right)\right],$$

(2)

where R_o is the radius of the oxygen ion (1.32 Å) [12], and r_A and r_B are the ionic radii of the tetrahedral (A site) and octahedral (B site) sites, respectively. The values of r_A and r_B will depend critically on the cation distribution of the system. The knowledge of cation distribution and spin alignment is essential to understand the magnetic properties of spinel ferrite. The investigation of cation distribution helps to develop materials with desired properties which are useful for many devices [13]. In order to calculate r_A and r_B, the following cation distribution is proposed:

$${\left({\mathrm{Zn}}_x^{2+}{\mathrm{Fe}}_{1-x}^{3+}\right)}_{\mathrm{A}}{\left[{\mathrm{Cu}}_{1-x}^{2+}{\mathrm{Fe}}_{1+x}^{3+}\right]}_{\mathrm{B}}{\mathrm{O}}_4^{2-},$$

(3)

where the brackets () and [ ] indicate the A site and B site, respectively. The cation distribution is based on the following:

• 1. CuFe₂O₄ [5] is an inverse spinel structure in which half of the ferric ions preferentially occupy the tetrahedral site (A sites) and the other half occupy the octahedral sites (B sites).

• 2. On the other hand, non-magnetic Zn ions prefer to occupy the tetrahedral sites [14, 15].

According to the cation distribution of Cu-Zn ferrites, the ionic radius of the A site (r_A) and B site (r_B) can be theoretically calculated using the following relations [16, 17]:

$$r_{\mathrm{A}}=C_{\mathrm{AZn}}r\left({\mathrm{Zn}}^{2+}\right)+C_{\mathrm{AFe}\text{'}}r\left({\mathrm{Fe}}^{3+}\right)$$

(4)

$$r_{\mathrm{B}}=\frac{1}{2}\left[C_{\mathrm{BCu}}r\left({\mathrm{Cu}}^{2+}\right)+C_{\mathrm{BFe}}r\left({\mathrm{Fe}}^{3+}\right)\right],$$

(5)

where r(Zn²⁺), r(Cu²⁺), and r(Fe³⁺) are ionic radii of Zn²⁺ (0.83) [12], Cu²⁺ (0.76) [12], and Fe³⁺ (0.67) [12], respectively, while C_AZn and C_AFe’ are the concentrations of Zn²⁺ and Fe³⁺ ions on A sites and C_BCu and C_BFe are the concentrations of Cu²⁺ and Fe³⁺ ions on B sites. Using these formulae, the ionic radius of the A site (r_A) and B site (r_B) were calculated and given in Table 1. The theoretical and experimental values of the lattice parameters (a_th and a_exp) are plotted against Zn concentration in Figure 2. It is noted that a_th and a_exp increase with increasing Zn²⁺ ion content, indicating that the present system obeys Vegard’s law [18]. This increase in the lattice parameter can be attributed to the ionic size differences since the unit cell has to expand when substituted by ions of large ionic radius [19]. Since the ionic radius of Zn²⁺ ions (0.83 Å) is larger than that of Cu²⁺ ions (0.76 Å), the substitution is expected to increase the lattice parameter with the increasing concentration of Zn. This behavior appeared clearly in the physical properties such as density, porosity, and magnetic properties. A similar linear variation has also been observed in Zn-Mg [20, 21], Li-Mg [22], Zn-Mg-Cu [23], and Li-Cd [24] ferrites. The experimentally determined lattice parameter value in the present study for the sample x = 0 is 8.385 Å has a good coincidence with that of the literature value 8.37 Å [12]. The difference between a_th and a_exp as shown in Figure 2 can be attributed to the deviation from the formula of cation distribution (3), and this deviation is related to the presence of divalent iron ions Fe²⁺[25] and other crystal imperfections.

Figure 2

Variation of theoretical parameter ( a _th ) and experimental lattice parameter ( a _exp ) with Zn content.

Table 1 Cation distribution, ionic radii, lattice parameters, X-ray density, bulk density, and porosity of Cu-Zn ferrite samples

Densification

Density plays a vital role in controlling the properties of polycrystalline ferrites. The effect of Zn substitution on the X-ray density, bulk density, and porosity is shown in Table 1. X-ray density (ρ_x) depends upon the lattice parameter. As the lattice parameter increases linearly with the increase of Zn concentration, a corresponding decrease of the X-ray density is expected. A similar result has been observed by Pandit et al. in Mg-Zn ferrite [26]. It is also observed that X-ray densities are higher in magnitude than the corresponding bulk densities. This may be due to the existence of pores which were formed and developed during the sample preparation or the sintering process [27]. This increase in X-ray density is also due to the difference in ionic radii between Cu and Zn [28].

Figure 3 shows the effect of Zn on the bulk density (ρ_B) and porosity (P) of the samples. It is observed that bulk density decreases with the increase in Zn content. The decrease in densities can be ascribed to the density of Zn²⁺ (7.14 gm/cm³), which are lower than those of Cu²⁺ (8.96 gm/cm³) and Fe³⁺ (7.86 gm/cm³) [12]. Other than the difference in specific density of the constituent ions, the bulk densities are also governed by the porosities of the sintered sample. The porosity values are found to increase significantly with increasing Zn content. The composition x = 0.0 has the highest density of 5.14 gm/cm³ and lowest porosity. During the sintering process, the discontinuous grain growth takes place. The intra-granular porosity is increased due to discontinuous grain growth. When the grain growth rate is very high, pores may be left behind by rapidly moving grain boundaries, resulting in pores that are trapped inside the grains. This contributes toward the reduction of bulk density which in turn increases the porosity. Moreover, this increase in porosity and decrease in bulk density are due to the increase in grain size because the grains may be of irregular shape and as the sintering proceeds, the grain growth takes place [27]. The inter-granular pores must also be capable of moving with the grain boundaries as the growth occurs. It requires that the pores move together and coalesce, where a different transport mechanism takes place. This consists of the transport of gaseous oxygen across the pores and the diffusion of cations around the pores; it is facilitated by high concentration of cation vacancies. Hence, it is concluded that porosity increases with the addition of Zn content due to the creation of more cation vacancies with the reduction of oxygen vacancies [29]. These results agree with earlier reported results in Mg-Cu-Zn ferrite by Qi et al. [30].

Figure 3

Variation of bulk density and porosity with Zn content in Cu _{1- x} Zn _x Fe ₂ O ₄ .

Temperature dependence of initial permeability

The magnitude of the initial permeability μ’ of a magnetic material is proportional to the square of the saturation magnetization and inversely proportional to the magnetic magnetocrystalline anisotropy constant. Both quantities vary with temperature, so μ’ is a complicated function of temperature [12]. The variation of μ’ with temperature can be expressed as follows: the anisotropy constant (κ₁) and saturation magnetization (M_s) usually decrease with increase in temperature. However, the decrease in κ₁ with temperature is faster than the decrease in M_s. When the anisotropy constant reaches zero, μ’ attains its maximum value and then drops off to the maximum value near the Curie point. The thermal variation of the initial permeability μ’ was recorded to determine Curie temperature, T_C, for the above investigated compositions of Cu-Zn ferrite in the shape of toroid samples which is shown in Figure 4. The Curie temperature mainly depends upon the strength of the A-B exchange interaction. According to Neel’s [31] sublattice field model, the A-B exchange interaction is stronger than the A-A or B-B interaction. As the concentration of Zn ions increases, the amount of Fe³⁺ increases in the B sites. This reduces the A-B interactions. From Figure 4, it can be seen that μ’ increases with increasing temperature, attaining a maximum value just below T_C. The maximum value of μ’ just below T_C is a manifestation of the Hopkinson peak attributed to the minimization of magnetocrystalline anisotropy energy with temperature. Beyond this peak, permeability sharply falls to a very low value indicating T_C. The sharp fall of the permeability at the Curie point indicates the degree of homogeneity in the sample composition [32]. From the curves of the initial permeability versus temperature, it can be seen that for samples up to x = 0.3, a second broadening peak (hump shape) other than the Hopkinson peak is found which may be attributed to structural transformation from tetragonal to cubic in these samples [33, 34]. From XRD analysis it has been shown that the samples with x = 0.1 to 0.6 are of cubic structure, while that with x = 0.0 is of tetragonal structure. Indeed, the samples with x = 0.0 to 0.3 have a mixed structure, between cubic and tetragonal, that could not be identified by XRD. However, by using a more sensitive measurement technique such as temperature dependence of initial permeability, tetragonal-cubic transformations have been fairly demonstrated with the appearance of a hump in the μ’-T curve [35]. This kind of phase transformation from a tetragonal to a cubic structure was previously observed by many researchers for different ferrite systems [36]. It has been mentioned earlier that though tetragonal deformation is not perceptible from X-ray diffraction patterns, it exists due to the Jahn-Teller deformation of Cu²⁺ ions, which has been identified from temperature dependence of initial permeability curves by Mazen et al. [37, 38]. The samples with x = 0.4 to 0.6 have a pure cubic structure, and the curves of μ’ do not show any phase transformation; so, μ’ increases continuously up to T_C.

Figure 4

Permeability vs. temperature for different compositions of Cu _{1- x} Zn _x Fe ₂ O ₄ .

Figure 5 shows the concentration dependence of T_C of the Cu_1-xZn _x Fe₂O₄ system. The linear decrease of T_C with Zn content is attributed to the progressive weakening of J_AB exchange interactions resulting from substitution of non-magnetic Zn in the tetrahedral (A site) occupancy [39, 40]. A similar trend in the variation of T_C has been observed by some workers in Mg-Zn [18], Li-Zn [41], Ni-Cd [42], Co-Cd [43], and Li-Cd [44] ferrites. A linear least square fitting of the Curie temperature with x gives an empirical relation for the whole Cu_1-xZn _x Fe₂O₄ system as follows:

$$T_{\mathrm{C}}\left(x\right)=T_{\mathrm{C}0}-638.57x,$$

(6)

where T_C0 is the Curie temperature of the pure Cu ferrite and T_C(x) corresponds to the Curie temperature of any composition having Zn concentration, x. From this empirical relation, the Curie temperature of CuFe₂O₄ is found to be 471°C. Our experimental result is 460°C which is very close to literature value of 455°C [12].

Figure 5

Variation of Curie temperature ( T _C ) with Zn content.

Figure 6 shows that T_C decreases with increasing sintering temperature (T_S) for the pure CuFe₂O₄ samples. This may be explained as due to the volatile nature of CuO at 1,026°C [45], which may have some effect on the compositional gradients of the ferrite samples, and these compositional gradients may have influence on the reduction of T_C. Another factor which affects the T_C is the existence of the Cu¹⁺ ions in the samples [46], i.e., Cu¹⁺ ions are non-magnetic due to completely filled 3d shells which might be migrated to the tetrahedral (A) site, reducing the strength of the A-B exchange interaction and accounting for the lowering of T_C.

Figure 6

Variation of Curie temperature ( T _C ) with sintering temperature of CuFe ₂ O ₄ .

B-H loop measurement

Measurement of a hysteresis loop is a very simple and fast method to characterize ferromagnetic materials. The hysteresis curves and their properties such as the retentivity (B_r), coercivity (H_c), and hysteresis loss are very useful information from the application point of view. The B-H loops at room temperature of the investigated compositions Cu_1-xZn _x Fe₂O₄ were measured at a constant frequency (f = 1 kHz), and the results are presented in Figure 7. From these loops, B_r, M_s, and H_c were determined. The area within the hysteresis loop is directly related to the hysteresis loss. In Figure 7, it can be observed that the retentivity as well as hysteresis loop area increases at first and then decreases significantly. For the composition up to x = 0.4, the retentivity, hysteresis loss, and saturation magnetization are found to increase and then drop to a lower value for higher Zn concentration [47]. The increase in magnetization with Zn content up to x = 0.4 is due to the dilution of magnetization of the A sublattice by non-magnetic Zn²⁺ ions, which can be explained on the basis of Neel’s sublattice model [31]. The reason for the decrease of magnetization beyond this limit is that the magnetization of the A sublattice is so dilute that the A-B lattice interaction is no longer stronger and thereby the B-B sublattice interaction becomes strong, which in turn disturbs the parallel arrangement of spin magnetic moments on the B site, and hence, canting of spin occurs. Almost all Zn²⁺- and Cd²⁺-substituted ferrites have shown a similar type of canting behavior above a certain limit of contents [24]. It is also known that all these properties are extrinsic and depend on the microstructure. Addition of Zn²⁺ ions reduces the density and increases the porosity which is deleterious for magnetic properties. Coercivity is found to decrease with Zn content. Saturation magnetization, M_s, may play a direct role in decreasing coercivity through Brown’s relation [48] which is given by

$${\mathrm{H}}_c\ge \frac{2{\kappa }_1}{\mu \text{'}{M}_{\mathrm{s}}}$$

(7)

Figure 7

B - H loops for Cu-Zn ferrites.

According to this relation, H_c is inversely proportional to M_s which we have found experimentally as shown in Table 2. Reduction of H_c is also connected to the reduction of anisotropy energy, κ₁. It is known that substitution of Zn in spinel ferrite reduces the anisotropy energy and magnetostriction constant [1]. The lower value of saturation magnetization, retentivity, and coercivity for higher Zn content reduces the area within the loop. This leads to the lower value of hysteresis loss with the increase in Zn content as shown in Figure 8.

Figure 8

Variation in hysteresis loss with Zn content.

Table 2 Saturation magnetization, coercivity, retentivity, initial permeability, and hysteresis loss of Cu-Zn ferrite samples

The hysteresis behavior and frequency-dependent initial permeability μ’ reveal the softer ferromagnetic nature of the studied materials with the increase of Zn content. The compositional variation of initial permeability and coercivity of the present samples is shown in Figure 9. It is observed that initial permeability increases as Zn content increases up to x = 0.4 and decreases with further increase of Zn. However, the variation of initial permeability with Zn content was not consistent with the variation of the bulk density and the porosity. From XRD analysis, we could see that porosity increases with Zn content which led to an increase of initial permeability. The dramatic change of permeability can be explained by the equation [49]

$$\mu \text{'}\propto \frac{M_{\mathrm{s}}^2}{\left(a{\kappa }_1+\mathit{b\lambda \sigma }\right)},$$

(8)

where M_s is the saturation magnetization, κ₁ is the magnetocrystalline anisotropy constant, λ is the magnetostriction constant, and σ is the inner stress. Therefore, with the increase of Zn content, the increase of permeability of Cu-Zn ferrites was attributed to the decrease of the magnetostriction constant. Nam et al. [50] studied that Zn substitution within a small range in composition plays a crucial role in properties of NiCuZn ferrites by reducing the magnetostriction effects. The dependence of H_c and initial permeability μ’ is inversely proportional as found in Figure 9 which is concomitant with the theoretical prediction, since H_c is the indicator of magnetic hardness, while μ’ is the indicator of magnetic softness.

Figure 9

Variation of initial permeability ( μ ’) and coercivity ( H _c ) with Zn content.

Conclusions

The presence of Zn ions causes appreciable changes in the structure and magnetic properties of the Zn-substituted Cu ferrite. Pure CuFe₂O₄ showed tetragonality, while the samples with x = 0.1 to 0.6 have a cubic structure. The lattice parameter is found to increase linearly with increasing Zn content. Curie temperature decreases with the increase of Zn content. Sintering temperature has great influence on the Curie temperature. The retentivity, hysteresis loss, and saturation magnetization are found to increases then drop to a lower value for higher Zn concentration. Coercivity decreases with the increase of Zn content.