Nanoparticle analysis for blood flow of Prandtl fluid model with stenosis

Abstract

In this article, we have discussed blood flow in the nano-Prandtl fluid flow analysis in tapered stenosed arteries. The occurrence of nanoparticle fraction and heat transfer was found. Gravitational effects were also considered because the tube was taken vertically upward. Homotopy perturbation method was used to find the analytical solution of coupled nonlinear differential equations. Physical features have been discussed through graphs of concentration profile σ, velocity profile w, resistance impedance λ, temperature profile θ, wall shear stress S _{r z} , wall shear stress at the stenosis throat τ _s , and the stream lines.

Background

Blood flow in the artery has some important aspects due to engineering as well as medical application points of view. The hemodynamic behavior of the blood flow is influenced by the presence of arterial stenosis. If stenosis is present in the artery, normal blood flow is disturbed. Thurston and Chien et al. [1, 2] present the viscoelastic properties of the blood. According to them, the arterial configuration is closely connected to blood flow. Arteries which are basically considered as living tissues need a supply of metabolites including oxygen and removal of waste products. Aroesty and Gross [3] have discussed the pulsatile flow of blood in the small blood vessels. Chaturani and Ponnalagar Samy [4] reported the theory of Aroesty and Gross [3] and studied the pulsatile flow of blood in stenosed arteries modeling blood as Casson fluid. Scott Blair and Spanner [5] discussed that blood as Casson fluid is valid for moderate shear rate, and the validity of Casson and Herschel-Bulkley theory for blood flow is the same. In another article, Siddiqui et al. [6] discussed Casson fluid in arterial stenosis. Pulsatile flow of blood for a modified second-grade fluid model is presented by Massoudi and Phuoc [7].

Mekheimer and El Kot [8] examined the micropolar fluid model for axisymmetric blood flow through an axially nonsymmetric but radially symmetric mild stenosis tapered artery. Mandal [9] presented unsteady flow analysis for blood by treating blood as a non-Newtonian fluid through tapered arteries with stenosis. He discussed the numerical solution for the flow equations. Varshney et al. [10] considered the generalized power law fluid model for blood flow in the artery considering multiple stenosis. They present a numerical study under the action of a transverse magnetic field. A power law fluid model for blood flow through a tapered artery with stenosis is recently developed by Nadeem et al. [11]. In another article, Nadeem and Akbar [12] revisited the flow analysis of Nadeem et al. [11] for Jeffrey fluid. Mustafa et al. [13] make the analysis of blood flow for the generalized Newtonian fluid through a couple of irregular arterial stenosis. Blood flow with an irregular stenosis in the presence of magnetic field has been touched by Abdullah et al. [14].

Nanofluids are the fluids of nanometer-sized particles of metals, oxides, carbides, nitrides, or nanotubes. Nowadays, nanofluids, among researchers, are considered an active area of research. In fact, nanofluids are a suspension of nanosized solid particles in a base fluid. The nanofluids have high thermal conductivity as compared to the base fluid. Nanofluids basically increase heat transfer rate. Recent articles on nanofluids have been cited [15–20].

The main theme of the present article is to discuss the nanofluid analysis for steady blood flow of the Prandtl model with stenosis. To the best of the authors’ knowledge, blood flow analysis for nanofluids has not been investigated so far. We arranged this article in the following manner. The ‘Methods’ section consists of mathematical formulation and the solution expressions for velocity, temperature, nanoparticle, resistance impedance, wall shear stress, and shearing stress at the stenosis throat. The ‘Results and discussion’ section analyzes the salient features of the problem by graphical illustration.

Methods

Formulation of the problem

Consider the flow of incompressible Prandtl fluid lying in a tube having the length L. We are considering the cylindrical coordinate system in such a way that $ũ$, $\tilde{v}$, and $\tilde{w}$ are the velocity components in $\bar{r}$, $\bar{\theta }$, and $\bar{z}$ directions. The governing equations of the steady incompressible Prandtl fluid are as follows [11]:

$$\begin{array}{ll}\frac{\mathrm{\partial ũ}}{\partial \bar{r}}+\frac{ũ}{\bar{r}}+\frac{\partial \tilde{w}}{\partial \bar{z}}& =0,\end{array}$$

(1)

$$\begin{array}{ll}\rho \left(ũ\frac{\mathrm{\partial ũ}}{\partial \bar{r}}+\tilde{w}\frac{\mathrm{\partial ũ}}{\partial \bar{z}}\right)& =-\frac{\partial \bar{p}}{\partial \bar{r}}+\frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}\left(\bar{r}{S}_{\bar{r}\bar{r}}\right)+\frac{\partial }{\partial \bar{z}}\left(\bar{r}{S}_{\bar{r}\bar{z}}\right)-\frac{S_{\bar{\theta }\bar{\theta }}}{\bar{r}},\end{array}$$

(2)

$$\begin{array}{ll}\rho \left(ũ\frac{\partial \tilde{w}}{\partial \bar{r}}+\tilde{w}\frac{\partial \tilde{w}}{\partial \bar{z}}\right)& =-\frac{\partial \bar{p}}{\partial \bar{z}}+\frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}\left(\bar{r}{S}_{\bar{r}\bar{z}}\right)+\frac{\partial }{\partial \bar{z}}\left(\bar{r}{S}_{\bar{z}\bar{z}}\right)\\ +\mathrm{\rho g}{\hat{\alpha }}_t(\tilde{T}-{\tilde{T}}_0)+\mathrm{\rho g}{\hat{\alpha }}_c(\tilde{C}-{\tilde{C}}_0),\end{array}$$

(3)

$$\begin{array}{ll}\left(ũ\frac{\partial \tilde{T}}{\partial \bar{r}}+\tilde{w}\frac{\partial \tilde{T}}{\partial \bar{z}}\right)& =\alpha \left(\frac{{\partial }^2\tilde{T}}{\partial {\bar{r}}^2}+\frac{1}{\bar{r}}\frac{\partial \tilde{T}}{\partial \bar{r}}+\frac{{\partial }^2\tilde{T}}{\partial {\bar{z}}^2}\right)\\ +\tau \left[D_B\left(\frac{\partial \tilde{C}}{\partial \bar{r}}\frac{\partial \tilde{T}}{\partial \bar{r}}+\frac{\partial \tilde{C}}{\partial \bar{z}}\frac{\partial \tilde{T}}{\partial \bar{z}}\right)\right.\\ \left.+\frac{D_{\tilde{T}}}{{\tilde{T}}_0}\left\{{\left(\frac{\partial \tilde{T}}{\partial \bar{r}}\right)}^2+{\left(\frac{\partial \tilde{T}}{\partial \bar{z}}\right)}^2\right\}\right],\end{array}$$

(4)

$$\begin{array}{ll}\left(ũ\frac{\partial \tilde{C}}{\partial \bar{r}}+\tilde{w}\frac{\partial \tilde{C}}{\partial \bar{z}}\right)& =D_B\left(\frac{{\partial }^2\tilde{C}}{\partial {\bar{r}}^2}+\frac{1}{\bar{r}}\frac{\partial \tilde{C}}{\partial \bar{r}}+\frac{{\partial }^2\tilde{C}}{\partial {\bar{z}}^2}\right)\\ +\frac{D_{\tilde{T}}}{{\tilde{T}}_0}\left(\frac{{\partial }^2\tilde{T}}{\partial {\bar{r}}^2}+\frac{1}{\bar{r}}\frac{\partial \tilde{T}}{\partial \bar{r}}+\frac{{\partial }^2\tilde{T}}{\partial {\bar{z}}^2}\right).\end{array}$$

(5)

In the presented equations, $\tau =\frac{{\left(\mathrm{\rho c}\right)}_p}{{\left(\mathrm{\rho c}\right)}_f}$ describes the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid, $D_{\hat{B}}$ as the Brownian diffusion coefficient, $D_{\hat{T}}$ as the thermophoretic diffusion coefficient, ${\hat{\alpha }}_t$ as the coefficient of thermal expansion, and ${\hat{\alpha }}_c$ as the coefficient of thermal expansion with nanoconcentration.

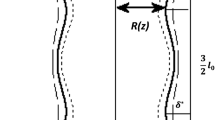
The geometry of stenosis is defined as follows [8]:

$$\begin{array}{ll}\overline{ĥ}\left(z\right)& =Q\left(z\right)[1-\eta (J_1^{n-1}(\bar{z}-J_0)-{(\bar{z}-J_0)}^n\left)\right],\\ J_0& \le \bar{z}\le J_0+J_1,\\ =Q\left(z\right),\text{otherwise}\end{array}$$

(6)

with

$$Q\left(z\right)=Q_0+\acute{\zeta }\bar{z},$$

(7)

where Q(z) be the radius of the tapered arterial section, Q₀ be the radius of the non-tapered arterial section, ζ be the tapering parameter, J₁ be the stenosis length, and J₀ indicates its place. The parameter η is defined as follows:

$$\eta =\frac{{\delta }^{\ast }{n}^{n-1}}{Q_0{J}_1^n(n-1)},$$

(8)

where δ denotes the maximum height of the stenosis located as follows:

$$\bar{z}=J_0+\frac{J_1}{n^{\frac{1}{n-1}}},$$

(9)

Non-dimensional variables are as follows:

$$\begin{array}{ll}r& =\frac{\bar{r}}{Q_o},z=\frac{\bar{z}}{J_1},w=\frac{\tilde{w}}{u_0},u=\frac{J_1ũ}{u_0\delta },p=\frac{Q_0\bar{p}}{u_0{J}_1\mu },ĥ=\frac{ĥ}{Q_0},\\ R_e& =\frac{J_1{u}_0\rho }{\mu },S_{\mathit{\text{rr}}}=\frac{J_1{\bar{S}}_{\mathit{\text{rr}}}}{u_0\mu },S_{\mathit{\text{rz}}}=\frac{Q_0{\bar{S}}_{\mathit{\text{rz}}}}{u_0\mu },S_{\mathit{\text{zz}}}=\frac{J_1{\bar{S}}_{\mathit{\text{zz}}}}{u_0\mu },\\ S_{\mathrm{\theta \theta }}& =\frac{J_1{\bar{S}}_{\mathrm{\theta \theta }}}{u_0\mu },\\ {\lambda }_2& =\frac{{\lambda }_2^{\star }{u}_0}{J_1},\theta =\frac{\tilde{T}-{\tilde{T}}_0}{{\tilde{T}}_0},\sigma =\frac{\tilde{C}-{\tilde{C}}_0}{{\tilde{C}}_0},N_t=\frac{{\left(\mathrm{\rho c}\right)}_p{D}_{\tilde{T}}}{{\left(\mathrm{\rho c}\right)}_f\alpha },\end{array}$$

$$\begin{array}{ll}\alpha & =\frac{k}{{\left(\mathrm{\rho c}\right)}_f},N_b=\frac{{\left(\mathrm{\rho c}\right)}_p{D}_B{\tilde{C}}_0}{{\left(\mathrm{\rho c}\right)}_f\alpha },{\alpha }_c=\frac{\mathrm{\rho g\alpha }{Q}_0{\tilde{C}}_0}{\mu u_0},\\ {\alpha }_t& =\frac{\mathrm{\rho g\alpha }{Q}_0{\tilde{T}}_0}{\mu u_0}.\end{array}$$

(10)

Making use of Equation 10 and after taking the condition, we get the following equation:

$$\frac{\text{Re}{\delta }^{\ast }{n}^{\left(\frac{1}{n-1}\right)}}{J_1}\ll 1,$$

(11a)

$$\frac{Q_0{n}^{(\frac{1}{n-1}})}{J_1}\backsim O\left(1\right).$$

(11b)

Equations 1 to 4, for the case of mild stenosis $(\frac{{\delta }^{\ast }}{Q_o}\ll 1)$, take the the following form:

$$\begin{array}{ll}\frac{\mathrm{\partial p}}{\mathrm{\partial r}}& =0,\end{array}$$

(12)

$$\begin{array}{ll}\frac{\mathrm{\partial p}}{\mathrm{\partial z}}& =\frac{1}{r}\frac{\partial }{\mathrm{\partial r}}\left[r\left(\alpha \left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)+\beta {\left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)}^3\right)\right]+G_r\theta +B_r\sigma ,\end{array}$$

(13)

$$\begin{array}{ll}0& =\frac{1}{r}\frac{\partial }{\mathrm{\partial r}}\left(r\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}\right)+N_b\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}\frac{\mathrm{\partial \sigma }}{\mathrm{\partial r}}+N_t{\left(\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}\right)}^2,\end{array}$$

(14)

$$\begin{array}{ll}0& =\frac{1}{r}\frac{\partial }{\mathrm{\partial r}}\left(\left(r\frac{\mathrm{\partial \sigma }}{\mathrm{\partial r}}\right)\right)+\frac{N_t}{N_b}\left(\frac{1}{r}\frac{\partial }{\mathrm{\partial r}}\left(r\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}\right)\right).\end{array}$$

(15)

In the above equations, N _t ,N _b ,B _r , and G _r are the defined thermophoresis parameter as Brownian motion parameter, as local nanoparticle Grashof number, and as local temperature Grashof number, respectively. The boundary conditions are as follows:

$$\begin{array}{ll}\frac{\mathrm{\partial w}}{\mathrm{\partial r}}& =0,\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}=0,\frac{\mathrm{\partial \sigma }}{\mathrm{\partial r}}=0\text{at}r=0,\end{array}$$

(16a)

$$\begin{array}{ll}w& =0,\theta =0,\sigma =0\text{at}r=ĥ,\end{array}$$

(16b)

where

$$\begin{array}{ll}ĥ\left(z\right)& =(1+\mathrm{\zeta z})[1-{\eta }_1(J_1^{n-1}(z-J_0)-{(z-J_0)}^n]\\ J_3& \le z\le J_3+1,\end{array}$$

(17)

and

$${\eta }_1=\frac{\delta n^{n-1}}{(n-1)},\delta =\frac{{\delta }^{\ast }}{Q_o},J_3=\frac{J_0}{J_1},\zeta =\frac{\acute{\zeta }{J}_1}{Q_o},\zeta =tan\varphi ,$$

(18)

where ϕ is the tapered angle and defined for the non-tapered artery (ϕ=0), for converging tapering (ϕ<0), and for diverging tapering (ϕ>0), as described in Figure 1.

Figure 1

Geometry of a nonsymmetric stenosis in the artery.

Solution of the problem

Homotopy perturbation solution

The homotopy perturbation method suggests that we may write Equations 13, 14, and 15 as follows [21, 22]:

$$\begin{array}{ll}ĥ(\text{Ķ},\theta )=& (1-\text{Ķ})\left[\text{Ł}\right(\theta )-\text{Ł}({\theta }_{10}\left)\right]\\ +\text{Ķ}\left[\text{Ł}\left(\theta \right)+N_b\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}\frac{\mathrm{\partial \sigma }}{\mathrm{\partial r}}+N_t{\left(\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}}\right)}^2\right],\end{array}$$

(19)

$$\begin{array}{ll}H(\text{Ķ},\sigma )=& (1-\text{Ķ})\left[\text{Ł}\left(\sigma \right)-\text{Ł}\left({\sigma }_{10}\right)\right]\\ +\text{Ķ}\left[\text{Ł}\left(\sigma \right)+\frac{N_t}{N_b}\left(\frac{1}{r}\frac{\partial }{\mathrm{\partial r}}\left(r\frac{\mathrm{\partial \theta }}{\mathrm{\partial r}})\right)\right)\right],\end{array}$$

(20)

$$\begin{array}{ll}H(\text{Ķ},w)=& (1-\text{Ķ})\left[\text{Ł}\right(w)-\text{Ł}(w_{10}\left)\right]\\ +\text{Ķ}\left[\text{Ł}\left(w\right)+\frac{1}{r}\frac{\partial }{\mathrm{\partial r}}\left(r\left(\beta {\left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)}^3\right)\right)\right.\\ \left.+G_r\theta +B_r\sigma -\frac{\mathrm{\partial p}}{\mathrm{\partial z}}\right],\end{array}$$

(21)

taking the following initial guesses:

$$\begin{array}{ll}{\theta }_{10}(r,z)& =-\left(\frac{r^2-{ĥ}^2}{4}\right),{\sigma }_{10}(r,z)=-\left(\frac{r^2-{ĥ}^2}{4}\right),\\ w_{10}(r,z)& =\frac{1}{\alpha }\left(\frac{r^2-{ĥ}^2}{4}\right)\frac{d{p}_0}{\mathit{\text{dz}}}.\end{array}$$

(22)

We define

$$\begin{array}{ll}w& =w_0+\text{Ķ}{w}_1+{\text{Ķ}}^2{w}_2+O{\left(\text{Ķ}\right)}^3,\end{array}$$

(23)

$$\begin{array}{ll}F& =F_0+\text{Ķ}{F}_1+{\text{Ķ}}^2{F}_2+O{\left(\text{Ķ}\right)}^3,\end{array}$$

(24)

$$\begin{array}{ll}\theta & ={\theta }_0+\text{Ķ}{\theta }_1+{\text{Ķ}}^2{\theta }_2+O{\left(\text{Ķ}\right)}^3,\end{array}$$

(25)

$$\begin{array}{ll}\sigma & ={\sigma }_0+\text{Ķ}{\sigma }_1+{\text{Ķ}}^2{\sigma }_2+O{\left(\text{Ķ}\right)}^3.\end{array}$$

(26)

Putting Equations 23 to 26 into Equations 19 to 21 and taking Ķ →1, the following form for temperature profile, concentration profile, velocity profile, and pressure gradient are written as follows:

$$\begin{array}{ll}w(r,z)=& \frac{1}{\alpha }\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\left(\frac{r^2-{ĥ}^2}{4}\right)+(\frac{{ê}_{20}}{\alpha }+{ê}_{10})(r^2-{ĥ}^2)\\ +(\frac{\beta {ê}_{17}+{ê}_{19}}{\alpha }+{ê}_{11})(r^4-{ĥ}^4)\\ +\frac{(\beta {ê}_{16}+{ê}_{18})}{\alpha }(r^6-{ĥ}^6),\end{array}$$

(27)

$$\begin{array}{ll}\theta (r,z)=& -\left(\frac{r^2-{ĥ}^2}{4}\right)+(2N_t+N_b)\left(\frac{r^4-{ĥ}^4}{64}\right)\\ +\left(\frac{r^2-{ĥ}^2}{4}\right)-\left(\frac{r^6-{ĥ}^6}{1152}\right)\\ (N_t+N_b)(2N_t+N_b),\end{array}$$

(28)

$$\begin{array}{ll}\sigma (r,z)=& -\left(\frac{r^2-{ĥ}^2}{4}\right)+\left(1+\frac{N_t}{N_b}\right)\left(\frac{r^2-{ĥ}^2}{4}\right)\\ -\frac{N_t}{N_b}\left\{\left(\frac{r^2-{ĥ}^2}{4}\right)-(N_t+N_b)\left(\frac{r^4-{ĥ}^4}{64}\right)\right\},\end{array}$$

(29)

$$\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}=-\frac{16\mathrm{F\alpha }}{{ĥ}^4}-\frac{16(\alpha {ê}_{21}+\beta {ê}_{22}+{ê}_{23})}{{ĥ}^4}.$$

(30)

Pressure drop (Δ p=p at z=0 and Δ p=−p and z=L) through the stenosis between the regions z=0 and z=L computed from Equation 30 can be written as follows:

$$\mathrm{\Delta p}=\underset{0}{\overset{L}{\int }}\left(-\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\right)\mathit{\text{dz}},$$

(31)

Resistance impedance

Using Equation 31, the expression for resistance impedance is given as follows:

$$\begin{array}{ll}\bar{\lambda }=\frac{\mathrm{\Delta p}}{F}=& \left\{\underset{0}{\overset{J_0}{\int }}E\left(z\right){\mid }_{ĥ=1}\mathit{\text{dz}}+\underset{J_0}{\overset{J_0+J_1}{\int }}E\left(z\right)\mathit{\text{dz}}\right.\\ \left.+\underset{J_0+J_1}{\overset{L}{\int }}E\left(z\right){\mid }_{ĥ=1}\mathit{\text{dz}}\right\},\end{array}$$

(32)

where

$$E\left(z\right)=\frac{16\alpha }{{ĥ}^4}+\frac{16(\alpha {ê}_{21}+\beta {ê}_{22}+{ê}_{23})}{{ĥ}^{4}F},$$

(33)

$$\begin{array}{ll}\bar{\lambda }=& \left\{(L-J_1)\left(16\alpha +\frac{16(\alpha {ê}_{21}+\beta {ê}_{22}+{ê}_{23}){|}_{ĥ=1}}{F}\right)\right.\\ \left.+\underset{J_0}{\overset{J_0+J_1}{\int }}E\left(z\right)\mathit{\text{dz}}\right\},\end{array}$$

(34)

Expression for the wall shear stress

Dimensionless shear stress is defined as follows:

$${\tilde{S}}_{\mathit{\text{rz}}}=\left(\alpha \left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)+\beta {\left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)}^3\right).$$

(35)

or

$${\tilde{S}}_{\mathit{\text{rz}}}={\left.\left[\left(\alpha \left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)+\beta {\left(\frac{\mathrm{\partial w}}{\mathrm{\partial r}}\right)}^3\right)\right]\right|}_{r=ĥ},$$

(36)

Using Equation 27, we obtain the following:

$${\tilde{S}}_{\mathit{\text{rz}}}=\frac{ĥ}{2}\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\left(1+\frac{\beta {ĥ}^2}{4{\alpha }^3}{\left(\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\right)}^2\right)+{ê}_{24}.$$

(37)

The shearing stress at the stenosis throat located at $z=\frac{J_0}{J_1}+\frac{1}{n^{\frac{1}{n-1}}}$ is defined as follows:

$${\tilde{\tau }}_s={\tilde{S}}_{\mathit{\text{rz}}}{\mid }_{ĥ=1-\delta },$$

(38)

or

$${\tilde{\tau }}_s={\left.\frac{ĥ}{2}\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\left(1+\frac{\beta {ĥ}^2}{4{\alpha }^3}{\left(\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\right)}^2\right)+{ê}_{24}\right|}_{ĥ=1-\delta }.$$

(39)

The final expression for λ, S _{r z} , and τ _s can be defined as follows:

$$S_{\mathit{\text{rz}}}=\frac{ĥ}{8F}\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\left(1+\frac{\beta {ĥ}^2}{4{\alpha }^3}{\left(\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\right)}^2\right)+\frac{{ê}_{24}}{4F},$$

(40)

$$\begin{array}{ll}\lambda =& \frac{1}{3}\left\{\left(1-\frac{J_1}{L}\right)\left(16\alpha +\frac{16(\alpha {ê}_{21}+\beta {ê}_{22}+{ê}_{23}){|}_{ĥ=1}}{F}\right)\right.\\ \left.+\frac{1}{L}\underset{J_0+J_1}{\overset{L}{\int }}R\left(z\right)\mathit{\text{dz}}\right\},\end{array}$$

(41)

$${\tau }_s={\left.\left\{\frac{ĥ}{8F}\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\left(1+\frac{\beta {ĥ}^2}{4{\alpha }^3}{\left(\frac{\mathit{\text{dp}}}{\mathit{\text{dz}}}\right)}^2\right)+\frac{{ê}_{24}}{4F}\right\}\right|}_{ĥ=(1-\delta )},$$

(42)

in which

$$\lambda =\frac{\bar{\lambda }}{{\lambda }_0},S_{\mathit{\text{rz}}}=\frac{{\tilde{S}}_{\mathit{\text{rz}}}}{{\tau }_0},{\tau }_s=\frac{{\tilde{\tau }}_s}{{\tau }_0},{\lambda }_0=3L,{\tau }_0=4\mathrm{F.}$$

(43)

Results and discussion

The quantitative results of the α, β, n, δ, N _t ,a n d N _b for diverging tapering, converging tapering, and non-tapered arteries are observed physically in Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, and 24. Variations of velocity profile for α, β, n, δ, N _t , and N _b for the cases of converging tapering, diverging tapering, and non-tapered arteries are displayed in Figures 2, 3, 4, 5, 6, and 7. In Figures 2, 3, 4, 5, 6, and 7, it is analyzed that with an increase in the thermophoresis parameter N _t and stenosis shape n, the velocity profile decreases, while velocity profile increases with an increase in the maximum height of the stenosis δ, Brownian motion parameter N _b , and Prandtl parameters α and β. It is also seen that for the case of converging tapering, it has a larger value as compared with the case of diverging tapering and non-tapered arteries. Figures 8, 9, 10, 11, 12, and 13 depict how the converging tapering, diverging tapering, and non-tapered arteries influence the wall shear stress S _{r z} . It is observed that with an increase in stenosis shape n, thermophoresis parameter N _t , stenosis height δ, and Prandtl parameter β, the shear stress decreases, while it increases with an increase in Prandtl parameter α and Brownian motion parameter N _b . Figures 14 and 15 depict variations of the shearing stress at the stenosis throat τ _s with δ. In these figures, it is analyzed that the shearing stress at the stenosis throat decreases with an increase in β and increases with an increase in α. Figures 16 and 17 show variations of concentration profile for the Brownian motion parameter N _b and thermophoresis parameter N _t . It is observed that with an increase in the Brownian motion parameter N _b , the concentration profile increases, while it decreases with an increase in the thermophoresis parameter N _t and the concentration profile gives a larger value for the converging tapering artery. Figures 18 and 19 depict variations of the temperature profile for the Brownian motion parameter N _b and thermophoresis parameter N _t . It is observed that with an increase in the Brownian motion parameter N _b and the thermophoresis parameter N _t , the temperature profile decreases. Figures 20, 21, 22, 23, and 24 describe the impedance resistance increases for non-tapered, diverging tapering, and converging tapering arteries when we increase the Prandtl parameters, α, and β, and Brownian motion parameter N _b , while it decreases with an increase in thermophoresis parameters, N _t and n.

Figure 2

Variation of velocity profile for F = 0.06, J ₃  = 0.03, n = 2, α = 0.6, β = 0.4 , N _t  = 0.9, N _b  = 0.9, B _r  = 2, z = 0.07, G _r  = 2 .

Figure 3

Variation of velocity profile for F = 0.06, J ₃  = 0.03, δ = 0.09, α = 0.6, β = 0.4 , N _t  = 0.9, N _b  = 0.9, B _r  = 2, z = 0.07, G _r  = 2 .

Figure 4

Variation of velocity profile for F = 0.07, J ₃  = 0.03, n = 2, δ = 0.01, β = 0.4 , N _t  = 0.9, N _b  = 0.9,B _r  = 2, z = 0.07, G _r  = 2 .

Figure 5

Variation of velocity profile for F = 0.07, J ₃  = 0.03, n = 2, α = 0.9, δ = 0.01 , N _t  = 0.9, N _b  = 0.9, B _r  = 2, z = 0.07, G _r  = 2 .

Figure 6

Variation of velocity profile for F = 0.07, J ₃  = 0.03, n = 2, α = 0.9, β = 0.4 , δ = 0.01, N _b  = 0.8, B _r  = 1, z = 0.07, G _r  = 1 .

Figure 7

Variation of velocity profile for F = 0.07, J ₃  = 0.03, n = 2, α = 0.9, β = 0.4 , N _t  = 0.9, δ = 0.09, B _r  = 1, z = 0.07, G _r  = 1 .

Figure 8

Variation of wall shear stress for F = 0.06, J ₃  = 0.01, n = 2, α = 0.9, β = 0.9 , N _t  = 0.9, N _b  = 0.9, B _r  = 1.0, G _r  = 1.0 .

Figure 9

Variation of wall shear stress for F = 0.06, J ₃  = 0.01, α=0.9, β=0.9, B _r  = 1.0 , G _r  = 1.0, δ = 0.01, N _t  = 0.9, N _b  = 0.9 .

Figure 10

Variation of wall shear stress for F = 0.06, δ = 0.01, N _t  = 0.9, B _r  = 1.0, G _r  = 1.0 , N _b  = 0.9, J ₃  = 0.01, β = 0.9 .

Figure 11

Variation of wall shear stress for F = 0.06, J ₃  = 0.01, n = 2, α = 0.9, G _r  = 1.0 , N _t  = 0.9, B _r  = 0.9, N _b  = 0.9 .

Figure 12

Variation of wall shear stress for F=0.06, J ₃  = 0.01, n = 2, α = 0.9, β = 0.9 , N _t  = 0.9, B _r  = 1.0, G _r  = 1.0, δ = 0.01 .

Figure 13

Variation of wall shear stress for F = 0.06, J ₃  = 0.01, N _t  = 0.9, β = 0.9, α = 0.9 , N _b  = 0.9, B _r  = 1.0, G _r  = 1.0, δ = 0.01 .

Figure 14

Variation of shear stress at the stenosis throat for F = 0.01, N _t  = 0.09, N _b  = 0.1 , B _r  = 0.03, G _r  = 0.05, α = 0.054 .

Figure 15

Variation of shear stress at the stenosis throat for F = 0.01, β = 0.01, N _t  = 0.09 , N _b  = 0.1, B _r  = 0.03, G _r  = 0.05 .

Figure 16

Variation of concentration profile for δ=0.01, J ₃  = 0.0, n = 2, z = 0.5, N _b  = 0.9 .

Figure 17

Variation of concentration profile for δ = 0.5, J ₃  = 0.0, n = 2, z = 0.5, N _t  = 0.5 .

Figure 18

Variation of temperature profile for δ = 0.5, J ₃  = 0.0, n = 2, z = 0.5, N _b  = 0.9 .

Figure 19

Variation of temperature profile for δ=0.5, J ₃ =0.0, n=2, z=0.5, N _t =0.5 .

Figure 20

Variation of resistance for F = 0.01, J ₃  = 0.09, B _r  = 0.3, G _r  = 0.1, L = 2 , N _t  = 0.01, N _b  = 0.1, α = 0.1, β = 0.03 .

Figure 21

Variation of resistance for F = 0.01, J ₃  = 0.09, B _r  = 0.3, G _r  = 0.1, n = 2 , L = 2, N _t  = 0.01, N _b  = 0.1, β = 0.01 .

Figure 22

Variation of resistance for F = 0.01, J ₃  = 0.09, B _r  = 0.3, G _r  = 0.1, n = 2 , L = 2, N _b  = 0.1, α = 0.1, N _t  = 0.01 .

Figure 23

Variation of resistance for F = 0.01, J ₃  = 0.09, B _r  = 0.3, G _r  = 0.1, n = 2 , L = 2, N _t  = 0.01, α = 0.13, β = 0.03 .

Figure 24

Variation of resistance for F = 0.01, J ₃  = 0.09, B _r  = 0.3, G _r  = 0.1, n = 2 , L = 2, N _b  = 0.1, α = 0.1, β = 0.03 .

Trapping

Trapping phenomena can be analyzed in Figures 24, 25, 26, 27, 28, 29, 30, 31. It is analyzed that with an increase in flow rate F, the number of trapping bolus increases. We also observed that with an increase in β, the size of trapping bolus increases, while the number of trapping bolus increases with an increase in α. It is also observed that with an increase in the Brownian motion parameter N _b , the number of trapping bolus increases, while with an increase in the thermophoresis parameter N _t the number of trapping bolus decreases. It is also analyzed that with local nanoparticle Grashof numbers B _r and G _r , the size of trapping bolus decreases.

Figure 25

Stream lines for different values of (a) F = 0.20 and (b) F = 0.21 . Other parameters are N _b  = 0.011, ϕ = π, α = 0.90, β = 2.4, J₃ = 0.01, δ = 0.01, n = 2, N _t  = 0.5, B _r  = 3.5, G _r  = 2.7.

Figure 26

Stream lines for different values of (a) β = 2.3 and (b) β = 2.5 .

Figure 27

Stream lines for different values of (a) α = 0.91 and (b) α = 0.92 . Other parameters are N _b  = 0.011, ϕ = π, F = 0.21, β = 2.4,J₃ = 0.01,δ = 0.01,n = 2, N _t  = 0.5, B _r  = 3.5,G _r  = 2.7.

Figure 28

Stream lines for different values of (a) N _t  = 0.4 and (b) N _t  = 0.6 . Other parameters are N _b  = 0.011, ϕ = π, F = 0.21, α = 0.90, J₃ = 0.01, δ = 0.01, n = 2, β = 2.4, B _r  = 3.5, G _r  = 2.7.

Figure 29

Stream lines for different values of (a) N _b  = 0.010 and (b) N _b  = 0.011 . Other parameters are N _t  = 0.6, ϕ = π,F = 0.21,α = 0.90,J₃ = 0.01,δ = 0.01,n = 2, β = 2.4,B _r  = 3.5,G _r  = 2.7.

Figure 30

Stream lines for different values of (a) B _r  = 3.4 and (b) B _r  = 3.6 . Other parameters are N _t  = 0.6, ϕ = π,F = 0.21,α = 0.90,J₃ = 0.01,δ = 0.01,n = 2, β = 2.4,G _r  = 2.7,N _b  = 0.011.

Figure 31

Stream lines for different values of (a) G _r  = 1.5 and (b) G _r  = 2.5 . Other parameters are N _t  = 0.6, ϕ = π, F = 0.21, α = 0.90, J₃ = 0.01, δ = 0.01, n = 2, β = 2.4, B _r  = 3.6,N _b  = 0.011.

Conclusions

The main points of the study that were examined are as follows:

• 1. It is analyzed that with an increase in the thermophoresis parameter N _t and stenosis shape n, the velocity profile decreases, while the velocity profile increases with an increase in the maximum height of the stenosis δ, the Brownian motion parameter N _b , and Prandtl parameters α and β.

• 2. It is analyzed that with an increase in stenosis shape n, the thermophoresis parameter N _t , stenosis height δ, and Prandtl parameter β, the shear stress decreases, while it increases with an increase in the Brownian motion parameter N _b and Prandtl parameter α.

• 3. It is analyzed that the shearing stress at the stenosis throat decreases with an increase in β and increases with an increase in α.

• 4. It is observed that with an increase in the Brownian motion parameter N _b , the concentration profile increases, while it decreases with an increase in the thermophoresis parameter N _t .

• 5. It is observed that with an increase in the Brownian motion parameter, the temperature profile decreases, while with an increase in the thermophoresis parameter, the temperature profile increases.

• 6. It is observed that with an increase in the Brownian motion parameter N _b and the thermophoresis parameter N _t , the temperature profile decreases.

• 7. It is analyzed that with an increase in flow rate F, Prandtl parameter α, and Brownian motion parameter N _b , the number of trapping bolus increases, while it decreases with an increase in the thermophoresis parameter N _t .

• 8. It is also analyzed that the size of trapping bolus decreases with an increase in the local nanoparticle Grashof numbers B _r and G _r , while the size of trapping bolus increases with an increase in the Prandtl parameter β.