The effect of silver and aluminum oxide nanoparticles on thermophysical properties of nanofluids

Abstract

The present paper describes experimental and theoretical aspects of the effective thermal conductivity, electrical conductivity, and viscosity of nanofluids. The thermal conductivity, electrical conductivity, and viscosity of nanofluids increase with the nanoparticle volume fraction. The nanofluid was prepared by synthesizing Al₂O₃ and Ag nanoparticles using microwave-assisted chemical precipitation method and then dispersed in distilled water using a sonicator. Water nanofluid with nominal diameters of 20 and 40 nm at various volume concentrations (0.25% to 5%) at a temperature of 15°C was used for the investigation. The thermal conductivity, electrical conductivity, and viscosity of nanofluids were measured, and it was found that the viscosity and electrical conductivity increase is substantially higher than the increase in thermal conductivity. The pure base fluid thermal conductivity displayed a Newtonian behavior at 15°C; it transformed to a non-Newtonian fluid with the addition of a small amount of nanoparticles φ > 3%.

Background

Nanoparticles have many remarkable properties because of their small size and very large specific surface areas[1]. Nanofluids have gained significant attention due to their enhanced thermal properties. Pak and Cho reported that convection increases transfer coefficient by 75% for an Al₂O₃ particle concentration of 2.7% at a fixed Reynolds number. Most published studies on nanofluids deal with viscose properties of nanoparticle suspensions at low temperature. Praveen and Namburu reported that with the heat transfer behavior including thermal conduction, phase change, heat transfer, and convection heat transfer from an application point of view, the ideal nanofluid should possess not only high thermal conductivity but also low viscosity. Until now, only few studies have addressed the viscosity of nanofluids which increases when the volume concentration of nanoparticles increases, for example, the viscosity of 6.12% copper oxide volume concentration is about four times the value of the base fluid at -35°C[2]. Although copper oxide nanofluids exhibit Newtonian behavior in ethylene glycol and water mixture for concentrations varying from 0% to 6.12%, they found that TiO₂ particles of 27-nm average diameter at a volumetric loading of 4.3% increased the viscosity of water by 60%. Pak found that for 10% volume concentration of nanoparticles, the viscosity of Al₂O₃ (13 nm) water- and TiO₂ (17 nm) water-based nanofluids is several times higher than that of water. The viscosity of nanofluids is an important transport property for applications of nanofluids as a new class of heating or cooling medium in thermal devices or systems such as heat exchangers or cooling systems. Determining the viscosity of nanofluids is essential to establishing adequate pumping power as well as the convective heat transfer coefficient, because the Prandtl and Reynolds numbers (functions of viscosity) will be influenced. Einstein proposed a viscosity correlation for particle suspensions in base fluid when the volume concentration is lower than 5%[3]:

$${\mu }_{\mathrm{s}}={\mu }_{\mathrm{f}}\left(1+2.5\phi \right),$$

(1)

Figure 1

Thermal conductivity ratio of Ag/water nanofluid as a function of volume concentration.

where μ_s is the suspension's viscosity, μ_f is the viscosity of the base fluid, and φ is the volume percentage of particles in base fluid. Brinkman extended Einstein's formula for use with moderate particle concentration as follows[4]:

$$\raisebox{1ex}{${\mu }_{\mathit{nf}}$}\!\left/ \!\raisebox{-1ex}{${\mu }_{\mathit{bf}}$}\right.={\left(1-\phi \right)}^{-2.5}.$$

(2)

Batchelor considered the effect of the Brownian motion of a particle on the bulk stress of an isotropic suspension of spherical particles and derived the viscosity expression as[5] follows:

$$\raisebox{1ex}{${\mu }_{\mathit{nf}}$}\!\left/ \!\raisebox{-1ex}{${\mu }_{\mathit{bf}}$}\right.=\left(1+2.5\phi +6.5{\phi }^2\right).$$

(3)

Various recent studies[6] suggest that the high viscosity of nanofluids is likely to be associated with the aggregation of nanoparticles for which the Krieger-Dougherty equation has been used by other authors[7]. The Krieger-Dougherty model has a form:

$$\frac{{\mu }_{\mathit{nf}}}{{\mu }_{\mathit{bf}}}={\left(1-\frac{{\phi }_n}{{\phi }_{\mathrm{m}}}\right)}^{-\left(\eta \right){\phi }_{\mathrm{m}}},$$

(4)

where φ_m is the maximum concentration at the flow, φ_a the effective volume fraction of aggregates, and η is the

Figure 2

Thermal conductivity ratio of Al ₂ O ₃ /water nanofluid as a function of volume concentration.

Figure 3

Viscosity of Ag/water nanofluid as a function of volume concentration.

intrinsic viscosity wherein for a monodisperse system, it has a typical value of 2.5.

Notice that all four correlations (Equations 1 to 4) were developed to relate viscosity as a function of volume percentage only. There is no consideration of temperature dependence. A correlation for pure fluids between viscosity and temperature is presented as follows[8]:

$$\mathrm{Ln}\frac{{\mu }_{\mathit{nf}}}{{\mu }_{\mathit{bf}}}\approx a+b\left(\frac{T_0}{T}\right)+C{\left(\frac{T_0}{T}\right)}^2,$$

(5)

where μ _bf and T₀ are reference values, and c is the dimensionless curve fitting constant. In this research, we report the rheological behavior of silver nanoparticles (40 nm) and Al₂O₃ (20 nm) suspended in water over a wide range of volumetric solid concentrations (φ = 0.25% to 5%). The nanoparticle suspensions generally exhibited a yield pseudoplastic behavior. We conducted a detailed investigation on their effects on the viscosity as a function of Al₂o₃ and Ag volume concentrations, shear rate, and temperature. Results have been discussed both in terms of several classical models and the theoretical prediction for viscosity of nanofluids proposed recently.

The research work on the measurement of thermophysical property, so far, has been done mostly on the effective thermal conductivity. Inspite of the scientific and technological importance of electrical conductivity

Figure 4

Viscosity of Al ₂ O ₃ /water nanofluid as a function of volume concentration.

Figure 5

Shear stress as a function of volume concentration for Al ₂ O ₃ .

characteristics of nanoparticle suspensions, the effective electrical conductivities of nanofluids have not been investigated thoroughly, and there are very few data which presented the electrical properties of nanofluids. In addition, among the transport properties, electrical conductivity may help to attain the understanding of dispersion state and stability of the particulate suspension[9].

Suvankar Ganguly et al.[10] investigated the effective electrical conductivity of alumina nanofluid at different volume fractions. It is seen that the electrical conductivity of alumina nanofluid increases almost linearly with increase in the volume fraction of the alumina nanoparticles. The experimental data also indicate that for a given volume fraction, the electrical conductivity of the suspension will increase with increases in the temperature. The highest value of electrical conductivity, 351 μS/cm, was recorded for a volume fraction of 0.03 at a temperature of 45°C; the corresponding value at room temperature (T = 24°C) was 258 μS/cm.

Results and discussion

In this paper, we have experimentally investigated the effective thermal conductivities, electrical conductivity, and viscosities of the water-based nanofluids containing Al₂O₃ and Ag nanoparticles (Al₂O₃ and Ag /water nanofluids).

Figure 6

Shear stress as a function of volume concentration for Ag.

Figure 7

Measured effective electrical conductivity of alumina nanofluid.

The thermal conductivity and viscosity of the nanofluid were measured using a KD2 Pro thermal property analyzer and Brookfield viscometer. Figures 1 and2 show the thermal conductivity of Al₂O₃ and Ag/water nanofluids as a function of particle volume concentration. The viscosity of nanofluids increases when the volume concentration of nanoparticles increases.

The results show that the thermal conductivity of nanofluids significantly increases linearly with increasing particle volume concentration. In contrast, Figures 3 and4 show that the viscosity was observed to have a nonlinear relation at a volume concentration greater than 2%.

Figures 5 and6 show the shear stress (τ) for various nanofluids with different volume concentrations of Al₂O₃ and Ag nanoparticles. We show the figures with a correlation coefficient R² > 0.98.

Figures 7 and8 show the effective electrical conductivity of alumina and silver nanofluids at different volume fractions and at 15°C. It can be found that the electrical conductivity of nanofluids increases linearly with an increase in the volume fraction of the alumina

Figure 8

Measured effective electrical conductivity of silver nanofluid.

Figure 9

Experimental setup for viscosity measurement of nanofluids.

nanoparticles. The enhancement in the electrical conductivity of the alumina and silver nanofluids is compared to that of the base fluid.

Conclusions

In this paper we have experimentally investigated the effective thermal conductivities and viscosities of water-based nanofluids containing Al₂O₃ and Ag nanoparticles:

• 1. Ideal nanofluids should not only possess high thermal conductivity but also should have low viscosity.

• 2. Al₂O₃ and Ag nanofluids exhibit Newtonian behavior in water for concentrations varying from 0.25% to 2% at 15°C.

• 3. The viscosity and thermal conductivity of nanofluids increase when the volume concentration of nanoparticles increases.

• 4. The viscosity of nanofluids is dependent on volume percentage. The higher the concentration of nanofluids, the higher viscosity.

• 5. The pure base fluids display Newtonian behavior at 15°C.

• 6. The viscosity is as critical as thermal conductivity in engineering systems that employ fluid flow.

• 7. Nanofluids (Ag and Al₂O₃) with different volume concentrations (0.25% to 5%) are appropriate for pumping in a heat exchanger setup.

• 8. The results show that the thermal conductivity of Ag nanofluids significantly increases linearly with increasing particle volume concentration.

• 9. The results indicate considerable enhancement of electrical conductivity with increase in volume fraction.

• 10. The experimental results show that the electrical conductivity of alumina and silver nanofluid is significantly greater than that of the base fluid.

Methods

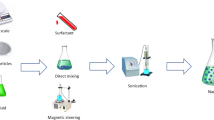
In our experiments, we used Al₂O₃ and Ag nanoparticles with an average diameter of 20 nm for Al₂O₃ and 40 nm for Ag. Nanofluids with different volume concentrations (0.25%, 0.5%, 1%, 2%, 3%, 4%, 5%) were dispersed in water. The suspension of nanofluids was then stirred and agitated thoroughly for 1 h with an ultrasonic agitator similar to a sonicator. This ensures uniform dispersion of nanoparticles in the base fluid. The viscosity of the nanofluids is measured using the Brookfield programmable

Table 1 Conductivity meter properties

Figure 10

Thermal conductivity meter and electrical conductivity meter.

viscometer (model: LVDV-II+, Brookfield Engineering Labs., Inc, Middleboro, MA, USA) connected to a PC-controlled Julabo temperature-controlled bath (JULABO GmbH, Seelbach, Germany) which can vary the fluid temperature control of 15°C. The viscometer drives a spindle immersed in nanofluids. When the spindle is rotated, the viscous drag of the fluid against the spindle is measured by the deflection of the calibrated spring. This viscometer has a viscosity measurement range of 1.5 and 30,000 mPas and can handle the viscosity measurement results within the temperature ranges of this experiment. The total volume of nanofluid required in a UL adapter is ≈20 ml. The viscometer contains a sample chamber and is carefully monitored using a RTD temperature sensor during the viscosity measurements. The spindle type and speed combinations will produce satisfactory results when the applied torque is between 10% and 100%; therefore, spindle types and speeds are selected in such way that the torque values lie in this prescribed range. A wide range of spindle speeds are available in this viscometer (0 to 200 RPM). Viscosity measurements were started at 15°C. The temperature of the fluid is measured by a calibrated pt100 temperature sensor. The viscometer is connected to another computer as shown in Figure 9. The operation of the viscometer and data collection, viscosity, shear stress, shear rate, RPM, torque, and temperature is performed using Wingather software. All the viscosity measurements were recorded at steady state conditions (Figure 9, Table 1).

Thermal conductivity measurement

The thermal conductivity of Al₂O₃ and Ag/water nanofluid was measured by using a KD2 Pro (Figure 10) thermal property analyzer (Decagon Devices, Inc., Pullman, WA, USA). It consists of a handheld microcontroller and sensor needles. The KD2 sensor needle contains both a heating element and a thermistor. The controller module contains a battery, a 16-bit microcontroller/AD converter, and power control circuitry. The sensor needle can be used for measuring thermal conductivity of fluids in the range of 0.2 to 2 W/mk with an accuracy of ±5%. Each measurement cycle consists of 90 s. During the first 30 s, the instrument will equilibrate which is then followed by heating and cooling of the sensor needle for 30 s each. At the end of the reading, the controller computes the thermal conductivity using the change in temperature (ΔT) time data from

$$k=\frac{q\left(\mathit{ln}{t}_2-\mathit{ln}{t}_1\right)}{4\pi \left(\Delta T_2-\Delta T_1\right)},$$

(6)

where q is the constant heat rate applied to an infinitely long and small ‘line’ source, and ΔT₁ and ΔT₂ are the changes in the temperature at times t₁ and t₂, respectively (Figure 10).

Measurements of the effective electrical conductivity of nanofluids

The 4510 is easy to use with the flexibility to meet the broadest range of applications, and for those where greater accuracy is required, the 4510 has automatic conductivity standard recognition and endpoint detection (Figure 10). Setup options include cell constant, temperature coefficient, and reference temperature to measure the electrical conductivity of nanofluids; a precision conductivity cell with an application range of 0.01 μS/cm to 2 S/cm has been used. Measurements of the electrical conductivity were carried out both as a function of nanoparticle volume fraction and temperature. The typical response time for measurement was about 20 s. The electrical conductivity of the Al₂O₃-water nanofluid was measured at a temperature of 15°C.