Background

Cytarabine is a chemotherapy agent utilized chiefly in the therapy of hematological malignancies like non-Hodgkin lymphoma and acute myeloid leukemia [1]. In addition, cytarabine has been known as Ara-C (arabinofuranosyl cytidine) [2]. In two randomized trials, the utilization of interferon and intermittent parenteral cytarabine has been estimated [3, 4]. This combination raises the cytogenetic response rate further, and in one trial [3], it enhanced overall survival compared with interferon alone. However, subcutaneously administered cytarabine has some defects. Following parenteral administration by the ubiquitous enzyme deoxycytidine deaminase, which results in a comparatively short serum half-life, it quickly undergoes systemic deamination [5]. It needs daily subcutaneous injection to render the drug and is also associated with upper gastrointestinal symptomatology, particularly mucositis and nausea [3]. In addition, carbon nanotubes (CNTs) have attracted an uninterrupted interest in different areas since their discovery because of their unique structure and electrical/mechanical characteristics [6, 7] which make them interesting for many potential usages in electronic devices, sensors, structural integrity [8], biomedical engineering [9–11], nanoinjectors [12], drug delivery [13], gene therapy [14], and in catalysis supports. We can categorize CNTs as single-wall carbon nanotubes (SWCNTs) and multiwall carbon nanotubes (MWCNTs) [15]. In fact, SWCNTs are grapheme cylinders with a wall thickness of 1 atomic layer and a diameter of around 1 nm. High aspect ratio, enormous surface, hollow geometry [6] are some their exciting characteristics. Other characteristics include high-current carrying capacity, superior thermal properties, fast response, and good reversibility [7, 16]. SWCNTs have three configurations. It will be in the form of an armchair if the nanotubes n = m and whenever n = 0 or m = 0, it will be in zigzag form with any other n and m, it will be in chiral variety. Each of these configurations has its own characteristics and properties [17, 18]. MWCNTs are made of multiple rolled layers (concentric tubes) of graphite. Using two models, we can depict the configurations of multiwall nanotubes. In one of these models, the Russian model, sheets of graphite are set in concentric cylinders, e.g., (0, 8) SWCNTs are within a larger (0, 17) single-wall nanotube. In the second model, the parchment model, a single sheet of graphite is rolled around itself, just like a scroll of parchment or a rolled newspaper. In multiwall nanotubes, the interlayer distance is somehow equal to the distance between grapheme layers in graphite, which is nearly 3.4 Å. Two concentric cylindrical grapheme layers conform to double-wall carbon nanotubes. Accordingly, they blend with the interesting electronic characteristic of SWCNTs with the superior mechanical strength of MWCNTs [19].

This paper is concentrated on the interaction of a carbon nanotube with an anticancer drug named cytarabine. Nowadays, in the universe of new medicine, carbon nanotubes have experimentally showed their capacity in passing through the cell shell. Accordingly, scientists believe that they can apply them in releasing active drug molecules in the cell, particularly in the most sensitive and essential molecules for special diseases such as cancer, AIDS. The physical and chemical nature of these nanotubes has been studied by many scientists in order to prepare this material for such a significant task. Scientists pay special attention to carbon nanotubes consisting of fullerenes [20] because of their unequaled electrical, optical, and thermal characteristics. Scientists are very hopeful to develop and utilize carbon nanotubes in releasing vaccines by conducting basic and fundamental projects. Releasing drugs in cancer cells without harming healthy cells of tissues under study is very significant. After a number of research, we can understand that nanotubes can do this task correctly [21, 22]. With the use of molecular mechanics (MM)/Monte Carlo (MC) simulation (in various force fields such as MM+, assisted model building with energy refinement (AMBER), and optimized potential for liquid simulations (OPLS)), the interaction of cytarabine with zigzag (5, 0) carbon nanotube was studied. Furthermore, we have studied the effects of solvents on their interaction by means of quantum mechanics (QM). We applied the self-consistent reaction field method (SCRF) for the simulation of solvent effects by QM method. Thus, it can be seen that we described the solvent effects on the thermodynamic values of this interaction using QM and MM methods.

Results and discussion

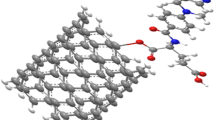
Here, the combination schema of cytarabine anticancer drug and zigzag (5, 0) carbon nanotube is shown in Figure 1. We have examined the thermodynamic values of the interaction of cytarabine with zigzag (5, 0) carbon nanotube in different dielectric constants.

Figure 1
figure 1

Shape of (cytarabine and SWCNT) system.

Full size image

In this work, we have done the said calculation by studying the following reaction:

Cytarabine + SWCNT → Cytarabine − SWCNT
(1)

Thus, in the first stage, we studied various force fields to estimate potential energy (kcal mol−1) and other kinds of geometrical parameters on the interaction of cytarabine with the zigzag (5, 0) carbon nanotube. By utilizing three various force fields, the potential energy of molecules will not be similar. Thus, to compare the calculated potential energy of one specific molecule with a special force field and with the potential energy of another molecule computed in another force field is neither reasonable nor possible. In this examination, we revealed the differences in force fields by comparing the calculated potential energy utilizing different force fields such as MM+, AMBER, and OPLS that are show in (Figures 2, 3, and 4). Thus, it can be observed which water solvent has the lowest value of potential energy alterations. Also, it can be seen why OPLS is the best force field in the comparison of potential energy alterations in the water solvent (Figure 5, Table 1). Using different force fields, we can obtain the theoretical potential energy values; these are done by the joining of or attraction of the Van Der Waals force caused by dipole-dipole interactions and the experimental repelling forces caused by Pauli repulsion. In the opposite direction of the encircling medium, a dipole moment is made by the thermodynamic values of solute dipole moment. Conversely, the medium polarizes the charge distribution in the solvent. The dipole moment values of cytarabine and zigzag (5, 0) carbon nanotube, (cytarabine/zigzag (5, 0) carbon nanotube) system in gas phase, and water and methanol at various temperatures have been related. It is revealed that dipole moment values in gas phase, water, and methanol increase with the increasing dielectric constant; we demonstrate these results in Table 2. A continuous dielectric constant signifies the presence of a solvent with a given dielectric constant in Onsager reaction field template. We must consider that the solute to be fixed into the cavity (usually with a spherical shape), with its radius in the molecule, and the electric field, which is related to the solute by the solvent dipole, will interact with the molecular dipole and will be directed to net stabilization. Now, it must be noted that salvation energy computed by SCRF method is the electrostatic distribution to the free energy of salvation. In this study, the cavity radii of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system were calculated and were then substituted while efficiency was improving. We have also achieved the volumes of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system. After computing the values of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system, we came up with these outcomes: 8.70, 5.06, 5.73 Å, respectively. We have reached the point wherein, along the increasing solvent dielectric constant, the dipole moment for the anticancer drug, cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) Carbon nanotube) system in different ranges of temperatures (between 299 and 314 K) also increased, which is based on the dipole moment data in Table 2. After computing the values for the Onsager template, the fact that Gibbs free energy, energy, enthalpy, and entropy values of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system are sensitive to the polarity of the encircling solvent. Thus, the Gibbs free energy, enthalpy, entropy, and energy values are revealed according to this approach in Table 3. All of these values have relationships with the dielectric constant. According to Table 3, everybody can understand that by increasing the temperature from 299 to 314K, the thermodynamic values of Gibbs free energy of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system in gas phase, water, and methanol will decrease. We can get the lowest amount of Gibbs free energy at 314 K. The achieved Gibbs free energy values decrease, in all inspected temperature, if the solvent dielectric constant increases. For example, Gibbs free energy obtains the most negative value whenever cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system are released in water solvent. More or less, Table 3 shows the obtained Gibbs free energy, enthalpy, energy, and entropy values in different solvents. According to the temperature that changed between 299 and 314 K, the changes of energy, enthalpy, and entropy of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system in gas phase, water, and methanol can be observed. Thus, we get to this point wherein the most positive value of energy, enthalpy, and entropy is 314 K if the temperature increases from 299 to 314 K. The other important point is that, after computing the values of energy, enthalpy, and entropy based on the solvent dielectric constant and increased values in temperature between 299 and 314 K, the value of energy and enthalpy becomes negative. The lowest values of energy and enthalpy and positive values of entropy can be obtained when cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system are in water solvent. In such cases, we can observe the most positive value of entropy.

Figure 2
figure 2

Potential energy alterations versus temperature in different solvents and MM + force field for reaction 1.

Full size image
Figure 3
figure 3

Potential energy alterations versus temperature in different solvents and AMBER force field for reaction 1.

Full size image
Figure 4
figure 4

Potential energy alterations versus temperature in different solvents and OPLS field for reaction 1.

Full size image
Figure 5
figure 5

Potential energy alterations versus temperature for water solution in different force fields for reaction 1.

Full size image
Table 1 Theoretical potential energy (kcal mol−1) values in different solvents and same force fields
Full size table
Table 2 Theoretical dipole moment μ (Debye) and Δμ (Debye) values in various temperatures for three phases
Full size table
Table 3 Theoretical thermodynamic parameters in various temperatures for three phases at HF/3-21G level of theory
Full size table

Study the following reaction:

Cytarabine + SWCNT → Cytarabine − SWCNT

In Table 4, we can observe the facts about the (cytarabine/zigzag (5, 0) carbon nanotube) system. If the solvent dielectric constant increases, the Gibbs free energy values of the interaction between solvent and solute molecules decrease. Noticeably, in Table 4, we can understand that the increase of solvent dielectric constant makes the enthalpy values of interaction between solvent and solute molecules move toward negative amounts. It reveals that the interaction between solvent and solute molecules is strong. According to Equation 1, the achieved entropy values are reasonable. In fact, the above reaction suggests that by coupling the anticancer drug of cytarabine with zigzag (5, 0) carbon nanotube, the entropy lessens. Now, we estimate and survey the data from another viewpoint on Equation 1:

Table 4 Theoretical thermodynamic parameter alterations in various temperatures for three phases at HF/3-21G level of theory
Full size table

We can see diagrams of Δμreaction, ΔGreaction, ΔHreaction, and ΔSreaction according to the temperature changes in Figures 6, 7, 8, and 9, respectively, in which the values of Δμreaction, ΔGreaction, ΔHreaction, and ΔSreaction are obtained on the basis of following function:

Δ J = Δ J cytarabine − SWCNT − Δ J cytarabine + Δ J SWCNT
Figure 6
figure 6

Dipole moment alterations calculated versus temperature for reaction 1.

Full size image
Figure 7
figure 7

Gibbs free energy alterations ( kcal mol −1 ) calculated versus temperature for reaction 1 for three phases.

Full size image
Figure 8
figure 8

Enthalpy alterations ( kcal mol −1 ) calculated versus temperature for reaction 1 for three phases.

Full size image
Figure 9
figure 9

Entropy alterations (kcal mol −1 K −1 ) calculated versus temperature for reaction 1 for three phases.

Full size image

In this function, the J parameter is equal to the dipole moment values μ for Figure 6, Gibbs free energy values G for Figure 7, enthalpy values H for Figure 8, and entropy values for Figure 9. In Figure 6, we can recognize which of the values will change by the increasing solvent constant, Δμreaction, in Figure 1 if the temperature is increased up to 314 K. Moreover, Figure 7 elaborates that the increase of temperature will also heighten the value of ΔGreaction. Thus, ΔGreaction has the lowest value at 299 K, and we then can reach to the point where the highest resistance for Equation 1 will occur. Also, Figure 9 reveals that the value of ΔSreaction declines with increasing temperature. The most positive value, ΔSreaction, in Equation 1 can be observed, and it is the more resistant rate. In Table 4, we must notice that the alteration of ΔGreaction, ΔHreaction, and ΔSreaction, in terms of solvent dielectric constant, will decline the value of the noted ΔGreaction in as much as the negative value of ΔGreaction is for water solvent; the water solvent is the best environment for Equation 1. According to Table 4, ΔHreaction and ΔSreaction values are reduced by the increase of solvent dielectric constant in temperature between 299 and 314 K. If Table 4 is considered, the fact that ΔSreaction at 299 K gains the most positive value is attained; thus, the temperature 299 K will be the choice for Figure 1.

Conclusions

In this article, cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system were studied by two methods, quantum mechanics and molecular mechanic/MC simulation. Diagrams were showed that ΔEPOT and thermodynamic values of the reaction were dependent to the solvent dielectric constant. The calculated ΔEPOT values for the reaction in water are more stable because the potential energy alterations become lower. The computed values of ΔEPOT from force fields MM+, AMBER, and OPLS in water solvent were compared, and they showed that the OPLS force field is the best force field for the study of Equation 1. In the next calculation, we investigated the obtained results by the HF/3-21G and Gaussian 98 showing that water is the best solvent when cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system are placed in it because they have the most negative Gibbs free energy and the most positive entropy in this solvent.

Methods

Computational method

We conducted all computations by quantum mechanics and molecular mechanics/Monte Carlo simulation (in various force fields such as MM+, AMBER, and OPLS) in various temperatures. At first level, we carried out all calculations using the program HYPER CHEM (Hypercube, Inc., Gainesville, FL, USA). In this study, different force fields were used to determine the potential energy. Thus, we can observe the difference in force field by comparing the computed potential energy with the applied force fields namely MM+, AMBER and OPLS. At the next level, using the Hartree-Fock (HF) method, we conducted calculations of the theoretical level. It is important to choose a level which is well matched with the molecular system being studied. Accurate geometry coordinates and energy parameters control conformational interconversions; in molecular systems, they are particularly important. Low-energy structures found on each surface were closed and exposed to unlimited quantum mechanical minimization using HF/3-21G SCRF [23]. To determine thermodynamic values of cytarabine, zigzag (5, 0) carbon nanotube, and (cytarabine/zigzag (5, 0) carbon nanotube) system, we performed a theoretical analysis at the HF/3-21 level. By means of the Onsager method as implemented in the Gaussian 98 program [24], we modeled the solvent effects. The geometries of the cytarabine and single-wall carbon nanotube and the interaction of a nanotube with an anticancer drug in various solvents were optimized using the Onsager model at the Hartree-Fock level of theory. We investigated the cytarabine single-wall carbon nanotube and interaction of a nanotube with an anticancer drug in gas phase (ϵ = 1) and various solvent media and dielectric constants: water (ϵ = 78.39) and methanol (ϵ = 32.63), at various temperatures.

Theoretical background

SCRF method

In using the SCRF model in the quantum chemical theory, the form and volume of the solute molecule needs to be determined specifically for any set of compounds; we know some of the approaches to calculate these properties, but no nonempirical method for their study had been developed. However, we can conclude from the results of the model calculations that the simple model that assumed a spherical or an ellipsoidal shape of the cavity for the solute molecule is likely satisfactory for comparatively tiny and strong molecules. We then selected this method in our computations [25]. In the past years, the Onsager-SCRF code elaborated by Wiberg and co-workers [26, 27] for the Gaussian computational code has been famous. The Onsager model describes the system as a molecule with a multipole moment inside a spherical cavity surrounded by a continuous dielectric. In some programs, only the dipole moment is used, and therefore, we cannot apply them for molecules with zero dipole moment. Qualitatively, the results from using the Onsager model and HF calculations are correct rules.

Molecular mechanics (Monte Carlo simulation)

By performing statistical sampling experiments, the Monte Carlo method provides approximate solutions to a variety of mathematical problems. Where statistical simulation is defined in quite general terms as a method that utilizes sequences of random numbers to conduct the simulation, we can loosely determine them as a statistical simulation method. We then can declare that the Monte Carlo method is a collection of various methods and unique processes. This process includes performing many simulations using random numbers and probabilities to get approximations of the answer to the problem. Our notion about defining the characteristic of the Monte Carlo method is its use of random numbers in its simulation. We apply the metropolis algorithm more than any other algorithm because of its simplicity in the Monte Carlo method [28]. By random displacement, we can determine the accuracy of the algorithm in small displacement; all moves are acceptable, but in huge cases, only the small moves are accepted. In this study, by comparing the computed potential energy using the force field MM+, AMBER, and OPLS in the Monte Carlo simulation, we illustrate the chemical calculation. Scientists use the HyperChem professional 7.1 in this investigation. Using this software, geometry optimization and Monte Carlo simulation have been performed. They have performed the quantum chemical calculations on the interaction of cytarabine with open-end SWCNT by means of the Gaussian 98 program package [29] using the standard 3-21G basis set. We apply a simple approximation in the Hartree-Fock level and in the Gaussian program, and in order to calculate the radius of cavity which forms the hypothetical surface of the molecule [30, 31]. We also utilize the volume of the solute. Both the solute and solvent are placed in the same cavity. How the SCRF approaches define the cavity and reaction field differ with each other. We take into account and consider the effect of the solvent in accordance with the self-consistent reaction field method. This method is based on the Onsager reaction field theory of electrostatic solvations. We consider the solvent as a uniform dielectric with a given dielectric constant, especially in this model. We then investigate solvent effects on the values of Gibbs free energy, enthalpy, entropy, energy, dipole moment of water, and methanol surrounding cytarabine open-end of the (SWCNT) system within the Onsager self-consistent reaction field model using the Hartree-Fock method as well as the various temperature effects on cytarabine open-end of SWCNT. We can compare the obtained thermodynamic values of cytarabine open-end of SWCNT in gas phase and in various solvents such as water and methanol.