Abstract
The freshwater reservoir effect can result in anomalously old radiocarbon ages of samples from lakes and rivers. This includes the bones of people whose subsistence was based on freshwater fish, and pottery in which fish was cooked. Water rich in dissolved ancient calcium carbonates, commonly known as hard water, is the most common reason for the freshwater reservoir effect. It is therefore also called hardwater effect. Although it has been known for more than 60 years, it is still less well-recognized by archaeologists than the marine reservoir effect. The aim of this study is to examine the order of magnitude and degree of variability of the freshwater reservoir effect over short and long timescales. Radiocarbon dating of recent water samples, aquatic plants, and animals, shows that age differences of up to 2000 14C years can occur within one river. The freshwater reservoir effect has also implications for radiocarbon dating of Mesolithic pottery from inland sites of the Ertebølle culture in Northern Germany. The surprisingly old ages of the earliest pottery most probably are caused by a freshwater reservoir effect. In a sediment core from the Limfjord, northern Denmark, the impact of the freshwater reservoir effect on radiocarbon dating in an estuarine environment is examined. Here, freshwater influence causes reservoir ages to vary between 250 and 700 14C years during the period 5400 BC - AD 700. The examples in this study show clearly that the freshwater reservoir effect can seriously corrupt radiocarbon dating at inland sites. Reservoir effects should therefore be considered whenever food remains on pottery or the bones of omnivores are radiocarbon dated - irrespective of the site’s distance to the coast.

Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Introduction
Throughout the entire history of radiocarbon dating, new sources of error have appeared, have been examined, and corrections have been found. Of particular interest and complexity are the so-called reservoir effects, which result in apparent ages that are too old.
One of the basic assumptions in radiocarbon dating is that a sample incorporates carbon in equilibrium with the atmosphere. This can be directly, e.g. in a plant via photosynthesis, or indirectly, e.g. when an animal feeds on plants. This type of sample is called terrestrial. If a sample obtains its carbon from another reservoir with a lower 14C level than the atmosphere, the basic assumption is no longer valid. The measured ages can be too old. This is typically the case for aquatic samples, originating in the sea (marine samples) or in freshwater systems such as lakes and rivers. This is of particular concern to archaeologists, as aquatic resources were an important contribution to human nutrition in Northern Europe, from Mesolithic hunter-gatherer-fishers to medieval Christians.
The marine reservoir effect is well-acknowledged among archaeologists, although the knee-jerk subtraction of 400 years from radiocarbon dates of marine samples might be too simplistic in some cases.
At least theoretically, the freshwater reservoir effect (FRE) has been known for a longer time than the marine reservoir effect. The most common cause of high apparent ages in freshwater systems is the presence of dissolved ancient carbonates, leading to the so-called hardwater effect. Under closed system conditions, calcite dissolution by carbonic acid leads to a 50% dilution of the 14C concentration [1, 2], causing a maximum FRE of one half-life of 14C, about 5,370 years. Under open system conditions, water DIC is continuously exchanging with the infinite reservoir of 14C-active soil CO2, causing no reservoir offset. In reality, freshwater systems have intermediate conditions, and a FRE between 0 and almost 6,000 years is possible [1].
The hardwater effect was already predicted by J. Iversen in a private communication to E. S. Deevey, October 5, 1949 [3]. The effect was considered by Godwin in 1951 [4] when discussing radiocarbon dates from the British Isles, and measured for the first time in 1954 on aquatic plants [5]. The marine reservoir effect was observed and discussed slightly later in the 1950s [6–8].
However, it took several decades before the FRE was measured and discussed in archaeologically relevant sample types, such as human bones [9–14] or food crusts on pottery [15–18]. In these cases, the consumption or preparation of large amounts of freshwater fish lead to spurious apparent ages of the bones and pottery.
Also aquatic plants which are incapable of assimilating carbonates, and rely on CO2, such as aquatic mosses, can show a substantial FRE [19]. High apparent ages can also be measured in carbonate-free groundwater and surface water [20], and apparent ages of up to 20,000 BP were reported from an Icelandic geothermal area [21].
In softwater lakes, the FRE can be caused by slow CO2 exchange between the atmosphere and the lake water due to a large depth-to-surface ratio, good wind protection or extended periods of lake ice cover [22, 23]. Other causes for a soft-water FRE are the inflow of old groundwater [22], the oxidisation of old organic matter [24], the inflow of water from a glacier containing old CO2, or old CO2 from volcanic activity [23].
Freshwater reservoir effects can vary significantly within one lake or river [18, 25, 26], even when only regarding submerged plants [26], or a single fish species from one lake [27]. Furthermore, the FRE influences radiocarbon dating in fjords and estuaries and can lead to site and time specific reservoir ages [28–30].
However, little attention has been paid to the temporal variability of the freshwater reservoir effect, and rivers have been underrepresented in studies of the FRE, with most studies focusing on lakes.
This study was designed to address some of these topics: the FRE in rivers; the short-term variability of the FRE; and the impact of the FRE on radiocarbon dating in estuarine environments. Therefore, modern river samples, archaeological samples from riparian sites, and samples from a fjord sediment core were radiocarbon dated. These radiocarbon dates were obtained as part of different studies from the author’s PhD project, all employing a variety of methods. See [17, 18, 31–33] for details on the individual sub-projects. For this paper, the radiocarbon dating results of the different sub-projects are extracted and discussed in the context of other authors’ studies on the FRE. This will provide an overview of use to archaeologists who consider dating materials which may be affected by a FRE. The author hopes that this paper can serve as a useful introduction to the FRE for researchers who are not familiar with this topic.
Location
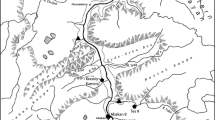
The locations examined in this study are mapped in Figure 1. Two main regions are in the focus of this paper, both located on the Jutland peninsula.
Map of the study area. Blank map of Europe by commons.wikimedia user Júlio Reis. a) The Limfjord region. Localities mentioned in the text are labelled. b) Detailed map of the Kilen core site. Own work, made with MapInfo Professional 7.8 using bathymetry data by Thorkild Høy, published in [34]. c) Map of the rivers Alster and Trave with the archaeological sites Kayhude/Alster (red cross, marked K) and Schlamersdorf/Trave (S). Main watersheds are indicated by yellow lines (after http://www.erneuerbare-energien.de/files/bilder/allgemein/image/gif/flussgebietseinheiten.gif, Umweltbundesamt, 2004). Map of Schleswig-Holstein by commons.wikimedia user NordNord-West, relief by commons.wikimedia user Lencer.
The first region this paper deals with is the southern part of the Jutland peninsula, the northernmost federal state of Germany, Schleswig-Holstein. Here, the short-term variability of the freshwater reservoir effect in the rivers Alster and Trave is measured. Both rivers run through a morainal landscape from the last two glaciations. The moraines have calcium carbonate contents of up to 20% ([35]; see [32] and [31] for details on the study area). In the same region, the impact of the freshwater reservoir effect on radiocarbon dating of pottery was studied. Mesolithic pottery, maybe the earliest in that region, was found at the sites Kayhude at the Alster and Schlamersdorf at the Trave. These sites are marked “K” and “S” on Figure 1.
The second region examined in this paper is the Limfjord, a sound through Northern Jutland. The study location Kilen is a former inlet of the Limfjord at 56∘30.005′N, 08∘34.089′E. Today, after the construction of a dam, Kilen is a brackish embayment. As Kilen was naturally protected from strong currents, storms and wave action in the past, a continuous sediment sequence has been preserved. It is therefore possible to study the influence of the freshwater reservoir effect on radiocarbon dates in the Limfjord over long time scales. Details on this study area are provided in [31, 33, 36, 37].
Materials and methods
This section describes the sample collection, chemical preparation, and measurement techniques. Modern samples of water, aquatic plants, fish and shellfish from the rivers Alster and Trave have been collected. Archaeological samples were provided from the Late Mesolithic sites of Kayhude/Alster and Schlamersdorf/Trave. Samples for studying the Limfjord were obtained from a sediment core.
Water
Dissolved inorganic carbon, DIC, is the carbon source for aquatic photosynthesis, and thus the material chosen for radiocarbon dating water samples. It comprises CO2(aq), H2CO3(aq), and . On 21 August 2007, 25 September 2008, 18 February 2009 and 6 July 2010, water samples were collected from the Northern German rivers Alster and Trave (Figure 1). They were sampled in 0.5L bottles and preserved with a few drops of a HgCl2 solution. This prevented the growth of algae, which would have converted some of the DIC into organic carbon. The samples were kept dark and cool until analysis. The water was acidified with 100% H3PO4, which converted all DIC into CO2. N2 was bubbled through the water to free the CO2, which was trapped cryogenically.
Modern plants and animals
Aquatic macrophytes and animals were collected at the same sites as the water samples. They were freeze-dried prior to analysis. No visible carbonate encrustations were found on the aquatic plants. HCl-pretreatment was therefore not considered necessary. Local fishermen provided fish from the rivers. Collagen was extracted from some modern fishbones, as this is the material used for analyses of archaeological bones. A modified Longin-procedure with ultrafiltration was used [38–40]. The samples were converted to CO2 by combustion in sealed evacuated quartz tubes containing CuO.
Sediment core from the Limfjord
In 2007, a 1560 cm long sediment sequence was obtained from Kilen, Limfjorden (Figure 1). The coring was made with a Russian peat sampler (chamber length 100 cm; [41]) in two parallel boreholes at a water depth of 390 cm below present sea level (bpsl). The sediments consist of homogenous grey-brown marine clay gyttja. This study focuses on the part between 467 and 1935 cm bpsl which was subsampled at 1–2 cm depth intervals. Material for AMS 14C dating was retrieved by wet sieving. Other sample types and measurements from this core, e.g. stable isotope measurements, are described in detail in [33, 36].
Shells
Both modern shells, collected from the Northern German rivers, and shells from the sediment core in the Limfjord were pretreated with the following method: Shells were cleaned with ultrasound in demineralised water. Depending on size, the outer 10–25% of the shell was dissolved with 1M HCl. Possible organic remains were removed with KMnO4 at 80∘C.13−−14 mg of pretreated shell was dissolved in 100% H3PO4 at 25∘C, to produce CO2 for 14C-dating.
Archaeological samples and terrestrial plant remains from the sediment core
Archaeological charcoal samples and plant remains from the sediment core were pre-treated with 1M HCl at 80∘C for one hour, 1M NaOH at 80∘C for at least three hours and 1M HCl at 20∘C overnight. Archaeological food crusts can be used for dating the last usage of the pottery. They were pre-treated like charcoal, but at 20∘C, and with only 0.5 or 0.2 M NaOH. Collagen was extracted from archaeological bones as described above for modern fish bones. The samples were converted to CO2 by combustion in sealed evacuated quartz tubes containing CuO.
Radiocarbon dating
For radiocarbon dating, CO2 from the combusted or acidified samples was converted to graphite with the H2 reduction method [42]. It was measured at the AMS 14C Dating Centre at Aarhus University (AAR-numbers) or at the 14CHRONO Centre, Queen’s University Belfast (UBA-numbers). The dating results are reported as conventional 14C dates in 14C yr BP [43]. Calibrated dates have been obtained using OxCal version 4 with IntCal09 [44, 45] and are quoted as cal AD/BC.
For the sediment core, an age model was calculated based on 13 radiocarbon dates on macrofossils of unequivocally terrestrial origin. To account for changes in accumulation rate, boundaries are inserted at 447, 552, 1055 and 1748 cm, based on major changes in the CaCO3 content (Figure 2). The age model was constructed using the P_sequence depositional model in OxCal 4.1 [44], with k values between 10 and 200. The final k value of 150 yielded an agreement index of 73.3%. The width of the green line in the age model, Figure 2, indicates the uncertainty of the age model.
Radiocarbon ages of molluscs and terrestrial samples. a) Radiocarbon ages of terrestrial samples and mollusc shells from a sediment core from Kilen, Limfjorden, Denmark. b) Age-to-depth model for the sediment core. See [33] for details on calculations. The calibrated ages are given as calibrated ages AD/BC.
Stable carbon isotope measurements
Measurements of the stable carbon isotope ratio, 13C/12C, are essential for normalising 14C-measurements. Furthermore, they provide information about the origin of a sample. They can for example distinguish between marine and terrestrial samples. Measurements were either performed on the pre-treated sample, using an elemental analyser, or on a CO2 aliquot from combustion or acidification.
The analyses on pre-treated samples were performed by combustion in a EuroVector elemental analyser coupled to an IsoPrime stable isotope ratio mass spectrometer at the AMS 14C Dating Centre at Aarhus University. Most samples yielded enough material for replicate measurements. δ13C values are reported as ‰ VPDB. δ15N values and C/N ratios were measured at the same time and are discussed in detail in other publications [31–33].
The analyses on a CO2 aliquot from the radiocarbon preparation were performed using a Dual Inlet IsoPrime stable isotope mass spectrometer at the AMS 14 Dating Centre at Aarhus University. δ13C values are reported as ‰ VPDB. The standard deviation of 0.05‰ was determined using internal laboratory standards.
Calculation of reservoir ages
The reservoir age R is the difference in 14C age between an aquatic sample and a contemporaneous terrestrial sample. It is calculated by subtracting the 14C age of a terrestrial sample from the 14C age of the contemporaneous aquatic sample :
Finding the 14C age of a contemporaneous terrestrial sample was challenging for all instances where reservoir ages were calculated: Modern samples are affected by bomb carbon [46, 47], while not all ancient aquatic samples are clearly associated with terrestrial samples. Therefore, the following two sections will elaborate on how to calculate reservoir ages in these cases.
Calculation of reservoir ages of modern samples
As post-bomb terrestrial 14C ages are negative, the 14C age measured on an aquatic sample would underestimate the reservoir effect. Therefore, both the aquatic sample and a modern terrestrial sample are dated. Measurements on atmospheric 14CO2 (e.g. [48]) provide a convenient record of terrestrial references. The reservoir age R in 14C years is calculated from the difference in 14C ratios, which are given as percent modern carbon, pmC (pmCA for the aquatic, pmCT for the terrestrial sample; see [43] for details on notation and reporting of radiocarbon data):
where 8033 is the conventional “Libby” mean life of 14C. The uncertainty of the calculated reservoir age R, s(R), is calculated by propagation of uncertainty from the measurement uncertainties ΔpmC:
For the 14C content of the contemporaneous atmosphere at the time of sample formation, pmC T , measurements from the Black Forest station Schauinsland are used ([48] and pers. comm. I. Levin 2012). In spite of the high altitude, they are assumed to be a better estimate than the available data from a low-altitude station, Heidelberg, in the heavily polluted Rhein-Neckar area, which is affected both by additional 14C from a nearby nuclear power plant and 14C-free CO2 from industry, heating and transport [49].
Water DIC 14C-concentrations measured in this study will be compared with those of the atmosphere in the month of sampling, and aquatic plant 14C-concentrations with the average atmospheric concentrations of the entire growing season during which the plant grew (April-September, or April-July/August in case of sampling in summer). The average atmospheric 14C levels used for these calculations are presented in Table 1. For calculations of the uncertainty of the reservoir age of water DIC, the uncertainty of ±2‰ of the atmospheric measurements was used [49]. In the case of aquatic flora and fauna, the standard deviation of the average atmospheric measurements throughout the growing season was used.
Calculation of reservoir ages for samples from a sediment core
In the case of mollusc samples from a sediment core, we need an independent control of the true age of the molluscs to calculate their reservoir ages. In some cases, shell and terrestrial material from the same depth are available. The reservoir age R direct is the difference between the 14C age of the mollusc, 14CM, and the 14C age of the contemporaneous atmosphere, as determined by the 14C age of a terrestrial sample, 14CT:
where t represents the calendar age as determined by the terrestrial age-depth model. When the contemporaneous 14C age of the atmosphere cannot be assessed directly, i.e. terrestrial material is not available at the same depth, 14CT(t) is determined using the age model (to estimate t, Figure 2) in conjunction with the atmospheric calibration curve IntCal09 [45] to calculate the reservoir age R(t) as
Similarly, the local 14C reservoir age deviation from the global ‘model’ ocean, δR(t), can be estimated as the difference between a measured marine 14C age, , and the contemporaneous marine 14C age of the global ‘model’ ocean, :
In this case, the calibrated age t of each mollusc sample is converted into a marine 14C age, , by applying the global marine calibration curve Marine09 [45]. Errors on the calculated δR(t) values are estimated using 95% confidence intervals on the calibrated terrestrial age of each mollusc sample together with the measurement uncertainty on 14CM, i.e. the error on the mollusc 14C date.
Results and discussion
This presentation of the results starts with modern samples from Northern Germany. Then archaeological samples from the same region are discussed to assess the effect on samples from the past. Finally, the importance of the freshwater reservoir effect for radiocarbon dating in an estuarine environment is examined.
Modern river samples
On three occasions, in August 2007, September 2008 and July 2010, plants and animals were collected from the Northern German rivers Alster and Trave. Water samples were as well collected on these occasions and additionally in February 2009. Radiocarbon dates and δ13C measurements on the modern river samples are presented in Table 1 and Figure 3. Radiocarbon ages between -70 and +2620 14C years lead to estimated reservoir ages of 350 to 3040 14C years. The atmospheric 14C levels used for estimating reservoir ages are given in Table 1 as well. The mallard feather is the sample with the youngest 14C age. It is not considered a truly aquatic sample and is therefore excluded from this discussion. The δ13C values of modern river samples span a large range from -34.2 to -8.9‰.
Radiocarbon dating of water, aquatic plants and animals. Radiocarbon ages (uncal. 14C years BP) and δ13C values of modern samples. The values of the water samples were measured on DIC, dissolved inorganic carbon, which is the carbon source for photosynthesis among aquatic plants. The three smaller graphs display the same measurements as the large one, divided after date of sampling. Note the different scales for the small graphs. In February 2009, only water samples were collected. This sampling date is therefore not represented by an extra graph. The error bars are in most cases smaller than the symbols and thus not visible on the graphs. See Table 1 for values and additional information about the samples, such as estimated reservoir ages.
The ranges in 14C ages for water DIC, plants and fauna overlap. In general, DIC samples are older and more enriched in δ13C than the biological materials from the same sampling date (Figure 3). Natural variations in 14C levels between different reservoirs are amplified today because of the presence of “bomb 14C”, an excess in atmospheric 14C concentrations due to atomic bomb testing [46, 47], which lead to a doubling of atmospheric 14C levels until the 1960s. The FRE measured today is therefore not directly translatable to prehistoric samples.
Water
The δ13C values and 14C ages of the water DIC are correlated [32]. This reflects most likely the carbon source: dissolved ancient limestone has infinite 14C ages and δ13C values around 0‰; CO2 from modern decaying organic matter has 14C ages close to zero and δ13C values around -25‰ (there is no fractionation between organic carbon and CO2 under soil conditions as the corresponding biochemical reactions usually proceed to the end [50]). Old apparent ages of water DIC have already been measured in the first studies of the FRE. In 1954, for example, water samples from a hardwater lake in North America yielded ages of 2,200 years [5].
This two-component model, however, is too simple to describe the factors governing the DIC radiocarbon age: The 14C age of Alster DIC is greater than that of Trave DIC for every sampling date but one, 2010; Alster DIC δ13C values are generally lower than Trave DIC, except for 2008 (Table 1). If the only source for large radiocarbon ages were dissolved carbonate minerals, and the only source for small radiocarbon ages soil CO2, then the low δ13C values of the Alster would be inconsistent with the large 14C ages. There are two possible explanations for this discrepancy: on the one hand, higher ages in the Alster could be caused by mineralisation of old organic matter, such as peat. On the other hand, lower ages in the Trave could be caused by the fact that the Trave flows through the shallow lake Wardersee [51]; this leads to a comparatively long residence time of the water, which facilitates exchange with atmospheric CO2.
When scrutinizing precipitation records for Schleswig-Holstein, it was found that the amount of precipitation in the week prior to sampling is correlated negatively with the radiocarbon age and the δ13C values of the water DIC. The more rain in the period before sampling, the younger the 14C age, and the more negative the δ13C values. During periods with less precipitation, on the other hand, the relative amount of groundwater with ancient dissolved carbonates appears to be larger in the rivers. See [32] for details.
Aquatic plants
Modern aquatic plants were found to have radiocarbon ages between -70 and +2270 BP, corresponding to estimated reservoir ages of 350–2690 14C years (Table 1). The average reservoir ages are 2490 ±200 14C years for the Alster and 1270 ±770 14C years for the Trave. A FRE of this order of magnitude is not uncommon for aquatic plants. From 14C measurements of living aquatic plants and the contemporaneous atmosphere by Olsson et al. [52, 53], reservoir ages of up to 2,000 years could be calculated for Swedish lakes. Also in Estonian hardwater lakes, a large range of reservoir ages, up to 2,700 14C years, has been measured [26].
The large age range, substantially more than 2000 14C years, and the great variability of 14C ages of aquatic plants, is most likely caused by the multitude of available carbon sources for these plants. These include atmospheric CO2, different DIC species in the water, CO2 from decaying organic matter in the sediment, and nutrients stored in the rhizome of e.g. Nuphar lutea. These different carbon sources have potentially very different 14C ages. Sediment organic matter, for example, can be recent, or some decades old and thus heavily affected by bomb carbon. However, as the plant samples were not pretreated (see page 11), minute amounts of DIC could have been present and might have caused older ages. Future studies will compare samples of aquatic plants with and without acid wash, and thus clarify this matter. The purely terrestrial date of a mallard feather that had been found floating on the river water, however, indicates that this risk is low.
The most striking result of the analysis of aquatic plants is the fact that floating leaves of aquatic plants do not have younger 14C ages than submerged plants. A submerged plant with an estimated reservoir age of only 350 14C years contrasts with a floating plant, collected on the same day at the same part of the river, with a much higher reservoir age of 1300 14C years (Table 1). Floating and submerged parts of the same plant have the same radiocarbon age, as exemplified by two individuals of Nuphar lutea, where both the tip of the leaf and the end of the petiole were dated (Table 1).
Water lilies add a complicating factor to the multitude of possible carbon sources, as atmospheric air is transported from the younger leaves through petioles and rhizome to the older leaves, where most of the CO2 from this transport is photosynthesized [54]. This continuous air transport is most likely the reason for petioles and leaves having the same 14C ages. The large ages of the water lilies (Table 1) indicate a surprisingly large contribution from water CO2 (CO2, and not bicarbonate, is the DIC species N. lutea uses for photosynthesis), and a surprisingly little contribution from sediment CO2. The CO2 concentration in the sediment is much larger than that in the water or atmosphere, and sediment organic matter can be some decades old and therefore have a considerable excess of 14C due to atomic bomb tests. It was reported that the aquatic plants which are capable of using sedimentary CO2 are inhabitants of softwater environments, such as isoetids or similar plants; so far, no hardwater or marine species have been found to show significant root uptake of carbon [55].
These results disagree with previous studies where emergent plants and floating leaves of N. lutea were found to have 14C contents in equilibrium with the atmosphere [5, 26]. The specimen of N. lutea analysed by Olsson and Kaup [26], however, originated from a softwater lake. The reservoir age of this water lily was calculated by comparing its 14C activity with the 14C activity of the contemporaneous atmosphere at Schauinsland [26, 56]. Its leaves had a reservoir age of 39 years, while the stems had a negative reservoir age of -416 years. This is most likely caused by the fact that the plant grew during the decreasing part of the bomb peak: the stem was build using nutrients from the preceding growing season, stored in the rhizome [26].
In another study, however, N. lutea showed a full hardwater effect of about 500 years, while the white water lily Nymphaea alba had a terrestrial radiocarbon age [57].
Howsoever, I strongly recommend not to regard the floating leaves of any aquatic plant as terrestrial samples, even though the respective species might be known to assimilate atmospheric CO2.
Aquatic animals
Radiocarbon ages between 70 and 1660 BP were measured on fish and molluscs from Alster and Trave. This leads to estimated reservoir ages between 490 and 2090 14C years (Table 1). The age range is thus almost as large as that of the aquatic plants. The average reservoir age of the animals from both rivers is 1120 ±620 14C years (excluding the mallard feather). For the Alster alone, the average reservoir age is 1060 ±520, and for the Trave, 1150 ±730. The large variability of radiocarbon ages for fish and other freshwater animals (Table 1) is not surprising, regarding the large variability on the basis of the food web, including water DIC and aquatic plants [58]. Furthermore, DIC (for photosynthesis of aquatic plants) is not the only carbon source for aquatic animals. Filter feeders can for example rely on organic carbon in the water. Variation of the FRE both between fish species as well as within species have been measured in modern and archaeological samples from lakes and rivers [59].
Some of the fish with high reservoir ages were used for cooking experiments, which showed that a food crust on pottery has the same reservoir age as the ingredients [18, 31, 60].
Interestingly, the average reservoir ages of water DIC and aquatic plants are equal in the Alster, while they differ substantially in the Trave. The animals from the Alster, however, have significantly lower reservoir ages than the plants. In the Trave, on the other hand, aquatic plants and animals have similar average reservoir ages. We have not yet been able to find a satisfactory explanation for these similarities and differences, and more samples are needed to draw any firm conclusions.
A high FRE has been measured in a multitude of other studies. Many modern mussels and fish from rivers and freshwater bodies from the Netherlands, for example, had apparent ages of over 2,000 years; the flesh of one fish even 4,430 years [61]. A present-day pike from Lake Aunsø, Denmark, had an apparent age of 684 14C years [62]. In Lake Tissø, Denmark, ten modern fish and mollusc samples had an average reservoir age of more than 1,000 14C years [16]. Aquatic plants collected from a river near Tereze, North Caucasus, have an estimated reservoir age of 800 years, while fish from the same river had a FRE of approximately 600 years [63]. At Elk Hills, California, a consistent freshwater reservoir offset of 340 ±20 14C years was measured for paired samples of freshwater shells and charcoal [64]. A FRE of 1,600 years in an Antarctic lake was probably caused by penguin guano, as the reservoir age of Antarctic sea water is between 1,000 and 1,700 years [23].
The degree of variability can expected to be lower for prehistoric samples, due to the absence of bomb 14C. However, some variability of the FRE has already been measured for Stone Age samples: the reservoir age on human bones from the graveyard of Ostorf varied between -103 and 835 years, only weakly correlated with δ13C and δ15N values, thus probably indicating different reservoir ages of e.g. fish from different lakes [13]. Also in archaeological fish bone from England, a time and space variable FRE has been measured [27]. Early Neolithic fish bones from Åkonge, Denmark, have a broad FRE range as well: 115–480 14C years [16]. Variations in the reservoir age of lakes are furthermore determined by variations of e.g. the ratio between lake surface and lake volume (i.e. water depth), as groundwater DIC can enter the lake from the total underground surrounding the lake, while atmospheric exchange only takes place on the surface [65]. If a river, which past FRE is to be reconstructed, runs through a lake, another complicating factor is therefore added to the temporal variability of the FRE.
δ13C values and the FRE
δ13C values of plants and animals from Alster and Trave span a large range between -34.2 and -13.2‰ (Table 2, Figure 3). When excluding the three most enriched values of one aquatic plant and two shell samples, a tendency can be seen: flora and fauna with more depleted δ13C values have older radiocarbon ages (Figure 3). The youngest samples have almost terrestrial δ13C values. This relation seems to be typical of water bodies in regions with developed soils, and it was already indicated many decades ago: Aquatic plants and organic lake mud have been measured to have δ13C values down to -30‰ [3], and fish that spent at least part of their live in freshwater systems were found to have δ13C values significantly more negative than marine fish [66].
In regions or periods with less soil organic matter in the watershed, higher δ13C values in the water and thus in the aquatic plants have to be expected. For example, aquatic plants from an early postglacial lake with age offsets of 1,500 to 2,000 years had average δ13C values of -15.3‰ [67]. This is caused by the fact that most of the CO2 for mineral weathering will be derived from the atmosphere in these cases, and not from decomposition of organic matter in the soil, as would be the case for mature vegetation and more developed soils [1, 68]. This might be the explanation for Early Mesolithic Danish pike and otter bones having δ13C values that would usually be classified as marine [62]. As a consequence, DIC δ13C in freshwater systems can vary greatly, and values between 0 and -25‰ have been measured [69].
Archaeological samples from Northern Germany
Archaeological samples from the sites Kayhude/Alster and Schlamersdorf/Trave were acquired from museum archives. Terrestrial samples, bones of freshwater fish, and pottery sherds with food crusts were selected for analysis. The radiocarbon dates of these samples are presented in Table 2 and Figure 4.
Radiocarbon ages of archaeological samples from Northern Germany. Uncalibrated radiocarbon ages BP of archaeological samples from Kayhude/Alster and Schlamersdorf/Trave, Northern Germany. Different sample types are marked with different colours. The graphs were made using OxCal 4.1.4 [75].
Kayhude/Alster
Two terrestrial samples, four food crusts on pottery and one freshwater fish bone from Kayhude were radiocarbon dated. The samples from Kayhude are believed to be contemporaneous, as they were found embedded in a stone layer (part of the soft ground close to the former river/lake had been stabilised by stones, and the dated samples originated from between those stones). Still, the two terrestrial samples have very different radiocarbon ages: 5440 and 9150 BP. The older sample must be an admixture from earlier layers, as it is older than the oldest finds of the entire Ertebølle culture. This exemplifies that this stone layer cannot be regarded as totally undisturbed. Direct 14C-dating of the pottery is thus necessary, as we cannot be sure which terrestrial samples are clearly associated with the pottery.
The pike bone collagen is about 3000 14C years older than the charcoal sample. Food crusts on pottery have the same or slightly larger 14C ages than the youngest terrestrial sample. None of the food crusts are as old as the fish bone.
The age divergence of the two terrestrial samples shows that the association of the samples is insecure. However, if we assume that the charcoal AAR-11480 gives the correct age of the find layer, then the food crust AAR-11479 is not affected by reservoir effects. For the three other food crusts, AAR-11403, AAR-11404 and AAR-14212, reservoir ages of the order of magnitude of 300 to 600 14C years can be estimated. Compared to the average reservoir age of modern Alster animals, 1060 ±520 14C years, this would indicate 30% to 60% aquatic ingredients in the food crust. If we assume that the pike bone AAR-11695 is contemporaneous with the charcoal and food crust samples, then the reservoir age in the Mesolithic at Kayhude would be about 3000 14C years. This is very high, but not unrealistic, when comparing with the largest 14C ages of modern plants and fish from this river. In this case, the reservoir ages of the food crusts AAR-11403, AAR-11404 and AAR-14212 would indicate only 10% to 20% aquatic ingredients. These are only thought experiments, though, and not secure calculations of percentage aquatic diet, due to the above-mentioned unsecurity of the context of the samples. If the charcoal sample was influenced by the old wood effect, for example, the reservoir effect calculated here would be underestimated by up to several hundred years.
The base-soluble fraction of three food crusts has also been dated. It may consist of partly original material, e.g. fatty substances [70], but also partly of contamination from the soil such as humic acid. The base-soluble fraction is in all cases older than the food crusts (Figure 4), indicating contamination with an older soil substance.
The calibrated ages of the three food crust samples are in the interval 5200–4000 cal BC, younger than the previously dated food crust sample with an age of 5400 cal BC [71].
Schlamersdorf/Trave
From Schlamersdorf at the river Trave, nine terrestrial samples, three fishbones and five food crusts on pottery were dated. The age range of terrestrial samples is very broad, about 1000 years (Figure 4). The food crusts have the same age as the terrestrial samples or are slightly older. The fishbone collagen is significantly older than the terrestrial samples. The terrestrial age range of Schlamersdorf complies with earlier charcoal dates from this site [72]. The broad age range measured here is unlikely to indicate an occupation period of 1000 years. The site was probably occupied repeatedly for shorter periods, as archaeological analysis indicated that the site was a hunting or fishing station. The broad terrestrial age range reveals the necessity of direct pottery dating: It is unclear whether the pottery from this site is associated with the older or with the younger terrestrial dates.
Three food crusts had previously been dated to around 5300 cal BC (6300–6100 uncal BP) [73]; their δ13C values between -28.6 and -31.9‰ indicate a possibility of freshwater ingredients and thus the possibility of a freshwater reservoir effect [74]. In some cases, also terrestrial ingredients can have such low δ13C values, e.g. caused by a canopy effect. However, this is unlikely, especially for δ13C = -31.9‰, as no terrestrial wood sample from Schlamersdorf has δ13C values below -29‰ (Table 2). Furthermore, the terrestrial animal with the lowest δ13C value, a red deer tooth collagen sample with δ13C = -23.6‰, would have a flesh value of about -29.1‰, assuming a flesh–bone collagen fractionation of 5.5‰. The δ13C value of one of the food crusts is thus significantly lower.
Two of the four food crusts radiocarbon dated from that site are from 5500–6000 BP (which would be about 4000–5000 cal BC), and two around 7000 BP (corresponding to an age range from 5600 to 6000 cal BC; Figure 4). However, as the average reservoir age in modern Trave animals is 1150 ±730 14C years, the old ages of the two oldest potsherds could have been caused by a reservoir effect. In case fish or other aquatic resources had been prepared in these pots, their reservoir age could likely be about one thousand 14C years. It is thus probable that the true ages of all the food crusts from Schlamersdorf are about the same, and lie within an interval of c. 4000–5000 cal BC.
An interesting case is the potsherd AAR-11481 of which both inner and outer crust have been dated. If one assumes that the outer crust is soot from the cooking fire, then it should give the date of cooking, or an older date in case old wood had been used. The reservoir effect would, in this case, be approximately 2000 years, or more, if the outer crust had been affected by an old wood effect. As this outer crust is younger than all the other terrestrial samples, it could be suspected to be influenced by modern contamination. However, if it had been modern contamination from the burial environment, from the handling during the excavation or later during storage in the archives, this contamination would be expected to have affected both sides of the sherd equally, if the carbon content of both samples was the same. Here, the carbon yield of the outer crust is with 4.8% significantly higher than that of the inner crust (1.7%). The outer crust would therefore be affected less by contamination. It is therefore unlikely that its surprisingly young age is caused by modern contamination.
In one of the sherds, AAR-11483, we were lucky to find some plant remains that presumably had been incorporated into the clay during the forming of the pottery. The 14C age of these plant remains is 6000 BP. The calibrated 2 σ age range is 4999–4766 cal BC (92.7%) and 4756–4729 cal BC (2.7%), calibrated with OxCal v4.1.2 [75] and the IntCal04 atmospheric curve [76]. The probability for the pottery being older than 5000 cal BC is thus less than 5%. Unfortunately, the food crust sample of AAR-11483 was lost during dating. It would otherwise have helped to measure the reservoir effect in food crusts directly, assuming that the time of forming and time of using the pottery were closely together.
The hardwater effect at Schlamersdorf and Kayhude seems to be larger than the effect reported by Fischer and Heinemeier (2003, [16]), at least for the fish bones. In their study area, the Åmose on Zealand, Denmark, the fish was 100 to 500 14C years older than the archaeological context, while the food crusts were up to 300 14C years older. However, the lack of clearly associated samples from Kayhude and Schlamersdorf makes it difficult to give more than rough estimates of the FRE.
Although some researchers doubt the existence of the FRE in food crusts on pottery [77], there seems to be more and more indications of its presence. For example, Sergant et al. 2006 [78] reported age offsets between pottery and short-lived terrestrial samples of several hundred years. Swifterbant pottery food crusts from a Belgian site were on average 320 ±159 14C years older than plant material, and only three food crust ages overlapped with the age range of terrestrial plants [15]. As all these food crusts had δ13C values below -25‰, the FRE was suggested to be the cause for the age offset [15]. On Åland, food crusts from Östra Jansmyra I and Vargstensslätten II were dated to around 5,000 BC, while hazelnut shells from Östra Jansmyra II were about 1,000 years younger [79]. The FRE might explain the surprisingly old food crust dates, although it is difficult to be certain, as the samples were not associated directly. Food crust dates on Estonian pottery with textile impressions were 1,000 years older than hitherto assumed [80].
The FRE is also a potential error source in radiocarbon dating of pottery from coastal sites, where a predominance of marine resources would be expected. On coastal Lithuanian sites such as Nida on the bank of the Currish Lagoon, δ13C values below -25‰ indicate freshwater resources, and food crust 14C dates appeared 400 to 500 years older than the earliest terrestrial dates from the same site [81]. Pottery from the Danish fjord sites Bjørnsholm and Norsminde showed evidence for the heating of fish oils, but interestingly, not for marine ingredients, in spite of the availiability of marine resources [82].
The marine reservoir effect in pottery should not be neglected, though. A special risk lies in the fact that partly marine food crusts can have the same δ13C values as the bone collagen of terrestrial animals. For example, δ13C values between -22.0 and -24.7‰ of food remains on pottery belonging to the Pitted Ware Culture were interpreted as reflecting terrestrial origin, although the radiocarbon dates were older than expected [83]. However, terrestrial plants and fat and flesh of terrestrial animals usually have more negative δ13C values, around ca. -25‰, while the bone collagen of terrestrial animals is more enriched. Food crust values which are more enriched than -25‰ indicate therefore the presence of marine resources. Similarly, the δ13C values of food crusts from Tybrind Vig, mean δ13C = -23 ±1‰, indicate a strong marine component [84], but were originally interpreted as being terrestrial [85].
FRE are also of possible concern in areas which are usually not connected with subsistence based on the exploitation of aquatic resources. Clay pots of the Catacomb Cultures of the North-West Caspian steppe, for example, contain evidence for fish processing such as bones and scale remains of freshwater fish [14]. Generally, fishing is almost always underrepresented in the archaeological record relative to traces of hunting [86].
Another complicating factor is the possibility of different pieces of food charring on different locations in the vessel. This has been found in experiments [31], but also in one prehistoric vessel: An age difference of 1100 years was measured on food crusts on sherds that were believed to belong to the same vessel [87]. Furthermore, some ingredients char more easily on the vessel walls than others [31, 60, 88].
Different experiments have shown that isotopic ratios of food only change slightly during cooking [88–92], and that food crust isotope ratios do not change during burial [89], or only change slightly [93]. Stable isotope measurements can therefore be useful for roughly distinguishing different food sources. It is important here not only to measure δ13C values, but also δ15N values, as “terrestrial” δ13C values can be the result of mixed marine and freshwater resources [61].
Sediment core samples from the Limfjord
As described in section “Materials and methods”, terrestrial samples and molluscs from the sediment core were radiocarbon dated, a terrestrial age model was constructed, and δR values were calculated. The radiocarbon results and the age model are shown in Figure 2.
The δR values range from -140 to 300 14C years (Figure 5), which is within the same order of magnitude as the values measured on 19th and 20th century (pre-bomb) shells from the Limfjord [28].
Palaeoenvironmental proxies and reservoir ages in the Limfjord. ΔR and supporting palaeoenvironmental proxies: δ13C, C/N and δ15N of bulk sediment organic matter, diatom-inferred salinity (DI-salinity) and percentage marine foraminifera species. The time axis is given as calibrated ages AD/BC. ΔR is the deviation from marine reservoir age, as described in section “Materials and methods”.
Based on the temporal variability of the local reservoir age deviation δR, the core has been visually divided into four time intervals, denoted zones 1–4 (Figure 5). This division is supported by other proxies, as described in [33] and [31]. Figure 5 displays the development of δR from c. 5400 BC to AD 700.
In zone 1, the reservoir age is slightly larger than the marine ‘model’ age. In zone 2, δR varies between -150 and +300 14C years, corresponding to reservoir ages between 250 and 700 14C years. Throughout zone 3, the reservoir age decreases slightly, but steadily, from small positive to small negative δR values. Variability increases again in zone 4.
In three cases, R direct can be calculated by comparing the 14C ages of a shell sample and a terrestrial sample from the same depth (Table 3). The differences between R direct and R(t) values are 8 ±151, -79 ±200 and 57 ±78 14C-years. The values thus agree within errors. There is no correlation between shell species and reservoir age, suggesting that species effects due to different feeding habits or burrowing depths have no significant influence on the reservoir age. A similar conclusion was reached by studies of three other Danish fjords [29] and the North Icelandic shelf [94]. In other studies, though, an influence of the habitat and diet of shellfish on the reservoir age has been observed (e.g. [95]).
During inferred marine conditions, it can be expected that the Kilen reservoir age R is c. 400 years (Δ R ≈ 0). More variable reservoir ages may be expected during inferred brackish conditions. Very high reservoir ages (Δ R>0) most likely indicate influence of 14C free carbonates, i.e. the hard-water effect, from groundwater or river discharge of dissolved carbonates. In contrast, low reservoir ages (Δ R<0) can be caused by increased CO2 exchange at the water-atmosphere boundary, or by surface-water runoff or mineralisation of contemporaneous terrestrial organic matter. Similar variations were found in other Danish fjords [29], with reservoir ages up to 900 years [28]. Other coastal environments show high reservoir ages as well: In a Swedish isostatically isolated basin, reservoir effects as high as R = 1,100 to 700 14C years were measured on clay gyttja that was deposited during the most saline coastal Litorina phase [96]. On the coast of Oman, a reservoir age of 645 ±40 14C years was measured on samples from graves from the 4th millennium BC [97].
In Norwegian mollusc samples, freshwater influence lowered the reservoir effect [98]: reservoir ages were found to be lower in the fresher, uppermost surface water along the inner coast and in the fjords (δR between -150 and -100 years). Also on the coast of central Queensland, Australia, estuarine 14C dates are highly complex due to variations in terrestrial carbon input and exchange with the open ocean [30].
Lastly, variations in the marine reservoir age itself should be kept in mind. Small fluctuations in the Kilen reservoir age might be result of these variations. However, this is more likely to happen in regions with variations in the upwelling of deep-sea water [95, 99, 100].
The supporting proxies presented in Figure 5 are stable isotope measurements on bulk sediment organic matter: δ13C, C/N ratio and δ15N; salinity reconstructed from diatom assemblages; and the percentage of all marine foraminifera species [33]. δ15N values most likely reflect δ15N values of source organic matter. Increasing δ15N values after c. 4000 cal. BP (c. 2000 BC) are here interpreted as a manuring signal from the surrounding grassland, due to increased dependence on cattle farming [33]. δ13C values and C/N ratios are strongly correlated [33]. They indicate source organic matter and distinguish between allochthonous terrestrial organic matter and autochthonous organic matter. A linear mixing of marine and terrestrial organic matter can be observed.
The percentage of marine foraminifera species indicates bottom-water salinity [33, 36]. The surface-water salinity was reconstructed from diatoms [36]. The δ13C values also correlate with a diatom-inferred quantitative reconstruction of surface salinity and can thus be used as a proxy for salinity estimation in the photic zone. During brackish conditions, sediment organic matter is dominated by terrestrial input, whereas marine conditions enhance autochthonous production [33]. The potential of sediment δ13C values as salinity proxy was already suggested by Hedenström and Possnert, 2001 [96], and further explored by e.g. Mackie et al. [101, 102].
The salinity changes observed in zones 3 to 4 are suggested to show increased marine influence in the western part of the Limfjord (through the western opening of the fjord towards the North Sea), whereas the northern openings diminished as a result of isostatic uplift, aeolian sand transport and redeposition of sediment by ocean currents, mainly the Jutland Current. Additionally, reduced connection of Kilen to the Limfjord should be considered. Further work from sites in the northern Limfjord is needed, however, to explore this.
As the reservoir ages are highly variable in zones 1, 2 and 4, no single value for a reservoir correction can be obtained. Between 5000 and 2000 cal yr BP, however, a marine reservoir age of δR=0 (R=400 14C years) can be applied to samples from the Limfjord.
Conclusion
In modern river samples, the freshwater reservoir effect is large and variable even on short time scales. The reservoir age of water DIC depends on precipitation amounts prior to sampling. Differences between adjacent rivers can be caused by differences in residence time, or differences in concentrations of 14C-deficient carbonates or organic material in the watershed. The radiocarbon age range of modern aquatic plants spans more than 2000 14C years. This is most likely caused by the multitude of carbon sources available for these plants, including different DIC species, atmospheric CO2, and CO2 from decaying vegetation in the river sediments or in the catchment. It should be stressed that floating leaves of aquatic plants, although assimilating atmospheric CO2, can not be regarded as terrestrial samples. These results indicate that it is impossible to find a single freshwater reservoir age for a given river system. A few samples of water, plants or fish from a river are not sufficient to characterise the 14C age of a water body. However, the freshwater reservoir effect might still be “correctable” for archaeological samples: Reservoir age fluctuations are expected to be less pronounced for pre-bomb samples; organic matter with an actual age of a few decades can be heavily affected by bomb carbon and thus reduce a sample’s radiocarbon age significantly. Furthermore, samples accumulating carbon over longer time scales, such as human bones, show average reservoir ages. These might be quite uniform for individuals with similar nutrition habits.
Analyses on archaeological samples indicate the necessity of direct pottery dating, as securely associated terrestrial samples are difficult to find for the assumedly earliest pottery in Northern Germany. A freshwater reservoir effect is likely for the food crusts on pottery from the Ertebølle sites Kayhude and Schlamersdorf. A strong indicator for this is a sherd where both inner and outer crust have been dated, yielding an age difference of approximately 2000 years. The true age of the pottery at Schlamersdorf might be indicated by the radiocarbon date of a plant remain found within the ceramic matrix. A radiocarbon age of about 6000 BP implies that the pottery most likely was produced after 5000 cal BC. In all probability, the earliest pottery from inland sites in Schleswig-Holstein has the same age as Ertebølle pottery from coastal sites. The origins of pottery in Schleswig-Holstein can thus equally likely derive from Eastern European hunter-gatherer pottery traditions, as well as from southwestern influences from agricultural communities in central Germany.
Reservoir age measurements from a core from the Limfjord exemplify that freshwater influence can cause fluctuations of the coast-near marine reservoir ages of up to several hundred years. Freshwater influence can both increase and decrease the reservoir age. A marine reservoir correction can thus not be applied to estuarine samples. So far, stable isotope measurements on shells or sediment organic matter can not be used to predict the reservoir effect. The variable coastal reservoir effect should be kept in mind when radiocarbon dating marine samples, pottery or human bones from coastal sites, as coast-near fishing and shell collection are ascertained for many prehistoric periods.
References
Clark ID, Fritz P: Environmental Isotopes in Hydrogeology. 1997, New York, Boca Raton: Lewis Publishers, CRC Press LLC
Broecker WS, Walton A: The geochemistry of C14 in fresh-water systems. Geochimica et Cosmochimica Acta. 1959, 16: 15-38. 10.1016/0016-7037(59)90044-4.
Oana S, Deevey ES: Carbon 13 in lake waters and its possible bearing on paleolimnology. Am J Sci. 1960, 258 (A): 253-272.
Godwin H: Comments on radiocarbon dating samples from the British Isles. Am J Sci. 1951, 249: 301-307. 10.2475/ajs.249.4.301.
Deevey ES, Gross MS, Hutchinson GE, Kraybill HL: The Natural C14 contents of materials from hard-water lakes. PNAS - Proc Natl Acad Sci USA. 1954, 40: 285-288. 10.1073/pnas.40.5.285.
Revelle R, Suess HE: Carbon dioxide exchange between atmosphere and ocean and the question of an increase of atmospheric CO2 during the past decades. Tellus. 1957, 9: 18-27. 10.1111/j.2153-3490.1957.tb01849.x.
Craig H: The natural distribution of radiocarbon and the exchange time of carbon dioxide between atmosphere and sea. Tellus. 1957, 9: 1-17. 10.1111/j.2153-3490.1957.tb01848.x.
Arnold JR, Anderson EC: The distribution of C14 in nature. Tellus. 1957, 9: 28-32. 10.1111/j.2153-3490.1957.tb01850.x.
Lanting JN, van der Plicht J: Wat hebben Floris V, skelet swifterbant S2 en visotters gemeen?. Palaeohistoria. 1995/1996, 37/38: 491-519.
Cook GT, Bonsall C, Hedges REM, McSweeney K, Boroneant V, Pettitt PB: A freshwater diet-derived 14C reservoir effect at the stone age sites in the Iron Gates Gorge. Radiocarbon. 2001, 43 (2A): 453-460.
Smits L, van der Plicht H: Mesolithic and Neolithic human remains in the Netherlands: physical anthropological and stable isotope investigations. J Archaeology Low Tries. 2009, 1: 55-85.
Olsen J, Heinemeier J: AMS dating of human bone from the Ostorf cemetery in the light of new information on dietary habits and freshwater reservoir effects. Innovation and Continuity. Non-Megalithic Mortuary Practices in the Baltic. Workshop Schwerin 24.-25. April 2006, Berichte der Römisch-Germanischen Kommission. Edited by: Larsson L, Lüth F, Terberger T. 2009, Darmstadt/Mainz: Philipp von Zabern
Olsen J, Heinemeier J, Lübke H, Lüth F, Terberger T: Dietary habits and freshwater reservoir effects in bones from a Neolithic Northern German cemetery. Radiocarbon. 2010, 52 (2–3): 635-644.
Shishlina NI, Van der Plicht J, Hedges REM, Zazovskaya EP, Sevastyanov VS, Chichagova OA: The catacomb cultures of the north-west Caspian steppe: 14C chronology, reservoir effect, and paleodiet. Radiocarbon. 2007, 49 (2): 713-726.
Boudin M, Strydonck MV, Crombé P: Radiocarbon dating of tery food crusts: reservoir effect or not? The case of Swifterbant pottery from Doel “Deurganckdok” (Belgium). Chronology and Evolution in the Mesolithic of North-West Europe. Proceedings of an International Meeting, Brussels, May 30-June 1st 2007. Edited by: Crombé P, Strydonck MV, Sergant J, Boudin M, Bats M. 2009, Newcastle upon Tyne: Cambridge Scholars Publishing, 753-772.
Fischer A, Heinemeier J: Freshwater reservoir effect in 14C dates of food residue on pottery. Radiocarbon. 2003, 45 (3): 449-466.
Philippsen B: Terminal mesolithic diet and radiocarbon dating at inland sites in Schleswig-Holstein. Landscapes and Human Development: The Contribution of European Archaeology. Proceedings of the International Workshop “Socio-Environmental Dynamics over the Last 12,000 Years: The Creation of Landscapes (1st - 4th April 2009)”, Volume 191 of Universitätsforschungen zur prähistorischen Archäologie. Aus der Graduiertenschule “Human Development in Landscapes” der Universität Kiel. 2010, Bonn: Dr. Rudolf Habelt GmbH, 21-36.
Philippsen B, Kjeldsen H, Hartz S, Paulsen H, Clausen I, Heinemeier J: The hardwater effect in AMS 14C dating of food crusts on pottery. Nucl Instrum Methods Phys Res Sect B: Beam Interact Mater Atoms. 2010, 268 (7–8): 995-998.
MacDonald GM, Beukens RP, Kieser WE, Vitt DH: Comparative radiocarbon dating of terrestrial plant macrofossils and aquatic moss from the “ice-free corridor” of western Canada. Geology. 1987, 15 (9): 837-840. 10.1130/0091-7613(1987)15<837:CRDOTP>2.0.CO;2.
Sveinbjörnsdóttir AE, Heinemeier J, Árnórsson S: Origin of 14C in Icelandic groundwater. Radiocarbon. 1995, 37 (2): 551-565.
Sveinbjörnsdottir AE, Heinemeier J, Rud N, Johnsen S: 14C anomalies observed for plants growing in Icelandic geothermal waters. Radiocarbon. 1992, 34 (3): 696-703.
Håkansson S: Radiocarbon activity in submerged plants from various South Swedish lakes. Radiocarbon dating - ninth international conference. Edited by: Berger R, Suess HE. 1976, Los Angeles and La Jolla: University of California Press, 433-443.
Björk S, Wohlfarth B: 14C chronostratigraphic techniques in paleolimnology. Basin Analysis, Coring, and Chronological Techniques, Volume 1 of Tracking Environmental Change Using Lake Sediments. Edited by: Last WM, Smol JP. 2001, Dordrecht: Kluwer Academic Publishers
Boaretto E, Thorling L, Sveinbjörnsdottir AE, Yechieli Y, Heinemeier J: Study of the effect of fossil organic carbon on 14C in groundwater from Hvinningdal, Denmark. Radiocarbon. 1998, 40 (2): 915-920.
Srdoč D, Obelic B, Horvatinčic N, Sliepčevic A: Radiocarbon dating of calcareous tufa: how reliable data can we expect?. Radiocarbon. 1980, 22 (3): 858-862.
Olsson IU, Kaup E: The varying radiocarbon activity of some recent submerged Estonian plants grown in the early 1990s. Radiocarbon. 2001, 43 (2B): 809-820.
Keaveney EM, Reimer PJ: Understanding the variability in freshwater radiocarbon reservoir offsets: a cautionary tale. J Archaeological Sci. 2012, 39 (5): 1306-1316. 10.1016/j.jas.2011.12.025. [http://dx.doi.org/10.1016/j.jas.2011.12.025]
Heier-Nielsen S, Heinemeier J, Nielsen HL, Rud N: Recent reservoir ages for Danish Fjords and marine waters. Radiocarbon. 1995, 37 (3): 875-882.
Olsen J, Rasmussen P, Heinemeier J: Holocene temporal and spatial variation in the radiocarbon reservoir age of three Danish fjords. Boreas. 2009, 38 (3): 458-470. 10.1111/j.1502-3885.2009.00088.x.
Ulm S: Marine and estuarine reservoir effects in central Queensland, Australia: determination of δR values. Geoarchaeology. 2002, 17 (4): 319-348. 10.1002/gea.10017.
Philippsen B: Variability of freshwater reservoir effects: Implications for radiocarbon dating of prehistoric pottery and organisms from estuarine environments. PhD thesis. Aarhus Universitet, 2012
Philippsen B, Heinemeier J: Freshwater reservoir effect variability in Northern Germany. Radiocarbon. 2013, 55 (3–4):
Philippsen B, Olsen J, Lewis JP, Rasmussen P, Ryves DB, Knudsen KL: Mid- to late-Holocene reservoir age variability and isotope-based palaeoenvironmental reconstruction in the Limfjord, Denmark. Holocene. 2013, 23 (7): 1015-1025.
Ringkjøbing Amtskommune, Teknik- og Miljøforvaltningen: Kilen. Miljøovervågning 1989. 1991, Vandmiljøovervågning
Stewig R: Landeskunde von Schleswig-Holstein, Volume 5 of Geocolleg. 1982, Berlin, Stuttgart: Gebrüder Borntraeger
Lewis JP, et al: Environmental change in the Limfjord, Denmark (ca 7,500-1,500 cal yrs BP): a multiproxy study. Quaternary Sci Rev. 2013, http://dx.doi.org/10.1016/j.quascirev.2013.05.020,
Lewis J: Holocene environmental change in coastal Denmark: interactions between land, sea and society. PhD thesis. Loughborough University, 2011
Longin R: New method of collagen extraction for radiocarbon dating. Nature. 1971, 230: 241-242. 10.1038/230241a0.
Brown TA, Nelson DE, Vogel JC, Southon JR: Improved collagen extraction by improved Longin method. Radiocarbon. 1988, 30: 171-177.
Jørkov MLS, Heinemeier J, Lynnerup N: Evaluating bone collagen extraction methods for stable isotope analysis in dietary studies. J Archaeological Sci. 2007, 34 (11): 1824-1829. 10.1016/j.jas.2006.12.020. [http://dx.doi.org/10.1016/j.jas.2006.12.020]
Jowsey PC: An improved peat sampler. New Phytol. 1966, 65 (2): 245-248. 10.1111/j.1469-8137.1966.tb06356.x.
Vogel JS, Southon JR, Nelson DE, Brown TA: Performance of catalytically condensed carbon for use in accelerator mass spectrometry. Nucl Instrum Methods Phys Res Section B: Beam Interact Mater Atoms. 1984, 5 (2): 289-293. 10.1016/0168-583X(84)90529-9.
Stuiver M, Polach HA: Discussion. Reporting of 14C data. Radiocarbon. 1977, 19 (3): 355-363.
Ramsey CB: Deposition models for chronological records. Quaternary Sci Rev. 2008, 27 (1–2): 42-60.
Reimer PJ, Baillie MGL, Bard E, Bayliss A, Beck JW, Blackwell PG, Bronk Ramsey C, Buck CE, Burr GS, Edwards RL, Friedrich M, Grootes PM, Guilderson TP, Hajdas I, Heaton TJ, Hogg AG, Hughen KA, Kaiser KF, Kromer B, McCormac FG, Manning SW, Reimer RW, Richards DA, Southon JR, Talamo S, Turney CSM, van der Plicht J, Weyhenmeyer CE: IntCal09 and Marine09 radiocarbon age calibration curves, 0–50,000 years cal BP. Radiocarbon. 2009, 51 (4): 1111-1150.
de Vries Hd: Atomic bomb effect: Variation of radiocarbon in plants, shells, and snails in the past 4 years. Science. 1958, 128 (3318): 250-251. 10.1126/science.128.3318.250.
Rafter TA, Fergusson GJ: “Atom bomb effect”–Recent increase of carbon-14 content of the atmosphere and biosphere. Science. 1957, 126 (3273): 557-558. 10.1126/science.126.3273.557.
Levin I, Naegler T, Kromer B, Diehl M, Francey RJ, Gomez-Pelaez AJ, Steele LP, Wagenbach D, Weller R, Worthy DE: Observations and modelling of the global distribution and long-term trend of atmospheric 14CO2. Tellus. 2010, 62 B: 26-46. [Tellus B]
Levin I, Hammer S, Kromer B, Meinhardt F: Radiocarbon observations in atmospheric CO2: Determining fossil fuel CO2 over Europe using Jungfraujoch observations as background. Sci Total Environ. 2008, 391 (2–3): 211-216.
Galimov EM: Carbon isotopes in soil CO2. Geochem Int. 1966, 3: 889-898. [Translated from Geokhimiya No. 9, pp.1110–1118, 1966]
Nixdorf B, Hemm M, Hoffmann A, Richter P: Dokumentation von Zustand und Entwicklung der wichtigsten Seen Deutschlands. 2003, Cottbus: Brandenburg University of Technology
Olsson IU, El-Gammal S, Göksu Yeter: Uppsala natural radiocarbon measurements IX. Radiocarbon. 1969, 11 (2): 515-544.
Olsson IU, Klasson M: Uppsala radiocarbon measurements X. Radiocarbon. 1970, 12: 281-284.
Dacey JWH: Internal winds in water lilies: an adaptation for life in anaerobic sediments. Science. 1980, 210 (4473): 1017-1019. 10.1126/science.210.4473.1017.
Farmer AM: Carbon uptake by roots. Plant Roots: The hidden half. Edited by: Waisel Y, Eshel A, Kafkaki U. 1996, New York: Marcel Dekker, Inc, 679-689.
Levin I, Kromer B: The tropospheric Δ14C level in mid-latitudes of the Northern Hemisphere (1959–2003). Radiocarbon. 2004, 46 (3): 1261-1272.
Törnqvist TE, de Jong AFM, Oosterbaan WA, Van der Borg K: Accurate dating of organic deposits by AMS 14C measurement of macrofossils. Radiocarbon. 1992, 34 (3): 566-577.
Keeley JE, Sandquist DR: Carbon: freshwater plants. Plant, Cell Environ. 1992, 15 (9): 1021-1035. 10.1111/j.1365-3040.1992.tb01653.x.
Keaveney EM: Investigations into Freshwater Radiocarbon Reservoir Offsets from Britain and Ireland. Dissertation. Queen’s University, 2009.
Philippsen B: Der Süßwasser-Reservoireffekt in der 14C-Datierung: neue Analysen und mesolithische Kochexperimente. Experimentelle Archäologie in Europa - Bilanz, Volume. 2013, Unteruhldingen: Europäische Vereinigung zur Förderung der Experimentellen Archäologie / European Association for the advancement of archaeology by experiment e.V. in press
Lanting JN, van der Plicht J: Reservoir effects and apparent ages. J Irish Archaeol. 1998, 9: 151-165.
Fischer A, Olsen J, Richards M, Heinemeier J, Sveinbjörnsdottir AE, Bennike P: Coast-inland mobility and diet in the Danish Mesolithic and Neolithic: evidence from stable isotope values of humans and dogs. J Archaeological Sci. 2007, 34: 2125-2150. 10.1016/j.jas.2007.02.028.
Higham T, Warren R, Belinskij A, Härke H: Radiocarbon dating, stable isotope analysis, and diet-derived offsetes in 14C ages from the Klin-Yar site, Russian North Caucasus. Radiocarbon. 2010, 52 (2–3): 653-670.
Culleton BJ: Implications of a freshwater radiocarbon reservoir correction for the timing of late Holocene settlement of the Elk Hills, Kern County, California. J Archaeological Sci. 2006, 33: 1331-1339. 10.1016/j.jas.2006.01.013.
Geyh MA, Schotterer U, Grosjean M: Temporal changes of the 14C reservoir effect in lakes. Radiocarbon. 1998, 40 (2): 921-931.
Schoeninger MJ, DeNiro MJ: Nitrogen and carbon isotopic composition of bone collagen from marine and terrestrial animals. Geochimica et Cosmochimica Acta. 1984, 48: 625-639. 10.1016/0016-7037(84)90091-7.
Day SP: Dogs, deer and diet at Star Carr: a reconsideration of C-isotope evidence from Early Mesolithic dog remains from the Vale of Pickering, Yorkshire, England. J Archaeological Sci. 1996, 23 (5): 783-787. 10.1006/jasc.1996.0072.
Turney CSM: Lacustrine bulk organic δ13C in the British Isles during the last glacial-holocene transition (14-9 ka 14C BP). Arctic, Antarctic, Alpine Res. 1999, 31: 71-81. 10.2307/1552624.
Tan FC: Stable carbon isotopes in dissolved organic carbon in marine and estuarine environments. The Marine Environment, A, Volume 3 of Handbook of Environmental Isotope Geochemistry. Edited by: Fritz P, Fontes JC. 1989, Amsterdam, Oxford, New York, Tokyo: Elsevier, 171-190.
Hallgren F, Possnert G: Pottery design and time. The pottery from the TRB site Skogsmossen, in view of the AMS-datings of organic remains on potsherds. Tor. 1997, 29: 113-136.
Clausen I: Steinzeitliches Alstervergnügen. Archäologie in Deutschland. 2007, 2: 54-
Hartz S: Inland-Ertebølle in Schleswig-Holstein. Die Fundstelle Schlamersdorf LA5, Kr. Stormarn. Archäologie in Schleswig [Symposium Wohlde]. 1993, 1/1991: 33-38.
Hartz S: Zehnter Arbeitsbericht des Archäologischen Landesamtes Schleswig-Holstein. Grabungsberichte der Jahre 1988–1993: Göksu, Travenbrück (Altgemeinde Schlamersdorf), Kr. Stormarn, Steinzeitliche Wohnplätze Travenbrück, LA5 und LA15. Offa. 1996, 53: 374-378.
Hartz S, Heinrich D, Lübke H: Coastal farmers – the neolithisation of northernmost Germany. The Neolithisation of Denmark. 150 years of debate. Edited by: Fischer A, Kristiansen K. 2002, Sheffield: J.R. Collis Publications, 321-340.
Bronk Ramsey C: Bayesian analysis of radiocarbon dates. Radiocarbon. 2009, 51: 337-360.
Reimer PJ, Baillie MGL, Bard E, Bayliss A, Beck JW, Bertrand CJH, Blackwell PG, Buck CE, Burr GS, Cutler KB, Damon PE, Edwards RL, Fairbanks RG, Friedrich M, Guilderson TP, Hogg AG, Hughen KA, Kromer B, McCormac G, Manning S, Bronk Ramsey C, Reimer RW, Remmele S, Southon JR, Stuiver M, Talamo S, Taylor FW, van der Plicht J, Weyhenmeyer CE: IntCal04 terrestrial radiocarbon age calibration, 0–26 cal kyr BP. Radiocarbon. 2004, 46 (3): 1029-1058.
Hart JP, Lovis WA: The freshwater reservoir and radiocarbon dates on cooking residues: old apparent ages or a single outlier? comments on Fischer and Heinemeier (2003). Radiocarbon. 2007, 49 (3): 1403-1410.
Sergant J, Crombé P, Perdaen Y: The sites of Doel “Deurganckdok” and the mesolithic/neolithic transition in the Sandy Lowlands of Belgium. La Néolithisation / The Neolithisation Process. Actes du XIVème Congrès UISPP, Université de Liège, Belgique, 2–8 Septembre 2001, Volume 1520 of BAR International Series. Edited by: van Berg G. 2006, Oxford: Archaeopress, 53-60.
Hallgren F: The introduction of ceramic technology around the Baltic Sea in the 6th millennium. Coast to coast - arrival. Proceedings of the Final Coast to Coast Conference 1–5 Oct. 2002 in Falköping, Sweden. Edited by: Knuttson H. 2004, Uppsala: Coast to Coast Project, 123-142.
Kriiska A, Lavento M, Peets J: New AMS dates of the neolithic and bronze age ceramics in Estonia: preliminary results and interpretations. Estonian J Archaeology. 2005, 9: 3-31.
Pilic̆iauskas G, Lavento M, Oinonen M, Griz̆as G: New 14C dates of neolithic and early metal period ceramics in Lithuania. Radiocarbon. 2011, 53 (4): 629-643.
Heron C, Craig OE, Forster M, Stern B, Andersen SH: Residue analysis of ceramics from prehistoric shell middens in Denmark: Initial investigations at Norsminde and Bjørnsholm. Shell Middens in, Atlantic Europe. Edited by: Milner N, Craig OE, Bailey GN. 2007, Norwich: Oxbow Books, 78-85.
Segerberg A, Possnert G, Arrhenius B, Lidén K: Ceramic chronology in view of 14C datings. Laborativ Arkeologi. 1991, 5: 83-91.
Craig OE, Forster M, Andersen SH, Koch E, Crombé P, Milner NJ, Stern B, Bailey GN, Heron CP: Molecular and isotopic demonstration of the processing of aquatic products in Northern European prehistoric pottery. Archaeometry. 2007, 49: 135-152. 10.1111/j.1475-4754.2007.00292.x.
Andersen SH, Malmros C: Madskorpe på Ertebøllekar fra Tybrind Vig. Aarbøger for Nordisk Oldkyndighed og Historie. 1984, 1984: 78-95.
Fischer A, Richards M, Olsen J, Robinson DE, Bennike P, Kubiak-Martens L, Heinemeier J: The composition of mesolithic food - evidence from a submerged settlement on the Argus Bank, Denmark. Acta Archaeologica. 2007, 78 (2): 163-178. 10.1111/j.1600-0390.2007.00104.x.
Nakamura T, Taniguchi Y, Tsuji S, Oda H: Radiocarbon dating of charred residues on the earliest pottery in Japan. Radiocarbon. 2001, 43 (2B): 1129-1138.
Morton JD, Schwarcz HP: Palaeodietary implications from stable isotopic analysis of residues on prehistoric Ontario ceramics. J Archaeological Sci. 2004, 31 (5): 503-517. 10.1016/j.jas.2003.10.001.
Hastorf CA, DeNiro MJ: Reconstruction of prehistoric plant production and cooking practices by a new isotopic method. Nature. 1985, 315: 489-491. 10.1038/315489a0.
Katzenberg MA, Saunders SR, Abonyi S: Bone chemistry, food and history: a case study from 19th century upper Canada. Biogeochemical Approaches to, Paleodietary Analysis. Edited by: Ambrose SH, Katzenberg MA. 2000, New York: Kluwer Academic/Plenum Publishers, 1-22.
Abonyi S: The effects of processing on stable isotope levels and mineral concentration in foods: implications for Palaeodietary reconstruction. PhD thesis. University of Calgary, 1993
Bonsall C, Lennon R, McSweeney K, Stewart C, Harkness D, Boroneant V, Bartosiewicz L, Payton R, Chapman J: Mesolithic and early neolithic in the Iron Gates: a palaeodietary perspective. J Eur Archaeology. 1997, 5: 50-92.
Whitney SE: A stable isotope examination of food residues on contemporary and archaeological pottery from southern Somalia. PhD thesis. Athens
Eiríksson J, Larsen G, Knudsen KL, Heinemeier J, Símonarson LA: Marine reservoir age variability and water mass distribution in the Iceland Sea. Quaternary Sci Rev. 2004, 23: 2247-2268. 10.1016/j.quascirev.2004.08.002.
Petchey F, Ulm S: Marine reservoir variation in the Bismarck region: an evaluation of spatial and temporal change in δR and R over the last 3000 years. Radiocarbon. 2012, 54: 45-58. 10.2458/azu_js_rc.v54i1.13050.
Hedenström A, Possnert G: Reservoir ages in Baltic Sea sediment - a case study from the Litorina stage. Quaternary Sci Rev. 2001, 20: 1779-1785. 10.1016/S0277-3791(01)00069-5.
Zazzo A, Munoz O, Saliège JF, Moreau C: Variability in the marine radiocarbon reservoir effect in Muscat (Sultanate of Oman) during the 4th millennium, BC: reflection of taphonomy or environment?. J Archaeological Sci. 2012, 39 (7): 2559-2567. 10.1016/j.jas.2012.01.043.
Mangerud J, Bondevik S, Gulliksen S, Hufthammer AK, Høisæter T: Marine 14C reservoir ages for 19th century whales and mollusks from the North Atlantic. Quaternary Sci Rev. 2006, 25: 3228-3245. 10.1016/j.quascirev.2006.03.010.
Soares AMM, Martins JMM: Radiocarbon dating of marine shell samples. The marine radiocarbon reservoir effect of coastal waters off Atlantic Iberia during Late Neolithic and Chalcolithic Periods. J Archaeological Sci. 2009, 36: 2875-2881. 10.1016/j.jas.2009.09.027.
Culleton BJ, Kennet DJ, Ingram BL, Erlandson JM, Southon JR: Intrashell radiocarbon variability in marine mollusks. Radiocarbon. 2006, 48: 387-400.
Mackie EAV, Leng MJ, Lloyd JM, Arrowsmith C: Bulk organic δ13C and C/N ratios as palaeosalinity indicators within a Scottish isolation basin. J Quaternary Sci. 2005, 20 (4): 303-312. 10.1002/jqs.919.
Mackie EAV, Lloyd JM, Leng MJ, Bentley MJ, Arrowsmith C: Assessment of δ13C and C/N ratios in bulk organic matter as palaeosalinity indicators in Holocene and Lateglacial isolation basin sediments, northwest Scotland. J Quaternary Sci. 2007, 22 (6): 579-591. 10.1002/jqs.1081.
Acknowledgements
I would like to thank my PhD supervisors Jan Heinemeier and Jesper Olsen for their support with the project about the freshwater reservoir effect in Northern Germany (JH) and the project about the Limfjord (JO). Furthermore, I would like to thank Sönke Hartz and Ingo Clausen for providing archaeological samples, Sönke Hartz for assistance with collecting modern samples from rivers, and the staff at the AMS 14C Dating Centre, Aarhus, and 14Chrono, Belfast, for their support. Three reviewers provided useful comments that helped to improve this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Philippsen, B. The freshwater reservoir effect in radiocarbon dating. herit sci 1, 24 (2013). https://doi.org/10.1186/2050-7445-1-24
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2050-7445-1-24