Soil-structure interaction modeling effects on seismic response of cable-stayed bridge tower

Abstract

A nonlinear dynamic analysis, including soil-structure interaction, is developed to estimate the seismic response characteristics and to predict the earthquake response of cable-stayed bridge towers with spread foundation. An incremental iterative finite element technique is adopted for a more realistic dynamic analysis of nonlinear soil-foundation-superstructure interaction system under great-earthquake ground motion. Two different approaches to model soil foundation interaction are considered: nonlinear Winkler soil foundation model and linear lumped-parameter soil model. The numerical results show that the simplified lumped-parameter-model analysis provides a good prediction for the peak response, but it overestimates the acceleration response and underestimates the uplift force at the anchor between superstructure and pier. The soil bearing stress beneath the footing base is dramatically increased due to footing base uplift. The predominant contribution to the vertical response at footing base resulted from the massive foundation rocking rather than from the vertical excitation.

Introduction

Long-span bridges, such as cable-stayed bridge structural systems, provide a valuable environment for the nonlinear behavior due to material and geometrical nonlinearities of the structures of relatively large deflection and forces (Ali and Abdel-Ghaffar 1995; Abdel Raheem and Hayashikawa 2003; Committee of Earthquake Engineering 1996). The Hyogoken-Nanbu (Kobe, Japan) earthquake on 17 January 1995 led to an increased awareness concerning the response of highway bridges subjected to earthquake ground motions. The dynamic analyses and ductility design have been reconsidered by Japan Road Association (Committee of Earthquake Engineering 1996; Japan Road Association 1996a, 1996b). Necessity has arisen to develop more efficient analysis procedures, which can lead to a thorough understanding and a realistic prediction of the nonlinear dynamic response of the bridge structural systems, to improve the bridge seismic performances.

Current design practice does not account for the nonlinear behavior of soil-foundation interface primarily due to the absence of reliable nonlinear soil-structure interaction modeling techniques that can predict the permanent and cyclic deformations of the soil as well as the effect of nonlinear soil-foundation interaction on the response of structural members. Safe and economic seismic designs of bridge structures directly depend on the understanding level of seismic excitation and the influence of supporting soil on the structural dynamic response. Long-span bridges are more susceptible to relatively severe soil-structure interaction effect during earthquakes when compared to buildings due to their spatial extent, varying soil condition at different supports, and possible incoherence in the seismic input. The necessity of incorporating soil-structure interaction in the design of a wide class of bridge structures has been pointed out by several post-earthquake investigations, experimental, and analytical studies (Committee of Earthquake Engineering 1996; Vlassis and Spyrakos 2001; Trifunac and Todorovska 1996; Megawati et al. 2001). Recently, several cable-stayed bridges have been constructed on relatively soft ground, which results in a great demand to evaluate the effect of soil-structure interaction on the seismic behavior of bridges and properly reflect it on seismic design to accurately capture the response, enhance the safety level, and reduce design and construction costs.

Due to material and geometrical nonlinearities, the dynamic characteristics of soil-structure system are changed during a severe earthquake. These nonlinearities are sometimes treated using an equivalent linear model (Abdel Raheem et al. 2002; Chaojin and Spyrakos 1996; Spyrakos 1997). However, the dynamic characteristics of soil-structure system are dependent on the soil stress level during a severe earthquake (Ahn and Gould 1992; Gazetas and Dobry 1984; Kobayashi et al. 2002). Foundation rocking and uplifting are important for short-period structures on a relatively soft soil site (Yim and Chopra 1984; Harden et al. 2006). For nonlinear structures, effects of soil-structure interaction due to rocking can result in significantly larger ductility demands under certain conditions (Tang and Zhang 2011; Zhang and Tang 2009). These findings necessitate the evaluation of structural responses considering soil-structure interaction using foundation models that can realistically capture the nonlinear force, displacement behaviors, and energy dissipation mechanisms. Nonlinear foundation movements and associated energy dissipation may be utilized to reduce force and ductility demands of a structure, particularly in high-intensity earthquake events (Raychowdhury 2011).

The purpose of this study is to assess the effects of soil-structure interaction on the seismic response and dynamic performance of the cable-stayed bridge towers with spread foundation. An incremental iterative finite element technique for a more realistic dynamic analysis of nonlinear soil-foundation-superstructure system subjected to earthquake ground motion is developed. Two different modeling approaches, nonlinear Winkler soil model and linear lumped-parameter soil model, for the soil foundation interaction are investigated. The seismic responses of the nonlinear Winkler soil model are compared to those of the simplified linear lumped-parameter model. In the lumped-parameter soil model, the soil-structure interaction is simulated with translational, rotational, and their coupling linear springs acting at the centroid of the spread foundation at footing base level. While in the nonlinear Winkler soil model, the soil structure interaction is simulated with continuous spring system (Winkler) along the embedded depth of tower pier and underneath the spread foundation. Soil strain-dependent material nonlinearity is considered through hysteretic element, while geometrical nonlinearity by basemat uplift is considered through a gap element. The massive pier of the tower model activates rocking response of the spread foundation under strong earthquake ground motion, hence, results in the foundation uplift and yield of the underlying soil (Kawashima and Hosoiri 2002; Gelagoti et al. 2012). The results of the nonlinear Winkler-soil-model approach are compared with those from the linear lumped-soil-model approach.

Methods

Finite element analysis procedure

Three-dimensional beam element tangent stiffness

A nonlinear dynamic finite element technique is developed to analyze the elastoplastic dynamic response of frame structures under strong earthquake excitation, in which the nonlinear three-dimensional beam elements are employed. A three-dimensional beam element has six degrees of freedom at each node, in which all couplings among bending, twisting, and stretching deformations for the beam element are incorporated according to the geometrical nonlinear beam theory. The element nodal displacement vector in local coordinate system is given as follows:

$$\mathbf{d}={\left\{{\overline{u}}_i{\overline{v}}_i{\overline{w}}_i{\overline{\theta }}_{\mathit{xi}}{\overline{\theta }}_{\mathit{yi}}{\overline{\theta }}_{\mathit{zi}}{\overline{u}}_j{\overline{v}}_j{\overline{w}}_j{\overline{\theta }}_{\mathit{xj}}{\overline{\theta }}_{\mathit{yj}}{\overline{\theta }}_{\mathit{zj}}\right\}}^T.$$

(1)

The displacements u, v, and w of a general point (x, y, and z) in the beam can be written as follows:

$$u=\overline{u}-y\cdot d\overline{v}/\mathit{dx}-z\cdot d\overline{w}/\mathit{dx},v=\overline{v},w=\overline{w},$$

(2)

where $\overline{u}$, $\overline{v}$, and $\overline{w}$ are the displacements of a point in the centroid axis of a beam corresponding to x-, y-, and z- axes, respectively. $\overline{\theta }$ is the cross-sectional rotation about the x-axis. The displacement transformation matrix of the beam element relates the element internal displacement to the nodal point displacement:

$$\overline{\mathbf{u}}={\left\{\overline{u}\overline{v}\overline{w}\overline{\theta }\right\}}^T={\left[{\overline{N}}_x{\overline{N}}_y{\overline{N}}_z{\overline{N}}_{\theta }\right]}^T\mathbf{d},$$

(3)

$$\begin{array}{l}{\overline{N}}_x=\left[N_{1}00000N_{2}00000\right],\\ {\overline{N}}_y=\left[0N_{3}000N_{4}0N_{5}000N_6\right],\\ {\overline{N}}_z=\left[00N_{3}0-N_{4}000N_{5}0-N_{6}0\right],\\ {\overline{N}}_{\theta }=\left[000N_{1}00000N_{2}00\right].\mathrm{(4)}\end{array}$$

(4)

The shape functions N _i (i = 1 to 6) are assumed for the local element displacements and given as follows:

$$\begin{array}{l}{N}_1=1-\zeta ,N_2=\zeta ,N_3=1-3{\zeta }^2+2{\zeta }^3,\zeta =x/l,\\ N_3=\left(\zeta -2{\zeta }^2+{\zeta }^3\right)l,N_5=3{\zeta }^2-2{\zeta }^3,N_6=(-{\zeta }^2+{\zeta }^3)l,\end{array}$$

(5)

in which l is the original length of the beam element.

$$\begin{array}{ll}\frac{d\overline{u}}{\mathit{dx}}& ={\mathbf{B}}_x\mathbf{d},\frac{d^2\overline{v}}{\mathit{dx}}={\mathbf{B}}_2\mathbf{d},\frac{d^2\overline{w}}{\mathit{dx}}={\mathbf{B}}_3\mathbf{d},\frac{d\overline{v}}{\mathit{dx}}={\mathbf{B}}_4\mathbf{d},\frac{d\overline{w}}{\mathit{dx}}\\ ={\mathbf{B}}_5\mathbf{d},\frac{d\overline{\theta }}{\mathit{dx}}={\mathbf{B}}_6\mathbf{d}.\end{array}$$

(6)

The strain in the deformed configuration ε _t can be expressed in terms of the displacement at the equilibrium state at any specified point in the beam cross section (x, y, and z) that defines the state of strain at any arbitrary point. The strain displacement equation (Green-Lagrange representation of axial strain ε _t ) is given in the following:

$${\epsilon }_t=\frac{d{u}_t}{\mathit{dx}}+\frac{1}{2}{\left(\frac{d{u}_t}{\mathit{dx}}\right)}^2+\frac{1}{2}{\left(\frac{d{v}_t}{\mathit{dx}}\right)}^2+\frac{1}{2}{\left(\frac{d{w}_t}{\mathit{dx}}\right)}^2,$$

(7)

where u _t , v _t , and w _t are the element displacement vectors in x-, y-, and z- axis directions, respectively; it is assumed that du _t / dx << 1. Thus, (du _t / dx)² is ignored compared to its linear term. The normal strain ε _t is then calculated. The unknown strain in t + 1 configuration can be written incrementally from configuration t as follows:

$${\epsilon }_{t+1}=\frac{d{u}_{t+1}}{\mathit{dx}}+\frac{1}{2}{\left(\frac{d{v}_{t+1}}{\mathit{dx}}\right)}^2+\frac{1}{2}{\left(\frac{d{w}_{t+1}}{\mathit{dx}}\right)}^2,$$

(8)

$$\begin{array}{rll}\delta {\epsilon }_{t+1}& =& \frac{\mathit{d\delta u}}{\mathit{dx}}+\frac{d{v}_t}{\mathit{dx}}\cdot \frac{\mathit{d\delta v}}{\mathit{dx}}+\frac{d{w}_t}{\mathit{dx}}\cdot \frac{\mathit{d\delta w}}{\mathit{dx}}\\ +\frac{1}{2}\delta {\left(\frac{\mathit{dv}}{\mathit{dx}}\right)}^2+\frac{1}{2}\delta {\left(\frac{\mathit{dw}}{\mathit{dx}}\right)}^2\\ =& \left({\mathbf{B}}_L+{\mathbf{B}}_{\mathit{NL}}\right)\delta \mathbf{d},\end{array}$$

(9)

$$\begin{array}{rl}{\mathbf{B}}_L=& {\mathbf{B}}_1-y{\mathbf{B}}_2-z{\mathbf{B}}_3,\\ {\mathbf{B}}_{\mathit{NL}}=& \left({\mathbf{B}}_4^T{\mathbf{B}}_4+{\mathbf{B}}_5^T{\mathbf{B}}_5\right)/2,\\ {\mathbf{B}}_1=& {\mathbf{B}}_x+\frac{d{v}_t}{\mathit{dx}}{\mathbf{B}}_4+\frac{d{w}_t}{\mathit{dx}}{\mathbf{B}}_5.\end{array}$$

(10)

From the principle of energy, the external work is equivalent to the internal work. The equilibrium equation in the deformed configuration t + 1 can be expressed in terms of the principle of virtual displacements:

$$\mathit{\delta U}-\mathit{\delta W}=0.,$$

(11)

$$\begin{array}{l}\underset{V}{\int }{\sigma }_{t+1}\delta {\epsilon }_{t+1}\mathit{dV}+\underset{l}{\int }{T}_{\mathit{sv}}\cdot \left(\mathit{d\theta }/\mathit{dx}\right)\mathit{dx}\\ +\frac{1}{2}{\displaystyle \underset{l}{\int }\mathit{GJ}{\left(\mathit{d\theta }/\mathit{dx}\right)}^2\mathit{dx}}-{\displaystyle \underset{S}{\int }{f}_{t+1}^T\delta {\mathbf{d}}_{t+1}\mathit{dS}=}0,\end{array}$$

(12)

where U is the internal work, W is the external virtual work, σ_t+1 is the axial Couchy stress, V is the volume, δ is the virtual quantity, f is the external applied force, and θ is the cross-sectional rotation about the x-axis. The unknown configuration is t + 1 which can be written incrementally from configuration t consistently with a nonlinear Lagrangian scheme as follows:

$$\begin{array}{l}{\displaystyle \underset{V}{\int }\left({\sigma }_t+\sigma \right)\delta {\epsilon }_{t+1}\mathit{dV}+{\displaystyle \underset{l}{\int }{T}_{\mathit{sv}}\frac{\mathit{d\theta }}{\mathit{dx}}\mathit{dx}+\frac{1}{2}{\displaystyle \underset{l}{\int }\mathit{GJ}{\left(\frac{\mathit{d\theta }}{\mathit{dx}}\right)}^2\mathit{dx}}}}\\ {\displaystyle -\underset{S}{\int }\left(f_t^T+f^T\right)\delta \left({\mathbf{d}}_t+\mathbf{d}\right)\mathit{dS}=}0,\end{array}$$

(13)

where σ is the second Piola-Kirchhoff axial stress:

$$\begin{array}{c}{\displaystyle \underset{V}{\int }\left\{\sigma {\mathbf{B}}_L+{\sigma }_t{\mathbf{B}}_{\mathit{NL}}\right\}\mathit{dV}+}\frac{1}{2}{\displaystyle \underset{l}{\int }\mathit{GJ}{\left(\frac{\mathit{d\theta }}{\mathit{dx}}\right)}^2\mathit{dx}}-\underset{S}{\int }{f}^T\delta \mathbf{d}\mathit{dS}\\ ={\displaystyle \underset{S}{\int }{f}_t^T\delta \mathbf{d}\mathit{dS}-}{\displaystyle \underset{V}{\int }{\sigma }_t{\mathbf{B}}_L\mathit{dV}-}{\displaystyle \underset{l}{\int }{T}_{\mathit{sv}}\frac{\mathit{d\theta }}{\mathit{dx}}\mathit{dx}},\end{array}$$

(14)

$$\begin{array}{l}\underset{V}{\int }\left\{\sigma {\mathbf{B}}_L+{\sigma }_t{\mathbf{B}}_{\mathit{NL}}\right\}\mathit{dV}+0.5{\displaystyle \underset{l}{\int }\mathit{GJ}{\left(\mathit{d\theta }/\mathit{dx}\right)}^2\mathit{dx}}\\ =\delta d^T\int \left\{E_1,{\mathbf{B}}_1^{\mathrm{T}},{\mathbf{B}}_1,-,E_2,\left({\mathbf{B}}_2^{\mathrm{T}}{\mathbf{B}}_1+{\mathbf{B}}_1^{\mathrm{T}}{\mathbf{B}}_2\right)\right.\\ +E_3{\mathbf{B}}_2^{\mathrm{T}}{\mathbf{B}}_2-E_4\left({\mathbf{B}}_3^{\mathrm{T}}{\mathbf{B}}_1+{\mathbf{B}}_1^{\mathrm{T}}{\mathbf{B}}_3\right)+E_5{\mathbf{B}}_3^{\mathrm{T}}{\mathbf{B}}_3\\ \left.+,E_6,\left({\mathbf{B}}_2^{\mathrm{T}}{\mathbf{B}}_3+{\mathbf{B}}_3^{\mathrm{T}}{\mathbf{B}}_2\right)\right\}d\mathit{dx}\\ +\delta d^T{\displaystyle \underset{l}{\int }{F}_x\left({\mathbf{B}}_4^{\mathrm{T}}{\mathbf{B}}_4+{\mathbf{B}}_5^{\mathrm{T}}{\mathbf{B}}_5\right)\mathit{dx}d}\\ +\delta d^T{\displaystyle \underset{l}{\int }\mathit{GJ}\left({\mathbf{B}}_6^{\mathrm{T}}{\mathbf{B}}_6\right)d\mathit{dx}},\end{array}$$

(15)

$$\begin{array}{l}{\displaystyle \underset{V}{\int }{\sigma }_t{\mathbf{B}}_{\mathrm{L}}\mathit{dV}}+{\displaystyle \underset{l}{\int }{T}_{\mathit{sv}}\left(\mathit{d\theta }/\mathit{dx}\right)\mathit{dx}}\\ =\delta d^T{\displaystyle \underset{V}{\int }{\sigma }_t\left({\mathbf{B}}_1^T-y{\mathbf{B}}_2^T-z{\mathbf{B}}_3^T\right)\mathit{dV}+\delta d^T{\displaystyle \underset{l}{\int }{T}_{\mathit{sv}}{\mathbf{B}}_6^T\mathit{dx}}}\\ =\delta d^T{\displaystyle \underset{l}{\int }\left(F_x{\mathbf{B}}_1^T-M_z{\mathbf{B}}_2^T-M_y{\mathbf{B}}_3^T+T_{\mathit{sv}}{\mathbf{B}}_6^T\right)\mathit{dx}},\mathrm{(16)}\end{array}$$

(16)

$$\begin{array}{l}{E}_1=E_T{\displaystyle \int \mathit{dydz}},E_2=E_T{\displaystyle \int \mathit{ydydz}},E_3=E_T{\displaystyle \int y^2\mathit{dydz}},\\ E_4=E_T{\displaystyle \int \mathit{zdydz}},E_5=E_T{\displaystyle \int z^2\mathit{ydydz}},E_6=E_T{\displaystyle \int \mathit{zydydz}},\\ F_x={\displaystyle \int {\sigma }_t\mathit{dydz}},{\mathrm{M}}_z={\displaystyle \int {\sigma }_t\mathit{ydydz}},{\mathrm{M}}_y={\displaystyle \int {\sigma }_t\mathit{zdydz}}\end{array}$$

(17)

which can be determined through numerical integration over the cross section of fiber segments. The tangent stiffness can be written as follows:

$$\begin{array}{ll}{k}_{\mathrm{t}}=& \int \mathbf{\{}{E}_1{\mathbf{B}}_1^{\mathrm{T}}{\mathbf{B}}_1-E_2\left({\mathbf{B}}_2^{\mathrm{T}}{\mathbf{B}}_1+{\mathbf{B}}_1^{\mathrm{T}}{\mathbf{B}}_2\right)\\ +E_3{\mathbf{B}}_2^{\mathrm{T}}{\mathbf{B}}_2-E_4\left({\mathbf{B}}_3^{\mathrm{T}}{\mathbf{B}}_1+{\mathbf{B}}_1^{\mathrm{T}}{\mathbf{B}}_3\right)+E_5{\mathbf{B}}_3^{\mathrm{T}}{\mathbf{B}}_3\\ +E_6\left({\mathbf{B}}_2^{\mathrm{T}}{\mathbf{B}}_3+{\mathbf{B}}_3^{\mathrm{T}}{\mathbf{B}}_2\right)+F_x\mathbf{(}{\mathbf{B}}_4^{\mathrm{T}}{\mathbf{B}}_4+{\mathbf{B}}_5^{\mathrm{T}}{\mathbf{B}}_5\mathbf{)}\\ +\mathit{GJ}\mathbf{\left(}{\mathbf{B}}_6^{\mathrm{T}}{\mathbf{B}}_6\mathbf{\right)}\mathbf{\}}\mathit{dx}.\mathrm{(18)}\end{array}$$

(18)

In order to capture the spread of plastic zone in individual element, the beam element is divided along its length and over its cross section directions. The stiffness quantities of the section are calculated based on the stress states of integration points over the cross section. The element stiffness quantities are then obtained by integrating along the length of the beam, where the plastic development of the material is automatically considered. The stiffness matrix calculations of the elements are completed by a numerical integration procedure. After obtaining the stiffness matrix of the elements with respect to the local coordinate system, the element coordinates are transformed from the local coordinate system to the global coordinate system. The stiffness matrix of the elements is then assembled using standard procedures and by getting the global stiffness matrix. In the nonlinear incremental analysis, the structure tangent stiffness matrix, which is assembled from the element tangent stiffness matrices, is used to predict the next incremental displacements under a loading increment.

Soil-structure interaction formulation

The interaction between the soil and the structure is simulated with translational, rotational, and their coupling spring system and equivalent viscous damping. The spring constants of the lumped-parameter model in both bridge axis and right-angle directions are calculated based on foundation geometry and soil profile underneath and along the embedded depth of the foundation, as specified in Japanese Highway Specification (Committee of Earthquake Engineering 1996; Japan Road Association 1996a). Soil properties from the standard penetration test (SPT) data and logs of boreholes at the tower site are used to determine the coefficients of vertical and horizontal subgrade reactions that are used in a spread foundation design. A set of spring elements along all the six degrees of freedom and the coupling of lateral and rotational directions constitutes the linear lumped soil model, and it is connected to the foundation centroid node at the footing base level. The influence of the soil flexibility in the global dynamic response is considered through the assembling of the stiffness matrix of the soil spring system using standard procedures getting the globe stiffness matrix (Abdel Raheem 2009; Abdel Raheem et al. 2002, 2003).

In the nonlinear Winkler soil model, three types of soil resistance displacement models could describe the soil characteristics: the first type represents the lateral soil pressure against the pier and the corresponding lateral pier displacement relationship, the second type represents the skin friction and the relative vertical displacement between the soil and the pier relationship, and the third type describes the bearing stress beneath the spread foundation and settlement relationship. All three types assume the soil behavior to be nonlinear and can be developed from the basic soil parameters. The soil-structure interaction is simulated with nonlinear spring-dashpot system along the embedded depth of the pier. Both strain-dependent material nonlinearity and geometrical nonlinearity by basemat uplift are considered through a beam on nonlinear Winkler soil element connected in series with gap element spring system (Abdel Raheem et al. 2002, 2003; Kobayashi et al. 2002). The spring constants in both bridge axis directions are calculated based on foundation geometry and soil profile underneath and along the embedded depth of the foundation as specified in Japanese Highway Specification (Committee of Earthquake Engineering 1996; Japan Road Association 1996a). The nonlinear soil-foundation model is described as the Winkler model that has nonlinear springs distributed along the embedded depth in the three directions of the local coordinate system. The reaction displacement model of the tensionless foundation at base level is considered.

The contribution of soil reactions to the foundation element equivalent nodal forces vector and the element tangent stiffness of the foundation, {f_soil} and [k_soil], respectively, can be given as follows:

$$\left\{f_{\mathrm{soil}}\right\}=-{\displaystyle \underset{l}{\int }{\left[N\right]}^T\left\{r\right\}\mathit{dx}}$$

(19)

and

$$\begin{array}{ll}\left[k_{\mathrm{soil}}\right]& =-\frac{\delta \left\{f_{\mathrm{soil}}\right\}}{\delta \left\{d\right\}}={\displaystyle \underset{l}{\int }{\left[N\right]}^T\frac{\delta \left\{r\right\}}{\delta \left\{d\right\}}\mathit{dx}}\\ ={\displaystyle \underset{l}{\int }{\left[N\right]}^T\left[k\right]\left[N\right]\mathit{dx}},\end{array}$$

(20)

where

$$\begin{array}{ll}\delta \left\{r\right\}& =\left[\begin{array}{l}{k}_x\\ k_y\\ k_z\end{array},\right]\left\{\begin{array}{l}\delta \overline{u}\\ \delta \overline{v}\\ \delta \overline{w}\end{array}\right\}=\left[k\right]\delta \left\{\overline{u}\right\}\\ =\left[k\right]\left[N\right]\left\{d\right\}.\end{array}$$

(21)

Equation of motion

The governing nonlinear dynamic equation of the tower structure response can be derived using the principle of energy, i.e., the external work is absorbed by the internal, inertial, and damping energy for any small admissible motion that satisfies compatibility and boundary condition. By assembling the element dynamic equilibrium equation at time t + Δt over all the elements, the incremental finite element method dynamic equilibrium equation (Abdel Raheem 2009; Chen 2000) can be obtained as follows:

$$\begin{array}{l}\left[\mathrm{M}\right]{\left\{ü\right\}}^{t+\mathit{\Delta t}}+\left[\mathrm{C}\right]{\left\{\dot{u}\right\}}^{t+\mathit{\Delta t}}+{\left[\mathrm{K}\right]}^{t+\mathit{\Delta t}}{\left\{\mathit{\Delta u}\right\}}^{t+\mathit{\Delta t}}\\ ={\left\{\mathrm{F}\right\}}^{t+\mathit{\Delta t}}-{\left\{\mathrm{F}\right\}}^t,\end{array}$$

(22)

where [M], [C], and [K]^t+Δt are the system mass, damping, and tangent stiffness matrices at time t + Δt, respectively;$\ddot{u}$, $\dot{u}$ and Δu are the accelerations, velocities, and incremental displacement vectors at time t + Δt, respectively. {F}^t+Δt − {F}^t is the unbalanced force vector. It can be noticed that the dynamic equilibrium equation of motion takes into consideration the different sources of nonlinearities (geometrical and material nonlinearities), which affect the calculation of the tangent stiffness and internal forces. The implicit Newmark step-by-step integration method is used to directly integrate the equation of motion, and then it is solved for the incremental displacement using the Newton–Raphson iteration method, in which the stiffness matrix is updated at each increment to consider the geometrical and material nonlinearities and to speed the convergence rate.

The tower structure damping mechanism is adapted to the Rayleigh damping; the damping coefficient is taken to be 2% for steel materials of tower superstructure and 10% for concrete materials of embedded pier substructure (Committee of Earthquake Engineering 1996; Japan Road Association 1996a, 1996b). Vibration periods of 2.5 and 0.50 s are considered to represent a broad range of high participation modes and the softening that takes place as the columns and soil yield. A common design approach of maintaining elastic behavior in the substructure is considered to avoid inelastic behavior below the ground surface, where the damage would be difficult to detect or to repair. A nonlinear dynamic analysis computer program is developed based on the above-mentioned formulation to predict the vibration behavior of framed structures as well as the nonlinear response under earthquake loadings. The program has been validated through a comparison with different commercial software EDYNA, DYNA2E, and DYNAS (Japanese software).

Input excitation

In the dynamic response analysis, the seismic motion by an inland direct-strike type earthquake that was recorded during the 1995 Hyogoken-Nanbu earthquake of high intensity but short duration is used as an input ground motion to assure the seismic safety of the bridges. The horizontal and the vertical accelerations recorded at the station of JR-Takatori observatory (Committee of Earthquake Engineering 1996; Japan Road Association 1996a, 1996b) are used for the dynamic response analysis of the cable-stayed bridge tower at a soil of type II, where the fundamental period of the site ranges from 0.2 to 0.6 s, and the mean value of shear wave velocity of 30 m of the soil deposit ranges from 200 to 600 m/s (Japan Road Association 1996a). It is considered to be capable of securing the required seismic performance during the bridge service life. The selected ground motion has maximum acceleration intensities of its components of 642 (N-S), 666 (E-W), and 290 gal (U-D). The kinematic interaction can be modeled by a transfer function, which can be used to modify a free-field ground motion so that an effective input motion for a soil-structure system can be obtained. A simple model based on analytical modeling of rigid foundation is adopted, in which the effective seismic motion is obtained starting from the free-field motion by an approximate analytical solution (Harada et al. 1981; Ganev et al. 1995) for embedded foundation with its base resting on a stiffer layer.

Finite element modeling of tower structure

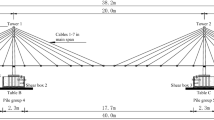
The steel tower of a three-span continuous-cable-stayed bridge located in Hokkaido, Japan is considered, in which the main span length is equal to 284 m. Figure 1 shows a schematic representation of the bridge elevation. The towers are H-shaped steel structures as shown in Figure 2. Each tower is founded on a spread foundation on good soil layer, and it consists of two steel legs and horizontally connected beam. The cross section of each leg has a hollow rectangular shape with an interior stiffener; the cross-sectional size varies over the height of the tower. Cable-stayed bridges represent highly redundant and mechanically nonhomogeneous structural systems; the tower, deck, and cable stays affect the structural response in a wide range of vibration modes (Ali and Abdel-Ghaffar 1995; Abdel Raheem and Hayashikawa 2003). The tower is taken out of the cable-stayed bridge, and a finite element model is constructed based on the design drawings, as shown in Figure 3. A flexural fiber element is developed for the tower characterization; the element incorporates both geometric and material nonlinearities. A bilinear model is adopted to describe the stress–strain relationship of the element. The yield stress and the modulus of elasticity are equal to 355 MPa (SM490) and 200 GPa, respectively; the plastic region strain hardening is 0.01. The nonlinearity of inclined cables is idealized using the equivalent modulus approach (Karoumi 1999). The nonlinearity of the cables originates with an increase in the loading followed by a decrease in the cable sag, resulting in an increase of the cable apparent axial stiffness. In this approach, each cable is simulated by a truss element with equivalent tangential modulus of elasticity E_eq that is given by (Ernst 1965) as follows:

$$E_{\mathrm{eq}}=E/\left\{1+\mathit{EA}{\left(\mathit{wL}\right)}^2/12T^3\right\},$$

(23)

where E is the material modulus of elasticity, L is the cable horizontal projected length, w is the weight per unit length of the cable, A is the cross section of the area of the cable, and T is the tension force in the cable. This tower has nine cables in each side of the tower. The stiffening girder dead load is considered to be equivalent to the vertical component of the pretension force of the cables acting at their joints and the two vertical components at stiffening girder-tower connection at the substructure top level. The tower steel superstructure has a rectangular hollow steel section of different dimensions along the different parts of the tower, as indicated in Table 1. In the numerical analysis, steel superstructure is modeled as a three-dimensional elastoplastic beam element, while concrete substructure is modeled as an elastic element.

Figure 1

Schematic representation of bridge elevation ( m ).

Figure 2

Tower geometry (a) and cross section (b) of steel tower of cable-stayed bridge.

Figure 3

Finite element model of bridge tower.

Table 1 Cross section dimension of different tower regions

Modeling of soil-structure interaction

A crucial goal of current seismic foundation design, particularly as entrenched in the respective codes (European Committee for Standardization 1998), is to avoid full mobilization of strength in the foundation by guiding failure to the aboveground structure. The designer must ensure that the (difficult to inspect) belowground support system will not even reach a number of thresholds that would statically imply failure: mobilization of the soil bearing capacity, significant foundation uplifting, and sliding or any of their combination are prohibited or severely limited. To this end, following the norms of capacity design, overstrength factors and safety factors (explicit or implicit) are introduced against those failure modes.

Linear lumped-parameter soil model

In the linear lumped-parameter soil model, the interaction between the soil and the structure is simulated with translational, rotational, and their coupling spring system. The spring stiffness values in both bridge axis and right-angle directions are given in Table 2. The stiffness is calculated based on foundation geometry and soil profile underneath and along the embedded depth of the foundation, as specified in Japanese Highway Specification (Japan Road Association 1996a, 1996b) and as shown in Figure 4.

Figure 4

Linear lumped-parameter soil model.

Table 2 Stiffness values of linear lumped-parameter soil model

Nonlinear Winkler model for soil-structure interaction

The soil-structure interaction is simulated with nonlinear spring-dashpot system along the pier embedded depth. Strain-dependent material nonlinearity is implemented using the nonlinear Hardin-Drnevich soil model (Hardin and Drnevich 1972a, 1972b). Geometrical nonlinearity by basemat uplift is considered through nonlinear soil element connected in series with gap element spring system, as shown in Figure 5. The spring constants in both bridge axis directions are calculated based on foundation geometry and soil profile underneath and along embedded depth of foundation, as specified in Japanese Highway Specification (Japan Road Association 1996a, 1996b). Soil properties from the SPT data and logs of boreholes at the tower site are used to determine the coefficients of vertical and horizontal sub-grade reactions. The subgrade reaction coefficients are obtained from the ground stiffness corresponding to the deformation caused in the ground during an earthquake.

Figure 5

Winkler model for soil-structure interaction.

Soil nonlinearity idealization

One of the most important factors in the analysis of soil-foundation interactive behavior is the nonlinear constitutive laws of the soil (material nonlinearity). In this study, the Hardin-Drnevich model is proposed to represent the soil material nonlinearity that is often used for its capacity to trace the degradation of stiffness. The parameters used to define the skeleton curve and family of hysteresis stress–strain curves are indicated in Figure 6. The skeleton curve is expressed as follows:

$$\tau =G_0\gamma /\left(1+|\gamma /{\gamma }_{\mathrm{r}}|\right),{\gamma }_{\mathrm{r}}={\tau }_{\max }/G_0,$$

(24)

where G₀ is the initial shear modulus, τ is the generalized soil shear stress, τ_max is the shear stress at failure, γ_r is the reference strain, and γ is the generalized strain. The hysteretic curve can be constructed using the Masing rule (Masing 1926) and is given as follows:

$$\tau \pm {\tau }_{\mathrm{m}}=G_0\left(\gamma \pm {\gamma }_{\mathrm{m}}\right)/\left\{1+|\left(\gamma \pm {\gamma }_{\mathrm{m}}\right)/2{\gamma }_{\mathrm{r}}|\right\},$$

(25)

where τ_m and γ_m indicate the coordinates of the origin of the curve, that is, the point of the most recent load reversal. The hysteresis curve is the same in shape as the skeleton curve but is enlarged twice. The nonlinear dynamic soil parameters including the dynamic shear moduli and the damping ratios for the employed soil models in this study are modulated based on the shear strain-dependent relationships for gravel, sand, and clay shown in Figure 7. Soil exhibits nonlinear nature even at small strains. The shear modulus (G) can be described as follows:

$$G/G_0=1/\left(1+{\gamma }_{\mathrm{m}}/{\gamma }_{\mathrm{r}}\right).$$

(26)

Figure 6

Hardin-Drnevich model and Masing rule hysteresis loop.

Figure 7

Strain-dependent soil material nonlinearity (rigidity and damping).

The soil element stiffness is idealized by the Winkler model. For practical use, frequency-independent spring coefficients are computed based on Japanese Specification for Highway Bridges (Japan Road Association 1996a, 1996b). Each spring consists of a gap element and a soil element. The gap element transmits no tensile stress, which can express the geometrical nonlinearity of basemat uplift.

Soil damping idealization

The hysteretic damping characteristic of the soil, which resulted from the deformations produced by interaction with the pier, is represented by nonlinear viscous dashpots. The damping ratio of the soil dashpot strain-dependent material nonlinearity is described by a simple relationship between the shear modulus and damping, as shown in Figure 8.

$$\begin{array}{ll}h& =\left(\mathit{\Delta w}/w\right)/2\pi \\ =\left(2/\pi \right)\left[\left(2G_0/G\right)\left\{\left({\gamma }_{\mathrm{r}}/{\gamma }_{\mathrm{m}}\right)-{\left({\gamma }_{\mathrm{r}}/{\gamma }_{\mathrm{m}}\right)}^2\log \left(1+g_{\mathrm{r}}/g_{\mathrm{m}}\right)\right\}-1\right].\end{array}$$

(27)

Figure 8

Hysteretic damping of soil.

The material-damping ratio h is defined as follows:

$$h=C_{\mathrm{m}}/C_{\mathrm{r}},C_{\mathrm{r}}=2{\left(k/m\right)}^{0.5},$$

(28)

in which C_m is the coefficient of material damping, C_r is the coefficient of material critical damping, and k and m are the soil spring stiffness and pier mass per unit length, respectively. The coefficient of material damping of the soil C_soil is obtained as follows:

$$C_{\mathrm{soil}}=2h_{\max }\left(1-k/k_0\right){\left(k/m\right)}^{0.5}.$$

(29)

The radiation-damping characteristic of soil is represented through an approximation of a para-axial boundary, where viscous dampers can be used to represent a suitable transmitting boundary for many applications involving both dilatational waves and shear waves. A one-dimensional viscous boundary model is selected for this study. It is assumed that a horizontally moving pier cross section would solely generate one-dimensional P waves traveling in the direction of shaking and one-dimensional S waves in the direction perpendicular to shaking, as shown in Figure 9. Based on the previous assumption, the coefficient of viscous dashpot that will absorb the energy of the waves originating at soil-pier interface is evaluated.

Figure 9

One-dimensional radiation-damping model.

Results and discussion

To study the effects of soil-foundation-structure interaction on the seismic behavior of the cable-stayed bridge towers, two different approaches for soil-foundation-interaction modeling (nonlinear Winkler model and linear lumped-parameter model) are considered. The soil-foundation-superstructure model with Winkler hypothesis for soil idealization is compared to a simplified lumped-parameter model, and dynamic response simulation is conducted by applying acceleration at the base level of the foundation. The following two different cases of soil idealization are analyzed:

Case I Seismic response with soil material and geometrical nonlinearities: nonlinear Winkler model.

Case II Seismic response of tower model with linear lumped-parameter soil model.

Soil-structure interaction modeling effects on global responses

The acceleration time history at the tower top, where the tower acceleration response is significantly decreased due to degradation of soil stiffness and energy dissipation through soil hysteresis, clarifies the effects of soil nonlinearity. The reduction of acceleration response of Winkler model (case I) related to soil nonlinearities (material and geometrical) approaches about 60% of that of the simplified model (case II), as illustrated in Figure 10. Moreover, the acceleration time history of case II is characterized by large peak acceleration that is associated with a short duration impulse of high frequency (acceleration spike). The Fourier acceleration response spectrum clarifies the significant contribution of high-frequency modes to the tower seismic response.

Figure 10

Acceleration time history and response spectra at tower top.

The displacement, moment ratio, and vertical force time histories of Winkler model (case I) at the tower superstructure base show the response nature to strong excitation. The moment ratio is defined as the ratio of moment demand to the moment capacity at the first yield of the cross section. The large pulse in the ground motion produces two or three cycles of large force response with rapidly decaying amplitudes of displacement, moment, and force after the peak excursions. The predominant contribution to the vertical force response at the tower superstructure base results from the in-plane rocking vibration rather than from the vertical excitation, and it is dominated by long-period in-plane vibration and slightly affected by high-frequency vertical excitation and vibration, as shown in Figures 11 and 12. However, the lumped-parameter-model analysis (case II) for tower superstructure base moment and axial force displays slight attenuation after peak response excursions, and the time history response is characterized by high-frequency spike. The simplified lumped-parameter-model analysis provides a good prediction for peak response but overestimates the acceleration response and underestimates the uplift force at the anchor between superstructure and pier. It can be obviously seen that foundation uplifting and plasticity have a significant effect on the reduction of seismic force of bridge tower. The foundation allowed uplifting, and yielding in design will protect tower pier and superstructures. The value of reduction of seismic force increases with the increase of seismic intensity.

Figure 11

Moment ratio time history at tower superstructure base.

Figure 12

Vertical force time history at tower superstructure base.

Soil nonlinearity effects on tower response

The uplift of the tower footing is investigated through vertical deformation and force resistance of the basement soil at the extreme right and left sides of the footing base (case I). Two aspects of foundation response to seismic excitation, rocking deformation and the accumulation of the permanent settlement can be distinguished. The permanent settlement was found to be the less significant in the total vertical displacement at the footing base level, as shown in Figures 13 and 14. It can be concluded that separation of the soil from the structure occurs under large dynamic loads leading to changes in the predominant vibration of the system. As a result of the decrease in soil support at the sidewalls of the foundation by stiffness degradation due to hysteresis, the stress caused by the structural weight on the bottom soil is increased during earthquakes. The reduction of the foundation width in contact during uplift induces an increase of the stresses under the foundation. This leads to a larger soil yielding, which itself modifies the uplift behavior of the foundation. The maximum uplift of not more than 5 mm clarifies that the tower foundation almost has sufficient structural loading to minimize the uplift. The soil layer at the footing base level has sufficient bearing capacity to prevent foundation excessive settlement.

Figure 13

Vertical displacement time history of footing extreme right and left at footing base level.

Figure 14

Vertical force per unit length time history of footing extreme right and left at footing base level.

Since the foundation structure is very rigid compared to the underlying foundation soil, the rocking motion of the foundation is significantly observed, which affects the characteristics of the foundation motion. The limited shear strength of soil also causes sliding of the foundation block, which could alter the characteristics of the foundation motion. In addition to the inertial soil-foundation interaction due to the existence of foundation mass, the size and stiffness of the foundation could also affect the foundation motion characteristics. From superstructure base (steel superstructure and concrete substructure connection joint) displacement time history (case I) as shown in Figure 15, it could be seen that the displacement could reach around 3.0 cm for soil-structure interaction model of the tower with both material and geometrical nonlinearities; this effect is totally ignored for fixed base model assumption. The limited shear strength of basement soil causes sliding of the foundation, which could be underestimated by elastic and linear soil assumption, as shown in Figure 16.

Figure 15

In-plane displacement time history at superstructure base.

Figure 16

Foundation sliding time history at footing base level.

From the Fourier spectra study of tower acceleration response at different levels of tower for nonlinear soil-foundation-superstructure interaction model (case I), it is shown that there is amplification of different modes over a wide frequency range, as seen in Figures 17 and 18. The in-plane superstructure base response spectrum is larger than that at the footing base at a spectral frequency less than 2.0 Hz because of amplification induced by flexible superstructure and massive rigid substructure interaction, while at high frequency above 2.0 Hz, the response spectra are slightly attenuated due to inertial interaction. The tower top response spectra are significantly amplified at low-frequency range and are almost totally attenuated at high-frequency range due to tower superstructure flexibility, as seen in Figure 18. The massive foundation has the effect of amplifying the response over a wide frequency band. The vertical acceleration response at the footing base level shows relatively high-frequency amplification as the response spectra within the frequency range of 2 to 3 Hz are slightly amplified at the superstructure base level, and they are dramatically amplified at the tower top. On the other hand, the response spectrum at high-frequency range is attenuated by superstructure flexibility filter of the tower response. The nonlinear seismic response of bridge piers is distinctly different from that of the linear response. There is a great difference whether it is in vibration amplitude or in frequency property. The nonlinear properties of foundations make the stiffness of the structure low, the response of rotational angle increase, and the response of bending moment decrease.

Figure 17

In-plane acceleration time history and response spectra (case I).

Figure 18

Vertical acceleration time history and response spectra (case I).

Conclusions

A finite element model to study the effects of soil-foundation-superstructure interaction on the seismic response of a cable-stayed bridge tower supported on spread foundation was presented, in which an incremental iterative technique was adopted for a more realistic analysis of the nonlinear soil-foundation-superstructure interaction. The problem was analyzed, employing the finite element method and taking account of material (soil, steel superstructure) and geometric (uplifting and P-Δ effects) nonlinearities. Two different modeling approaches for soil foundation interaction, nonlinear Winkler model and linear lumped-parameter model, were investigated. The seismic responses of Winkler soil model were compared to those of the simplified linear lumped-parameter model. In the lumped-parameter soil model, the soil-structure interaction is simulated with translational, rotational, and their coupling spring system acting at centroid of spread foundation at the footing base level while in the Winkler soil model, the soil-structure interaction is simulated with continuous spring system (Winkler) along embedded depth of tower pier and underneath the spread foundation. Soil yielding under the foundation and along the embedded depth was modeled using the Hardin-Drnevich model to express nonlinear soil characteristics. The contact nonlinearity induced by the uplift of the foundation was integrated using gap element. Radiation damping associated with wave propagation was accounted for implicitly through viscous damping while the energy dissipation through soil material nonlinearity was explicitly modeled. The interaction effects generated by the normal and tangential resistance of the soil against all active sides of the footing were taken into account. The following conclusions can be drawn as follows:

The analysis with simplified linear lumped-parameter model provides a good prediction for the peak response but overestimates the acceleration response and underestimates the uplift force at the anchor between superstructure and pier. The nonlinear soil-foundation interaction effect is very remarkable when uplifting and yielding of supporting soil are considered. The analysis using the nonlinear interaction Winkler model shows that the foundation uplift alters tower displacement seismic response and reduces structural member forces. Compared with the linear analysis, the stiffness of the tower-soil system degrades in each cycle after considering uplifting and yielding. The nonlinear analysis displays larger rotational angles and smaller bending moments compared with the linear lumped-parameter-model analysis. The inclusion of massive foundation and nonlinearity of soil effects leads to the amplification of higher modes of vibration and activates the high-frequency translational motion of the input ground motion and generates foundation-rocking responses. The rocking vibration dominates the lateral bearing stress for the soil along the embedded depth of the tower pier. The predominant contribution to the vertical response at the footing base resulted from the massive foundation rocking rather than from the vertical excitation; the permanent settlement is found to be less significant. The soil bearing stress demand beneath the spread foundation is significantly increased due to footing base uplift. The bearing stress under the foundation should be checked considering both soil material and geometrical nonlinearities with an appropriate factor of safety to avoid catastrophic foundation failure. The soil at the foundation level should have sufficient bearing capacity to prevent foundation excessive settlement.

From the nonlinear Winkler soil model, it is concluded that the soil interaction effect is very remarkable when uplifting and yielding of supporting soil are considered. Compared with the linear lumped soil model, the stiffness of tower foundation-soil model degrades in each cycle after considering uplifting and yielding. It is shown that the nonlinear analysis can get larger rotational angles and smaller bending moments compared with the linear analysis. The nonlinear modeling of soil-foundation interface shows that the soil structure interaction effect may play an important role in altering the force and displacement demand, indicating the necessity for consideration of foundation behavior in the modern design codes to accomplish a more economic yet safe structural design. For more general and versatile conclusions, different input excitations and different ground conditions at bridge construction site should be considered.

Authors’ information

SEAR is an associate professor in Earthquake, Bridge, Structural and Geotechnical Engineering since 2009 at the Civil Engineering Department in Assiut University, Egypt. He acquired his Doctorate in Engineering in 2003 and was a Japan Society for the Promotion of Science fellow in 2006 in Hokkaido University, Japan. He was an Alexander von Humboldt fellow in 2005 in Kassel University, Germany. He has published more than 60 papers in the field of structural engineering, structural analysis, earthquake engineering, soil structure interaction, seismic pounding, structural control, and nonlinear dynamic of offshore structures. He is a previous member of the Japan Society of Civil Engineers. He reviewed many papers for international journals. He is currently working as an engineering counselor at the general project management of Taibah University, Medina, Saudi Arabia. TH is a professor in Earthquake, Bridge, Structural and Geotechnical Engineering since 2004. He acquired his Doctorate in Engineering in 1984 in Hokkaido University, Japan. He was a visiting research fellow at Princeton University, USA in 1985. His research works/interests include Response of Cable-Stayed Bridges under Great Earthquake Ground Motion; Seismic Isolation Design; Energy Dissipation System and Performance-Based Design of Steel Structures; Damage Identification of Highway Bridge; and Bridge Management System Vibration Control and Intelligential Structure of Steel Bridges. He is a fellow member of the Japan Society of Civil Engineers. He reviewed many papers for international journals.