On a sequence of approximate solutions: bending of a simply supported square plate

Abstract

The solution from Kirchhoff’s theory for a simple textbook problem of bending of a simply supported square plate under doubly sinusoidal vertical load is re-examined concerning the exact solution of the three-dimensional problem. Well-known deficiencies in widely used classical theories such as Reissner’s theory and first-order shear deformation theory (FSDT) along with Kirchhoff’s theory are highlighted. These theories are based on the stationary property of relevant total potential. They do not provide proper initial solutions for the generation of a sequence of approximate solutions converging to the exact solution. The aim of the present work is to eliminate deficiencies in these classical theories. A sixth-order system consisting of three second-order equations is initially formulated with the aid of a normal strain ignored in FSDT. These second-order equations, uncoupled from transverse deflection in Kirchhoff’s theory, govern in-plane displacements and transverse stresses. A supplementary problem consisting of a fourth-order system of equations is included to rectify inadequacies of polynomial expansions in the thickness-wise distribution of approximate solutions. More realistic and practical edge conditions are considered. An auxiliary problem is formulated, and its solution is used in the generation of a proper sequence of two-dimensional problems. Higher-order corrections to primary solutions are proposed through an iterative procedure.

Introduction

One finds several theories reported in the literature for the analysis of bending of plates within the classical small deformation theory of elasticity. These theories are generally based on making suitable assumptions about thickness-wise distribution of displacements and/or stresses (or strains) to derive two-dimensional plate equations from three-dimensional equations. They are primarily intended to overcome inherent limitations in the theory of Kirchhoff (1850) which is simple and continuously used to obtain design information. For a brief survey of most of these theories, one may refer to the following reviews: Reissner (1985), Lo et al. (19771978), Lewinski (19861987), Blocki (1992), Kienzler (2002), and Batista (2010).

Kirchhoff’s theory consists of a single-variable model in which in-plane displacements are expressed in terms of gradients of vertical deflection w₀(x, y) from the assumption of zero transverse shear strains. Solution for w₀ is such that zero face shear conditions and edge support conditions are satisfied. It is governed by a fourth-order equation associated with two edge conditions instead of three edge conditions required in a 3-D problem. A consequence of this lacuna is the well-known Poisson-Kirchhoff boundary conditions paradox unresolved satisfactorily over the past 16 decades.

Reissner (1985) in his article felt that inclusion of transverse shear deformation effects was directly (or by implication) presumed to be the key in resolving Poisson-Kirchhoff’s boundary conditions paradox. In his pioneering work, Reissner (1944) brought out the use of transverse shear stresses in deriving a sixth-order plate theory. Equations governing (average) displacements in his sixth-order theory (Reissner 1945) consist of Kirchhoff’s fourth-order equation and a second-order equation coupled through edge conditions. They correspond to plate element equations governing stress resultants consistent in the reduction of 3-D equations through calculus of variations. After Reissner (19441945), several sixth- and higher-order shear deformation theories were reported. Governing equations derived either from using calculus of variations or from statics correspond to errors in satisfying in-plane equilibrium equations and/or constitutive relations.

The assumption of zero transverse shear strains is discarded, resulting in a three-variable model of the widely used first-order shear deformation theory (FSDT), based on Hencky (1947). In this theory, w₀ and in-plane displacements [u, v] = z[u₁(x, y), v₁(x, y)] are coupled in governing differential equations and boundary conditions. In Reissner’s sixth-order theory (Reissner 1945) and FSDT, applied in-plane shear is combined with transverse shear resulting in a 'torsion-type’ problem in flexure instead of in-plane shear combining with reactive vertical shear implied in Kelvin and Tait’s (Love 1934) physical interpretation of contracted boundary condition in Kirchhoff’s theory. In fact, torsion problem is associated with flexure problem (Vijayakumar 2011b), whereas flexure problem (unlike that directly or indirectly implied in the energy methods) is independent of the torsion problem. This torsion problem is, however, an approximation to the associated torsion problem in the bending of plates and results in unrealistic vertical deflection of the plate. In fact, a solution of the associated torsion problem is to nullify the effect due to applied or reactive edge stress τ_xy in the flexure problem (In this connection, a pertinent observation is that Kirchhoff’s theory and FSDT are valid for the analysis of hard and soft, simply supported plates, respectively). This can be inferred from numerical results reported by Lewinski (1990) in which higher-order theories give decreasing values of vertical deflection. Recently, Kirchhoff’s theory is modified such that the resulting sixth-order theory of bending and St. Venant’s theory of torsion are mutually exclusive to each other (Vijayakumar 2009).

In the present author’s recently developed theory designated as 'Poisson’s theory of plates in bending’, reactive transverse shear stresses are initially determined independent of material constants retaining their thickness-wise parabolic distributions. Dependence on material constants is through higher-order corrections to these stresses. These higher-order corrections are determined through an iterative procedure based on the equilibrium of a 3-D infinitesimal element instead of on the use of the stationary property of total potential in the energy methods. Dependence of analysis on vertical deflection w₀(x, y) is eliminated (one should note that the coupling of analysis with w₀ in energy methods is due to the work done by the applied transverse stresses during deformation and also the root cause for Poisson-Kirchhoff’s boundary conditions paradox). Also, the coupling between flexure problem and associated torsion problem is eliminated through an iterative method (Vijayakumar 2011a). The problem at each stage of iteration is defined by a sixth-order system of equations using a solution at the preceding stage of iteration. In the earlier investigations (Vijayakumar 20092011ab), in-plane displacements are expressed in terms of gradients of two functions, ψ and φ, in which ψ is related to w and φ is required to decouple bending and torsion problems. The function φ is an auxiliary plane harmonic function from zero rotation (v, _x - u, _y ) denoted by ω _z about z-axis. The function φ was introduced earlier by Reissner (1947) as a 'stress function’ governed by a 'wave equation’ with imaginary velocity of propagation. Kirchhoff’s theory, FSDT, Reissner’s theory, and other shear deformation theories and reported higher-order theories based on energy principles are definitely not useful (explained later) in the generation of a proper sequence of 2-D problems converging to a 3-D problem.

In Kirchhoff’s theory and shear deformation theories including the widely used FSDT, vertical deflection w₀ (average displacement in Reissner’s sixth-order theory) is same in the face parallel planes. However, it is known physically that neutral plane deflection has to be higher than face deflection. This is due to the fact that an elastic medium is on either side of the neutral plane, whereas it is on one side of each of the top and bottom faces. Proper estimation of neutral plane deflection is dependent on normal strain ε_z ignored in Kirchhoff’s theory and shear deformation theories. In an earlier investigation (Vijayakumar 2011a), it is shown that the expansion of displacements in polynomials of thickness coordinate z is not adequate to properly estimate face and neutral plane deflections. This fact is overlooked in the analysis of even isotropic homogeneous plates through the widely used FSDT and other shear deformation theories. A solution to a supplementary problem is required to obtain neutral plane deflection. It is, however, observed that the error in the estimation of face deflection is much higher than that of neutral plane deflection. However, it is desirable to provide uniform approximation to deformations through thickness of the plate. It appears to the author’s knowledge that no suitable 2-D modeling which gives more or less the same percentage of approximation to thickness-wise distribution of a displacement variable is reported until now. Proper higher-order theories are to reduce only maximum error in the estimation of a physical variable to a desirable level.

Variational methods based on the principle of virtual work consist of virtual increments in displacement variables. Due to arbitrary virtual increments, one derives static equations governing real displacements independent of these virtual displacements which do not participate in these equations. If a 3-D variable, for example, u(x, y, z) is expressed in infinite series with sum on (i, j, k = 0, 1, 2, ∙∙∙∙∙∙)

$$u\left(x,y,z\right)=\left({{\displaystyle \sum \alpha }}_i{x}^i\right)\left({{\displaystyle \sum b}}_j{y}^j\right)\left({{\displaystyle \sum c}}_k{z}^k\right)$$

then determination of real constants (a _i , b _j , c _k ) from relevant algebraic equations generated in the numerical methods such as finite difference methods, finite element methods, etc. is presumably valid for solutions of such 3-D variables. However, expansion of displacements based on polynomials of thickness coordinate z is not adequate as mentioned earlier in obtaining proper solutions of displacements. Moreover, sequence of 2-D problems derived from variational principles do not converge to 3-D problems since

$$\begin{array}{l}\mathit{\delta }\left[\left({\displaystyle \sum }{a}_i{x}^i\right)\left({\displaystyle \sum }{b}_j{y}^j\right)\left({\displaystyle \sum }{c}_k{z}^k\right)\right]\ne \sum z^k\mathit{\delta }\left[\left({\displaystyle \sum }{a}_{\mathit{ik}}{x}^i\right)\left({\displaystyle \sum }{b}_{\mathit{jk}}{y}^j\right)\right],\\ \left(i,j,k=0,1,2,······\right).\end{array}$$

Hence, it is necessary to consider equilibrium equations of a 3-D infinitesimal element (instead of plate element) to generate proper sequence of 2-D problems governing 2-D displacement variables.

The condition zero ω _z decoupling flexure from the torsion problem is satisfied in Kirchhoff’s theory. By imposing this condition in FSDT, the sum of in-plane normal strains (ε _x + ε _y ) in isotropic plates is governed by a second-order equation due to applied transverse loads. Using this sum of in-plane strains together with condition ω _z = 0 gives uncoupled second-order equations governing in-plane displacements. Reactive transverse shear stresses are gradients of (ε _x + ε _y ) uncoupled from w₀.

In Poisson’s theory mentioned earlier, in-plane distribution of (ε _x + ε _y ) is denoted by ψ(x, y) so that the gradients ψ_,x and ψ_,y give in-plane distributions of transverse shear stresses independent of material constants. The function ψ is related to normal strain ε _z , and ψ = 0 implies ε _z = 0 along the supported edge. The condition ε _z = 0 in place of w₀ = 0 is mathematically valid and more so at point supports along the wall of the plate.

In the bending problem of a simply supported square plate under doubly sinusoidal vertical load, accuracy achieved in the estimation of face deflection (Vijayakumar 2011a) is much less than that of neutral plane deflection at the end of the first stage of iteration. This is likely to persist even in higher-order approximations. This deficiency is rectified earlier (briefly described and used later in the present analysis) through solution of an auxiliary bending problem (Vijayakumar 2013). This auxiliary problem is based on consideration of the influence of σ _z = ± zq/2 satisfying face load conditions and associated constant transverse shear stresses on the preliminary solutions of primary bending problems. These transverse stresses are treated as virtual quantities since they do not participate in the static in-plane equilibrium equations as the above-mentioned virtual incremental displacements in the application of principle of virtual work. Constant transverse shear stresses, however, contribute in the integrated equilibrium equations, and linear σ _z contributes in the in-plane normal stress–strain relations. These transverse stresses are absent in Kirchhoff’s theory.

Bending of a simply supported square plate

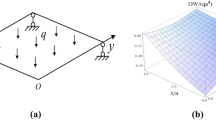
A square plate bounded within 0 ≤ X, Y ≤ a, Z = ±h planes with reference to the Cartesian coordinate system (X, Y, Z) is considered. The material of the plate is homogeneous and isotropic with elastic constants E (Young’s modulus), ν (Poisson’s ratio), and G (Shear modulus) that are related to each other by E = 2(1 + ν) G. For convenience, coordinates X, Y, Z and displacements (U, V, W) in non-dimensional form x = X/a, y = Y/a, z = Z/h, (u, v, w) = (U, V, W)/h and half-thickness ratio α = (h/a) are used. With the above notation and ⇄ indicating interchange, equilibrium equations in stress components are (with 3-D stress components as functions of coordinates x, y, and z)

$$\mathit{\alpha }\left({\mathit{\sigma }}_x{,}_x+{\mathit{\tau }}_{\mathit{xy}}{,}_y\right)+{\mathit{\tau }}_{\mathit{xz}}{,}_z=0\rightleftarrows \left(x,y\right)$$

(1a)

$$\mathit{\alpha }\left({\mathit{\tau }}_{\mathit{xz}}{,}_x+{\mathit{\tau }}_{\mathit{yz}}{,}_y\right)+{\mathit{\sigma }}_z{,}_z=0$$

(1b)

in which the suffix after ' , ’ denotes the partial derivative operator.

The plate is subjected to asymmetric load σ _z = ± (q₀/2) sin (πx/a) sin (πy/a) and zero shear stresses along z = ±1 faces. In a simply supported plate, conditions along x (and y) constant edges are

$${\mathit{\sigma }}_x=0\rightleftarrows \left(x,y\right),v=0\rightleftarrows \left(v,u\right),w=0$$

(2)

In displacement-based models, stress components are expressed in displacements via six stress–strain constitutive relations and six strain–displacement relations. These relations within the classical small deformation theory of elasticity are as follows:

Constitutive relations:

$$E{\epsilon }_x={\mathit{\sigma }}_x-\nu \left({\mathit{\sigma }}_y+{\mathit{\sigma }}_z\right)\rightleftarrows \left(x,y\right)$$

(3a)

$$E{\epsilon }_z={\mathit{\sigma }}_z-\nu \left({\mathit{\sigma }}_x+{\mathit{\sigma }}_y\right)$$

(3b)

$$\left[{\mathit{\tau }}_{\mathit{xy}},{\mathit{\tau }}_{\mathit{xz}},{\mathit{\tau }}_{\mathit{yz}}\right]=G\left[{\mathit{\gamma }}_{\mathit{xy}},{\mathit{\gamma }}_{\mathit{xz}},{\mathit{\gamma }}_{\mathit{yz}}\right]$$

(4)

Strain–displacement relations:

$$\left[{\mathit{\epsilon }}_x,{\mathit{\epsilon }}_y,{\mathit{\epsilon }}_z\right]=\left[u{,}_x,v{,}_y,w{,}_z\right]$$

(5)

$$\left[{\mathit{\gamma }}_{\mathit{xy}},{\mathit{\gamma }}_{\mathit{xz}},{\mathit{\gamma }}_{\mathit{yz}}\right]=\left[u{,}_y+v{,}_x,u{,}_z+w{,}_x,v{,}_z+w{,}_y\right]$$

(6)

Methods

Analysis consists of exact solutions of 3-D equations of bending problem with and without torsion, 2-D equations from Poisson’s theory and extended Poisson’s theory.

Exact solutions

With reference to the proper sequence of 2-D problems converging to a 3-D problem, an exact solution of the above-mentioned problem of a simply supported square plate presented briefly earlier (Vijayakumar 2011a) is described here to assess solutions of the present 2-D problems. Equilibrium equations in displacements in the 3-D problem are

$$\begin{array}{l}{\mathit{\alpha }}^2\mathit{\Delta u}+u{,}_{\mathit{zz}}+\frac{1}{1-2\nu }\mathit{\alpha }\left(\mathit{\alpha }u{,}_{\mathit{xx}}+\alpha v{,}_{\mathit{yx}}+w{,}_{\mathit{zx}}\right)\\ =0\rightleftarrows \left(x,y\right),\left(u,v\right)\end{array}$$

(7)

$${\mathit{\alpha }}^2\mathit{\Delta w}+w{,}_{\mathit{zz}}+\frac{1}{1-2\nu }\left(\mathit{\alpha }u{,}_{\mathit{xz}}+\mathit{\alpha }v{,}_{\mathit{yz}}+w{,}_{\mathit{zz}}\right)=0$$

(8)

Displacements are expressed in the form with $\mathit{\beta }=\sqrt{2}\alpha \pi$

$$\begin{array}{l}\mathrm{u}=\left({\mathrm{A}}_1\mathrm{sinh\beta z}+{\mathrm{A}}_2\mathrm{z}\mathrm{cosh\beta z}\right)\mathrm{cos\pi x}\mathrm{sin\pi y}\\ \rightleftarrows \left(\mathrm{x},\mathrm{y}\right),\left(\mathrm{u},\mathrm{v}\right)\end{array}$$

(9)

$$\mathrm{w}=\left({\mathrm{C}}_1\cosh \mathrm{\beta z}+{\mathrm{C}}_2\mathrm{z}\sinh \mathrm{\beta z}\right)\sin \mathrm{\pi x}\sin \mathrm{\pi y}$$

(10)

From satisfying the above equilibrium equations, one gets C₂ = √2A₂ = (2α π A₁ - β C₁) / (3–4 ν).

Zero shear stresses and vertical load condition along faces give

$$\begin{array}{l}{C}_1=\frac{\mathit{\beta }\tanh \mathit{\beta }+2\left(1-\nu \right)}{\mathit{\beta }tanh\mathit{\beta }-\left(1-2\nu \right)}\sqrt{2}{A}_1\\ =\left(1+\nu \right)\frac{\mathit{\beta }sinh\mathit{\beta }+2\left(1-\nu \right)cosh\mathit{\beta }}{\mathit{\beta }\left(sinh\mathit{\beta }cosh\mathit{\beta }-\mathit{\beta }\right)}\left(q_0/2E\right)\end{array}$$

(11)

From the above solutions, one obtains with ν = 0.3 and α = 1/6 (i.e., plate thickness ratio 2h/a = 1/3)

$$\begin{array}{l}\left(\mathrm{E}/2{\mathrm{q}}_0\right)\mathrm{w}\left(\mathrm{a}/2,\mathrm{a}/2,0\right)=3.49\\ \left(\mathrm{E}/2{\mathrm{q}}_0\right)\mathrm{w}\left(\mathrm{a}/2,\mathrm{a}/2,1\right)=2.37\end{array}$$

The above estimates correspond to those from the associate torsion problem since ω _z ≠ 0 in Equations 7 and 8. In the case ω _z = 0 decoupling bending and torsion problems, equilibrium equations are in terms of (u, v, σ _z ) given by

$$\begin{array}{l}\mathrm{E}\text{'}{\mathrm{\alpha }}^2\mathrm{\Delta u}+\mathrm{\mu \alpha }{\mathrm{\sigma }}_{\mathrm{z}}{,}_{\mathrm{x}}+{\mathrm{\tau }}_{\mathrm{xz},\mathrm{z}}=0\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)\\ \mathrm{\alpha }\left({\mathrm{\tau }}_{\mathrm{xz}}{,}_{\mathrm{x}}+{\mathrm{\tau }}_{\mathrm{yz}}{,}_{\mathrm{y}}\right)+{\mathrm{\sigma }}_{\mathrm{z}}{,}_{\mathrm{z}}=0\end{array}$$

Estimated vertical deflection parameters from solutions of the above equations are

$$\begin{array}{l}\left(\mathrm{E}/2{\mathrm{q}}_0\right)\mathrm{w}\left(\mathrm{a}/2,\mathrm{a}/2,0\right)=4.49\\ \left(\mathrm{E}/2{\mathrm{q}}_0\right)\mathrm{w}\left(\mathrm{a}/2,\mathrm{a}/2,1\right)=4.17\end{array}$$

Estimates from Kirchhoff’s theory and FSDT

The above face deflection parameter from Kirchhoff’s theory is 2.27. It is the same in all face parallel planes. Correction due to coupling with torsion is 1.45 (Vijayakumar 2011b), whereas it is 1.42 from FSDT and other sixth-order theories (Lewinski 1990). With reference to numerical values reported in Lewinski’s article, the above correction is less than 1.23 in Reissner’s 12th-order and other higher-order theories. It clearly shows that shear deformation theories and other higher-order theories do not lead to the solutions of bending problems. It is to be noted that vertical deflection w₀ from FSDT is usually considered to be w_0N, but its estimated value (3.69) of the deflection parameter is much nearer the w_0F.

Poisson’s theory

In Kirchhoff’s theory, the basic variable is w₀(x, y), and [u, v] are from [γ _xz , γ _yz ] ≡ 0 in the plate. In FSDT, w₀ is associated with z[u₁, v₁] through [γ _xz , γ _yz ]. In these theories and other shear deformation theories, σ _z is neglected in constitutive relations. In the present analysis, as in Kirchhoff’s theory and FSDT, σ _z is neglected initially in the semi-inverted constitutive relations

$${\mathrm{\sigma }}_{\mathrm{x}}=\mathrm{E}\text{'}\left({\mathrm{\epsilon }}_{\mathrm{x}}+\mathrm{\nu }{\mathrm{\epsilon }}_{\mathrm{y}}\right)+\mathrm{\mu }{\mathrm{\sigma }}_{\mathrm{z}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(12a)

$${\mathrm{\epsilon }}_{\mathrm{z}}=–\mathrm{\mu }\mathrm{e}+\left(1–2\mathrm{\nu }\mathrm{\mu }\right){\mathrm{\sigma }}_{\mathrm{z}}/\mathrm{E}$$

(12b)

in which e = (ε _x + ε _y ), E^′ = E / (1 - ν²) and μ = ν / (1 - ν).

In-plane variables (u₁, v₁) uncoupled from w₀ are basic variables as in earlier investigations (Vijayakumar 20092011a, b). Due to the condition ω _z = 0 required to decouple bending and torsion problems, one obtains reactive transverse stresses from thickness-wise integration of equilibrium equations

$${\mathrm{\tau }}_{\mathrm{xz}}=\mathrm{E}\text{'}{\mathrm{f}}_2\left(\mathrm{z}\right)\mathrm{\alpha }{\mathrm{e}}_1{,}_{\mathrm{x}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(13)

$${\mathrm{\sigma }}_{\mathrm{z}3}=–\mathrm{E}\text{'}{\mathrm{f}}_3\left(\mathrm{z}\right){\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{e}}_1$$

(14)

in which f₂ = (1 - z²) / 2 and f₃ = (z - z³/3) / 2.

Constitutive relation gives ε _z = -μ f₁e₁ with f₁ = z and e₁ = ε_{z 1}. From satisfying face load condition, one gets the equation governing e₁ as

$$\left(2/3\right)\mathrm{E}\text{'}{\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{e}}_1+\mathrm{q}=0$$

(15)

In Poisson’s theory, e₁ in the above equation is replaced by ψ₂(x, y), and it is solved with edge condition ψ₂ = 0 in the simply supported plate problem. As mentioned earlier, the function ψ₂ is related to normal strain ε _z and ψ₂ = 0 implies ε _z = 0.

Equations governing u₁ and v₁ are given by

$$\mathrm{\alpha }\left({\mathrm{u}}_1{,}_{\mathrm{x}}+{\mathrm{v}}_1{,}_{\mathrm{y}}\right)={\mathrm{\psi }}_2,\mathrm{\alpha }\left({\mathrm{u}}_1{,}_{\mathrm{y}}–{\mathrm{v}}_1{,}_{\mathrm{x}}\right)=0$$

(16)

so that

$${\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{u}}_1=\mathrm{\alpha }{\mathrm{\psi }}_2{,}_{\mathrm{x}},{\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{v}}_1=\mathrm{\alpha }{\mathrm{\psi }}_2{,}_{\mathrm{y}}$$

(17)

Homogeneous equations show that u₁ and v₁ are conjugate harmonic functions coupled through conditions (2) on u₁ and v₁ along x (and y) constant edge

$${\mathrm{u}}_1=0\mathrm{or}\mathrm{E}\text{'}{\mathrm{u}}_1{,}_{\mathrm{x}}={\mathrm{T}}_{\mathrm{x}}\left(\mathrm{y}\right)\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),\left(\mathrm{u},\mathrm{v}\right)$$

(18a)

$${\mathrm{v}}_1=0\mathrm{or}2\mathrm{G}{\mathrm{v}}_1{,}_{\mathrm{x}}={\mathrm{T}}_{\mathrm{xy}}\left(\mathrm{y}\right)\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),\left(\mathrm{u},\mathrm{v}\right)$$

(18b)

In the above equations, T _x and T _xy are prescribed stress distributions.

From zero face shear conditions, one obtains w₀(x, y) in terms of known [u₁, v₁] in the form

$$\mathrm{\alpha }{\mathrm{w}}_0\left(\mathrm{x},\mathrm{y}\right)=-\int \left[{\mathrm{u}}_1\mathrm{dx}+{\mathrm{v}}_1\mathrm{dy}\right]$$

(19)

The vertical deflection thus obtained corresponds to face deflection (note that zero face shear conditions do not participate in the 3-D domain equations unlike in Kirchhoff’s theory). Its zero value along the edge requires simply a support to prevent vertical deflection of intersection of the face with the wall of the plate. Such a support also ensures zero deflection of the neutral plane along its edge. It is because the face and neutral plane deflections (w_0F, w_0N) are one and the same since w(x, y, z) with (w₂ + ε_{z 1})= 0 can be expressed as

$$\begin{array}{l}\mathrm{w}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)={\mathrm{w}}_{0\mathrm{F}}\left(\mathrm{x},\mathrm{y}\right)+{\mathrm{f}}_2\left(\mathrm{z}\right){\mathrm{w}}_2\\ ={\mathrm{w}}_{0\mathrm{N}}\left(\mathrm{x},\mathrm{y}\right)–{\mathrm{z}}^2{\mathrm{\epsilon }}_{\mathrm{z}1}/2\end{array}$$

(20)

However, f₂(z) of the second-order correction w₂ to the vertical deflection w is parabolic; thereby, the applied or reactive transverse shear stress along an edge is parabolic.

Equations 15 and 17 form a sixth-order system to determine ψ₂, u₁, and v₁. Relevant three edge conditions correspond to those required by Poisson. Hence, the theory is designated as 'Poisson's theory of plates in bending’, parallel to Kirchhoff's theory. It is significant to note that the condition w ₀ = 0 prescribed along segments of the edge has no effect on the displacements [u ₁ , v ₁ , w ₀ ] obtained from the present Poisson’s theory. It is to be noted that Poisson’s theory gives an additional value of 0.27 to w(x, y, 1) due to ε_{z 1} to the earlier w_0F estimate from Kirchhoff’s theory.

Numerical results and discussion

After the first stage of iteration involving f₃(z)[u_3,v₃] in the earlier work (Vijayakumar 2011a), higher-order correction to w₀ uncoupled from torsion is 1.26 so that total correction to the value from Kirchhoff’s theory is about 1.54. Neutral plane deflection w_0N is corrected from the solution of a supplementary problem. Here the total correction over face deflection is about 0.66 giving a value of 4.46 which is very close to the exact value 4.49. Hence, it is safe to conclude that second-order corrections in the displacements and transverse stresses from the iterative method serve the purpose of assessing data from Kirchhoff’s theory and FSDT.

Solution for w₀ consists of satisfying (i) zero face shear conditions and (ii) edge support conditions in w₀. In Kirchhoff’s theory, both of these requirements are met through the single variable w₀ governed by a fourth-order equation. In Reissner (1945), the average vertical displacement satisfies condition (ii), and in FSDT, condition (i) is not satisfied but its effect is included through shear energy correction factor. In any case, both of them are approximations to associated torsion problem (Vijayakumar 2011b). The present analysis provides some clarity with regard to the preliminary solution of primary flexure problem. It shows that determining in-plane displacements, bending stresses, and reactive transverse stresses from integration of equilibrium equations is uncoupled from w₀. However, edge condition w₀ = 0 or contracted stress resultant V _x = V _xo in Kirchhoff’s theory is different from the condition along x (and y) = constant edge

$${\mathrm{\epsilon }}_{\mathrm{z}}=0\mathrm{or}{\mathrm{\tau }}_{\mathrm{xz}2}={\mathrm{T}}_{\mathrm{xz}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

Error in the estimated value (=3.81) of w_0F is relatively high compared to the accuracy achieved in neutral plane deflection. In the earlier work (Vijayakumar 2011a), estimation of w_0F is further improved by modifying in-plane displacements (u*_3,v*₃) such that (τ_{xz 2}, τ_{yz 2}) are independent of ε_{z 1}. In the present example, correction to the face deflection changes to 1.43 so that face deflection value is 3.97 (=2.27 + 0.27 + 1.43) which is under 4.7% from the exact value. The correction 1.43 to the face deflection is due to ε_{z 3} from the constitutive relation. Determination of ε_{z 3} in terms of (σ_{z 3}, u₃, v₃) involves lengthy algebra and arithmetical work.

The above analysis consists of a basic sixth-order system and a supplementary fourth-order system. Since the second-order corrections are mainly due to inclusion of σ_{z 1} in the in-plane constitutive relations, it is much simpler to find its effect from the following extended Poisson’s theory without consideration of higher-order displacement components (u₃, v₃).

Improved estimates

The analysis presented here eliminates the assumptions in Kirchhoff’s theory. Preliminary solution consists of a combination of solutions of four problems presented elsewhere (Vijayakumar 2013) in the analysis of bending of symmetric laminates with anisotropic plies in which the analysis of the present title problem is included as illustrative example. The first one is a solution of an auxiliary problem to account for thickness-wise linear distribution of σ _z = z q(x, y) / 2 neglected in the constitutive relations in Kirchhoff’s theory and shear deformation theories. The second one is concerned with determining [u_1c, v_1c] due to σ _z = z q(x, y) / 2 in the in-plane constitutive relations. In the case of a simply supported plate, [u_1c, v_1c] are governed by a fourth-order system with homogeneous in-plane edge conditions. The third one consists of solution of a fourth-order system of finding [u₁, v₁] _b due to transverse stresses obtained in the second problem. Finally, the fourth one consists of solution of a fourth-order system of a supplementary problem to obtain a more or less uniform approximation of thickness-wise distributions of deformations in the plate.

Auxiliary problem

One finds that σ_{z 1} is neglected in shear deformation theories. Moreover, transverse shear stress conditions along the edges are specified with reference to reactive (statically equivalent) stresses in the form of parabolic distributions, though mathematically valid but not practical. Kirchhoff’s theory is based on assuming identically zero transverse shear strains and neglecting σ_{z 1} in the constitutive relations. The former assumption results in highly constrained deformations of the plate.

In view of the above observations, transverse shears along faces of the plate are initially assumed in the form [τ_{xz 0}, τ_{yz 0}] = [T _xz (x, y), T _yz (x, y)]. It is more reasonable and practical to assume that they are the same in face parallel planes instead of w₀(x, y). Correspondingly, [τ_{xz 0}, τ_{yz 0}] along constant x (and y) edges are

$${\mathrm{\tau }}_{\mathrm{xz}0}={\mathrm{T}}_{\mathrm{xz}}\left(\mathrm{y}\right)\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(21)

They are more realistic edge conditions and more practical if they are independent of in-plane coordinates. In view of Equation 1b, [τ_{xz 0}, τ_{yz 0}] are expressed as

$$\left[{\mathrm{\tau }}_{\mathrm{xz}0},{\mathrm{\tau }}_{\mathrm{yz}0}\right]=\mathrm{\alpha }\left[{\mathrm{\psi }}_0{,}_{\mathrm{x}},{\mathrm{\psi }}_0{,}_{\mathrm{y}}\right]$$

(22)

so that ψ₀(x, y) is governed by

$${\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{\psi }}_0+{\mathrm{\sigma }}_{\mathrm{z}1}=0$$

(23)

in which ∆ is the plane Laplace operator (∂²/∂x² + ∂²/∂y²) and σ_{z 1} = q/2 with σ _z = z σ_{z 1}.

The above equation is to be solved with edge condition either ψ₀ = 0 or its normal gradient equal to the applied transverse shear stress along the edge. It is to be noted that the assumed face stresses [T _xz , T _yz ] correspond to [τ_{xz 0}, τ_{yz 0}] in Equation 21 consistent with applied or reactive vertical shears along the edges.

The condition ψ₀ = 0 is different from the usual condition w₀ = 0 in Kirchhoff’s theory. The function ψ₀ is related to normal strain ε _z which is proportional to ∆w₀. If the plate is free of applied transverse stresses, that is, the plate is subjected to bending and twisting moments only, ψ₀(x, y), thereby, ∆w₀ ≡ 0 from Equation 2 (In Kirchhoff’s theory, the tangential gradient of ∆w₀ is proportional to the corresponding gradient of applied τ _xy along the edge of the plate implied from Kelvin and Tait’s physical interpretation of the contracted transverse shear condition). This Laplace equation is not adequate to satisfy two in-plane edge conditions. One needs its conjugate harmonic functions implying v₁, _x = u₁, _y to express in-plane displacements in the form

$$\left[{\mathrm{u}}_1,{\mathrm{v}}_1\right]=-\mathrm{\alpha z}\left[{\mathrm{w}}_{0,\mathrm{x}}+{\mathrm{\phi }}_{0,\mathrm{y}},{\mathrm{w}}_{0,\mathrm{y}}-{\mathrm{\phi }}_{0,\mathrm{x}}\right]$$

(24)

The function φ₀ was introduced earlier by Reissner (1945) as a stress function in satisfying Equation 2.

After finding w₀ and φ₀ from solving in-plane equilibrium equations (Equation 1a,b), correction w_0c to w₀ from zero face shear conditions is given by

$${\mathrm{w}}_{0\mathrm{c}}=\int \left[{\mathrm{\phi }}_{0,\mathrm{y}}\mathrm{dx}-{\mathrm{\phi }}_{0,\mathrm{x}}\mathrm{dy}\right]$$

(25)

One should note here that w(x, y) = w₀ + w_0c is the face deflection. It does not satisfy the prescribed w = 0 edge condition. As mentioned in Poisson’s theory, its zero value along the edge requires only a support to prevent the vertical deflection of intersection of the face with the wall of the plate. Correction w_0c is obviously due to the tangential gradient of τ _xy in vertical shear V_x(y). In Kirchhoff’s theory, w(x, y) is a bi-harmonic function. It is obtained in the simply supported (hard type) plate satisfying w = 0 along with in-plane condition along the x (and y) constant edge

$$\mathrm{w}{,}_{\mathrm{x}}=0\mathrm{or}\mathrm{E}\text{'}\mathrm{w}{,}_{\mathrm{xx}}={\mathrm{T}}_{\mathrm{x}}\left(\mathrm{y}\right)\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(26)

In Kirchhoff’s theory, w(x, y) obtained above corresponds to neutral plane deflection w_0N with edge condition w_0N = 0. Obviously, this edge condition is not required to obtain [u₁, v₁] and face deflection. With reference to the present analysis, it is relevant to note the following observations: In the preliminary solution, σ _z , α[τ _xz , τ _yz ], α²[σ _x , σ _y , τ _xy ] are of O(1). As such, estimation of in-plane stresses, thereby, in-plane displacements, are not dependent on w₀. The support condition w₀ = 0 along the plate edge does not play any role in the estimation of in-plane displacements. In fact, Kirchhoff’s theory gives only a lower bound for α for the validity of small deformation theory. Validity of its application is a questionable proposition for small values of α even slightly higher than this lower bound since the theory gives highly constrained solutions for displacements. Shear deformations are included in FSDT in which face shear conditions are not satisfied and Reissner’s theory in which edge condition on w₀ is not satisfied. Both of these theories give more or less the same maximum vertical deflection. It shows that satisfying either edge condition on w₀ or face shear conditions has equal effect on deformations. In each of these theories, both conditions are satisfied only in the limit. Limiting process, however, nullifies the effect due to the applied or reactive edge stress τ _xy in the bending problem. Moreover, linear variation of σ _z in z is neglected in constitutive relations. The present analysis shows that this linear σ _z results in more flexible plate deformations in conjunction with zero face shear conditions.

In 3-D problems of homogeneous plates, w₀(x, y, 0) and w₀(x, y, 1) are the neutral plane deflection w_0N and face deflection w_0F, respectively. Both of them are 2-D functions and they are from the thickness-wise integration of ε _z in a 2-D problem. Determination of w_0N used as an unknown variable is dependent on edge support condition and that of w_0F on zero face shear conditions. The present analysis is with reference to finding w_0F and the need to satisfy that edge condition on w_0N does not exist.

[u_1c, v_1c] due to transverse stresses [τ_{xz 0}, τ_{yz 0}, zσ_{z 1}]

With reference to the second problem mentioned earlier, the in-plane displacements to be determined are z(u₁, v₁) _c . Here transverse stresses are expressed in the form

$${\mathrm{\tau }}_{\mathrm{xz}}={\mathrm{\tau }}_{\mathrm{xz}0}+{\mathrm{f}}_2{\mathrm{\tau }}_{\mathrm{xz}2\mathrm{c}}$$

(27)

$${\mathrm{\tau }}_{\mathrm{yz}}={\mathrm{\tau }}_{\mathrm{yz}0}+{\mathrm{f}}_2{\mathrm{\tau }}_{\mathrm{yz}2\mathrm{c}}$$

(28)

$${\mathrm{\sigma }}_{\mathrm{z}}=\mathrm{z}{\mathrm{\sigma }}_{\mathrm{z}1}+{\mathrm{f}}_3{\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}$$

(29)

in which (τ_{xz 2}, τ_{yz 2}, σ_{z 3})_c yet to be determined are corrections due to (u₁, v₁)_c. Since the added terms are dependent on material constants, the above transverse shear stresses are no longer applied stresses along the edges.

In order to keep σ_{z 3c} as a free variable, the function f₃(z) in Equation 29 is replaced by f₃*(z) = (f₃ - z/3) so that f₃*(±1) = 0. Then the face load condition is satisfied with

$${\mathrm{\sigma }}_{\mathrm{z}}=\mathrm{z}\left(\mathrm{q}/2\right)+\left[{\mathrm{f}}_3*{\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}\right]$$

(30)

In further analysis, it is convenient to express σ _z with β₁ = 1/3 in the form

$${\mathrm{\sigma }}_{\mathrm{z}}=\left[\mathrm{q}/2-{\mathrm{\beta }}_1{\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}\right]\mathrm{z}+{\mathrm{f}}_3\left(\mathrm{z}\right){\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}$$

(31)

In-plane distributions [u₁, v₁] _c are modified in the form with

$${\mathrm{u}}_{1\mathrm{c}}*={\mathrm{u}}_{1\mathrm{c}}+{\mathrm{\tau }}_{\mathrm{xz}0}/\mathrm{G}–\mathrm{\alpha }{\mathrm{w}}_{0,\mathrm{x}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),\left(\mathrm{u},\mathrm{v}\right)$$

(32)

The introduction of w₀(x, y) term in the above equation is to avoid its participation in the static in-plane equilibrium equations. Modified transverse shear stresses from stress–strain and strain–displacement relations are

$${\mathrm{\tau }}_{\mathrm{xz}2\mathrm{c}}=\mathrm{G}{\mathrm{u}}_{1\mathrm{c}}+{\mathrm{\tau }}_{\mathrm{xz}0}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),\left(\mathrm{u},\mathrm{v}\right)$$

(33)

Substitution of the above shear stresses in Equation 1b with σ _z = z[q/2 - β₁σ_{z 3c}] and e_1c = (ε_{x 1} + ε_{y 1}) _c gives

$$\mathrm{G}{\mathrm{e}}_{1\mathrm{c}}={\mathrm{\beta }}_1{\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}$$

(34)

For the use of [u₁*, v₁*] _c in the integration of equilibrium equations (Equation 1a,b), displacements [u₁, v₁] _c due to the requirement of v_1c,x = u_1c,y to decouple bending and torsion problems are expressed in the form

$${\left[{\mathrm{u}}_1,{\mathrm{v}}_1\right]}_{\mathrm{c}}=-\mathrm{\alpha }{\left[{\mathrm{\psi }}_1{,}_{\mathrm{x}},{\mathrm{\psi }}_1{,}_{\mathrm{y}}\right]}_{\mathrm{c}}$$

(35)

in the case of hard and/or soft simply supported edge conditions.

Contributions of ψ_1c and w₀ in [u₁, v₁] _c * are one and the same in giving corrections to w(x, y, z) and transverse stresses (in fact, the contribution of w₀ is through strain–displacement relations in static equilibrium equations and through constitutive relations in through-thickness integration of equilibrium equations). Since w₀ does not participate in the in-plane static equations, its contribution is through [u₁, v₁] _c in the integrated in-plane equilibrium equations. Hence, w₀ in [u₁, v₁] _c * is replaced by ψ_1c (so as to be independent of w₀ used in strain–displacement relations) so that [u₁, v₁, ε_{x 1}, ε_{y 1}, γ_{xy 1}] _c * are

$${\mathrm{u}}_{1\mathrm{c}}*=\left(2{\mathrm{u}}_{1\mathrm{c}}+{\mathrm{\gamma }}_{\mathrm{xz}0}\right)\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),\left(\mathrm{u},\mathrm{v}\right)$$

(36)

$${\mathrm{\epsilon }}_{\mathrm{x}1\mathrm{c}}*=\left(2{\mathrm{\epsilon }}_{\mathrm{x}1\mathrm{c}}+\mathrm{\alpha }{\mathrm{\gamma }}_{\mathrm{xz}0,\mathrm{x}}\right)\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(37a)

$${\mathrm{\gamma }}_{\mathrm{xy}1\mathrm{c}}*=\left[2{\mathrm{\gamma }}_{\mathrm{xy}1\mathrm{c}}+\mathrm{\alpha }\left({\mathrm{\gamma }}_{\mathrm{xz}0}{,}_{\mathrm{y}}+{\mathrm{\gamma }}_{\mathrm{yz}0}{,}_{\mathrm{x}}\right)\right]$$

(37b)

From the integration of Equation 1a using the above strains in Equation 12a along with v₁, _x = u₁, _y , reactive transverse stresses are

$${\mathrm{\tau }}_{\mathrm{xz}2\mathrm{c}}=\mathrm{\alpha }\left(\mathrm{E}\text{'}{\mathrm{e}}_{1\mathrm{c}}*+\mathrm{\mu }{\mathrm{\sigma }}_{\mathrm{z}1}\right){,}_{\mathrm{x}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(38)

$$\mathrm{\alpha }{\left({\mathrm{\tau }}_{\mathrm{xz}2}{,}_{\mathrm{x}}+{\mathrm{\tau }}_{\mathrm{yz}2}{,}_{\mathrm{y}}\right)}_{\mathrm{c}}*+{\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}=0$$

(39)

One equation governing in-plane displacements (u₁, v₁), noting that σ_{z 3} from Equation 29 is negative of the one from Equation 34 due to (f₃, _zz + f₁) = 0, is given by

$$\mathrm{\alpha }{\mathrm{\beta }}_1{\left({\mathrm{\tau }}_{\mathrm{xz}2}{,}_{\mathrm{x}}+{\mathrm{\tau }}_{\mathrm{yz}2}{,}_{\mathrm{y}}\right)}_{\mathrm{c}}=\mathrm{G}{\mathrm{e}}_{1\mathrm{c}}$$

From Equations 29, 34, and 39, one gets

$$\mathrm{E}\text{'}{\mathrm{\beta }}_1{\mathrm{\alpha }}^4\mathrm{\Delta \Delta }\left(2{\mathrm{\psi }}_{1\mathrm{c}}+{\mathrm{\psi }}_0/\mathrm{G}\right)+\mathrm{G}{\mathrm{e}}_{1\mathrm{c}}-\mathrm{\mu }{\mathrm{\beta }}_1{\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{\sigma }}_{\mathrm{z}1}=0$$

(40)

The above equation becomes a fourth-order equation in ψ_1c to be solved with two in-plane conditions along constant x (and y) edges

$${\mathrm{\sigma }}_{\mathrm{x}1\mathrm{c}}*=0\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),{\mathrm{v}}_{1\mathrm{c}}*=0\rightleftarrows \left(\mathrm{u},\mathrm{v}\right)$$

(41)

After some algebra with G = E/2(1 + ν), μ = ν/(1 - ν) and ψ_1c = c_1c sin (πx) sin (πy), the equation governing c_1c becomes

$$[{\mathrm{\beta }}^2+\frac{3\left(1-\mathit{v}\right)}{4}{\mathrm{c}}_{1\mathrm{c}}-\frac{\left(1+\mathit{v}\right)}{8}\left(2-\mathit{v}\right)\left(2{\mathrm{q}}_0/\mathrm{E}\right)=0$$

(42)

From the above equation, one gets c_1c = 0.26(2q₀/E) with ν = 0.3 and α = 1/6.

Face deflection w_0c from the integration of transverse shear strain–displacement relations is

$${\mathrm{w}}_0=\left\{\left[\left(1+\mathrm{\nu }\right)/2{\mathrm{\beta }}^2\right]\left(2{\mathrm{q}}_0/\mathrm{E}\right)+{\mathrm{c}}_{1\mathrm{c}}\right\}$$

(43)

from which w_0c = 1.39(2q₀/E) in the present example.

Primary displacements z(u₁, v₁)_b

In the absence of higher-order in-plane displacement terms, transverse stresses in the bending problem are

$${\mathrm{\tau }}_{\mathrm{xz}2\mathrm{b}}={\mathrm{\tau }}_{\mathrm{xz}0}+{\mathrm{\tau }}_{\mathrm{xz}2\mathrm{c}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(44)

$${\mathrm{\sigma }}_{\mathrm{z}3\mathrm{b}}={\mathrm{\sigma }}_{\mathrm{z}1}+{\mathrm{\sigma }}_{\mathrm{z}3\mathrm{c}}$$

(45)

Since the added terms are dependent on material constants, above transverse shear stresses are no longer applied stresses along the edges but they are completely known. By expressing [τ_{xz 2}, τ_{yz 2}] _b as gradients of a function ψ_2b, one obtains

$$\mathrm{\alpha }{\mathrm{\psi }}_{2\mathrm{b}}=\int \left({\mathrm{\tau }}_{\mathrm{xz}2\mathrm{b}}\mathrm{dx}+{\mathrm{\tau }}_{\mathrm{yz}2\mathrm{b}}\mathrm{dy}\right)$$

(46)

Equations governing u_1b and v_1b as in the above Poisson’s theory are given by

$$\begin{array}{l}\mathrm{\alpha }\left({\mathrm{u}}_{1\mathrm{b}}{,}_{\mathrm{x}}+{\mathrm{v}}_{1\mathrm{b}}{,}_{\mathrm{y}}\right)=\left(\mathrm{G}/\mathrm{E}\text{'}\right){\mathrm{\psi }}_{2\mathrm{b}},\\ \mathrm{\alpha }\left({\mathrm{u}}_{1\mathrm{b}}{,}_{\mathrm{y}}‒{\mathrm{v}}_{1\mathrm{b}}{,}_{\mathrm{x}}\right)=0\end{array}$$

(47)

so that

$${\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{u}}_{1\mathrm{b}}=\left(\mathrm{G}/\mathrm{E}\text{'}\right)\mathrm{\alpha }{\mathrm{\psi }}_{2\mathrm{b}}{,}_{\mathrm{x}},$$

(48a)

$${\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{v}}_{1\mathrm{b}}=\left(\mathrm{G}/\mathrm{E}\text{'}\right)\mathrm{\alpha }{\mathrm{\psi }}_{2\mathrm{b}}{,}_{\mathrm{y}}$$

(48b)

In the case of a simply supported plate, solutions for [u₁, v₁] _b from the above pair of second-order equations are coupled through conditions along x (and y) constant edges

$${\mathrm{u}}_{1\mathrm{b}}{,}_{\mathrm{x}}=0,{\mathrm{v}}_{1\mathrm{b}}=0\rightleftarrows \left(\mathrm{u},\mathrm{v}\right)$$

(49)

w_0b due to (u_1b, v_1b)

Here it is convenient to take (u_1b, v_1b) = -α[ψ₁, _x , ψ₁, _y ] _b as in Kirchhoff’s theory so that one obtains the equation governing ψ₁ as

$$\mathrm{E}\text{'}{\mathrm{\alpha }}^4\mathrm{\Delta \Delta }{\mathrm{\psi }}_{1\mathrm{b}}=3\left[\mathrm{q}/2+\mathrm{G}{\mathrm{e}}_{1\mathrm{c}}/{\mathrm{\beta }}_1\right]$$

(50)

The above equation is expressed in the form

$${\mathrm{\alpha }}^4\mathrm{\Delta \Delta }{\mathrm{\psi }}_{1\mathrm{b}}=\frac{3\left(1-\mathit{v}\right)\left(1+\mathit{v}\right)}{4}\left(2\mathrm{q}/\mathrm{E}\right)-\frac{3\left(1-\mathit{v}\right)}{2}{\mathrm{\alpha }}^2\mathrm{\Delta }{\mathrm{\psi }}_{1\mathrm{c}}$$

(51)

from which

$${\mathrm{c}}_{1\mathrm{b}}=\left[\frac{3\left(1-\mathit{v}\right)\left(1+\mathit{v}\right)}{4}\left(2\mathrm{q}/\mathrm{E}\right)+\frac{3\left(1-\mathit{v}\right)}{2}{\mathrm{\beta }}^2{\mathrm{c}}_{1\mathrm{c}}\right]/{\mathrm{\beta }}^4$$

(52)

In the present example, the estimated c_1b is 2.42(2q₀/E), (=2.27 + 0.15). It is also equal to w_0b from the integration of strain–displacement relations.

The estimated face deflection (E/2q₀) w_F = 4.08 (=2.27 + 0.27 + 1.39 + 0.15) which is fairly close to the exact value (4.17). It shows that the solution to w from the present analysis provides proper correction to the estimation of face deflection. It is underestimated by 2.16%.

Supplementary problem

Corrective in-plane displacements in the supplementary problem are assumed in the form

$${\mathrm{u}}_{\mathrm{s}}={\mathrm{u}}_{1\mathrm{s}}\sin \left(\mathrm{\pi }\mathrm{z}/2\right)\rightleftarrows \left(\mathrm{u},\mathrm{v}\right)$$

(53)

In-plane stresses are

$${\mathrm{\sigma }}_{1\mathrm{si}}=\left(\mathrm{E}\text{'}{\mathrm{\epsilon }}_{1\mathrm{sj}}+\mathrm{\mu }{\mathrm{\sigma }}_{\mathrm{z}1}\right)\sin \left(\mathrm{\pi }\mathrm{z}/2\right)$$

(54)

With the above in-plane stresses along with [τ _xz , τ _yz ] = [τ_{xz 2}, τ_{yz 2}] _s cos (π z/2) and σ_{z 3} = σ_{z 3s} sin (π z/2), the integration of equilibrium equations gives

$${\mathrm{\tau }}_{\mathrm{xz}2\mathrm{s}}=-\left(2/\mathrm{\pi }\right)\mathrm{\alpha }\left(\mathrm{E}\text{'}{\mathrm{e}}_{1\mathrm{s}}+\mathrm{\mu }{\mathrm{\sigma }}_{\mathrm{z}1}\right){,}_{\mathrm{x}}\rightleftarrows \left(\mathrm{x},\mathrm{y}\right)$$

(55)

$${\mathrm{\sigma }}_{\mathrm{z}3\mathrm{s}}={\left(2/\mathrm{\pi }\right)}^2{\mathrm{\alpha }}^2\mathrm{\Delta }\left(\mathrm{E}\text{'}{\mathrm{e}}_{1\mathrm{s}}+\mathrm{\mu }{\mathrm{\sigma }}_{\mathrm{z}1}\right)$$

(56)

In-plane distributions u_1s and v_1s are added as corrections to the known in-plane displacements (u₁*, v₁*) so that (u, v) in the supplementary problem are

$$\mathrm{u}=\left({\mathrm{u}}_1*+{\mathrm{u}}_{1\mathrm{s}}\right)\sin \left(\mathrm{\pi z}/2\right)\rightleftarrows \left(\mathrm{u},\mathrm{v}\right)$$

(57)

in which u₁* = (u_1c* + u_1b).

By equating σ_{z 3s} (from the integration of Equation 1a,b with s variables) with β₁σ_{z 3} (from static equations with * variables), one equation governing [u_1s, v_1s] is

$${\left(2/\mathrm{\pi }\right)}^2{\mathrm{\alpha }}^2\mathrm{\Delta }\left(\mathrm{E}\text{'}{\mathrm{e}}_{1\mathrm{sj}}+\mathrm{\mu }{\mathrm{\sigma }}_{\mathrm{z}1}\right)={\mathrm{\beta }}_1{\mathrm{\sigma }}_{\mathrm{z}3}$$

(58)

By expressing [u_1s, v_1s] = -α [ψ_1s, _x , ψ_1s, _y ] due to the second equation v_1s, _x = u_1s, _y , Equation 58 becomes a fourth-order equation in ψ_1s to be solved with two in-plane conditions along constant x (and y) edges in the present example

$${\mathrm{\sigma }}_{\mathrm{x}1\mathrm{s}}=0\rightleftarrows \left(\mathrm{x},\mathrm{y}\right),{\mathrm{v}}_{1\mathrm{s}}=0\rightleftarrows \left(\mathrm{v},\mathrm{u}\right)$$

(59)

ψ_1s is related to e_1c by the equation

$$\mathrm{E}\text{'}\left(4/{\mathrm{\pi }}^2\right){\mathrm{\alpha }}^4\mathrm{\Delta \Delta }{\mathrm{\psi }}_{1\mathrm{s}}=\mathrm{G}{\mathrm{e}}_{1\mathrm{c}}$$

(60)

c_1s is related to c_1c by the equation

$$\left(\mathrm{E}/2{\mathrm{q}}_0\right){\mathrm{c}}_{1\mathrm{s}}=\left[\frac{1-\mathrm{v}}{2}{\mathrm{\pi }}^2-{\mathrm{\beta }}_1{}^2\right]\left(\mathrm{E}/2{\mathrm{q}}_0\right){\mathrm{c}}_{1\mathrm{c}}$$

(61)

so that c_1s = 0.55(2q₀/E) with ν = 0.3 and α = 1/6. Neutral plane deflection w_0N = 4.36(2q₀/E), (=2.27 + 0.15 + 1.39 + 0.55) is underestimated by 2.90% from the exact value (4.49).

Evaluation of neutral plane deflection involves u_1c and u_1s associated with f₂(z) and cos (πz/2) distributions of transverse shear stresses, respectively. As such, the solution of the present auxiliary problem provides second-order corrections to the solutions of the primary problem. It is to be noted that the wide variation of percentage of errors from 0.67 to 4.80 in w along the vertical line from the neutral plane to the face plane at the first stage of iteration using (u₃, v₃) in Poisson’s theory is reduced from 2.16 to 2.90 from the face plane to the neutral plane without using (u₃, v₃) in extended Poisson’s theory. One iteration using (u₃, v₃) is expected to reduce this gap even further along with decreased percentage of errors. A significant implication of this observation is that solution of the present auxiliary problem is necessary so as to obtain a more or less uniform approximation to thickness-wise distributions of deformations.

The fourteenth-order system of equations in the analysis of a simply supported plate presented here forms the initial set in the iterative procedure. Moreover, the analysis clearly establishes that the second-order corrections in Kirchhoff’s theory are mainly due to inclusion of σ _z = z σ_{z 1}in the constitutive relations and not due to consideration of shear deformations presumed in FSDT and Reissner’s theory. It is possible to decrease the percentage of errors in the estimation of w(x, y z) by considering the influence of in-plane displacements thus obtained in estimation of transverse stresses. Successive iterative steps consist of a pair of fourth-order system of equations forming a proper sequence of sets of 2-D problems converging to a 3-D problem.

Conclusions

Estimation of transverse stresses in the preliminary solution is independent of material constants through Poisson’s theory in the analysis of primary bending problem defined from Kirchhoff’s theory. Hence, it is unaltered in the analysis of bending of homogeneous and laminated plates with orthotropic and anisotropic materials. Application of transverse shear stress independent of thickness coordinate z along the edges of the plate is more practical instead of stress resultants which have no unique z-distributions. Coupling of w₀(x, y) in obtaining in-plane displacements which are the root cause for the Poisson-Kirchhoff boundary condition paradox is eliminated. In addition, inclusion of the tangential gradient of applied in-plane shear stress in transverse shear in Kirchhoff’s theory is removed. Vertical stress σ _z linear in z neglected in Kirchhoff’s theory and shear deformation theories gives primary second-order corrections instead of shear deformations. Thickness-wise distributions of displacements in terms of polynomials in z are not adequate to reduce 3-D problems into a sequence of 2-D problems.