The discussion on optimization models of pure bending beam

Abstract

This article is devoted to shape optimization design of pure bending beams under single loading condition. Compliance minimization with material volume constraint, the maximum stress minimization problem, and the maximum displacement are considered. In the case of trusses, it has been shown that the former two problems have the same optimal topology. The possibility of extending this result for pure bending beam problems is examined in the present work. First, the comparison of the optimum design results between the maximum displacement, the conventional mean compliance, and the maximum stress is carried out by an example of optimal cross-sectional design of a continuous beam. Then, geometric average displacement (GAD) is introduced in optimization models of linearly elastic structures. The elevated accuracy in results achieved with GAD is shown in this article.

Introduction

Structural optimization is one of the most challenging research topics in the field of computational mechanics. It has received more and more attention recently because of its great potential application in many industrial areas. Its importance lies in the fact that the appropriate result of structural design is generally the most decisive factor that influences the product efficiency.

Structural optimization, especially topology optimization, is being used increasingly in aerospace vehicles, maritime carriers, wind turbine blades, and various mechanical equipment where high strength, high stiffness, and low weight are important. In such applications, the problem of selecting a suitable optimization model has been investigated for a long time. In the vast literature on structural optimization model, arguably the two most studied problems are stress-constrained weight minimization and material volume-constrained compliance minimization. Indeed, Cox (1965) succeeded to prove that results attained via compliance minimization model would be equivalent to Michell's truss (stress-constrained weight minimization result) in 1965.It has been shown a long time ago that these seemingly different problems possess equal optimal topologies (result), when the truss is subject to a single loading condition and the allowable stresses in tension and compression are equal (Dorn et al. 1964; Hemp 1973). This result has been extended by Achtziger (1996) for cases where the allowable stresses in tension and compression are not equal.

Despite these successes, most of the topology optimization problems were modeled to minimize the compliance of the structures, following the methods adopted by Bendsøe and Kikuchi. The optimization problems of minimum compliance have been widely studied in the relevant literature (Xie et al. 2012; Bendsøe 1989; Eschenauer and Olhoff 2001; Sethian and Wiegmann 2000; Xie and Steven 1993; Gerzen and Barthold 2012; Gain and Paulino 2012; Lee et al. 2012; Bruggi and Duysinx 2012).

Given all that, in most static structure design examples, the ultimate goal is to find the structures with maximum stiffness, or with minimum weight under stress constraint. Most of the current designs were modeled by minimum compliance and achieved the desired results by solving the minimum compliance problems. Although many good results have been attained in this way, stiffness is more accurately characterized by the maximum displacement of a structure under load. Moreover, Mela and Koski (2012) have suggested that the stress-constrained minimum weight problem and the compliance minimization problem do not have equal optimal topologies of truss under multiple loading conditions.

The main purpose of the present paper is to show that the maximum stress minimization problem and the compliance minimization problem have equal optimal results of pure bending beam under a single loading condition. Compared to them, the maximum displacement minimization problem does not have equal optimal results, and it is necessary to find the appropriate index as approximation of the maximum displacement.

The paper is organized as follows: the optimal design results attained via the different models is presented and discussed in detail in the ‘Methods’ section. The main result of the paper is presented in the ‘Results and discussion’ section, where a cantilever beam is minimized separately for the maximum displacement, maximum stress, compliance, and so on. To illustrate the application of the proposed index as appropriate approximation of the maximum displacement in the static structure optimization, a power index parameter is solved in the ‘Results and discussion’ section. Finally, the results are summarized with discussion in the ‘Conclusions’ section.

Methods

Cross-sectional design of the cantilever beam

Problem description

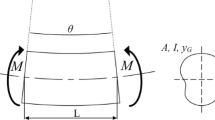
In order to present the differences in optimal design results attained via the maximum displacement, maximum stress, and conventional mean compliance methods, a cantilever beam was studied with varying square cross sections, with ends x = 0 and x = L, where x is the abscissa measured along the beam axis and subjected to a distributed constant line load q, as shown in Figure 1a. The equation of bending moment and bending moment diagram are given in Figure 1b. The objective of this example is to obtain the excellent mechanical performance of the cantilever beam by changing the cross-sectional areas along the x-axis.

Figure 1

A Cantilever beam with varying sections. (a) A cantilever beam under uniformly distributed load. (b) Equation of bending moment.

The exact differential equation of the deflection (displacement of the y-axis) curve can be described as

$$\mathit{EI}\left(x\right)\frac{{\partial }^{2}v}{\partial x^2}=M\left(x\right)=-\frac{1}{2}q{x}^2.$$

(1)

Here, v is the displacement of any point along the x-axis, q is the load line density, and E is Young's modulus of the material. Here, moments of inertia I(x) can also be stated as

$$I\left(x\right)=\frac{A^2\left(x\right)}{12}.$$

(2)

Here, A(x) is the continuously differentiable function of the area of the square cross section along the x-axis.

Then, the mechanical optimization problem can be formulated as

$$\begin{array}{cc}\hfill \mathrm{find}:\hfill & \hfill A\left(x\right)\hfill \\ \hfill min:\hfill & \hfill f\left(A\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.:\hfill & \hfill {\displaystyle {\int }_{\mathrm{0}}^{\mathit{L}}A\left(x\right)\mathit{dx}=W_0}.\hfill \end{array}$$

(3)

Here, f(A) denotes a mechanical behavior index, and the material volume is limited by W₀. With the Lagrange multiplier method, the solution of the cross-sectional areas of cantilever beam is attained by

$${\delta }_{\mathrm{A}}\left(f\left(A\right)\right)+\lambda {\displaystyle {\int }_{\mathit{0}}^{\mathit{L}}\mathit{\delta Adx}}=0,\mathit{\delta \lambda }\left({\displaystyle {\int }_{\mathit{0}}^{\mathit{L}}A\left(x\right)\mathit{dx}}-W_0\right)=0.$$

(4)

Here, δA is the variation function of A(x), and δ_A(f(A))denotes the Fréchet derivative of f(A) with respect to A(x).The constrained optimization problem (3) is transformed into an equivalent equation (4) by making use of the Karush-Kuhn-Tucker conditions of the constrained optimization. The optimal cross-sectional area fields A(x) in problem (3) can be obtained by solving Equation 4.

Minimization of the maximum displacement

In many practical cases, a commonly used design criterion is that the maximum displacement of the structure should not exceed a specified value. Thus, maximum displacement is naturally the ideal objective function of optimization models. According to the elementary theory of the beam, the maximum displacement is located in the boundary of x = 0 and can be written as

$$v_{max}\left(\mathit{A}\right)={\displaystyle {\int }_0^{\mathit{L}}\frac{\overline{M}\left(x\right)M\left(x\right)}{\mathit{EI}}\mathit{dx}}={\displaystyle {\int }_0^{\mathit{L}}\frac{6q{x}^3}{E{A}^2}\mathit{dx}},$$

(5)

where $\overline{M}\left(x\right)$ is the bending moment produced by a unit load applied on the free end of the beam (x = 0) and is of the form

$$\overline{M}\left(x\right)=-x.$$

(6)

Substituting Equations 5 and 6 into Equation 4 gives

$${\displaystyle {\int }_0^{\mathit{L}}\left(-\frac{12q{x}^3}{E{A}^3}+\lambda \right)\mathit{\delta Adx}}=0$$

(7)

and

$${\displaystyle {\int }_0^{\mathit{L}}\mathit{Adx}}-W_0=0.$$

(8)

Since δA is an arbitrary function, A(x) can be written as

$$A={\left(\frac{12q}{\mathit{\lambda E}}\right)}^{1/3}x.$$

(9)

Here, λ is an unknown variable. Substituting Equation 9 into Equation 8, the optimal cross-sectional area fields $A_{v_{\max }}\left(x\right)$. and λ can be expressed as

$$\begin{array}{l}\lambda =\frac{8q{L}^6}{2E{M}^3}\\ A_{v_{max}}\left(x\right)=\frac{2W_0}{L^2}x\end{array}$$

(10)

and the corresponding displacement function is

$$v_{v_{max}}=\frac{3q{L}^4}{4E{W}_0^2}{\left(x-L\right)}^2.$$

(11)

The sectional maximum stress is found at the location on the cross section where y is the largest and can be written as

$${\sigma }_{v_{max}}=\frac{M{y}_{max}}{I}=\frac{6M{A}^{\frac{1}{2}}}{A^2}=\sqrt{\frac{9}{8}}\frac{q{L}^{\frac{7}{2}}}{W_0^{\frac{3}{2}}}{\left(\frac{x}{L}\right)}^{\frac{1}{2}}$$

(12)

Introducing a dimensionless parameter

$$\tilde{x}=\frac{x}{L},$$

(13)

the cross-sectional area fields and the corresponding displacement function can be expressed in the dimensionless space as

$${\tilde{A}}_{v_{max}}\left(\tilde{x}\right)=\frac{A_{v_{max}}\left(\tilde{x}\right)L}{W_0}=2\tilde{x},$$

(14)

$${\tilde{v}}_{v_{max}}\left(\tilde{x}\right)=\frac{v_{v_{max}}\left(\tilde{x}\right)E{W}_0^2}{q{L}^6}=\frac{3}{4}{\left(\tilde{x}-1\right)}^2,$$

(15)

and

$${\tilde{\sigma }}_{v_{max}}=\frac{{\sigma }_{v_{max}}\left(\tilde{x}\right)W_0^{\frac{3}{2}}}{q{L}^{\frac{7}{2}}}=\sqrt{\frac{9}{8}}{\tilde{x}}^{\frac{1}{2}}.$$

(16)

Here, the subscript v_max shows that the optimization objective is to minimize the maximum displacement.

Minimization of the maximum stress

In many practical cases, a commonly used design criterion is that the maximum stress of the structure should not exceed a specified value (strength criterion). Thus, maximum stress is naturally the ideal objective function of optimization models. However, the location of the maximum stress usually will not be fixed with the change of material distribution in the optimization process. Therefore, the maximum stress is an implicit function with respect to material distribution. Hence, to resolve this problem, a performance index called geometric average sectional maximum stress instead of a direct optimization of the maximum stress is proposed, which is expressed as

$$\begin{array}{c}{f}_{{\sigma }_{\text{max}}}=\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}\left(\frac{1}{L}{\displaystyle {\int }_0^{\mathit{L}}{\left({\sigma }_{\text{max}}\right)}^n\mathit{dx}}\right){}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\\ =\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\left(\frac{1}{L}{\displaystyle {\int }_0^{\mathit{L}}{\left(\frac{6M}{A^{\frac{3}{2}}}\right)}^n\mathit{dx}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}.\end{array}$$

(17)

Theoretically, geometric average displacement (GAD) tends to geometric average stress when n tends to infinity (Gentile 2003; Li and Fang 1997).

Substituting Equation 17 into Equation 4 gives

$$\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\displaystyle {\int }_0^{\mathit{L}}\left(-Z\frac{x^{2n}}{A^{\frac{3}{2}n+1}}+\lambda \right)\mathit{\delta Adx}}=0,$$

(18)

where

$$Z=\frac{3{\left(3q\right)}^n}{2L}{\left(\frac{1}{L}{\displaystyle {\int }_{\mathit{0}}^{\mathit{L}}{\left(\frac{3q{x}^2}{A^{\frac{3}{2}}}\right)}^n\mathit{dx}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.-1}.$$

(19)

Since δA is an arbitrary function, A(x) can be written as

$$A=\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\left(\frac{Z}{\lambda }\right)}^{\frac{2}{3n+2}}{x}^{\frac{4n}{3n+2}}=H{x}^{\frac{4}{3}},$$

(20)

where H is an unknown variable:

$$H=\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\left(\frac{Z}{\lambda }\right)}^{\frac{2}{3n+2}}.$$

(21)

Substituting Equation 20 into Equation 8 gives

$$\begin{array}{l}H=\frac{7W_0}{3L^{7/3}}\\ A_{{\sigma }_{\text{max}}}\left(x\right)=\frac{7W_0}{3L^{7/3}}{x}^{4/3}.\end{array}$$

(22)

The corresponding displacement function and the sectional maximum stress function are

$$\begin{array}{l}{v}_{{\sigma }_{max}}=\frac{81q{L}^{14/3}}{98E{W}_0^2}\left(3x^{4/3}-4L^{1/3}x+L^{1/3}\right)\\ {\sigma }_{{\sigma }_{max}}=\sqrt{\frac{243}{343}}\frac{q{L}^{\frac{7}{2}}}{W_0^{\frac{3}{2}}}.\end{array}$$

(23)

As shown in Equation 22, we can obtain an iso-stress (the sectional maximum stress function is constant) design via the maximum stress-based model. The dimensionless cross-sectional area fields, displacement function, and the sectional maximum stress function are

$$\begin{array}{l}{\tilde{A}}_{{\sigma }_{max}}\left(\tilde{x}\right)=\frac{A_{{\sigma }_{max}}\left(\tilde{x}\right)L}{W_0}=\frac{7}{3}{\tilde{x}}^{4/3}\\ {\tilde{v}}_{{\sigma }_{max}}\left(\tilde{x}\right)=\frac{81}{98}(3{\tilde{x}}^{4/3}-4\tilde{x}+1)\\ {\tilde{\sigma }}_{{\sigma }_{max}}=\sqrt{\frac{243}{343}}.\end{array}$$

(24)

Here, the subscript σ_max shows that the optimization objective is to minimize the maximum stress.

Minimization of the compliance

For the cantilever beam in Figure 1, the compliance can also be expressed as

$$f\left(A\right)=C={\displaystyle {\int }_{\mathit{0}}^{\mathit{L}}\frac{M\left(x\right)M\left(x\right)}{2\mathit{EI}}\mathit{dx}}={\displaystyle {\int }_{\mathit{0}}^{\mathit{L}}\frac{3q^2{x}^4}{2E{A}^2}\mathit{dx}}.$$

(25)

Here, the compliance is used as an optimization objective function. The optimal cross-sectional area fields A(x) should obey the following necessary conditions:

$${\displaystyle {\int }_0^{\mathit{L}}\left(-\frac{3q^2{x}^4}{E{A}^3}+\lambda \right)\mathit{\delta Adx}}=0,{\displaystyle {\int }_0^{\mathit{L}}\mathit{Adx}}-W_0=0.$$

(26)

The cross-sectional area fields can be obtained by solving Equation 26, which is

$$A_{\mathrm{C}}\left(x\right)=\frac{7W_0}{3L^{7/3}}{x}^{4/3}$$

(27)

Compared with Equation 22, the compliance minimization problem and the maximum stress minimization problem have equal optimal results in this example. To amplify this highly simplified conclusion, the contrast between the compliance minimization problem and the maximum stress minimizaion problem can be formulated as

$$\left\{\begin{array}{lll}\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\displaystyle {\int }_0^{\mathit{L}}\left(-Z\frac{M^n}{{\left(A_{{\sigma }_{\text{max}}}\right)}^{\frac{3n+2}{2}}}+{\lambda }_{{\sigma }_{max}}\right)\mathit{\delta Adx}}\hfill & Z=\frac{3{\left(6\right)}^n}{2L}\left(\frac{1}{L}{\displaystyle {\int }_0^{\mathit{L}}{\left(\frac{6M}{A_{{\sigma }_{\text{max}}}^{\frac{3}{2}}}\right)}^n\mathit{dx}}\right){}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.-1}\hfill & {\displaystyle {\int }_0^{\mathit{L}}{A}_{{\sigma }_{\text{max}}}\mathit{dx}}-W_0=0\hfill \\ {\displaystyle {\int }_0^{\mathit{L}}\left(-\frac{12M^2}{E{A}_{\mathrm{C}}^3}+{\lambda }_{\mathrm{C}}\right)\mathit{\delta Adx}}=0,\hfill & {\displaystyle {\int }_0^{\mathit{L}}{A}_{\mathrm{C}}\mathit{dx}}-W_0=0\hfill \end{array}\right.$$

(28)

then

$$\left\{\begin{array}{ll}{A}_{{\sigma }_{\text{max}}}=\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\left(\frac{Z{M}^n}{{\lambda }_{{\sigma }_{max}}}\right)}^{\frac{2}{3n+2}}=H_{{\sigma }_{max}}{M}^{\frac{2}{3}}\hfill & H_{{\sigma }_{max}}=\underset{n\to \infty }{{\displaystyle \mathbf{\text{lim}}}}{\left(\frac{Z}{{\lambda }_{{\sigma }_{max}}}\right)}^{\frac{2}{3n+2}}\hfill \\ A_C={\left(\frac{12M^2}{E{\lambda }_{\mathrm{C}}}\right)}^{\frac{1}{3}}=H_{\mathrm{C}}{M}^{\frac{2}{3}}\hfill & H_{\mathrm{C}}={\left(\frac{12}{E{\lambda }_{\mathrm{C}}}\right)}^{\frac{1}{3}}\hfill \end{array}\right..$$

(29)

Substituting Equation 29 into Equation 4 gives

$$\left\{\begin{array}{l}{H}_{{\sigma }_{max}}=H_{\mathrm{C}}\\ A_{{\sigma }_{max}}=A_{\mathrm{C}}\end{array}\right..$$

(30)

Therefore, the first example helps us draw the conclusion that in this kind of problem (pure bending beam), the optimal design generated from the compliance formulation and the maximum are identical, same to the truss problems (Cox 1965; Dorn et al. 1964; Hemp 1973).

Comparisons of the results

Comparing these results, it shows that the optimization models with compliance (maximum stress) and the maximum displacement as objective function sometimes does not give the same optimal results in this kind of problem, and we find significant differences in the cross-sectional area fields, displacement, and the sectional maximum stress function. To be more specific, from the results, the maximum displacement of the optimal design generated from maximum displacement decreases by extra 10% in comparison with the design obtained by conventional compliance (maximum stress). Furthermore, the maximum stress of the optimal design generated from maximum displacement with the extra increase of 26% is presented to demonstrate the validity of this example, as shown in Figure 2.

Figure 2

Comparisons of design results of objectives. (a) Comparisons of displacement function. (b) Comparisons of cross-sectional area fields. (c) Comparisons of the sectional maximum stress function.

Results and discussion

The optimization model of the geometric average displacement

In many practical cases, a commonly used design criterion is the maximum displacement of the structure which does not exceed a specified value (stiffness criterion). Thus, maximum displacement is naturally the ideal objective function of optimization models. However, the location of the maximum displacement usually changes with the change of material distribution in the optimization process, resulting in a discontinuous maximum displacement function, especially for topology optimization. Hence, to achieve a good balance between the optimization performance and numerical cost, a performance index called GADU_GAD, instead of a direct optimization of the maximum displacement, is proposed, which is expressed as

$$U_{\mathrm{GAD}}={\left(\frac{1}{\left|\Omega \right|}{\displaystyle {\int }_{\Omega }{\left(u\left(x\right)\right)}^n\mathit{d}\mathbf{\Omega }}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.},x\in \mathbf{\Omega }.$$

(31)

Here, |Ω| denotes the area (or volume) of the design region, and the displacement of a general point can be described in terms of u(x). Theoretically, GAD tends to the maximum displacement when n tends to infinity (Li and Fang 1997), i.e., $U_{\mathrm{GAD}}\stackrel{n\to \infty }{\to }max\left(u\left(x\right)\right),x\in \mathrm{\Omega }$. When n is big enough, GAD is an appropriate approximation of the maximum displacement.

In order to present the validity of GAD, a cantilever beam was studied again with varying square cross sections and subjected to a distributed linear load, as shown in Figure 3a. The equation of bending moment and bending moment diagram are given in Figure 3b.

Figure 3

Cantilever beam with varying sections subjected to a distributed linear load. (a) A cantilever beam under uniformly distributed load. (b) Equation of bending moment.

First, the conventional compliance formulation is applied under a given weight constraint. Then, the same problem in Figure 3 is solved using the minimization of the maximum displacement. Finally, to discuss the influence of the objective functions, a GAD-based optimization model is carried out to find the maximum stiffness design with the different power indices n (1,2,3,4).

For the cantilever beam in Figure 3, the compliance can also be expressed as

$$\begin{array}{c}{f}_{\mathrm{c}}\left(A\right)=C={\displaystyle {\int }_0^{\mathit{L}}\frac{M\left(x\right)M\left(x\right)}{2\mathit{EI}}\mathit{dx}}\\ ={\displaystyle {\int }_0^{\mathit{L}}\frac{Q^2{x}^6}{6E{L}^2{A}^2}\mathit{dx}}.\end{array}$$

(32)

The cross-sectional area fields can be obtained by substituting Equation 32 into Equation 4, which is

$$A_{\mathrm{C}}\left(x\right)=\frac{3W_0}{L^3}{x}^2.$$

(33)

The corresponding displacement function and the sectional maximum stress function are

$$\begin{array}{l}{v}_C=\frac{2Q{L}^5}{9E{W}_0^2}\left(x{ln}^x+L-x-x{ln}^L\right)\\ {\sigma }_C=\sqrt{\frac{1}{27}}\frac{Q{L}^{\frac{7}{2}}}{W_0^{\frac{3}{2}}}.\end{array}$$

(34)

We also obtain an iso-stress design via compliance-based model as the former example. The dimensionless cross-sectional area fields, displacement function, and the sectional maximum stress function of compliance are

$$\begin{array}{l}{\tilde{A}}_C\left(\tilde{x}\right)=3{\tilde{x}}^2\\ {\tilde{v}}_{{\sigma }_{max}}\left(\tilde{x}\right)=\left\{\begin{array}{ll}\frac{2}{9}\left(\tilde{x}{ln}^{\tilde{x}}-\tilde{x}+1\right)\hfill & \tilde{x}\ne 1\hfill \\ \frac{2}{9}\hfill & \tilde{x}=1\hfill \end{array}\right.\\ {\tilde{\sigma }}_{{\sigma }_{max}}=\sqrt{\frac{1}{27}}.\end{array}$$

(35)

According to Equations 28 to 30, the compliance minimization problem and the maximum stress minimization problem will have equal optimal results in this example. Wherefore, it is useless to solve this problem again via the maximum stress-based model.

For the cantilever beam in Figure 3, the maximum displacement can also be expressed as

$$\begin{array}{c}{f}_{v_{max}}\left(A\right)={\left.v\left(x\right)\right|}_{x=L}={\displaystyle {\int }_0^{\mathit{L}}\frac{\overline{M}\left(x\right)M\left(x\right)}{\mathit{EI}}\mathit{dx}}\\ ={\displaystyle {\int }_0^{\mathit{L}}\frac{2Q{x}^4}{\mathit{EL}{A}^2}\mathit{dx}}.\hfill \end{array}$$

(36)

The cross-sectional area fields can be obtained by substituting Equation 32 into Equation 4, which is

$$A_{v_{max}}\left(x\right)=\frac{7W_0}{3L^{\frac{7}{3}}}{x}^{\frac{4}{3}}.$$

(37)

The corresponding displacement function and the sectional maximum stress function are

$$\begin{array}{l}{v}_{v_{max}}=\frac{27Q{L}^{\frac{11}{3}}}{686E{W}_0^2}\left(3x^{\frac{7}{3}}-7L^{\frac{4}{3}}x+4L^{\frac{7}{3}}\right)\\ {\sigma }_{v_{max}}=\sqrt{\frac{27}{243}}\frac{Q{L}^{\frac{7}{2}}}{W_0^{\frac{3}{2}}}x.\end{array}$$

(38)

The dimensionless cross-sectional area fields, displacement function, and the sectional maximum stress function of compliance are

$$\begin{array}{l}{\tilde{A}}_{v_{max}}\left(\tilde{x}\right)=\frac{7}{3}{\tilde{x}}^{\frac{4}{3}}\\ {\tilde{v}}_{v_{max}}\left(\tilde{x}\right)=\frac{27}{686}(3{\tilde{x}}^{\frac{7}{3}}-7\tilde{x}+4)\\ {\tilde{\sigma }}_{v_{max}}=\sqrt{\frac{27}{243}}\tilde{x}.\end{array}$$

(39)

In order to illustrate that GAD is an appropriate approximation of the maximum displacement, the problem is modeled again to minimize GAD as follows:

$$f_{\mathrm{GAD}}^n={\left(\frac{1}{L}{\displaystyle {\int }_{\mathit{0}}^{\mathit{L}}{v}^n\left(x\right)\mathit{dx}}\right)}^{\frac{1}{n}}.$$

(40)

Based on the optimal result generated by the maximum displacement, we can assume the optimal cross-sectional area fields obtained by GAD as follows:

$$A_{\mathrm{GAD}}^n=H\left(m\right)x^{\frac{m}{2}},$$

(41)

where the superscript n denotes a power index parameter in Equation 40, and m is the evaluated variable. Substituting Equation 41 into Equation 4 gives

$$H\left(m\right)=\frac{\left(m+2\right)W_0}{2L^{\frac{m+2}{2}}},$$

(42)

and the corresponding displacement function is

$$v_{\mathrm{GAD}}=\left\{\begin{array}{ll}\frac{8Q{L}^{m+1}}{E{W}_0^2\left(4-m\right)\left(5-m\right){\left(m+2\right)}^2}(x^{5-m}-\left(5-m\right)L^{4-m}x+(4-m\left)L^{5-m}\right)\hfill & m<4\hfill \\ \left.\begin{array}{ll}\frac{2Q{L}^5}{9E{W}_0^2}\left(x{ln}^x+L-x-x{ln}^L\right)\hfill & x\ne 0\hfill \\ \frac{2Q{L}^6}{9E{W}_0^2}\hfill & x\ne 0\hfill \end{array}\right\}\hfill & m=4\hfill \end{array}\right..$$

(43)

The geometric average displacement can be rewritten as

$$f_{\mathrm{GAD}}^{\mathit{n}}=f_{\mathrm{GAD}}^{\mathit{n}}\left(n,m\right)=\left\{\begin{array}{ll}\frac{8Q{L}^6}{E{W}_0^2\left(4-m\right)\left(5-m\right){\left(m+2\right)}^2}{\left(\frac{1}{L}{\displaystyle {\int }_0^1{\left({\tilde{x}}^{5-m}-\left(5-m\right)\tilde{x}+\left(4-m\right)\right)}^{n}d\tilde{x}}\right)}^{\frac{1}{n}}\hfill & m<4\hfill \\ \frac{2Q{L}^6}{9E{W}_0^2}{\left(\frac{1}{L}{\displaystyle {\int }_0^1{\left(\tilde{x}{ln}^{\tilde{\mathit{x}}}-\tilde{x}+1\right)}^{n}d\tilde{x}}\right)}^{\frac{1}{n}}\hfill & m=4\hfill \end{array}\right.,$$

(44)

and the evaluated variable m in the optimal cross-sectional area fields can be solved by

$$\frac{\partial f_{\mathrm{GAD}}^n\left(n,m\right)}{\partial m}=0.$$

(45)

To facilitate the comparisons, the solutions of the optimization models with the compliance (the maximum stress), the maximum displacement, and GAD as objective functions are shown in Table 1 and Figure 4. It can be seen that the compliance design experiences large displacement under the applied force, whereas the compliance and GAD design have only very slight displacement that implies a much stiffer design. To be more specific, the maximum displacement of the optimal design generated from GAD decreases by an extra 32% in comparison with the design obtained by compliance. Furthermore, the maximum stress of the optimal design generated from GAD, and the compliance with the extra increase of 21% is presented to demonstrate the validity of this example. With the increase in power index n, the material distribution and the displacement field obtained by the GAD-based model rapidly move close to the convergence of results obtained by the maximum displacement. Since the approximate level tends to stability with the increasing power index n, an appropriate value n is required to be selected in the practical optimization process.

Table 1 Results obtained by geometric average displacement for varying n

Figure 4

Comparisons of design results of objectives. (a) Comparisons of displacement function. (b) Comparisons of cross-sectional area fields. (c) Comparisons of the sectional maximum stress function.

Conclusions

The classic test problems indicate that for the pure bending beam under single loading condition, the maximum stress minimization problem and the compliance minimization problem have equal optimal results, and the maximum displacement minimization problem and the compliance minimization problem do not have equal optimal results. This anticipated result has so far been without the proof that the test problems provide. The implication of the conclusion is that the designer can rely on finding the stress-constrained minimum weight solution by performing optimization for the compliance minimization problem, and it is necessary to propose an appropriate index as approximation of the maximum displacement for the complex problems. Through a classic example, it was shown that the solutions achieved via the model utilizing GAD rapidly move close to the convergence of results obtained by the maximum displacement.