Wave propagation in laminated composite plates

Abstract

In this article, the dispersion of propagation waves in an arbitrary direction in laminated composite plates is studied in the framework of elasticity. Three-dimensional field equations of elasticity are considered, and the characteristic equation is obtained on employing the continuity of displacements and stresses at the layers' interfaces. Obtained characteristic equation is further simplified by making use of the properties of the block matrices. Some important particular cases such as of free waves on reducing plates to single layer and the surface waves when thickness tends to infinity are also discussed. Numerical results are also obtained and represented graphically.

Introduction

The growing practical applications of laminated composite materials and their uses because of advanced high strength, high modulus layered structures must go a careful inspection to sort out manufacturing defects and in-service degradation in the design of engineering structures. Composite materials are also becoming indispensible in modern industries such as aerospace, infrastructure, and energy because of their ability to customize the physical properties in addition to light weight, directional stiffness, and long fatigue life. The potential of such advanced laminated composites and fiber-reinforced materials as important structural members, wherein an internal layer provides structural strength and the outside layer provide protection against the surrounding media, has motivated an extensive amount of research in the field of mechanics. To modify composite structures or in order to meet particular demands, the design of structures has encouraged the studies of impact and wave propagation in such materials.

Also the lightweight, high strength, and corrosion resistance of fiber-reinforced polymers (FRP) make them ideally suited for quick and effective structural repairs. Investigations on the protection of historical and monumental buildings made of masonry material through the adoption of FRP composite provisions have inspired a wide scientific literature on the subject, with many theoretical as well as experimental contributions and developments of original approaches, techniques, and numerical tools in addressing the problem of masonry constructions; the planning and design of adequate protection techniques are studied in Foti (2013a), Baratta and Corbi (2005, 2010, 2011), Baratta et al. (2008). Foti (2011) studied the behavior fiber-reinforced concrete structures. They obtained results of some tests for an approach to a broader testing on the possibility of using fibers from polyethylene terephthalate (PET) bottles to increase the ductility of the concrete. The use of recycled waste PET bottle fibers for the reinforcement of concrete is studied by Foti (2013b). A series of tests have been performed with the aim to define the best solution in strengthening a deteriorated structure with a rheoplastic mortar reinforcement by Foti and Vacca (2013) and three types of possible structural reinforcing renovation on reinforced concrete pillars have been considered, with special attention to adhesion between materials with different chemical-physical and mechanical characteristics. The crack patterns obtained on the specimens have been analyzed to demonstrate the relevance of an appropriate thickness of the reinforcement to obtain an effective mechanical behavior of the reinforced concrete element over time.

Since composites consist of different materials, they are inhomogeneous and anisotropic. As a consequence, different mechanical properties among the constituents and the environmental changes can create residual stresses, which may lead to interface de-bonding in the structures, leading to failure of the system. Therefore, it is of interest to investigate the feasibility of non-destructively monitoring mechanical aging in composites. The study of wave propagation and vibration in plates, half-spaces, and laminates is an area of considerable recent research activity. The propagation of the plane waves in unbounded homogeneous layered media is well known, and many methods have been proposed. On the dynamic behavior of anisotropic plates, extensive review of the plate theories can be found in Achenbach (1973), Auld (1973), Fedorov (1968), Nayfeh (1995), and Wooster (1973), and wave propagation problems in periodically layered anisotropic media have been considered by the authors Norris (1992, 1993), Wang and Rokhlin (2002), and Braga and Hermann (1988). Several problems on the theories of laminated and composite plates have been considered, and their dynamic behavior was studied by authors Reddy (1987, 1990), Liu et al. (1990), Postma (1955), Rytov (1956), and Sun et al. (1968). There also have been a reasonable number of investigations of such advanced materials, and their analysis was reported by Sve (1971), Jones (1975), Graff (1991), and Reddy (1997). Nayfeh (1991) developed a transfer matrix technique to obtain the dispersion relation curves of elastic wave propagating in multilayered anisotropic media, i.e., composite laminate. Detailed review on the wave propagation in layered anisotropic media/anisotropic laminates is given by Liu and Xi (2002). Yamada and Nasser (1981) have studied harmonic wave's propagation direction in orthotropic composites, and Verma (1999) considered the similar problem in thermoelastic heat conducting material.

Similar formulations using Floquet's theorem are employed to analyze the wave motions of two-phase slender periodic structures that has been made by Tourafte (1986) and Tassilly (1987). Dispersion equation has been represented by the vanishing of a 12 × 12 determinant. Yamada and Nasser (1981) considered an orthotropic, periodically layered composite with two layers in a unit cell, and the dispersion equation corresponds to a 12 × 12 characteristic determinant. These approaches lead to important results but had limitation due to the size of the matrices that must be manipulated when the unit cell has more than two layers, or when the layers are anisotropic. In this paper, the above said limitation has been resolved by simplifying the obtained characteristic equation using the basic properties of block matrices. Thus, in order to solve the problem numerically, it is sufficient to consider the 6 × 6 determinant only instead of taking the 12 × 12 determinant, thus reducing the numerical work considerably. Further, some of the important particular cases of free waves and the surface waves are also derived and discussed from the obtained results.

Following Yamada and Nasser (1981), in this article, the propagation of waves in layered laminated composites, where the direction of the corresponding harmonic waves makes an arbitrary angle with respect to the layers, is examined. Three-dimensional field equations of elasticity are considered for this study, and the corresponding characteristic equation on employing the continuity of displacements at the layers' interface is obtained. Obtained characteristic equation is further simplified using the basic properties of block matrices, and in order to solve the problem numerically, it is sufficient to consider the determinant of the 6 × 6 matrix instead of taking the determinant 12 × 12 matrix. Some important particular cases such as of free waves on reducing plates to single layer and the surface waves when thickness tends to infinity are also discussed. Numerical results are also obtained and represented graphically.

Methods

Formulation

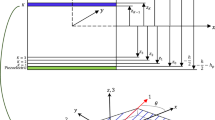
Consider a set of Cartesian coordinate system x _i = (x₁, x₂, x₃) in such a manner that x₃- axis is normal to the layering. The coordinate axes x₁, x₂, and x₃ of the model are chosen as to be analogous with the principal axes x, y, and z, with z- axis being normal to the plate. The displacement field vector u = (u₁, u₂, u₃) satisfies the basic field equation of motion for an infinite generally anisotropic medium in the absence of body forces, which is

$${\displaystyle \sum _{j=1}^3\left(\frac{\partial {\tau }_{\mathit{ij}}\left(\mathbf{u}\right)}{\partial x_j}\right)}=\rho \frac{{\partial }^2{u}_i}{\partial t^2}i=1,2,3.$$

(2.1)

Constitutive relations for anisotropic materials

$${\tau }_{\mathit{ij}}=C_{\mathit{ijkl}}{e}_{\mathit{kl}},\mathit{i},j,k,l=1,2,3.$$

(2.2)

ρ is the density, t is time, u _i is the displacement in the x _i direction; τ _ij , and e _kl are the stress and strain tensor respectively; and the fourth order tensor of the elasticity C _ijkl satisfies the (Green) symmetry conditions:

$$c_{\mathit{ijkl}}=c_{\mathit{klij}}=c_{\mathit{ijlk}}=c_{\mathit{jikl}}.$$

(2.3)

Strain–displacement relation

$$e_{\mathit{ij}}=\frac{1}{2}\left(\raisebox{1ex}{$\mathit{\partial }{u}_i$}\!\left/ \!\raisebox{-1ex}{$\mathit{\partial }{x}_j$}\right.+\raisebox{1ex}{$\mathit{\partial }{u}_j$}\!\left/ \!\raisebox{-1ex}{$\mathit{\partial }{x}_i$}\right.\right).$$

(2.4)

In addition, at the interface between two layers the tractions, displacements must be continuous.

For orthotropic media, the stress equation for an orthotropic material in the symmetric coordinate system can be expressed by

$$\left[\begin{array}{c}\hfill {\tau }_{11}\hfill \\ \hfill {\tau }_{22}\hfill \\ \hfill {\tau }_{33}\hfill \\ \hfill {\tau }_{23}\hfill \\ \hfill {\tau }_{13}\hfill \\ \hfill {\tau }_{12}\hfill \end{array}\right]=\left[\begin{array}{cccccc}\hfill c_{11}\hfill & \hfill c_{12}\hfill & \hfill c_{13}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill c_{12}\hfill & \hfill c_{22}\hfill & \hfill c_{23}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill c_{13}\hfill & \hfill c_{23}\hfill & \hfill c_{33}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill c_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill c_{55}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill c_{55}\hfill \end{array}\right]\left[\begin{array}{c}\hfill e_{11}\hfill \\ \hfill e_{22}\hfill \\ \hfill e_{33}\hfill \\ \hfill 2e_{23}\hfill \\ \hfill 2e_{13}\hfill \\ \hfill 2e_{12}\hfill \end{array}\right].$$

(2.5)

Analysis

For harmonic waves propagating in an arbitrary direction, the displacement components u₁, u₂, and u₃ are written as

$$\left(u_1,u_2,u_3\right)=\left\{U_1\left(x_3\right),U_2\left(x_3\right),U_3\left(x_3\right)\right\}{e}^{\mathit{i\xi }\left(l_1{x}_1+l_2{x}_2+l_3{x}_3-\mathit{ct}\right)},$$

(3.1)

where ξ is the wave number, c is the phase velocity ( = ω/ξ), $i=\sqrt{-1},\omega$ is the circular frequency, l₁, l₂, and l₃ are the direction cosine defining the propagation direction.

U _j are the constants related to the amplitudes of displacement, Floquet's theory requires functions U _j (j = 1, 2, 3) to have the same periodicity as the layering. Hence, the problem is reduced to that of one pair of layers, where

$$U_j={\overline{U}}_j{e}^{-\mathit{i\xi }\left(l_3+\alpha \right)x_3},j=1,2,3,$$

(3.2)

where ${\overline{U}}_j$ are constants. On substitution of Equations (3.2) into Equations (2.1), via (2.2) to (2.4) and specializing the equations for orthotropic media, it follows that

$$M_{\mathit{mn}}\left(\alpha \right){\overline{U}}_n=0,m,n=1,2,3,$$

(3.3)

where

$$\begin{array}{l}{M}_{11}=\left(l_1^2+l_2^2{\overline{c}}_{66}+{\alpha }^2{\overline{c}}_{55}-{\zeta }^2\right),M_{12}=({\overline{c}}_{12}+{\overline{c}}_{66})l_1{l}_2,\\ M_{13}=-({\overline{c}}_{13}+{\overline{c}}_{55})l_1\alpha ,\\ M_{22}=\left(l_1^2{\overline{c}}_{66}+l_2^2{\overline{c}}_{22}+{\alpha }^2{\overline{c}}_{44}-{\zeta }^2\right),\\ M_{23}=-({\overline{c}}_{23}+{\overline{c}}_{44})l_2\alpha ,\\ M_{33}=\left(l_1^2{\overline{c}}_{55}+l_2^2{\overline{c}}_{44}+{\alpha }^2{\overline{c}}_{33}-{\zeta }^2\right),\end{array}$$

(3.4)

where ${\zeta }^2=\frac{\rho c^2}{c_{11}}$. The existence of nontrivial solutions for ${\overline{U}}_j$ (j = 1, 2, and 3) demands the vanishing of the determinant in Equation (3.3) and yields the sixth degree polynomial equation

$$\Delta {\alpha }^6+F_1{\alpha }^4+F_2{\alpha }^2+F_3=0,$$

(3.5)

where

$$\Delta =c_{33}{c}_{44}{c}_{55},$$

$$\begin{array}{l}{F}_1=\left[\left(c_{22}{c}_{33}-2c_{23}{c}_{44}-c_{23}^2\right)c_{55}+c_{33}{c}_{44}{c}_{66}\right]l_2^2\\ +\left[\left(c_{33}-2c_{13}{c}_{55}-c_{13}^2\right)c_{44}+c_{33}{c}_{55}{c}_{66}\right]l_1^2\\ -\left(c_{33}{c}_{44}+c_{33}{c}_{55}+c_{44}{c}_{55}\right){\zeta }^2\end{array}$$

$$\begin{array}{l}{F}_2=\left[\left(c_{33}-2c_{13}{c}_{55}-c_{13}^2\right)c_{66}+c_{44}{c}_{55}\right]l_1^4\\ +\left[\left(c_{22}{c}_{33}-2c_{23}{c}_{44}-c_{23}^2\right)c_{66}+c_{22}{c}_{55}{c}_{44}\right]l_2^4\\ +\left[\left(-c_{12}^2{c}_{33}-2(c_{33}{c}_{44}-c_{66}{c}_{23}{c}_{55}-c_{12}{c}_{44}{c}_{55}\right.\right.\\ +c_{13}{c}_{22}{c}_{55}-2c_{44}{c}_{55}{c}_{66}-c_{13}{c}_{44}{c}_{66}\\ +c_{12}{c}_{33}{c}_{66}-c_{12}{c}_{13}{c}_{44}-c_{13}{c}_{23}{c}_{66}-c_{12}{c}_{23}{c}_{55}\\ \left.\left.-c_{12}{c}_{13}{c}_{23}\right)-c_{13}^2{c}_{22}+c_{22}{c}_{33}-c_{23}^2\right]l_1^2{l}_2^2\\ +\left[\begin{array}{l}\left({2\mathrm{c}}_{13}{\mathrm{c}}_{55}-c_{66}{c}_{33}-{\mathrm{c}}_{55}{\mathrm{c}}_{44}-{\mathrm{c}}_{44}\right.\\ \left.-{\mathrm{c}}_{33}-c_{66}{c}_{55}+c_{13}^2\right)l_1^2\\ +\left(2c_{23}{c}_{44}+c_{23}^2-c_{22}{c}_{33}-c_{22}{c}_{55}\right.\\ \left.-c_{66}{c}_{44}-{\mathrm{c}}_{55}{\mathrm{c}}_{44}-c_{33}{c}_{66}\right)l_2^2\\ +\left(c_{33}+c_{44}+c_{55}\right){\zeta }^4\end{array}\right]{\zeta }^2\end{array}$$

$$\begin{array}{l}{F}_3=\left(c_{55}{l}_1^2+c_{44}{l}_2^2-{\zeta }^2\right)\left\{\left(\left(1+c_{66}\right)l_1^2+\left(c_{22}+c_{66}\right)l_2^2\right){\zeta }^2-{\zeta }^4\right.\\ +\left.\left[\left(2c_{22}{c}_{66}+c_{12}^2-c_{22}\right)c_{55}\right]l_1^2{l}_2^2-c_{22}{c}_{66}{l}_2^4-c_{66}{l}_1^4\right\}\end{array}$$

Equation (3.2) can be rewritten as

$$\left(U_1,U_2,U_3\right)={\displaystyle \sum _{q=1}^8\left({\overline{U}}_{1q},{\overline{U}}_{2q},{\overline{U}}_{3q}\right)e^{-\mathit{i\xi }\left(l_3+{\alpha }_q\right)x_3}}$$

(3.6)

For each α_q,q = 1, 2,....6, we can use the Equations (3.3) and express the displacements ratios

$$\frac{D_1}{D}=\frac{{\overline{U}}_{2q}}{{\overline{U}}_{1q}}={\gamma }_q,\frac{D_2}{D}=\frac{{\overline{U}}_{3q}}{{\overline{U}}_{1q}}={\delta }_q,q=1,2....6.$$

(3.7)

$$\begin{array}{l}{D}_1\left({\alpha }_q\right)=M_{13}\left({\alpha }_q\right)M_{23}\left({\alpha }_q\right)-M_{12}\left({\alpha }_q\right)M_{33}\left({\alpha }_q\right),\\ D_2\left({\alpha }_q\right)=M_{12}\left({\alpha }_q\right)M_{23}\left({\alpha }_q\right)-M_{13}\left({\alpha }_q\right)M_{22}\left({\alpha }_q\right)\\ D_3\left({\alpha }_q\right)=0,D\left({\alpha }_q\right)=M_{22}\left({\alpha }_q\right)M_{33}\left({\alpha }_q\right)-M^2{}_{23}\left({\alpha }_q\right).\end{array}$$

(3.8)

Therefore, the solution is

$$\left(U_1,U_2,U_3\right)={\displaystyle \sum _{q=1}^8\left(1,{\gamma }_q,{\delta }_q\right){\overline{U}}_{1q}{e}^{-\mathit{i\xi }\left(l_3+{\alpha }_q\right)x_3}}.$$

(3.9)

In view of the continuity of the displacement components, tractions across the interface of the two layers, the following conditions must be satisfied:

$${}_u^{j_{\mathrm{I}}}{}_{{}_{x_3=\stackrel{-}{0}}}=u_j^{\mathrm{II}}{}_{{}_{x_3=\stackrel{+}{0}}},$$

(3.10)

$${\tau }_{3j}^{\mathrm{I}}{}_{{}_{x_3=\stackrel{-}{0}}}={\tau }_{3j}^{\mathrm{II}}{}_{x_3=\stackrel{-}{0}},$$

(3.11)

where superscripts I and II refer to layers one and two, respectively; 0⁺ and 0⁻ are values of x₃ near zero. Because of the periodicity of the deformation and stress fields, additional conditions obtained are

$$u_j^{\mathrm{I}}{}_{{}_{x_3=\stackrel{-}{h_1}}}=u_j^{\mathrm{II}}{}_{{}_{x_3=-\stackrel{+}{h_2}}},$$

(3.12)

$${\tau }_{3j}^{\mathrm{I}}{}_{x_3=\stackrel{-}{h_1}}={\tau }_{3j_{x_3=-\stackrel{+}{h_2}}}^{\mathrm{II}},j=1,2,3.$$

(3.13)

Following Yamada and Nasser (1981) on substituting the displacements, stress components into Equations (3.10) to (3.11) and linear homogeneous equations for twelve constants $U_{11}^{\mathrm{I}},U_{12}^{\mathrm{I}},\dots ,U_{15}^{\mathrm{II}}$ and $U_{16}^{\mathrm{II}}$ are obtained. For nontrivial solutions, the determinant of the coefficients must vanish. This yields the following characteristic equation:

$$det\left(\begin{array}{cc}\hfill P_{\mathit{jk}}\hfill & \hfill -{\overline{P}}_{\mathit{jk}}\hfill \\ \hfill Q_{\mathit{jk}}\hfill & \hfill -{\overline{Q}}_{\mathit{jk}}\hfill \end{array}\right)=0j,k=1,2\dots 6.$$

(3.14)

The entries of the 6 × 6 matrices $P_{\mathit{jk}},{\overline{P}}_{\mathit{jk}},Q_{\mathit{jk}}$ and ${\overline{Q}}_{\mathit{jk}}$ are

$$\begin{array}{l}{P}_{1j}=1,P_{2j}={\gamma }_j^{\mathrm{I}},P_{3j}={\delta }_j^I,P_{4j}=b_{1j}^{\mathrm{I}}{c}_{55}^{\mathrm{I}},P_{5j}=b_{2j}^{\mathrm{I}}{c}_{44}^{\mathrm{I}},\\ P_{6j}=b_{3j}^{\mathrm{I}},{\overline{P}}_{1j}=1,{\overline{P}}_{2j}={\gamma }_j^{\mathrm{II}},{\overline{P}}_{3j}={\delta }_j^{\mathrm{II}},{\overline{P}}_{4j}=\eta b_{1j}^{\mathrm{II}}{c}_{55}^{\mathrm{II}},\\ {\overline{P}}_{7j}=\eta b_{2j}^{\mathrm{II}}{c}_{44}^{\mathrm{II}},{\overline{P}}_{6j}=\eta b_{3j}^{\mathrm{II}},Q_{\mathit{jk}}=P_{\mathit{jk}}{E}_k^{-},{\overline{Q}}_{\mathit{jk}}={\overline{P}}_{\mathit{jk}}{E}_k^{+}\end{array}$$

(3.15a)

where

$$\begin{array}{l}{E}_j^{-}=e^{-\mathit{iQ}\left(l_3+{\alpha }_j^{\left(1\right)}\right)h_1/h},Q=\xi \left(h_1+h_2\right),\\ E_j^{+}=e^{-\mathit{iQ}\left(l_3+{\alpha }_j^{\mathrm{II}}\right)h_2/h},\eta =c_{11}^{\mathrm{II}}/c_{11}^{\mathrm{I}}{b}_{1j}^{\left(m\right)}\\ =l_1{\delta }_j^{\left(m\right)}-{\alpha }_j^{\left(m\right)}{b}_{1j}^{\left(m\right)}=l_1{\delta }_j^{\left(m\right)}-{\alpha }_j^{\left(m\right)},\\ b_{3j}^{\left(m\right)}={\overline{c}}_{13}^{\left(m\right)}{l}_1+{\overline{c}}_{23}^{\left(m\right)}{l}_2{\gamma }_j^{\left(m\right)}-{\overline{c}}_{33}^{\left(m\right)}{\alpha }_j^{\left(m\right)}{\delta }_j^{\left(m\right)},\\ {\overline{c}}_{\mathit{jk}}^{\left(m\right)}=c_{\mathit{jk}}^{\left(m\right)}/c_{11}^{\left(m\right)}\end{array}$$

(3.15b)

From Equation (3.14), we have

$$det\left[P_{\mathit{jk}}\right]det\left(\left[-{\overline{Q}}_{\mathit{jk}}\right]-\left[Q_{\mathit{jk}}\right]{\left[P_{\mathit{jk}}\right]}^{-1}\left[-{\overline{P}}_{\mathit{jk}}\right]\right)=0$$

(3.16a)

which implies that either

$$det\left[P_{\mathit{jk}}\right]=0,$$

(3.16b)

or

$$det\left(\left[-{\overline{Q}}_{\mathit{jk}}\right]-\left[Q_{\mathit{jk}}\right]{\left[P_{\mathit{jk}}\right]}^{-1}\left[-{\overline{P}}_{\mathit{jk}}\right]\right)=0.$$

(3.16c)

If equation (3.16b) holds true, then the problem reduces to a free wave propagation of single plate of thickness h₁, and in this case, $\left(\left[-{\overline{Q}}_{\mathit{jk}}\right]-\left[Q_{\mathit{jk}}\right]{\left[P_{\mathit{jk}}\right]}^{-1}\left[-{\overline{P}}_{\mathit{jk}}\right]\right)$ will not exist as P _jk singular. On the other hand, if P _jk is nonsingular, [P _jk ]⁻¹ exists and accordingly

$$det\left(\left[-{\overline{Q}}_{\mathit{jk}}\right]-\left[Q_{\mathit{jk}}\right]{\left[P_{\mathit{jk}}\right]}^{-1}\left[-{\overline{P}}_{\mathit{jk}}\right]\right)=0.$$

(3.17a)

Similarly, Equation (3.14) can also be written as

$$det\left[-{\overline{Q}}_{\mathit{jk}}\right]det\left(\left[P_{\mathit{jk}}\right]-\left[-{\overline{P}}_{\mathit{jk}}\right]{\left[-{\overline{Q}}_{\mathit{jk}}\right]}^{-1}\left[Q_{\mathit{jk}}\right]\right)=0,$$

(3.17b)

which implies that either

$$det\left[-{\overline{Q}}_{\mathit{jk}}\right]=0,$$

(3.17c)

or

$$det\left(\left[P_{\mathit{jk}}\right]-\left[-{\overline{P}}_{\mathit{jk}}\right]{\left[-{\overline{Q}}_{\mathit{jk}}\right]}^{-1}\left[Q_{\mathit{jk}}\right]\right)=0.$$

(3.17d)

If Equation (3.17b) holds true, then the problem reduces to a free wave propagation of single plate of thickness h₂, and $\left(\left[-{\overline{Q}}_{\mathit{jk}}\right]-\left[Q_{\mathit{jk}}\right]{\left[P_{\mathit{jk}}\right]}^{-1}\left[-{\overline{P}}_{\mathit{jk}}\right]\right)$ will not exist as ${\overline{Q}}_{\mathit{jk}}$ is singular.

On the other hand, if ${\overline{Q}}_{\mathit{jk}}$ is nonsingular, therefore

$$det\left(\left[-{\overline{Q}}_{\mathit{jk}}\right]-\left[Q_{\mathit{jk}}\right]{\left[P_{\mathit{jk}}\right]}^{-1}\left[-{\overline{P}}_{\mathit{jk}}\right]\right)=0.$$

(3.18)

In order to solve the problem numerically, it is sufficient to consider either Equation (3.17a) or Equation (3.18) for composite plates, and for free plate, Equation (3.16b) or Equation (3.17b) can be considered.

Particular cases

Free waves

When layer I = II and h₁ = h₂ (say h), then the thickness of the layer is 2h, considering the origin at the middle of the plate, then the above analysis reduces to a single plate. In this case, the eight roots of Equation (3.5) can be arranged in four pairs as α_{j + 1} = − α _j , (j = 1, 3, 5).

It is observed from Equation (3.4) that M₁₃ and M₂₃ are odd functions of α _j , and the other M_ij are even functions of α _j . On employing stresses and free surfaces conditions,

$${\sigma }_{3j}=0,x_3=\pm h,j=1,2,3,$$

(4.1)

corresponding relations to (3.7), we have

$${\gamma }_{q+1}={\gamma }_q\mathrm{and}{\delta }_{q+1}=-{\delta }_q$$

(4.2)

Hence, from (3.16)

$$\begin{array}{l}{b}_{1q+1}=-b_{1q},b_{2q+1}=-b_{2q},b_{3q+1}=b_{3q},b_{1j}\\ =l_1{\delta }_j-{\alpha }_j,b_{2j}=l_2{\delta }_j-{\alpha }_j{\gamma }_j,\end{array}$$

(4.3)

$$b_{3j}={\overline{c}}_{13}{l}_1+{\overline{c}}_{23}{l}_2{\gamma }_j-{\overline{c}}_{33}{\alpha }_j{\delta }_j,{\overline{c}}_{\mathit{jk}}=c_{\mathit{jk}}/c_{11},$$

(4.4)

$$\det \left[P_{\mathit{jk}}\right]=0.$$

(4.5a)

After simple mathematical manipulations, this equation reduces to

$${\Delta }_E{\alpha }^6+A_{E1}{\alpha }^4+A_{E2}{\alpha }^2+A_{3E}=0$$

(4.5b)

$$\begin{array}{l}{A}_{E1}=\left(c_1{c}_6{F}_{11}-c_6{F}_{13}^2+c_5{F}_{13}{F}_{23}-c_5^2{F}_{33}\right.\\ \left.-c_2{F}_{23}^2-2c_1{c}_5{F}_{12}+c_5{F}_{21}{F}_{23}+c_2{c}_6{F}_{33}\right)\end{array}$$

$$\begin{array}{l}{A}_{E2}=\left(F_{23}^2{F}_{11}-F_{22}{F}_{13}^2+c_6{F}_{11}{F}_{33}+c_1{F}_{11}{F}_{22}\right.\\ \left.-c_1{F}_{12}^2+2F_{12}{F}_{13}{F}_{23}+2c_5{F}_{12}{F}_{33}+c_2{F}_{22}{F}_{33}\right)\end{array}$$

$$A_{E3}=\left(F_{11}{F}_{22}-F_{12}^2\right)F_{33},{\Delta }_E=\left(c_2{c}_6-c_5^2\right)c_1,$$

where A _Ej , j = 1,2,3 and Δ _E are parameters defined in Verma (2008).

Equation (4.5) is the corresponding characteristic equation for free waves in elastic plate. Further, if thickness d(=h₁ + h₂) → ∞, in Equation (4.5), then the problem reduces to that of surfaces waves.

On applying appropriate boundary conditions on the plate outer boundaries, a large variety of important physical problems can be solved.

Higher symmetry materials

Results for higher symmetry materials such as transversely isotropic, cubic, and isotropic can be obtained as special cases with the following restrictions for transverse isotropy symmetry:

$$c_{33}=c_{22},{\mathrm{c}}_{13}=c_{12},{\mathrm{c}}_{55}=c_{66},{\mathrm{c}}_{22}-c_{23}=2c_{44};$$

(4.6)

for cubic symmetry,

$$\begin{array}{l}{c}_{11}=c_{22}=c_{33},c_{12}=c_{13}=c_{23},c_{44}=c_{55}\\ =c_{66};\mathrm{and}\end{array}$$

(4.7)

for isotropic symmetry,

$$\begin{array}{l}{c}_{11}=c_{22}=c_{33}=\lambda +2\mu ,\\ c_{12}=c_{13}=c_{23}=\lambda ,c_{44}=c_{55}=c_{66}=\mu .\end{array}$$

(4.8)

Results and discussion

Using Equation (3.17a), numerical results are presented to exhibit the dependence of dispersion with the angle of propagation. The materials chosen for this purpose is aluminum epoxy composite as layer I (h₁ = 0.6) and carbon steel as layer II (h₂ = 0.4).

Since the distinction among the wave mode types of thermoelastic waves in anisotropic plates is somewhat artificial, as the elastic wave modes are generally coupled, they are referred to as quasi-longitudinal, quasi-transverse, and quasi-shear horizontal modes. For a wave to propagate in the direction of higher symmetry, some wave types revert to pure modes and lead to a simple characteristic equation of lower order, and consequently, the loss of pure wave modes for general propagation direction in such cases. Here, Figure 1 depicts the dispersion curves with the direction cosines of propagation l₁ = 0.259, l₂ = 0.542, and l₃ = 0.799, whereas dispersion curves with the direction cosines of propagation l₁ = 0.195, l₂ = 0.515, and l₃ = 0.834 are shown in Figure 2. Similarly, dispersion curves with the direction cosines of propagation l₁ = 0.125, l₂ = 0.707, and l₃ = 0.696 are shown in Figure 3.

Figure 1

Phase velocity versus wave number for the direction cosine l ₁ = 0.259, l ₂ = 0.542, and l ₃ = 0.799.

Figure 2

Phase velocity versus wave number for the direction cosine l ₁ = 0.195, l ₂ = 0.515, and l ₃ = 0.834.

Figure 3

Phase velocity versus wave number for the direction cosine l ₁ = 0.125, l ₂ = 0.707, and l ₃ = 0.696.

The dispersion behavior of wave speed modes with different angles of propagation is demonstrated in Figures 1, 23. It is observed that at zero wave number limits, each figure (Figures 1, 23) displays three wave speeds corresponding to one quasi-longitudinal and two quasi-transverses. It is apparent that the largest value corresponds to the quasi-longitudinal. At low wave number limits, modes are found to be highly influenced and also vary with direction. From these figures, it is also observed that at low wave number limits, wave speed modes are dispersive. It is also observed that with the change in the propagation direction, lower modes appear to be highly influenced than the higher modes, where a small change is noticed. Thus, at low values of the wave number, only the lower modes got affected, and the little change is observed at the relatively high values of the wave number. Thus, the low value region of the wave number is found to be of more physical interest. Further, at high wave number limits, there is no effect in the laminated composite plates. A small change is observed in these mode values as wave number increases, and other higher modes appear; one of the modes seemed to be associated with quick change in the slope.

Conclusions

The propagation of waves in layered laminated composites, where the direction of the corresponding harmonic waves makes an arbitrary angle with respect to the layers, is studied. Three-dimensional field equations of elasticity are considered for this study and the corresponding characteristic equation is obtained on employing the continuity of displacements at the layers' interface. Obtained characteristic equation is further analytically simplified using the basic properties of block matrices, and in order to solve the problem numerically, it is sufficient to consider the determinant of the 6 × 6 matrix instead of taking the determinant 12 × 12 matrix, which reduces the numerical work considerably. Important cases such as of free waves and surface waves on reducing plates to single layer and when thickness tends to infinity are also discussed. It is found that at zero wave number limits, each figure displays three wave speeds corresponding to one quasi-longitudinal and two quasi-transverses. It is apparent that the largest value corresponds to the quasi-longitudinal. At low wave number limits, modes are found to be highly influenced and also vary with the direction. It is observed that with the change in the propagation direction, lower modes appear to have more influence than the higher modes where a small change is noticed. Therefore, at the lower value region of the wave number, it is found to be of more physical interest than at high wave number limits, on the laminated composites plates.

The study may find applications in damage identification in laminated composite, as the laminated composites possess characteristics that make them particularly useful for applications in nondestructive evaluation of such defects in plate-like structures and provide a means of inspection of an otherwise inaccessible area. In order to use waves in ultrasonic nondestructive applications, it is necessary to investigate the phenomenon of scattering of these waves in arbitrary directions.

Future work will be dedicated on enhancing the current models, especially for the heat-conducting materials in the context of generalized thermoelasticity, viscoelasticity, and orthotropic piezoelectric material. Further steps will be taken to develop a 3D model to observe the wave propagation behavior along different directions, including models of damage, to evaluate the sensitivity of auxetic laminates for damage tolerance applications. From the experimental point of view, Lamb wave propagation will be shortly evaluated for different classes of auxetic laminates with special stacking layer sequences, for comparison with the developed models. It is important to realize that, although the results presented here have been derived for a periodically layered composite with two layers in a unit cell, Floquet theory can be applied to the mathematical modeling of periodically layered structures. This can be done by finding the appropriate linear combination of Floquet waves that satisfy a set of boundary conditions prescribed at planes normal to the layering. Applying appropriate boundary conditions on the plate outer boundaries, a large variety of important physical problems can be solved, which include free waves in layered plates and in periodic media constructed from a repetition of the layered plate.

Authors' information

KL Verma gained the Ph.D. in Engineering from the Nagoya Institute of Technology, Nagoya, Japan and Masters in Philosophy and M.Sc. in Mathematics from Panjab University Chandigarh (UT), India and is presently working as an associate professor in Mathematics, Government Post Graduate College Hamirpur (HP), India. Area of specialization is in solid mechanics.