Diversity between shell-like and beam-like regions for a cantilever cylindrical shell under follower forces

Abstract

The effect of length and thickness on dynamic stability analysis of cantilever cylindrical shells under follower forces is addressed. Beck's, Leipholz's, and Hauger's problems were solved for cylindrical shells with different length-to-radius and thicknesses-to-radius ratios using the Galerkin method. First-order shear theory was used, and rotary inertias were considered in deriving the differential equations. Critical circumferential and longitudinal mode numbers and loads were evaluated for each case. Diagrams containing nondimensional load parameters vs. length and thickness parameters were plotted for each problem. For some shells with small length-to-radius ratios, flutter occurred in high longitudinal mode numbers where the first-order shear theory may not suffice to accurately evaluate the deformations. However, for long and moderately thick shells, there are ranges in which the shell can be analyzed using the simplified equivalent beam model.

Introduction

A prevailing position of potential instability is when a structure, especially a column, a reservoir, or an aerospace structure such as a projectile, undergoes an axial follower force. The most well-known physical state of follower force is Beck's problem, in which a concentrated follower force is applied at the free end of a cantilever. Practical applications of this problem include the thrust applied at the end of a projectile or missile by a rocket, the thrust applied on the body of aircraft structures by a jet engine or a gas turbine rotor, the gripping force in disk brakes, the eccentric load exerted on a platform by a tip mass, etc. Also, Leipholz's and Hauger's problems can be applied to cantilever reservoirs conveying fluid with constant or linearly varying velocity, respectively Simkins and Anderson (1975); Seyranian and Elishakoff (2002); Simitses and Hodges (2006). Two basic types of instability may exist in the case of a follower force: one characterized with zero frequency, called divergence, and the other with nonzero frequency, known as flutter. However, the prevailing instability type in these structures is flutter, which occurs in high-speed fluid flows Elfesoufi and Azrar (2005). When undergoing follower forces, the only instability type in structures with moderate thickness amounts is flutter, which is, for the most part, limited to columns, reservoirs, and aerospace structures, especially projectiles such as missiles Park and Kim (2000).

Another boundary condition in structures under follower forces is free-free at the two ends. Free-free beams or shells can also be analyzed with the equivalent cantilever model, which is rather overestimating Seyranian and Elishakoff (2002).

Most of the research on the three above-mentioned problems is concerned with beams and plates. Sugiyama and Kawagoe (1975) studied the dynamic stability of elastic columns with different boundary conditions under the simultaneous effect of conservative and nonconservative (follower) axial loads using the finite difference method. Kounadis and Katsikadelis (1976) considered the effects of shear deformation and rotary inertia on the critical Beck's load for columns with open sections and different slenderness ratios. Sugiyama and Mladenov (1983) studied the dynamic stability of elastic columns under Hauger's loading. Ryu and Sugiyama (1994) studied the dynamic stability of cantilever Timoshenko beams under Beck's loading by modeling the effect of the rocket-throwing engine as a follower load and a concentrated mass.

Altman and De Oliviera (1988), (1990) studied the dynamic stability of cantilever cylindrical and conical panels with and without slight internal damping. They asserted that due to numerical defects, the critical load calculated becomes occasionally very small. To overcome this problem, a slight damping matrix proportional to the stiffness matrix can be used in the solution Altman and De Oliviera (1988), (1990). The dynamic stability of thin cylindrical panels with different boundary conditions under concentrated and distributed follower forces was first studied by Bismark Nasr (1995) using the finite element method with C¹ continuity. The dynamic stability of free-free cylindrical shells under end-follower forces was studied by Park and Kim (2000). They used the finite element method with first-order shear theory (FST) theory. They extracted the critical loads, critical sequential modes, and critical circumferential mode numbers for different length-to-radius (L/R) and thickness-to-radius (h/R) ratios. They concluded that FST is valid only for L/R > 20, and for L/R > 40, the cylindrical shell can be analyzed with the beam theory in certain regions of h/R. The same problem for cylindrical shells was studied by considering the fluid-shell interaction by Jung et al. (2005). They gathered that, in most cases except those with very low filling ratios, the presence of liquid in the cylinder increases the stability. Bochkarev and Matveenko (2008) also studied the dynamic stability of cylindrical shells conveying fluid for free-free and clamped-free boundary conditions using the perturbation of velocity potential method.

Although rockets, missiles, and fluid reservoirs are mostly cylindrical shells rather than beams, to the best of the authors' knowledge, it seems the dynamic stability of complete cylindrical shells undergoing follower forces has not been studied to the sufficient extent. Specifically, actual shell-like and beam-like geometric regions in cylindrical shells for all three kinds of follower forces have not been sophisticatedly defined for cantilever structures.

In the present research, the dynamic instability of cantilever cylindrical shells is solved for Beck's, Leipholz's, and Hauger's problems to find out the geometrical regions in which the structure acts as a general shell-like or simplified beam-like model. Flutter loads are plotted for different L/R and h/R ratios. Tables containing critical sequential modes and critical circumferential mode numbers are collected for different L/R and h/R ratios. For each L/R, specific h/R regions could be found in which the structure can be analyzed simply with an equivalent beam model. This region is found to be almost independent of the loading scheme (i.e., almost the same in Beck's, Leipholz's, or Hauger's problems).

Methods

Formulation

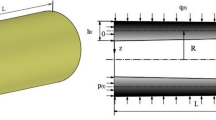
Consider a cylindrical shell with radius R, thickness h, and length L. In case that the coordinate system is taken to be as shown in Figure1a, then using FST, the deformation components of any point can be written as follows Reddy (2007):

$$\begin{array}{ll}u\left(x,\theta ,z,t\right)\hfill & =u_0\left(x,\theta ,t\right)+z{\phi }_x\left(x,\theta ,t\right)\hfill \\ v\left(x,\theta ,z,t\right)\hfill & =v_0\left(x,\theta ,t\right)+z{\phi }_{\theta }\left(x,\theta ,t\right)\hfill \\ w\left(x,\theta ,z,t\right)\hfill & =w_0\left(x,\theta ,t\right),\hfill \end{array}$$

(1)

where u₀, v₀, and w₀ are the displacement components of the middle surface, and ϕ _x and ϕ _θ are changes in the slope of the normal to the middle surface around θ and x axes, respectively. The strain resultants per unit length for a cylindrical shell are shown in Figure1b.

Figure 1

The coordinate system (a) and strain resultants (b) considered for cylindrical shells.

For the strain components, Love's hypotheses are used. These hypotheses express the following Reddy (2007):

• The transverse normal is inextensible.

• Normals to the reference surface of the shell before deformation remain straight, but not necessarily normal, after deformation.

• Deflections and strains are infinitesimal.

• The transverse normal stress is negligible (plane-stress state is invoked).

Using Equation 1 and by considering Love's hypotheses expressed above, the strain tensor elements can be written as follows Reddy (2007):

$$\begin{array}{l}{\epsilon }_1={\epsilon }_1^0+z{\epsilon }_1^1,{\epsilon }_2=\frac{1}{1+z/R}\left({\epsilon }_2^0+z{\epsilon }_2^1\right)\hfill \\ {\epsilon }_6={\omega }_1^0+z{\omega }_1^1+\frac{1}{1+z/R}\left({\omega }_2^0+z{\omega }_2^1\right)\hfill \\ {\epsilon }_4=\frac{1}{1+z/R}{\epsilon }_4^0,{\epsilon }_5={\epsilon }_4,\hfill \end{array}$$

(2)

where the superscripted components are defined as follows Reddy (2007):

$$\begin{array}{ll}{\epsilon }_1^0\hfill & =\frac{\partial u_0}{\partial x},{\epsilon }_2^0=\frac{1}{R}\left(\frac{1}{R}\frac{\partial v_0}{\partial \theta }+\frac{\partial R}{\partial x}{u}_0+w_0\right)\hfill \\ {\epsilon }_4^0\hfill & =\frac{1}{R}\left(\frac{1}{R}\frac{\partial w_0}{\partial \theta }+R{\phi }_{\theta }-v_0\right),{\epsilon }_5^0=\frac{\partial w_0}{\partial x}+{\phi }_x\hfill \\ {\omega }_1^0\hfill & =\frac{\partial v_0}{\partial x},{\omega }_2^0=\frac{1}{R^2}\frac{\partial u_0}{\partial \theta }\hfill \\ {\epsilon }_1^1\hfill & =\frac{\partial {\phi }_x}{\partial x},{\epsilon }_2^1=\frac{1}{R^2}\frac{\partial {\phi }_{\theta }}{\partial \theta }\hfill \\ {\omega }_1^1\hfill & =\frac{\partial {\phi }_{\theta }}{\partial x},{\omega }_2^1=\frac{1}{R^2}\frac{\partial {\phi }_x}{\partial \theta }.\hfill \end{array}$$

(3)

The stress resultant vectors in unit length (of the shell circumference), N, M, and Q, can be obtained in terms of strain components using the ABD matrix as follows Reddy (2007):

$$\begin{array}{ll}\left[\begin{array}{l}\left\{N\right\}\hfill \\ \left\{M\right\}\hfill \end{array}\right]\hfill & =\left[\begin{array}{cc}\hfill \begin{array}{l}\left[A\right]\hfill \\ \left[B\right]\hfill \end{array}\hfill & \hfill \begin{array}{l}\left[B\right]\hfill \\ \left[D\right]\hfill \end{array}\hfill \end{array}\right]\left[\begin{array}{l}\left\{{\epsilon }^0\right\}\hfill \\ \left\{{\epsilon }^1\right\}\hfill \end{array}\right],\left\{{\epsilon }^0\right\}=\left\{\begin{array}{l}{\epsilon }_1^0\hfill \\ {\epsilon }_2^0\hfill \\ {\epsilon }_6^0\hfill \end{array}\right\},\hfill \\ \left\{{\epsilon }^1\right\}\hfill & =\left\{\begin{array}{l}{\epsilon }_1^1\hfill \\ {\epsilon }_2^1\hfill \\ {\epsilon }_6^1\hfill \end{array}\right\},{\epsilon }_6^0={\omega }_1^0+{\omega }_2^0,{\epsilon }_6^1={\omega }_1^1+{\omega }_2^1\hfill \\ \left\{\begin{array}{l}{Q}_2\hfill \\ Q_1\hfill \end{array}\right\}\hfill & =K_s\left[\begin{array}{cc}\hfill \begin{array}{l}{A}_{44}\hfill \\ A_{45}\hfill \end{array}\hfill & \hfill \begin{array}{l}{A}_{45}\hfill \\ A_{55}\hfill \end{array}\hfill \end{array}\right]\left\{\begin{array}{l}{\epsilon }_4^0\hfill \\ {\epsilon }_5^0\hfill \end{array}\right\}\hfill \end{array}$$

(4)

where the components are defined as follows Reddy (2007):

$$\begin{array}{ll}\left(A_{\mathit{ij}},B_{\mathit{ij}},D_{\mathit{ij}}\right)\hfill & ={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}{S}_{\mathit{ij}}\left(z\right)\left(1,z,z^2\right)\mathit{dz}},(i,j=1,2,6)\hfill \\ A_{\mathit{ij}}\hfill & ={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}{S}_{\mathit{ij}}\left(z\right)\mathit{dz}},(i,j=4,5)\hfill \\ S_{11}\hfill & =S_{22}=\frac{E}{1-{\upsilon }^2},{\mathrm{S}}_{12}=S_{21}=\frac{\mathit{\upsilon E}}{1-{\upsilon }^2},\hfill \\ {\mathrm{S}}_{44}\hfill & =S_{55}=S_{66}=\frac{E}{2\left(1+\upsilon \right)},\hfill \end{array}$$

(5)

where K _s is the shear correction factor, which is π²/12 for cylindrical shells Park and Kim (2000), and υ is Poisson's ratio, which was taken as 0.3 (for mild steel) in this research.

In order to derive the governing equations of motion, Hamilton's principle is used as follows Reddy (2007):

$${\displaystyle \underset{0}{\overset{T}{\int }}\left[\mathit{\delta K}-\mathit{\delta U}+\delta W_{\mathit{\text{nc}}}\right]\mathit{\text{dt}}}=0,$$

(6)

where δK and δU are variations of kinetic energy and strain energy, respectively, defined as follows:

$$\begin{array}{cc}\delta K\hfill & =\underset{0}{\overset{L}{\int }}\underset{0}{\overset{2\pi }{\int }}\left[I_0,\left({\dot{u}}_0\delta {\dot{u}}_0+{\dot{v}}_0\delta {\dot{v}}_0+{\dot{w}}_0\delta {\dot{w}}_0\right)\right.\hfill \\ +I_1\left({\dot{\phi }}_x\delta {\dot{u}}_0+{\dot{u}}_0\delta {\dot{\phi }}_x+{\dot{\phi }}_{\theta }\delta {\dot{v}}_0+{\dot{v}}_0\delta {\dot{\phi }}_{\theta }\right)\hfill \\ \left.+I_2\left({\dot{\phi }}_x\delta {\dot{\phi }}_x+{\dot{\phi }}_{\theta }\delta {\dot{\phi }}_{\theta }\right)\right]\mathit{\text{Rdxdθ}}\hfill \\ \delta U\hfill & =\underset{0}{\overset{L}{\int }}\underset{0}{\overset{2\pi }{\int }}\left[N_x\delta {\epsilon }_1^0+M_x\delta {\epsilon }_1^1+N_{\theta }\delta {\epsilon }_2^0+M_{\theta }\delta {\epsilon }_2^1\right.\hfill \\ +\left(N_{\mathit{x\theta }}\delta {\omega }_1^0+N_{\mathit{\theta x}}\delta {\omega }_2^0\right)+\left(M_{\mathit{x\theta }}\delta {\omega }_1^1+M_{\mathit{\theta x}}\delta {\omega }_2^1\right)\hfill \\ \left.+Q_{\theta }\delta {\epsilon }_4^0+Q_x\delta {\epsilon }_5^0\right]\mathit{\text{Rdxdθ}}\hfill \\ I_i\hfill & ={\displaystyle \underset{-h/2}{\overset{h/2}{\int }}\rho \left(z\right)\left(1+\frac{z}{R}\right){\left(z\right)}^i\mathit{dz},\left(i=0,1,2\right)}\hfill \end{array}$$

(7)

where the dot superscript shows differentiation with respect to time. δW _nc is the variation of the work done by nonconservative forces. δW _nc in Beck's, Leipholz's, and Hauger's problems for cylindrical shells are obtained after integration by parts as follows Simitses and Hodges (2006; Altman and De Oliviera (1988); Park and Kim (2000):

$$\begin{array}{c}\delta W_{\mathit{\text{nc}}}=-\bar{P}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(\frac{{\partial }^{2}v}{\partial x^2}\mathit{\delta v}+\frac{{\partial }^{2}w}{\partial x^2}\mathit{\delta w}\right)}\mathit{\text{Rdxdθ}}}\hfill \\ \text{for}\text{Beck}’\mathrm{s}\text{problem},\hfill \end{array}$$

(8)

$$\begin{array}{c}\delta W_{\mathit{\text{nc}}}=-\bar{p}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(L-x\right)\left(\frac{{\partial }^{2}v}{\partial x^2}\mathit{\delta v}+\frac{{\partial }^{2}w}{\partial x^2}\mathit{\delta w}\right)}\mathit{\text{Rdxdθ}}}\hfill \\ \text{for}\text{Leipholz}’\mathrm{s}\text{problem},\hfill \end{array}$$

(9)

$$\begin{array}{c}\delta W_{\mathit{\text{nc}}}=-\frac{\bar{g}}{2}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left(L-x\right)}^2\left(\frac{{\partial }^{2}v}{\partial x^2}\mathit{\delta v}+\frac{{\partial }^{2}w}{\partial x^2}\mathit{\delta w}\right)}\mathit{\text{Rdxdθ}}}\hfill \\ \text{for}\text{Hauger}’\mathrm{s}\text{problem},\hfill \end{array}$$

(10)

where$\bar{P}=P/2\mathit{\pi R}$,$\bar{p}=p/2\mathit{\pi R}$, and$\bar{g}=g/2\mathit{\pi R}$ are the forces per unit length of the shell circumference, on the premise that the axial stress is uniformly distributed along the thickness. We note that$\bar{p}$ and$\bar{g}$ are forces per unit length and unit square length of the shell, respectively. Stated another way, if the resultant force per unit length of the shell cross section circumference is of an equal magnitude$\bar{P}$ in all three cases, then$\bar{p}$ and$\bar{g}$ will be$\bar{P}/L$ and$2\bar{P}/L^2$, respectively. Figure2 includes the scheme of each follower loading.

Figure 2

Schematic shape of follower loading. (a) Beck's problem, (b) Leipholz's problem, (c) Hauger's problem.

Thus, Equations 8, 9 and 10 can be rewritten as follows:

$$\begin{array}{c}\delta W_{\mathit{\text{nc}}}=-\bar{P}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(\frac{{\partial }^{2}v}{\partial x^2}\mathit{\delta v}+\frac{{\partial }^{2}w}{\partial x^2}\mathit{\delta w}\right)}\mathit{\text{Rdxdθ}}}\hfill \\ \text{for}\text{Beck}’\mathrm{s}\text{problem},\hfill \end{array}$$

(11)

$$\begin{array}{c}\delta W_{\mathit{\text{nc}}}=-\bar{P}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(1-\frac{x}{L}\right)\left(\frac{{\partial }^{2}v}{\partial x^2}\mathit{\delta v}+\frac{{\partial }^{2}w}{\partial x^2}\mathit{\delta w}\right)}\mathit{\text{Rdxdθ}}}\hfill \\ \text{for}\text{Leipholz}’\mathrm{s}\text{problem},\hfill \end{array}$$

(12)

$$\begin{array}{c}\delta W_{\mathit{\text{nc}}}=-\bar{P}{\displaystyle \underset{0}{\overset{L}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left(1-\frac{x}{L}\right)}^2\left(\frac{{\partial }^{2}v}{\partial x^2}\mathit{\delta v}+\frac{{\partial }^{2}w}{\partial x^2}\mathit{\delta w}\right)}\mathit{\text{Rdxdθ}}}\hfill \\ \text{for}\text{Hauger}’\mathrm{s}\text{problem}.\hfill \end{array}$$

(13)

In order to derive the equations of motion correctly, an additional constraint equation must be added to δU as follows:

$${\displaystyle \int {\displaystyle \int \left(\frac{M_{\mathit{\theta x}}}{R}+N_{\mathit{\theta x}}-N_{\mathit{x\theta }}\right)\delta {\phi }_n\mathit{\text{Rdxdθ}}}},$$

(14)

where δφ _n denotes the rotation about the transverse normal to the shell surface. For thin shells, M _xθ  = M _θx , N _xθ  = N _θx . Using Equation 2 to write the strain components of Equation 3 in terms of displacements, the following system of differential equations will be derived:

$$\begin{array}{c}\underset{t_1}{\overset{t_2}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\int }}\left\{\frac{\partial N_x}{\partial x}+\frac{1}{R}\frac{\partial }{\partial \theta }\left(N_{\mathit{x\theta }}-\frac{1}{2R}{M}_{\mathit{x\theta }}\right)-F\left(x\right)\frac{{\partial }^2{u}_0}{\partial x^2}\right.\hfill \\ \left.-\left(I_0\frac{{\partial }^2{u}_0}{\partial t^2}+I_1\frac{{\partial }^2{\phi }_x}{\partial t^2}\right)\right\}\mathit{\text{dxRdθdt}}\hfill \\ +\underset{0}{\overset{t}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\left[-N_x\right]}}\mathit{\text{Rdθdt}}=0\hfill \\ \delta v_0:\underset{t_1}{\overset{t_2}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\int }}\left\{\frac{\partial }{\partial x}\left(N_{\mathit{x\theta }}+\frac{1}{2R}{M}_{\mathit{x\theta }}\right)+\frac{1}{R}\frac{\partial N_{\theta }}{\partial \theta }+\frac{Q_{\theta }}{R}\right.\hfill \\ \left.-F\left(x\right)\frac{{\partial }^2{v}_0}{\partial x^2}-\left(I_0\frac{{\partial }^2{v}_0}{\partial t^2}+I_1\frac{{\partial }^2{\phi }_{\theta }}{\partial t^2}\right)\right\}\mathit{\text{dxRdθdt}}\hfill \\ +\underset{0}{\overset{t}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\left[-N_{\mathit{x\theta }}\right]}}\mathit{\text{Rdθdt}}=0\hfill \\ \delta w_0:\underset{t_1}{\overset{t_2}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\int }}\left\{\frac{\partial Q_x}{\partial x}+\frac{1}{R}\frac{\partial Q_{\theta }}{\partial \theta }-\frac{N_{\theta }}{R}+q-F\left(x\right)\frac{{\partial }^2{w}_0}{\partial x^2}\right.\hfill \\ \left.-I_0\frac{{\partial }^2{w}_0}{\partial t^2}\right\}\mathit{\text{dxRdθdt}}+\underset{0}{\overset{t}{\int }}\underset{0}{\overset{2\pi }{\int }}{\left[-Q_x\right]}_0^L\mathit{\text{Rdθdt}}=0\hfill \\ \delta {\phi }_1:\underset{t_1}{\overset{t_2}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\int }}\left\{\frac{\partial M_x}{\partial x}+\frac{1}{R}\frac{\partial M_{\mathit{x\theta }}}{\partial \theta }\right.-Q_x-\left(I_2\frac{{\partial }^2{\phi }_x}{\partial t^2}\right.\hfill \\ \left.\left.+I_1\frac{{\partial }^2{u}_0}{\partial t^2}\right)\right\}dxRd\theta dt+\underset{0}{\overset{t}{\int }}\underset{0}{\overset{2\pi }{\int }}{\left[-M_x\right]}_0^L\mathit{\text{Rdθdt}}=0\hfill \\ \delta {\phi }_2:\underset{t_1}{\overset{t_2}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{L}{\int }}\left\{\frac{\partial M_{\mathit{x\theta }}}{\partial x}+\frac{1}{R}\frac{\partial M_{\theta }}{\partial \theta }-Q_{\theta }-\left(I_2\frac{{\partial }^2{\phi }_{\theta }}{\partial t^2}\right.\right.\hfill \\ \left.\left.+I_1\frac{{\partial }^2{v}_0}{\partial t^2}\right)\right\}dxRd\theta dt+\underset{0}{\overset{t}{\int }}\underset{0}{\overset{2\pi }{\int }}{\left[-M_{\mathit{x\theta }}\right]}_0^L\mathit{\text{Rdθdt}}=0,\hfill \end{array}$$

(15)

where []₀^L denotes the value at x = 0 subtracted from the value at x = L, and F(x) is$\bar{P}$,$\bar{P}\left(1-x/L\right)$, and$\bar{P}{\left(1-x/L\right)}^2$ in Beck's, Leipholz's, and Hauger's problems, respectively. Since the mode shapes used in the present research do not satisfy natural boundary conditions, the boundary equations have been added to the domain equations. After replacing the stress resultants by their strain equivalents (Equation 4) and replacing strain components in terms of deformations (Equation 1), the following differential operators will be derived:

$$\begin{array}{c}{\displaystyle \underset{t_1}{\overset{t_2}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left({\displaystyle \underset{0}{\overset{L}{\int }}\left[L\right]\left\{\text{Δ}\right\}\mathit{dx}}+{\left[\left[L^{\prime }\right]\left\{\text{Δ}\right\}\right]}_0^L\right)\mathit{\text{Rdθdt}}}}=\left\{0\right\},\hfill \\ \left\{\text{Δ}\right\}={\left\{u_0,v_0,w_0,{\phi }_x,{\phi }_{\theta }\right\}}^T\hfill \end{array}$$

(16)

where L and L^′ matrices are differential operators of the domain and boundary, respectively, whose elements are defined in the Appendix.

Solution method

It can be proved that all of the equations are orthogonal in terms of θ if the displacements are defined using alternative sine and cosine functions as stated in Equation 17. Thus, we can choose base functions and mode shape functions as follows:

$$\begin{array}{ll}{u}_0\hfill & ={\displaystyle {\sum }_{j=1}^q{U}_j\left(x\right)}\text{cos}\left(\mathit{n\theta }\right)e^{\mathit{\omega t}},U_j\left(x\right)=a_j^1{\psi }_j^1\left(x\right)\hfill \\ v_0\hfill & ={\displaystyle {\sum }_{j=1}^q{V}_j\left(x\right)}\text{sin}\left(\mathit{n\theta }\right)e^{\mathit{\omega t}},V_j\left(x\right)=a_j^2{\psi }_j^2\left(x\right)\hfill \\ w_0\hfill & ={\displaystyle {\sum }_{j=1}^q{W}_j\left(x\right)}\text{cos}\left(\mathit{n\theta }\right)e^{\mathit{\omega t}},W_j\left(x\right)=a_j^3{\psi }_j^3\left(x\right)\hfill \\ {\phi }_x\hfill & ={\displaystyle {\sum }_{j=1}^q{X}_j\left(x\right)}\text{cos}\left(\mathit{n\theta }\right)e^{\mathit{\omega t}},X_j\left(x\right)=a_j^4{\psi }_j^4\left(x\right)\hfill \\ {\phi }_{\theta }\hfill & ={\displaystyle {\sum }_{j=1}^q{Y}_j\left(x\right)}\text{sin}\left(\mathit{n\theta }\right)e^{\mathit{\omega t}},Y_j\left(x\right)=a_j^5{\psi }_j^5\left(x\right).\hfill \end{array}$$

(17)

The superscripts denote functions corresponding to u ₀ , …, and φ _θ , and a _j ⁱ (i = 1…5) are the unknown coefficients that could be determined by exerting any approximation method such as the Galerkin method. For the mode shape functions, ψ _j ⁱ(x) (i = 1…5) that satisfy the essential boundary conditions of the cantilever cylinder, the following polynomials have been taken (Altman and De Oliviera, 1988):

$${\psi }_j^1={\psi }_j^2=x^j,{\psi }_j^3=x^{j+1},{\psi }_j^4=\frac{d{\phi }_j^3}{\mathit{dx}},{\psi }_j^5={\psi }_j^3.$$

(18)

After application of the Galerkin method, stiffness and mass matrices can be defined as functions of n. The stiffness matrix is also a function of$\bar{P}$. The equations obtained by the application of the so-called generalized Galerkin method are algebraic equations in terms of a _j ⁱ (i = 1…5). Setting the determinant of the coefficient matrix to zero to impose the condition of nontrivial solution, as stated in Equation 19, ω will be obtained:

$$\text{det}\left({\mathit{K}}_{\left(\bar{P},n\right)}+{\omega }^2{\mathit{M}}_{\left(n\right)}\right)=0.$$

(19)

ω is a complex number with a zero real part until the shell loses its stability under the applied follower forces. As soon as instability occurs, the real part begins to become positive or negative. In order to facilitate verification for future works, the nondimensional load parameter β _s for the shell model can be considered as the comparator, which is defined as follows Park and Kim (2000):

$${\beta }_s=\frac{1-{\nu }^2}{\mathit{\text{Eh}}}\bar{P}.$$

(20)

Results and discussion

Calculations in the present study that demonstrated the optimum number of terms needed for convergence in the Galerkin method is 6, which is confirmed in the study of Altman and De Oliviera (1988). The ‘Free vibration of shells’ and ‘Flutter of very long shells (equivalent beam model)’ subsections comprise verification of results with previous works.

Free vibration of shells

The minimum natural frequency (pertaining to the first mode) vs. the circumferential mode number for a shell with the following properties is shown in Figure3. The results were verified with those of the work of Leissa (1973).

Figure 3

Minimum natural frequency (Hz) for free vibration of cantilever shell vs. circumferential mode number ( R / h  = 400,  L / R  = 2.23,  h  = 0.254 mm ).

Flutter of very long shells (equivalent beam model)

When the imaginary part of the natural frequency (ω) of two sequential modes becomes zero and the real part gets greater than zero, the vibration amplitude approaches infinity and divergence occurs. Alternatively, when the imaginary parts of the natural frequency of two sequential modes become equal and the real part gets greater than zero, the vibration amplitude approaches infinity and flutter occurs. Results demonstrated that instability under follower forces can be flutter or divergence. However, flutter always takes place before divergence in shells with moderate thicknesses. In order to verify the present computational approach, the problem was firstly solved for long shells, and the results were compared with those obtained with the beam model. The nondimensional load and frequency parameters in the beam model have been defined in the literature as follows Simitses and Hodges (2006):

$${\beta }_b=\frac{P{L}^2}{\mathit{\text{EI}}},{\Omega }_b=\omega L^2\sqrt{\frac{\mu }{\mathit{\text{EI}}}}$$

(21)

where μ is the mass per unit length (μ = 2πRhρ). In order to analyze very long shells with the equivalent beam model, the following identity can be used:

$$A=2\mathit{\text{πRh}},I=\pi R^{3}h\Rightarrow \frac{I}{A{L}^2}=\frac{1}{2}{\left(\frac{R}{L}\right)}^2.$$

(22)

Therefore, the relation between the two nondimensional loads is as follows:

$${\beta }_b=\frac{2{\left(L/R\right)}^2}{1-{\nu }^2}{\beta }_s.$$

(23)

Figures4,5, and6 show the results for Beck's, Leipholz's, and Hauger's problems, respectively. In all three figures, the minimum flutter load occurs between the first and second longitudinal modes. Thus, the upper and lower branches of Im(Ω_b) pertain to the first and second longitudinal modes, respectively. Present results for Hauger's problem have been compared with those of the work of De Rosa and Franciosi (1990). However, based on the alternative definition of Hauger's loading in the work of De Rosa and Franciosi (1990), twice the load calculated in the present research is given in that reference.

Figure 4

Variation of the imaginary and real parts of Ω _b vs. β _b for Beck's problem.

Figure 5

Variation of the imaginary and real parts of Ω _b vs. β _b for Leipholz's problem.

Figure 6

Variation of the imaginary and real parts of Ωb vs. βb for Hauger's problem ( β _bcr (De Rosa and Franciosi) = 75.4 ).

Results for shells

Tables1 and2 include critical circumferential mode numbers (n _cr ) and critical longitudinal mode numbers (M _cr ), those corresponding to the minimum flutter load, for the three problems of shells with different L/R and h/R ratios. The shell has the following geometric parameters (which belong to mild steel):

$$\begin{array}{c}h=0.01\mathrm{m},E=2.03\times {10}^{11}\mathrm{Pa},\nu =0.3,\hfill \\ \rho =7,850\mathit{\text{kg}}/{\mathrm{m}}^3.\hfill \end{array}$$

Table 1 Critical circumferential mode numbers ( n _cr ) for all three problems

Table 2 Numbers of the first two critical modes for all three problems

Tables1 and2 reveal the following results:

• For a given L/R and h/R ratio, n _cr is identical for all three problems for short shells (L/R ≤ 1). However, for longer shells, n _cr tends to increase when the loading function's degree rises, and the increase in n _cr is the most rigorous for L/R = 1. In other words, L/R = 1 is the most sensitive case towards changing the load function (to Leipholz's and Hauger's loadings).

• For short shells (L/R ≤ 1), critical longitudinal mode numbers tend to increase when the loading degree increases. However, they remain constant for longer shells.

• When h/R increases and L/R decreases, the effect of shear deformations on the vibration gets increased. Since this effect is prevalent in higher modes, in large values of h/R and small values of L/R, the number of critical modes approaches higher modes, i.e., higher-than-5 modes. It is quite obvious that the critical load obtained in those cases based on the FST theory is not accurate enough since shear theories of higher degrees are needed to account for higher modes Park and Kim (2000). For instance, for a shell under Beck's loading, with h/R = 0.075 and L/R = 1, the nondimensional frequencies for the first 11 modes are demonstrated in Figure7. For more convenience, Ω_b has been plotted instead of Ω _s using Equation 22. Also, the below-mentioned results can be observed.

• In the 0 < h/R ≤ 0.03 interval, all answers have sufficient precision with the FST theory since the instability longitudinal mode numbers are low, and thus flexural deformations are much more significant than shear deformations [2]. In the 0.03 < h/R ≤ 0.05 interval, answers for L/R ≥ 0.25 are valid. In the 0.05 < h/R ≤ 0.15 interval, answers for L/R ≥ 5 are valid. Finally, in the h/R > 0.15 interval, answers for L/R ≥ 10 are valid.

• For thin shells (0 < h/R ≤ 0.03), critical longitudinal mode numbers increase (to second and third) from L/R = 0.5 to L/R = 1 and decrease (to first and second) onwards. Expressed in another way, flutter in thin shells occurs in the second and third modes only for L/R of about unity and occurs in the first and second modes for other L/R ratios. All the same, for shells with h/R > 0.03, flutter always takes place in the first and second modes.

• For L/R ≥ 5, for a specified L/R ratio, n _cr decreases with h/R, and conversely, for a specified h/R ratio, n _cr decreases with L/R. Altogether, for large h/R and L/R ratios, flutter always occurs in n _cr of unity, which signifies that the structure is approaching the beam-like model.

Figure 7

Nondimensional frequencies for the first 11 modes for a shell. The shell has the following components: h = 0.01 m, E = 2.03 × 10¹¹ Pa, ν = 0.3, ρ = 7, 850 kg/m³, h/R = 0.075, L/R = 1.

The critical nondimensional load parameters and β _scr of shells with the geometric parameters stated in Equation 24 are depicted against L/R and h/R in Figures8,9, and10 and Figures11,12 and13, respectively.

Figure 8

Variation of β _scr against L / R for different h / R ratios in Beck's problem.

Figure 9

Variation of β _scr against L / R for different h / R ratios in Leipholz's problem.

Figure 10

Variation of β _scr against L / R for different h / R ratios in Hauger's problem.

Figure 11

Variation of β _scr against h / R for different L / R ratios in Beck's problem.

Figure 12

Variation of β _scr against h / R for different L / R ratios in Leipholz's problem.

Figure 13

Variation of β _scr against h / R for different L / R ratios in Hauger's problem.

It was observed in the outcomes that with a specified h/R and L/R, β _s is independent of the thickness. The reason is that in case h/R and L/R are both constant, h, R, and L will all be changed to the same extent when h changes. Thus, for h^′ other than 0.01 m

$${\beta }_s\left(h/R,L/R,h^{\prime }\right)={\beta }_s\left(h/R,L/R,0.01\right)$$

(24)

From Figures8,9,10,11,12, and13, the following results can be drawn:

In a constant h/R, the nondimensional load β _scr gets decreased with L/R. However, in a constant L/R, β _scr gets increased with h/R.

By increasing L/R ratio, for L/R > 10, β _scr magnitudes approach an envelope curve, which is in fact the curve pertaining to the equivalent beam.

Since β _scr is independent of h/R in beams, it can be deduced that, in Figures11,12, and13, the ranges which are constant with h/R can be considered as beam-like ranges, i.e., the ranges in which the structure can be analyzed with a simple equivalent beam model. This eliminates the complicated shell differential equations which are much more difficult to solve than beam equations Park and Kim (2000). It can be easily observed that this range is almost independent of the loading scheme, i.e., almost the same in Beck's, Leipholz's, and Hauger's loadings. It can also be observed that the FST theory is valid for all h/R and L/R ratios in beam-like ranges.

Tables3 and4 include the ratio of β _scr in Leipholz's problem to that in Beck's problem and the ratio of β _scr in Hauger's problem to that in Beck's problem, respectively.

Table 3 Ratio of β _scr (Leipholz) to β _scr (Beck)

Table 4 Ratio of β _scr (Hauger) to β _scr (Beck)

It can be observed from Tables3 and4 that the so-defined ratios in very thin and short shells (h/R < 0.03, L/R ≤ 0.5) and very long and moderately thick (beam-like) shells are almost equal.

Also, it was observed in the numerical results that the nondimensional frequency parameter is the same, i.e., approximately 12, for all the three problems in the beam-like ranges.

Conclusions

Inclusive work on the dynamic stability of cantilever cylindrical shells considering all types of follower loads and wide ranges of length and thickness ratios does not meet the needs. In this paper, dynamic stability of clamped-free cylindrical shells was studied to bring out the geometric regions in which the structure acts as a general shell or a beam. In developing the equations of motion, FST theory was used and rotary inertias were considered. The results for the equivalent beam were in complete agreement with those in the literature. Results consisted of tables containing critical longitudinal mode numbers and critical circumferential mode numbers, and also diagrams showing flutter load parameters against vast intervals of length and thickness ratios. Raising the load function degree increased critical circumferential mode numbers and critical longitudinal mode numbers in specific ranges of thickness and length ratios. The flutter load parameter decreased by increasing the length ratio and decreasing the thickness ratio. In some ranges of small length ratios, results obtained based on FST theory should be more carefully dealt with since the critical longitudinal mode numbers are obtained to be higher than 5, in which FST seems not to be accurate enough. For long and moderately thick shells, ranges of thickness ratios exist in which the shell can be analyzed with a simple equivalent beam model, which is almost independent of the loading scheme. For very short and thin shells, and also for beam-like (long and moderately thick) shells, the ratios of Leipholz's to Beck's, and Hauger's to Beck's nondimensional critical loads are the same as their corresponding values in beams. Moreover, the nondimensional frequency parameters in beam-like shells are equal in all three problems.

Appendix

$$\begin{array}{l}{L}_{11}=A_{11}\frac{{\partial }^2}{\partial x^2}+\left(\frac{A_{66}}{R^2}-\frac{1}{2}\frac{B_{66}}{R^3}\right)\frac{{\partial }^2}{\partial {\theta }^2}-I_0\frac{{\partial }^2}{\partial t^2},L_{12}=\left(\frac{A_{12}+A_{66}}{R}-\frac{1}{2}\frac{B_{66}}{R^2}\right)\frac{{\partial }^2}{\partial x\partial \theta }\hfill \\ L_{13}=\frac{A_{12}}{R}\frac{\partial }{\partial x},L_{14}=B_{11}\frac{{\partial }^2}{\partial x^2}+\left(\frac{B_{66}}{R^2}-\frac{D_{66}}{R^3}\right)\frac{{\partial }^2}{\partial {\theta }^2}-I_1\frac{{\partial }^2}{\partial t^2},L_{15}=\left(\frac{B_{12}+B_{66}}{R}-\frac{1}{2}\frac{D_{66}}{R^2}\right)\frac{{\partial }^2}{\partial x\partial \theta }\hfill \\ L_{21}=\left(\frac{A_{12}+A_{66}}{R}+\frac{1}{2}\frac{B_{66}}{R^2}\right)\frac{{\partial }^2}{\partial x\partial \theta },L_{22}=\left(A_{66}+\frac{1}{2}\frac{B_{66}}{R}-F\left(x\right)\right)\frac{{\partial }^2}{\partial x^2}+\frac{A_{22}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}-\frac{K_s{A}_{44}}{R^2}-I_0\frac{{\partial }^2}{\partial t^2},\hfill \\ L_{23}=\left(\frac{A_{22}}{R^2}+\frac{K_s{A}_{44}}{R^2}\right)\frac{\partial }{\partial \theta },L_{24}=\left(\frac{B_{12}+B_{66}}{R}+\frac{1}{2}\frac{D_{66}}{R^2}\right)\frac{{\partial }^2}{\partial x\partial \theta },L_{25}=\left(B_{66}+\frac{1}{2}\frac{D_{66}}{R}\right)\frac{{\partial }^2}{\partial x^2}+\frac{B_{22}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}+\frac{K_s{A}_{44}}{R}-I_1\frac{{\partial }^2}{\partial t^2}\hfill \\ L_{31}=-L_{13},L_{32}=-L_{23},L_{33}=\left(K_s{A}_{55}-F\left(x\right)\right)\frac{{\partial }^2}{\partial x^2}-\frac{A_{22}}{R^2}+\frac{K_s{A}_{44}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}-I_0\frac{{\partial }^2}{\partial t^2}\hfill \\ L_{34}=\left(-\frac{B_{12}}{R}+K_s{A}_{55}\right)\frac{\partial }{\partial x},L_{35}=\left(-\frac{B_{22}}{R^2}+\frac{K_s{A}_{44}}{R}\right)\frac{\partial }{\partial \theta }\hfill \\ L_{41}=B_{11}\frac{{\partial }^2}{\partial x^2}+\frac{B_{66}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}-I_1\frac{{\partial }^2}{\partial t^2},L_{42}=\left(\frac{B_{12}+B_{66}}{R}\right)\frac{{\partial }^2}{\partial x\partial \theta },L_{43}=-L_{34}\hfill \\ L_{44}=-K_s{A}_{55}+D_{11}\frac{{\partial }^2}{\partial x^2}+\frac{D_{66}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}-I_2\frac{{\partial }^2}{\partial t^2},L_{45}=\left(\frac{D_{12}+D_{66}}{R}\right)\frac{{\partial }^2}{\partial x\partial \theta }\hfill \\ L_{51}=\left(\frac{B_{12}+B_{66}}{R}\right)\frac{{\partial }^2}{\partial x\partial \theta },L_{52}=B_{66}\frac{{\partial }^2}{\partial x^2}+\frac{B_{22}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}+\frac{K_s{A}_{44}}{R}-I_1\frac{{\partial }^2}{\partial t^2},L_{53}=-L_{35}\hfill \\ L_{54}=L_{45},L_{55}=-K_s{A}_{44}+D_{66}\frac{{\partial }^2}{\partial x^2}+\frac{D_{22}}{R^2}\frac{{\partial }^2}{\partial {\theta }^2}-I_2\frac{{\partial }^2}{\partial t^2}\hfill \\ {L^{\prime }}_{11}=-A_{11}\frac{\partial }{\partial x},{L^{\prime }}_{12}=-\frac{A_{12}}{R}\frac{\partial }{\partial \theta },{L^{\prime }}_{13}=-\frac{A_{12}}{R},{L^{\prime }}_{14}=-B_{11}\frac{\partial }{\partial x},{L^{\prime }}_{15}=-\frac{B_{12}}{R}\frac{\partial }{\partial \theta }\hfill \\ {L^{\prime }}_{21}=-\frac{A_{66}}{R}\frac{\partial }{\partial \theta },{L^{\prime }}_{22}=A_{66}\frac{\partial }{\partial x},{L^{\prime }}_{23}=0,{L^{\prime }}_{24}=-\frac{B_{66}}{R}\frac{\partial }{\partial \theta },{L^{\prime }}_{25}=-B_{66}\frac{\partial }{\partial x}\hfill \\ {L^{\prime }}_{31}={L^{\prime }}_{32}=0,{L^{\prime }}_{33}=-K_s{A}_{55}\frac{\partial }{\partial x},{L^{\prime }}_{34}=-K_s{A}_{55},{L^{\prime }}_{35}=0\hfill \\ {L^{\prime }}_{41}={L^{\prime }}_{14},{L^{\prime }}_{42}=-\frac{B_{12}}{R}\frac{\partial }{\partial \theta },{L^{\prime }}_{43}=-\frac{B_{12}}{R},{L^{\prime }}_{44}=-D_{11}\frac{\partial }{\partial x},{L^{\prime }}_{45}=-\frac{D_{12}}{R}\frac{\partial }{\partial \theta }\hfill \\ {L^{\prime }}_{51}=-\frac{B_{66}}{R}\frac{\partial }{\partial \theta },{L^{\prime }}_{52}={L^{\prime }}_{25},{L^{\prime }}_{53}=0,{L^{\prime }}_{54}=-\frac{D_{66}}{R}\frac{\partial }{\partial \theta },{L^{\prime }}_{55}=-D_{66}\frac{\partial }{\partial x}\hfill \end{array}$$

Authors' information

MET is an MSc graduate in civil engineering. He received his MSc from Sharif University of Technology, Tehran, Iran. His research interests include mechanical properties of composite structures. MTK is an associate professor of civil engineering at Sharif university of Technology, Tehran, Iran. He received his PhD degree from North-Western University. His research interests include plasticity, reinforced concrete, and composite structures. SM is a PhD student of aerospace structural engineering at Sharif University of Technology, Tehran, Iran. He received his MSc from Sharif University of Technology. His research interests include thermomechanical properties of functionally graded materials.