Abstract
Background
DIALIGN-T is a reimplementation of the multiple-alignment program DIALIGN. Due to several algorithmic improvements, it produces significantly better alignments on locally and globally related sequence sets than previous versions of DIALIGN. However, like the original implementation of the program, DIALIGN-T uses a a straight-forward greedy approach to assemble multiple alignments from local pairwise sequence similarities. Such greedy approaches may be vulnerable to spurious random similarities and can therefore lead to suboptimal results. In this paper, we present DIALIGN-TX, a substantial improvement of DIALIGN-T that combines our previous greedy algorithm with a progressive alignment approach.
Results
Our new heuristic produces significantly better alignments, especially on globally related sequences, without increasing the CPU time and memory consumption exceedingly. The new method is based on a guide tree; to detect possible spurious sequence similarities, it employs a vertex-cover approximation on a conflict graph. We performed benchmarking tests on a large set of nucleic acid and protein sequences For protein benchmarks we used the benchmark database BALIBASE 3 and an updated release of the database IRMBASE 2 for assessing the quality on globally and locally related sequences, respectively. For alignment of nucleic acid sequences, we used BRAliBase II for global alignment and a newly developed database of locally related sequences called DIRM-BASE 1. IRMBASE 2 and DIRMBASE 1 are constructed by implanting highly conserved motives at random positions in long unalignable sequences.
Conclusion
On BALIBASE3, our new program performs significantly better than the previous program DIALIGN-T and outperforms the popular global aligner CLUSTAL W, though it is still outperformed by programs that focus on global alignment like MAFFT, MUSCLE and T-COFFEE. On the locally related test sets in IRMBASE 2 and DIRM-BASE 1, our method outperforms all other programs while MAFFT E-INSi is the only method that comes close to the performance of DIALIGN-TX.
Similar content being viewed by others
1 Introduction
DIALIGN is a widely used software for multiple alignment of nucleic acid and protein sequences [1, 2] that combines local and global alignment features. Pairwise or multiple alignments are composed by aligning local pairwise similarities. More precisely, pairwise local gap-free alignments called fragment alignments or fragments are used as building blocks to assemble multiple alignments. Each possible fragment is given a score that is related to the P values used by BLAST [3, 4], and the program then tries to find a consistent set of fragments from all possible sequence pairs, maximizing the total score of these fragments. Gaps are not penalized. Here, consistency means that a set of fragment alignments can be included into one single alignment without contradictions, see for example [5] for a more formal definition of our notion of consistency.
The main difference between DIALIGN and more traditional alignment approaches is the underlying scoring scheme or objective function. Instead of summing up substitution scores for aligned residues and subtracting gap penalties, the score of an alignment is based on P-values of local sequence similarities. Only those parts of the sequences are aligned that share some statistically significant similarity, unrelated parts of the sequences remain unaligned. This way, the method can produce global as well as local alignments of the input sequences, whatever seems more appropriate. Combining local and global alignment features is particularly important if genomic sequences are aligned where islands of conserved homologies may be separated by non-related parts of the sequences. Thus, DIALIGN has been used for comparative genomics [6], for example to find protein-coding genes in eukaryotes [7–9].
As with traditional objective functions for sequence alignment, numerically optimal pairwise alignments can be calculated efficiently in the segment-based approach. In DIALIGN, this is done by a space-efficient fragment-chaining algorithms [10, 11]. However, it is computationally not feasible to find mathematically optimal multiple alignments. Thus, heuristics must be used if more than two sequences are to be aligned. All previous versions of DIALIGN used a greedy algorithm for multiple alignment. In an initial step, optimal pairwise alignments are calculated for all possible pairs of input sequences. Since these pairwise alignments are completely independent of each other, they can be calculated on parallel processors [12]. Fragments from these pairwise alignments are then sorted by their scores, i.e. based on their P-values, and then included one-by-one into a growing consistent set of fragments involving all pairs of sequences – provided they are consistent with the previously included fragments.
The greedy algorithm used in DIALIGN is vulnerable to spurious random similarities. It has been shown, that the numerical score of alignments produced by this heuristic can be far below the optimum [5, 13]. Consequently, alternative optimization algorithms have been applied to the optimization problem defined by the DIALIGN approach, e.g. Integer Linear Programming [14].
2 Assembling alignments from fragments
Formally, we consider the following optimization problem: we are given a set S = {s1, . . ., s k } of input sequences where l i is the length of sequence s i . A fragment f is a pair of two equal-length segments from two different input sequences. Thus, a fragment represents a local pairwise gap-free alignment of these two sequences. Each possible fragment f is assigned a weight score w(f) which, in our approach, depends on the probability P(f) of random occurrence of such a fragment. More precisely, if f is a local alignment of sequences s i and s j , then P (f) is the probability of finding a fragment of the same length as f with at least the same sum of matches or similarity values for amino acids in random sequences of length l i and l j , respectively. For protein alignment, a standard substitution matrix is used. Let F be the set of all possible fragments. The optimization problem is then to find a consistent set A ⊂ F of fragments with maximum total weight, i.e. a consistent set A maximizing
A set of fragments is called consistent if all fragments can be included into one single alignment, see [15]. Fragments in A are allowed to overlap if different pairs of sequences are involved. That is, if two fragments f1, f2∈ A involve sequence pairs s i , s j and s j , s k , respectively, then f1 and f2 are allowed to overlap in sequence s j . If two fragments involve the same pair of sequences, no overlap is allowed. It can be shown that the problem of finding an optimal consistent set A of fragments is NP-complete (Constructing multiple sequence alignments from pairwise data, Subramanian et al., in preparation). Therefore, we are motivated in finding intelligent approximations that deliver a good tradeoff between alignment quality and CPU time.
To decrease the computational complexity of this problem, we restrict ourselves to a reduced subset F' ⊂ F and we will first search for a consistent subset A ⊂ F' with maximum total score. As in previous versions of DIALIGN, we use pairwise optimal alignments as a filter. In other words, the set F' is defined as the set of all fragments contained in any of the optimal pairwise alignments of the sequences in our input data set. Here, we also restrict the length of fragments using some suitable constant.
For multiple alignment, previous versions of DIALIGN used the above outlined greedy approach. We call this approach a direct greedy approach, as opposed to the progressive greedy approach that we introduce in this paper. A modification of this 'direct greedy' approach was also used in our reimplementation DIALIGN-T. Here, we considered not only the weight scores of individual fragments (or their overlap weights [1]) but also took into account the overall degree of similarity between the two sequences involved in the fragment. The rationale behind this approach is that a fragment from a sequence pair with high overall similarity is less likely to be a random artefact than a fragment from an otherwise non-related sequence pair, see [16] for details.
2.1 Combining segment-based greedy and progressive alignment
To overcome the difficulties of a 'direct' greedy algorithm for multiple alignment, we combined greedy features with a 'progressive' alignment approach [17–20]. Roughly outlined, the new method we developed first computes a guide tree for the set of input sequences based on their pairwise similarity scores. The sequences are then aligned in the order defined by the guide tree. We divide the set of fragments contained in the respective optimal pairwise alignments into two subsets F0 and F1 where F0 consists of all fragments with weight scores below the average fragment score in all pairwise alignments, and F1 consists of the fragments with a weight above or equal to the average weight. In a first step, the set F1 is used to calculate an initial multiple alignment A1 in a 'progressive' manner. The low-scoring fragments from set F0 are added later to A1 in a 'direct' greedy way, provided they are consistent with A1. In addition, we construct an alternative multiple alignment A0 using the 'direct' greedy approach implemented in previous versions of DIALIGN and DIALIGN-T, respectively. The program finally returns either A0 or A1, depending on which one of these two alignments has the highest score.
To construct a guide tree for the progressive alignment algorithm, we use straight-forward hierarchical clustering. Here, we use a weighted combination of complete-linkage and average-linkage clustering based on pairwise similarity values R(p, q) for pairs of cluster (C p , C q ). Initially, each cluster C i consists of one sequence s i only. The similarity R(i, j) between clusters C i and C j (or leaves i and j in our tree) is defined to be the score of the optimal pairwise alignment of s i and s j according to our objective function, i.e. the sum of the weights of the fragments in an optimal chain of fragments for these two sequences. In every step, we merge the two sequence clusters C i and C j with the maximum similarity value R(i, j) into a new cluster. Whenever a new cluster C p is created by merging clusters q and r (or a node p in the tree is created with children q and r), we define the similarity between p and all other remaining clusters m to be
The choice of this function has been inspired by MAFFT [21, 22]; it also worked very well in our situation on globally and locally related sequences after experiments on BALIBASE 3, BRAliBase II, IRMBASE 2 and DIRMBASE 1.
2.2 Merging two sub-alignments
The final multiple alignment of our input sequence set S is constructed bottom-up along the guide tree. Thus, the crucial step is to combine two sub-alignments represented by nodes q and r in our tree whenever a new node p is created. In the traditional 'progressive' alignment approach, this is done by calculating a pairwise alignment of profiles, but this procedure cannot be directly adapted to our segment-based approach. Let A q and A r be the existing subalignments of the sequences in clusters C q and C r , respectively, at the time where these clusters are merged to a new cluster C p . Let F q, r be the set of all fragments f ∈ F connecting one sequence from cluster C q with another sequence from cluster C r . Now, our main goal is to find a subset F p ⊂ Fq,rwith maximum total weight score that is consistent with the existing alignments A q and A r . In other words, we are looking for a subset F p ⊂ F q, r with maximum total weight such that
A p = A q ∪ A r ∪ F p
describes a valid multiple sequence alignment of the sequence set represented by node p.
It is easy to see that at this time, before clusters A q and A r are merged, every single fragment f ∈ Fq,ris consistent with the existing (partial) alignments A q and A r and therefore consistent with the set of all fragments accepted so far. Only groups of at least two fragments from Fq,rcan lead to inconsistencies with the previously accepted fragments. Thus, there are different subtypes of consistency conflicts in Fq,rthat may arise when A q and A r are fixed. There are pairs, triples or, in general, l-tuples of fragments of Fq,rthat give rise to a conflict in the sense that the conflict can be resolved by removing exactly one fragment of such a conflicting l-tuple. Statistically, pairs of conflicting fragments are the most frequent type of conflict, so we will take care of them more intelligently rather than using only a greedy method. Since in our approach, the length of fragments is limited, we can easily determine in constant time for any pair of fragments (f1, f2) if the set
A q ∪ A r ∪ {f1, f2}
is consistent, i.e. if it forms a valid alignment, or if there is a pairwise conflict between f1 and f2. Here, the data structures described in [23] are used. With unbounded fragment length, the consistency check for the new fragments (f1, f2) would take O(|f1| × |f2|) time where |f| is the length of a fragment f .
This gives rise to a conflict graph Gq,rthat has a weighted node n f for every fragment f ∈ Fq,r. The weight w(n f ) of node n f is defined to be the weight score w(f) of f, and for any two fragments f1, f2 there exists an edge connecting and iff there is a pairwise conflict between f1 and f2, i.e. if the set A q ∪ A r ∪ {f1, f2} is inconsistent. We are now interested in finding a good subset of Fq,rthat does not contain any pairwise conflicts in the above sense. The optimum solution would be obtained by removing a minimal weighted vertex cover from Gq,r. Since the weighted vertex cover problem is NP-complete we apply the 2-approximation given by Clarkson [24]. This algorithm roughly works as follows: in order to obtain the vertex cover C, the algorithm iteratively adds the node v with the maximum value
to C. For any edge (v, u) that connects a node u with v the weight w(u) is updated to
and the edge (u, v) is deleted. This iteration is followed as long as there are edges left.
Note that it is not sufficient to remove the vertex cover C from Fq,rto obtain a valid alignment since in the construction of C, only inconsistent pairs of fragments were considered. We therefore first remove C from Fq,rand we subsequently remove further inconsistent fragments from Fq,rusing our 'direct' greedy alignment as described in [16]. A consequence of this further reduction of the set Fq,ris that fragments that were previously removed because of pairwise inconsistencies, may became consistent again. A node may have been included into the set C and therefore removed from the alignment as the corresponding fragment f1 is part of an inconsistent fragment pair (f1, f2). However, after subtracting the set C from F q, r , the algorithm may detect that fragment f2 is part of a larger inconsistent group, and f2 is removed as well. In this case, it may be possible to include f1 again into the alignment. Therefore, our algorithm reconsiders in a final step the set C to see if some of the previously excluded fragments can now be reincluded into the alignment. This is again done using our 'direct' greedy method.
2.3 The overall algorithm
In the previous section, we discussed all ingredients that are necessary to give a high-level description of our algorithm to compute a multiple sequence alignment. For clarity, we omit algorithmical details and data structures such as the consistency frontiers or consistency boundaries, respectively, that are used to check for consistency as these features have been described elsewhere [23]. We use a subroutine PAIRWISE_ALIGNMENT (s i , s j , A) that takes two sequences s i and s j and (optionally) an existing consistent set of fragments A as input and calculates an optimal alignment of s i and s j under the side constraint that this alignment is consistent with A and that only those positions in the sequences are aligned that are not yet aligned by a fragment from A. Note that in DIALIGN, an alignment is defined as an equivalence relation on the set of all sequence positions, so a consistent set of fragments corresponds to an alignment. Therefore, we do not formally distinguish between alignments and sets of fragments.
Next, a subroutine GREEDY_ALIGNMENT (A, F') takes an alignment A and a set of fragments F' as arguments and returns a new alignment A' ⊃ A by adding fragments from the set F' in a 'directly' greedy fashion. For details on these subroutines see also [16]. Furthermore we use a subroutine BUILD_UPGMA (F') that takes a set F' of fragments as arguments and returns a tree and a subroutine MERGE(p, F') that takes the parent node p and the set of fragments F' as argument and returns an alignment of the set of sequences represented by node p. Those two subroutines are described in the previous two subsections. A pseudo-code description of the complete algorithm for multiple alignment is given in Figure 1. As in the original version of DIALIGN [1], the process of pairwise alignment and consistency filtering is carried out iteratively. Once a valid alignment A has been constructed by removing inconsistent fragments from the set F' of the fragments that are part of the respective optimal pairwise alignments, this procedure is repeated until no new fragments can be found. In the second and subsequent iteration steps, only those parts of the sequences are considered that are not yet aligned and optimal pairwise alignments are calculated under the consistency constraints imposed by the existing alignment A.
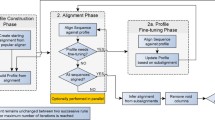
High-level description of our algorithm to calculate a multiple alignment of a set of input sequences s1, . . ., s k . The algorithm calculates a first alignment A0 using our novel progressive approach and a second alignment A1 with the greedy method previously used in DIALIGN. Finally, the alignment with the higher numerical score is returned. For the progressive method, fragments, i.e. local gap-free pairwise alignments from the respective optimal pairwise alignments are considered. Fragments with a weight score above the average fragment score are processed first following a guide tree as described in the main text. Lower-scoring fragments are added later, provided they are consistent with the previously included high-scoring fragments. Note that the output of the sub-routine PAIRWISE_ALIGNMENT is a chain of fragments. This is equivalent to a pairwise alignment in the sense of DIALIGN.
3 Further program features
Beside the above described improvements of the optimization algorithm, we incorporated new features into DIALIGN-TX that were already part of the original implementation of DIALIGN. DIALIGN-TX now supports anchor points the same way DIALIGN 2.2 does [5, 15]. Anchor points can be used for various purposes, e.g. to speed up alignment of large genomic sequences [25, 6], or to incorporate information about locally conserved motifs. This can been done, for example, using the N-local-decoding approach [26, 27] or other methods for motif finding.
DIALIGN-TX also now comes with an option to specify a threshold parameter T in order to exclude low-scoring fragments from the alignment. Following an approach proposed in [28], the alignment procedure can be iterated, starting with a high value of T and with lower values in subsequent iteration steps. By default, in the first iteration step of our algorithm, we use a value of T = -log2(0.5) for the pairwise alignment phase, while in all subsequent iteration steps, a value of T = 0 is usedd. With a user-specified threshold of T = 2 for the first iteration step, the threshold value remains -log2 (0.5) in all subsequent steps, and with a chosen threshold value of T = 1, the value for the subsequent iteration steps is set to -log2 (0.75).
An optimal pairwise alignment in the sense of our fragment-based approach is a chain of fragments with maximum total weight score. Calculating such an optimal alignment takes O(l3) time if l is the (maximum) length of the two sequences since all possible fragments are to be considered. If the length of fragments is bounded by a constant L, the complexity is reduced to O(l2 × L). In practice, however, it is not meaningful to consider all possible fragments. Our algorithm processes fragments starting at a pair of positions i and j, respectively, with increasing fragment length. To reduce the number of fragments considered, our algorithm stops processing longer fragments starting at i and j if the previously visited short fragments starting at the same positions have low scores. More precisely, we consider the average substitution score of aligned amino acids or the average number of matches for DNA or RNA alignment, respectively, to decide if further fragments starting at i and j are considered.
To reduce the run time for pairwise alignments, we implemented an option called fast mode. This option uses a lower threshold value for the average subsitution scores or number of matches. By default, during the pairwise alignment phase, fragments under consideration are extended until their average substitution score is at least 4 for amino acids (note that our BLOSUM62 matrix has 0 for the lowest score possible) and 0.25 for nucleotides, respectively. With the fast mode option, this threshold is increased by 0.25 which has the effect that the extension of fragments during the pairwise alignment phase is interrupted far more often than by default. This option, however, reduces the sensitivity of the program. We observed speed-ups up to factor 10 on various benchmark data when using this option while the alignment quality was still reasonably high, in the sense that the average sum-of-pair score and average column score on our benchmarks deteroriated around 5% – 10% only. We recommend to use this option for large input data containing sequences that are not too distantly related. Hence, this option is not advisable for strictly locally related sequences where we observed a reduction of the alignment quality almost down to a score of zero. However in the latter case this option is not necessary since the original similarity score thresholds of 4 and 0.25, respectively, are effective enough to prevent DIALIGN-TX of unnecessarily looking at too many spurious fragments.
4 Benchmark results
In order to evaluate the improvements of the new heuristics we had several benchmarks on various reference sets and compared DIALIGN-TX with its predecessor DIALIGN-T 0.2.2 [16], DIALIGN 2.2 [29], CLUSTAL W2 [30], MUSCLE 3.7 [31], T-COFFEE 5.56 [32] POA V2 [33, 34], PROBCONS 1.12 [35] & PROBCONSRNA 1.10, MAFFT 6.240 L-INSi and E-INSi [21, 22]. We performed benchmarks for DNA as well as for protein alignment. As globally related benchmark sets we used BRAliBase II [36, 37] for RNA and BALIBASE 3 [38] for protein sequences.
The benchmarks on locally related sequence sets were run on IRMBASE 2 for proteins and DIRMBASE 1 for DNA sequences, which have been constructed in a very similar way as IRMBASE 1 [16] by implanting highly conserved motifs generated by ROSE [39] in long random sequences. IRMBASE 2 and DIRM-BASE 1 both consist of four reference sets ref1, ref2, ref3 and ref4 with one, two, three and four (respectively) randomly implanted ROSE motives. The major difference compared to the old IRMBASE 1 lies in the fact that in 1/s cases the occurrence of a motive in a sequence has been omitted randomly, whereby s is the number of sequences in the sequence family. The results on IRMBASE 2 and DIRMBASE 1 now tell us how the alignment programs perform in cases when it is unknown if every motive occurs in every sequence thus providing a more realistic basis for assessing the alignment quality on locally related sequences compared to the situation in the old IRMBASE 1 where every motive always occurred in every sequence.
Each reference set in IRMBASE 2 and DIRMBASE 1 consists of 48 sequence families, 24 of which contain ROSE motifs of length 30 while the remaining families contain motifs of length 60. 16 sequence families in each of the reference sets consist of 4 sequences each, another 16 families consist of 8 sequences while the remaining 16 families consist of 16 sequences. In ref1, random sequences of length 400 are added to the conserved ROSE motif while for ref2 and ref3, random seqences of length 500 are added. In ref4 random sequences of length 600 are added.
For both BAliBASE and IRMBASE, we used two different criteria to evaluate multi-alignment software tools. We used the sum-of-pair score where the percentage of correctly aligned pairs of residues is taken as a quality measure for alignments. In addition, we used the column score where the percentage of correct columns in an alignment is the criterion for alignment quality. Both scoring schemes were restricted to core blocks within the reference sequences where the 'true' alignment is known. For IRMBASE 2 and DIRMBASE 1, the core blocks are defined as the conserved ROSE motifs. To compare the output of different programs to the respective benchmark alignments, we used C. Notredame's program aln_compare [32].
4.1 Results on locally related sequence families
The quality results of our benchmarks of DIALIGN-TX and various alignment programs on the local aligment databases can be found in Tables 1 and 2 for the local protein database IRMBASE 2 and in Tables 3 and 4 for the local DNA database DIRMBASE 1. The average CPU times of the tested methods are listed in Table 5. When looking at the results DIALIGN-TX clearly outperforms all other methods on sum-of-pairs score (SPS) and column score (CS) with the only exception that MAFFT E-INSi outperforms DIALIGN-TX on the SPS on IRMBASE 2 whilst in turn DIALIGN-TX is around 3.5 times faster and significantly outperforms MAFFT-EINSi on the CS. The superiority of DIALIGN-TX compared to DIALIGN-T 0.2.2 is not statistically significant on IRMBASE 2, however it is on DIRMBASE 1 which is due to a very low sensitivity threshold parameter for the DNA case set by default in DIALIGN-T 0.2.2 that allowed fragments solely comprised of matches. In all other comparisons DIALIGN-TX is significantly superior to the other programs with respect to the Wilcoxon Matched Pairs Signed Rank Test [40]. DIALIGN 2.2, DIALIGN-T 0.2.2 (only for protein), MAFFT L-INSi and MAFFT E-INSi were the only other methods that produced reasonable results.
On IRMBASE 2 our new program DIALIGN-TX is around 1.64 times slower compared to DIALIGN-T however it is still faster than DIALIGN 2.2, on DIRM-BASE 1 we observed that DIALIGN-TX is 4.26 times slower than DIALIGN-T (which is due to the reduced sensitivity in DIALIGN-T 0.2.2) and we also see that DIALIGN-TX is around 2.04 slower than DIALIGN 2.2. Although IRMBASE 2 and DIRMBASE 1 are constructed in a similar way we see that T-COFFEE and PROBCONS behave quite well on the protein alignments whereas the perform very poorly in the DNA case while the other methods ranked mostly equal in the protein and DNA case. Overall, we conclude from our benchmarks that DIALIGN-TX is the dominant program on locally related sequence protein and DNA families that consist of closely related motives embedded in long unalignable sequences.
4.2 Results on globally related sequence families
The results of our benchmark on the global alignment databases are listed in the Tables 6, 7 for BALIBASE 3 and in Tables 8, 9 for core blocks of BRAliBase II. The average CPU times of all methods can be found in Table 10. According to the Wilcoxon Matched Pairs Signed Rank Test DIALIGN-TX outperforms DIALIGN-T 0.2.2, DIALIGN 2.2, POA and CLUSTAL W2 on BALIBASE3 whereby DIALIGN-TX is the only method following the DIALIGN approach that significantly outperforms CLUSTAL W2. Since the methods T-COFFEE, PROBCONS, MAFFT and MUSCLE are focused on global alignments, they significantly outperform DIALIGN-TX on BALIBASE 3. Overall PROBCONS, MAFFT L-INSi and E-INSi are the superior methods on BALIBASE 3. On BALIBASE 3 the new DIALIGN-TX program is around 1.22 times slower than the previous version of DIALIGN-T and around 1.36 times faster than DIALIGN 2.2.
We have a slightly different picture in the RNA case we examined using BRAliBase II benchmark database that has an even stronger global character and is the only benchmark database that we used that does not come with core blocks. DIALIGN-TX significantly outperforms POA and all other versions of DIALIGN approach whereas it is still inferior to the global methods CLUSTAL W2, MAFFT, MUSCLE and PROBCONSRNA. The difference between T-COFFEE and DIALIGN-TX on BRAliBase II is quite small, i.e. T-COFFEE outperforms DIALIGN-TX only on the SPS whereas there is no significant different on the CS. Since MAFFT and PROBCONSRNA have been trained on BRAliBase II the dominance of those methods (especially PROBCONSRNA) is not very surprising. Regarding CPU time DIALIGN-TX is approximately 1.7 times slower than DIALIGN-T 0.2.2 and DIALIGN 2.2 on BRAliBase II.
5 Conclusion
In this paper, we introduced a new optimization algorithm for the segment-based multiple-alignment problem. Since the first release of the program DIALIGN in 1996, a 'direct' greedy approach has been used where local pairwise alignments (fragments) are checked for consistency one-by-one to see if they can be included into a valid multiple alignment. In this approach, the order in which fragments are checked for consistency is basically determined by their individual weight scores. Some modifications have been introduced, such as overlap weights [1] and a more context-sensitive approach that takes into account the overal significance of the pairwise alignment to which a fragment belongs [16]. Nevertheless, a 'direct' greedy approach is always sensitive to spurious pairwise random similarities and may lead to alignments with scores far below the possible optimal score (e.g. [13, 5], Pöhler and Morgenstern, unpublished data).
The optimization method that we introduced herein is inspired by the so-called progressive approach to multiple alignment introduced in the 1980s for the classical multiple-alignment problem [17]. We adapted this alignment strategy to our segment-based approach using an existing graph-theoretical optimization algorithm and combined it with our previous 'direct' greedy approach. As a result, we obtain a new version of our program that achieves significantly better results than the previous versions of the program, DIALIGN 2 and DIALIGN-T.
To test our method, we used standard benchmark databases for multiple alignment of protein and nucleic-acid sequences. Since these databases are heavily biased towards global alignment, we also used a benchmark database with simulated local homologies. The test results on these data confirm some of the known results on the performance of multiple-alignment programs. On the globally related sequence sets from BAliBASE and BRALIBASE, the segment-based approach is outperformed by classical, strictly global alignment methods. However, even on these data, we could achieve a considerable improvement with the new optimization algorithm used in DIALIGN-TX. On the simulated local homologies, our method clearly outperforms other alignment approaches, and again the new algorithm introduced in this paper achieved significantly better results than older versions of DIALIGN. Among the methods for global multiple alignment, the program MAFFT [21, 22] performed remarkably well, not only on globally, but also on locally related sequences.
We will conduct further studies to investigate to what extent the optimization algorithms used in the different versions of DIALIGN can be improved and which alternative algorithms can be applied to the optimization problem given by the segment-based alignment approach.
Program availability
DIALIGN-TX is online available at Göttingen Bioinformatics Compute Server ( GOBICS ) at [41] The program source code and our benchmark databases IRMBASE 2 and DIRMBASE 1 are downloadable from the same web site.
References
Morgenstern B, Dress A, Werner T: Multiple DNA and protein sequence alignment based on segment-to-segment comparison. Proc Natl Acad Sci USA. 1996, 93: 12098-12103.
Morgenstern B: DIALIGN: Multiple DNA and Protein Sequence Alignment at BiBiServ. Nuc Acids Res. 2004, 33 (Web Sever issue): W33-W36.
Altschul SF, Gish W, Miller W, Myers EM, Lipman DJ: Basic Local Alignment Search Tool. J Mol Biol. 1990, 215: 403-410.
Karlin S, Altschul SF: Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc Natl Acad Sci USA. 1990, 87: 2264-2268.
Morgenstern B, Prohaska SJ, Pöhler D, Stadler PF: Multiple sequence alignment with user-defined anchor points. Algorithms for Molecular Biology. 2006, 1: 6-
Brudno M, Chapman M, Göttgens B, Batzoglou S, Morgenstern B: Fast and sensitive multiple alignment of large genomic sequences. BMC Bioinformatics. 2003, 4: 66-
Taher L, Rinner O, Gargh S, Sczyrba A, Brudno M, Batzoglou S, Morgenstern B: AGenDA: Homology-based gene prediction. Bioinformatics. 2003, 19: 1575-1577.
Stanke M, Schöffmann O, Morgenstern B, Waack S: Gene prediction in eukaryotes with a Generalized Hidden Markov Model that uses hints from external sources. BMC Bioinformatics. 2006, 7: 62-
Stanke M, Tzvetkova A, Morgenstern B: AUGUSTUS+ at EGASP: using EST, protein and genomic alignments for improved gene prediction in the human genome. Genome Biology. 2006, 7: S11-
Morgenstern B: A Space-Efficient Algorithm for Aligning Large Genomic Sequences. Bioinformatics. 2000, 16: 948-949.
Morgenstern B: A simple and space-efficient fragment-chaining algorithm for alignment of DNA and protein sequences. Applied Mathematics Letters. 2002, 15: 11-16. 10.1016/S0893-9659(01)00085-4.
Schmollinger M, Nieselt K, Kaufmann M, Morgenstern B: DIALIGN P: fast pairwise and multiple sequence alignment using parallel processors. BMC Bioinformatics. 2004, 5: 128-
Wagner H, Dress A, Morgenstern B: Stability of Multiple Alignments and Phylogenetic Trees: An Analysis of ABC-Transporter Proteins.
Lenhof HP, Morgenstern B, Reinert K: An exact solution for the segment-to-segment multiple sequence alignment problem. Bioinformatics. 1999, 15: 203-210.
Morgenstern B, Werner N, Prohaska SJ, Schneider RSI, Subramanian AR, Stadler PF, Weyer-Menkhoff J: Multiple sequence alignment with user-defined constraints at GOBICS. Bioinformatics. 2005, 21: 1271-1273.
Subramanian AR, Weyer-Menkhoff J, Kaufmann M, Morgenstern B: DIALIGN-T: An improved algorithm for segment-based multiple sequence alignment. BMC Bioinformatics. 2005, 6: 66-
Feng DF, Doolittle RF: Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J Mol Evol. 1987, 25: 351-360.
Taylor WR: A flexible method to align large numbers of biological sequences. J Mol Evol. 1988, 28: 161-169.
Corpet F: Multiple sequence alignment with hierarchical clustering. Nuc Acids Research. 1988, 16: 10881-10890. 10.1093/nar/16.22.10881.
Higgins D, Sharp P: CLUSTAL – A PACKAGE FOR PERFORMING MULTIPLE SEQUENCE ALIGNMENT ON A MICROCOMPUTER. Gene. 1988, 73: 237-244.
Katoh K, Misawa K, Kuma K, Miyata T: MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002, 30 (14): 3059-3066.
Katoh K, Kuma K, Toh H, Miyata T: MAFFT version 5: improvement in accuracy of multiple sequence alignment. Nucleic Acids Res. 2005, 33 (2): 511-518.
Abdeddaïm S, Morgenstern B: Speeding up the DIALIGN multiple alignment program by using the 'Greedy Alignment of BIOlogical Sequences LIBrary' (GABIOS-LIB). Lecture Notes in Computer Science. 2001, 2066: 1-11.
Clarkson KL: A Modification of the Greedy Algorithm for Vertex Cover. Information Processing Letters. 1983, 16: 23-25. 10.1016/0020-0190(83)90007-8.
Brudno M, Steinkamp R, Morgenstern B: The CHAOS/DIALIGN WWW server for Multiple Alignment of Genomic Sequences. Nucleic Acids Research. 2004, 32: W41-W44.
Corel E, El Fegalhi R, Gérardin F, Hoebeke M, Nadal M, Grossmann A, Devauchelle C: Local Similarities and Clustering of Biological Sequences: New Insights from N-local Decoding. The First International Symposium on Optimization and Systems Biology. 2007, 189-195. Beijing, China
Didier G, Laprevotte I, Pupin M, Hénaut A: Local Decoding of sequences and alignment-free comparison. J Comput Biol. 2006, 13 (8): 1465-1476.
Morgenstern B, Rinner O, Abdeddaïm S, Haase D, Mayer K, Dress A, Mewes HW: Exon Discovery by Genomic Sequence Alignment. Bioinformatics. 2002, 18: 777-787.
Morgenstern B: DIALIGN 2: improvement of the segment-to-segment approach to multiple sequence alignment. Bioinformatics. 1999, 15: 211-218.
Thompson JD, Higgins DG, Gibson TJ: CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Research. 1994, 22: 4673-4680.
Edgar R: MUSCLE: Multiple sequence alignment with high score accuracy and high throughput. Nucleic Acids Res. 2004, 32 (5): 1792-1797.
Notredame C, Higgins D, Heringa J: T-Coffee: a novel algorithm for multiple sequence alignment. J Mol Biol. 2000, 302: 205-217.
Grasso C, Lee C: Combining partial order alignment and progressive multiple sequence alignment increases alignment speed and scalability to very large alignment problems. Bioinformatics. 2004, 20: 1546-1556.
Lee C, Grasso C, Sharlow MF: Multiple sequence alignment using partial order graphs. Bioinformatics. 2002, 18 (3): 452-464.
Do CB, Mahabhashyam MS, Brudno M, Batzoglou S: ProbCons: Probabilistic consistency-based multiple sequence alignment. Genome Research. 2005, 15: 330-340.
Gardner PP, Wilm A, Washietl S: A benchmark of multiple sequence alignment programs upon structural RNAs. Nucleic Acids Res. 2005, 33: 2433-2439.
Wilm A, Mainz I, Steger G: An enhanced RNA alignment benchmark for sequence alignment programs. Algorithms Mol Biol. 2006, 2: 19-10.1186/1748-7188-1-19.
Thompson JD, Plewniak F, Poch O: A benchmark alignment database for the evaluation of multiple sequence alignment programs. Bioinformatics. 1999, 15: 87-88.
Stoye J, Evers D, Meyer F: Rose: Generating Sequence Families. Bioinformatics. 1998, 14: 157-163.
Wilcoxon F: Individual Comparisons by Ranking Methods. Biometrics. 1945, 1: 80-83. 10.2307/3001968.
DIALIGN-TX. http://dialign-tx.gobics.de/
Acknowledgements
We would like to thank C. Notredame for providing his software tool aln_compare and R. Steinkamp for helping us with the web server at GOBICS. The work was partially supported by BMBF grant 01AK803G (MEDIGRID).
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
ARS conceived the new methods, implemented the program, constructed IRM-BASE 2 and DIRMBASE 1, did the evaluation and wrote parts of the manuscript, MK and BM supervised the work, provided resources and wrote parts of the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Subramanian, A.R., Kaufmann, M. & Morgenstern, B. DIALIGN-TX: greedy and progressive approaches for segment-based multiple sequence alignment. Algorithms Mol Biol 3, 6 (2008). https://doi.org/10.1186/1748-7188-3-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1748-7188-3-6