Abstract
Waveform design is studied for a cognitive multiple-input multiple-output (MIMO) radar system faced with a combination of additive Gaussian noise and signal dependent clutter. The linear frequency modulation (LFM) signals are employed as transmitted waveforms. Based on the sensed statistics of the target and clutter-plus-noise, assuming the LFM waveforms transmitted at different transmitters can have different starting frequencies and bandwidths, these waveform parameters are designed to maximize the signal-to-clutter-plus-noise ratio at the receiver of the cognitive MIMO radar system. The constraints of the allowable range of operating frequency and total transmit energy are considered. We show that in the tested examples, the designed waveforms are nonorthogonal which leads to superior performance compared with that of the frequency spread LFM waveforms commonly used in the traditional MIMO radar systems.
Similar content being viewed by others
1 Introduction
The advantages of multiple-input multiple-output (MIMO) radar have drawn considerable attention in the last decade [1–7]. MIMO radar systems employ multiple antennas on both the transmit and receive sides. The antennas can be either co-located or widely separated. Geometry gains can be obtained for the former since the antennas are located in several different directions with respect to a target, while waveform gains can be produced for the latter by sending different waveforms with different antennas.
Waveform design is a key issue in radar signal processing. The transmit waveforms of MIMO radar are usually optimized for specific goals, such as improving the signal-to-clutter-plus-noise ratio (SCNR) [8], increasing the resolution in the spatial and temporal domains, enhancing the detection performance [5], reducing the estimation error when approximating a desired beam-pattern [4], or maximizing the mutual information (MI) between the random target impulse response and the reflected waveforms [9].
The concept of cognitive radar (CR) was proposed in [10] for optimizing the performance of a radar system faced with interference and the constraint of limited resources. The CR system can intelligently learn the state of the environment and store the information in the database. The stored information can be used as an available prior knowledge for the designs of radar systems and transmit waveforms, which is helpful for improving the performance of target detection and parameter estimation. There have been many researches on waveform design for CR systems [11–14]. In [11], the transmit signals are designed by minimizing the mean-square error of the estimate of the target reflection coefficient.
In [12], the waveform is designed to minimize the average ambiguity of the transmitted signal over certain range Doppler bins. In [13, 14], the waveform is optimized by maximizing the signal-to-interference-plus-noise ratio for CR radar systems.
The cognitive technique has been introduced to MIMO radar systems [15–18] to enhance the robustness and adaptability. During the learning process of a cognitive MIMO radar system, the information of the environment, such as the prior knowledge of clutter and target impulse responses and noise, are collected by multiple receive antennas, which are transferred to multiple transmit antennas through a feedback mechanism for adjusting system parameters. In [15], the authors present an adaptive waveform design method to improve the target recognition performance of the cognitive MIMO radar. In [16], artificial intelligence algorithm is employed to improve the robustness of target detection for the cognitive MIMO radar system. In [17], the authors optimize the waveforms based on the Bayesian Cramer-Rao bound and the Reuven-Messer bound for cognitive MIMO radar systems. In [18], a waveform optimization approach is provided for cognitive MIMO radar based on the MI between the target impulse response and the received echoes and the MI between successive backscatter signals.
As a very common waveform for radar system, the linear frequency modulation (LFM) signal can provide advantages of high-resolution, anti-jamming, far detecting distance, etc. [19–23]. Moreover, the LFM signal can be conveniently generated and it has constant modulus. For MIMO radar, the frequency spread (FS) LFM signals are usually employed as a set of orthogonal signals for transmission [24, 25]. The orthogonality of the FS LFM signals can be obtained by increasing the frequency offset between two waveforms transmitted by the adjective antennas [26]. However, the maximum allowable operating bandwidth for radar system is often limited as the frequency band source becomes more and more crowded with the development of the communication and radar applications. Therefore, it is important to know how one can improve the radar performance through waveform design when the range of operating frequency is constrained.
In this paper, the waveforms are designed for the cognitive MIMO radar system. Since the detection probability is a nondecreasing function of the SCNR under the log-likelihood ratio test [27], we employ the SCNR maximization as the objective of the optimization problem to improve the detection performance. LFM signals are employed as the transmit waveforms. Unlike the FS LFM signals usually adopted in MIMO radars [24, 25], where each of the transmit LFM signals has identical bandwidth and transmit energy and equally spaced starting frequencies, we propose to construct the transmit waveforms as a set of LFM signals whose starting frequencies, bandwidths, and energies can be different and are to be optimized. The prior information about the target and clutter obtained by the cognitive process is used for the waveform optimization. The constraints of the total transmit energy and the allowable range of operating frequency impose restrictions on our optimization problem.
The rest of the paper is organized as follows. In Section 2, the signal model of the cognitive MIMO radar is introduced. In Section 3, the LFM-based waveform design for limited maximum allowable frequency band and total transmit energy is presented, and the algorithm for solving the optimization problem is given. In Section 4, we show the superior SCNR performance of our designed waveforms over the FS LFM signals through numerical examples. The effects of the number of transmit antennas are also analyzed. Finally conclusions are drawn in Section 5.
Notation: Throughout this paper, we use superscripts (·) H, (·) ∗, and (·) T to denote the complex conjugate transpose, conjugate, and transpose of a matrix, respectively. The ⌊·⌋ denotes the operation of rounding down the value to the nearest integer. The (i mod j) represents the remainder of division of i by j. We use for expectation with respect to all the random variables within the brackets. The symbol stands for the convolution operator and ⊗ for the Kronecker product operator. We let diag{·} denotes diagonal matrix. Finally, (A) ij denotes the ij th entry of A , and I N denotes the identity matrix of size N × N.
2 Signal model
Consider a cognitive MIMO radar equipped with M transmit antennas and L receive antennas. Each of the transmitted waveforms is assumed to be narrowband. The discrete-time waveform transmitted by the m th transmit antenna is denoted by s m [n], 0 ≤ n ≤ N - 1, where N is the total number of time samples. Assume that the signal propagation in the considered scenario is stable during the observation interval so that the target and clutter returns associated with each transmitter-to-receiver path can be regarded as the responses of two linear time-invariant (LTI) systems with the transmitted signal as input. Define ht,ml[n] and hc,ml[n] as the target and clutter impulse responses associated with the m-th (m = 1,…,M) transmitter and the l th (l = 1,…,L) receiver. Then the signal received by the l th receiver can be formulated as
where xt,ml[n] and xc,ml[n] denote the target and clutter returns corresponding to the ml th transmitter-to-receiver path, and z l [n] is the noise at receiver l. Stacking the N R observations (the choice of N R is discussed in Section 2.1) that contain the target return for all L receive antennas into a column vector, the LN R × 1 overall received signal vector can be expressed as
where x t denotes the target return vector, x c denotes the clutter return vector, z = (z1 [0],…,z L [0],…,z1 [N R -1],…,z L [N R -1])T is the noise vector, the waveform vector
The H t and H c in (2) are LN R × M N matrices, the expressions of which are given in Appendix 1.
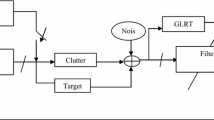
To enhance the system performance, a receive filter with impulse response
is used to process the receiver signal r at the receive end [12, 28], as shown in Figure 1. Thus, the SCNR at the output of the receive filter is defined as
As a cognitive MIMO radar system has the ability of learning, the prior knowledge of the environment state can be obtained from previous measurements. Using a specific environment database which contains the statistics of the target and clutter impulse responses and noise, the statistics of the target return x t and the clutter return x t can be derived. Next, we discuss the statistics of the target impulse response h t [n], the clutter impulse response h c [n], and the noise z.
2.1 Statistics of target return
Consider an extended target and assume the length of the target impulse response of the potential extended target is N t such that h t [n] ≠ 0 for n in [0,N t -1] and h t [n] = 0 otherwise. Then it can be shown from (1) that the target return xt,m[n] = 0 for all m and l when n is outside [0,N + N t -2]. So the number of the observations can be chosen as N R =N + N t -1. Define the target impulse response vector
From (2), the statistic of the target return vector x t is determined by the statistic of the target impulse response vector h t , as described in the following lemma.
Lemma 1
Given H ε , s, and h ε as in (2), (3), and (6)/(9), the can be defined in terms of , where the ij th entry of is given by
where , , , and .
Proof of Lemma
See (S Wang, Q He, Z He, RS Blum, Waveform design for MIMO over-the-horizon radar detection, submitted).
In this paper, the target impulse response h t is assumed to be zero-mean complex Gaussian distributed with covariance matrix . Since any linear transformation of a complex Gaussian random vector produces another complex Gaussian random variable [29], the x t in (2) also follows a zero-mean complex Gaussian distribution, whose covariance matrix
can be computed using Lemma 1.
2.2 Statistics of clutter return
Define the clutter impulse response vector
From (2), the statistic of the clutter return vector x c is determined by the statistic of the clutter impulse response vector h c , as described in Lemma 1.
Assume the clutter impulse response vector h c is zero-mean complex Gaussian distributed with known covariance matrix . Thus, x c also follows a zero-mean complex Gaussian distribution, whose covariance matrix
can be computed using Lemma 1.
2.3 Statistics of noise
The noise term z = (z1 [0],…,z L [0],…,z1 [N R -1],…,z L [N R -1])T is assumed to obey complex Gaussian distribution with mean zero and covariance matrix , which is assumed to be independent of the target and clutter returns.
3 Waveform design with constrained bandwidth
In this section, waveform design for the SCNR maximization problem is introduced for cognitive MIMO radar systems. The waveforms are constructed as LFM signals where the starting frequencies and bandwidths for each of the LFM signals will be optimized. The optimization problem with the constraints of the allowable range of operating frequency and total transmit energy is presented. The method to solve the optimization problem is given subsequently.
3.1 Waveform design for SCNR maximization
Design the waveform transmitted by the m th transmit antenna at the n th, n = 0,…,N - 1, discrete-time sample as
where E
m
is the transmitted energy of the m th waveform within the time duration T, Ts is the sampling period, and f
m
and b
m
are the staring frequency and bandwidth of the m th waveform s
m
[n], such that the frequency band occupied by s
m
[n] is [f
m
,f
m
+ b
m
]. Use  to denote the set of allowable operating frequencies. Thus, for any m, m = 1,…,M, the frequency band [f
m
,f
m
+ b
m
] should be within the set
to denote the set of allowable operating frequencies. Thus, for any m, m = 1,…,M, the frequency band [f
m
,f
m
+ b
m
] should be within the set  . Considering fixed total transmit energy and the constrained allowable frequency band, our goal is to optimize the waveform parameter vector p= [f1,…,f
M
,b1,…,b
M
,E1,…,E
M
] and the receiver impulse response vector h
r
to maximize the SCNR as defined in (5). The optimization problem is given by
. Considering fixed total transmit energy and the constrained allowable frequency band, our goal is to optimize the waveform parameter vector p= [f1,…,f
M
,b1,…,b
M
,E1,…,E
M
] and the receiver impulse response vector h
r
to maximize the SCNR as defined in (5). The optimization problem is given by
where E0 is the total transmit energy. The objective function in (12) is not a convex function, so that the convex optimization approaches do not work for this problem. Instead, we adopt the iterative approach proposed in [28] to solve the optimization problem in (12). We first fix the waveform p to optimize the receiver impulse response h r , and then fix h r to optimized p. These two steps are executed iteratively until the stopping criterion is met.
3.2 Optimization with fixed waveform
When the waveform parameter vector p is fixed, the problem in (12) is reduced to
From (8) and (10), the problem in (13) can be rewritten as
Defining where Y is a lower triangular matrix which satisfies Y YH= R c + R z , the optimization problem can be expressed in terms of u as
where Φ = Y-1 R t (YH)-1. Solving the problem in (15) with Lagrange multiplier method, the solution of u is obtained as
where ϕmax is the eigenvector corresponding to the largest eigenvalue of Φ. Thus, the solution of h r is given by
3.3 Optimization with fixed h r
When the receiver impulse response h r is fixed, the problem in (12) can be recast to
where the expressions of and  are also determined by the statistics of h
t
in (6) and h
c
in (9), as described in the following lemma.
are also determined by the statistics of h
t
in (6) and h
c
in (9), as described in the following lemma.
Lemma 2
Given H ε in (2), h r in (4), and h ε in (6) or (9), the can be defined in terms of , where the ij th entry of is given by
where , , , and .
Proof of Lemma
See (S Wang, Q He, Z He, RS Blum, Waveform design for MIMO over-the-horizon radar detection, submitted to IEEE Transactions on Aerospace and Electronic Systems).
As the problem in (18) is highly nonlinear, it is solved numerically using the interior point method. The optimized solution is denoted as p⋆.
3.4 Summary of the iterative method
The above discussed iterative method that solves the problem in (12) can be summarized in the following algorithm:

Then, both of the optimized waveform parameter vector popt and receiving impulse response vector hr,opt are achieved. The optimized waveform sopt can be obtained by plugging popt into (11).
4 Simulations
In this section, we present a few numerical results. Assume the cognitive MIMO radar has L = 2 receive antennas and M = 4 transmit antennas. The total transmit energy is E0 = 4. Suppose the allowable operating frequency band is . Assume the time duration of transmit waveforms N = 40 and the length of the target impulse response N t = 8. The number of the observation is N R = N + N t - 1 = 47. Assume the in the noise covariance matrix is . Assume the covariance matrix of the clutter impulse response vector h c in (9) satisfies R hc = C T ⊗ C S , where C S denotes the spatial correlation between clutter impulse responses corresponding to different transmitter to receiver paths for a fixed time index, and C T denotes the temporal correlation between clutter impulse responses corresponding to different time delays for a fixed spatial index [30]. Assume the ij th element of the spatial correlation matrix C S is
where and ρ S = 0.9 denotes one-lag correlation coefficient. The temporal correlation matrix C T is considered by the conventional time-varying autoregressive (TVAR) [31, 32] modeling (see [33] for details).
4.1 Optimal waveform design
According to the theoretical analysis in Section 3, the optimal waveforms should satisfy the optimization problem in (12), which can be solved by applying Algorithm 1. In the simulations, the parameter ε in the stopping condition of Algorithms is set to be 10-3. The SCNR obtained at each iteration is plotted in Figure 2. Obviously, the value of the SCNR has been converged well before the 51th iteration, so that the parameter vectors obtained at the 51th iteration can be regarded as the optimized parameters popt and hr,opt. The optimized starting frequency, bandwidth, and transmit energy for each of the waveforms in vector popt are listed in Table 1. Plugging popt into (11), the designed LFM signals are obtained. The real parts and frequencies of the designed LFM signals are shown in Figure 3.
For comparison, the real parts and frequencies of the FS LFM signals, which are commonly used in MIMO radar systems, are plotted in Figure 4. The low-pass component of the m th FS LFM signal at the n th, n = 0,…,N - 1, discrete-time sample is set as [24–26]
where Δ f is the frequency offset between the waveforms sent from two adjacent transmit antennas which is fixed to k/T to attain approximate orthogonality [26], where k is a positive integer. When the operating frequency is constrained in , the B u should satisfy B u + (M-1)Δ f ≤ B. In this example, we let Δ f = 2/T, B u = B - (M-1) Δ f, and the value of the other parameters are the same as those in the previous example. Obviously, the optimized LFM signals in Figure 3 and the FS LFM signals in Figure 4 are very different. Unlike the FS LFM signals, where each waveform has identical bandwidth and the frequency offset between adjacent waveforms are identical, the optimized LFM signals may have different bandwidths and the offsets between different pairs of adjacent waveforms may be different, providing more degrees of freedom, which may lead to superior system performance.
4.2 SCNR performance
Now, we compare the SCNR performance of the cognitive MIMO radar using the LFM waveforms designed by the proposed method with that of the system using FS LFM signals. Assume that the other parameters are the same as the previous examples. For different values of M and , the waveforms are designed and the resulting SCNRs (solid curves) are plotted in Figure 5. The SCNRs obtained using the FS LFM signals (dashed curves) are plotted in the same figure for comparison. The curves with points marked with circles and stars correspond to the cases for M = 2 and 4. It is seen that the SCNR curves of the systems employing the optimized LFM signals are uniformly higher than that of the systems employing FS LFM signals, indicating the superiority of our designed signals over the conventionally used FS LFM signals for any tested value of M. In the studied examples, the SCNR performance is improved when the number of transmitter M is increased from 2 to 4. Thus, employing more transmit antennas can be helpful in increasing the SCNR.
In Figure 6, we consider a cognitive MIMO radar with M = 2 transmitters. For different values of (20), which is a scaling factor of the clutter covariance matrix, the LFM waveforms are designed using the proposed method and the resulting SCNRs (solid curve with point marked with circle) are plotted in Figure 6. The other simulation settings are the same as those used in Figure 5. The SCNRs obtained using the FS LFM signals (dashed curve with point marked with square) are plotted in the same figure for comparison. It is observed that the SCNR decreases with the increase of the clutter covariance scaling factor . The SCNR performance of the system using our designed signals is better than that of the system using FS LFM signals for all the tested values of .
5 Conclusions
In this paper, the waveforms are proposed to be constructed by a group of LFM signals with undetermined starting frequencies, bandwidths, and transmit energies. The waveform parameters and the receiver impulse response are jointly designed by maximizing the SCNR performance of a cognitive MIMO radar system under the constraints of allowable range of operating frequency and total transmit energy. The algorithm for solving the waveform optimization problem was presented. We showed through numerical examples that the systems using the proposed waveforms have superior SCNR performance than the systems using the FS LFM signals.
Appendix 1
Convolution matrices
From (1), letting ε = t or c, the target or clutter return received by the l th receiver can be expressed as
where s[n] = (s1 [n],…,s M [n])T. Based on (22), the LN R × 1 overall target/clutter vector can be expressed as
where s is the overall waveform vector as defined in (3) and H ε denotes the convolution matrix for target or clutter, in which hε,ml[n] is defined in (1).
References
Aubry A, Lops M, Tulino AM, Venturino L: On MIMO detection under non-Gaussian target scattering. IEEE Trans. Inform. Theor 2010, 56(11):5822-5838.
Yu Y, Petropulu AP, Poor HV: Power allocation for CS-based colocated MIMO radar system. In IEEE Sensor Array and Multichannel Signal Processing Workshop. Hoboken, New Jersey; June 2012:217-220.
Aittomaki T, Koivunen V: Performance of MIMO radar with angular diversity under Swerling scattering models. IEEE J. Sel. Top. Signal. Process 2010, 4(1):101-114.
Stoica P, Li J, Xie Y: On probing signal design for MIMO radar. IEEE Trans. Signal Process 2007, 55(8):4151-4161.
Maio AD, Lops M, Ventura L: Diversity-integration trade-off in MIMO detection. IEEE Trans. Signal Process 2008, 56(10):4151-4161.
He Q, Blum RS, Godrich H, Haimovich AM: Target velocity estimation and antenna placement for MIMO radar with widely separated antennas. IEEE J. Sel. Top. Signal. Process 2010, 4(1):79-100.
He Q, Blum RS: Diversity gain for MIMO Neyman-Pearson signal detection. IEEE Trans. Signal Process 2011, 59(3):869-881.
Friedlander B: Waveform design for MIMO radars. IEEE Trans. Aero. Electron. Syst 2007, 43(5):1227-1238.
Yang Y, Blum RS: MIMO radar waveform design based on mutual information and minimum mean-square error estimation. IEEE Trans. Aero. Electron. Syst 2007, 43: 330-343.
Haykin S: Cognitive radar: a way of the future. IEEE Signal Process. Mag 2006, 23(1):30-40.
Stoica P, Hao H, Li J: Optimization of the receive filter and transmit sequence for active sensing. IEEE Trans. Signal Process 2012, 60(4):1730-1740.
Aubry A, Maio AD, Piezzo M, Farina A, Wicks M: Ambiguity function shaping for cognitive radar via complex quartic optimization. IEEE Trans. Signal Process 2013, 61(22):5603-5619.
Aubry A, Maio AD, Farina A, Wicks M: Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter. IEEE Trans. Aero. Electron. Syst 2013, 49(1):93-117.
Aubry A, Maio AD, Piezzo M, Farina A, Wicks M: Cognitive design of the receive filter and transmitted phase code in reverberating environment. IET Radar Sonar Navig 2012, 6(9):822-833. 10.1049/iet-rsn.2012.0029
Bae J, Goodman NA: Widely separated MIMO radar with adaptive waveform for target classification. In IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing. San Juan, Puerto Rico; December 2011:21-24.
Li W, Chen G, Blasch E, Lynch R: Cognitive MIMO sonar based robust target detection for harbor and maritime surveillance applications. In IEEE Aerospace Conference. Big Sky, Montana; March 2009:1-9.
Huleihel W, Tabrikian J, Shavit R: Optimal adaptive waveform design for cognitive MIMO radar. IEEE Trans. Signal Process 2013, 61(20):5075-5089.
Nijsure YA: Cognitive radar network design and applications. PhD thesis, Newcastle University. 2012.
Skolnik M: Radar Handbook. McGraw-Hill, New York; 2008.
Babur G, Krasnov OA, Yarovoy A, Aubry P: Nearly orthogonal waveforms for MIMO FWCW radar. IEEE Trans. Aero. Electron. Syst 2013, 49(3):1426-1437.
Geroleo FG, Brandt-Pearce M: Detection and estimation of LFMCW radar signals. IEEE Trans. Aero. Electron. Syst 2012, 48(1):405-418.
Wang Z, Tigrek F, Krasnov O, Van Der Zwan F, Van Genderen P, Yarovoy A: Interleaved OFDM radar signals for simultaneous polarimetric measurements. IEEE Trans. Aero. Electron. Syst 2012, 48(3):2085-2099.
Govoni MA, Li H, Kosinski JA: Low probability of interception of an advanced noise radar waveform with linear-FM. IEEE Trans. Aero. Electron. Syst 2013, 49(2):1351-1356.
Chen C, Vaidyanathan PP: MIMO radar ambiguity properties and optimization using frequency-hopping waveforms. IEEE Trans. Signal Process 2008, 56(12):5926-5936.
Wit JJMD, van Rossum WL, Jong AJD: Orthogonal waveforms for FMCW MIMO radar. In Radar Conference. IEEE,, Kansas City, Missouri; May 2011:686-691.
Liu B, He Z, Li J: Mitigation of autocorrelation sidelobe peaks of orthogonal discrete frequency-coding waveform for MIMO radar. In Radar Conference. IEEE; 2008:1-6.
Tree HLV: Detection, Estimation, and Modulation Theory, Part I. Wiley-Interscience, New York; 2001.
Chen C, Vaidyanathan PP: MIMO radar waveform optimization with prior information of the extended target and clutter. IEEE Trans. Signal Process 2009, 57(9):3533-3544.
Kay S: Fundamentals of Statistical Signal Processing: Detection Theory. Prentice-Hall, Upper Saddle River; 1998.
Wang S, He Q, He Z, Blum RS: MIMO over-the horizon radar waveform design for target detection. In IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). Vancouver, Canada; May 2013:4134-4138.
Eom KB: Time-varying autoregressive modeling of HRR radar signatures. IEEE Trans. Aero. Electron. Syst 1999, 35(3):974-988. 10.1109/7.784067
Fouladi SH, Hajiramezanali M, Amindavar H, Ritcey JA, Arabshahi P: Denoising based on multivariate stochastic volatility modeling of multiwavelet coefficients. IEEE Trans. Signal Process 2013, 61(22):5678-5589.
Wang S, He Q, He Z, Blum RS: Waveform design for MIMO over-the-horizon radar detection in signal dependent clutter and colored noise. In IET Radar Conference. Cincinnati, Ohio; May 2014:1-6.
Acknowledgements
This work was supported by the National Nature Science Foundation of China under Grants 61032010 and 61102142, the International Science and Technology Cooperation and Exchange Research Program of Sichuan Province under Grant 2013HH0006, and by the Fundamental Research Funds for the Central Universities under Grant ZYGX2013J015.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, S., He, Q. & He, Z. LFM-based waveform design for cognitive MIMO radar with constrained bandwidth. EURASIP J. Adv. Signal Process. 2014, 89 (2014). https://doi.org/10.1186/1687-6180-2014-89
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2014-89