Using information theoretic distance measures for solving the permutation problem of blind source separation of speech signals

Abstract

The problem of blind source separation (BSS) of convolved acoustic signals is of great interest for many classes of applications. Due to the convolutive mixing process, the source separation is performed in the frequency domain, using independent component analysis (ICA). However, frequency domain BSS involves several major problems that must be solved. One of these is the permutation problem. The permutation ambiguity of ICA needs to be resolved so that each separated signal contains the frequency components of only one source signal. This article presents a class of methods for solving the permutation problem based on information theoretic distance measures. The proposed algorithms have been tested on different real-room speech mixtures with different reverberation times in conjunction with different ICA algorithms.

1 Introduction

Blind source separation (BSS) is a technique of recovering the source signals using only observed mixtures when both the mixing process and the sources are unknown. Due to a large number of applications for example in medical and speech signal processing, BSS has gained great attention. This article considers the case of BSS for acoustic signals observed in a real environment, i.e., convolutive mixtures, focusing on speech signals in particular. In recent years, the problem has been widely studied and a number of different approaches have been proposed [1, 2]. Many state-of-the-art unmixing methods of acoustic signals are based on independent component analysis (ICA) in the frequency domain, where the convolutions of the source signals with the room impulse response are reduced to multiplications with the corresponding transfer functions. So for each frequency bin, an individual instantaneous ICA problem arises [2].

Due to the nature of ICA algorithms, obtaining a consistent ordering of the recovered signals is highly unlikely. In case of frequency domain source separation, this means that the ordering of outputs may change for each frequency bin. In order to correctly estimate source signals in the time domain, all separated frequency bins need to be put in a consistent order. This problem is also known as the permutation problem.

There exist several classes of algorithms giving a solution for the permutation problem. Approaches presented in [3–6] try to find permutations by considering the cross statistics (such as cross correlation or cross cumulants etc.) of the spectral envelopes of adjacent frequency bins. In [7] algorithms were proposed, that make use of the spectral distance between neighboring bins and try to make the impulse response of the mixing filters short, which corresponds to smooth transfer functions of the mixing system in the frequency domain. The algorithm proposed by Kamata et al. [8] solves the problem using the continuity in power between adjacent frequency components of the same source. A similar method was presented by Pham et al. [9]. Baumann et al. [10] proposed a solution by comparing the directivity patterns resulting from the estimated demixing matrix in each frequency bin. Similar algorithms were presented in [11–13]. In [14] it was suggested to use the direction of arrival (DOA) of source signals, determined from the estimated mixing matrices, for the problem solution. The approach in [15] is to exploit the continuity of the frequency response of the mixing filter. A similar approach was presented in [16] using the minimum of the L₁-norm of the resulting mixing filter and in [17] using the minimum distance between the adjacent filter coefficients. In [18] the authors suggest to use the cosine between the demixing coefficients of different frequencies as a cost function for the problem solution. Sawada et al. [19] proposed an approach based on basis vector clustering of the normalized estimated mixing matrices. In [20] a hybrid approach combines spectral continuity, temporal envelope and beamforming alignment with a psychoacoustic post-filter, and in [21] the permutation problem was solved using a maximum-likelihood-ratio between the adjacent frequency bins.

However with growing number of the independent components, the complexity of the solution grows. This is true not only because of the factorial increase of permutations to be considered, but also because of the degradation of the ICA performance. So not all of the approaches mentioned above perform equally well for an increasing number of sources.

The goal of this article is to investigate the usefulness of information theoretic distance measures for the solution of the permutation ambiguity problem. For this purpose it is assumed that the amplitudes of the estimated independent signals possess a Rayleigh distribution [22] and the logarithms of the amplitudes possess a generalized Gaussian distribution (GGD). It should be noted that the approach in [23] is based on a similar assumption, namely that the extracted signals are generalized Gaussian distributed. The authors handle the problem by comparing the parameters of the GGD of each frequency bin. However the resulting algorithm solves the permutation problem only partially and requires a combination with another approach, for instance [24].^a In contrast, the algorithms proposed in this article deal with the problem in a self-contained way and require no completion by other approaches.

The resulting approaches will be tested on different speech mixtures recorded in real environments with different reverberation times in combination with different ICA algorithms, such as JADE [25], INFOMAX [4, 26], and FastICA [27, 28].

2 Problem formulation

This section provides an introduction into the problem of blind separation of acoustic signals.

At first a general situation will be considered. In a reverberant (real) room, N acoustic signals s(t) = [s₁(t),...s _N (t)] are simultaneously active (t represents the time index). The vector of the source signals s(t) is recorded with M microphones placed in the room, so that an observation vector x(t) = [x₁(t), ... x _M (t)] results. Due to the time delay and to the signal reflections, the resulting mixture x(t) is a result of a convolution of the source signal s(t) with an unknown filter tensor $\underset{}{\underset{}{\mathbf{a}}}=\left({\underset{}{\mathbf{a}}}_1\dots {\underset{}{\mathbf{a}}}_K\right)$ where ${\underset{}{\mathbf{a}}}_k$ is the k-th (k ∈ [1...K]) M × N matrix with filter coefficients and K is the filter length. This problem can be summarized by

$$\mathbf{x}\left(t\right)=\sum _{k=0}^{K-1}{\underset{}{\mathbf{a}}}_{k+1}\mathbf{s}\left(t-k\right)+\mathbf{n}\left(t\right).$$

(1)

The term n(t) denotes the additive sensor noise. Now the problem is to find a filter matrix $\underset{}{\underset{}{\mathbf{w}}}=\left({\underset{}{\mathbf{w}}}_1\cdots {\underset{}{\mathbf{w}}}_{K^{\prime }}\right)$ so that by applying it to the observation vector x(t), the source signals can be estimated via

$$\mathbf{y}\left(t\right)=\sum _{k^{\prime }=0}^{K^{\prime }-1}{\underset{}{\mathbf{w}}}_{k^{\prime }+1}\mathbf{x}\left(t-k^{\prime }\right).$$

(2)

In other words, for the estimated vector y(t) and the source vector s(t), y(t) ≈ s(t) should hold.

This problem is also known as cocktail-party-problem. A common way to deal with the problem is to reduce it to a set of instantaneous separation problems, for which efficient approaches exist.

For this purpose, the time-domain observation vectors x(t) are transformed into a frequency domain time series by means of the short time Fourier transform (STFT)

$$\mathbf{X}\left(\Omega ,\tau \right)=\sum _{t=-\infty }^{\infty }\mathbf{x}\left(t\right)w\left(t-\tau R\right)e^{-j\Omega t},$$

(3)

where Ω is the angular frequency, τ represents the frame index, and w(t) is a window function (e.g., Hanning window) of length N_FFT, τ represents the frame index and corresponds to the time shift of he window and R is the shift size, in samples, between successive windows [29]. Transforming Equation (1) into the frequency domain reduces the convolutions to multiplications with the corresponding transfer functions, so that for each frequency bin an individual instantaneous ICA problem

$$\mathbf{X}\left(\Omega ,\tau \right)\approx \mathbf{A}\left(\Omega \right)\mathbf{S}\left(\Omega ,\tau \right)+\mathbf{N}\left(\Omega ,\tau \right)$$

(4)

arises. A(Ω) is the mixing matrix in the frequency domain, S(Ω, τ) = [S₁(Ω, τ), ..., S _N (Ω, τ)] represents the source signals, X(Ω, τ) = [X₁(Ω, τ), ..., X _M (Ω, τ)], denotes the observed signals, and N(Ω, τ) is the frequency domain representation of the additive sensor noise. In order to reconstruct the source signals unmixing matrix W(Ω) ≈ P^-1(Ω)A^-1(Ω) is derived using complex-valued ICA, so that

$$\widehat{\mathbf{Y}}\left(\Omega ,\tau \right)=\mathbf{W}\left(\Omega \right)\mathbf{X}\left(\Omega ,\tau \right)$$

(5)

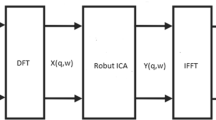
holds. Here Ŷ(Ω, τ) = [Ŷ₁(Ω, τ), ..., Ŷ _N (Ω, τ)] is the time frequency representation of the permutated ICA outputs. In order to solve the permutation problem a correction matrix P(Ω) for each frequency bin has to be found, which is the main topic of this article. The data flow of the whole application is shown in Figure 1.

Figure 1

Block diagram with data flow.

3 Permutation correction

This section gives an overview over the applied permutation correction methods. To resolve the permutations, the probability density functions (pdfs) of the magnitudes or of the logarithms of the magnitudes of the resulting frequency bins are compared. At this point, the assumption is made that adjacent frequency bins of the same source signal possess similar distributions.

3.1 Speech density modeling

3.1.1 Distribution of the speech magnitudes

As shown in [22], for speech signals the distribution of the magnitudes of spectral components can be described by the Rayleigh distribution. The pdf of the Rayleigh distribution of a random variable x is given by

$$f\left(x|\sigma \right)=\frac{x}{{\sigma }^2}\text{exp}\left\{-\frac{x^2}{2{\sigma }^2}\right\},$$

(6)

where σ is a shape parameter that can be estimated e.g., by using the maximum likelihood estimator [30].

For the vector of random variables x = (x₁, x₂,... x _N ), the multivariate Rayleigh distribution can be written as follows

$$f\left(\mathbf{x}|\Sigma \right)=\text{det}{\Sigma }^{-1/2}\prod _{i=1}^N\frac{{\tilde{x}}_i}{{\tilde{\sigma }}_i^2}\text{exp}\left\{-\frac{{\tilde{x}}_i^2}{2{\tilde{\sigma }}_i^2}\right\}{\left[\sum _{j=1}^N\text{exp}\left\{-\frac{{\tilde{x}}_i^2}{2{\tilde{\sigma }}_i^2}\right\}-N+1\right]}^{-\left(N+1\right)}$$

(7)

where

$$\Sigma ={\left(\mathbf{x}-\mu \right)}^T\left(\mathbf{x}-\mu \right)$$

(8)

is the symmetric positive definite covariance matrix of x,

$$\tilde{\mathbf{x}}={\Sigma }^{-1/2}\left(\mathbf{x}-\mu \right)$$

(9)

is a vector of the decorrelated random variables and ${\tilde{\sigma }}_i$ is the shape parameter for the signal ${\tilde{x}}_i$[31][32].^b

3.1.2 Distribution of the logarithms of the speech magnitudes

For the approximation of the logarithms of the speech magnitudes the GGD is applied. The PDF of the GGD of a random variable x is given by

$$f\left(x|\mu ,\sigma ,\beta \right)=\frac{\beta }{2a\Gamma \left(1/\beta \right)}\text{exp}\left\{-{\left|\frac{x-\mu }{a}\right|}^{\beta }\right\},$$

(10)

where μ is the mathematical expectation of x. The scale parameter a is obtained by

$$a=\sigma \sqrt{\frac{\Gamma \left(1/\beta \right)}{\Gamma \left(3/\beta \right)}},$$

(11)

and the Gamma function is given by

$$\Gamma \left(z\right)=\underset{0}{\overset{\infty }{\int }}{u}^{z-1}{e}^{-u}du.$$

(12)

The β-parameter describes the distribution shape and σ is the standard deviation of x. However, the β-parameter is unknown and needs to be estimated e.g., by using the maximum likelihood estimator [33] or the moment estimator [34, 35].

For the vector of random variables x = (x₁, x₂,... x _N ), the multivariate generalized Gaussian PDF can be written as follows

$$f\left(\mathbf{x}|\mu ,\Sigma ,{\beta }_1\dots {\beta }_N\right)=\text{det}{\Sigma }^{-1/2}\prod _{i=1}^N\left[\frac{{\beta }_i}{2a_i\Gamma \left(1/{\beta }_i\right)}\text{exp}\left\{-{\left|\frac{{\tilde{x}}_i}{a_i}\right|}^{{\beta }_i}\right\}\right],$$

(13)

where Σ is the covariance matrix of x and $\tilde{\mathbf{x}}$ is a vector of the decorrelated random variables (Equation (9)) [33].

3.2 Distance measures

Suppose the pdfs of magnitudes in two adjacent frequency bins

$$f\left(\left|\widehat{\mathbf{Y}}\left({\Omega }_k,\tau \right)\right|\right)=\left[f\left(\left|{Ŷ}_1\left({\Omega }_k,\tau \right)\right|\right),\dots ,f\left(\left|{Ŷ}_N\left({\Omega }_k,\tau \right)\right|\right)\right]$$

(14)

and

$$f\left(\left|\widehat{\mathbf{Y}}\left({\Omega }_{k+1},\tau \right)\right|\right)=\left[f\left(\left|{Ŷ}_1\left({\Omega }_{k+1},\tau \right)\right|\right),\dots ,f\left(\left|{Ŷ}_N\left({\Omega }_{k+1},\tau \right)\right|\right)\right]$$

(15)

of separated speech signals Ŷ(Ω, τ) are known. To solve the permutation ambiguity problem, it is necessary to define a pairwise similarity measure d(·, ·) between two PDFs, so the overall dependence (distance) results in

$$D\left(f\left(\left|{\widehat{\mathbf{Y}}}^P\left({\Omega }_k,\tau \right)\right|\right),f\left(\left|\widehat{\mathbf{Y}}\left({\Omega }_{k+1},\tau \right)\right|\right)\right)=\sum _{n=1}^{N}d\left(f\left(\left|{Ŷ}_n^P\left({\Omega }_k,\tau \right)\right|\right),f\left(\left|{Ŷ}_N\left({\Omega }_{k+1},\tau \right)\right|\right)\right),$$

(16)

where k ∈ [1, N_FFT - 1] is the frequency index,

$${\widehat{\mathbf{Y}}}^P\left({\Omega }_k,\tau \right)=\pi \left(\widehat{\mathbf{Y}}\left({\Omega }_k,\tau \right)\right)$$

(17)

is a permutation of Ŷ(Ω _k , τ), π(x) defines a permutation of the components of the vector x and N is the number of separated signals. The total distance D between a permutated vector of frequency bins, Ŷ^P(Ω _k , τ), and a reference vector in bin k + 1, is a sum of distances between each pair ${Ŷ}_n^P\left({\Omega }_k,\tau \right)$ and Ŷ _n (Ω_k+1, τ).

Below, several information theoretic similarity measures will be considered, which seem to be suitable for the solution of the permutation ambiguity problem. But first a definition of entropy or "self-information" is necessary.

The generalized formulation of entropy was given by Rényi and is known as the Rényi entropy in information theory [36, 37]. The Rényi differential entropy of order α, where α ≥ 0, for a random variable with a pdf f(x) whose support is a set , is defined as

$$H_{\alpha }\left(f\left(x\right)\right)=\frac{1}{1-\alpha }\text{log}\left(\underset{\mathbb{X}}{\int }{f}^{\alpha }\left(x\right)dx\right).$$

(18)

It can be shown, that in limit for α → 1, H _α (f(x)) converges to the Shannon entropy [37, 38],

$$H_1\left(f\left(x\right)\right)=-\underset{\mathbb{X}}{\int }f\left(x\right)\text{log}f\left(x\right)dx.$$

(19)

Similarly to the marginal entropy above, the joint entropy of a vector of random variables x = (x₁, x₂, ..., x _N ) is defined as

$$H_{\alpha }\left(f\left(\mathbf{x}\right)\right)=\frac{1}{1-\alpha }\text{log}\left(\underset{\mathbb{X}}{\int }{f}^{\alpha }\left(\mathbf{x}\right)d\mathbf{x}\right),$$

(20)

where f(x) is the multivariate pdf.

At this point it is possible to introduce the necessary dependence measures that will be used as the pairwise similarity measure d(·, ·) in Equation (16):

• Rényi generalized divergence between two distributions f(x) and g(x) of order α, where α ≥ 0, is defined [36] as

  $$d_{\alpha }\left(f\left(x\right)\left|\right|g\left(x\right)\right)=\frac{1}{\alpha -1}\text{log}\left(\int f^{\alpha }\left(x\right)g^{1-\alpha }\left(x\right)dx\right).$$

  (21)

Special cases of Equation (21) [39] are the

• Bhattacharyya coefficient

  $$d_{1/2}\left(f\left(x\right)\left|\right|g\left(x\right)\right)=-2\text{log}\left(\int \sqrt{f\left(x\right)g\left(x\right)}dx\right),$$

  (22)

• Kullback-Leibler divergence

  $$d_1\left(f\left(x\right)\left|\right|g\left(x\right)\right)=\int f\left(x\right)\text{log}\frac{f\left(x\right)}{g\left(x\right)}dx,$$

  (23)

• Log distance

  $$d_2\left(f\left(x\right)\left|\right|g\left(x\right)\right)=\text{log}E\left[\frac{f\left(x\right)}{g\left(x\right)}\right],$$

  (24)

where E [·] denotes the statistical expectation according to f(x),

• and log of the maximum ratio

  $$d_{\infty }\left(f\left(x\right)\left|\right|g\left(x\right)\right)=\text{log}\underset{x}{\text{sup}}\frac{f\left(x\right)}{g\left(x\right)}.$$

  (25)

Rényi's divergence describes the alikeness between two distributions. The smaller the Rényi divergence, the more similar the distributions are. The main advantage of the Rényi divergence is the small computational burden. The problem in using the Rényi divergence is the fact that this measure is not symmetric, so typically d _α (f(x)||g(x)) ≠ d _α (g(x)||f(x)), and not bounded, so infinite values can arise.

• Mutual information for a vector of random variables X = (X₁, X₂, ..., X _K ) is defined as the Kullback-Leibler divergence between the product of the distribution functions ${\prod }_{i=1}^K{f}_{X_i}\left(x_i\right)$ and the multivariate distribution f _x (x)

  $$I\left(\mathbf{X}\right)=d_1\left(f_{\mathbf{x}}\left(\mathbf{x}\right)∥\prod _{i=1}^K{f}_{X_i}\left(x_i\right)\right)$$

  (26)
  $$=\int f_{\mathbf{x}}\left(\mathbf{x}\right)\text{log}\frac{f_{\mathbf{X}}\left(\mathbf{x}\right)}{{\prod }_{i=1}^K{f}_{X_i}\left(x_i\right)}d\mathbf{X}$$

  (27)
  $$=\int f_{\mathbf{x}}\left(\mathbf{x}\right)\text{log}{f}_{\mathbf{x}}\left(\mathbf{x}\right)d\mathbf{x}-\int f_{\mathbf{X}}\left(\mathbf{x}\right)\text{log}\prod _{i=1}^K{f}_{X_i}\left(x_i\right)d\mathbf{x}$$

  (28)
  $$=\sum _{i=1}^K{H}_1\left(f_{X_i}\left(x_i\right)\right)-H_1\left(f_{\mathbf{x}}\left(\mathbf{x}\right)\right)$$

  (29)

where $H_1\left(f_{X_i}\left(x_i\right)\right)$ is the marginal entropy and H₁(f _x (x)) is the joint entropy of X.

Mutual information gives the amount of information contained in the random variables of X. Since for the computation of the term f _x (x) is taken into account i.e., the dependencies are considered, the mutual information is a stronger cost function than Rényi divergence and using it for resolving the permutations, better results are to be expected.

• The Jensen-Rényi divergence of the vector of random variables X = (X₁, X₂, ..., X _K ) of order α, where α ≥ 0, is defined [40] as

  $$d_{J{R}_{\alpha }}\left(\mathbf{X}\right)=H_{\alpha }\left(\frac{1}{K}\sum _{i=1}^K{f}_{X_i}\left(x_i\right)\right)-\frac{1}{K}\sum _{i=1}^K{H}_{\alpha }\left(f_{X_i}\left(x\right)\right).$$

  (30)

The Jensen-Rényi divergence is based on the Kullback-Leibler divergence and can be seen as an extension of it with the difference that it is symmetric^c and always of finite value. On the other hand, due to the fact that the distributions of the random variables are compared indirectly using the average $\frac{1}{K}{\sum }_{i=1}^K{f}_{X_i}\left(x\right)$, the Jensen-Rényi divergence can be seen as an alternative to the mutual information [41]. In fact, as shown in [42], both measures show similar characteristics.

• The modified Jensen-Rényi divergence. The Jensen-Rényi-divergence from the Equation (30) measures the distance between two distributions f _X (x) and f _Y (x) in respect to a third point in the distribution space. In this case, the third point is chosen as the average of the two distributions. This approach is justified because of the concavity of the entropy in distribution space

  $$H\alpha \left(\frac{f_X\left(x\right)+f_Y\left(x\right)}{2}\right)\ge \frac{H_{\alpha }\left(f_X\left(x\right)\right)+H_{\alpha }\left(f_Y\left(x\right)\right)}{2}.$$

  (31)

In principle, it is possible to define the distance in respect to any other point, if the assumption of the concavity for this point holds. Such a point can be chosen as an average over the random variables, the distributions of which are currently analyzed.

For the entropy of a random variable X

$$H_{\alpha }\left(f_X\left(x\right)\right)\propto \left|\right|f_X\left(x\right)|{|}_{\alpha }$$

(32)

holds, and for the entropy of the sum of two random variables X and Y [38, 43]

$$H_{\alpha }\left(f_{X+Y}\left(x\right)\right)\propto \left|\right|f_X\left(x\right)*f_Y\left(x\right)|{|}_{\alpha }.$$

(33)

||·||_α denotes the α norm operator and ٭ stands for convolution. Using the entropy power inequality [38] for the case of α = 1, and extending Young's inequality [44] for the case of α ≠ 1, it can be shown [45], that

$$H_{\alpha }\left(f_{X+Y}\left(x\right)\right)\ge \text{max}\left(H_{\alpha }\left(f_X\left(x\right)\right),H_{\alpha }\left(f_Y\left(x\right)\right)\right).$$

(34)

Since

$$\text{max}\left(a,b\right)\ge \frac{a+b}{2}$$

(35)

holds, the inequality in Equation (34) can be rewritten as

$$H_{\alpha }\left(f_{X+Y}\left(x\right)\right)\ge \frac{H_{\alpha }\left(f_X\left(x\right)\right)+H_{\alpha }\left(f_Y\left(x\right)\right)}{2}.$$

(36)

So, at this point a modification of the Jensen-Rényi divergence is proposed. This distance measure of the vector of random variables X = (X₁, X₂, ..., X _K ) of order α, where α ≥ 0, is defined as

$$d_{mJR\alpha }\left(\mathbf{X}\right)=H_{\alpha }\left(f_{\bar{X}}\left(x\right)\right)-\frac{1}{K}\sum _{i=1}^K{H}_{\alpha }\left(f_{X_i}\left(x\right)\right)$$

(37)

where $\bar{X}=\frac{1}{K}{\sum }_{i=1}^K{X}_i$ In the way the modified Jensen-Rényi divergence is used here, this distance measure describes the amount of new information coming to a spectrogram if an adjacent frequency bin Y(Ω_k+1, τ) is included. The lesser the new information provided, the closer the frequency bins are. This modification has less computational burden than the classical Jensen-Rényi divergence, since for $H_{\alpha }\left(f_{\tilde{X}}\left(x\right)\right)$, only one pdf has to be calculated instead of K in the Jensen-Rényi divergence. Furthermore, for the entropy $H_{\alpha }\left(f_{\bar{X}}\left(x\right)\right)$ there exists an analytical solution, which improves the accuracy of the results.

3.3 The Permutation correction algorithm

In this section the actual permutation correction algorithm will be discussed. As mentioned before, it will be assumed that subsequent frequency bins of the same source signal possess similar distributions. The similarity between the frequency bins is measured by applying the measures given in Equations (21),(29), (30), and (37) in the optimization of Equation (16).

However, as mentioned in [14] the use of only one frequency bin as a reference bin for the correction causes a risk of a misalignment of the algorithm. To avoid this problem, the approach presented in [5] uses an average value of the already corrected frequency bins. So, the Equation (16) will be redefined as

$$D\left[f\left(\left|{\widehat{\mathbf{Y}}}^P\left({\Omega }_k,\tau \right)\right|\right),f\left(\frac{1}{L}\sum _{l=k+1}^{k+1+L}\left|\widehat{\mathbf{Y}}\left({\Omega }_l,\tau \right)\right|\right)\right]=\sum _{n=1}^{N}d\left[f\left(\left|{Ŷ}_n^P\left({\Omega }_k,\tau \right)\right|\right),f\left(\frac{1}{L}\sum _{l=k+1}^{k+1+L}\left|{Ŷ}_n\left({\Omega }_l,\tau \right)\right|\right)\right]$$

(38)

where L is the number of the already corrected frequency bins to be used for the averaging. Then the correction algorithm can be implemented as described in Algorithm 1.

Algorithm 1

• 1. Initialization: Start with the frequency^d Set k = N_FFT/2.

• 2. Estimate the parameters of the Rayleigh distribution of |Ŷ(Ω _k , τ)| and of the average of L already corrected bins $\frac{1}{\widehat{L}}{\sum }_{l=k+1}^{\widehat{L}}\left|{Ŷ}_n\left({\Omega }_l,\tau \right)\right|$, with $\widehat{L}=\text{min}\left(k+1+L,N_{\text{FFT}}/2+1\right)-\left(k+1\right)$ using Equations (6)-(9).

• 3. Calculate $D\left[f\left(\left|{\widehat{\mathbf{Y}}}^P\left({\Omega }_k,\tau \right)\right|\right),f\left(\frac{1}{\widehat{L}}{\sum }_{l=k+1}^{\widehat{L}}\left|\widehat{\mathbf{Y}}\left({\Omega }_l,\tau \right)\right|\right)\right]$ as defined in Equation (38) for all possible permutations of |Ŷ(Ω _k , τ)|.

• 4. Choose the permutation π₊(|Ŷ(Ω _k , τ)|) with the most dependent value of D.

• 5. Correct the current frequency bin in order with the best permutation π₊(|Ŷ(Ω _k , τ)|).

• 6. Decrement k and if k ≠ 0 go to Step 2.

The same scheme can be applied on the logarithms of the spectral magnitudes of the signals log |Ŷ(Ω _k , τ)| instead of |Ŷ(Ω _k , τ)| and using generalized Gaussian instead of Rayleigh distributions. In that case Algorithm 2 results.

Algorithm 2

• 1. Initialization: Start with the frequency k = N_FFT/2.

• 2. Estimate the GGD parameters of log |Ŷ(Ω _k , τ)| and of the average of L already corrected bins $\text{log}\left(\frac{1}{\widehat{L}}{\sum }_{l=k+1}^{\widehat{L}}\left|{Ŷ}_n\left({\Omega }_l,\tau \right)\right|\right)$, with $\widehat{L}=\text{min}\left(k+1+L,N_{\text{FFT}}/2+1\right)-\left(k+1\right)$ using Equations (10)-(13).^e

• 3. Calculate $D\left[f\left(\text{log}\left|{\widehat{\mathbf{Y}}}^P\left({\Omega }_k,\tau \right)\right|\right),f\left(\text{log}\left(\frac{1}{\widehat{L}}{\sum }_{l=k+1}^{\widehat{L}}\left|\widehat{\mathbf{Y}}\left({\Omega }_l,\tau \right)\right|\right)\right)\right]$ as defined in Equation (38) for all possible permutations of |Ŷ(Ω _k , τ)|.

• 4. Choose the permutation π₊(log |Ŷ(Ω _k , τ)|) with the most dependent value of D.

• 5. Correct the current frequency bin in order with the best permutation π₊(log |Ŷ(Ω _k , τ)|).

• 6. Decrement k and if k ≠ 0 go to Step 2.

The Algorithms 1 and 2 will be used in the following sections for the experimental comparison of the distance measures given in Equations (21),(29), (30), and (37).

4 Experiments and results

4.1 Conditions

For the evaluation of the proposed approaches, two different sets of recordings were used. In the first data set, different audio files from the TIDigits database [46] were used and mixtures with up to four speakers were recorded under real room conditions. The distance between speakers and the center of a linear microphone array was varied between 0.9 and 2 m. The second dataset was recorded by Sawada [47]. Here also mixtures with up to four speakers are presented. All of the mixtures were made with the same number of microphones as the number of speakers in the mixture (M = N), i.e., in each mixture a determined problem is considered so the classical ICA algorithms for source separation can be applied. The experimental setups are presented schematically in Figure 2 and the experimental conditions are summarized in Tables 1, 2, 3, and 4.

Figure 2

Experimental Setup. L _i is the distance between speaker i and array center. θ _i is the angular position of the speaker i. d is the distance between microphones.

Table 1 Mixture characteristics

Table 2 Mixture characteristics

Table 3 Mixture characteristics

Table 4 Mixture characteristics

4.2 Parameter settings

The algorithms were tested on all recordings, which were first transformed to the frequency domain at a resolution of N_FFT = 1, 024. For calculating the spectrogram, the signals were divided into overlapping frames with a Hanning window and an overlap of 3/4 · N_FFT.

4.3 ICA performance measurement

For calculation of the effectiveness of the proposed algorithm, the improvement Δ SIR of the signal to interference ratio

$$\Delta \text{SI}{\text{R}}_i=10{\text{log}}_{10}\frac{{\sum }_n{y}_{i,s_i}^2\left(n\right)}{{\sum }_{j\ne i}{\sum }_n{y}_{i,s_j}^2\left(n\right)}-10{\text{log}}_{10}\frac{{\sum }_n{x}_{i,s_i}^2\left(n\right)}{{\sum }_{j\ne i}{\sum }_n{x}_{i,s_j}^2\left(n\right)}$$

(39)

was used as a measure of the separation performance and the signal to distortion ratio (SDR)

$$\text{SD}{\text{R}}_i=10{\text{log}}_{10}\frac{{\sum }_n{x}_{k{s}_i}^2\left(n\right)}{{\sum }_n{\left(x_{k{s}_i}\left(n\right)-\alpha y_{i{s}_i}\left(n-\delta \right)\right)}^2}$$

(40)

as a measure of the signal quality. Here $y_{i,s_j}$ is the i-th separated signal with only the source s _j active, and $x_{k,s_j}$ is the observation obtained by microphone k when only s _j is active. α and δ are parameters for phase and amplitude chosen to optimally compensate the difference between $y_{i,s_j}$ and $x_{k,s_j}$ [19].

For measuring the performance of the proposed algorithms on all speakers present in a mixture recording, an average Δ SIR

$$\Delta \text{SIR}=\frac{1}{N}\sum _{i=1}^N\Delta \text{SI}{\text{R}}_i$$

(41)

and SDR

$$\text{SDR}=\frac{1}{N}\sum _{i=1}^N\text{SD}{\text{R}}_i$$

(42)

were used, where N is the number of speakers in the considered mixture.

4.4 Experimental results

In this section the experimental results of the signal separation will be compared. All the mixtures from Tables 1, 2, 3, and 4 were separated by JADE, INFOMAX, and the FastICA algorithm and the permutation problem was solved using either Algorithm 1 or 2 from Section 3.3 and distance measures from Equations (21), (29), (30), and (37). For each result the performance is calculated using Equations (39) and (40).

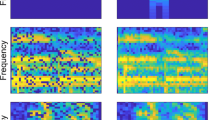
Figures 3 and 4 show the behavior of three different approaches in terms of Δ SIR and SDR (Equations (41) and (42)) over the mixtures for the Infomax approach.

Figure 3

Results obtained by Infomax and Algorithm 1 using ' ٭ ' mutual information with α = 1 , ' Δ ' Jensen-Rényi divergence with α = 1 and ' ο ' modified Jensen-Rényi divergence with α = 1 over the mixtures.

Figure 4

Results obtained by Infomax and Algorithm 2 using ' ٭ ' mutual information with α = 1 , ' Δ ' Jensen-Rényi divergence with α = 1 and ' ο ' modified Jensen-Rényi divergence with α = 1 over the mixtures.

In Tables 5 and 6, the separation results are averaged for each distance measure for the mixtures of 2, 3, and 4 signals separately. M₂ in Tables 5 and 6 contains the average Δ SIR/SDR of the separation results of Mix. 1, Mix. 4, Mix. 7 and Mix. 10, cf. Tables 1, 2, 3, and 4. Similarly, M₃ contains the separation results of Mix. 2, Mix. 5, Mix. 8 and Mix. 11, and M₄ those of Mix. 3, Mix. 6, Mix. 9 and Mix. 12.

Table 5 Average values of the obtained results of Algorithm 1 in terms of Δ SIR and SDR for each distance measure

Table 6 Average values of the obtained results of Algorithm 2 in terms of Δ SIR and SDR for each distance measure

4.5 Discussion

The calculated results show the usefulness of the proposed method for permutation correction, though not all of the applied distance measures perform equally. As already mentioned above, the best results were achieved using mutual information and the modified Jensen-Rényi divergence, while results obtained using generalized Rényi divergence are rather poor. This is especially the case, if α = 2 is used. Of all the applied distance measures based on the generalized Rényi divergence, the best performance was achieved in the case of the Bhattacharyya coefficient, i.e., α = 0.5. A similar tendency can be seen with "classical" Jensen-Rényi divergence. Here the best results were achieved using α = 1. In contrast, correction based on mutual information and the modified Jensen-Rényi divergence provides stable good results.

The poor performance in the case of generalized Rényi divergence can be explained by fact that the assumed models of the probability distribution of the amplitudes and log amplitudes are not exact enough to be used with generalized Rényi divergence for a successful solution of the permutation problem. As can be seen in Figure 5, the distribution of the lower frequency bins of a speech signal can be only roughly modeled with Rayleigh pdf. In contrast the higher frequencies can be seen as Rayleigh distributed variables. This causes a high error rate in the permutation correction at lower frequencies, when the generalized Rényi divergence is used. Since, as shown in [48], the lower frequencies play a more significant role in BSS of the speech signals than the higher frequencies, the low values of the SIR and SDR are explainable. The same holds for the distribution of the log amplitudes. This problem can be solved using a more exact model for the pdf of the speech signals such as Rayleigh mixture models (RMM) for the amplitudes or Gaussian mixture models (GMM) for the log amplitudes and is the subject of the future study.

Figure 5

Comparison of the assumed pdfs and the histograms of the speech signal at different frequencies. Histograms of the amplitudes of a clean speech signal (white bar) and the Rayleigh probability distribution functions (black line) that were calculated for the clean speech data at (a) 1,000 Hz, (b) 2,000 Hz, (c) 3,000 Hz and (d) 4,000 Hz

Furthermore, the effects of the various reverberation times on the performance of different distance measures are going to be studied in the future. While, as it can be seen in Figures 3 and 4, the performance of the separation system decreases with a growing reverberation time of the environment, the effect of reverberation time on different methods of permutation correction should be analyzed in a more exact way.

On the other hand, the assumption of the Rayleigh distribution and GGD is good enough for permutation correction with mutual information and the modified Jensen-Rényi divergence, since these distance measures are not as sensitive to the inter frequency-bin pdf perturbations as the generalized Rényi divergence. Furthermore, in this case there exists an analytical solution for modified Jensen-Rényi divergence, which reduces the computational burden of the algorithm and improves the accuracy of the solution.

As it can be seen in Tables 5 and 6, the separation performance of Algorithm 1 is slightly better than the performance of Algorithm 2. A possible explanation for this issue is the fact that for the Rayleigh pdf just one parameter has to be estimated instead of 2 parameters in case of GGD. Furthermore the estimation of the GGD parameters is more complicated than the estimation of the σ in case of Rayleigh distribution. These might cause the uncertainties and errors in the permutation correction.

In the next step, the best four of the proposed methods were compared with some other approaches from Section 1. In Table 7, the results of the comparison are shown. As can be seen, the proposed method (Algorithm 1 with the modified Jensen-Rényi divergence, α = 2) performs better than other algorithms in terms of Δ SIR in most cases.

Table 7 Average values of the obtained results in terms of Δ SIR and SDR for each distance measure

5 Conclusions

In this article, a method for the permutation correction in convolutive source separation has been presented. The approach is based on the assumption that magnitudes of speech signals adhere to a Rayleigh distribution and the logarithms of magnitudes can be modeled by a GGD. The assumption of Rayleigh or GG distributed signals allows to use information theoretic similarity measures. The information theoretic distance measures are used to detect similarities in subsequent frequency bins after bin-wise source separation is completed, in order to group the frequency bins coming from the same source. Beside the existing information theoretic distance measures, a modification of the Jensen-Rényi divergence is proposed. This modified distance measure shows very good results for the considered problem.

The proposed method has been tested on different reverberant speech mixtures in connection with different ICA algorithms. The experimental results and the comparison with today's state-of-the-art approaches for permutation correction show the usefulness of the proposed method. Further, the experimental results have shown that the method performs best using either the mutual information or the modified Jensen-Rényi divergence criterion (Tables 5 and 6). This fact may be explained at least partially by the ability of the Jensen-Renyi divergence and the mutual information to utilize temporal dependence structure, which puts these two criteria ahead of the Rényi generalized divergence and its special cases of the Kullback-Leibler divergence and the log maximum ratio, which we considered as alternatives.

Appendix 1

To calculate the distance measures from Equation (21), (29), (30), and (37), in most cases an integral has to be solved. The Rényi differential entropy (Equation (18)) in case of the Rayleigh distribution is calculated as

$$H_{\alpha }\left(X\right)=\frac{1}{1-\alpha }\text{log}\left(\underset{X}{\int }{f}_X^{\alpha }\left(x\right)dx\right)$$

(43)

$$=\text{log}\left(\frac{\sigma }{\sqrt{2}}\right)+\frac{1}{1-\alpha }\text{log}A+\frac{1}{1-\alpha }\text{log}\left(\Gamma \left(\alpha -\frac{\alpha }{2}+\frac{1}{2}\right)\right),$$

(44)

where σ is the shape parameter of the Rayleigh distribution and

$$A={\alpha }^{\left(-\alpha +\frac{\alpha }{2}-\frac{1}{2}\right)}.$$

(45)

Setting α → 1 the Equation (44) becomes

$$H_1\left(x\right)=1+\text{log}\frac{\alpha }{\sqrt{2}}+\frac{\gamma }{2},$$

(46)

where γ is the Euler-Mascheroni constant γ ≈ 0.57722.

For the GG distribution, the entropies can be computed as

$$H_{\alpha }^R\left(X\right)=\frac{1}{1-\alpha }\text{log}\left(\underset{X}{\int }{f}_X^{\alpha }\left(x\right)dx\right)$$

(47)

$$=\frac{1}{1-\alpha }\text{log}{\alpha }^{-1/{\beta }_X}-\text{log}\left(\frac{{\beta }_X}{2a\Gamma \left(1/{\beta }_X\right)}\right)$$

(48)

and

$$H_1\left(X\right)=\frac{1}{{\beta }_X}-\text{log}\left(\frac{{\beta }_X}{2a\Gamma \left(1/{\beta }_X\right)}\right).$$

(49)

The solution of the Equation (46) is given in [38]. The solutions of the Equations (44) and (48) were derived using MATHEMATICA. For the distance measures without an analytical solution the trapezoidal rule for numerical integration was applied [49].

Appendix 2

Since information theoretic similarity measures make use only of the pdfs of the signals, a question may arise, as to whether temporal dependence structures of the signals are utilized at all in the suggested framework. The temporal structure is taken into account indirectly in the applied similarity measures, since each of the measures contains a term where either the joint probability, the pdf of the mean value of the random variables (Equation (37)), the mean of the pdf or a quotient of the pdfs is considered. These are the terms where the values of the distribution functions produced at the same time domain window are "compared".

To demonstrate this issue, the following example was constructed: We compare signal U₁(τ), which contains amplitudes of a speech signal at the frequency f = 3219.2 Hz, U₂(τ) which is the same signal as U₁(τ) but time delayed, and U₃(τ), which contains a amplitudes of the same speech signal as U₁(τ) at the frequency f = 3230 Hz, the next frequency bin, with additional Gaussian noise, see Figure 6.

Figure 6

Constructed signals for demonstration. (a) Signal U₁(τ) is a speech signal at the frequency f = 3, 219.2 Hz, (b) U₂(τ) is the same signal as U₁(τ) but time delayed and (c) signal U₃(τ) contains amplitudes of the same speech signal as U₁(τ) at the frequency f = 3, 230 Hz (the next frequency bin) with an additional Gaussian noise.

For each signal pair 〈U₁(τ), U₂(τ)〉, 〈U₁(τ), U₃(τ)〉, 〈log(U₁(τ)), log(U₂(τ))〉 and 〈log(U₁(τ)), log(U₃(τ))〉, the similarity measures from Equations (21), (29), (30), and (37) were applied. The results of the signal comparison can be found in Tables 8 and 9.

Table 8 Comparison of signal pairs 〈 U ₁ ( τ ), U ₂ ( τ ) 〉 and 〈 U ₁ ( τ ), U ₃ ( τ ) 〉 with each distance measure

Table 9 Comparison of signal pairs 〈log( U ₁ ( τ )), log( U ₂ ( τ ))〉 and 〈log( U ₁ ( τ )), log( U ₃ ( τ ))〉 with each distance measure

As can be seen, for this example each similarity measure that was considered in this article rates U₁(τ) more similar to U₃(τ) than to U₂(τ),^f which implies that the temporal dependencies and correlations were not ignored during the computation of the probability distribution functions.

In contrast to the other measures, in the case of the Rényi generalized divergence defined in Equation (21), and in its special cases of the Kullback-Leibler divergence and the log maximum ratio, the time dependency can not be taken into account in this manner. Still, these similarity measures can also be used for permutation correction, since the situation we considered in the example above is rather artificial and cannot be expected for realistic situations with two speech signals as the desired sources.

Endnotes

^aIn the cases where no permutation correction by the means of the comparison of the GGD parameters is possible, the problem is handled by applying the correlation based permutation correction approach. ^bEquation (7) is a special case of the multivariate Weibull distribution with α = 1 and c _i = 2 [32, Equation (14)]. ^cE.g. $d_{J{R}_{\alpha }}\left(X_1,X_2\right)=d_{J{R}_{\alpha }}\left(X_2,X_1\right)$. ^dThe proposed algorithm solves the permutations problem starting with the higher frequency bins. The first frequency bin in this case is the bin with k = N_FFT/2 + 1. Since there is no other definition of the correct order of the signals, the signal order in frequency bin k = N_FFT/2+1 will be assumed as correct. ^eFor the experiments from the Section 4 the parameter β was calculated using the approximation for the inverse function as proposed in [34]. ^fThe more dependent the signals are, the higher the value of the mutual information Equation (29) becomes, while simultaneously, the values of the similarity measures from (21), (30), and (37) decrease.