Detection and localization of double compression in MP3 audio tracks

Abstract

In this work, by exploiting the traces left by double compression in the statistics of quantized modified discrete cosine transform coefficients, a single measure has been derived that allows to decide whether an MP3 file is singly or doubly compressed and, in the last case, to devise also the bit-rate of the first compression. Moreover, the proposed method as well as two state-of-the-art methods have been applied to analyze short temporal windows of the track, allowing the localization of possible tampered portions in the MP3 file under analysis. Experiments confirm the good performance of the proposed scheme and demonstrate that current detection methods are useful for tampering localization, thus offering a new tool for the forensic analysis of MP3 audio tracks.

1 Introduction

In the last years, the research in multimedia forensics started to consider audio contents for investigating their origin and authenticity. In particular, similarly to the image forensic field, the analysis of the artifacts due to double compression has received a lot of attention. Basing on such digital footprints, in this paper, we will assume the role of the forensic analyst that wants to discover two of the main forgeries that a MP3 audio track can undergo: (i) fake quality, i.e., the audio file is recompressed at higher bit-rate to pass it off as a high-quality track and (ii) tampering, i.e., a portion of the audio track has been edited or deleted. In particular, our aim is to propose a forensic scheme able to detect fake quality audio tracks and to provide information on the first compression bit-rate, as well as to localize possible tampered portions in audio files.

The works dealing with MP3 audio files and double audio compression proposed in the current literature are briefly reported in the following. In[1], to defeat fake quality MP3, authors observed that there are many more quantized modified discrete cosine transform (MDCT) coefficients with small values in a singly compressed MP3 file than in a fake quality MP3 file, no matter which bit-rate the fake quality MP3 was transcoded from. According to this, a detector was proposed that just measures the number of MDCT coefficients assuming ±1 values and compares this value to a given threshold T: if it is lower than T, the file is a fake quality one, otherwise it is a singly compressed one. The same authors in[2] proposed to detect double MP3 compression through the use of support vector machine classifiers with feature vectors formed by the distributions of the first digits of quantized MDCT coefficients; in particular, a global method was proposed, where the statistics on the first digits of all quantized MDCT coefficients are taken, and the computed probability distributions of nine digits are used as features (nine dimensions) for training a support vector machine (SVM). A so-called band distribution method is also proposed, where a procedure of band division is added before computing the statistics on the first digits, allowing to increase the performance. In[3, 4], to detect double MP3 compression, some statistical features of the MDCT are extracted and a SVM is applied to the extracted features for classification. A set of statistical features of zero MDCT coefficients and nonzero MDCT coefficients from the frequency range as well as individual scale bands are adopted. In[5, 6], a forgery detection method for MP3 audio files is proposed. Based on the observation that forgeries break the original frame segmentation, frame offsets are used to locate forgeries automatically, allowing to detect most common forgeries, such as deletion, insertion, substitution, and splicing. However, experimental results are carried out in audio files that have not been reencoded in MP3 format after the manipulation. In[7], a method is presented to determine the encoder of MP3 data on the basis of statistical features extracted from the data; the work also addresses the classification of MP3 files recompressed with different encoders but considering the same value of bit-rate for the second compression. Finally, in[8], the inverse decoder problem is considered. In this scenario, only the uncompressed samples are known to the analyst and the goal is to recover the parameters of a possible previous compression. The same problem is tackled in[9], where some properties of the frequency spectrum of the track under analysis are exploited; the same classifier used to differentiate between different MP3 quality levels is also applied to detect transcoded MP3s, but for this scenario, the presented experiments are rather limited.

In this work, which is an extension of a previous work[10], we propose an approach exploiting the effect of double compression in the statistical properties of quantized MDCT coefficients in MP3 audio files. The method, that will be presented in Section 2, relies on a single measure derived from the statistics of MDCT coefficients, allowing us to apply a simple threshold detector to decide whether a given MP3 file is singly compressed or it has been doubly compressed, without resorting to SVM classifiers. Moreover, the proposed method is able to derive the bit-rate of the first compression by means of a nearest neighbour classifier. The ability of the algorithm to detect doubly MP3 compressed files remains valid also on tracks of reduced length, allowing its application to the localization of singly/doubly compressed segments within a MP3 audio file, as shown in Section 3.

In Section 4, the performance of the proposed method is evaluated and compared to two previously proposed schemes, namely Yang et al.[2] and Liu et al.[3, 4] in the fake quality detection scenario. In order to do the same comparison in the audio tampering scenario, in the same section, we present also the application of the proposed scheme and of the two state-of-the-art algorithms to the forgery scenario we have considered: in particular, we tested the accuracy of such doubly compressed audio file detectors when the audio track length is reduced and we exploited their use for tampering localization.

Finally, in Section 5, some conclusions about our research are drawn.

2 Detection and classification of double compression

The core idea of the algorithm is to measure the similarity between the histogram of quantized MDCT coefficients of the MP3 file under analysis, that has possibly undergone a double compression, and the histogram of the MDCT coefficients computed on a singly compressed version of the same file, that is of the singly compressed MDCT coefficients. Intuitively, if the distance between the two distributions is low, this will indicate that the file under analysis has not been MP3 encoded twice; vice versa, the file will be considered as doubly compressed.

Obtaining a reliable estimate of the distribution of the singly quantized MDCT coefficients from the corresponding quantized or doubly quantized coefficients appears to be a difficult task. However, it has already been observed in the image forensic literature[11, 12] that the DCT coefficients obtained by applying a slight shift to the grid used for computing the block DCT usually do not exhibit quantization artifacts. In a similar way, the distribution of the singly compressed MDCT coefficients can be approximated by generating a simulated singly compressed file, starting from the file under analysis. This can be achieved by decompressing the MP3 file, removing a given number of pulse code modulation (PCM) samples of the decompressed version, and then recompressing the remaining samples to the same compression quality of the file under analysis.

To demonstrate that the idea is effective, an uncompressed audio track, 4 s long, has been MP3 compressed at several bit-rates in the set [64, 96, 128, 192] kbit/s, and then recompressed to 160 kbit/s, in such a way to obtain four doubly compressed versions, three with increasing bit-rate, and one with decreasing bit-rate. Then, the uncompressed file is also singly compressed to 160 kbit/s. To each of these MP3 files, the previous procedure has been applied to obtain a simulated singly compressed file, by removing the first ten PCM samples to the decompressed file and recompressing the remaining samples to 160 kbit/s. Then, the histograms of MDCT coefficients extracted from the input original files and from the corresponding simulated singly compressed files have been compared.In Figure1, the histograms related to the MP3 file doubly compressed at 64 kbit/s and then to 160 kbit/s (left) and to the simulated MP3 file singly compressed at 160 kbit/s (right) are shown. It is evident that the first histogram exhibits the characteristic pattern of a distribution of coefficients that have undergone a double compression, whereas in the second one, these artifacts have been removed, and thus the difference between the two histograms is significant. Similar results are obtained when the first compression was done with higher bit-rates but still lower than 160 kbit/s, even if the effect of the double quantization becomes smaller.On the contrary, if the same procedure is applied to a singly compressed MP3 file, it will happen that the histograms of the input file (left) and the corresponding simulated one (right) are very similar, as it is shown in Figure2.A similar situation shows up when a double compression has been applied, but with the first bit-rate (i.e., 192 kbit/s) equal or higher than the second one (i.e., 160 kbit/s), see Figure3: in this case, the histogram of the MP3 file under analysis (left) does not exhibit the double compression artifacts, so that the histograms of the two files are very similar, thus not allowing to detect the double compression. The removal of these artifacts is due to the fact that the second compression is so strong that deletes the traces left by the previous one.

Figure 1

MDCT histograms for doubly compressed file with increasing bit-rate and simulated singly compressed file.

Figure 2

MDCT histograms for singly compressed file and simulated singly compressed file.

Figure 3

MDCT histograms for doubly compressed file with decreasing bit-rate and simulated singly compressed file.

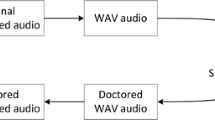
According to the previous analysis, an algorithm composed by the processing blocks illustrated in Figure4 has been derived: the MP3 file to be analyzed is decompressed obtaining a sequence of PCM samples. Next, the Trimming removes a given number of PCM samples starting from the beginning of the PCM sequence in such a way that the trimmed sequence is no more aligned with the MP3 frame borders. The Filterbank + MDCT block takes the PCM samples and applies filtering and the MDCT transform, achieving a set of unquantized MDCT coefficients. The steps of trimming and recompression allow to remove possible double quantization artifacts, while maintaining the original characteristics of the signal. The Parameter extraction allows to extract from the original MP3 bitstream the quantization parameters, i.e., the quantization pattern and the original quantization values. This information is needed by the Re-quantizer to simulate a distribution of MDCT coefficients that have undergone only a single compression. In addition, the Re-quantizer smooths the sequence of simulated coefficients through a Laplace Smoothing[13], a technique used to smooth categorical data (in particular, the smoothing parameter α equal to 1 was adopted). This operation aims at filling possible empty bins present in the data histogram and thus avoiding numerical errors in the following computations. The original quantized values and the simulated singly quantized values are then compared through the Histograms distances block.

Figure 4

Scheme of the proposed method.

Indicating with X and Y respectively the observed and the simulated distributions of MDCT coefficients, their histograms are built, and a similarity measure is computed. Among the possible measures that can be used to compute the distance between two histograms, we adopted the chi-square distance D _χ (X,Y)[14], defined as:

$$D_{\chi }(X,Y)=\sum _{i=1}^N\frac{{\left(X_i-Y_i\right)}^2}{2\left(X_i+Y_i\right)}$$

(1)

where N is the number of bins of the histograms.

The computed distance measure represents the feature the proposed method uses to detect whether a MP3 file has been singly or doubly compressed.

The proposed feature (as it will be shown in Section 4) is able to provide additional information about the compression suffered by the analyzed MP3 file, in particular concerning the difference between the second and the first bit-rate (Δ = BR 2 - BR 1): when such a value is positive the proposed algorithm is able to classify doubly compressed MP3 audio tracks with respect to the first compression bit-rate. In fact, the values assumed by the feature range quite differently according to the second bit-rate and the Δ factor, thus allowing to cluster doubly compressed MP3 audio tracks by applying a nearest neighbour classifier.

3 Application to tampering localization

Knowledge about double encoding of an MP3 track can also provide evidence of local tampering. Let us assume that a part of an MP3 track has been edited in such a way as to alter the original audio recording. It is reasonable to assume that the editing operation will also remove the features due to MP3 compression. If such a track is recompressed in MP3 format, then the original part will exhibit the typical artifacts of double compression, whereas the edited part will be very similar to a singly compressed track. A similar behavior can be expected also when a portion of an audio track is deleted: with a very high probability, such a deletion will introduce a desynchronization of the audio frames; hence, in case of recompression, the audio frames up to the deletion point will be doubly compressed, whereas the audio frames after the deletion point will appear as singly compressed ones.In order to use the proposed feature for tampering localization, a natural strategy is to divide the analyzed audio track into several short segments and to compute a different value of the feature for each segment. In the presence of a genuine audio track, the feature is expected to have similar values on all audio segments. Conversely, in the presence of tampering, the segments corresponding to the manipulated part will have different values of the feature with respect to the original part. In particular, according to the above tampering model, we will assume that a tampered part is characterized by a lower value of the feature, corresponding to singly compressed audio tracks. An example of this behavior is visible in Figure5, where we show the values of the proposed feature, analyzed by using audio segments 1/8 s long, for a genuine audio track, where all segments are singly compressed (top), and an audio track where the central part has been edited and recompressed (bottom). Since the editing operation removes the features due to compression, then the original segments exhibit the artifacts of double compression, whereas the edited ones are similar to a singly compressed track.

Figure 5

Feature values over temporal windows for a genuine file and a tampered file.

In the following, we propose a simple automatic procedure to localize the manipulated parts in possibly tampered MP3 tracks. The first step is to divide the to be analyzed track into several audio segments and to compute the value of the feature for each segment. The set of values obtained in such a way are then clustered using the expectation maximization (EM) algorithm[15]. Namely, we will assume that the distribution of the proposed feature can be modelled as a mixture of two approximately Gaussian components, corresponding to the original part and the tampered part. The EM algorithm will produce two clusters of feature values characterized by the respective cluster centers, D₁ and D₂, corresponding to the mean value of the Gaussian component representing each cluster.

Let us assume, without loss of generality, that the cluster centers satisfy D₂ > D₁. According to the previous analysis, a given audio track will be classified as tampered if the EM algorithm finds two nonempty clusters. Furthermore, when a track is classified as tampered, the audio segments belonging to the cluster with the lower mean, i.e., D₁, will reveal the position of the tampered part.The rationale of the proposed approach is evident by looking at Figure6, showing the distributions of the feature values for an original (top) audio track and a tampered audio track (bottom), where the different colors highlight the two Gaussian components found by the EM algorithm. In the case of a genuine MP3 track, all the values of the feature will be similar, so that the EM algorithm will usually find a single cluster. Conversely, in the case of a tampered MP3 track, the values of the feature form two distinct clusters, corresponding to the original part and the manipulated part, which are well separated by the EM algorithm.

Figure 6

Histogram of feature values on a genuine file and a tampered file.

4 Experimental results

To validate the ideas proposed in the previous section, an audio dataset has been built, trying to represent as much as possible heterogeneous sources. To this aim, the database includes uncompressed audio files belonging to four different categories: Music, royalty free music audio tracks, with five different musical styles[16]; Speech, music audio files containing dialogues; Outdoor, audio files relative to recording outdoors; and Commercial, files containing dialogues combined with music, as often happens in advertising. Each category collects about 17 min of audio. Throughout all the experiments, we employed the latest release of the lame codec (available athttp://lame.sourceforge.net), namely version 3.99.5. This choice was motivated by the widespread adoption of this codec and by the fact that it is an open source project.

4.1 Double compression detection and first compression bit-rate classification

In order to evaluate the performance of our method in detecting double compression, we divided each audio file into 250 segments 4 s long, for a total of 1,000 uncompressed audio files. Each file has been compressed, in dual mono, with bit-rate BR1 chosen in [64, 96, 128, 160, 192] kbit/s, obtaining 5,000 singly compressed MP3 files. Finally, these files have been compressed again using as BR2 one of the previous bit-rate values (also the same value as the first one was considered) achieving 25,000 MP3 doubly compressed files. Among these, 10,000 files have a difference Δ = BR2-BR1 between the second and the first bit-rate which is positive, taking value in [32, 64, 96, 128] kbit/s; 10,000 files have a negative difference Δ taking value in [-128, -96, -64, -32] kbit/s and 5,000 files have Δ = 0. The overall dataset is thus composed by 30,000 MP3 files, including 5,000 singly compressed files.

As a first experiment, we computed the values assumed by the proposed feature for all the 30,000 files belonging to the test dataset. The chi-square distance has been calculated by evaluating the MDCT histograms on 2,000 bins, with step size equal to one. In Figure7, the chi-square distances are visualized: singly compressed files and doubly compressed files with negative or zero Δ show a distance D near to zero, whereas the other files have D rather higher than zero. By comparing D with a threshold τ, it is possible to discriminate these two kinds of files: doubly compressed files with Δ > 0 and the other ones.

Figure 7

Chi-square distances computed for the 30,000 audio segments composing the dataset.

By adopting a variable threshold τ, we then computed a receiver operating characteristic (ROC) curve, representing the capacity of the detector to separate singly compressed from doubly compressed MP3 files (including Δ > or ≤ 0). The trend of the obtained ROC curve is shown in Figure8 (left): it reflects the bimodal distribution of distances of doubly compressed files (blue and green colored in Figure7) and highlights that the detector is able to distinguish only one of the two components (the one with Δ > 0). If we separate the previous ROC in one relating to files doubly compressed with positive Δ and one to files doubly compressed with negative or zero Δ, as is shown in Figure8 (right), when doubly compressed files with positive Δ are considered, we obtain an almost perfect classifier, while when the cases with negative or zero Δ are analyzed, we are next to the random classifier.

Figure 8

ROC curve. ROC curve obtained by varying the threshold τ of the classifier (left). Separation of cases with positive Δ and negative or zero Δ (right).

As anticipated in Section 2, the distance representing the proposed feature assumes a large range of values, as it can be clearly observed in Figure7. In order to highlight the relationship between the values taken by the feature and the compression parameters (i.e., BR2 and Δ), we examined in more detail the 10,000 doubly compressed files with positive Δ, plotting their chi-square distances in Figure9. Such values were plotted according to the different Δ: in particular, there are 4,000 files with Δ = 32 (yellow), 3,000 files with Δ = 64 (violet), 2,000 files with Δ = 96 (sky-blue), and finally 1,000 files with Δ = 128 (black) and grouped for different BR2: [96, 128, 160, 192]. Figure9 shows that the values of chi-square distance tend to cluster for different Δ factors and different BR2 values (see plotting with same color). On the one hand, the increasing Δ values correspond to increasing Chi-square distances between the observed and simulated distribution. On the other hand, given a value of Δ, for different bit-rate of the second compression, slightly different values of distance are obtained. This suggests the possibility of optimizing the detector by considering a specific threshold for each bit-rate of the second compression (a parameter observable from the bitstream). Moreover, the different values of the feature for different Δ factors can be used to classify the bit-rate of the first compression, as detailed in the following sections.

Figure 9

Chi-square distances computed for doubly compressed files with positive Δ.

As to detection, we performed a set of experiments in order to compare the detection accuracy of the proposed scheme with respect to the detection accuracy of the methods proposed in[3, 4] by Liu et al. (LSQ method) and in[2] by Yang et al. (YSH method). Corresponding results are shown in Tables1,2, and3 respectively. The classifiers have been trained on 80% of the dataset and tested on the remaining 20%. Results have been averaged over 20 independent trials. In our method, different thresholds have been employed for different BR2 values, while for the other methods, different SVMs have been trained for different BR2 values. The proposed method achieves nearly optimal performances for all combinations with Δ>0. Also, the other methods generally achieve good performances for Δ>0, especially the LSQ method. Conversely, for Δ<0, the proposed method is not able to reliably detect double MP3 compression, whereas the other methods have better performances.

Table 1 Detection accuracy of the proposed method for different bit-rates

Table 2 Detection accuracy of LSQ method for different bit-rates

Table 3 Detection accuracy of YSH method for different bit-rates

All the results shown in Tables1,2, and3 have been achieved considering audio tracks 4 s long. We evaluated the degradation of the performance of the three detectors when the duration of the audio segments is reduced from 4 s to [2, 1, 1/2, 1/4, 1/8, 1/16] s. The reason behind this experiment is that analyzing very small portions of audio potentially opens the door to fine-resolution splicing localization (i.e., detect if part of an audio file has been tampered). Practically, instead of taking all the MDCT coefficients of the 4-s long segment, only the coefficients belonging to a subpart of the segment are retained, where the subpart is just one half, one fourth, and so on. For BR2 = 192 kbit/s and BR2 = 128 kbit/s, the detection accuracies (averaged with respect to BR1) have been plotted with varying audio file duration in Figure10 for our method, the LSQ method, and the YSH method.

Figure 10

Detection accuracy with varying audio file duration for BR2 = 192 kbit/s and BR2 = 128 kbit/s.

The proposed method and LSQ achieve a nearly constant detection performance up to 1/8-s audio segments, whereas the performance of the YSH method drops for audio segments under 2 s. Our method achieves very good performance in the case of high-quality MP3 files: indeed, for BR2 equal to 192 kbit/s, our method achieves an almost perfect classification performance irrespective of the audio segment duration. Conversely, For BR2 equal to 128 kbit/s, even if the performance is only slightly affected by the segment duration, the proposed method remains inferior with respect to the other two methods.

By taking into account the feature distribution highlighted in Figure9, we then considered the capability of the proposed feature to classify the doubly compressed file according to the first compression bit-rate, as BR1 = BR2- Δ. A nearest neighbour classifier has been adopted for each different BR2 and the corresponding classification accuracy results are shown in Table4 for BR2 = 192 kbit/s and Table5 for BR2 = 128 kbit/s. The rows of the tables represent the actual bit-rate of the first compression and the columns the values assigned by the classifier. A comment about this experiment is in order: as shown in the previous section, the proposed method will hardly detect double compression for negative or zero Δ. Similarly, the output of the classifier on doubly encoded files with negative or zero Δ is not reliable. In particular, since a singly compressed file can be considered like having undergone a (virtual) first compression at infinite quality, the classifier cannot distinguish between singly encoded files and doubly encoded files with negative Δ.

Table 4 Classification accuracy of the proposed method for BR2 = 192

Table 5 Classification accuracy of the proposed method for BR2 = 128

For comparison, only the LSQ method is considered since the YSH method was not proposed for compression classification. The corresponding results obtained on 4-s audio segments for BR2 = 192, 128 kbit/s are shown in Tables6 and7, respectively.As in the case of detection, we experimented how the classification performances vary with respect to audio file duration. The average classification accuracy for different BR2 (i.e., [192, 160, 128, 96, 64] kbit/s) and decreased audio file duration (i.e., [4, 2, 1, 1/2, 1/4, 1/8, 1/16] s) are shown in Figure11 for both our method (top) and LSQ method (bottom). The accuracy is averaged over every possible BR1 in the dataset, thus providing a fair overall index of classification accuracy, that can be used to compare different methods and show a clear performance trend for different audio segment lengths.

Table 6 Classification accuracy of LSQ method for BR2 = 192

Table 7 Classification accuracy of LSQ method for BR2 = 128

Figure 11

Accuracy of the proposed and LSQ classifiers with varying audio file duration.

In this scenario, LSQ appears to have a better classification performance, even if the proposed method performs reasonably well for the higher bit-rates. It is also worth noting that the performances of both methods suffer only a slight degradation for the shorter audio segments, which suggests good localization capabilities.

4.2 Tampering localization

As explained in Section 3, the proposed method for double compression analysis can be used as a tool for audio forgery localization. Although this possibility was not considered in the respective papers, previous experiments seem to prove that also the methods YSH and LSQ can be used for such a task, by analyzing the track using small windows. We thus designed a set of experiments to test the applicability of each of the considered algorithms to forgery localization: we divided the uncompressed files mentioned at the beginning of this section in segments of 10 s each, obtaining 100 files. Among these, 60 were chosen at random to build a training set, while the rest were used as the test set. Since the goal is to localize tampered segments within a file, test files were created as follows:

• 1. The file was MP3 compressed at a bit-rate BR1 ∈ {96, 128, 160} kbit/s.

• 2. The file was decoded and a portion of 1 s, located at the center of the track, was replaced with the same-positioned samples coming from the uncompressed file.

• 3. The resulting track was re-compressed at a bit-rate BR1 + Δ, with Δ taking values in {-32, 0, 32} kbit/s.

In such a way, we created a cut-and-paste tampering that is virtually undetectable by a human listener (the pasted content is the same, just without the first compression); this also avoids facilitating the detector by introducing abrupt changes in audio content.

The above procedure creates files where 1/10 of the track is tampered, and the rest is untouched. While this scenario is reasonable for testing localization capabilities, it does not fit well to training a classifier (needed for methods YSH and LSQ), where a more balanced distribution of positive and negative examples is preferable. Keeping in mind that each file will be analyzed using small windows, and that each window will be classified as singly or doubly encoded, we generated the training dataset as follows:

• 1. The file was MP3 compressed at a bit-rate BR1 ∈ {96, 128, 160} kbit/s.

• 2. The file was decoded and the part of the track between second 5 and 6 was cut and appended at the end of the file.

• 3. The resulting track was re-compressed at a bit-rate BR1 + Δ, with Δ taking values in {-32, 0, 32} kbit/s.

In such a way, samples in the first half of the track will show traces of double encoding, while samples in the second half will not, due to the induced misalignment of the quantization pattern.

Similarly to what we did in previous experiments, it is of interest to evaluate the localization performance of each algorithm for different sizes of the analysis window: a smaller size causes noisier measurements but higher temporal resolution, allowing the analyst to detect subtle modifications, like turning into a voice recording a word ‘yes’ into a ‘no’. The set {1/4, 1/8, 1/16} s was then chosen as possible values for the size of the window. When analyzing a file, the analyst knows both the size of the window he wants to employ and the bit-rate of the last compression undergone by the file. In light of this, the training procedure for algorithms LSQ and YSH can be done separately, creating a SVM for each BR2 (in our case, BR2 ∈{64,96,128,160,192}) and for each size of the analysis window. We chose RBF kernels and used fivefold cross validation to determine the best values for C ∈ {2³,2⁴,…2¹²} and γ ∈ {2^-4,2^-3,…,2⁵}. Concerning the proposed algorithm, we used the training samples to get a good initialization point for the expectation-maximization algorithm: specifically, we computed the average value of the χ² distance obtained for singly compressed sequences and doubly compressed sequences available in the training set, resulting in μ₁ = 0.004 and μ₂ = 0.015, respectively. The algorithm stops when either the log likelihood stabilizes (difference between two iterations lower than 10^-15) or a maximum of 500 iterations is reached.

Performance of YSH and LSQ algorithms were evaluated as follows: given a test file, the proper SVM was selected based on the observed bit-rate and the chosen window size; then the file was decoded and coefficients were classified, moving the analysis window. After repeating the same approach for all the files, we computed the probability of correctly classifying a window as tampered, denoted by Pr(T) and the probability of correctly classifying a window as original, denoted by Pr(O). Since by using probabilities we are normalizing the different size of each class, the final accuracy can be simply calculated as

$$\text{ACC}=\frac{\text{Pr}\left(O\right)+\text{Pr}\left(T\right)}{2}.$$

A similar approach was used to evaluate performance of the proposed algorithm. After executing the EM algorithm, if a mixture of two Gaussians was found, we labelled as tampered those windows belonging to the model with lower mean; if only one Gaussian component was found, all the windows were classified as untouched. Finally, the localization accuracy of the algorithm was computed with the same formula described above.

Results are reported in Table8, for different sizes of the analysis window. Results are separated according to the difference between the first and second compression bit-rate (main rows), while the final value of BR2 is given in the columns (this is the only information available to the analyst). Since possible values for BR1 were limited to be in {96, 128, 160}, some combinations of BR2 and Δ are not explored. As we can see, the proposed algorithm yields comparable performance to the method YSH and outperforms LSQ when BR2 is higher than BR1. For zero or negative Δs, coherently with previous results, the proposed model is not able to discriminate forged regions.

Table 8 Tampering localization accuracy obtained by each algorithm for different window sizes

5 Conclusions

In this paper, a method to localize the presence of double compression artifacts in a MP3 audio file has been presented, with the aim of uncovering possibly tampered parts. We proposed an algorithm based on a simple statistical feature measuring the effect of double compression that allows to decide whether a MP3 file is singly compressed or it has been doubly compressed and also to derive the bit-rate of the first compression. In addition, the proposed scheme as well as two state-of-the-art methods designed for detecting doubly compressed MP3 files have been applied to analyze short temporal windows, in such a way to allow the localization of tampered portions in the MP3 file under analysis.

The proposed algorithm is very effective when the bit-rate of the second compression is higher than the bit-rate of the first one but offers limited performance in the opposite case, where it is outperformed by state-of-the-art methods, based on SVM classifiers. On the other hand, we must keep in mind that the proposed approach does not exploit machine learning techniques, as the previous schemes did, so that its performance is less affected than other methods by the choice of a suitable training set.

In our opinion, the main contribution of the paper regards the tampering localization scenario. To the best of our knowledge, this is the first time that techniques used for detecting double compression in MP3 audio files are used in this kind of scenario. We also point out that the authors in[3, 4] and[2] did not investigate how their methods would perform on very short audio segments. The results provide some interesting insights. For example, we see that more complex features, which achieve very good results in the simple detection scenario, may not be well suited for the localization scenario. This is evident in the performance of LSQ features for localization, which is sensibly lower than the performance achieved in the simple detection scenario. We believe that this is due to the difficulty of providing a good training set for the localization scenario, which negatively affects methods based on machine learning. Moreover, we also see that in the high-quality scenario, a simple feature based on calibration may obtain a performance very close to that of state-of-the-art features, without requiring a SVM.

There are some interesting issues that can be considered for further research. For example, the detection and localization accuracies of the different algorithms may be affected by the actual codec(s) used in the first and second compressions. Since the proposed feature is based on a simple histogram distance, we believe that different encoder/decoders should not affect much the performance. Nevertheless, more complex features may be affected by the encoder, especially if the detector is trained on a different encoder that the one actually used. Another aspect is the use of a variable bit-rate (VBR) encoding strategy: since the proposed approach does not consider the MDCT coefficients according to the different quantization factors, but compute global histograms, we think that the different quantization factors induced by VBR will not affect significantly the proposed approach. However, we leave analysis of VBR to future work.