Universal distortion function for steganography in an arbitrary domain

Abstract

Currently, the most successful approach to steganography in empirical objects, such as digital media, is to embed the payload while minimizing a suitably defined distortion function. The design of the distortion is essentially the only task left to the steganographer since efficient practical codes exist that embed near the payload-distortion bound. The practitioner’s goal is to design the distortion to obtain a scheme with a high empirical statistical detectability. In this paper, we propose a universal distortion design called universal wavelet relative distortion (UNIWARD) that can be applied for embedding in an arbitrary domain. The embedding distortion is computed as a sum of relative changes of coefficients in a directional filter bank decomposition of the cover image. The directionality forces the embedding changes to such parts of the cover object that are difficult to model in multiple directions, such as textures or noisy regions, while avoiding smooth regions or clean edges. We demonstrate experimentally using rich models as well as targeted attacks that steganographic methods built using UNIWARD match or outperform the current state of the art in the spatial domain, JPEG domain, and side-informed JPEG domain.

1 Introduction

Designing steganographic algorithms for empirical cover sources[1] is very challenging due to the fundamental lack of accurate models. The most successful approach today avoids estimating (and preserving) the cover source distribution because this task is infeasible for complex and highly non-stationary sources, such as digital images. Instead, message embedding is formulated as source coding with a fidelity constraint[2] - the sender hides her message while minimizing an embedding distortion. Practical embedding algorithms that operate near the theoretical payload-distortion bound are available for a rather general class of distortion functions[3, 4].

The key element of this general framework is the distortion, which needs to be designed in such a way that tests on real imagery indicate a high level of security^a. In[5], a heuristically defined distortion function was parametrized and then optimized to obtain the smallest detectability in terms of a margin between classes within a selected feature space (cover model). However, unless the cover model is a complete statistical descriptor of the empirical source, such optimized schemes may, paradoxically, end up being more detectable if the warden designs the detector ‘outside of the model’[6, 7], which brings us back to the main and rather difficult problem - modeling the source.

In the JPEG domain, by far the most successful paradigm is to minimize the rounding distortion with respect to the raw, uncompressed image, if available[8–12]. In fact, this ‘side-informed embedding’ can be applied whenever the sender possesses a higher-quality ‘precover’^b that is quantized to obtain the cover^c. Currently, the most secure embedding method for JPEG images that does not use any side information is the uniform embedding distortion (UED)[13] that substantially improved upon the nsF5 algorithm[14] - the previous state of the art. Note that most embedding algorithms for the JPEG format use only non-zero DCT coefficients, which makes them naturally content-adaptive.

In the spatial domain, embedding costs are typically required to be low in complex textures or ‘noisy’ areas and high in smooth regions. For example, HUGO[15] defines the distortion as a weighted norm between higher-order statistics of pixel differences in cover and stego images[16], with high weights assigned to well-populated bins and low weights to sparsely populated bins that correspond to more complex content. An alternative model-free approach called wavelet obtained weights (WOW)[17] uses a bank of directional high-pass filters to obtain the so-called directional residuals, which assess the content around each pixel along multiple different directions. By measuring the impact of embedding on every directional residual and by suitably aggregating these impacts, WOW forces the distortion to be high where the content is predictable in at least one direction (smooth areas and clean edges) and low where the content is unpredictable in every direction (as in textures). The resulting algorithm is highly adaptive and has been shown to better resists steganalysis using rich models[18] than HUGO[17].

The distortion function proposed in this paper bears similarity to that of WOW but is simpler and suitable for embedding in an arbitrary domain. Since the distortion is in the form of a sum of relative changes between the stego and cover images represented in the wavelet domain, hence its name universal wavelet relative distortion (UNIWARD).

After introducing the basic notation and terminology in Section 2, we describe the distortion function in its most general form in Section 3 - one suitable for embedding in both the spatial and JPEG domains and the other for side-informed JPEG steganography. We also describe the additive approximation of UNIWARD that will be exclusively used in this paper. In Section 4, we introduce the common core of all experiments - the cover source, steganalysis features, the classifier used to build the detectors, and the empirical measure of security. A study of the best settings for UNIWARD, formed by the choice of the directional filter bank and a stabilizing constant, appears in Section 5. Section 6 contains the results of all experiments in the spatial, JPEG, and side-informed JPEG domains as well as the comparison with previous art. The security is measured empirically using classifiers trained with rich media models on a range of payloads and quality factors. The paper is concluded in Section 7.

This paper is an extended and adjusted version of an article presented at the First ACM Information Hiding and Multimedia Security Workshop in Montpellier in June 2013[19].

2 Preliminaries

2.1 Notation

Capital and lowercase boldface symbols stand for matrices and vectors, respectively. The symbols\mathbf{X}=(X_{\mathit{\text{ij}}}),\mathbf{Y}=(Y_{\mathit{\text{ij}}})\in {\mathcal{I}}^{n_1\times n_2} will always be used for a cover (and the corresponding stego) image with n₁ × n₂ elements attaining values in a finite set. The image elements will be either 8-bit pixel values, in which case\mathcal{I}=\{0,\dots ,255\}, or quantized JPEG DCT coefficients,\mathcal{I}=\{-1,024,\dots ,1,023\}, arranged into an n₁ × n₂ matrix by replacing each 8 × 8 pixel block with the corresponding block of quantized coefficients. For simplicity and without loss on generality, we will assume that n₁ and n₂ are multiples of 8.

For side-informed JPEG steganography, a precover (raw, uncompressed) image will be denoted as\mathbf{P}=(P_{\mathit{\text{ij}}})\in {\mathcal{I}}^{n_1\times n_2}. When compressing P, first a blockwise DCT transform is executed for each 8 × 8 block of pixels from a fixed grid. Then, the DCT coefficients are divided by quantization steps and rounded to integers. Let P^(b) be the b th 8 × 8 block when ordering the blocks, e.g., in a row-by-row fashion (b = 1,…,n₁ · n₂/64). With a luminance quantization matrix Q = {q _kl }, 1 ≤ k,l ≤ 8, we denote D^(b) = DCT(P^(b))./Q the raw (non-rounded) values of DCT coefficients. Here, the operation ^′./^′ is an elementwise division of matrices and DCT(.) is the DCT transform used in the JPEG compressor. Furthermore, we denote X^(b) = [D^(b)] the quantized DCT coefficients rounded to integers. We use the symbols D and X to denote the arrays of all raw and quantized DCT coefficients when arranging all blocks D^(b) and X^(b) in the same manner as the 8 × 8 pixel blocks in the uncompressed image. We will use the symbol J^-1(X) for the JPEG image represented using quantized DCT coefficients X when decompressed to the spatial domain^d.

For matrix A, A^T is its transpose, and |A| = (|a _ij |) is the matrix of absolute values. The indices i,j will be used solely to index pixels or DCT coefficients, while u,v will be exclusively used to index coefficients in a wavelet decomposition.

2.2 DCT transform

We would like to point out that the JPEG format allows several different implementations of the DCT transform, DCT(.). The specific choice of the transform implementation may especially impact the security of side-informed steganography. In this paper, we work with the DCT(.) implemented as ‘dct2’ in Matlab when feeding in pixels represented as ‘double’. In particular, a block of 8 × 8 DCT coefficients is computed from a precover block P^(b) as

\begin{array}{ll}\text{DCT}{({\mathbf{P}}^{(b)})}_{\mathit{\text{kl}}}& =\sum _{i,j=0}^7\frac{w_k{w}_l}{4}cos\frac{\pi k(2i+1)}{16}\\ \times cos\frac{\pi l(2j+1)}{16}{P}_{\mathit{\text{ij}}}^{(b)},\end{array}

(1)

where k,l ∈ {0,…,7} index the DCT mode andw_0=1/\sqrt{2}, w _k  = 1 for k > 0.

To obtain an actual JPEG image from a two-dimensional array of quantized coefficients X (cover) or Y (stego), we first create an (arbitrary) JPEG image of the same dimensions n₁ × n₂ using Matlab’s ‘imwrite’ with the same quality factor, read its JPEG structure using Sallee’s Matlab JPEG Toolbox (http://dde.binghamton.edu/download/jpeg_toolbox.zip) and then merely replace the array of quantized coefficients in this structure with X and Y to obtain the cover and stego images, respectively. This way, we guarantee that both images were created using the same JPEG compressor and that all that we will be detecting are the embedding changes rather than compressor artifacts.

3 Universal distortion function UNIWARD

In this section, we provide a general description of the proposed universal distortion function UNIWARD and explain how it can be used to embed in the JPEG and the side-informed JPEG domains. The distortion depends on the choice of a directional filter bank and one scalar parameter whose purpose is stabilizing the numerical computations. The distortion design is finished in Section 5, which investigates the effect of the filter bank and the stabilizing constant on empirical security.

Since rich models[18, 20–22] currently used in steganalysis are capable of detecting changes along ‘clean edges’ that can be well fitted using locally polynomial models, whenever possible the embedding algorithm should embed into textured/noisy areas that are not easily modellable in any direction. We quantify this using outputs of a directional filter bank and construct the distortion function in this manner.

3.1 Directional filter bank

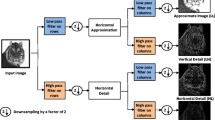
By a directional filter bank, we understand a set of three linear shift-invariant filters represented with their kernels\mathcal{B}=\{{\mathbf{K}}^{(1)},{\mathbf{K}}^{(2)},{\mathbf{K}}^{(3)}\}. They are used to evaluate the smoothness of a given image X along the horizontal, vertical, and diagonal directions by computing the so-called directional residuals W^(k) = K^(k) ⋆ X, where ‘ ⋆’ is a mirror-padded convolution so that W^(k) has again n₁ × n₂ elements. The mirror padding prevents introducing embedding artifacts at the image boundary.

While it is possible to use arbitrary filter banks, we will exclusively use kernels built from one-dimensional low-pass (and high-pass) wavelet decomposition filters h (and g):

{\mathbf{K}}^{(1)}=\mathbf{h}·{\mathbf{g}}^{\mathrm{T}},{\mathbf{K}}^{(2)}=\mathbf{g}·{\mathbf{h}}^{\mathrm{T}},{\mathbf{K}}^{(3)}=\mathbf{g}·{\mathbf{g}}^{\mathrm{T}}.

(2)

In this case, the filters correspond, respectively, to two-dimensional LH, HL, and HH wavelet directional high-pass filters, and the residuals coincide with the first-level undecimated wavelet LH, HL, and HH directional decomposition of X. We constrained ourselves to wavelet filter banks because wavelet representations are known to provide good decorrelation and energy compactification for images of natural scenes (see, e.g., Chapter 7 in[23]).

3.2 Distortion function (non-side-informed embedding)

We are now ready to describe the universal distortion function. We do so first for embedding that does not use any precover. Given a pair of cover and stego images, X and Y, represented in the spatial (pixel) domain, we will denote withW_{\mathit{\text{uv}}}^{(k)}(\mathbf{X}) andW_{\mathit{\text{uv}}}^{(k)}(\mathbf{Y}), k = 1,2,3, u ∈ {1,…,n₁}, v ∈ {1,…,n₂}, their corresponding uv th wavelet coefficient in the k th subband of the first decomposition level. The UNIWARD distortion function is the sum of relative changes of all wavelet coefficients with respect to the cover image:

D(\mathbf{X},\mathbf{Y})\triangleq \sum _{k=1}^3\sum _{u=1}^{n_1}\sum _{v=1}^{n_2}\frac{|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{X})-W_{\mathit{\text{uv}}}^{(k)}(\mathbf{Y})|}{\sigma +|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{X})|},

(3)

where σ > 0 is a constant stabilizing the numerical calculations.

The ratio in (3) is smaller when a large cover wavelet coefficient is changed (where texture and edges appear). Embedding changes are discouraged in regions where|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{X})| is small for at least one k, which corresponds to a direction along which the content is modellable.

For JPEG images, the distortion between the two arrays of quantized DCT coefficients, X and Y, is computed by first decompressing the JPEG files to the spatial domain, and evaluating the distortion between the decompressed images, J^-1(X) and J^-1(Y), in the same manner as in (3):

D(\mathbf{X},\mathbf{Y})\triangleq D\left(J^{-1}(\mathbf{X}),J^{-1}(\mathbf{Y})\right).

(4)

Note that the distortion (3) is non-additive because changing pixel X _ij will affect s × s wavelet coefficients, where s × s is the size of the 2D wavelet support. Also, changing a JPEG coefficient X _ij will affect a block of 8×8 pixels and therefore a block of (8 + s - 1) × (8 + s - 1) wavelet coefficients. It is thus apparent that when changing neighboring pixels (or DCT coefficients), the embedding changes ‘interact,’ hence the non-additivity of D.

3.3 Distortion function (JPEG side-informed embedding)

By side-informed embedding in JPEG domain, we understand the following general principle. Given the raw DCT coefficient D _ij obtained from the precover P, the embedder has the choice of rounding D _ij up or down to modulate its parity (usually the least significant bit of the rounded value). We denote with e _ij  = |D _ij  - X _ij |, e _ij  ∈ [0,0.5], the rounding error for the ij th coefficient when compressing the precover P to the cover image X. Rounding ‘to the other side’ leads to an embedding change, Y _ij  = X _ij  + sign(D _ij  - X _ij ), which corresponds to a ‘rounding error’ 1 - e _ij . Thus, every embedding change increases the distortion with respect to the precover by the difference between both rounding errors: |D _ij  - Y _ij | - |D _ij -X _ij | = 1 - 2e _ij . For the side-informed embedding in JPEG domain, we therefore define the distortion as the difference:

\begin{array}{l}{D}^{(\text{SI})}(\mathbf{X},\mathbf{Y})\triangleq D\left(\mathbf{P},J^{-1}(\mathbf{Y})\right)-D\left(\mathbf{P},J^{-1}(\mathbf{X})\right)\\ =\sum _{k=1}^3\sum _{u=1}^{n_1}\sum _{v=1}^{n_2}\left[\frac{|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{P})-W_{\mathit{\text{uv}}}^{(k)}\left(J^{-1}(\mathbf{Y})\right)|}{\sigma +|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{P})|}\right.\\ -\left.\frac{|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{P})-W_{\mathit{\text{uv}}}^{(k)}\left(J^{-1}(\mathbf{X})\right)|}{\sigma +|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{P})|}\right].\end{array}

(5)

Note that the linearity of DCT and the wavelet transforms guarantee that D^(SI)(X,Y) ≥ 0. This is because rounding a DCT coefficient (to obtain X) corresponds to adding a certain pattern (that depends on the modified DCT mode) in the wavelet domain. Rounding to the other side (to obtain Y) corresponds to subtracting the same pattern but with a larger amplitude. This is why|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{P})-W_{\mathit{\text{uv}}}^{(k)}(J^{-1}(\mathbf{Y}))|-|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{P})-W_{\mathit{\text{uv}}}^{(k)}(J^{-1}(\mathbf{X}))|\ge 0 for all k,u,v.

We note at this point that (5) bears some similarity to the distortion used in Normalized Perturbed Quantization (NPQ)[11, 12], where the authors also proposed the distortion as a relative change of cover DCT coefficients. The main difference is that we compute the distortion using a directional filter bank, allowing thus directional sensitivity and potentially better content adaptability. Furthermore, we do not eliminate DCT coefficients that are zeros in the cover. Finally, and most importantly, in contrast to NPQ, our design naturally incorporates the effect of the quantization step because the wavelet coefficients are computed from the decompressed JPEG image.

3.3.1 Technical issues with zero embedding costs

When running experiments with any side-informed JPEG steganography in which the embedding cost is zero, when e _ij  = 1/2, we discovered a technical problem that, to the best knowledge of the authors, has not been disclosed elsewhere. The problem is connected to the fact that when e _ij  = 1/2 the cost of rounding D _ij ‘down’ instead of ‘up’ should not be zero because, after all, this does constitute an embedding change. This does not affect the security much when the number of such DCT coefficients is small. With an increasing number of coefficients with e _ij  = 1/2 (we will call them 1/2-coefficients), however, 1-2e _ij is no longer a good measure of statistical detectability and one starts observing a rather pathological behavior - with payload approaching zero, the detection error does not saturate at 50% (random guessing) but rather at a lower value and only reaches 50% for payloads nearly equal to zero^e. The strength with which this phenomenon manifests depends on how many 1/2-coefficients are in the image, which in turn depends on two factors - the implementation of the DCT used to compute the costs and the JPEG quality factor. When using the slow DCT (implemented using ‘dct2’ in Matlab), the number 1/2-coefficients is small and does not affect security at least for low-quality factors. However, in the fast-integer implementation of DCT (e.g., Matlab’s imwrite), all D _ij are multiples of 1/8. Thus, with decreasing quantization step (increasing JPEG quality factor), the number of 1/2-coefficients increases.

To avoid dealing with this issue in this paper, we used the slow DCT implemented using Matlab’s dct2 as explained in Section 2.2 to obtain the costs. Even with the slow DCT, however, 1/2-coefficients do cause problems when the quality factor is high. As one can easily verify from the formula for the DCT (1), when k,l ∈ {0,4}, the value of D _kl is always a rational number because the cosines are either 1 or\sqrt{2}/2, which, together with the multiplicative weights w, gives again a rational number. In particular, the DC coefficient (mode 00) is always a multiple of 1/4, the coefficients of modes 04 and 40 are multiples of 1/8, and the coefficients corresponding to mode 44 are multiples of 1/16. For all other combinations of k,l ∈ {0,…,7}, D _ij is an irrational number. In practice, any embedding whose costs are zero for 1/2-coefficients will thus strongly prefer these four DCT modes, causing a highly uneven distribution of embedding changes among the DCT coefficients. Because rich JPEG models[24] utilize statistics collected for each mode separately, they are capable of detecting this statistical peculiarity even at low payloads. This problem becomes more serious with increasing quality factor.

These above embedding artifacts can be largely suppressed by prohibiting embedding changes in all 1/2-coefficients in modes 00, 04, 40, and 44^f. In Figure1, where we show the comparison of various side-informed embedding methods for quality factor 95, we intentionally included the detection errors for all tested schemes where this measure was not enforced to prove the validity of the above arguments.

Figure 1

Comparison of various side-informed embedding methods. Detection error E_OOB for SI-UNIWARD and four other methods with the union of SRMQ1 and JRM and the ensemble classifier for JPEG quality factors 75, 85, and 95. The dashed lines in the graph for QF 95 correspond to the case when all the embedding methods use all coefficients, including the DCT modes 00, 04, 40, and 44 independently of the value of the rounding error e _ij .

The solution of the problem with 1/2-coefficients, which is clearly not optimal, is related to the more fundamental problem, which is how exactly the side information in the form of an uncompressed image should be utilized for the design of steganographic distortion functions. The authors postpone a detailed study of this quite intriguing problem to a separate paper.

3.4 Additive approximation of UNIWARD

Any distortion function D(X,Y) can be used for embedding in its additive approximation[4] using D to compute the cost ρ _ij of changing each pixel/DCT coefficient X _ij . A significant advantage of using an additive approximation is the simplicity of the overall design. The embedding can be implemented in a straightforward manner by applying nowadays a standard tool in steganography - the Syndrome-Trellis Codes (STCs)[3]. All experiments in this paper are carried out with additive approximations of UNIWARD.

The cost of changing X _ij to Y _ij and leaving all other cover elements unchanged is

{\rho }_{\mathit{\text{ij}}}(\mathbf{X},Y_{\mathit{\text{ij}}})\triangleq D(\mathbf{X},{\mathbf{X}}_{\sim \mathit{\text{ij}}}{Y}_{\mathit{\text{ij}}}),

(6)

where X_{∼i j}Y _ij is the cover image X with only its ij th element changed: X _ij  → Y _ij ^g. Note that ρ _ij  = 0 when X = Y. The additive approximation to (3) and (5) will be denoted as D_A(X,Y) andD_{\mathrm{A}}^{(\text{SI})}(\mathbf{X},\mathbf{Y}), respectively. For example,

D_{\mathrm{A}}(\mathbf{X},\mathbf{Y})=\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}{\rho }_{\mathit{\text{ij}}}(\mathbf{X},Y_{\mathit{\text{ij}}})[X_{\mathit{\text{ij}}}\ne Y_{\mathit{\text{ij}}}],

(7)

where [S] is the Iverson bracket equal to 1 when the statement S is true and 0 when S is false.

Note that, due to the absolute values in D(X,Y) (3), ρ _ij (X,X _ij  + 1) = ρ _ij (X,X _ij  - 1), which permits us to use a ternary embedding operation for the spatial and JPEG domains^h. Practical embedding algorithms can be constructed using the ternary multi-layered version of STCs (Section 4 in[3]).

On the other hand, for the side-informed JPEG steganography,D_{\mathrm{A}}^{(\text{SI})}(\mathbf{X},\mathbf{Y}) is inherently limited to a binary embedding operation because D _ij is either rounded up or down.

The embedding methods that use the additive approximation of UNIWARD for the spatial, JPEG, and side-informed JPEG domain will be called S-UNIWARD, J-UNIWARD, and SI-UNIWARD, respectively.

3.5 Relationship of UNIWARD to WOW

The distortion function of WOW bears some similarity to UNIWARD in the sense that the embedding costs are also computed from three directional residuals. The WOW embedding costs are, however, computed a different way that makes it rather difficult to use it for embedding in other domains, such as the JPEG domainⁱ.

To obtain a cost of changing pixel X _ij  → Y _ij , WOW first computes the embedding distortion in the wavelet domain weighted by the wavelet coefficients of the cover. This is implemented as a convolution{\xi }_{\mathit{\text{ij}}}^{(k)}=|W_{\mathit{\text{uv}}}^{(k)}(\mathbf{X})|\star |W_{\mathit{\text{uv}}}^{(k)}(\mathbf{X})-W_{\mathit{\text{uv}}}^{(k)}({\mathbf{X}}_{\sim \mathit{\text{ij}}}{Y}_{\mathit{\text{ij}}})| (see Equation 2 in[17]). These so-called embedding suitabilities{\xi }_{\mathit{\text{ij}}}^{(k)} are then aggregated over all three subbands using the reciprocal Hölder norm,{\rho }_{\mathit{\text{ij}}}^{(\text{WOW})}={\sum }_{k=1}^{3}1/{\xi }_{\mathit{\text{ij}}}^{(k)} to give WOW the proper content adaptivity in the spatial domain.

In principle, this approach could be used for embedding in the JPEG (or some other) domain in a similar way as in UNIWARD. However, notice that the suitabilities{\xi }_{\mathit{\text{ij}}}^{(k)} increase with increasing JPEG quantization step (increasing spatial frequency), giving the high-frequency DCT coefficients smaller costs,{\rho }_{\mathit{\text{ij}}}^{(\text{WOW})}, and thus a higher embedding probability than for the low-frequency coefficients. This creates both visible and statistically detectable artifacts. In contrast, the embedding costs in UNIWARD are higher for high-frequency DCT coefficients, desirably discouraging embedding changes in coefficients which are largely zeros.

4 Common core of all experiments

Before we move to the experimental part of this paper, which appears in Sections 5 and 6, we introduce the common core of all experiments: the cover source, steganalysis features, the classifier used to build the steganography detectors, and an empirical measure of security.

4.1 Cover source

All experiments are conducted on the BOSSbase database ver. 1.01[25] containing 10,000 512 × 512 8-bit grayscale images coming from eight different cameras. This database is very convenient for our purposes because it contains uncompressed images that serve as precovers for side-informed JPEG embedding. Also, the images can be compressed to any desirable quality factor for the JPEG domain.

The steganographic security is evaluated empirically using binary classifiers trained on a given cover source and its stego version embedded with a fixed payload. Even though this setup is artificial and does not correspond to real-life applications, it allows assessment of security with respect to the payload size, which is the goal of academic investigations of this type^j.

4.2 Steganalysis features

Spatial domain steganography methods will be analyzed using the spatial rich model (SRM)[18] consisting of 39 symmetrized sub-models quantized with three different quantization factors with a total dimension of 34,671^k. JPEG domain methods (including the side-informed algorithms) will be steganalyzed using the union of a downscaled version of the SRM with a single quantization step q = 1 (SRMQ1) with dimension 12,753 and the JPEG rich model (JRM)[24] with dimension 22,510, giving the total feature dimension of 35,263.

4.3 Machine learning

All classifiers will be implemented using the ensemble[26] with Fisher linear discriminant as the base learner. The security is quantified using the ensemble’s ‘out-of-bag’ (OOB) error E_OOB, which is an unbiased estimate of the minimal total testing error under equal priors,P_{\mathrm{E}}={min}_{P_{\text{FA}}}\frac{1}{2}(P_{\text{FA}}+P_{\text{MD}})[26]. The statistical detectability is usually displayed graphically by plotting E_OOB as a function of the relative payload. With the feature dimensionality and the database size, the statistical scatter of E_OOB over multiple ensemble runs with different seeds was typically so small that drawing error bars around the data points in the graphs would not show two visually discernible horizontal lines, which is why we omit this information in our graphs. As will be seen later, the differences in detectability between the proposed methods and prior art are so large that there should be no doubt about the statistical significance of the improvement. The code for extractors of all rich models as well as the ensemble is available athttp://dde.binghamton.edu/download.

5 Determining the parameters of UNIWARD

In this section, we study how the wavelet basis and the stabilizing constant σ in the distortion function UNIWARD affect the empirical security. We first focus on the parameter σ and then on the filter bank.

The original role of σ in UNIWARD[19] was to stabilize the numerical computations when evaluating the relative change of wavelet coefficients (3). As the following experiment shows, however, σ also strongly affects the content adaptivity of the embedding algorithm. In Figure2, we show the embedding change probabilities for payload α = 0.4 bpp (bits per pixel) for six values of the parameter σ. For this experiment, we selected the 8-tap Daubechies wavelet filter bank whose 1D filters are shown in Figure3^l. Note that a small value of σ makes the embedding change probabilities undesirably sensitive to content. They exhibit unusual interleaved streaks of high and low values. This is clearly undesirable since the content (shown in the upper left corner of Figure2) does not change as abruptly. On the other hand, a large σ makes the embedding change probabilities ‘too smooth,’ permitting thus UNIWARD to embed in regions with less complex content. Intuitively, we need to choose some middle ground for σ to avoid introducing a weakness into the embedding algorithm.

Figure 2

Embedding change probabilities. The effect of the stabilizing constant σ on the character of the embedding change probabilities for a 128 × 128 cover image shown in the upper left corner. The numerical values are the E_OOB obtained using the content-selective residual (CSR) and the SRM on BOSSbase 1.01 for relative payload α = 0.4 bpp.

Figure 3

Daubechies wavelet filter bank. UNIWARD uses the Daubechies 8-tap wavelet directional filter bank built from one-dimensional low-pass and high-pass filters, h and g.

Because the SRM consists of statistics collected from the noise residuals of all pixels in the image, it ‘does not see’ the artifacts in the embedding probabilities - the interleaved bands of high and low values. Notice that the position of the bands is tied to the content and does not correspond to any fixed (content-independent) checkerboard pattern. Thus, we decided to introduce a new type of steganalysis features designed specifically to utilize the artifacts in the embedding probabilities to probe the security of this unusual selection channel for small values of σ.

5.1 Content-selective residuals

The idea behind the attack on the selection channel is to compute the statistics of noise residuals separately for pixels with a small embedding probability and then for pixels with a large embedding probability. The former will serve as a reference for the latter, giving strength to this attack. While it is true that the embedding probabilities estimated from the stego image will generally not exactly match those computed from the corresponding cover image^m, they will be close and ‘good enough’ for the attack to work.

We will use the first-order noise residuals (differences among neighboring pixels):

\begin{array}{l}{R}_{\mathit{\text{ij}}}=X_{i,j}-X_{i,j+1},i\in \{1,\dots ,n_1\},j\in \{1,\dots ,n_2-1\}.\end{array}

(8)

To curb the residuals’ range and allow a compact statistical representation, R _ij will be truncated to the range [-T,T], R _ij  ← trunc _T (R _ij ), where T is a positive integer, and

(9)

Since this residual involves two adjacent pixels, we will divide all horizontally adjacent pixels in the image into four classes and compute the histogram for each class separately. Letp_{\mathit{\text{ij}}}(\mathbf{X},\overline{\alpha }) denote the embedding change probability computed from image X when embedding payload of\overline{\alpha } bpp. Given two thresholds 0 < t _s  < t _L  < 1, we define the following four sets of residuals:

(10)

(11)

(12)

\begin{array}{l}{\mathcal{R}}_{\mathit{\text{LL}}}=\{R_{\mathit{\text{ij}}}|p_{\mathit{\text{ij}}}(\mathbf{X},\overline{\alpha })>t_L\wedge p_{i,j+1}(\mathbf{X},\overline{\alpha })>t_L\}.\end{array}

(13)

The so-called content-selective residual (CSR) features will be formed by the histograms of residuals in each set. Because the marginal distribution of each residual is symmetrical about zero, one can merge the histograms of residuals from{\mathcal{R}}_{\mathit{\text{sL}}} and{\mathcal{R}}_{\mathit{\text{Ls}}}. The feature vector is thus the concatenation of 3 × (2T + 1) histogram bins, l = -T,…,T:

\begin{array}{l}{h}_s(l)=\left|\{R_{\mathit{\text{ij}}}|R_{\mathit{\text{ij}}}=l\wedge R_{\mathit{\text{ij}}}\in {\mathcal{R}}_{\mathit{\text{ss}}}\}\right|\end{array}

(14)

\begin{array}{l}{h}_L(l)=\left|\{R_{\mathit{\text{ij}}}|R_{\mathit{\text{ij}}}=l\wedge R_{\mathit{\text{ij}}}\in {\mathcal{R}}_{\mathit{\text{LL}}}\}\right|\end{array}

(15)

\begin{array}{l}{h}_{\mathit{\text{sL}}}(l)=\left|\{R_{\mathit{\text{ij}}}|R_{\mathit{\text{ij}}}=l\wedge R_{\mathit{\text{ij}}}\in {\mathcal{R}}_{\mathit{\text{sL}}}\cup {\mathcal{R}}_{\mathit{\text{Ls}}}\}\right|.\end{array}

(16)

The set{\mathcal{R}}_{\mathit{\text{ss}}} holds the residual values computed from pixels with a small embedding change probability, while the other sets hold residuals that are likely affected by embedding - their tails will become thicker.

All that remains is to specify the values of the parameters t _s , t _L , and\overline{\alpha }. Since the steganalyst will generally not know the payload embedded in the stego imageⁿ, we need to choose a fixed value of\overline{\alpha } that gives an overall good performance over a wide range of payloads. In our experiments, a medium value of\overline{\alpha }=0.4 generally provided a good estimate of the interleaved bands in the embedding change probabilities. Finally, we conducted a grid search on images from BOSSbase to determine t _s and t _L . The found optimum was rather flat and located around t _s  = 0.05, t _L  = 0.06. The threshold T for trunc _T (x) was kept fixed at T = 10.

For the value of σ as originally proposed in the workshop version of this paper[19], σ = 10 · eps ≈ 2 × 10^-15 (‘eps’ defined as in Matlab), the detection error of the 3 × (2 × 10 + 1) = 63-dimensional CSR feature vector turned out to be a reliable detection statistic. Figure4 shows the detection error E_OOB as a function of the relative payload. This confirms our intuition that too small a value of σ introduces strong banding artifacts, the stego scheme becomes overly sensitive to content, and an approximate knowledge on the faulty selection channel can be used to successfully attack S-UNIWARD.

Figure 4

Detection error E _OOB obtained using CSR features as a function of relative payload for σ = 10 · eps.

As can be seen from Figure2, the artifacts in the embedding change probabilities become gradually suppressed when increasing the value of the stabilizing constant σ. To determine the proper value of σ, we steganalyzed S-UNIWARD with both the CSR and SRM feature sets (and their union) on payload α = 0.4 bpp as a function of σ (see Figure5)^o. The detection error using both the SRM and the CSR is basically constant until σ becomes close to 2^-14 when a further increase of σ makes the CSR features ineffective for steganalysis. From σ = 1 the SRM starts detecting the embedding more accurately as the adaptivity of the scheme becomes lower. Also, at this value of σ, adding the CSR does not lower the detection error of the SRM. Based on this analysis, we decided to set the stabilizing constant of S-UNIWARD to σ = 1 and kept it at this value for the rest of the experiments in the spatial domain reported in this paper.

Figure 5

Detection error of S-UNIWARD. Payload 0.4 bpp implemented with various values of σ for the CSR and SRM features and their union.

The attack based on content-selective residuals could be expanded to other residuals than pixel differences, and one could use higher-order statistics instead of histograms[27]^p. While the detection error for the original S-UNIWARD setting σ = 10 · eps can, indeed, be made smaller this way, expanding the CSR feature set has virtually no effect on the security of S-UNIWARD for σ = 1 and the optimality of this value.

We note that constructing a similar targeted attack against JPEG implementations of UNIWARD is likely not feasible because the distortion caused by a change in a DCT coefficient affects a block of 8 × 8 pixels and, consequently, 23 × 23 wavelet coefficients. The distortion ‘averages out’ and no banding artefacts show up in the embedding probability map. Steganalysis of J-UNIWARD with JSRM shown in Figure6 indicates that the optimal σ for J-UNIWARD is 2^-6, which we selected for all experiments with J-UNIWARD and SI-UNIWARD in this paper.

Figure 6

Steganalysis of J-UNIWARD with JSRM. Detection error E_OOB obtained using the merger of JRM and SRMQ1 (JSRM) features as a function σ for J-UNIWARD with payload α = 0.4 bpnzAC and JPEG quality factor 75.

5.2 Effect of the filter bank

As a final experiment of this section aimed at finding the best settings of UNIWARD, we studied the influence of the directional filter bank. We did so for a fixed payload α = 0.4 bpp and two values of σ when steganalyzing using the CSR and SRM features. Table1 shows the results for five different wavelet bases (http://wavelets.pybytes.com/wavelet/db8/) with varying parameters (support size s). The best results have been achieved with the 8-tap Daubechies wavelet, whose 1D low- and high-pass filters are displayed in Figure3.

Table 1 Detection error E _OOB obtained using CSR and SRM features when using different filter banks in UNIWARD

6 Experiments

In this section, we test the steganography using UNIWARD implemented with the 8-tap Daubechies directional filter bank and σ = 1 for S-UNIWARD and σ = 2^-6 for J- and SI-UNIWARD. We report the results on a range of relative payloads 0.05, 0.1, 0.2, …, 0.5 bpp, while JPEG domain (and side-informed JPEG) methods will be tested on the same payloads expressed in bits per non-zero cover AC DCT coefficient (bpnzAC).

6.1 Spatial domain

In the spatial domain, we compare the proposed method with HUGO[15], HUGO implemented using the Gibbs construction with bounding distortion (HUGO BD)[4], WOW[17], LSB matching (LSBM), and the edge-adaptive (EA) algorithm[28]. With the exception of the EA algorithm, in which the costs and the embedding algorithm are inseparable, the results of all other algorithms are reported for embedding simulators that operate at the theoretical payload-distortion bound. The only algorithm that we implemented using STCs (with constraint height h = 12) to assess the coding loss is the proposed S-UNIWARD method.

For HUGO, we used the embedding simulator[25] with default settings γ = 1, σ = 1 and the switch --T with T = 255 to remove the weakness reported in[7]. HUGO BD starts with a distortion measure implemented as a weighted norm in the SPAM feature space, which is non-additive and not locally supported either. The bounding distortion is a method (see Section 7 in[4]) to give the distortion the form needed for the Gibbs construction to work - the local supportedness. HUGO BD was implemented using the Gibbs construction with two sweeps as described in the original publication with the same parameter settings as for HUGO. The non-adaptive LSBM was simulated at the ternary bound corresponding to uniform costs, ρ _ij  = 1 for all i,j.

Figure7 shows the E_OOB error for all stego methods as a function of the relative payload expressed in bits per pixel. While the security of the S-UNIWARD and WOW is practically the same due to the similarity of their distortion functions, the improvement over both versions of HUGO is quite apparent. HUGO BD performs better than HUGO especially for large payloads, where its detectability becomes comparable to that of S-UNIWARD. As expected, the non-adaptive LSBM performs poorly across all payloads, while EA appears only marginally better than LSBM.

Figure 7

E _OOB error for all stego methods. Detection error E_OOB using SRM as a function of relative payload for S-UNIWARD and five other spatial domain steganographic schemes.

In Figure8, we contrast the probability of embedding changes for HUGO, WOW, and S-UNIWARD. The selected cover image has numerous horizontal and vertical edges and also some textured areas. Note that while HUGO embeds with high probability into the pillar edges as well as the horizontal lines above the pillars, S-UNIWARD directional costs force the changes solely into the textured areas. The placement of embedding changes for WOW and S-UNIWARD is quite similar, which is correspondingly reflected in their similar empirical security.

Figure 8

Embedding probability for payload 0.4 bpp. HUGO (top right), WOW (bottom left), and S-UNIWARD (bottom right) for a 128 × 128 grayscale cover image (top left).

6.2 JPEG domain (non-side-informed)

For the JPEG domain without side information, we compare J-UNIWARD with nsF5[14] and the recently proposed UED algorithm[13]. Since the costs used in UED are independent of the embedding change direction, we decided to include for comparison the UED implemented using ternary codes rather than binary, which indeed produced a more secure embedding algorithm^q. All methods were again simulated at their corresponding payload-distortion bounds. The costs for nsF5 were uniform over all non-zero DCTs with zeros as the wet elements[29]. Figure9 shows the results for JPEG quality factors 75, 85, and 95. As in the spatial domain, J-UNIWARD clearly outperformed both nsF5 and both versions of UED by a sizeable margin across all three quality factors. Furthermore, when using STCs with constraint height h = 12, the coding loss appears rather small.

Figure 9

Results for JPEG quality factors 75, 85, and 95. Testing error E_OOB for J-UNIWARD, nsF5, and binary (ternary) UED on BOSSbase 1.01 with the union of SRMQ1 and JRM and ensemble classifier for quality factors 75, 85, and 95.

6.3 JPEG domain (side-informed)

Working with the same three quality factors, we compare SI-UNIWARD with four other methods - the block entropy-weighted method of[10] (EBS), the NPQ[11], BCHopt[9], and the fourth method, which can be viewed as a modification (or simplification) of[9] or as[10] in which the normalization by block entropy has been removed. Following is a list of cost assignments for these four embedding methods;{\rho }_{\mathit{\text{ij}}}^{(\mathit{\text{kl}})} is the cost of changing DCT coefficient ij corresponding to DCT mode kl.

• 1. {\rho }_{\mathit{\text{ij}}}^{(\mathit{\text{kl}})}={\left(\frac{q_{\mathit{\text{kl}}}(0.5-|e_{\mathit{\text{ij}}}|)}{H({\mathbf{X}}^{(b)})}\right)}^2

• 2. {\rho }_{\mathit{\text{ij}}}^{(\mathit{\text{kl}})}=\frac{q_{\mathit{\text{kl}}}^{{\lambda }_1}(1-2|e_{\mathit{\text{ij}}}|)}{{(\mu +|X_{\mathit{\text{ij}}}|)}^{{\lambda }_2}}

• 3. {\rho }_{\mathit{\text{ij}}}^{(\mathit{\text{kl}})} as defined in [9]

• 4. {\rho }_{\mathit{\text{ij}}}^{(\mathit{\text{kl}})}={\left(q_{\mathit{\text{kl}}}(1-2|e_{\mathit{\text{ij}}}|)\right)}^2

In method 1 (EBS), H(X^(b)) is the block entropy defined asH({\mathbf{X}}^{(b)})=-{\sum }_i{h}_i^{(b)}log{h}_i^{(b)}, whereh_i^{(b)} is the normalized histogram of all non-zero DCT coefficients in block X^(b). Per the experiments in[11], we set μ = 0 as NPQ embeds only in non-zero AC DCT coefficients, and λ₁ = λ₂ = 1/2 as this setting seemed to produce the most secure NPQ scheme for most payloads when tested with various feature sets. The cost ρ _ij for methods 1 to 4 is equal to zero when e _ij  = 1/2. Methods 1 and 4 embed into all DCT coefficients, including the DC term and coefficients that would otherwise round to zero (X _ij  = 0). We remind from Section 3.3.1 that methods 1, 2, and 4 avoid embedding into 1/2-coefficients from DCT modes 00, 04, 40, and 44. Since the cost assignment in method 3 (BCHopt) is inherently connected to its coding scheme, we kept this algorithm unchanged in our tests.

Figure1 shows that SI-UNIWARD achieves the best security among the tested methods for all payloads and all JPEG quality factors. The coding loss is also quite negligible. Curiously, the weighting by block entropy in the EBS method paid off only for quality factor 95. For factors 85 and 75, the weighting actually increases the statistical detectability using our feature vector (c.f., the ‘Square’ and ‘EBS’ curves). The dashed curves for quality factor 95 in Figure1 are included to show the negative effect when 1/2-coefficients from DCT modes 00, 04, 40, and 44 are used for embedding (see the discussion in Section 3.3.1). In this case, the detection error levels off at approximately 25% to 30% for small-medium payloads because most embedding changes are executed at the above four DCT modes. Note that NPQ and BCHopt do not exhibit the pathological error saturation as strongly because they do not embed into the DC term (mode 00).

7 Conclusion

Perfect security seems unachievable for empirical cover sources, examples of which are digital images. Currently, the best the steganographer can do for such sources is to minimize the detectability when embedding a required payload. A standard way to approach this problem is to embed while minimizing a carefully crafted distortion function, which is tied to empirical statistical detectability. This converts the problem of secure steganography to one that has been largely resolved in terms of known bounds and general near-optimal practical coding constructions.

The contribution of this paper is a clean and universal design of the distortion function called UNIWARD, which is independent of the embedding domain. The distortion is always computed in the wavelet domain as a sum of relative changes of wavelet coefficients in the highest frequency undecimated subbands. The directionality of wavelet basis functions permits the sender to assess the neighborhood of each pixel for the presence of discontinuities in multiple directions (textures and ‘noisy’ regions) and thus avoid making embedding changes in those parts of the image that can be modeled along at least one direction (clean edges and smooth regions). This model-free heuristic approach has been implemented in the spatial, JPEG, and side-informed JPEG domains. In all three domains, the proposed steganographic schemes matched or outperformed current state-of-the-art steganographic methods. A quite significant improvement was especially obtained for the JPEG and side-informed JPEG domains. As demonstrated by experiments, the innovative concept to assess the costs of changing a JPEG coefficient in an alternative domain seems to be quite promising.

Although all proposed methods were implemented and tested with an additive approximation of UNIWARD, this distortion function is naturally defined in its non-additive version, meaning that changes made to neighboring pixels (DCT coefficients) interact in the sense that the total imposed distortion is not a sum of distortions of individual changes. This potentially allows UNIWARD to embed while taking into account the interaction among the changed image elements. We plan to explore this direction as part of our future effort.

Last but not the least, we have discovered a new phenomenon that hampers the performance of side-informed JPEG steganography that computes embedding costs based solely on the quantization error of DCT coefficients. When unquantized DCT coefficients that lie exactly in the middle of the quantization intervals are assigned zero costs, any embedding that minimizes distortion starts introducing embedding artifacts that are quite detectable using the JPEG rich model. While the makeshift solution proposed in this article is by no means optimal, it raises an important open question, which is how to best utilize the side information in the form of an uncompressed image when embedding data into the JPEG compressed form. The authors postpone detailed investigation of this phenomenon into their future effort.

Endnotes

^aFor a given empirical cover source, the statistical detectability is typically evaluated empirically using classifiers trained on cover and stego examples from the source.

^bThe concept of precover was used for the first time by Ker[30].

^cHistorically, the first side-informed embedding method was the embedding while dithering algorithm[31], in which a message was embedded to minimize the color quantization error when converting a true-color image to a palette image.

^dThe process J^-1 involves rounding to integers and clipping to the dynamic range.

^eThis is because the embedding strongly prefers 1/2-coefficients.

^fIn practice, we assign very large costs to such coefficients.

^gThis notation was used in[4] and is also standard in the literature on Markov random fields[32].

^hOne might (seemingly rightfully) argue that the cost should depend on the polarity of the change. On the other hand, since the embedding changes with UNIWARD are restricted to textures, the equal costs are in fact plausible.

ⁱThis is one of the reasons why UNIWARD was conceived.

^jBuilding a universal detector of steganography is not the goal of this paper.

^k In Section 5, we will describe and work with another small feature set whose sole purpose will be to probe the security of the selection channel and to determine the proper value of the stabilizing constant σ.

^lThis filter bank was previously shown to provide the highest level of security for WOW[17] from among several tested filter banks. We thus selected the same bank here as a good initial candidate for the experiments.

^mAlso because the embedded payload α is unknown to the steganalyst.

ⁿA study on building steganalyzers when the payload is not known appears in[33].

^oWhen steganalyzing with the union of CSR and SRM using the ensemble classifier, we made sure that all 63 CSR features were included in each random feature subspace to avoid ‘diluting’ their strength in this type of classifier.Also, the value of σ for extracting the embedding change probabilitiesp_{\mathit{\text{ij}}}(\mathbf{X};\overline{\alpha }) was always fixed at σ = 10 · eps as the location of interleaved bands of high and low probabilities are more accurately estimated this way than with the value used in S-UNIWARD for the actual message embedding.

^pNote for reviewers: A preprint of this article is available upon request.

^qThe authors of UED were apparently unaware of this possibility to further boost the security of their algorithm.