Discretization of forced Duffing system with fractional-order damping

Abstract

In this paper we are interested in studying the effect of the fractional-order damping in the forced Duffing oscillator before and after applying a discretization process to it. Fixed points and their stability are discussed for the discrete system obtained. Finally, numerical simulations using Matlab are carried out to investigate the dynamic behavior such as bifurcation, chaos, and chaotic attractors. We note that on increasing the value of the fractional-order parameter, the resulting discrete system is stabilized.

1 Introduction

In recent years differential equations with fractional-order have attracted the attention of many researchers because of their applications in many areas of science and engineering. Analytical and numerical techniques have been implemented to study such equations. The fractional calculus has allowed the operations of integration and differentiation to be applied upon any fractional-order. For the existence of solutions for fractional differential equations, see [1, 2].

As regards the development of existence theorems for fractional functional-differential equations, many contributions exist and can be referred to [3–5]. Many applications of fractional calculus amount to replacing the time derivative in a given evolution equation by a derivative of fractional-order.

We recall the basic definitions (Caputo) and properties of fractional-order differentiation and integration.

Definition 1 The fractional integral of order $\beta \in {\mathbb{R}}^{+}$ of the function $f(t)$, $t>0$, is defined by

$$I^{\beta }f(t)={\int }_0^t\frac{{(t-s)}^{\beta -1}}{\mathrm{\Gamma }(\beta )}f(s)ds,$$

and the fractional derivative of order $\alpha \in (0,1)$ of $f(t)$, $t>0$, is defined by

$$D^{\alpha }f(t)=I^{1-\alpha }\frac{df(t)}{dt}.$$

To solve fractional-order differential equations there are two famous methods: frequency domain methods [6] and time domain methods [7]. In recent years it has been shown that the second method is more effective because the first method is not always reliable in detecting chaos [8] and [9].

Often it is not desirable to solve a differential equation analytically, and one turns to numerical or computational methods. In [10], a numerical method for nonlinear fractional-order differential equations with constant or time-varying delay was devised. It should be noticed that the fractional differential equations tend to lower the dimensionality of the differential equations in question, however, introducing delay in differential equations makes it infinite dimensional. So, even a single ordinary differential equation with delay could display chaos.

A lot of differential equations with Caputo fractional derivative were simulated by the predictor-corrector scheme, such as the fractional Chua system, the fractional Chen system, the Lorenz system, and so on. We should note that the predictor-corrector method is an approximation for the fractional-order integration, however, our approach is an approximation for the right-hand side.

Indeed, fractional-order systems are useful in studying the anomalous behavior of dynamical systems in electrochemistry, biology, viscoelasticity, and chaotic systems; see for example [11]. Dealing with fractional-order differential equations as dynamical systems is somewhat new and has motivated the leading research literature recently; see for example [12–26]. The nonlocal property of fractional differential equations means that the next state of a system not only depends on its current state but also on its history states. This property is very closely resembling to the real world and thus fractional differential equations have become popular and have been applied to dynamical systems.

On the other hand, some examples of dynamical systems generated by piecewise constant arguments have been studied in [27–30]. Here we propose a discretization process to obtain the discrete version of the system under study. Meanwhile, we apply the discretization process to discretize the fractional-order logistic differential equation.

2 Forced Duffing oscillator with fractional-order damping

The Duffing oscillator is an example of a periodically forced oscillator with nonlinear elasticity. It is one of the prototype systems of nonlinear dynamics. It first became popular for studying harmonic oscillations and, later, chaotic nonlinear dynamics in the wake of early studies by the engineer Georg Duffing [31]. The system has been successfully used to model a variety of physical processes, such as stiffening springs, beam buckling, nonlinear electronic circuits, superconducting Josephson parametric amplifiers, and ionization waves in plasmas. Despite the simplicity of the Duffing oscillator, the dynamical behavior is extremely rich and research is still going on today [32].

Forced Duffing oscillators are much harder to analyze analytically, because of the periodic force involved. It is far better to use computer approximations of the system to analyze how the forced Duffing oscillator is behaving under certain conditions. The Duffing equation, a well-known nonlinear differential equation, is used for describing many physical, engineering, and even biological problems [33].

Originally the Duffing equation was introduced by German electrical engineer Duffing in 1918. The equation is given by

$$x^{\cdot \cdot }+\mu x^{\cdot }+\lambda x+b{x}^3=\gamma sin(\omega t),$$

(2.1)

where the constants μ, λ, b, and γ are the damping coefficient, linear stiffness, nonlinear stiffness, excitation amplitude, and excitation frequency, respectively. All previous constants, assumed to be positive except λ, can also be negative.

Here we are concerned with the forced Duffing oscillator with fractional-order damping given by

$$x^{\cdot \cdot }+\mu D^{\alpha }x+\lambda x+b{x}^3=\gamma sin(\omega t),$$

(2.2)

where $\alpha \in (0,1)$ is the fractional-order parameter. First of all, we split (2.2) into a system of three equations, as follows:

$$\begin{array}{c}{D}^{\alpha }x=y,\hfill \\ D^{1-\alpha }y=z,\hfill \\ \frac{dz}{dt}=-\mu y-\lambda x-b{x}^3+\gamma sin(\omega t).\hfill \end{array}$$

(2.3)

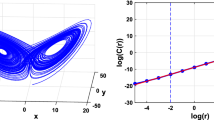
The solution of system (2.3) with $\alpha =0.85$ is simulated using the Grünwald-Letnikov method described in [34] and is shown in Figures 1 and 2.

Figure 1

State trajectory of system ( 2.3 ) in 3D state space with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ .

Figure 2

Solution of system ( 2.3 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ .

2.1 Bifurcation and chaos

The nonlinear dynamic of the duffing oscillator with fractional-order damping is simulated using Matlab. We firstly fix the parameters $\mu =0.9$, $\lambda =-1$, $b=1$, $\omega =1$, $\gamma =0.6$, and the initial state is $x(0)=y(0)=z(0)=0$. When $\alpha =1$, the system is described by the classical Duffing equation. Now vary the fractional-order parameter α from 0 to 1 with step size $\mathrm{\Delta }\alpha =0.005$, and the bifurcation can easily be detected by examining the relationship between α and x. Figure 3 shows the effect of the fractional-order parameter on the dynamics of the system.

Figure 3

Bifurcation of system ( 2.3 ) w.r.t. α .

Bifurcation diagrams with other control parameters, ω with $\alpha =0.80$; step size $\mathrm{\Delta }\omega =0.1$ and γ with $\alpha =0.85$; step size $\mathrm{\Delta }\gamma =0.005$ are shown in Figures 4 and 5. Figure 3 shows the strong effect of the fractional-order parameter on the dynamic of system (2.3); it stabilizes the system as $\alpha \to 1$. Figure 4 shows an oscillating behavior of the bifurcation diagram as expected because ω is the excitation frequency inside the sine function.

Figure 4

Bifurcation of system ( 2.3 ) w.r.t. ω with $\mathit{\alpha }\mathbf{=}\mathbf{0.80}$ .

Figure 5

Bifurcation of system ( 2.3 ) w.r.t. γ with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ .

3 Discretization process

In [35], a discretization process is introduced to discretize the fractional-order differential equations and we take Riccati’s fractional-order differential equations as an example. We notice that when the fractional-order parameter $\alpha \to 1$, Euler’s discretization method is obtained. In [36], the same discretization method is applied to the logistic fractional-order differential equation. We conclude that Euler’s method is able to discretize first order difference equations, however, we succeeded in discretizing a second order difference equation. Finally, in [37], we applied the same procedure to the fractional-order Chua system to get the same results as in the two previous papers, and we showed that when $\alpha \to 1$ the system will be stabilized.

Here we are very interested in applying the dicretization method to a system of differential equations like the Chua system.

Now let $\alpha \in (0,1)$ and consider the differential equation of fractional order

$$\begin{array}{r}{D}^{\alpha }x(t)=f(x(t)),t>0,\\ x(0)=x_0,t\le 0.\end{array}$$

(3.1)

The corresponding equation with piecewise constant argument is

$$D^{\alpha }x(t)=f\left(x\left(r\left[\frac{t}{r}\right]\right)\right),x(t)=x_0,t\le 0.$$

(3.2)

Let $t\in [0,r)$, then $\frac{t}{r}\in [0,1)$. So, we get

$$D^{\alpha }x(t)=f(x_0),t\in [0,r).$$

Thus

$$x_1(t)=x_0+\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}f(x_0).$$

Let $t\in [r,2r)$, then $\frac{t}{r}\in [1,2)$. Thus, we get

$$D^{\alpha }x(t)=f(x_1(r)),t\in [r,2r).$$

Thus

$$x_2(t)=x_1(r)+\frac{{(t-r)}^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}f(x_1(r)).$$

Let $t\in [2r,3r)$, then $\frac{t}{r}\in [2,3)$. So, we get

$$D^{\alpha }x(t)=f(x_2(r)),t\in [2r,3r).$$

Thus

$$x_3(t)=x_1(r)+\frac{{(t-2r)}^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}f(x_2(r)).$$

Repeating the process we get this result: when $t\in [nr,(n+1)r)$, then $\frac{t}{r}\in [n,n+1)$. So, we get

$$D^{\alpha }x(t)=f(x_n(nr)),t\in [nr,(n+1)r).$$

Thus

$$x_{n+1}(t)=x_n(r)+\frac{{(t-nr)}^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}f(x_n(r)).$$

We are interested in discretizing (3.1) with piecewise constant arguments given in the form

$$\begin{array}{c}{D}^{\alpha }x=y\left(r\left[\frac{t}{r}\right]\right),\hfill \\ D^{1-\alpha }y=z\left(r\left[\frac{t}{r}\right]\right),\hfill \\ \frac{dz}{dt}=-\mu y\left(r\left[\frac{t}{r}\right]\right)-\lambda x\left(r\left[\frac{t}{r}\right]\right)-bx{\left(r\left[\frac{t}{r}\right]\right)}^3+\gamma sin\left(\omega \left(r\left[\frac{t}{r}\right]\right)\right),\hfill \end{array}$$

(3.3)

with initial conditions $x(0)=0$, $y(0)=0$, and $z(0)=0$.

Applying the above mentioned discretization process and letting $t\to (n+1)r$ we obtain the discrete system

$$\begin{array}{c}{x}_{n+1}=x_n+\frac{r^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}{y}_n,\hfill \\ y_{n+1}=y_n+\frac{r^{1-\alpha }}{\mathrm{\Gamma }(2-\alpha )}{z}_n,\hfill \\ z_{n+1}=z_n+r(-\mu y-\lambda x-b{x}^3+\gamma sin(\omega n)).\hfill \end{array}$$

(3.4)

Indeed, there are other discretization methods for discretizing fractional-order differential equations, for example:

• The Grünwald-Letnikov definition (GL) which is a generalization of the derivative. The idea behind is that h, the step size, should approach 0 as n approaches infinity.

• The predictor-corrector method is an approximation for the fractional-order integration.

As a matter of fact, our approach is an approximation for the right-hand side.

4 Stability of fixed points

Now we study the asymptotic stability of the fixed points of the system (3.4) in the unforced case, that is, $sin(\mathrm{\Omega }t)=0$, which has three fixed point namely, ${\mathit{fix}}_1=(0,0,0)$, ${\mathit{fix}}_2=(\frac{\lambda }{b}i,0,0)$, and ${\mathit{fix}}_3=(\frac{-\lambda }{b}i,0,0)$.

By considering the Jacobian matrix for these fixed points and calculating its eigenvalues, we can investigate the stability of it based on the roots of the system’s characteristic equation [38]. The Jacobian matrix is given by

$$\left(\begin{array}{ccc}1& \frac{r^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}& 0\\ 0& 1& \frac{r^{1-\alpha }}{\mathrm{\Gamma }(2-\alpha )}\\ -r\lambda -3br{x}^2& -r\mu & 1\end{array}\right).$$

Linearizing the unforced system about ${\mathit{fix}}_1$ yields the following characteristic equation:

$$P(\mathrm{\Lambda })={\mathrm{\Lambda }}^3-3{\mathrm{\Lambda }}^2+(1+r\mu l)\mathrm{\Lambda }+(srl\lambda +1-r\mu l)=0,$$

(4.1)

where $s=\frac{r^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}$ and $l=\frac{r^{1-\alpha }}{\mathrm{\Gamma }(2-\alpha )}$. Let

$$\begin{array}{c}{a}_1=-3,\hfill \\ a_2=(1+r\mu l),\hfill \\ a_3=(srl\lambda +1-r\mu l).\hfill \end{array}$$

From the Jury test, if $P(1)>0$, $P(-1)<0$, and $a_3<1$, $|b_3|>b_1$, $c_3>|c_2|$, where $b_3=1-a_3^2$, $b_2=a_1-a_3{a}_2$, $b_1=a_2-a_3{a}_1$, $c_3=b_3^2-b_1^2$, and $c_2=b_3{b}_2-b_1{b}_2$, then the roots of $P(\mathrm{\Lambda })$ satisfy $\mathrm{\Lambda }<1$ and thus ${\mathit{fix}}_1$ is asymptotically stable. This is not satisfied here since $a_3>1$. That is, ${\mathit{fix}}_1$ is unstable.

While linearizing the same unforced system about ${\mathit{fix}}_2$ or ${\mathit{fix}}_3$ yields the following characteristic equation:

$$F(\mathrm{\Lambda })={\mathrm{\Lambda }}^3-3{\mathrm{\Lambda }}^2+(3+r\mu l)\mathrm{\Lambda }-(1+r\mu l+2sr\lambda l)=0.$$

(4.2)

We let $a_{11}=-3$, $a_{22}=3+r\mu l$, and $a_{33}=-(1+r\mu l+2sr\lambda l)$. From the Jury test, if $F(1)>0$, $F(-1)<0$, and $a_{33}<1$, $|b_{33}|>b_{11}$, $c_{33}>|c_{22}|$, where $b_{33}=1-a_{33}^2$, $b_{22}=a_{11}-a_{33}{a}_{22}$, $b_{11}=a_{22}-a_{33}{a}_{11}$, $c_{33}=b_{33}^2-b_{11}^2$, and $c_{22}=b_{33}{b}_{22}-b_{11}{b}_{22}$, then the roots of $F(\mathrm{\Lambda })$ satisfy $\mathrm{\Lambda }<1$ and thus ${\mathit{fix}}_2$ or ${\mathit{fix}}_3$ is asymptotically stable. We can check easily that $F(1)<0$, that is, both ${\mathit{fix}}_2$ and ${\mathit{fix}}_3$ are unstable.

5 Attractors, bifurcation, and chaos

In this section we show some dynamic behavior of the system (3.4) such as attractors, bifurcation and chaos for different α and r (see Figures 6-14). The effect of taking a fractional order on the system dynamics is investigated using phase diagrams and bifurcation diagrams. The bifurcation diagram is also used to examine the effect of the excitation amplitude and the frequency on the Duffing system with fractional-order damping. We show bifurcation and chaos of the dynamical system (3.4) by means of bifurcation diagrams first with respect to the parameter μ, then with respect to the fractional-order parameter α, and finally with respect to the parameter γ.

Figure 6

Attractor of ( 3.4 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ , $\mathit{r}\mathbf{=}\mathbf{0.25}$ , $\mathit{\mu }\mathbf{=}\mathbf{4}$ .

Figure 7

Attractor of ( 3.4 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ , $\mathit{r}\mathbf{=}\mathbf{0.3}$ , $\mathit{\mu }\mathbf{=}\mathbf{4}$ .

Figure 8

Chaotic attractor of ( 3.4 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.75}$ , $\mathit{r}\mathbf{=}\mathbf{0.3}$ , $\mathit{\mu }\mathbf{=}\mathbf{4}$ .

Figure 9

Chaotic attractor of ( 3.4 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ , $\mathit{r}\mathbf{=}\mathbf{0.25}$ , $\mathit{\mu }\mathbf{=}\mathbf{3}$ .

Figure 10

Chaotic attractor of ( 3.4 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ , $\mathit{r}\mathbf{=}\mathbf{0.25}$ , $\mathit{\mu }\mathbf{=}\mathbf{3.5}$ .

Figure 11

Chaotic attractor of ( 3.4 ) with $\mathit{\alpha }\mathbf{=}\mathbf{0.85}$ , $\mathit{r}\mathbf{=}\mathbf{0.1}$ , $\mathit{\mu }\mathbf{=}\mathbf{3}$ .

Let $r=0.25$ be fixed and vary α from 0.70 to 0.95 and μ from 2 to 8. The initial state of the system (3.4) is $(x_0,y_0,z_0)=(0,0,0)$. The step size for ρ is 0.01, the resulting bifurcation diagrams are shown in Figure 12(a)-(f). It is observed from the figures that increasing the fractional-order parameter α and fixing the parameter r stabilize the chaotic system.

Figure 12

Bifurcation diagram of ( 3.4 ) w.r.t. the parameter μ .

Now vary the fractional-order parameter α from 0.70 to 0.95, but with a fixed system parameter μ and change the parameter r from 0.15 to 0.30; the resulting bifurcation diagrams are shown in Figure 12(a)-(d).

Then vary the fractional-order parameter α from 0.85 to 0.95, but with a fixed system parameter $r=0.25$ and vary the parameter γ from 0 to 2; the resulting bifurcation diagrams are shown in Figure 12(a)-(d).

It is clear from Figure 13 that increasing the value of the fractional-order parameter α transforms the system into its stable behavior, exactly as in the case of the fractional-order system (3.1).

Figure 13

Bifurcation diagram of system ( 3.4 ) as a function of the fractional-order parameter α with different values of the parameters r and μ .

Figure 14

Bifurcation diagram of system ( 3.4 ) as a function of the parameter γ with different values of the fractional-order parameters α .

6 Conclusion

A discretization method is applied in this paper to the forced Duffing oscillator with fractional-order damping. The dynamics of the discretized fractionally damped Duffing equation has been examined numerically. Also, the conclusion of bifurcation of the parameter-dependent system has been drawn numerically. Increasing the value of the fractional-order damping term stabilizes the system under study in both cases: fractional-order system and discretized system.