The threshold of a stochastic SIQS epidemic model

Abstract

In this paper, we discuss the dynamics of a stochastic SIQS epidemic model. When the noise is large, the infective decays exponentially to zero regardless of the magnitude of $R_0$. When the noise is small, sufficient conditions for extinction exponentially and persistence in the mean are established. The results are illustrated by computer simulations.

MSC:34F05, 37H10, 60H10, 92D25, 92D30.

1 Introduction

One intervention procedure to control the spread of infectious diseases is to isolate some infectives, in order to reduce transmissions of the infection to susceptibles. Isolation may have been the first infection control method. Over the centuries quarantine has been used to reduce the transmission of human diseases such as leprosy, plague, cholera, typhus, yellow fever, smallpox, diphtheria, tuberculosis, measles, mumps, ebola, and lassa fever. Quarantine has also been used for animal diseases such as rinderpest, foot and mouth, psittacosis, Newcastle disease, and rabies. Studies of epidemic models with quarantine have become an important area in the mathematical theory of epidemiology, and they have largely been inspired by Refs. [1–4].

Hethcote et al. in [5] discuss an SIQS epidemic model:

$$\{\begin{array}{l}\dot{S}(t)=A-\beta S(t)I(t)-\mu S(t)+\gamma I(t)+\epsilon Q(t),\\ \dot{I}(t)=\beta S(t)I(t)-(\mu +\delta +\gamma +\alpha )I(t),\\ \dot{Q}(t)=\delta I(t)-(\mu +\epsilon +\alpha )Q(t),\end{array}$$

(1.1)

where parameters A, μ, and β are positive constants, and α, γ, ε, and δ are non-negative constants. Here $S(t)$ denotes the number of members who are susceptible to an infection at time t. $I(t)$ denotes the number of members who are infective at time t. $Q(t)$ denotes the number of members who are removed and isolated either voluntarily or coercively from the infectious class. The parameters in the model are summarized in the following list:

A: the recruitment rate of susceptibles corresponding to births and immigration;

β: transmission coefficient between compartments S and I;

μ: the per capita natural mortality rate;

δ: the rate for individuals leaving the infective compartment I for the quarantine compartment Q;

γ: recovery rate of infectious individuals;

ε: the rate at which individuals return to susceptible compartment S from compartments Q;

α: disease-caused death rate of infectious individuals.

In a simple epidemic model, there is generally the basic reproduction number (or the threshold) $R_0$. If $R_0\le 1$, the disease-free equilibrium is a unique equilibrium in this type of epidemic model and it is globally asymptotically stable; if $R_0>1$, this type of model has also a unique endemic equilibrium, which is globally asymptotically stable. The threshold of system (1.1) is

$$R_0=\frac{\beta A}{\mu (\mu +\delta +\gamma +\alpha )}.$$

(1.2)

In [5], the system (1.1) always has the disease-free equilibrium $P_0=(S_0,I_0,Q_0)=(\frac{A}{\mu },0,0)$. If $R_0⩽1$, then $P_0$ is the unique equilibrium of (1.1) and it is globally stable in invariant set Γ, where

$$\mathrm{\Gamma }=\{(S,I,Q):S>0,I\ge 0,Q\ge 0,S+I+Q\le \frac{A}{\mu }\}.$$

If $R_0>1$, then $P_0$ is unstable and there is an endemic equilibrium

$$P^{\ast }=(S^{\ast },I^{\ast },Q^{\ast })=(\frac{\mu +\delta +\gamma +\alpha }{\beta },\frac{A(1-\frac{1}{R_0})}{(\mu +\alpha )(1+\frac{\delta }{\mu +\epsilon +\alpha })},\frac{\delta I^{\ast }}{\mu +\epsilon +\alpha }),$$

which is globally asymptotically stable under a sufficient condition in invariant set Γ.

In fact, epidemic models are inevitably affected by environmental white noise which is an important component in realism, because it can provide an additional degree of realism in comparison to their deterministic counterparts. Many stochastic models for epidemic populations have been developed in [6–17]. Dalal et al. [6] have previously used the technique of parameter perturbation to examine the effect of environmental stochasticity in a model of AIDS and condom use. They found that the introduction of stochastic noise changes the basic reproduction number of the disease and can stabilize an otherwise unstable system. Tornatore et al. [9] propose a stochastic disease model where vaccination is included. They prove existence, uniqueness, and positivity of the solution and the stability of the disease-free equilibrium. Zhao et al. [7] discuss the dynamics of a stochastic SIS epidemic model with vaccination. They obtain the condition of the disease extinction and persistence according to the threshold of the deterministic system and the noise. Ji et al. [10] discuss the SDE SIR model with no delay. They obtain if $\beta <\gamma +\mu -{\sigma }^2/2$, then the disease-free equilibrium is stochastically asymptotically stable in the large and exponentially mean-square stable. If $\beta >\gamma +\mu$, then the solution of the system is fluctuating around $(S^{\ast },I^{\ast },R^{\ast })$, which is the endemic equilibrium of the corresponding deterministic system. The disease will prevail if the white noise is small.

However, compared to deterministic systems, it is difficult to give the threshold of stochastic systems. Recently, Gray et al. in [11] investigate the stochastic SIS epidemic model with fluctuations around the transmission coefficient β. They prove that this model has a unique global positive solution and establish conditions for extinction and persistence of $I(t)$ according to the threshold of the stochastic model. In the case of persistence they show the existence of a stationary distribution and derive expressions for its mean and variance. Zhao and Jiang [12] continue to discuss the stochastic SIS epidemic model with vaccination. When the noise is small, they obtain a threshold of the stochastic system which determines the extinction and persistence of the epidemic. Besides, they find that large noise will suppress the epidemic from prevailing.

In this paper, taking into account the effect of randomly fluctuating environment, we assume that fluctuations in the environment will manifest themselves mainly as fluctuations in the parameter β,

$$\beta \to \beta +\sigma \dot{B}(t),$$

where $B(t)$ is standard Brownian motions with $B(0)=0$, and with intensity of white noise ${\sigma }^2>0$. The stochastic version corresponding to the deterministic model (1.1) takes the following form:

$$\{\begin{array}{l}dS(t)=(A-\beta S(t)I(t)-\mu S(t)+\gamma I(t)+\epsilon Q(t))dt-\sigma S(t)I(t)dB(t),\\ dI(t)=(\beta S(t)I(t)-(\mu +\delta +\gamma +\alpha )I(t))dt+\sigma S(t)I(t)dB(t),\\ dQ(t)=(\delta I(t)-(\mu +\epsilon +\alpha )Q(t))dt,\end{array}$$

(1.3)

This paper is organized as follows. In Section 2, we show there is a unique positive solution of system (1.3). In Section 3, we investigate system (1.3) is exponential stability when the noise is large. In this case, the infective decays exponentially to zero. When the noise is small, we deduce the condition ${\tilde{R}}_0<1$ which will enable the disease to die out exponentially in Section 3 and the condition ${\tilde{R}}_0>1$ for the disease being persistent is given in Sections 4. Throughout the paper, outcomes of numerical simulations are reported to support the analytical results.

Next, we give some basic theory in stochastic differential equations (see [18]).

Throughout this paper, unless otherwise specified, let $(\mathrm{\Omega },{\{{\mathcal{F}}_t\}}_{t\ge 0},P)$ be a complete probability space with a filtration ${\{{\mathcal{F}}_t\}}_{t\ge 0}$ satisfying the usual conditions (i.e. it is right continuous and ${\mathcal{F}}_0$ contains all P-null sets). Let

$${\mathbb{R}}_{+}^d=\{x\in {\mathbb{R}}^d:x_i>0\text{ for all }1⩽i⩽d\},{\overline{\mathbb{R}}}_{+}^d=\{x\in {\mathbb{R}}^d:x_i\ge 0\text{ for all }1⩽i⩽d\}.$$

In general, consider the n-dimensional stochastic differential equation

$$dx(t)=f(x(t),t)dt+g(x(t),t)dB(t),\text{for }t\ge t_0,$$

(1.4)

with initial value $x(t_0)=x_0\in R^d$. $B(t)$ denotes n dimensional standard Brownian motion defined on the above probability space. Define the differential operator L associated with (1.4) by

$$L=\frac{\partial }{\partial t}+\sum _{i=1}^d{f}_i(x,t)\frac{\partial }{\partial x_i}+\frac{1}{2}\sum _{i,j=1}^d{[g^T(x,t)g(x,t)]}_{ij}\frac{{\partial }^2}{\partial x_i\partial x_j}.$$

If L acts on a function $V\in C^{2,1}({\mathbb{R}}^d\times {\overline{\mathbb{R}}}_{+};{\overline{\mathbb{R}}}_{+})$, then

$$LV(x,t)=V_t(x,t)+V_x(x,t)f(x,t)+\frac{1}{2}trace[g^T(x,t)V_{xx}(x,t)g(x,t)],$$

where $V_t=\frac{\partial V}{\partial t}$, $V_x=(\frac{\partial V}{\partial x_1},\dots ,\frac{\partial V}{\partial x_d})$, $V_{xx}={(\frac{{\partial }^{2}V}{\partial x_i\partial x_j})}_{d\times d}$. By Itô’s formula, if $x(t)\in R^d$, then

$$dV(x(t),t)=LV(x(t),t)dt+V_x(x(t),t)g(x(t),t)dB(t).$$

Consider (1.4), assume $f(0,t)=0$ and $g(0,t)=0$ for all $t\ge t_0$. So $x(t)\equiv 0$ is a solution of (1.4), called the trivial solution or equilibrium position.

2 Existence and uniqueness of positive solution

In this section we first show that the solution of system (1.3) is global and positive. To get a unique global (i.e. no explosion in a finite time) solution for any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and local Lipschitz condition (cf. [18]). However, the coefficients of system (1.3) do not satisfy the linear growth condition, though they are locally Lipschitz continuous, so the solution of system (1.3) may explode in finite time. In this section, using the Lyapunov analysis method (mentioned in [11, 14]), we show the solution of system (1.3) is positive and global.

Theorem 2.1 There is a unique solution $(S(t),I(t),Q(t))$ of system (1.3) on $t⩾0$ for any initial value $(S(0),I(0),Q(0))\in {\mathbb{R}}_{+}^3$, and the solution will remain in ${\mathbb{R}}_{+}^3$ with probability 1, namely, $(S(t),I(t),Q(t))\in {\mathbb{R}}_{+}^3$ for all $t⩾0$ almost surely.

Proof Since the coefficients of the equation are locally Lipschitz continuous for any given initial value $(S(0),I(0),Q(0))\in {\mathbb{R}}_{+}^3$, there is a unique local solution $(S(t),I(t),Q(t))$ on $t\in [0,{\tau }_e)$, where ${\tau }_e$ is the explosion time (see [18]). To show this solution is global, we need to show that ${\tau }_e=\mathrm{\infty }$ a.s. Let $k_0\ge 0$ be sufficiently large so that $S(0)$, $I(0)$, and $Q(0)$ all lie within the interval $[1/k_0,k_0]$. For each integer $k⩾k_0$, define the stopping time

$${\tau }_k=inf\{t\in [0,{\tau }_e):min\{S(t),I(t),Q(t)\}\le \frac{1}{k}\text{ or }max\{S(t),I(t),Q(t)\}\ge k\},$$

where, throughout this paper, we set $inf\mathrm{\varnothing }=\mathrm{\infty }$ (as usual ∅ denotes the empty set). According to the definition, ${\tau }_k$ is increasing as $k\to \mathrm{\infty }$. Set ${\tau }_{\mathrm{\infty }}={lim}_{k\to \mathrm{\infty }}{\tau }_k$, whence ${\tau }_{\mathrm{\infty }}⩽{\tau }_e$ a.s. If we can show that ${\tau }_{\mathrm{\infty }}=\mathrm{\infty }$ a.s., then ${\tau }_e=\mathrm{\infty }$ and $(S(t),I(t),Q(t))\in {\mathbb{R}}_{+}^3$ a.s. for all $t⩾0$. In other words, to complete the proof all we need to show is that ${\tau }_{\mathrm{\infty }}=\mathrm{\infty }$ a.s. If this statement is false, then there exist a pair of constants $T>0$ and $\epsilon \in (0,1)$ such that

$$P\{{\tau }_{\mathrm{\infty }}⩽T\}>\epsilon .$$

Hence there is an integer $k_1⩾k_0$ such that

$$P\{{\tau }_k⩽T\}⩾\epsilon \text{for all }k⩾k_1.$$

(2.1)

For $t\le {\tau }_k$, we can see, for each k,

$$d(S+I+Q)=[A-\mu (S+I+Q)-\alpha (I+Q)]dt\le [A-\mu (S+I+Q)]dt$$

and so

$$S(t)+I(t)+Q(t)\le \{\begin{array}{ll}\frac{A}{\mu },& \text{if }S(0)+I(0)+Q(0)\le \frac{A}{\mu },\\ S(0)+I(0)+Q(0),& \text{if }S(0)+I(0)+Q(0)>\frac{A}{\mu }\end{array}:=M.$$

Define a $C^2$-function $V:{\mathbb{R}}_{+}^3\to {\overline{\mathbb{R}}}_{+}$ by

$$V(S,I,Q)=(S-1-logS)+(I-1-logI)+(Q-1-logQ).$$

The nonnegativity of this function can be seen from $u-1-logu⩾0$, $\mathrm{\forall }u>0$. Let $k⩾k_0$ and $T>0$ be arbitrary. Applying the Itô formula, we obtain

$$\begin{array}{rcl}dV(S,I,Q)& =& (1-\frac{1}{S})dS+\frac{1}{2S^2}{(dS)}^2+(1-\frac{1}{I})dI+\frac{1}{2I^2}{(dI)}^2+(1-\frac{1}{Q})dQ\\ =& LVdt+\sigma (I-S)dB(t),\end{array}$$

(2.2)

where $LV:{\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+}$ is defined by

$$\begin{array}{rcl}LV& =& (1-\frac{1}{S})(A-\beta SI-\mu S+\gamma I+\epsilon Q)+\frac{1}{2}{\sigma }^2{I}^2+(1-\frac{1}{I})[\beta SI-(\mu +\delta +\gamma +\alpha )I]\\ +\frac{1}{2}{\sigma }^2{S}^2+(1-\frac{1}{Q})[\delta I-(\mu +\epsilon +\alpha )Q]\\ =& A-\beta SI-\mu S+\gamma I+\epsilon Q-\frac{A}{S}+\beta I+\mu -\gamma \frac{I}{S}-\epsilon \frac{Q}{S}+\frac{1}{2}{\sigma }^2{I}^2\\ +\beta SI-(\mu +\delta +\gamma +\alpha )I\\ -\beta S+(\mu +\delta +\gamma +\alpha )+\frac{1}{2}{\sigma }^2{S}^2+\delta I-(\mu +\epsilon +\alpha )Q-\delta \frac{I}{Q}+(\mu +\epsilon +\alpha )\\ \le & A+3\mu +2\alpha +\delta +\gamma +\epsilon +(\gamma +\epsilon +\beta +\delta )M+{\sigma }^2{M}^2\\ :=& K.\end{array}$$

The remainder of the proof follows that in Ji et al. [14]. □

Remark 2.1 From Theorem 2.1, for any initial value $(S(0),I(0),Q(0))\in {\mathbb{R}}_{+}^3$, there is a unique global solution $(S(t),I(t),Q(t))\in {\mathbb{R}}_{+}^3$ almost surely of system (1.3). Hence

$$d(S+I+Q)\le [A-\mu (S+I+Q)]dt$$

and

$$S(t)+I(t)+Q(t)\le \frac{A}{\mu }+e^{-\mu t}(S(0)+I(0)+Q(0)-\frac{A}{\mu }).$$

If $S(0)+I(0)+Q(0)\le \frac{A}{\mu }$, then $S(t)+I(t)+Q(t)\le \frac{A}{\mu }$ a.s. so the region

$${\mathrm{\Gamma }}^{\ast }=\{(S,I,Q):S>0,I>0,Q>0,S+I+Q\le \frac{A}{\mu }\text{ a.s.}\}$$

(2.3)

is a positively invariant set of system (1.3) on ${\mathrm{\Gamma }}^{\ast }$, which is similar to Γ of system (1.1).

From now on, we always assume that $(S(0),I(0),Q(0))\in {\mathrm{\Gamma }}^{\ast }$.

3 Extinction

In this section, we investigate the conditions for the extinction of the disease. For convenience we introduce the notation:

$$〈x(t)〉=\frac{1}{t}{\int }_0^{t}x(r)dr,{\tilde{R}}_0=\beta \left(\frac{A}{\mu }\right)\frac{1}{(\mu +\gamma +\delta +\alpha )+\frac{1}{2}{\sigma }^2{(\frac{A}{\mu })}^2}.$$

We first give a useful lemma.

Lemma 3.1 ([18] (Strong Law of Large Numbers))

Let $M={\{M_t\}}_{t\ge 0}$ be a real-value continuous local martingale vanishing at $t=0$. Then

$$\underset{t\to \mathrm{\infty }}{lim}{〈M,M〉}_t=\mathrm{\infty }\mathit{\text{a.s.}}\Rightarrow \underset{t\to \mathrm{\infty }}{lim}\frac{M_t}{{〈M,M〉}_t}=0\mathit{\text{a.s.}}$$

and also

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{{〈M,M〉}_t}{t}<\mathrm{\infty }\mathit{\text{a.s.}}\Rightarrow \underset{t\to \mathrm{\infty }}{lim}\frac{M_t}{t}=0\mathit{\text{a.s.}}$$

The following is the main theorem of this section.

Theorem 3.1 Let $(S(t),I(t),Q(t))$ be the solution of system (1.3) with initial value $(S(0),I(0),Q(0))\in {\mathrm{\Gamma }}^{\ast }$. If

• (a) ${\sigma }^2>max\{\frac{{\beta }^2}{2(\gamma +\delta +\mu +\alpha )},\frac{\beta \mu }{A}\}$, or

• (b) ${\tilde{R}}_0<1$ and ${\sigma }^2\le \frac{\beta \mu }{A}$.

Then

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{logI(t)}{t}⩽-(\mu +\gamma +\alpha +\delta )+\frac{{\beta }^2}{2{\sigma }^2}<0\mathit{\text{a.s. if }}(\mathrm{a})\mathit{\text{ holds}};$$

(3.1)

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{logI(t)}{t}⩽\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})<0\mathit{\text{a.s. if }}(\mathrm{b})\mathit{\text{ holds}};$$

(3.2)

namely, $I(t)$ tends to zero exponentially a.s. i.e., the disease will die out with probability one. In addition

$$\underset{t\to \mathrm{\infty }}{lim}S(t)=\frac{A}{\mu }=S_0,\underset{t\to \mathrm{\infty }}{lim}I(t)=0,\underset{t\to \mathrm{\infty }}{lim}Q(t)=0\mathit{\text{a.s.}}$$

Proof An integration of the system (1.3) yields

$$\begin{array}{r}\frac{S(t)-S(0)}{t}=A-\beta 〈S(t)I(t)〉-\mu 〈S(t)〉+\gamma 〈I(t)〉+\epsilon 〈Q(t)〉-\frac{\sigma }{t}{\int }_0^{t}S(r)I(r)dB(r),\\ \frac{I(t)-I(0)}{t}=\beta 〈S(t)I(t)〉-(\gamma +\delta +\mu +\alpha )〈I(t)〉+\frac{\sigma }{t}{\int }_0^{t}S(r)I(r)dB(r),\\ \frac{Q(t)-Q(0)}{t}=\delta 〈I(t)〉-(\mu +\epsilon +\alpha )〈Q(t)〉,\end{array}$$

(3.3)

then we have

$$\begin{array}{r}\frac{\mu +\epsilon +\alpha }{\epsilon }[\frac{S(t)-S(0)}{t}+\frac{I(t)-I(0)}{t}]+\frac{Q(t)-Q(0)}{t}\\ =\frac{\mu +\epsilon +\alpha }{\epsilon }A-\frac{(\mu +\epsilon +\alpha )\mu }{\epsilon }〈S(t)〉-\frac{(\mu +\epsilon +\alpha )(\alpha +\delta +\alpha )}{\epsilon }〈I(t)〉+\delta 〈I(t)〉.\end{array}$$

We compute that

$$〈S(t)〉=\frac{A}{\mu }-\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }〈I(t)〉+\phi (t),$$

(3.4)

where $\phi (t)$ is defined by

$$\begin{array}{rcl}\phi (t)& =& -\frac{\epsilon }{\mu (\mu +\epsilon +\alpha )}\{\frac{\mu +\epsilon +\alpha }{\epsilon }[\frac{S(t)-S(0)}{t}+\frac{I(t)-I(0)}{t}]+\frac{Q(t)-Q(0)}{t}\}\\ =& -\frac{1}{\mu }[\frac{S(t)-S(0)}{t}+\frac{I(t)-I(0)}{t}]-\frac{\epsilon }{\mu (\mu +\epsilon +\alpha )}\frac{Q(t)-Q(0)}{t}.\end{array}$$

Obviously $\phi (t)\to 0$, $t\to \mathrm{\infty }$. Applying Itô’s formula to system (1.3) leads to

$$dlogI=[[\beta S-(\gamma +\delta +\mu +\alpha )]dt-\frac{1}{2}{\sigma }^2{S}^2]dt+\sigma SdB(t).$$

(3.5)

Integrating this from 0 to t and dividing t on the both sides, we have

$$\begin{array}{rcl}\frac{logI(t)-logI(0)}{t}& =& \beta 〈S(t)〉-(\mu +\gamma +\delta +\alpha )-\frac{1}{2}{\sigma }^2〈S^2(t)〉+\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r)\\ \le & \beta 〈S(t)〉-(\mu +\gamma +\delta +\alpha )-\frac{1}{2}{\sigma }^2{〈S(t)〉}^2+\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r).\end{array}$$

(3.6)

Substituting (3.4) into (3.6) yields

$$\begin{array}{r}\frac{logI(t)-logI(0)}{t}\\ =\beta [\frac{A}{\mu }-\frac{\mu +\alpha }{\mu }(1+\frac{\delta }{\mu +\epsilon +\alpha })〈I(t)〉+\phi (t)]-(\mu +\gamma +\delta +\alpha )\\ -\frac{1}{2}{\sigma }^2{[\frac{A}{\mu }-\frac{\mu +\alpha }{\mu }(1+\frac{\delta }{\mu +\epsilon +\alpha })〈I(t)〉+\phi (t)]}^2+\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r)\\ =\beta [\frac{A}{\mu }-\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }〈I(t)〉+\phi (t)]-(\mu +\sigma +\delta +\alpha )-\frac{1}{2}{\sigma }^2[{\left(\frac{A}{\mu }\right)}^2\\ +{\left(\frac{\mu +\alpha }{\mu }\right)}^2{\left(\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }\right)}^2{〈I(t)〉}^2+\phi {(t)}^2-\left(\frac{2A}{\mu }\right)\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }〈I(t)〉\\ +\frac{2A}{\mu }\phi (t)-2\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }〈I(t)〉\phi (t)]+\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r)\\ =\frac{\beta A}{\mu }-(\mu +\gamma +\delta +\alpha )-\frac{1}{2}{\sigma }^2{\left(\frac{A}{\mu }\right)}^2-\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }(\beta -{\sigma }^2\frac{A}{\mu })〈I(t)〉\\ -\frac{1}{2}{\sigma }^2{\left(\frac{\mu +\alpha }{\mu }\right)}^2{\left(\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }\right)}^2{〈I(t)〉}^2+\beta \phi (t)-\frac{1}{2}{\sigma }^2\phi {(t)}^2-{\sigma }^2\left(\frac{A}{\mu }\right)\phi (t)\\ +{\sigma }^2\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }〈I(t)〉\phi (t)+\frac{\sigma M(t)}{t}\\ \le \frac{\beta A}{\mu }(1-\frac{1}{{\tilde{R}}_0})-\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }(\beta -{\sigma }^2\frac{A}{\mu })〈I(t)〉+\mathrm{\Phi }(t)+\frac{\sigma M(t)}{t},\end{array}$$

(3.7)

where

$$\begin{array}{c}\mathrm{\Phi }(t)=\beta \phi (t)-\frac{{\sigma }^2}{2}{\phi }^2(t)+{\sigma }^2\frac{(\mu +\epsilon )(\mu +\alpha )}{\mu (\mu +\epsilon +p)}〈I(t)〉\phi (t)-{\sigma }^2\frac{A}{\mu }\phi (t),\hfill \\ M(t)={\int }_0^{t}S(r)dB(r).\hfill \end{array}$$

If the condition (b) is satisfied, we have

$$\frac{logI(t)-logI(0)}{t}\le \beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})+\mathrm{\Phi }(t)+\frac{\sigma M(t)}{t}.$$

(3.8)

Moreover,

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{{〈M,M〉}_t}{t}⩽\frac{{\sigma }^2{A}^2}{{\mu }^2}<\mathrm{\infty }\text{a.s.}$$

By Lemma 3.1 and $\phi (t)\to 0$, $t\to \mathrm{\infty }$, we obtain

$$\underset{t\to \mathrm{\infty }}{lim}\frac{M(t)}{t}=0\text{and}\underset{t\to \mathrm{\infty }}{lim}\mathrm{\Phi }(t)=0\text{a.s.}$$

(3.9)

It follows from (3.8) and (3.9) that

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{logI(t)}{t}⩽\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})<0\text{a.s.}$$

Conclusion (3.2) is proved.

Next, according to (3.6), we obtain

$$\begin{array}{rcl}\frac{logI(t)-logI(0)}{t}& \le & \beta 〈S(t)〉-(\mu +\gamma +\delta +\alpha )-\frac{1}{2}{\sigma }^2{〈S(t)〉}^2+\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r)\\ =& -\frac{1}{2}{\sigma }^2{(〈S(t)〉-\frac{\beta }{{\sigma }^2})}^2+\frac{{\beta }^2}{2{\sigma }^2}-(\gamma +\delta +\mu +\alpha ).\end{array}$$

If the condition (a) is satisfied, we have

$$\frac{logI(t)}{t}\le \frac{{\beta }^2}{2{\sigma }^2}-(\gamma +\delta +\mu +\alpha )+\sigma \frac{M(t)}{t}+\frac{logI(0)}{t}.$$

Conclusion (3.1) is proved.

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{logI(t)}{t}⩽-(\mu +\gamma +\alpha +\delta )+\frac{{\beta }^2}{2{\sigma }^2}<0\text{a.s.}$$

According to (3.1) and (3.2), they implies

$$\underset{t\to \mathrm{\infty }}{lim}I(t)=0\text{a.s.}$$

(3.10)

Next, let us prove the last assertion. We solve the last equation of system (1.3), then

$$Q(t)=e^{-(\mu +\epsilon +\alpha )t}[Q(0)+{\int }_0^t\delta I(s)e^{(\mu +\epsilon +\alpha )s}ds].$$

Applying L’Hospital’s rule and (3.10), we get

$$\underset{t\to \mathrm{\infty }}{lim}Q(t)=\underset{t\to \mathrm{\infty }}{lim}\frac{Q(0)+{\int }_0^t\delta I(s)e^{(\mu +\epsilon +\alpha )s}ds}{e^{(\mu +\epsilon +\alpha )t}}=\underset{t\to \mathrm{\infty }}{lim}\frac{\delta I(t)}{\mu +\epsilon +\alpha }=0.$$

According to system (1.3), we obtain

$$d(S+I+Q)=[A-\mu (S+I+Q)-\alpha (I+Q)]dt,$$

then

$$S(t)+I(t)+Q(t)=e^{-\mu t}\{[S(0)+I(0)+Q(0)]+{\int }_0^t[A-\alpha (I(s)+Q(s))]e^{\mu s}ds\},$$

then

$$\begin{array}{rcl}\underset{t\to \mathrm{\infty }}{lim}S(t)& =& \underset{t\to \mathrm{\infty }}{lim}\{\frac{[S(0)+I(0)+Q(0)]+{\int }_0^t[A-\alpha (I(s)+Q(s))]e^{\mu s}ds}{e^{\mu t}}-I(t)-Q(t)\}\\ =& \underset{t\to \mathrm{\infty }}{lim}\frac{A-\alpha (I(s)+Q(s))}{\mu }\\ =& \frac{A}{\mu }\text{a.s.}\end{array}$$

This finishes the proof of Theorem 3.1. □

Remark 3.2 Theorem 3.1 tells us the disease will die out if ${\tilde{R}}_0<1$ and the white noise is not large satisfied ${\sigma }^2\le \frac{\beta \mu }{A}$. Moreover, we notice the conditions for $I(t)$ to become extinct in the SDE model (1.3) are weaker than in the corresponding deterministic model. When the white noise is large enough such that ${\sigma }^2>max\{\frac{{\beta }^2}{2(\gamma +\delta +\mu +\alpha )},\frac{\beta \mu }{A}\}$ is satisfied, the disease will also die out. The following examples illustrate this result more explicitly.

Example 3.3 Throughout the paper we shall assume that the unit of time is one day and the population sizes are measured in units of 1 million. Choose the parameters in system (1.3) as follows:

$$\begin{array}{r}A=0.8,\beta =0.6,\mu =0.4,\alpha =0.2,\gamma =0.3,\\ \epsilon =0.2,\delta =0.1,\sigma =0.4.\end{array}$$

(3.11)

Note that

$${\tilde{R}}_0=\beta \left(\frac{A}{\mu }\right)\frac{1}{(\mu +\gamma +\delta +\alpha )+\frac{1}{2}{\sigma }^2{(\frac{A}{\mu })}^2}=0.9091<1\text{and}{\sigma }^2=0.16\le \frac{\beta \mu }{A}=0.3,$$

then by Theorem 3.1, the solution $(S(t),I(t),Q(t))$ of system (1.3) obeys

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{logI(t)}{t}⩽\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})=-0.12<0,\text{a.s.}$$

and

$$\underset{t\to \mathrm{\infty }}{lim}S(t)=\frac{A}{\mu }=2,\underset{t\to \mathrm{\infty }}{lim}Q(t)=0\text{a.s.}$$

with any initial value $(S(0),I(0),Q(0))=(0.8,0.4,0.5)\in {\mathrm{\Gamma }}^{\ast }$. That is, $I(t)$ will tend to zero exponentially with probability one.

On the other hand, for the corresponding deterministic model (1.1),

$$R_0=\frac{\beta A}{\mu (\mu +\delta +\gamma +\alpha )}=1.2>1,$$

(3.12)

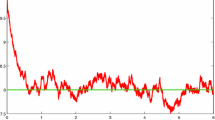
then the endemic equilibrium $(S^{\ast },I^{\ast },Q^{\ast })$ is globally asymptotically stable in Γ. Using the method mentioned in [19], we give the simulations shown in Figure 1 to support our results.

Figure 1

Computer simulation of the path $\mathit{S}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{I}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{Q}\mathbf{(}\mathit{t}\mathbf{)}$ for model ( 1.3 ) and ( 1.1 ) for parameter values $\mathit{A}\mathbf{=}\mathbf{0.8}$ , $\mathit{\beta }\mathbf{=}\mathbf{0.6}$ , $\mathit{\mu }\mathbf{=}\mathbf{0.4}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.2}$ , $\mathit{\gamma }\mathbf{=}\mathbf{0.3}$ , $\mathit{\epsilon }\mathbf{=}\mathbf{0.2}$ , $\mathit{\delta }\mathbf{=}\mathbf{0.1}$ and $\mathit{\sigma }\mathbf{=}\mathbf{0.4}$ , with step size $\mathbf{\Delta }\mathit{t}\mathbf{=}\mathbf{0.001}$ and initial value $\mathbf{(}\mathit{S}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{,}\mathit{I}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{,}\mathit{Q}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{)}\mathbf{=}\mathbf{(}\mathbf{0.8}\mathbf{,}\mathbf{0.4}\mathbf{,}\mathbf{0.5}\mathbf{)}$ .

Example 3.4 We keep all the parameters of (3.11) unchanged but increase σ to 0.6. Note that ${\sigma }^2=0.36>0.3=max\{\frac{{\beta }^2}{2(\gamma +\delta +\mu +\alpha )},\frac{\beta \mu }{A}\}$, then by Theorem 3.1, the solution $(S(t),I(t),Q(t))$ of system (1.3) obeys

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{logI(t)}{t}⩽-(\mu +\gamma +\alpha +\delta )+\frac{{\beta }^2}{2{\sigma }^2}=-0.5<0\text{a.s.}$$

That is, $I(t)$ will tend to zero exponentially with probability one. But, for the corresponding deterministic model (1.1), note (3.12), $R_0=1.2>1$, then the endemic equilibrium $(S^{\ast },I^{\ast },Q^{\ast })$ is globally asymptotically stable in Γ. Using the method mentioned in [19], we give the simulations shown in Figure 2 to support our results.

Figure 2

Computer simulation of the path $\mathit{S}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{I}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{Q}\mathbf{(}\mathit{t}\mathbf{)}$ for model ( 1.3 ) and ( 1.1 ) for parameter values $\mathit{A}\mathbf{=}\mathbf{0.5}$ , $\mathit{q}\mathbf{=}\mathbf{0.8}$ , $\mathit{\beta }\mathbf{=}\mathbf{0.5}$ , $\mathit{\mu }\mathbf{=}\mathbf{0.1}$ , $\mathit{p}\mathbf{=}\mathbf{0.6}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.2}$ , $\mathit{\gamma }\mathbf{=}\mathbf{0.3}$ , $\mathit{\epsilon }\mathbf{=}\mathbf{0.2}$ , and $\mathit{\sigma }\mathbf{=}\mathbf{0.6}$ , with step size $\mathbf{\Delta }\mathit{t}\mathbf{=}\mathbf{0.001}$ and initial value $\mathbf{(}\mathit{S}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{,}\mathit{I}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{,}\mathit{Q}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{)}\mathbf{=}\mathbf{(}\mathbf{0.8}\mathbf{,}\mathbf{0.4}\mathbf{,}\mathbf{0.5}\mathbf{)}$ .

4 Persistence

Since there is no internal equilibrium model in the stochastic infectious disease model, how to choose the appropriate scale to reflect the widespread prevalence of the disease is a key issue. We first give a definition of persistence in the mean and a lemma to be used in proof.

Definition 4.1 System (1.3) is said to be persistent in the mean, if

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\frac{1}{t}{\int }_0^{t}I(r)dr>0\text{a.s.}$$

Lemma 4.2 [7]

Let $f\in C[[0,\mathrm{\infty })\times \mathrm{\Omega },(0,\mathrm{\infty })]$ and $F(t)\in C([0,\mathrm{\infty })\times \mathrm{\Omega },R)$. If there exist positive constants ${\lambda }_0$, λ, and T such that

$$logf(t)\le \lambda t-{\lambda }_0{\int }_0^{t}f(s)ds+F(t)\mathit{\text{a.s.}}$$

for all $t\ge T$, and ${lim}_{t\to \mathrm{\infty }}\frac{F(t)}{t}=0$ a.s., then

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{1}{t}{\int }_0^{t}f(s)ds\le \frac{\lambda }{{\lambda }_0}\mathit{\text{a.s.}}$$

Theorem 4.1 If ${\tilde{R}}_0>1$ and ${\sigma }^2<\frac{\beta \mu }{A}$, then for any initial value $(S(0),I(0),Q(0))\in {\mathrm{\Gamma }}^{\ast }$, the solution $(S(t),I(t),Q(t))$ of system (1.3) has the following property:

$${\tilde{I}}_{\ast }\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈I(t)〉\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈I(t)〉\le {\tilde{I}}^{\ast }\mathit{\text{a.s.}},$$

(4.1)

where

$${\tilde{I}}_{\ast }=\frac{\frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})}{(\frac{\mu +\alpha }{\mu })\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }},{\tilde{I}}^{\ast }=\frac{\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})}{(\frac{\mu +\alpha }{\mu })\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }(\beta -{\sigma }^2\frac{A}{\mu })}.$$

Moreover,

$$\frac{A}{\mu }-\frac{\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})}{\beta -{\sigma }^2\frac{A}{\mu }}\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈S(t)〉\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈S(t)〉\le \frac{A}{\mu {\tilde{R}}_0}\mathit{\text{a.s.}},$$

(4.2)

and

$$\begin{array}{rl}\frac{A\delta (1-\frac{1}{{\tilde{R}}_0})}{(\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}& \le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈Q(t)〉\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈Q(t)〉\\ \le \frac{\beta A\delta (1-\frac{1}{{\tilde{R}}_0})}{(\mu +\alpha )(\mu +\epsilon +\alpha +\delta )(\beta -{\sigma }^2\frac{A}{\mu })}\mathit{\text{a.s.}}\end{array}$$

(4.3)

Proof By the last inequality of (3.7), we have

$$\begin{array}{rl}\frac{logI(t)}{t}\le & \beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})-\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }[\beta -{\sigma }^2\frac{A}{\mu }]〈I(t)〉\\ +\mathrm{\Phi }(t)+\frac{\sigma M(t)}{t}+\frac{logI(0)}{t}.\end{array}$$

If ${\tilde{R}}_0>1$ and ${\sigma }^2<\frac{\beta \mu }{A}$, together with Lemma 4.2 and (3.9), then

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈I(t)〉⩽\frac{\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})}{(\frac{\mu +\alpha }{\mu })\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }(\beta -{\sigma }^2\frac{A}{\mu })}.$$

(4.4)

On the other hand, substituting (3.4) into the first equality of (3.6), then

$$\begin{array}{rcl}\frac{logI(t)-logI(0)}{t}& \le & \beta [\frac{A}{\mu }-\left(\frac{\mu +\alpha }{\mu }\right)\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }〈I(t)〉+\phi (t)]\\ -(\mu +\gamma +\delta +\alpha )-\frac{1}{2}{\left(\frac{A}{\mu }\right)}^2+\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r).\end{array}$$

We compute that

$$\begin{array}{rcl}〈I(t)〉& \ge & \frac{\mu (\mu +\epsilon +\alpha )}{\beta (\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}[\beta \frac{A}{\mu }-(\mu +\gamma +\delta +\alpha )-\frac{1}{2}{\sigma }^2{\left(\frac{A}{\mu }\right)}^2+\beta \phi (t)\\ +\frac{\sigma }{t}{\int }_0^{t}S(r)dB(r)-\frac{logI(t)-logI(0)}{t}]\\ =& \frac{\mu (\mu +\epsilon +\alpha )}{\beta (\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}[\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})+\beta \phi (t)\\ +\frac{\sigma }{t}M(t)-\frac{logI(t)-logI(0)}{t}].\end{array}$$

(4.5)

If ${\tilde{R}}_0>1$ and ${\sigma }^2<\frac{\beta \mu }{A}$, taking the limit inferior of both sides (4.5) leads to

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈I(t)〉\ge \frac{\mu (\mu +\epsilon +\alpha )}{\beta (\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})=\frac{\frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})}{\frac{(\mu +\alpha )}{\mu }\frac{\mu +\epsilon +\alpha +\delta }{\mu +\epsilon +\alpha }}.$$

(4.6)

Combining (4.4) with (4.6), conclusion (4.1) is proved.

Moreover, due to equality (3.4) and inequalities (4.4), (4.6), we have

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈S(t)〉=\frac{A}{\mu }-\frac{(\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}{\mu (\mu +\epsilon +\alpha )}\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈I(t)〉\ge \frac{A}{\mu }-\frac{\beta \frac{A}{\mu }(1-\frac{1}{{\tilde{R}}_0})}{\beta -{\sigma }^2\frac{A}{\mu }}$$

and

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈S(t)〉=\frac{A}{\mu }-\frac{(\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}{\mu (\mu +\epsilon +\alpha )}\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈I(t)〉\le \frac{A}{\mu {\tilde{R}}_0}.$$

In view of (3.3), (4.3), and (4.4), we get

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈Q(t)〉=\frac{\delta }{\mu +\epsilon +\alpha }\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈I(t)〉\ge \frac{A\delta (1-\frac{1}{{\tilde{R}}_0})}{(\mu +\alpha )(\mu +\epsilon +\alpha +\delta )}$$

and

$$\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈Q(t)〉=\frac{\delta }{\mu +\epsilon +\alpha }\underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈I(t)〉\le \frac{\beta A\delta (1-\frac{1}{{\tilde{R}}_0})}{(\mu +\alpha )(\mu +\epsilon +\alpha +\delta )(\beta -{\sigma }^2\frac{A}{\mu })}.$$

This finishes the proof of Theorem 4.1. □

Remark 4.3 From Theorem 3.1 and Theorem 4.1, we can see when the noise is so small that ${\sigma }^2<\frac{\beta \mu }{A}$, then the value of ${\tilde{R}}_0<1$ will lead to the disease dying out and the value of ${\tilde{R}}_0>1$ will lead to the disease prevailing. So we consider ${\tilde{R}}_0$ as the threshold of stochastic system (1.3).

Example 4.4 Assume that the parameters of system (1.3) are given by

$$\begin{array}{r}A=0.8,\beta =0.8,\mu =0.2,\alpha =0.2,\gamma =0.3,\\ \epsilon =0.2,\delta =0.1,\sigma =0.1.\end{array}$$

(4.7)

Note that

$${\tilde{R}}_0=\beta \left(\frac{A}{\mu }\right)\frac{1}{(\mu +\gamma +\delta +\alpha )+\frac{1}{2}{\sigma }^2{(\frac{A}{\mu })}^2}=3.6364>1\text{and}{\sigma }^2=0.01<\frac{\beta \mu }{A}=0.2,$$

then by Theorem 4.1, for any initial value $(S(0),I(0),Q(0))=(0.8,0.4,0.5)\in {\mathrm{\Gamma }}^{\ast }$, we conclude that the solution $(S(t),I(t),Q(t))$ of system (1.3) obeys

$$1.2428\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}inf}〈I(t)〉\le \underset{t\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈I(t)〉\le 1.5081\text{a.s.}$$

That is to say, the disease will prevail.

To further illustrate the effect of the noise intensity σ on the model (1.3), we keep all the parameters of (4.7) unchanged but increase σ to 0.05. Using the method mentioned in [19], we give the simulations to support our results in Figure 3. Comparing the first picture and the second picture in Figure 3, with the noise getting smaller, the fluctuation of the solution of system (1.3) is getting weaker.

Figure 3

Computer simulation of the path $\mathit{S}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{I}\mathbf{(}\mathit{t}\mathbf{)}$ , $\mathit{Q}\mathbf{(}\mathit{t}\mathbf{)}$ for model ( 1.3 ) and ( 1.1 ) for parameter values $\mathit{A}\mathbf{=}\mathbf{0.8}$ , $\mathit{\beta }\mathbf{=}\mathbf{0.8}$ , $\mathit{\mu }\mathbf{=}\mathbf{0.2}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.2}$ , $\mathit{\gamma }\mathbf{=}\mathbf{0.3}$ , $\mathit{\epsilon }\mathbf{=}\mathbf{0.2}$ , $\mathit{\delta }\mathbf{=}\mathbf{0.1}$ , $\mathit{\sigma }\mathbf{=}\mathbf{0.1}$ , and $\mathit{\sigma }\mathbf{=}\mathbf{0.05}$ , with step size $\mathbf{\Delta }\mathit{t}\mathbf{=}\mathbf{0.001}$ and initial value $\mathbf{(}\mathit{S}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{,}\mathit{I}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{,}\mathit{Q}\mathbf{(}\mathbf{0}\mathbf{)}\mathbf{)}\mathbf{=}\mathbf{(}\mathbf{0.8}\mathbf{,}\mathbf{0.4}\mathbf{,}\mathbf{0.5}\mathbf{)}$ .