Analytic and numerical solutions of nonlinear diffusion equations via symmetry reductions

Abstract

In this article, the authors study analytic and numerical solutions of nonlinear diffusion equations of Fisher’s type with the help of classical Lie symmetry method. Lie symmetries are used to reduce the equations into ordinary differential equations (ODEs). Lie group classification with respect to time dependent coefficient and optimal system of one-dimensional sub-algebras is obtained. Then sub-algebras are used to construct symmetry reduction and analytic solutions. Finally, numerical solutions of nonlinear diffusion equations are obtained by using one of the differential quadrature methods.

1 Introduction

Consider the nonlinear diffusion equation

$$\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial x^2}+g(u).$$

(1)

When $g(u)=\alpha u(1-u)$, (1) stands for the Fisher equation, put forward by Fisher [1] as a model for the spatial and temporal propagation of a viral gene in an infinite medium. This equation also expresses a one-dimensional reaction-diffusion model for the evolution of the infected population. The equation is defined by

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+\alpha u(1-u)$$

(2)

in which $\alpha >0$ is a parameter. Kawahara and Tanaka [2] found an exact solution describing the coalescence of two traveling wave fronts of (2). Applications of traveling wave fronts appear in biology, chemistry, and medicine [3]. Such wave fronts were studied by Fisher for the first time in 1930s by considering (2).

The Fisher equation (2) appears in chemical kinetics [4], in logistic population growth models [5], autocatalytic chemical reactions, branching Brownian motion processes, flame propagation, and neurophysiology. The reaction-diffusion equation (2) also expresses a model equation for the evolution of a neutron population in a nuclear reactor [6] and also arises in the study of chemical wave propagation [7]. This equation includes the effects of linear diffusion via $u_{xx}$ and nonlinear local multiplication or reaction via $u(1-u)$.

There is a large cycle of works on mathematical properties and discussion of the Fisher equation in the literature. Larson [8], Kawahara and Tanaka [2], and Brazhnik and Tyson [5] provided excellent summaries of the Fisher equation. Ablowitz and Zepetella [9] gave the presentation of explicit solutions of the Fisher equation for a special wave speed. For the generalized the Fisher equation, Wang [10] presented the exact and explicit solitary wave solutions. Then Wazwaz and Gorguis [11] considered an analytic study of the Fisher equation by using the Adomian decomposition method. But it was not before 1974 when numerical solutions of the Fisher equation were available in the literature. Gazdag and Canosa [12] were the first to study numerical solutions of the Fisher equation with a pseudo-spectral approach. Afterwards, a lot of researchers have studied numerical solutions on the Fisher equation. Hagstrom and Keller [13] presented asymptotic boundary conditions by using a centered finite-difference algorithm. Afterwards, Evans and Sahimi [14] used an alternating group explicit iterative method to solve (2) and obtained satisfactory results, of a qualitatively similar nature. The numerical scheme considered in [14] is quite complicated and it causes unexpected high-frequency oscillations, which must be filtered out at each time step. Next, Parekh and Puri [15] and Twizell et al. [16] developed implicit and explicit finite differences algorithms for numerically solving the Fisher equation. Then Tang and Weber [17] proposed a Galerkin finite element method. Mickens [18] put forward a best finite-difference scheme for the Fisher equation. Afterwards, Garey and Shen [19] used a least-squares finite element method and Qiu and Sloan [20] used a moving mesh method for numerical solution of the Fisher equation. Rizwan [21] compared the nodal integral method and non-standard finite-difference schemes, and Khaled [22] proposed the Sinc collocation method. Daniel et al. [23] proposed a pseudo-spectral method for the numerical solution of the Fisher equation. Mittal and Kumar [24] studied the Fisher equation by applying wavelet Galerkin method, while Jiwari et al. [25–30] studied numerical solutions of some nonlinear evolution equations by using differential quadrature method. Finally, for numerical solutions of the nonlinear Fisher reaction-diffusion equation, Mittal and Jain [31] proposed a numerical method, based on collocation of modified cubic B-splines over finite elements.

The purpose of this paper is to present analytic and numerical solutions via symmetry reductions of nonlinear diffusion equations of Fisher’s type defined as:

F1: Fisher’s equation

$$u_t-u_{xx}-\alpha u(1-u)=0;$$

(3)

F2: Fisher’s type equation

$$u_{t.}-u_{xx}-u^2(1-u)=0;$$

(4)

F3: Fisher’s type equation

$$u_{t.}-u_{xx}-u(u-a)(1-u)=0$$

(5)

in which a is a parameter.

Lie symmetries are used to reduce the equations to ordinary differential equations (ODEs). In the next section, lie group classification with respect to time dependent coefficient and optimal system of one-dimensional sub-algebras is obtained. Then, in Section 3, sub-algebras are used to construct symmetry reduction and analytic solutions. In Section 4, numerical solutions of nonlinear diffusion equations are obtained by using polynomial differential quadrature method. Finally, in Section 5, absolute, root mean square (RMS), and $L_{\mathrm{\infty }}$ errors are calculated.

2 Method of Lie symmetries

In this section, we recall the general procedure for determining symmetries for any system of partial differential equation. To begin, let us consider that the general case of a nonlinear system of partial differential equations of order n in p-independent and q-dependent variables is given as a system of equations,

$${\mathrm{\Delta }}_v(x,u^{(n)})=0,v=1,\dots ,l.$$

(6)

This entails $x=(x^1,\dots ,x^p)$, $u=(u^1,\dots ,u^q)$, and the derivatives of u with respect to x up to n, where $u^{(n)}$ expresses all the derivatives of u of all orders from 0 to n. We consider a one-parameter Lie group of infinitesimal transformation acting on the independent and dependent variables of the system (6)

$$\begin{array}{r}{(x^{\ast })}^i=x^i+s{\xi }^i(x,u)+O\left(s^2\right),i=1,\dots ,p,\\ {(u^{\ast })}^j=u^j+s{\eta }^j(x,u)+O\left(s^2\right),j=1,\dots ,q,\end{array}$$

(7)

where s is the parameter of transformation and ${\xi }^i$, ${\eta }^j$ are infinitesimals of transformation for the independent and dependent variables, respectively. The invariance of the system (6) under the infinitesimal transformation leads to the invariance conditions

$$p_r^{(n)}\left[{\mathrm{\Delta }}_v(x,u^{(n)})\right]=0,v=1,\dots ,l\text{ whenever }{\mathrm{\Delta }}_v(x,u^{(n)})=0,$$

(8)

where $p_r^{(n)}$ is called the n th-order prolongation of infinitesimal generator given by

$$p_r^{(n)}=v+\sum _{\alpha =1}^q\sum {\varphi }_{\alpha }^j(x,u^{(n)})\partial u_j^{\alpha },$$

(9)

where $j=(j_1,\dots ,j_k)$, $1\le j_k\le p$, $1\le k\le n$, and the sum is over all orders of j. If $j=k$ the coefficients ${\varphi }_j^{\alpha }$ of $\partial u_j^{\alpha }$ will only depend on k th- and lower-order derivatives of u;

$${\varphi }_{\alpha }^j(x,u^{(n)})=D_j({\varphi }_{\alpha }-\sum _{i=1}^p{\xi }^i{u}_i^{\alpha })+\sum _{i=1}^p{\xi }^i{u}_{j,i}^{\alpha },$$

(10)

where $u_i^{\alpha }=\frac{\partial u^{\alpha }}{\partial x^i}$ and $u_{j,i}^{\alpha }=\frac{\partial u_j^{\alpha }}{\partial x^i}$.

One of the most important properties of these infinitesimal symmetries is that they form a Lie algebra under the usual Lie bracket.

3 Polynomial differential quadrature method

Differential quadrature method is a numerical technique to find the numerical solution of differential equations. The technique is used for the discretization of the spatial derivatives. The polynomial differential quadrature discretization of the first and the second derivatives at a point $x_i$ is given by the following equations:

$$u_x(x_i,t)=\sum _{j=1}^N{a}_{ij}u(x_j,t),u_{xx}(x_i,t)=\sum _{j=1}^N{b}_{ij}u(x_j,t),$$

(11)

where $a_{ij}$ and $b_{ij}$ express the weighting coefficients [32], $i=1,2,\dots ,N$. The following basis functions are used to obtain the weighting coefficients:

$$g_k(x)=\frac{L(x)}{(x-x_k)L^{(1)}(x_k)},k=1,2,\dots ,N,$$

(12)

where

$$L(x)=(x-x_1)(x-x_2)\cdots (x-x_N),$$

(13)

$$L^{(1)}(x_i)=\prod _{k=1,k\ne i}^N(x_i-x_k)$$

(14)

when $x\ne x_i$ and then

$$g_k(x)=x^k,k=1,2,\dots ,N$$

(15)

since both test functions given in (12) and (15) span the problem domain. The off-diagonal weighting coefficients for the first-order derivative are determined by using the set of basis functions given in (12) and the off-diagonal weighting coefficients of the first-order derivative are found as [32]

$$a_{ij}=\frac{L^{(1)}(x_i)}{(x_i-x_j)L^{(1)}(x_j)},k=1,2,\dots ,N,i\ne j.$$

(16)

The set of basis functions given in (15) are used to find the following diagonal weighting coefficients:

$$a_{ii}=-\sum _{j=1,j\ne i}^N{a}_{ij},i=1,2,\dots ,N.$$

(17)

In the same way the weighting coefficients of the second-order derivative are derived by the same basis functions and the weighting coefficients are found as [32]

$$b_{ij}=2a_{ij}(a_{ii}-\frac{1}{x_i-x_j}),i,j=1,2,\dots ,N,i\ne j,$$

(18)

$$b_{ii}=-\sum _{j=1,j\ne i}^N{b}_{ij},i=1,2,\dots ,N.$$

(19)

Similarly, Shu [32] proposed the weighting coefficients of higher-order derivatives in the explicit form

$$w_{ij}^{(r)}=r[a_{ij}{w}_{ii}^{(r-1)}-\frac{w_{ii}^{(r-1)}}{x_i-x_j}],\text{for }i\ne j,i,j=1,2,\dots ,N;r=3,4,\dots ,N-1,$$

(20)

$$w_{ii}^{(r)}=-\sum _{j=1,j\ne i}^N{w}_{ij}^{(r)},\text{for }i=j,$$

(21)

where $a_{ij}$ and $w_{ij}^{(r)}$ are the weighting coefficients of the first-order derivative and r th-order derivative, respectively.

4 Lie classical analysis for nonlinear diffusion Fisher’s type equations

In this section, we study the infinitesimal transformations and reductions by one-dimensional sub-algebras of (3)-(5) by applying the classical Lie symmetry method [33] one by one. Consider the one-parameter group of infinitesimal transformations in $(x,t,u)$ given by

$$\begin{array}{r}{x}^{\ast }=x+\epsilon \xi (x,t,u)+O({\epsilon }^2),\\ t^{\ast }=t+\epsilon \tau (x,t,u)+O({\epsilon }^2),\\ u^{\ast }=u+\epsilon \eta (x,t,u)+O({\epsilon }^2),\end{array}$$

(22)

where ε is the group parameter. The functions ξ, τ, η are the infinitesimals of the transformations for the variables x, t, and u, respectively. We shall denote the infinitesimals for $u_t$, $u_{xx}$ by ${\eta }^x$, ${\eta }^{xx}$. The infinitesimals are as follows:

$$\begin{array}{r}{\eta }^x\equiv {(\eta -\xi u_x-\tau u_t)}_x+\xi u_{xx}+\tau u_{tx},\\ {\eta }^{xx}\equiv {(\eta -\xi u_x-\tau u_t)}_{xx}+\xi u_{xxx}+\tau u_{txx}.\end{array}$$

(23)

Using these various extensions, the infinitesimal criterion for the invariance of (3)-(5) under the group (22) is given by

$$VH{|}_{H=0}\equiv 0,$$

(24)

where $H=(x^{\ast },t^{\ast },v^{\ast },v_{x^{\ast }},v_{t^{\ast }},v_{x^{\ast }{x}^{\ast }})$ and $v=\theta (x^{\ast },t^{\ast })$ are also solutions of (3)-(5). In (24), the prolongation of the tangent vector field V is given by

$$V=\xi \frac{\partial }{\partial x}+\tau \frac{\partial }{\partial t}+{\eta }^x\frac{\partial }{\partial u_x}+{\eta }^t\frac{\partial }{\partial u_t}+{\eta }^{xx}\frac{\partial }{\partial u_{xx}}+\cdots .$$

(25)

Now, substitute (23) and (25) into (24). Then we collect together the coefficients of u, $u_x$, $u_t$, $u_{xx}$, $u_{tt}$ and set all of them to zero. Finally, we get a system of linear partial differential equations from which we can find ξ, τ, and η in practice.

Next we will use the above method to find the Lie symmetry group of the Fisher type equations (3)-(5). The prolongation of the tangent vector field of (3) is given by

$$V=\xi \frac{\partial }{\partial x}+\tau \frac{\partial }{\partial t}+{\eta }^x\frac{\partial }{\partial u_x}+{\eta }^t\frac{\partial }{\partial u_t}+{\eta }^{xx}\frac{\partial }{\partial u_{xx}}+{\eta }^{tt}\frac{\partial }{\partial u_{tt}}.$$

(26)

After substituting (23) and (26) into (24), we have

$${\eta }^t-{\eta }^{xx}-\eta +2u\eta =0.$$

(27)

Now, substituting (23) in (27), we get a system of linear partial differential equations. We set all the coefficients of u, $u_x$, $u_t$, $u_{xx}$ to zero. Then we obtain

$$\xi =a,\tau =b,\eta =0,$$

where a and b are arbitrary constants. The associated vector fields for the one-parameter Lie group of infinitesimal transformations are $V_1$ and $V_2$ as given by

$$V_1=\frac{\partial }{\partial x},V_2=\frac{\partial }{\partial t}.$$

Firstly, we construct an optimal system to classify the group-invariant solutions of (3) and the problem of finding an optimal subgroup is equivalent to that of finding an optimal system of sub-algebras. Here, by using the method presented in [33], we will construct an optimal system of one-dimensional sub-algebras of (22). The general one-parameter group of symmetries can be obtained by considering the linear combination $V=a_1{V}_1+a_2{V}_2$ of given vector fields. But the explicit formulas for the above transformations are very complicated. Factually, they can be expressed uniquely in the form

$$g=exp({\epsilon }_1{V}_1)+exp({\epsilon }_2{V}_2).$$

(28)

Our task is to simplify as many of the coefficients ${\epsilon }_i$, $i=1,2$ as possible though judicious applications of adjoint maps to V. By taking $a_2\ne 0$, $a_2=1$, we have $V_2+a_1{V}_1$.

4.1 Reductions by one-dimensional sub-algebras

Case 1: Thus making use of this group transformation, the similarity variable and similarity solution are given by

$$\zeta =x-ct,u(x,t)=F(\zeta ).$$

(29)

After substituting these similarity variables in (3), the equation reduced into ordinary differential equation (ODE) given by

$$-c{F}^{\prime }(\zeta )-F^{″}(\zeta )-\alpha F(\zeta )(1-F(\zeta ))=0.$$

(30)

The exact solution corresponding to this ODE is given by

$$c=-\frac{5\sqrt{\alpha }}{\sqrt{6}},F(\zeta )=\frac{1}{4}-\frac{1}{2}tanh(-c_1+\frac{1}{12}\sqrt{6\alpha }\zeta )+\frac{1}{4}tanh{(-c_1+\frac{1}{12}\sqrt{6\alpha }\zeta )}^2,$$

(31)

where $c_1$ is a constant.

Thus, the exact solution of Fisher equation (3) is given by

$$u(x,t)=\frac{1}{4}-\frac{1}{2}tanh(-c_1+\frac{1}{12}\sqrt{6\alpha }(x-ct))+\frac{1}{4}tanh{(c_1+\frac{1}{12}\sqrt{6\alpha }(x-ct))}^2.$$

(32)

In this similar way, we can apply the Lie classical method to (4) and (5) and can study the exact solutions of these equations.

Case 2: Now, by applying the Lie classical method to (4), the following vector fields are obtained:

$$V_1=\frac{\partial }{\partial x},V_2=\frac{\partial }{\partial t}.$$

The optimal system of these vector fields is

$$(\mathrm{i})V_2+a_2{V}_1,$$

where $a_2$ is an arbitrary constant.

$$(\mathrm{ii})V_1.$$

The similarity variable and similarity solution corresponding to the basic vector field $V_2+a_2{V}_1$ are given by

$$\zeta =x-lt,u(x,t)=F(\zeta ),$$

where $l=\frac{1}{a_2}$, $a_2\ne 0$. On using this similarity variable and similarity solution into (4), this equation reduces to

$$-l{F}^{\prime }(\zeta )-F^{″}(\zeta )-F^2(\zeta )(1-F(\zeta ))=0.$$

(33)

The solution of the above ODE is given by

$$l=\frac{1}{\sqrt{2}},F(\zeta )=\frac{1}{2}-\frac{1}{2}tanh(c_2+\frac{1}{4}\sqrt{2}\zeta ).$$

(34)

Thus, the exact solution of the Fisher equation (4) is given by

$$u(x,t)=\frac{1}{2}-\frac{1}{2}tanh(c_2+\frac{1}{4}\sqrt{2}(x-\frac{1}{\sqrt{2}}t)),$$

(35)

where $c_2$ is a constant.

Corresponding to the basic vector field $V_1$ in the optimal system, we can obtain only a constant solution.

Case 3: After utilizing the Lie classical method for (5), the following vector fields are obtained:

$$V_1=\frac{\partial }{\partial x},V_2=\frac{\partial }{\partial t}.$$

The optimal systems of these vector fields contain the following sub-algebras:

$$(\mathrm{i})V_2+a_3{V}_1,$$

where $a_3$ is an arbitrary constant.

$$(\mathrm{ii})V_1.$$

For the sub-algebra, $V_2+a_3{V}_1$, the similarity variable and similarity solution are

$$\zeta =x-mt,u(x,t)=F(\zeta ),\text{where }m=\frac{1}{a_3},a_3\ne 0.$$

Using these similarity variables in the nonlinear diffusion equation (5), the reduced ODE is

$$-m{F}^{\prime }(\zeta )-F^{″}(\zeta )-F(\zeta )(1-F(\zeta ))(F(\zeta )-a)=0.$$

(36)

The exact solution of the above ODE is given as

$$m=\frac{1}{\sqrt{2}}(1+a),F(\zeta )=\frac{1}{2}+\frac{1}{2}a+(\frac{1}{2}-\frac{1}{2}a)tanh(c_3+\frac{1}{4}\sqrt{2}(-1+a)\zeta ),$$

(37)

where $c_3$ is an arbitrary constant.

Now, the exact solution of the nonlinear diffusion equation (5) is given by

$$u(x,t)=\frac{1}{2}+\frac{1}{2}a+(\frac{1}{2}-\frac{1}{2}a)tanh(c_3+\frac{1}{4}\sqrt{2}(-1+a)(x-mt)).$$

(38)

For the sub-algebra $V_1$, only a constant can be obtained.

5 Comparative study of exact and numerical solutions of Fisher’s type equations

In this section, a comparative study of exact and numerical solutions is made by finding a numerical solution of the equations with the help of the polynomial differential quadrature method. For this purpose, the exact solutions obtained in Section 4 are used for initial and boundary conditions to find the numerical solution by polynomial differential quadrature method (PDQM). Discretizing the spatial derivatives of equations (3)-(5) by using PDQM at the point $x_i$, we have

$$\frac{d{u}_i}{dt}=\sum _{j=1}^N{b}_{ij}{u}_j+\alpha u_i(1-u_i),i=1,2,\dots ,N,$$

(39)

$$\frac{d{u}_{i.}}{dt}=\sum _{j=1}^N{b}_{ij}{u}_j+u_i^2(1-u_i),i=1,2,\dots ,N,$$

(40)

$$\frac{d{u}_{i.}}{dt}=\sum _{j=1}^N{b}_{ij}{u}_j+u_i(1-u_i)(u_i-a),i=1,2,\dots ,N,$$

(41)

where α, a are parameters, $b_{ij}$ are weighting coefficients of the second-order partial derivative and $u_i=u(x_i,t)$. Equations (39)-(40) are systems of first-order nonlinear differential equations. The initial and boundary conditions are taken from the analytic solutions obtained by Lie symmetry method in Section 4. Finally, the systems of initial and boundary value problems are solved by Pike and Roe’s fourth-stage RK4 [34].

5.1 Numerical experiments and discussion

In this subsection, three particular numerical examples are considered with fixed values of the arbitrary constants occurring in the solutions of (3)-(5) and numerical solutions are obtained by using the polynomial differential quadrature method. The whole computation work is done by the MATLAB and DEV C++ software. Absolute errors $L_{\mathrm{\infty }}$, root mean square error (RMS), and $L_2$ are computed according to the following formulas:

$$\begin{array}{c}{L}_{\mathrm{\infty }}-Error=\underset{1\le i\le n}{max}|e_i|,RMS-Error={\left(\sum _{i=1}^n\frac{e_i^2}{n}\right)}^{1/2},\text{and}\hfill \\ L_2-Error={\left(\sum _{i=1}^n{e}_i^2\right)}^{1/2},\hfill \end{array}$$

where $e_i=(u_i-U_i)$, $u_i$ are approximated solutions and $U_i$ are exact solutions.

Example 1 Consider (3) over the domain $[0,1]$ with the following initial conditions:

$$u(x,0)=\frac{1}{4}-\frac{1}{2}tanh(-c_1+\frac{1}{12}\sqrt{6\alpha }(x))+\frac{1}{4}tanh{(c_1+\frac{1}{12}\sqrt{6\alpha }(x))}^2$$

and boundary conditions:

$$\begin{array}{c}u(0,t)=\frac{1}{4}-\frac{1}{2}tanh(-c_1+\frac{1}{12}\sqrt{6\alpha }(-ct))+\frac{1}{4}tanh{(c_1+\frac{1}{12}\sqrt{6\alpha }(-ct))}^2,\hfill \\ u(1,t)=\frac{1}{4}-\frac{1}{2}tanh(-c_1+\frac{1}{12}\sqrt{6\alpha }(1-ct))+\frac{1}{4}tanh{(c_1+\frac{1}{12}\sqrt{6\alpha }(1-ct))}^2,\hfill \end{array}$$

where $c=\frac{-5\sqrt{\alpha }}{\sqrt{6}}$ and $c_1$ is an arbitrary constant.

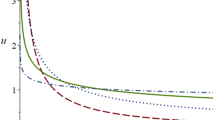
The exact solution of the equation is taken from (32). Numerical solutions in the form of errors of the example are given in Table 1. The table shows that the errors are small and negligible. Figure 1 compares the numerical and exact solutions in 3D form and it is concluded that the solutions are very similar.

Figure 1

Numerical (left) and exact (right) solutions of Example 1 for ${\mathit{c}}_{\mathbf{1}}\mathbf{=}\mathit{\alpha }\mathbf{=}\mathbf{1}$ up to time $\mathit{t}\mathbf{=}\mathbf{1}$ .

Table 1 ${\mathit{L}}_{\mathbf{\infty }}$ , RMS, and ${\mathit{L}}_{\mathbf{2}}$ errors of Example 1 at different times t and for different constants

Example 2 In this example, we have considered the Fisher equation (4) over the domain $[0,1]$ with the following initial conditions:

$$u(x,t)=\frac{1}{2}-\frac{1}{2}tanh(c_2+\frac{1}{4}\sqrt{2}(x))$$

and boundary conditions:

$$\begin{array}{c}u(0,t)=\frac{1}{2}-\frac{1}{2}tanh(c_2+\frac{1}{4}\sqrt{2}(-\frac{1}{\sqrt{2}}t)),\hfill \\ u(1,t)=\frac{1}{2}-\frac{1}{2}tanh(c_2+\frac{1}{4}\sqrt{2}(1-\frac{1}{\sqrt{2}}t)).\hfill \end{array}$$

The exact solution of the equation is taken from (35). Numerical solutions of the example are given in Table 2 and Figure 2. Table 2 presents the errors at different times and parameter values which are small and negligible. Figure 2 depicts a comparison of numerical and exact solutions in 3D form and it is concluded that the solutions are very similar.

Figure 2

Numerical (left) and exact (right) solutions of Example 2 for ${\mathit{c}}_{\mathbf{2}}\mathbf{=}\mathbf{1}$ up to time $\mathit{t}\mathbf{=}\mathbf{1}$ .

Table 2 ${\mathit{L}}_{\mathbf{\infty }}$ , RMS, and ${\mathit{L}}_{\mathbf{2}}$ errors of Example 2 at different times t and for different constants

Example 3 Consider the Fisher equation (5) over the domain $[0,1]$ with the following initial and boundary conditions:

$$\begin{array}{c}u(x,0)=\frac{1}{2}+\frac{1}{2}a+(\frac{1}{2}-\frac{1}{2}a)tanh(c_3+\frac{1}{4}\sqrt{2}(-1+a)(x)),\hfill \\ u(0,t)=\frac{1}{2}+\frac{1}{2}a+(\frac{1}{2}-\frac{1}{2}a)tanh(c_3+\frac{1}{4}\sqrt{2}(-1+a)(-mt)),\hfill \\ u(1,t)=\frac{1}{2}+\frac{1}{2}a+(\frac{1}{2}-\frac{1}{2}a)tanh(c_3+\frac{1}{4}\sqrt{2}(-1+a)(1-mt)).\hfill \end{array}$$

In this example, the exact solution is taken from (38). Table 3 and Figure 3 present the numerical results of the example. Table 3 presents the errors at different times and parameter values which are small and negligible. Figure 3 depicts a comparison of the numerical and exact solutions in 3D form and it is concluded that the solutions are very similar.

Figure 3

Numerical (left) and exact (right) solutions of Example 3 for ${\mathit{c}}_{\mathbf{3}}\mathbf{=}\mathbf{1}$ , $\mathit{a}\mathbf{=}\mathbf{0.5}$ up to time $\mathit{t}\mathbf{=}\mathbf{1}$ .

Table 3 ${\mathit{L}}_{\mathbf{\infty }}$ , RMS, and ${\mathit{L}}_{\mathbf{2}}$ errors of Example 3 at different times t and for different constants

6 Conclusion

In this article, the authors studied analytic and numerical solutions of the Fisher type equations with the help of the classical Lie symmetry method and the polynomial differential quadrature method. The Lie symmetry method is utilized to investigate the symmetries and invariant solutions of the equations. By determining the transformation group under which a given system is invariant, information about the invariants and symmetries of that equation is obtained. This information, in turn, is used to determine similarity variables that reduce the number of independent variables. The vector fields of the optimal system lead to a reduction of the nonlinear system of partial differential equations to ordinary differential equations. The infinitesimal generators in the optimal system are used for reductions and exact solutions. Finally, the polynomial differential quadrature method is used to find the numerical solutions of the Fisher type equations with the help of initial and boundary conditions taken from the analytic solutions obtained by the classical Lie symmetry method. It is concluded that the numerical solutions are in good agreement with the analytical solutions. $L_{\mathrm{\infty }}$, RMS, and $L_2$ errors are calculated for each equation with particular values of arbitrary constants, which are small and negligible.