Critical extinction exponents for a nonlocal reaction-diffusion equation with nonlocal source and interior absorption

Abstract

This paper is concerned with a nonlocal reaction-diffusion equation with nonlocal source and interior absorption $u_t={\int }_{{\mathbb{R}}^N}J(x-y)(u(y,t)-u(x,t))dy+\lambda {\int }_{\mathrm{\Omega }}{u}^{q}dx-u^p$, $x\in \mathrm{\Omega }$, $t>0$, $u(x,t)=0$, $x\notin \mathrm{\Omega }$, $t\ge 0$, $u(x,0)=u_0(x)$, $x\in \mathrm{\Omega }$. We investigate the critical extinction exponents for the problem based on some adequate supersolutions and subsolutions.

MSC:35K57, 35B33, 35K10.

1 Introduction

Our goal is to study the critical extinction exponents of the nonlocal heat equation with nonlocal source and interior absorption, namely,

$$\{\begin{array}{l}{u}_t={\int }_{{\mathbb{R}}^N}J(x-y)(u(y,t)-u(x,t))dy+\lambda {\int }_{\mathrm{\Omega }}{u}^{q}dx-u^p,x\in \mathrm{\Omega },t>0,\\ u(x,t)=0,x\notin \mathrm{\Omega },t\ge 0,\\ u(x,0)=u_0(x),x\in \mathrm{\Omega },\end{array}$$

(1.1)

where $J:{\mathbb{R}}^N\to \mathbb{R}$ is a nonnegative, smooth, symmetric radially function with ${\int }_{{\mathbb{R}}^N}J(z)dz=1$ and supported in the unitary ball, $\lambda ,p,q>0$. We assume that $u_0\in C(\mathrm{\Omega })$ is a nonnegative function.

Since the long-rang effects are taken into account, nonlocal diffusion equations of the form

$$\frac{\partial }{\partial t}u(x,t)=J\ast u-u(x,t)={\int }_{{\mathbb{R}}^N}J(x-y)(u(y,t)-u(x,t))dy$$

(1.2)

have been widely used to model the diffusion processes (see [1–6] and references therein). More precisely, as stated in [6], if $u(x,t)$ is thought of as the density of a species at the point x at time t, and $J(x-y)$ is thought of as the probability distribution of jumping from location y to location x, then ${\int }_{{\mathbb{R}}^N}J(x-y)u(y,t)dy$ and $-u(x,t)=-{\int }_{{\mathbb{R}}^N}J(x-y)u(x,t)dy$ is the rate at which individuals are arriving at position x from all other places and at which they are leaving location x to travel to all other sites, respectively. It is well known that equation (1.2) shares many properties with the classical heat equation, $u_t=\mathrm{△}u$, such as the bounded stationary solutions and the maximum principle [6]. In the last few years, a lot of works have been devoted to the study of properties of solutions to parabolic problems involving nonlocal terms. Especially, García-Melián and Rossi [7] discussed the existence of a critical exponent of Fujita type for the nonlocal diffusion problem with local source. Zhang and Wang [8] studied the critical exponent for the nonlocal diffusion equation

$$\{\begin{array}{l}{u}_t={\int }_{{\mathbb{R}}^N}J(x-y)(u(y,t)-u(x,t))dy+e^{\beta t}{u}^p,x\in \mathrm{\Omega },t>0,\\ u(x,t)=0,x\notin \mathrm{\Omega },t\ge 0,\\ u(x,0)=u_0(x),x\in \mathrm{\Omega },\end{array}$$

(1.3)

with $p>1$, $\beta >0$ and obtained the critical exponent $p_{\beta }^{\ast }$. Recently, Fang and Xu [9] investigated the extinction behavior of solutions for the homogeneous Dirichlet boundary value problem of the non-Newtonian filtration equation with nonlocal sources. More recently, Antontsev and Shmarev [10] discussed the behavior of energy solutions of the homogeneous Dirichlet problem for the anisotropic doubly degenerate parabolic equation

$$\frac{d}{dt}({|v|}^{m(x,t)}signv)=\sum _{i=1}^n{D}_i(a_i(x,t){|D_{i}v|}^{p_i(x,t)-2}{D}_{i}v)+b(x,t){|v|}^{\sigma (x,t)-2}v+g(x,t)$$

with $m(x,t)>0$, $p_i(x,t)>1$ and $\sigma (x,t)>1$. They derived the sufficient conditions of the finite time blow-up or vanishing and established the decay rates as $t\to \mathrm{\infty }$. More results on the extinction for the degenerate parabolic equations have also been obtained by many researchers, and we may refer to [11–16] and the references therein. We point out that Liu [17] investigated the extinction properties of solutions for the homogeneous Dirichlet boundary value problem of the nonlocal reaction-diffusion equation

$$u_t-d\mathrm{△}u+k{u}^p={\int }_{\mathrm{\Omega }}{u}^{q}dx$$

with $p,q\in (0,1)$ and $k,d>0$ and showed that $q=p$ is the critical extinction exponent by invoking the regularizing effect. In this paper under the appropriate hypotheses $p,q>0$, we discuss problem (1.1) and obtain the extinction condition by using the principal eigenvalue of the nonlocal heat equation, and thus avoid using the regularizing effect, since there is no regularizing effect in general [18]. It is noted that our approach can be adopted to deal with the blow-up behavior of solutions of nonlocal reaction-diffusion equations with nonlocal source or local source, which was considered in [7, 19].

Motivated by the above works, the purpose of this paper is to analyze the extinction exponent for problem (1.1), that is, we want to show that problem (1.1) shares many important properties with the corresponding local reaction-diffusion system,

$$\{\begin{array}{l}{u}_t=\mathrm{△}u+\lambda {\int }_{\mathrm{\Omega }}{u}^{q}dx-u^p,x\in \mathrm{\Omega },t>0,\\ u(x,t)=0,x\in \partial \mathrm{\Omega },t\ge 0,\\ u(x,0)=u_0(x),x\in \mathrm{\Omega },\end{array}$$

(1.4)

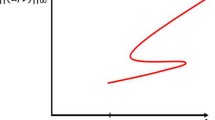
such as the extinction condition [17]. Through the main points, we see that there exists a critical curvilinear line $q^{\ast }=min(p,1)$ such that the $(q,p)$-parameter plane is divided into three parts, with the bottom part corresponding to a nonextinction solution and the top part of the line corresponding to all the infinite time extinctions or the finite time extinction. Moreover, there exists a critical point on this line such that the line is also divided into three parts, which exhibits different features of extinction phenomena (see Figure 1).

Figure 1

The critical extinction exponents of extinction phenomena.

Now our main results can be stated as follows.

2 Main results

Theorem 2.1 (1) If $q=1$, then the solution of problem (1.1) vanishes in infinite time for any nonnegative initial data provided that $\lambda >0$ is appropriately small.

• (2) If $q>1$, then the solution of problem (1.1) vanishes in infinite time for any appropriately small initial data.

Theorem 2.2 (1) If $q=p<1$, then the solution of problem (1.1) vanishes in finite time for any nonnegative initial data provided that $\lambda >0$ is appropriately small.

• (2) If $p<q<1$, then the solution of problem (1.1) vanishes in finite time for any conveniently small initial data.

Remark 1 (1) The small condition on initial data $u_0$ in Theorem 2.1 and Theorem 2.2 can be removed if $\lambda >0$ is sufficiently small.

• (2) That $u(x,t)$ vanishes in infinite time means that ${lim}_{t\to +\mathrm{\infty }}u(x,t)=0$ for any $x\in \mathrm{\Omega }$.

• (3) That $u(x,t)$ vanishes in finite time means that there exists $0<T^{\ast }<+\mathrm{\infty }$, such that $u(x,t)=0$ for any $x\in \mathrm{\Omega }$ and $t>T^{\ast }$.

Theorem 2.3 (Nonextinction)

• (1) If $q=p<1$, then problem (1.1) admits at least one nonextinction solution for any nonnegative initial data provided that $\lambda >0$ is appropriately large.

• (2) If $q=1<p$, then problem (1.1) admits at least one nonextinction solution for any nonnegative initial data provided that λ is appropriately large.

• (3) If $q<min\{1,p\}$, then problem (1.1) admits at least one nonextinction solution for any nonnegative initial data.

• (4) If $q=p=1$, then problem (1.1) admits at least one nonextinction solution for any nonnegative initial data provided that $\lambda >0$ is sufficiently large.

Preliminary lemmas

Before proving our main results, we will give some preliminary lemmas, which play a crucial role in the following proofs. As for the proofs of these lemmas, we will not repeat them again.

Let $\psi (x)$ satisfy

$$\{\begin{array}{l}{\int }_{{\mathbb{R}}^N}J(x-y)(\psi (y)-\psi (x))dy=-{\lambda }_1\psi (x),x\in \mathrm{\Omega },\\ \psi (x)=0,x\notin \overline{\mathrm{\Omega }}.\end{array}$$

(2.1)

Using results in [7, 20] and $\psi (x)>0$ in $\overline{\mathrm{\Omega }}$, we can always assume

$$m=\underset{\overline{\mathrm{\Omega }}}{min}\psi (x)>0,M=\underset{\overline{\mathrm{\Omega }}}{max}\psi (x)>0.$$

Applying almost exactly the same arguments as in the proof of Lemma 5 in [21], we conclude to the following lemma.

Lemma 2.1 Let $y(t)$ be a solution of the following problem:

$$\{\begin{array}{l}\frac{dy}{dt}+\alpha y+\beta y^p=\gamma y^q,t\ge 0,\\ y(t)>0,t>0,\\ y(0)\ge 0,\end{array}$$

where $\alpha ,\beta ,\gamma >0$ and $0<q<min\{p,1\}$. Then the above ODE problem has at least one non-constant solution.

Next, our aim is to prove the local existence of solutions to equation (1.1) and the validity of the comparison principle. First, we give the definition of supersolution and subsolution.

Definition 2.1 A nonnegative function

$$\overline{u}\in C(0,T;L^1(\mathrm{\Omega }))\cap W^{1,1}(0,T;L^1(\mathrm{\Omega }))$$

is a supersolution of problem (1.1) if it is a supersolution of problem (1.1), which satisfies

$$\{\begin{array}{l}\frac{\partial }{\partial t}\overline{u}(x,t)\ge {\int }_{\mathrm{\Omega }}J(x-y)(\overline{u}(y,t)-\overline{u}(x,t))dy\\ \phantom{\frac{\partial }{\partial t}\overline{u}(x,t)\ge }-{\int }_{{\mathbb{R}}^N\setminus \mathrm{\Omega }}J(x-y)\overline{u}(x,t)dy+\lambda {\int }_{\mathrm{\Omega }}{\overline{u}}^{q}dx-{\overline{u}}^p,(x,t)\in Q_T,\\ \overline{u}(x,0)\ge u_0(x),x\in \mathrm{\Omega },\end{array}$$

(2.2)

where $Q_T:=\mathrm{\Omega }\times (0,T)$. The subsolution is defined similarly by reversing the inequalities. Furthermore, if u is a supersolution as well as a subsolution, then we call it a solution of problem (1.1).

The existence of the solution of problem (1.1) will be obtained via the successive approximation which comes from [22].

Lemma 2.2 Let $0\le u_0\in C(\overline{\mathrm{\Omega }})$. Then there exists $T=T(\lambda ,p,q)>0$, such that problem (1.1) has nonnegative solutions.

Proof Let

$$R=2{(1+{\parallel u_0\parallel }_{L^{\mathrm{\infty }}})}^q|\mathrm{\Omega }|,T=\frac{1}{R}\text{and}{u}_0(x,t)={\parallel u_0\parallel }_{L^{\mathrm{\infty }}}+Rt.$$

Then for any $m\ge 1$, we consider the following successive approximation problem:

$$\{\begin{array}{l}{u}_{mt}(x,t)={\int }_{\mathrm{\Omega }}J(x-y)(u_m(y,t)-u_m(x,t))dy\\ \phantom{u_{mt}(x,t)=}-{\int }_{{\mathbb{R}}^N\setminus \mathrm{\Omega }}J(x-y)dy{u}_m(x,t)\\ \phantom{u_{mt}(x,t)=}+\lambda {\int }_{\mathrm{\Omega }}{u}_{m-1}^q(x,t)dx-u_m^p(x,t),(x,t)\in Q_T,\\ u_m(x,t)=0,x\notin \mathrm{\Omega },t\ge 0,\\ u_m(x,0)=u_0(x),x\in \mathrm{\Omega }.\end{array}$$

(2.3)

Applying almost exactly the same arguments as in the proof of Theorem 1.1 in [22], we derive that equation (2.3) possesses a unique solution $u_m\in C(0,T;L^1(\mathrm{\Omega }))\cap W^{1,1}(0,T;L^1(\mathrm{\Omega }))$. Now we turn to proving that

$$0\le u_m(x,t)\le u_{m-1}(x,t)\le u_0(x,t)\text{in }{Q}_T.$$

In fact, if $m=1$, then it is easier to see that $u_0(x,t)={\parallel u_0\parallel }_{L^{\mathrm{\infty }}}+Rt$ and 0 are a supersolution and a subsolution of equation (2.3), respectively. Then by the comparison principle, we have $0\le u_1(x,t)\le u_0(x,t)$. The fact that $0\le u_m(x,t)\le u_{m-1}(x,t)\le u_0(x,t)$ in $Q_T$ can be shown by mathematical induction. Therefore, $u(x,t):={lim}_{m\to \mathrm{\infty }}{u}_m(x,t)$ is the solution of equation (1.1). In fact $u_m(x,t)$ is the solution of the following problem:

$$\begin{array}{rcl}{u}_m(x,t)& =& u_0(x)+{\int }_0^t{\int }_{\mathrm{\Omega }}J(x-y)(u_m(y,s)-u_m(x,s))dyds\\ -{\int }_0^t{\int }_{{\mathbb{R}}^N\setminus \mathrm{\Omega }}J(x-y)dy{u}_m(x,t)ds+{\int }_0^t(\lambda {\int }_{\mathrm{\Omega }}{u}_{m-1}^q(x,t)dx-u_m^p(x,t))ds\end{array}$$

with $0\le u_m(x,t)\le {\parallel u_0\parallel }_{L^{\mathrm{\infty }}}+1$ for all most $(x,t)\in Q_T$. Then it follows from the Lebesgue dominated convergence theorem that $u(x,t)$ is the solution of problem (1.1). □

In the following, we conclude that a comparison principle holds for solutions to problem (1.1).

Lemma 2.3 Let $\overline{u}$, $\underline{u}$ be the supersolution and the subsolution to equation (1.1), respectively. If either $q\ge 1$ and $\overline{u}$ is upper bounded or $0<q<1$ and $\underline{u}$ has a positive lower bound, then $\underline{u}(x,t)\le \overline{u}(x,t)$ in $Q_T$.

Proof Let $v=\underline{u}-\overline{u}$. Then due to the Definition 2.1, we have

$$v_t+{\int }_{{\mathbb{R}}^N}J(x-y)(v(y,t)-v(x,t))dy\le \lambda {\int }_{\mathrm{\Omega }}({\underline{u}}^q-{\overline{u}}^q)dx-({\underline{u}}^p-{\overline{u}}^p).$$

(2.4)

If $q>1$ and $\overline{u}$ is bounded, multiplying equation (2.4) by ${(\underline{u}-\overline{u})}_{+}$ and integrating it over Ω, we derive

$$\begin{array}{c}\frac{1}{2}\frac{d}{dt}{\int }_{\mathrm{\Omega }}{v}_{+}^2(x,t)dx+{\int }_{\mathrm{\Omega }}({\int }_{{\mathbb{R}}^N}J(x-y)(v(y,t)-v(x,t))dy)v_{+}dx\hfill \\ \le \lambda {\int }_{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}({\underline{u}}^q(x,t)-{\overline{u}}^q(x,t))dx{(\underline{u}-\overline{u})}_{+}(x,t)dx-{\int }_{\mathrm{\Omega }}({\underline{u}}^p-{\overline{u}}^p){(\underline{u}-\overline{u})}_{+}dx\hfill \\ \le \lambda {\int }_{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}({\underline{u}}^q(x,t)-{\overline{u}}^q(x,t))dx{(\underline{u}-\overline{u})}_{+}(x,t)dx\hfill \\ \le \lambda q{M}^{q-1}|\mathrm{\Omega }|{\int }_{\mathrm{\Omega }}{v}_{+}^2(x,t)dx,\hfill \end{array}$$

and M depends only on $\overline{u}$, where $s_{+}=max\{s,0\}$ and $M>0$. It then follows from Gronwall’s inequality that

$$\frac{1}{2}\frac{d}{dt}{\int }_{\mathrm{\Omega }}{v}_{+}^2(x,t)dx\le C,$$

which implies that $\underline{u}(x,t)\le \overline{u}(x,t)$ in $Q_T$. The assertion can be proved similarly for the case $0<q<1$ and $\underline{u}$ has a positive lower bound. Thus the proof of this lemma is completed. □

Once the existence of the solution to problem (1.1) and the comparison principle are ensured, we begin to analyze the extinction exponents for nonnegative solutions. As a first step we discuss the infinite time extinction of the solution.

Proof of Theorem 2.1 The proof can be divided into two steps:

Step I: $q=1$ with $\lambda <\frac{{\lambda }_{1}m}{{\int }_{\mathrm{\Omega }}\psi (x)dx}$. Let $v(x,t)=f(t)\psi (x)$, where $f(t)$ satisfies

$$\{\begin{array}{l}{f}^{\prime }(t)+({\lambda }_1-\lambda \frac{{\int }_{\mathrm{\Omega }}\psi (x)dx}{m})f(t)=0,t\ge 0,\\ f(0)=f_0>0.\end{array}$$

Obviously, $f(t)$ is nonincreasing and ${lim}_{t\to +\mathrm{\infty }}f(t)=0$. Then it can be observed that $v(x,t)$ is the supersolution of equation (1.1) provided that $f_0\ge \frac{{\parallel u_0\parallel }_{L^{\mathrm{\infty }}(\mathrm{\Omega })}}{m}$. To this end, due to $q=1$, we obtain

$$\begin{array}{rcl}Pv& =& v_t(x,t)-[{\int }_{{\mathbb{R}}^N}J(x-y)(v(y,t)-v(x,t))dy+\lambda {\int }_{\mathrm{\Omega }}vdx-v^p]\\ =& f^{\prime }(t)\psi (x)+{\lambda }_{1}f(t)\psi (x)-\lambda f(t){\int }_{\mathrm{\Omega }}\psi (x)dx+f^p(t){\psi }^p(x)\\ \ge & \psi (x)[f^{\prime }(t)+({\lambda }_1-\frac{\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx}{\psi (x)})f(t)]\\ \ge & \psi (x)[f^{\prime }(t)+({\lambda }_1-\frac{\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx}{m})f(t)]\\ =& 0.\end{array}$$

Therefore, applying Lemma 2.3 to equation (1.1) in $Q_T$, we have $u(x,t)\le v(x,t)$ for $(x,t)\in Q_T$, which implies ${lim}_{T\to +\mathrm{\infty }}u(x,T)=0$. Hence the solution of equation (1.1) vanishes in infinite time provided that $\lambda <\frac{{\lambda }_{1}m}{{\int }_{\mathrm{\Omega }}\psi (x)dx}$.

Step II: $q>1$. Assume that $u(x,t)$ is the solution of equation (1.1) with the initial datum $u_0(x)$. Let $v(x,t)=A\psi (x)$ with

$$A={\left[\frac{{\lambda }_{1}m}{(\frac{2M^{q-1}{\int }_{\mathrm{\Omega }}\psi (x)dx}{{\int }_{\mathrm{\Omega }}{\psi }^q(x)dx}+1)\lambda {\int }_{\mathrm{\Omega }}{\psi }^q(x)dx}\right]}^{\frac{1}{q-1}}.$$

Then $v(x,t)$ is a supersolution of equation (1.1) provided that ${\parallel u_0\parallel }_{L^{\mathrm{\infty }}(\mathrm{\Omega })}\le Am$. Invoking Lemma 2.3 to equation (1.1) in Q, we obtain $u(x,t)\le v(x,t)$ for $(x,t)\in Q$, which implies that $u(x,t)\le AM$. Therefore $u(x,t)$ satisfies

$$u_t-{\int }_{{\mathbb{R}}^N}J(x-y)(u(y,t)-u(x,t))dy-\frac{{\lambda }_{1}m}{2{\int }_{\mathrm{\Omega }}\psi (x)dx}{\int }_{\mathrm{\Omega }}udx+u^p\le 0,x\in \mathrm{\Omega },t>0,$$

and then by Step I, we end up with that the solution $u(x,t)$ of equation (1.1) vanishes in infinite time. The proof of this theorem is completed. □

Proof of Theorem 2.2 The proof is similar to that of Theorem 2.1, so we sketch it briefly here. We will prove the theorem in two cases.

Case I: If $q=p<1$ and $\lambda <\frac{m^p}{{\int }_{\mathrm{\Omega }}{\psi }^q(x)dx}$. Let $w(x,t)=g(t)\psi (x)$, where $g(t)$ satisfies the following ODE problem:

$$\{\begin{array}{l}{g}^{\prime }(t)+\frac{m^p-\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{M}{g}^p(t)=0,t>0,\\ g(0)=g_0>0.\end{array}$$

(2.5)

Due to $p<1$, $g(t)$ is nonincreasing and $g(t)=0$ for all $t\ge T^{\ast }=\frac{M}{(m^p-\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx)(1-p)}{g}_0^{1-p}$. Hence, we can infer that $w(x,t)$ is the supersolution of equation (1.1) provided that $g_0\ge \frac{{\parallel u_0\parallel }_{L^{\mathrm{\infty }}(\mathrm{\Omega })}}{m}$. In fact, with the help of $q=p$, we readily find that

$$\begin{array}{rcl}Pw& =& w_t(x,t)-[{\int }_{{\mathbb{R}}^N}J(x-y)(w(y,t)-w(x,t))dy+\lambda {\int }_{\mathrm{\Omega }}{w}^{p}dx-w^p]\\ \ge & \psi (x)[g^{\prime }(t)+\frac{m^p-\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{M}{g}^p]\\ =& 0.\end{array}$$

Thus, thanks to Lemma 2.3, we derive $u(x,t)\le w(x,t)$ ($(x,t)\in Q_T$), for any fixed $T<T^{\ast }$. Therefore, $u(x,T)\le w(x,T)$, which, together with the arbitrariness of $T<T^{\ast }$ and $w(x,T^{\ast })=0$ implies that $u(x,T^{\ast })=0$. Furthermore, setting $\tilde{u}(x,t)=u(x,t+T^{\ast })$, then $\tilde{u}(x,t)$ satisfies equation (1.1). According to the above proof, we claim that $\tilde{u}(x,t)\le w(x,t)$ with any $g_0>0$. Now, by virtue of the relation of the extinction time $T^{\ast }$ of $w(x,t)$ to $g_0$, we finally conclude that $\tilde{u}(x,t)=0$ for any $t>0$, namely $u(x,t)=0$ for all $t\ge T^{\ast }$.

Case II: Set $0<p<q<1$. Suppose that $u(x,t)$ is the solution of equation (1.1) with the initial datum $u_0(x)$ and

$$B={\left[\frac{m^p}{(\frac{2M^{q-p}{\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{{\int }_{\mathrm{\Omega }}{\psi }^q(x)dx}+1)\lambda {\int }_{\mathrm{\Omega }}{\psi }^q(x)dx}\right]}^{\frac{1}{q-p}}.$$

Let $w(x,t)=B\psi (x)$. By the arguments as those in the proof of Theorem 2.1, we get

$$u_t-{\int }_{{\mathbb{R}}^N}J(x-y)(u(y,t)-u(x,t))dy-\frac{m^p}{2{\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{\int }_{\mathrm{\Omega }}{u}^{p}dx+u^p\le 0.$$

According to the above results, the solution $u(x,t)$ of equation (1.1) vanishes in finite time. This completes the proof of Theorem 2.2. □

Proof of Theorem 2.3 The proof can be divided into four cases.

Case I: In the case $q=p<1$ with $\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx-M{m}^{p-1}>0$, we shall prove that problem (1.1) admits at least one nonextinction solution for any nonnegative initial data by constructing a suitable subsolution of equation (1.1). Let $w(x,t)=g(t)\psi (x)$, where $g(t)$ satisfies

$$\{\begin{array}{l}{g}^{\prime }(t)=(\frac{\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{M}-m^{p-1})g^p(t)-{\lambda }_{1}g(t),t>0,\\ g(t)>0,t>0,\\ g(0)=0.\end{array}$$

With the help of $p<1$ and $\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx-M{m}^{p-1}>0$, we derive that $g(t)$ is nondecreasing and $g(t)\le {(\frac{\frac{\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{M}-m^{p-1}}{{\lambda }_1})}^{\frac{1}{1-p}}$. Simple calculations show that

$$\begin{array}{rcl}Pv& =& v_t(x,t)-[{\int }_{{\mathbb{R}}^N}J(x-y)(v(y,t)-v(x,t))dy+\lambda {\int }_{\mathrm{\Omega }}{v}^{p}dx-v^p]\\ =& g^{\prime }(t)\psi (x)+{\lambda }_{1}g(t)\psi (x)-\lambda g^p(t){\int }_{\mathrm{\Omega }}{\psi }^p(x)dx+g^p(t){\psi }^p(x)\\ \le & \psi (x)[g^{\prime }(t)+{\lambda }_{1}g(t)-(\frac{\lambda {\int }_{\mathrm{\Omega }}{\psi }^p(x)dx}{M}-m^{p-1})g^p(t)]\\ =& 0,\end{array}$$

which implies w is a subsolution of problem (1.1). Therefore problem (1.1) admits a solution $u(x,t)$ satisfying $u(x,t)\ge w(x,t)$, which, combined with $w(x,t)>0$ ($\mathrm{\Omega }\times (0,+\mathrm{\infty })$) implies that $u(x,t)$ is a nonextinction solution of equation (1.1) for any nonnegative initial data provided that $\lambda >0$ is appropriately large.

Case II: Suppose that $q=1<p$, $\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx-{\lambda }_{1}M>0$ and $g(t)$ is the solution of the following ODE problem:

$$\{\begin{array}{l}{g}^{\prime }(t)=(\frac{\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx}{M}-{\lambda }_1)g(t)-m^{p-1}{g}^p(t),t>0,\\ g(t)>0,t>0,\\ g(0)=0.\end{array}$$

Since $p>1$ and $\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx-{\lambda }_{1}M>0$, we conclude that $g(t)$ is a nondecreasing and $g(t)\le {(\frac{\frac{\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx}{M}-{\lambda }_1}{m^{p-1}})}^{\frac{1}{p-1}}$. Let $w(x,t)=g(t)\psi (x)$. Then we can easily derive $u(x,t)\ge w(x,t)$. Therefore, $u(x,t)$ is a nonextinction solution of equation (1.1) for any nonnegative initial data provided that $\lambda >0$ is appropriately large.

Case III: Suppose that $q<min\{p,1\}$ and let $w(x,t)=g(t)\psi (x)$, where $g(t)$ is given by

$$\{\begin{array}{l}{g}^{\prime }(t)=-{\lambda }_{1}g(t)+\frac{\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx}{M}{g}^q(t)-m^{p-1}{g}^p(t),t>0,\\ g(t)>0,t>0,\\ g(0)=0.\end{array}$$

(2.6)

Applying Lemma 2.1 to equation (2.6), we have $g(t)>0$ ($t>0$). Then the same argument as in the derivation of Case I shows that $u(x,t)$ is a nonextinction solution of equation (1.1) for any nonnegative initial data.

Case IV: If $q=p=1$ and $\lambda {\int }_{\mathrm{\Omega }}\psi (x)dx-({\lambda }_1+1)M>0$, employing exactly the same arguments as in the proof of Case I, we finally conclude the result. □