Robust stability analysis for Lur’e systems with interval time-varying delays via Wirtinger-based inequality

Abstract

This paper considers the problem of robust stability for Lur’e systems with interval time-varying delays and parameter uncertainties. It is assumed that the parameter uncertainties are norm bounded. By constructing a newly augmented Lyapunov-Krasovskii functional, less conservative sufficient stability conditions of the concerned systems are introduced within the framework of linear matrix inequalities (LMIs). Three numerical examples are given to show the improvements over the existing ones and the effectiveness of the proposed methods.

1 Introduction

The Lur’e system is one of a significant class of nonlinear systems and has a nonlinear element satisfying certain sector bounded constraints. Since the Lur’e system and absolute stability were firstly introduced by [1, 2], the study of the absolute stability for Lur’e system has attracted many researchers. Most nonlinear systems consist of feedback connections of linear dynamic systems and nonlinear elements. Thus, as regards practical systems, there are various kinds of nonlinearities it takes to operate various tasks of systems. For this reason, during a few decades, Lur’e system has received a great deal of attention due to its extensive applications [3, 4]. Moreover, we need to pay close attention to a delay in the time, which is a natural concomitant of the finite speed of information processing and/or amplifier switching in the implementation of the systems in various systems such as physical and biological systems, population dynamics, neural networks, networked control systems, and so on. It is well known that the time delay often causes undesirable dynamic behavior, such as performance degradation and instability of the systems. Therefore, the study on stability analysis for systems with time delay has been widely investigated. For more details, see the literature [5–14] and references therein. The recent remarkable result in the delay-dependent stability analysis of dynamic systems is the Wirtinger-based integral inequality [15]. This method provides a tighter lower bound of the integral terms of the quadratic form. It was shown that this method can be applied and effectively reduce the conservatism of various problems such as stability analysis of systems with constant and known delay or a time-varying delay, stabilization of sampled-data systems, and so on.

Returning to the Lur’e system, this system is also booked for the stability problem with time delay [16–29]. Above all, in [16], the time-delayed Lur’e systems are dealt with sector and slope restricted nonlinearities and uncertainties. Li et al. [19] investigated the problem of delay-dependent absolute and robust stability for time-delay Lur’e system and the relaxed conditions were presented some previously ignored terms when estimating the triple integral Lyapunov-Krasovskii functional terms’ derivative. In [23], the problems of master-slave synchronization of Lur’e systems under time-varying delay-feedback controllers were investigated in the framework of LMIs. Ramakrishnan and Ray [29] proposed an improved delay-dependent sufficient stability condition for a class of Lur’e systems of neutral type by imposing tighter bounding on the time derivative of the Lyapunov-Krasovskii functional without neglecting any useful terms with a delay-partitioning approach. However, there is room for further improvements in stability analysis of Lur’e system with time delay.

With the motivation mentioned above, in this paper, the problem to get improved delay-dependent sufficient stability conditions for a class of Lur’e systems with interval time-varying delays and parameter uncertainties are considered. Here, stability or stabilization of a system with interval time-varying delays has been a focused topic of theoretical and practical importance [30] in very recent years. The system with interval time-varying delays means that the lower bounds of the time delay which guarantees the stability of system is not restricted to zero, and they include the networked control system as one of the typical examples. Moreover, the analyses of systems with time delay can be classified as delay-dependent and delay-independent analysis [31]. To achieve this, by construction of a newly augmented Lyapunov-Krasovskii functional and utilization of a Wirtinger-based inequality [15] and a reciprocally convex approach [5], new delay-dependent robust sufficient stability conditions are derived in terms of LMIs, which can be formulated as convex optimization algorithms which are amenable to computer solution [32]. Finally, three numerical examples are included to show the effectiveness of the proposed methods.

Notation ${\mathbb{R}}^n$ is the n-dimensional Euclidean space, and ${\mathbb{R}}^{m\times n}$ denotes the set of all $m\times n$ real matrices. $X>0$ (respectively, $X\ge 0$) means that the matrix X is a real symmetric positive definite (respectively, semidefinite) matrix. $I_n$ and 0 denote $n\times n$ identity matrix and zero matrix of appropriate dimension, respectively. $\parallel \cdot \parallel$ refers to the Euclidean vector norm or the induced matrix norm. $\mathtt{diag}\{\cdots \}$ denotes the block diagonal matrix. For square matrix X, $\mathtt{sym}\{X\}$ means the sum of X and its symmetric matrix $X^T$, i.e., $\mathtt{sym}\{X\}=X+X^T$. For any vectors $x_i\in {\mathbb{R}}^m$ ($i=1,2,\dots ,n$), $\mathtt{col}\{x_1,x_2,\dots ,x_n\}$ means the column vector ${[x_1^T,x_2^T,\dots ,x_n^T]}^T\in {\mathbb{R}}^{mn}$. $X_{[f(t)]}\in {\mathbb{R}}^{m\times n}$ means that the elements of matrix $X_{[f(t)]}$ include the scalar value of $f(t)$, i.e., $X_{[f_0]}=X_{[f(t)=f_0]}$.

2 Preliminaries and problem statement

Consider the uncertain Lur’e systems with time-varying delays given by

$$\begin{array}{r}\dot{x}(t)=(A+\mathrm{\Delta }A(t))x(t)+(A_d+\mathrm{\Delta }{A}_d(t))x(t-h(t))+(B+\mathrm{\Delta }B(t))\psi (y(t)),\\ y(t)=Cx(t),\end{array}$$

(1)

where $x(t)\in {\mathbb{R}}^n$ is the state vector, $y(t)\in {\mathbb{R}}^{n_y}$ is the output vector, $\psi (\cdot )\in {\mathbb{R}}^{n_y}$ denotes the nonlinearity, which satisfies ${\psi }_i(0)=0$ ($i=1,\dots ,n_y$), and

$${\gamma }_i^{-}\le \frac{{\psi }_i(u)-{\psi }_i(v)}{u-v}\le {\gamma }_i^{+},u\ne v,\mathrm{\forall }u,v\in \mathbb{R}$$

(2)

where ${\gamma }_i^{-}$ and ${\gamma }_i^{+}$ are given constants. Here, for simplicity, let us define ${\mathrm{\Gamma }}^{-}=\mathtt{diag}\{{\gamma }_1^{-},\dots ,{\gamma }_n^{-}\}$ and ${\mathrm{\Gamma }}^{+}=\mathtt{diag}\{{\gamma }_1^{+},\dots ,{\gamma }_n^{+}\}$. $A,A_d\in {\mathbb{R}}^{n\times n}$, $B\in {\mathbb{R}}^{n\times n_y}$, and $C\in {\mathbb{R}}^{n_y\times n}$ are the system matrices; and $\mathrm{\Delta }A(t)$, $\mathrm{\Delta }{A}_d(t)$, and $\mathrm{\Delta }B(t)$ are the parameter uncertainties of the form

$$[\mathrm{\Delta }A(t),\mathrm{\Delta }{A}_d(t),\mathrm{\Delta }B(t)]=DF(t)[E_a,E_d,E_b],$$

(3)

where $D\in {\mathbb{R}}^{n\times n_u}$, $E_a\in {\mathbb{R}}^{n_u\times n}$, $E_d\in {\mathbb{R}}^{n_u\times n}$, and $E_b\in {\mathbb{R}}^{n_u\times n_y}$ are real known constant matrices; and $F(t)\in {\mathbb{R}}^{n_u\times n_u}$ is a real uncertain matrix function with Lebesgue measurable elements satisfying $F^T(t)F(t)\le I_{n_u}$.

The delay $h(t)$ is a time-varying continuous function satisfying

$$0\le h_m\le h(t)\le h_M,d_m\le \dot{h}(t)\le d_M,$$

(4)

where $h_m$, $h_M$, $d_m$, and $d_M$ are known constant values.

The aim of this paper is to investigate the delay-dependent stability analysis of system (1) with interval time-varying delays and parameter uncertainties.

For simplicity of the system’s representation, the system can be formulated as follows:

$$\begin{array}{c}\dot{x}(t)=Ax(t)+A_{d}x(t-h(t))+B\psi (y(t))+Dp(t),\hfill \\ p(t)=F(t)q(t),\hfill \\ q(t)=E_{a}x(t)+E_{d}x(t-h(t))+E_b\psi (y(t)).\hfill \end{array}$$

(5)

Also, before deriving our main results, the following lemmas will be used in main results.

Lemma 1 ([15])

For a given matrix $M>0$, the following inequality holds for all continuously differentiable function x in $[a,b]\to {\mathbb{R}}^n$:

$${\int }_a^b{\dot{x}}^T(s)M\dot{x}(s)ds\ge \frac{1}{b-a}{\xi }_1^{T}M{\xi }_1+\frac{3}{b-a}{\xi }_2^{T}M{\xi }_2,$$

where ${\xi }_1=x(b)-x(a)$ and ${\xi }_2=x(b)+x(a)-\frac{2}{b-a}{\int }_a^{b}x(s)ds$.

Lemma 2 ([33])

Let $\zeta \in {\mathbb{R}}^n$, $\mathrm{\Phi }={\mathrm{\Phi }}^T\in {\mathbb{R}}^{n\times n}$ and $B\in {\mathbb{R}}^{m\times n}$ such that $\mathtt{rank}(B)<n$. The following statements are equivalent:

• (i) ${\zeta }^T\mathrm{\Phi }\zeta <0$, $\mathrm{\forall }B\zeta =0$, $\zeta \ne 0$,

• (ii) ${B^{\perp }}^T\mathrm{\Phi }{B}^{\perp }<0$, where $B^{\perp }$ is a right orthogonal complement of B,

• (iii) $\mathrm{\exists }X\in {\mathbb{R}}^{n\times m}$: $\mathrm{\Phi }+XB+{(XB)}^T<0$.

3 Main results

In this section, new sufficient stability conditions for the system (5) will be derived. For convenience, the notations of several matrices are defined as

$$\begin{array}{c}\zeta (t)=\mathtt{col}\{x(t),x(t-h_m),x(t-h(t)),x(k-h_M),\dot{x}(t),\frac{1}{h_m}{\int }_{t-h_m}^{t}x(s)ds,\hfill \\ \phantom{\zeta (t)=}\frac{1}{h(t)-h_m}{\int }_{t-h(t)}^{t-h_m}x(s)ds,\frac{1}{h_M-h(t)}{\int }_{t-h_M}^{t-h(t)}x(s)ds,\psi (y(t)),p(t)\},\hfill \\ \eta (t)=\mathtt{col}\{x(t),{\int }_{t-h_m}^{t}x(s)ds,{\int }_{t-h(t)}^{t-h_m}x(s)ds,{\int }_{t-h_M}^{t-h(t)}x(s)ds\},\hfill \\ {\mathrm{\Pi }}_{1,1[h(t)]}=[e_1,h_m{e}_6,(h(t)-h_m)e_7,(h_M-h(t))e_8],\hfill \\ {\mathrm{\Pi }}_{1,2[\dot{h}(t)]}=[e_5,e_1-e_2,e_2-(1-\dot{h}(t))e_3,(1-\dot{h}(t))e_3-e_4],\hfill \\ {\mathrm{\Pi }}_{2,1}=[e_1-e_2,e_1+e_2-2e_6],\hfill \\ {\mathrm{\Pi }}_{2,2}=[e_2-e_3,e_2+e_3-2e_7,e_3-e_4,e_3+e_4-2e_8],\hfill \\ {\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}=\mathtt{sym}\left\{{\mathrm{\Pi }}_{1,1[h(t)]}\mathcal{P}{\mathrm{\Pi }}_{1,2[\dot{h}(t)]}^T\right\}\hfill \\ \phantom{{\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}=}+[e_2,e_1-e_2]{\mathcal{Q}}_2{[e_2,e_1-e_2]}^T-(1-\dot{h}(t))[e_3,e_1-e_3]{\mathcal{Q}}_2{[e_3,e_1-e_3]}^T\hfill \\ \phantom{{\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}=}+\mathtt{sym}\{[e_7,e_1-e_7](h(t)-h_m){\mathcal{Q}}_2{[0,e_5]}^T\}\hfill \\ \phantom{{\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}=}+(1-\dot{h}(t))[e_3,e_1-e_3]{\mathcal{Q}}_4{[e_3,e_1-e_3]}^T-[e_4,e_1-e_4]{\mathcal{Q}}_4{[e_4,e_1-e_4]}^T\hfill \\ \phantom{{\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}=}+\mathtt{sym}\{[e_8,e_1-e_8](h_M-h(t)){\mathcal{Q}}_4{[0,e_5]}^T\},\hfill \\ {\mathrm{\Xi }}_2=e_1{Q}_1{e}_1^T-e_2{Q}_1{e}_2^T+e_2{Q}_3{e}_2^T-e_4{Q}_3{e}_4^T\hfill \\ \phantom{{\mathrm{\Xi }}_2=}+\mathtt{sym}\{[e_9-e_1{C}^T{\mathrm{\Gamma }}^{-}]L_{1}C{e}_5^T+[e_1{C}^T{\mathrm{\Gamma }}^{+}-e_9]L_{2}C{e}_5^T\}\hfill \\ \phantom{{\mathrm{\Xi }}_2=}+h_m^2{e}_5{R}_1{e}_5^T+{(h_M-h_m)}^2{e}_5{R}_2{e}_5^T,\hfill \\ \mathrm{\Psi }=\left[\begin{array}{cc}\mathtt{diag}\{R_2,3R_2\}& M\\ M^T& \mathtt{diag}\{R_2,3R_2\}\end{array}\right],\hfill \\ {\mathrm{\Xi }}_3=-{\mathrm{\Pi }}_{2,1}\mathtt{diag}\{R_1,3R_1\}{\mathrm{\Pi }}_{2,1}^T-{\mathrm{\Pi }}_{2,2}\mathrm{\Psi }{\mathrm{\Pi }}_{2,2}^T,\hfill \\ \mathrm{\Omega }=-\mathtt{sym}\left\{[e_9-e_1{C}^T{\mathrm{\Gamma }}^{-}]K{[e_9-e_1{C}^T{\mathrm{\Gamma }}^{+}]}^T\right\},\hfill \\ \mathrm{\Sigma }=ϵ\{{(E_a{e}_1^T+E_d{e}_3^T+E_b{e}_9^T)}^T(E_a{e}_1^T+E_d{e}_3^T+E_b{e}_9^T)-e_{10}{I}_{n_u}{e}_{10}^T\},\hfill \\ {\mathbf{\Xi }}_{[h(t),\dot{h}(t)]}={\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}+{\mathrm{\Xi }}_2+{\mathrm{\Xi }}_3+\mathrm{\Omega }+\mathrm{\Sigma },\hfill \\ \mathrm{\Upsilon }=A{e}_1^T+A_d{e}_3^T-I_n{e}_5^T+B{e}_9^T+D{e}_{10}^T,\hfill \end{array}$$

(6)

where $e_i\in {\mathbb{R}}^{(8n+n_y+n_u)\times n}$ ($i=1,2,\dots ,10$) are defined as block entry matrices, e.g., $e_3^T\zeta (t)=x(t-h(t))$.

Then the following theorem is given as the main result.

Theorem 1 For given scalars $0\le h_m\le h_M$, $d_m\le d_M$, diagonal matrices ${\mathrm{\Gamma }}^{-}$ and ${\mathrm{\Gamma }}^{+}$, the system (5) is asymptotically stable for (4), if there exist a positive scalar ϵ, positive definite matrices $\mathcal{P}\in {\mathbb{R}}^{4n\times 4n}$, $Q_i\in {\mathbb{R}}^{n\times n}$ ($i=1,3$), ${\mathcal{Q}}_i\in {\mathbb{R}}^{2n\times 2n}$ ($i=2,4$), $R_i\in {\mathbb{R}}^{n\times n}$ ($i=1,2$), positive definite diagonal matrices $L_i\in {\mathbb{R}}^{n_y\times n_y}$ ($i=1,2$), $K\in {\mathbb{R}}^{n_y\times n_y}$, and any matrix $M\in {\mathbb{R}}^{2n\times 2n}$ satisfying the following LMIs:

$${{\mathrm{\Upsilon }}^{\perp }}^T{\mathbf{\Xi }}_{j,k}{\mathrm{\Upsilon }}^{\perp }<0(j,k=1,2),$$

(7)

$$\mathrm{\Psi }\ge 0,$$

(8)

where ${\mathbf{\Xi }}_{j,k}$ are the four vertices of ${\mathbf{\Xi }}_{[h(t),\dot{h}(t)]}$ with the bounds of $h(t)$ and $\dot{h}(t)$, that is, $h_M$ and $h_D$ when $j=k=1$, $h_M$ and $-h_D$ when $j<k$, $h_m$ and $h_D$ when $j>k$, and $h_m$ and $-h_D$ when $j=k=2$.

Proof Let us consider the following Lyapunov-Krasovskii functional candidate:

$$\begin{array}{rcl}V& =& {\eta }^T(t)\mathcal{P}\eta (t)\\ +{\int }_{t-h_m}^t{x}^T(s)Q_{1}x(s)ds+{\int }_{t-h(t)}^{t-h_m}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]ds\\ +{\int }_{t-h_M}^{t-h_m}{x}^T(s)Q_{3}x(s)ds+{\int }_{t-h_M}^{t-h(t)}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]ds\\ +h_m{\int }_{t-h_m}^t{\int }_s^t{\dot{x}}^T(u)R_1\dot{x}(u)duds+(h_M-h_m){\int }_{t-h_M}^{t-h_m}{\int }_s^t{\dot{x}}^T(u)R_2\dot{x}(u)duds\\ +2\sum _{i=1}^n{\int }_0^{C_i^{T}x(t)}[l_{1i}({\psi }_i(s)-{\gamma }_i^{-}s)+l_{2i}({\gamma }_i^{+}s-{\psi }_i(s))]ds.\end{array}$$

(9)

It should be noted that

$$\begin{array}{rcl}\eta (t)& =& \left[\begin{array}{c}x(t)\\ {\int }_{t-h_m}^{t}x(s)ds\\ {\int }_{t-h(t)}^{t-h_m}x(s)ds\\ {\int }_{t-h_M}^{t-h(t)}x(s)ds\end{array}\right]\\ =& \left[\begin{array}{c}x(t)\\ {\int }_{t-h_m}^{t}x(s)ds\\ (\frac{1}{h(t)-h_m}{\int }_{t-h(t)}^{t-h_m}x(s)ds)(h(t)-h_m)\\ (\frac{1}{h_M-h(t)}{\int }_{t-h_M}^{t-h(t)}x(s)ds)(h_M-h(t))\end{array}\right]\\ =& {\underset{{\mathrm{\Pi }}_{1,1[h(t)]}}{\underbrace{[e_1,h_m{e}_6,(h(t)-h_m)e_7,(h_M-h(t))e_8]}}}^T\zeta (t)\end{array}$$

(10)

and

$$\begin{array}{rcl}\dot{\eta }(t)& =& \left[\begin{array}{c}\dot{x}(t)\\ x(t)-x(t-h_m)\\ x(t-h_m)-(1-\dot{h}(t))x(t-h(t))\\ (1-\dot{h}(t))x(t-h(t))-x(t-h_M)\end{array}\right]\\ =& {\underset{{\mathrm{\Pi }}_{1,2[\dot{h}(t)]}}{\underbrace{[e_5,e_1-e_2,e_2-(1-\dot{h}(t))e_3,(1-\dot{h}(t))e_3-e_4]}}}^T\zeta (t).\end{array}$$

(11)

The time derivative of V can be calculated as

$$\begin{array}{rcl}\dot{V}& =& 2{\eta }^T(t)\mathcal{P}\dot{\eta }(t)\\ +x^T(t)Q_{1}x(t)-x^T(t-h_m)Q_{1}x(t-h_m)\\ +{\left[\begin{array}{c}x(t-h_m)\\ {\int }_{t-h_m}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}x(t-h_m)\\ {\int }_{t-h_m}^t\dot{x}(s)ds\end{array}\right]\\ -(1-\dot{h}(t)){\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]\\ +2{\int }_{t-h(t)}^{t-h_m}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}0\\ \dot{x}(t)\end{array}\right]ds\\ +x^T(t-h_m)Q_{3}x(t-h_m)-x^T(t-h_M)Q_{3}x(t-h_M)\\ +(1-\dot{h}(t)){\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]\\ -{\left[\begin{array}{c}x(t-h_M)\\ {\int }_{t-h_M}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}x(t-h_M)\\ {\int }_{t-h_M}^t\dot{x}(s)ds\end{array}\right]\\ +2{\int }_{t-h_M}^{t-h(t)}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}0\\ \dot{x}(t)\end{array}\right]ds\\ +h_m^2{\dot{x}}^T(t)R_1\dot{x}(t)-h_m{\int }_{t-h_m}^t{\dot{x}}^T(s)R_1\dot{x}(s)ds\\ +{(h_M-h_m)}^2{\dot{x}}^T(t)R_2\dot{x}(t)-(h_M-h_m){\int }_{t-h_M}^{t-h_m}{\dot{x}}^T(s)R_2\dot{x}(s)ds\\ +2{[\psi (Cx(t))-{\mathrm{\Gamma }}^{-}Cx(t)]}^T{L}_{1}C\dot{x}(t)\\ +2{[{\mathrm{\Gamma }}^{+}Cx(t)-\psi (Cx(t))]}^T{L}_{2}C\dot{x}(t)\\ =& {\zeta }^T(t)({\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}+{\mathrm{\Xi }}_2)\zeta (t)-h_m{\int }_{t-h_m}^t{\dot{x}}^T(s)R_1\dot{x}(s)ds\\ -(h_M-h_m){\int }_{t-h(t)}^{t-h_m}{\dot{x}}^T(s)R_2\dot{x}(s)ds-(h_M-h_m){\int }_{t-h_M}^{t-h(t)}{\dot{x}}^T(s)R_2\dot{x}(s)ds.\end{array}$$

(12)

By Lemma 1, the integral terms of the $\dot{V}$ are bounded as

$$-h_m{\int }_{t-h_m}^t{\dot{x}}^T(s)R_1\dot{x}(s)ds\le -{\xi }_{1,1}^T(t)R_1{\xi }_{1,1}(t)-3{\xi }_{1,2}^T(t)R_1{\xi }_{1,2}(t)$$

(13)

and

$$\begin{array}{c}-(h_M-h_m){\int }_{t-h(t)}^{t-h_m}{\dot{x}}^T(s)R_2\dot{x}(s)ds-(h_M-h_m){\int }_{t-h_M}^{t-h(t)}{\dot{x}}^T(s)R_2\dot{x}(s)ds\hfill \\ \le -\frac{h_M-h_m}{h(t)-h_m}{\xi }_{2,1}^T(t)R_2{\xi }_{2,1}(t)-\frac{3(h_M-h_m)}{h(t)-h_m}{\xi }_{2,2}^T(t)R_2{\xi }_{2,2}(t)\hfill \\ -\frac{h_M-h_m}{h_M-h(t)}{\xi }_{3,1}^T(t)R_2{\xi }_{3,1}(t)-\frac{3(h_M-h_m)}{h_M-h(t)}{\xi }_{3,2}^T(t)R_2{\xi }_{3,2}(t),\hfill \end{array}$$

(14)

where

$$\begin{array}{c}{\xi }_{1,1}(t)=x(t)-x(t-h_m)={(e_1-e_2)}^T\zeta (t),\hfill \\ {\xi }_{1,2}(t)=x(t)+x(t-h_m)-\frac{2}{h_m}{\int }_{t-h_m}^{t}x(s)ds={(e_1+e_2-2e_6)}^T\zeta (t),\hfill \\ {\xi }_{2,1}(t)=x(t-h_m)-x(t-h(t))={(e_2-e_3)}^T\zeta (t),\hfill \\ {\xi }_{2,2}(t)=x(t-h_m)+x(t-h(t))-\frac{2}{h(t)-h_m}{\int }_{t-h(t)}^{t-h_m}x(s)ds={(e_2+e_3-2e_7)}^T\zeta (t),\hfill \\ {\xi }_{3,1}(t)=x(t-h(t))-x(t-h_M)={(e_3-e_4)}^T\zeta (t),\hfill \\ {\xi }_{3,2}(t)=x(t-h(t))+x(t-h_M)-\frac{2}{h_M-h(t)}{\int }_{t-h_M}^{t-h(t)}x(s)ds={(e_3+e_4-2e_8)}^T\zeta (t).\hfill \end{array}$$

Furthermore, if the inequality (8) holds, applying the reciprocally convex approach in [5] to (14) leads to

$$\begin{array}{c}-\frac{1}{\alpha (t)}\{{\xi }_{2,1}^T(t)R_2{\xi }_{2,1}(t)+3{\xi }_{2,2}^T(t)R_2{\xi }_{2,2}(t)\}\hfill \\ -\frac{1}{1-\alpha (t)}\{{\xi }_{3,1}^T(t)R_2{\xi }_{3,1}(t)+3{\xi }_{3,2}^T(t)R_2{\xi }_{3,2}(t)\}\hfill \\ =-{\left[\begin{array}{c}{\xi }_{2,1}\\ {\xi }_{2,2}\\ {\xi }_{3,1}\\ {\xi }_{3,2}\end{array}\right]}^T\left[\begin{array}{cc}\frac{1}{\alpha (t)}\mathtt{diag}\{R_2,3R_2\}& 0\\ 0& \frac{1}{1-\alpha (t)}\mathtt{diag}\{R_2,3R_2\}\end{array}\right]\left[\begin{array}{c}{\xi }_{2,1}\\ {\xi }_{2,2}\\ {\xi }_{3,1}\\ {\xi }_{3,2}\end{array}\right]\hfill \\ \le -{\left[\begin{array}{c}{\xi }_{2,1}\\ {\xi }_{2,2}\\ {\xi }_{3,1}\\ {\xi }_{3,2}\end{array}\right]}^T\left[\begin{array}{cc}\mathtt{diag}\{R_2,3R_2\}& M\\ M^T& \mathtt{diag}\{R_2,3R_2\}\end{array}\right]\left[\begin{array}{c}{\xi }_{2,1}\\ {\xi }_{2,2}\\ {\xi }_{3,1}\\ {\xi }_{3,2}\end{array}\right]\hfill \\ ={\zeta }^T(t){\mathrm{\Xi }}_3\zeta (t)\hfill \end{array}$$

(15)

for any $2n\times 2n$ matrix M, where $\frac{1}{\alpha (t)}=\frac{h_M-h_m}{h(t)-h_m}$.

In addition, the following inequality holds for any positive diagonal matrix K:

$$\begin{array}{rcl}0& \le & -2{[\psi (Cx(t))-{\mathrm{\Gamma }}^{-}Cx(t)]}^{T}K[\psi (Cx(t))-{\mathrm{\Gamma }}^{+}Cx(t)]\\ =& {\zeta }^T(t)\underset{\mathrm{\Omega }}{\underbrace{[-\mathtt{sym}\left\{[e_9-e_1{C}^T{\mathrm{\Gamma }}^{-}]K{[e_9-e_1{C}^T{\mathrm{\Gamma }}^{+}]}^T\right\}]}}\zeta (t)\\ =& {\zeta }^T(t)\mathrm{\Omega }\zeta (t).\end{array}$$

(16)

Moreover, with the relational expression between $p(t)$ and $q(t)$, $p^T(t)p(t)\le q^T(t)q(t)$, from the system (5), there exists a scalar $ϵ>0$ satisfying the following inequality:

$$\begin{array}{rcl}0& \le & ϵ\{q^T(t)q(t)-p^T(t)p(t)\}\\ =& ϵ{(E_{a}x(t)+E_{d}x(t-h(t))+E_b\psi (y(t)))}^T(E_{a}x(t)+E_{d}x(t-h(t))+E_b\psi (y(t)))\\ -ϵp^T(t)p(t)\\ =& {\zeta }^T(t)\left[\underset{\mathrm{\Sigma }}{\underbrace{ϵ\{{(E_a{e}_1^T+E_d{e}_3^T+E_b{e}_9^T)}^T(E_a{e}_1^T+E_d{e}_3^T+E_b{e}_9^T)-e_{10}{I}_{n_u}{e}_{10}^T\}}}\right]\zeta (t)\\ =& {\zeta }^T(t)\mathrm{\Sigma }\zeta (t).\end{array}$$

(17)

From (12) to (17) and by applying the S-procedure [32], $\dot{V}$ has a new upper bound:

$$\dot{V}\le {\zeta }^T(t)({\mathrm{\Xi }}_{1[h(t),\dot{h}(t)]}+{\mathrm{\Xi }}_2+{\mathrm{\Xi }}_3+\mathrm{\Omega }+\mathrm{\Sigma })\zeta (t).$$

(18)

Then a new stability condition for the system (1) can be written:

$${\zeta }^T(t){\mathbf{\Xi }}_{[h(t),\dot{h}(t)]}\zeta (t)<0$$

(19)

subject to $\mathrm{\Upsilon }\zeta (t)=0$.

Here, the above condition is affinely dependent on $h(t)$ and $\dot{h}(t)$. Also, from (i) and (iii) of Lemma 2, if the inequality (19) holds, then for any free matrix X with appropriate dimension, the condition (19) is equivalent to

$${\mathbf{\Xi }}_{j,k}+\mathtt{sym}\{X\mathrm{\Upsilon }\}={\mathrm{\Omega }}_{j,k}<0(j,k=1,2).$$

(20)

From (18) to (20), if (20) holds, then there exist positive scalars ${\epsilon }_{j,k}$ ($j,k=1,2$) such that $\dot{V}\le {\zeta }^T(t){\mathrm{\Omega }}_{j,k}\zeta (t)<-{\epsilon }_{j,k}{\parallel x(t)\parallel }^2$ ($j,k=1,2$). Therefore, it can be seen that for all time t, if (20) holds, then $\dot{V}<-{min}_{j,k=1,2}\{{\epsilon }_{j,k}\}{\parallel x(t)\parallel }^2$. From the Lyapunov stability theory, it can be concluded that if (20) holds, then the system (5) is asymptotically stable.

Lastly, by utilizing (ii) and (iii) of Lemma 2, one can confirm that the inequality (19) is equivalent to the inequality (7). This completes our proof. □

Remark 1 To reduce the conservatism of sufficient stability conditions, the very simple Lyapunov-Krasovskii functional with a Wirtinger-based inequality was utilized in the work [15], but a new Lyapunov-Krasovskii functional was not introduced. In view of this, the main difference between this work and [15] is the use of ${\int }_{t-h(t)}^{t-h_m}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]ds$ and ${\int }_{t-h_M}^{t-h(t)}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]ds$ included in the new Lyapunov-Krasovskii functional (9). In other words, by calculating their time derivatives, some cross terms such as

$$\begin{array}{c}{\left[\begin{array}{c}x(t-h_m)\\ {\int }_{t-h_m}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}x(t-h_m)\\ {\int }_{t-h_m}^t\dot{x}(s)ds\end{array}\right]\hfill \\ -(1-\dot{h}(t)){\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]\hfill \\ +2{\int }_{t-h(t)}^{t-h_m}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_2\left[\begin{array}{c}0\\ \dot{x}(t)\end{array}\right]ds\hfill \end{array}$$

and

$$\begin{array}{c}(1-\dot{h}(t)){\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}x(t-h(t))\\ {\int }_{t-h(t)}^t\dot{x}(s)ds\end{array}\right]\hfill \\ -{\left[\begin{array}{c}x(t-h_M)\\ {\int }_{t-h_M}^t\dot{x}(s)ds\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}x(t-h_M)\\ {\int }_{t-h_M}^t\dot{x}(s)ds\end{array}\right]\hfill \\ +2{\int }_{t-h_M}^{t-h(t)}{\left[\begin{array}{c}x(s)\\ {\int }_s^t\dot{x}(u)du\end{array}\right]}^T{\mathcal{Q}}_4\left[\begin{array}{c}0\\ \dot{x}(t)\end{array}\right]ds\hfill \end{array}$$

are obtained and utilized in estimating the time derivative of the proposed Lyapunov-Krasovkii functional (9).

As a special case of Theorem 1, when the system (1) is the nominal form and the information about $\dot{h}(t)$ is unknown, then, based on a new Lyapunov-Krasovskii functional candidate given by

$$\begin{array}{rcl}V& =& {\left[\begin{array}{c}x(t)\\ {\int }_{t-h_m}^{t}x(s)ds\\ {\int }_{t-h_M}^{t-h_m}x(s)ds\end{array}\right]}^T\mathcal{P}\left[\begin{array}{c}x(t)\\ {\int }_{t-h_m}^{t}x(s)ds\\ {\int }_{t-h_M}^{t-h_m}x(s)ds\end{array}\right]\\ +{\int }_{t-h_m}^t{x}^T(s)Q_{1}x(s)ds+{\int }_{t-h_M}^{t-h_m}{x}^T(s)Q_{3}x(s)ds\\ +h_m{\int }_{t-h_m}^t{\int }_s^t{\dot{x}}^T(u)R_1\dot{x}(u)duds\\ +(h_M-h_m){\int }_{t-h_M}^{t-h_m}{\int }_s^t{\dot{x}}^T(u)R_2\dot{x}(u)duds\\ +2\sum _{i=1}^n{\int }_0^{C_i^{T}x(t)}[l_{1i}({\psi }_i(s)-{\gamma }_i^{-}s)+l_{2i}({\gamma }_i^{+}s-{\psi }_i(s))]ds,\end{array}$$

(21)

the following theorem can be obtained.

Theorem 2 For given scalars $0\le h_m\le h_M$, diagonal matrices ${\mathrm{\Gamma }}^{-}$ and ${\mathrm{\Gamma }}^{+}$, the nominal form of the system (1) is asymptotically stable for $h_m\le h(t)\le h_M$, if there exist positive definite matrices $\mathcal{P}\in {\mathbb{R}}^{3n\times 3n}$, $Q_i\in {\mathbb{R}}^{n\times n}$ ($i=1,3$), $R_i\in {\mathbb{R}}^{n\times n}$ ($i=1,2$), positive definite diagonal matrices $L_i\in {\mathbb{R}}^{n_y\times n_y}$ ($i=1,2$), $K\in {\mathbb{R}}^{n_y\times n_y}$, and any matrix $M\in {\mathbb{R}}^{2n\times 2n}$ satisfying the LMIs (8) and

$${{\hat{\mathrm{\Upsilon }}}^{\perp }}^T{\hat{\mathbf{\Xi }}}_i{\hat{\mathrm{\Upsilon }}}^{\perp }<0(i=1,2),$$

(22)

where ${\hat{\mathbf{\Xi }}}_i$ are the two vertices of ${\hat{\mathbf{\Xi }}}_{[h(t)]}$ with the bounds of $h(t)$, that is, $h_M$ when $i=1$ and $h_M$ when $i=2$, and $\hat{\mathrm{\Upsilon }}=A{e}_1^T+A_d{e}_3^T-I_n{e}_5^T+B{e}_9^T$.

Proof The new upper bound of the time derivative of (21) can be calculated as

$$\dot{V}\le {\hat{\zeta }}^T(t){\hat{\mathbf{\Xi }}}_{[h(t)]}\hat{\zeta }(t),$$

(23)

where

$$\begin{array}{c}\hat{\zeta }(t)=\mathtt{col}\{x(t),x(t-h_m),x(t-h(t)),x(k-h_M),\dot{x}(t),\frac{1}{h_m}{\int }_{t-h_m}^{t}x(s)ds,\hfill \\ \phantom{\hat{\zeta }(t)=}\frac{1}{h(t)-h_m}{\int }_{t-h(t)}^{t-h_m}x(s)ds,\frac{1}{h_M-h(t)}{\int }_{t-h_M}^{t-h(t)}x(s)ds,\psi (y(t))\},\hfill \\ {\hat{\mathbf{\Xi }}}_{[h(t)]}=\mathtt{sym}\left\{[e_1,h_m{e}_6,(h(t)-h_m)e_7+(h_M-h(t))e_8]\mathcal{P}{[e_5,e_1-e_2,e_2-e_4]}^T\right\}\hfill \\ \phantom{{\hat{\mathbf{\Xi }}}_{[h(t)]}=}+{\mathrm{\Xi }}_2+{\mathrm{\Xi }}_3+\mathrm{\Omega }\hfill \end{array}$$

with replacing the block entry matrices to $e_i\in {\mathbb{R}}^{(8n+n_y)\times n}$ ($i=1,\dots ,9$), which is very similar to the proof of Theorem 1, so it is omitted. □

4 Illustrative examples

Example 1 Consider the system (1) with

$$\begin{array}{c}A=\left[\begin{array}{cc}-1.2& 0\\ 0.8& -1\end{array}\right],A_d=\left[\begin{array}{cc}-1& 0.6\\ -0.6& -1\end{array}\right],B=-I_2,C=I_2,\hfill \\ D=\mathtt{diag}\{\theta ,\theta \},E_a=\mathtt{diag}\{0.2,0.2\},E_d=E_b=\mathtt{diag}\{0.03,0.03\},\hfill \\ {\mathrm{\Gamma }}^{-}=0,{\mathrm{\Gamma }}^{+}=\mathtt{diag}\{1,3\}.\hfill \end{array}$$

(24)

Table 1 shows the results of the maximum allowable delay bounds with various θ and fixed $h_m=d_m=0$ for the above system. It can be seen that Theorem 1 in this work provides a larger delay bound than the existing works. This indicates that the presented conditions relieve the conservativeness of the stability caused by time delay.

Table 1 Maximum allowable delay bounds with fixed ${\mathit{h}}_{\mathit{m}}\mathbf{=}{\mathit{d}}_{\mathit{m}}\mathbf{=}\mathbf{0}$ (Example 1)

Example 2 Consider the Chua circuit [34] given by

$$\begin{array}{c}{\dot{x}}_1(t)=\alpha (x_2(t)-h(x_1(t))),\hfill \\ {\dot{x}}_2(t)=x_1(t)-x_2(t)+x_3(t),\hfill \\ {\dot{x}}_3(t)=-\beta x_2(t)\hfill \end{array}$$

with the nonlinear function $h(x_1(t))=m_1{x}_1(t)+\frac{1}{2}(m_0-m_1)(|x_1(t)+c|-|x_1(t)-c|)$, where the parameters are $m_0=-\frac{1}{7}$, $m_1=\frac{2}{7}$, $\alpha =9$, $\beta =14.28$, and $c=1$; its Lur’e form can be rewritten with

$$\begin{array}{c}A=\left[\begin{array}{ccc}-\alpha m_1& \alpha & 0\\ 1& -1& 1\\ 0& -\beta & 0\end{array}\right],A_d=0_3,\hfill \\ B=\left[\begin{array}{c}-\alpha (m_0-m_1)\\ 0\\ 0\end{array}\right],C=[\begin{array}{ccc}1& 0& 0\end{array}].\hfill \end{array}$$

Furthermore, according to the works [23, 29], a master-slave error system using static error feedback control with time-varying delay is presented as

$$\begin{array}{c}\dot{m}(t)=Am(t)+B\psi (Cm(t)),\hfill \\ \dot{s}(t)=As(t)+B\psi (Cs(t))-K(m(t)-s(t))+L(Cm(t-h(t))-Cs(t-h(t)))\hfill \end{array}$$

and defining $e(t)=m(t)-s(t)$ leads to

$$\dot{e}(t)=(A+K)e(t)-LCe(t-h(t))+B\psi (Ce(t)).$$

Here, $\psi (s)$ belongs to the sector bound $[0,1]$.

For comparison with the existing works, the controller gains are selected by

$$K=\mathtt{diag}\{-1,-1,-1\},L={[\begin{array}{ccc}6.0029& 1.3367& -2.1264\end{array}]}^T.$$

Synthetically, the above error system is equal to the nominal form of system (1) with

$$\begin{array}{r}A=\left[\begin{array}{ccc}-\alpha m_1-1& \alpha & 0\\ 1& -2& 1\\ 0& -\beta & -1\end{array}\right],A_d=\left[\begin{array}{ccc}-6.0029& 0& 0\\ -1.3367& 0& 0\\ 2.1264& 0& 0\end{array}\right],\\ B=\left[\begin{array}{c}-\alpha (m_0-m_1)\\ 0\\ 0\end{array}\right],C=[\begin{array}{ccc}1& 0& 0\end{array}].\end{array}$$

(25)

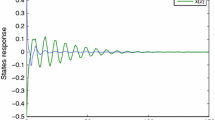
For system (1) with (25), the result of the maximum allowable delay bound with fixed $h_m=0$, unknown $d_m$ and $d_M$ obtained by Theorem 2 is listed in Table 2. One can see that our result for this example gives a larger maximum allowable delay bound than those of [23] and [29]. Even though the number of decision variables of Theorem 2 is larger than that of [23], it is smaller than that of [29]. To confirm the obtained result, a simulation result when the time delay is $h(t)=0.0895sin(11.1794t)+0.0895$ and the initial value $x(0)={[-1,0.5,1]}^T$ is given in Figure 1.

Figure 1

Phase trajectory (Example 2).

Table 2 Maximum allowable delay bounds with fixed ${\mathit{h}}_{\mathit{m}}\mathbf{=}\mathbf{0}$ , unknown ${\mathit{d}}_{\mathit{m}}$ and ${\mathit{d}}_{\mathit{M}}$ (Example 2)

Example 3 Consider the nominal form of system (1) with

$$A=\left[\begin{array}{cc}0& 1\\ -1& -2\end{array}\right],A_d=\left[\begin{array}{cc}0& 0\\ -1& 1\end{array}\right].$$

(26)

For the above system, the results of the maximum allowable delay bound with various $h_m=0$, unknown $d_m$ and $d_M$ are compared with the previous results in Table 3. It can also be shown that the proposed sufficient stability condition improves the stability region. Furthermore, the number of utilized decision variables in Theorem 2 is much smaller than those of [19, 22], and [21].

Table 3 Maximum allowable delay bounds with unknown ${\mathit{d}}_{\mathit{m}}$ and ${\mathit{d}}_{\mathit{M}}$ (Example 3)

5 Conclusions

In this paper, the delay-dependent stability problem for the Lur’e systems with interval time-varying delays and parameter uncertainties was dealt. In Theorem 1, the improved robust sufficient stability condition for the concerned systems was proposed by introducing the augmented Lyapunov-Krasovskii functional and using some approaches. In Theorem 2, based on the result of Theorem 1, the sufficient stability condition for the nominal form of Lur’e systems with interval time-varying delays having a constraint on the unknown $\dot{h}(t)$ was presented. Three illustrative examples have been given to show the effectiveness and usefulness of the presented sufficient conditions.