Abstract
This paper considers the problems of determining the robust exponential stability and estimating the exponential convergence rate for delayed neural networks with parametric uncertainties and time delay. The relationship among the time-varying delay, its upper bound, and their difference is taken into account. Theoretic analysis shows that our result includes a previous result derived in the literature. As illustrations, the results are applied to several concrete models studied in the literature, and a comparison of results is given.
Similar content being viewed by others
1 Introduction
Time delays are often encountered in various practical systems such as chemical processes, neural networks, and long transmission lines in pneumatic systems. It has been shown that the existence of time delays may lead to oscillations, divergences, or instabilities. This motivates the stability analysis problem for linear systems affected by time delays. During the last decade, increasing research interests have been aroused in the stability analysis and control design of time delay systems [1–17]. It is well known that neural networks have been extensively studied over the past few decades and have been successfully applied to many areas, such as signal processing, static processing, pattern recognition, combinatorial optimization, and so on [18]. So, it is important to study the stability of neural networks. In biological and artificial neural networks, time delays often arise in the processing of information storage and transmission.
Recently, a considerable number of sufficient conditions on the existence, uniqueness, and global asymptotic stability of equilibrium point for neural networks with constant delays or time-varying delays were reported under some assumptions; for example, see [3, 4, 6, 8, 9, 11, 15–17] and references therein. In the design of delayed neural networks (DNNs), however, one is interested not only in the global asymptotic stability of the neural network, but also in some other performances. In particular, it is often desirable that the neural network converges fast enough in order to achieve a fast response [15]. It is well known that exponential stability gives a fast convergence rate to the equilibrium point. Therefore, some researchers studied the exponential stability analysis problem for time delay systems with constant delays or time-varying delays, and a great number of results on this topic have been given in the literature; for example, see [3, 7, 9–11, 14–17] and references therein. The exponential stability problems of switched positive continuous time [12] and discrete-time [13, 14] linear systems with time delay were considered. In [16], exponential stability criteria for DNNs with time-varying delay are derived, but the constraint on a time-varying delay was imposed. Such a restriction is very conservative and has physical limitations.
In practical implementations, uncertainties are inevitable in neural networks because of the existence of modeling errors and external disturbance. It is important to ensure the neural networks system is stable under these uncertainties. Both time delays and uncertainties can destroy the stability of neural networks in an electronic implementation. Therefore, it is of great theoretical and practical importance to investigate the robust stability for delayed neural networks with uncertainties [11].
Recently, a free-weighting matrix approach [3] has been employed to study the exponential stability problem for neural networks with a time-varying delay [4]. However, as mentioned in [5], some useful terms in the derivative of the Lyapunov functional were ignored in [4, 6, 17]. The derivative of with was estimated as and the negative term was ignored in [17], which may lead to considerable conservativeness. Although in [4] and [6] the negative term was retained, the other term, , was ignored, which may also lead to considerable conservativeness. On the other hand, if the free-weighting method introduces too many free-weighting matrices in the theoretical derivation, some of them sometimes have no effect on reducing the conservatism of the obtained results; on the contrary, they mathematically complicate the system analysis and consequently lead to a significant increase in the computational demand [8]. How to overcome the aforementioned disadvantages of the integral inequality approach (IIA) is an important research topic in the delay-dependent related problem and also motivates the work of this paper on exponential stability analysis. Furthermore, the restriction of is released in the proposed scheme.
In this paper, a global robust exponential stability of the delayed neural networks with time-varying delays is proposed. By constructing a suitable augmented Lyapunov functional, a delay-dependent criterion is derived in terms of linear matrix inequalities (LMIs) and the integral inequality approach (IIA), which can be solved efficiently by using the generalized eigenvalue problem (GEVP). Furthermore, examples with simulation are given to show that the proposed stability criteria are less conservative than some recent ones in the literature.
Notation: Throughout this paper, stands for the transpose of the matrix N, denotes the n-dimensional Euclidean space, means that the matrix P is positive definite, I is an appropriately dimensioned identity matrix, and denotes a block diagonal matrix.
2 Problem formulations and preliminaries
Consider continuous neural networks with time-varying delays can be described by the following state equations:
or equivalently
where is the neuron state vector, is for the activation functions, , is a constant input vector, is a positive diagonal matrix, and are the interconnection matrices representing the weight coefficients of the neurons. The matrices , , and are the uncertainties of the system and have the form
where D, , , and are known constant real matrices with appropriate dimensions and is an unknown matrix function with Lebesgue-measurable elements bounded by
where I is an appropriately dimensioned identity matrix.
The time delay is a time-varying differentiable function that satisfies
where h and are constants.
Assumption 1 Throughout this paper, it is assumed that each of the activation functions () possesses the following condition:
where () are positive constants.
Next, the equilibrium point of system (2.1) is shifted to the origin through the transformation , then system (2.1) can be equivalently written as the following system:
where , , , . It is obvious that the function () satisfies the following condition:
which is equivalent to
To obtain the main results, the following lemmas are needed. First, we introduce a technical lemma of the integral inequality approach (IIA), which will be used in the proof of ours.
For any semi-positive definite matrices
the following integral inequality holds:
Secondarily, we introduce the following Schur complement which is essential in the proofs of our results.
Lemma 2 [1]
The following matrix inequality:
where , and depend in an affine way on x, is equivalent to
and
Finally, Lemma 3 will be used to handle the parametrical perturbation.
Lemma 3 [18]
Given symmetric matrices Ω and D, E, of appropriate dimensions, we have
for all satisfying , if and only if there exists some such that
Firstly, we consider the nominal from system (2.7):
For the nominal system (2.18), we will give a stability condition by using an integral inequality approach as follows.
Theorem 1 For given scalars h, α, and , system (2.18) is exponentially stable if there exist symmetry positive-definite matrices , , , , , diagonal matrices , , , and
and
such that the following LMIs hold:
where
Proof Choose the following Lyapunov-Kravoskii functional candidate:
where
Then taking the time derivative of with respect to t along the system (2.18) yields
First, the derivative of is
Second, we get the bound of differential on as
Third, the bound of differential on is as follows:
Using Lemma 2, the term can be written as
Similarly, we have
The operator for the term is as follows:
From (2.9) for appropriately dimensioned diagonal matrices (), we have
and
Combining (2.24)-(2.31) yields
From (2.32) and the Schur complement, it is easy to see that holds if , . □
3 Exponential robust stability analysis
Based on Theorem 1, we have the following result for uncertain neural networks with time-varying delay (2.7).
Theorem 2 For given positive scalars h, α, and , the uncertain delayed neural networks with time-varying delay (2.7) is exponentially robust stable if there exist symmetric positive-definite matrices , , , , , diagonal matrices , , , a scalar and
such that the following LMIs are true:
and
where (; ) are defined in (2.19).
It is, incidentally, worth noting that the uncertain delayed neural networks with time-varying delay (2.7) is exponential stable, that is, the uncertain parts of the nominal system can be tolerated within allowable time delay h and exponential convergence rate α.
Proof Replacing A, B, and C in (2.19) with , , and , respectively, we apply Lemma 2 for system (2.7) and the result is equivalent to the following condition:
where and .
According to Lemma 3, (3.4) is true if there exists a scalar such that the following inequality holds:
Applying the Schur complement shows that (3.5) is equivalent to (3.1). This completes the proof. □
If the upper bound of the derivative of time-varying delay is unknown, Theorem 2 can be reduced to the result with and , we have the following Corollary 1.
Corollary 1 For given positive scalars h and α, the system (2.7) is exponentially robust stable if there exist symmetric positive-definite matrices , , , diagonal matrices , , , and
such that the following LMIs are true:
and
where
Proof If the matrix is selected in (2.22). This proof can be completed in a formulation similar to Theorem 1 and Theorem 2. □
Based on that, a convex optimization problem is formulated to find the bound on the allowable delay time h and exponential convergence rate α which maintains the recurrent neural network time delay with parameter uncertainties systems (2.7).
Remark 1 It is interesting to note that h and α appear linearly in (2.19), (3.1), and (3.6). Thus a generalized eigenvalue problem (GEVP) as defined in Boyd et al. [1] can be formulated to solve the minimum acceptable (or ) and therefore the maximum h (or α) to maintain robust stability as judged by these conditions.
The lower bound of exponential convergence rate or the allowable time delay conditions can be determined by solving the following three optimization problems.
Case 1: estimate the lower bound of exponential convergence rate .
Case 2: estimate the allowable maximum time delay h.
Case 3: estimate the allowable maximum change rate of time delay .
If the change rate of time delay is equal to 0, i.e., , then the system (2.7) reduces to the neural networks with constant delay, and, consequently, Theorem 1 reduces to Corollary 1.
The lower bound of exponential convergence rate or the allowable time delay conditions can be determined by solving the following two optimization problems.
Case 4: estimate the lower bound of exponential convergence rate .
Case 5: estimate the allowable maximum time delay h.
Remark 2 All the above optimization problems (Op1-Op5) can be solved by the MATLAB LMI toolbox. Especially, Op1 and Op4 can estimate the lower bound of the global exponential convergence rate α, which means that the exponential convergence rate of any neural network included in (2.7) is at least equal to α. It is useful in real-time optimal computation.
4 Numerical examples
This section provides four numerical examples to demonstrate the effectiveness of the presented criterion.
Example 1 Consider the delayed neural network (2.18) as follows:
where
The neuron activation functions are assumed to satisfy Assumption 1 with .
Solution: It is assumed that the upper bound is fixed as 1. The exponential convergence rates for various ’s obtained from Theorem 1 and those in [4, 11, 17] are listed in Table 1. In the following, in Tables 1-2, ‘-’ means that the results are not applicable to the corresponding cases, and ‘unknown ’ means that can have arbitrary values, even is very large or is not differentiable.
On the other hand, if the exponential convergence rate of α is fixed as 0.8, the upper bounds of for various ’s from Theorem 1 and those in [4, 11, 17] are listed in Table 2.
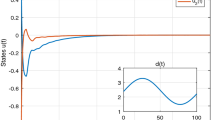
From Table 1, it is clear that when the delay is time-invariant, i.e., , the obtained result in Theorem 1 is much better than that in [17]. Furthermore, when the delay is time varying, the theorem in [17] fails to obtain the allowable exponential convergence rate of the exponential stable neural network system, but Theorem 1 in this paper can also obtain significantly better results than that in [4, 11], which guarantees the exponential stability of the neural networks. Moreover, when the exponential convergence rate of α is fixed as 0.8, the upper bounds of for various ’s derived by Theorem 1 are also better than those in [4, 11, 17] from Table 2. The reason is that, compared with [4, 11, 17], our results not only do not ignore any useful terms in the derivative of Lyapunov-Krasovskii functional but also consider the relationship among , , and . Figure 1 shows the state response of Example 1 with time delay , when the initial value is .
Example 2 Consider the delayed neural network (2.18) as follows:
where
The neuron activation functions are assumed to satisfy Assumption 1 with .
Solution: It is assumed that the exponential convergence rate of α is fixed as zero. The upper bounds of h for various ’s from Theorem 1 and those in [4–6, 11] are listed in Table 3. It is also clear that the obtained upper bounds of in this paper are better than those in [4–6, 11], which guarantee the asymptotic stability of neural networks. The reason is that our results do not ignore any useful negative terms in the derivative of Lyapunov-Krasovskii functional compared with [4, 6], and our results also consider the relationship among , , and compared with [5, 11].
Example 3 Consider the following uncertain delayed neural network:
where
The neuron activation functions are assumed to satisfy Assumption 1 with .
Solution: We let and as [9] did and, by Theorem 2, we can obtain the maximum allowable exponential convergence rate (MAECR) size to be . However, applying the criteria in [9], the maximum value of for the above system is 0.1. This example demonstrates that our robust stability condition gives a less conservative result. Hence, it is obvious that the results obtained from our simple method are less conservative than those obtained by existing methods. The maximum allowable exponential convergence rate (MAECR) for various h from Theorem 2 are listed in Table 4.
Example 4 Consider the following delayed neural network:
where
The neuron activation functions are assumed to satisfy Assumption 1 with .
Solution: Let and . Using the MATLAB LMI toolbox, the conditions of Theorem 2 can be met, and then we get the global robust exponential stability in this example for and
For this case, it can be verified that the stability conditions in [10, 13] are not applicable when . This implies that for this example the stability condition in Theorem 2 in this paper is less conservative than those in [10, 13].
Remark 3 In this paper, we are mainly concerned with exponential stability. For this reason another practical background and other definitions have not been introduced. Among them, exponential stability provides a useful measure for the decaying rate, or convergence speed. It is also worth pointing out that the main results in this paper can easily be extended to exponential stability for neural networks with time-varying delays by the same approach used in [8]. Note that we mainly focus on the effects brought about by the maximum allowable delay bound (MADB) and exponential convergence rate (MAECR) in this paper.
Remark 4 Some comparisons have been made with the same examples that appear in many recent papers. Our results show them to be less conservative than those reports.
5 Conclusion
In this paper, we have proposed some new delay dependent sufficient conditions for the global robust exponential stability analysis of a class of delayed neural networks with time-varying delays and parameter uncertainties. We have discussed the advantage of the assumption condition investigated in our paper over those in previous studies in the literature. Some global exponential stability criteria, which depend on time delay, are derived via the approach of the Lyapunov-Krasovskii functional. Four numerical examples are given to show the significant improvement over some existing results in the literature. In addition, the method proposed in this paper can easily be extended to solve the stability or exponential stability problem for delayed neural networks with distributed delay.
References
Boyd S, El Ghaoui L, Feron E, Balakrishnan V SIAM Studies in Applied Mathematics. In Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia; 1994.
Gahinet P, Nemirovski A, Laub A, Chilali M: LMI Control Toolbox User’s Guide. The Mathworks, Natick; 1995.
He Y, Wu M, She JH, Liu GP: Parameter-dependent Lyapunov functional for stability of time-delay systems with polytopic-type uncertainties. IEEE Trans. Autom. Control 2004, 49: 828–832. 10.1109/TAC.2004.828317
He Y, Wu M, She JH: Delay-dependent exponential stability of delayed neural networks with time-varying delay. IEEE Trans. Circuits Syst. II, Express Briefs 2006, 53: 553–557.
He Y, Liu GP, Rees D: New delay-dependent stability criteria for neutral networks with time-varying delay. IEEE Trans. Neural Netw. 2007, 18: 310–314.
Hua CC, Long CN, Guan XP: New results on stability analysis of neural networks with time-varying delays. Phys. Lett. A 2006, 352: 335–340. 10.1016/j.physleta.2005.12.005
Liu PL: Robust exponential stability for uncertain time-varying delay systems with delay dependence. J. Franklin Inst. 2009, 346: 958–968. 10.1016/j.jfranklin.2009.04.005
Liu PL: Improved delay-dependent robust stability criteria for recurrent neural networks with time-varying delays. ISA Trans. 2013, 52: 30–35. 10.1016/j.isatra.2012.07.007
Park JH: Further note on global exponential stability of uncertain cellular neural networks with variable delays. Appl. Math. Comput. 2007, 188: 850–854. 10.1016/j.amc.2006.10.036
Song QK: Exponential stability of recurrent neural networks with both time-varying delays and general activation functions via LMI approach. Neurocomputing 2008, 71: 2823–2830. 10.1016/j.neucom.2007.08.024
Xiang M, Xiang ZR:Stability, -gain and control synthesis for positive switched systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2013, 9(1):9–17.
Xiang ZR, Liu SL, Chen QW: An improved exponential stability criterion for discrete-time switched non-linear systems with time-varying delays. Trans. Inst. Meas. Control 2013, 35(3):353–359. 10.1177/0142331212448271
Xiang M, Xiang ZR: Exponential stability of discrete-time switched linear positive systems with time-delay. Appl. Math. Comput. 2014, 230: 193–199.
Wu X, Wang YN, Huang LH, Zuo Y: Robust exponential stability criterion for uncertain neural networks with discontinuous activation functions and time-varying delays. Neurocomputing 2010, 73: 1265–1271. 10.1016/j.neucom.2010.01.002
Xu SY, Lam J: A new approach to exponential stability analysis of neural networks with time-varying delays. Neural Netw. 2006, 19: 76–83. 10.1016/j.neunet.2005.05.005
Yuan K, Cao J, Deng J: Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays. Neurocomputing 2006, 69: 1619–1627. 10.1016/j.neucom.2005.05.011
Zhang Q, Wei X, Xu J: Delay-dependent exponential stability of cellular neural networks with time-varying delays. Chaos Solitons Fractals 2005, 23: 1363–1369. 10.1016/j.chaos.2004.06.036
Chua L, Yang L: Cellular neural networks: theory. IEEE Trans. Circuits Syst. 1988, 35: 1257–1272. 10.1109/31.7600
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xie, JC., Chen, CP., Liu, PL. et al. Robust exponential stability analysis for delayed neural networks with time-varying delay. Adv Differ Equ 2014, 131 (2014). https://doi.org/10.1186/1687-1847-2014-131
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-131