Abstract
This paper studies the problem for exponential stability of switched recurrent neural networks with interval time-varying delay. The time delay is a continuous function belonging to a given interval, but not necessarily differentiable. By constructing a set of argumented Lyapunov-Krasovskii functionals combined with the Newton-Leibniz formula, a switching rule for exponential stability of switched recurrent neural networks with interval time-varying delay is designed via linear matrix inequalities, and new sufficient conditions for the exponential stability of switched recurrent neural networks with interval time-varying delay via linear matrix inequalities (LMIs) are derived. A numerical example is given to illustrate the effectiveness of the obtained result.
Similar content being viewed by others
1 Introduction
In recent years, neural networks (especially recurrent neural networks, Hopfield neural networks, and cellular neural networks) have been successfully applied in many areas such as signal processing, image processing, pattern recognition, fault diagnosis, associative memory, and combinatorial optimization; see, for example, [1–6]. One of the best important works in these applications is to study the stability of the equilibrium point of neural networks. A major purpose is to find stability conditions i.e., the conditions for the stability of the equilibrium point of neural networks. The stability and control of recurrent neural networks with time delay have attracted considerable attention in recent years [1–10]. In many practical systems, it is desirable to design neural networks which are not only asymptotically or exponentially stable but can also guarantee an adequate level of system performance. In the area of control, signal processing, pattern recognition, and image processing, delayed neural networks have many useful applications. Some of these applications require the equilibrium points of the designed network to be stable. In both biological and artificial neural systems, time delays due to integration and communication are ubiquitous and often become a source of instability. The time delays in electronic neural networks are usually time-varying and sometimes vary violently with respect to time due to the finite switching speed of amplifiers and faults in the electrical circuitry. The Lyapunov-Krasovskii functional technique has been among the popular and effective tools in the design of guaranteed cost controls for neural networks with time delay. Nevertheless, despite such diversity of results available, most existing works either assumed that the time delays are constant or differentiable [9–14]. To the best of our knowledge, a switching rule and exponential stability for switched recurrent neural networks with interval time-varying delay, non-differentiable time-varying delays have not been fully studied yet (see, e.g., [4–9, 13–25] and the references therein), and they are important in both theories and applications. This motivates our research.
In this paper, we investigate the exponential stability for a switched recurrent neural networks problem. The novel features here are that the delayed neural network under consideration is with various globally Lipschitz continuous activation functions, and the time-varying delay function is interval, non-differentiable. Based on constructing a set of augmented Lyapunov-Krasovskii functionals combined with Newton-Leibniz formula, a switching rule for exponential stability of switched recurrent neural networks with interval time-varying delay and new delay-dependent exponential stability criteria for switched recurrent neural networks with interval time-varying delay are established in terms of LMIs, which allow simultaneous computation of two bounds that characterize the exponential stability rate of the solution and can be easily determined by utilizing MATLABs LMI control toolbox.
The outline of the paper is as follows. Section 2 presents definitions and some well-known technical propositions needed for the proof of the main result. LMI delay-dependent exponential stability criteria for switched recurrent neural networks with interval time-varying delay criteria, a switching rule for exponential stability of switched recurrent neural networks with interval time-varying delay, and a numerical example showing the effectiveness of the result are presented in Section 3. The paper ends with conclusions and cited references.
2 Preliminaries
The following notations will be used in this paper. denotes the set of all real non-negative numbers; denotes the n-dimensional space with the scalar product or of two vectors x, y and the vector norm ; denotes the space of all matrices of -dimensions. denotes the transpose of matrix A; A is symmetric if ; I denotes the identity matrix; denotes the set of all eigenvalues of A; , . , ; denotes the set of all -valued continuously differentiable functions on ; denotes the set of all the -valued square integrable functions on .
Matrix A is called semi-positive definite () if for all ; A is positive definite () if for all ; means . The notation stands for a block-diagonal matrix. The symmetric term in a matrix is denoted by ∗.
Consider the following switched recurrent neural networks with interval time-varying delay:
where is the state of the neural, n is the number of neurals, and
are the activation functions; is the switching rule, which is a function depending on the state at each time and will be designed. A switching function is a rule which determines a switching sequence for a given switching system. Moreover, implies that the system realization is chosen as the j th system, . It is seen that the system (2.1) can be viewed as an autonomous switched system in which the effective subsystem changes when the state hits predefined boundaries.
, represents the self-feedback term; , denote the connection weights, the discretely delayed connection weights, and the distributively delayed connection weight, respectively. The time-varying delay function satisfies the condition
The initial functions with the norm
In this paper, we consider various activation functions and assume that the activation functions , are Lipschitzian with the Lipschitz constants :
Definition 2.1 The zero solution of switched recurrent neural networks with interval time-varying delay (2.1) is α-exponentially stable if there exist two positive numbers , such that every solution satisfies the following condition:
We introduce the following technical well-known propositions, which will be used in the proof of our results.
Proposition 2.1 (Schur complement lemma [26])
Given constant matrices X, Y, Z with appropriate dimensions satisfying . Then if and only if
Proposition 2.2 (Integral matrix inequality [27])
For any symmetric positive definite matrix , scalar and vector function such that the integrations concerned are well defined, the following inequality holds:
3 Main results
Let us set
Theorem 3.1 The zero solution of the switched recurrent neural networks with interval time-varying delay (2.1) is α-exponentially stable if there exist a positive number , symmetric positive definite matrices P, U, , , , , and diagonal positive definite matrices , satisfying the following LMIs:
the switching rule is chosen as . Moreover, the solution of the system satisfies
Proof Let , . We consider the following Lyapunov-Krasovskii functional:
It is easy to check that
Taking the derivative of , we have
Applying Proposition 2.2 and the Leibniz-Newton formula
we have, for ,
Note that
Applying Proposition 2.2 gives
Since , we have
then
Similarly, we have
Then we have
Using equation (2.1),
and multiplying both sides by , we have
Adding all the zero items of (3.5) into (3.4) for the following estimations:
we obtain
where , and
Therefore, by condition (3.1), we obtain from (3.6) that
Integrating both sides of (3.7) from 0 to t, we obtain
Furthermore, taking condition (3.2) into account, we have
then
which concludes the exponential stability of (2.1). This completes the proof of the theorem. □
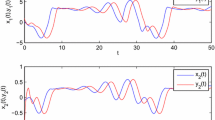
Example 3.1 Consider the switched recurrent neural networks with interval time-varying delay (2.1) for , where
Note that is non-differentiable, therefore, the stability criteria proposed in [5–9, 11–14, 17–25] are not applicable to this system. We choose that , , . By using the Matlab LMI toolbox, we can solve linear matrix inequalities for P, U, , , , , and which satisfy the conditions (3.1) in Theorem 3.1. A set of solutions is as follows:
By Theorem 3.1, the switched recurrent neural networks with interval time-varying delay are exponentially stable and the switching rule is chosen as . Moreover, the solution of the system satisfies
4 Conclusion
In this paper, the problem of exponential stability for switched recurrent neural networks with interval non-differentiable time-varying delay has been studied. By constructing a set of time-varying Lyapunov-Krasovskii functional combined with Newton-Leibniz formula, a switching rule for exponential stability of switched recurrent neural networks with interval time-varying delay has been presented and new sufficient conditions for the exponential stability for the system have been derived in terms of LMIs.
References
Hopfield JJ: Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79: 2554-2558. 10.1073/pnas.79.8.2554
Ratchagit K: Asymptotic stability of delay-difference system of Hopfield neural networks via matrix inequalities and application. Int. J. Neural Syst. 2007, 17: 425-430. 10.1142/S0129065707001263
Kevin G: An Introduction to Neural Networks. CRC Press, Boca Raton; 1997.
Wu M, He Y, She JH: Stability Analysis and Robust Control of Time-Delay Systems. Springer, Berlin; 2010.
Arik S: An improved global stability result for delayed cellular neural networks. IEEE Trans. Circuits Syst. 2002, 499: 1211-1218.
He Y, Wang QG, Wu M: LMI-based stability criteria for neural networks with multiple time-varying delays. Physica D 2005, 112: 126-131.
Kwon OM, Park JH: Exponential stability analysis for uncertain neural networks with interval time-varying delays. Appl. Math. Comput. 2009, 212: 530-541. 10.1016/j.amc.2009.02.043
Phat VN, Trinh H: Exponential stabilization of neural networks with various activation functions and mixed time-varying delays. IEEE Trans. Neural Netw. 2010, 21: 1180-1185.
Botmart T, Niamsup P: Robust exponential stability and stabilizability of linear parameter dependent systems with delays. Appl. Math. Comput. 2010, 217: 2551-2566. 10.1016/j.amc.2010.07.068
Fridman E, Orlov Y: Exponential stability of linear distributed parameter systems with time-varying delays. Automatica 2009, 45: 194-201. 10.1016/j.automatica.2008.06.006
Xu S, Lam J: A survey of linear matrix inequality techniques in stability analysis of delay systems. Int. J. Syst. Sci. 2008, 39(12):1095-1113. 10.1080/00207720802300370
Xie JS, Fan BQ, Young SL, Yang J: Guaranteed cost controller design of networked control systems with state delay. Acta Autom. Sin. 2007, 33: 170-174.
Yu L, Gao F: Optimal guaranteed cost control of discrete-time uncertain systems with both state and input delays. J. Franklin Inst. 2001, 338: 101-110. 10.1016/S0016-0032(00)00073-9
Park JH, Kwon OM, Lee SM, Won SC:On robust filter design for uncertain neural systems: LMI optimization approach. Appl. Math. Comput. 2004, 159: 625-639. 10.1016/j.amc.2003.09.025
Park JH: Further result on asymptotic stability criterion of cellular neural networks with time-varying discrete and distributed delays. Appl. Math. Comput. 2006, 182: 1661-1666. 10.1016/j.amc.2006.06.005
Ratchagit K, Phat VN: Robust stability and stabilization of linear polytopic delay-difference equations with interval time-varying delays. Neural Parallel Sci. Comput. 2011, 19: 361-372.
Phat VN, Ratchagit K: Stability and stabilization of switched linear discrete-time systems with interval time-varying delay. Nonlinear Anal. Hybrid Syst. 2011, 5: 605-612. 10.1016/j.nahs.2011.05.006
Tian L, Liang J, Cao J: Robust observer for discrete-time Markovian jumping neural networks with mixed mode-dependent delays. Nonlinear Dyn. 2012, 67: 47-61. 10.1007/s11071-011-9956-y
Rajchakit M, Rajchakit G: Mean square exponential stability of stochastic switched system with interval time-varying delays. Abstr. Appl. Anal. 2012., 2012: Article ID 623014. doi:10.1155/2012/623014
Phat VN, Kongtham Y, Ratchagit K: LMI approach to exponential stability of linear systems with interval time-varying delays. Linear Algebra Appl. 2012, 436: 243-251. 10.1016/j.laa.2011.07.016
Wu H, Li N, Wang K, Xu G, Guo Q: Global robust stability of switched interval neural networks with discrete and distributed time-varying delays of neural type. Math. Probl. Eng. 2012., 2012: Article ID 361871. doi:10.1155/2012/361871
Xu H, Wu H, Li N: Switched exponential state estimation and robust stability for interval neural networks with discrete and distributed time delays. Abstr. Appl. Anal. 2012., 2012: Article ID 103542. doi:10.1155/2012/103542
Rajchakit M, Niamsup P, Rojsiraphisal T, Rajchakit G: Delay-dependent guaranteed cost controller design for uncertain neural networks with interval time-varying delay. Abstr. Appl. Anal. 2012., 2012: Article ID 587426. doi:10.1155/2012/587426
Zhang H, Wang Z, Liu D: Robust exponential stability of recurrent neural networks with multiple time-varying delays. IEEE Trans. Circuits Syst. II, Express Briefs 2007, 54(8):730-734.
Gau R-S, Lien C-H, Hsieh J-G: Novel stability conditions for interval delayed neural networks with multiple time-varying delays. Int. J. Innov. Comput. Inf. Control 2011, 7(1):433-444.
Boyd S, El Ghaoui L, Feron E, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia; 1994.
Gu K, Kharitonov V, Chen J: Stability of Time-Delay Systems. Birkhäuser, Berlin; 2003.
Acknowledgements
This work was supported by the Office of Agricultural Research and Extension Maejo University Chiang Mai Thailand, the National Research Council of Thailand, the Thailand Research Fund Grant, the Higher Education Commission and Faculty of Science, Maejo University, Thailand. The authors thank anonymous reviewers for valuable comments and suggestions, which allowed us to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors contributed equally and significantly in writing this paper. The authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rajchakit, M., Niamsup, P. & Rajchakit, G. A switching rule for exponential stability of switched recurrent neural networks with interval time-varying delay. Adv Differ Equ 2013, 44 (2013). https://doi.org/10.1186/1687-1847-2013-44
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-44