Numerical solution of fractional partial differential equations by numerical Laplace inversion technique

Abstract

In this paper, we propose a numerical method for solving fractional partial differential equations. This method is based on the homotopy perturbation method and Laplace transform. The transformed problem obtained by means of temporal Laplace transform is solved by the homotopy perturbation method. Then we use Stehfest’s numerical algorithm for calculating inverse Laplace transform to retrieve the time domain solution. The approximate solutions obtained by our proposed method are in excellent agreement with the exact solutions. It is worthwhile to note that our method is applicable to a variety of fractional partial differential equations occurring in fluid mechanics, signal processing, system identification, control robotics, etc. The utility of the method is shown by solving some interesting examples.

MSC:34A08, 44A10.

1 Introduction

Fractional differential equations are found to be an effective tool to describe certain physical phenomena such as damping laws, rheology, diffusion processes, and so on. Several methods have been developed to solve fractional differential equations. Lin and Xu [1] proposed the numerical solution for a time-fractional diffusion equation. In [2], an unconditionally stable finite element (FEM) approach for solving a one-dimensional Caputo-type fractional differential equation with singularity at the boundary was presented. Kexue and Jigen [3] discussed the Laplace transform (LT) method for solving fractional differential equations with constant coefficients. Jafari et al. [4] applied the homotopy analysis method to obtain the solution of a multi-order fractional differential equation in the Caputo sense. Merrikh-Bayat [5] developed a low-cost numerical algorithm to find the series solution of nonlinear fractional differential equations with delay. In [6], the Riemann-Liouville fractional integral for repeated fractional integration was expanded in block pulse functions to yield the block pulse operational matrices for the fractional order integration. Esmaeili et al. [7] developed a computational technique based on the collocation method and Muntz polynomials for the solution of fractional differential equations. In [8], three different numerical methods were used to solve a singularly perturbed Able Volterra integral equation, presented by a fractional differential equation. Ibrahim [9] discussed holomorphic solutions for nonlinear singular fractional differential equations.

Homotopy perturbation method (HPM) has been applied by several researchers to solve different kinds of functional equations. This method was further developed and improved by He [10] and applied to develop a coupling method for a homotopy technique [11], limit cycle and bifurcation of nonlinear problems [12], nonlinear wave equation [13], boundary value problems [14], chemical kinetics system [15], oscillators with discontinuities [16], Riccati equation with fractional orders [17], neutron transport equation [18], nonlinear singular fourth order four-point boundary value problems [19], systems of partial differential equations [20], nonlinear ill-posed operator equations [21] and stiff systems of ordinary differential equations [22].

The Laplace transform method has been applied to a wide class of ordinary differential equations (ODEs), partial differential equations (PDEs), integral equations (IEs) and integro-differential equations (IDEs). In these problems it is necessary to calculate the Laplace transform and inverse Laplace transform of certain functions. The inverse of Laplace transform is usually difficult to compute by using the techniques of complex analysis, and there exist numerous numerical methods for its evaluation [23, 24]. Sastre et al. [25] developed an application of Laguerre matrix polynomial series to the numerical inversion of Laplace transforms of matrix functions. Laguerre matrix polynomials were introduced in [26] and theorems for the expansion of matrix functions in series of Laguerre matrix polynomials can be found in [27, 28]. In [29], the dynamical differential equations with initial conditions were converted into the model of linear operator action, in which the linear operator is just the infinitesimal generator for the solver of the differential equations, and the resolvent of the linear operator is the Laplace transform of the solver of original differential equations. In [30], a method for the numerical inversion of Laplace transform on the real line of heavytailed (probability) density functions is presented. The method assumes a finite set of real values of the Laplace transform and chooses the analytical form of the approximant maximizing Shannon-entropy, so that positivity of the approximant itself is guaranteed. In [31], a Laplace homotopy perturbation method is employed for solving one-dimensional non-homogeneous partial differential equations with a variable coefficient. This method is a combination of the Laplace transform and the homotopy perturbation method (LHPM). LHPM presents an accurate methodology to solve non-homogeneous partial differential equations with a variable coefficient. Sheng et al. [32] proposed an application of numerical inverse Laplace transform algorithms and obtained an easy way to solve the complicated fractional-order differential equations numerically. Weeks numerical inversion of Laplace transform algorithm was established by using the Laguerre expansion and bilinear transformations [33]. The authors of [34] developed an accurate numerical inversion of Laplace transforms. Tagliani [35] proposed a numerical method for inversion of Laplace transform with probability densities. The maximum entropy technique provides an analytical form of the approximate solution. Fractional moments are mainly investigated. Entropy and cross-entropy convergence are proved. Valko et al. [36] proposed a new algorithm for the numerical inversion of Laplace transforms by using multi-precision computational environment and provided controlled accuracy, that is, the inversion can be carried out to yield any pre-specified number of significant digits. The fundamental collocation method was extended to handle two-dimensional transient heat conduction problems in solids in [37]. The method was applied in the Laplace transform domain, followed by an inversion technique to retrieve the time-domain solution. In [38], the authors developed a numerical algorithm for inverting a Laplace transform, based on Laguerre polynomial series expansion of the inverse function under the assumption that the Laplace transform is known on the real axis only. The main contribution of the paper is to provide computable estimates of truncation, discretization, conditioning and roundoff errors introduced by numerical computations. In the present work, we apply the Stehfest [39] algorithm for numerical inversion of Laplace transform.

In this paper, the method for numerical solution of fractional partial differential equations is based on Laplace transform (LT), the homotopy perturbation method (HPM) and Stehfest’s numerical algorithm for calculating inverse Laplace transform. The accuracy and efficiency of the method is verified by solving some examples of physical interest.

2 Homotopy perturbation technique

In this section, we describe the homotopy perturbation method [10–16] for a general type of the nonlinear differential equation with boundary conditions

$$A(u)-f(r)=0,r\in \mathrm{\Omega },$$

(1)

$$B(u,\frac{\partial u}{\partial n})=0,r\in \mathrm{\Gamma },$$

(2)

where A is a general differential operator, B is a boundary operator, $f(r)$ is a known analytical function and Γ is the boundary of the domain Ω. The operator A can be divided into two parts L and N, where L is a linear operator and N is a nonlinear operator. Therefore, Eq. (1) can be rewritten as follows:

$$L(u)+N(u)-f(r)=0.$$

(3)

By the homotopy technique, we define a homotopy $H(r,p):\mathrm{\Omega }\times [0,1]\to R$ as follows:

$$H(u,p)=(1-p)[L(u)-L(u_0)]+p[A(u)-f(r)]=0,p\in [0,1],r\in \mathrm{\Omega },$$

(4)

or

$$H(u,p)=L(u)-L(u_0)+pL(u_0)+p[N(u)-f(r)]=0,p\in [0,1],r\in \mathrm{\Omega },$$

(5)

where $p\in [0,1]$ is an embedding parameter, and ${\overline{u}}_0$ is an initial approximation for Eq. (1) with

$$H(u,0)=L(u)-L(u_0)=0,H(u,1)=A(u)-f(r)=0.$$

(6)

Note that the process of varying the values of p from zero to unity corresponds to that of $u(r,p)$ from ${\overline{u}}_0(r)$ to $u(r)$. We assume that the solution of Eq. (1) can be written as a power series in p, that is,

$$v=\sum _{k=0}^{\mathrm{\infty }}{p}^k{u}_k.$$

(7)

Substituting (7) in (5) and comparing the coefficients of powers of p yields a successive procedure to determine $u_k$. Finally, by setting $p=1$ in (7), we obtain the solution of Eq. (1).

3 Preliminaries

In this section, we recall some basic concepts of fractional calculus [40–44] and Laplace transform.

Definition 1 For $\mu \in R$, a function $f:R\to R^{+}$ is said to be in the space $C_{\mu }$ if it can be written as $f(x)=x^p{f}_1(x)$ with $p>\mu$, $f_1(x)\in C[0,\mathrm{\infty })$, and it is said to be in the space $C_{\mu }^m$ if $f^{(m)}\in C_{\mu }$ for $m\in N\cup \{0\}$.

Definition 2 The Riemann-Liouville fractional integral of order $\alpha >0$ for a function $f\in C_{\mu }$ with $\mu \ge -1$ is defined as

$$\begin{array}{r}{J}^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-\tau )}^{\alpha -1}f(\tau )d\tau ,\alpha >0,t>0,\\ J^{0}f(t)=f(t).\end{array}$$

(8)

Definition 3 The Riemann-Liouville fractional derivative of order $\alpha >0$ for a function $f\in C_{-1}^m$ with $m\in N\cup \{0\}$ is defined as

$$D_{\ast }^{\alpha }f(t)=\frac{d^m}{d{t}^m}{J}^{m-\alpha }f(t),m-1<\alpha \le m,m\in N.$$

(9)

Definition 4 The Caputo fractional derivative of order $\alpha >0$ for a function $f\in C_{-1}^m$ with $m\in N\cup \{0\}$ is defined as

$$D^{\alpha }f(t)=\{\begin{array}{cc}{J}^{m-\alpha }{f}^{(m)}(t),\hfill & m-1<\alpha \le m,m\in N,\hfill \\ \frac{d^{m}f(t)}{d{t}^m},\hfill & \alpha =m.\hfill \end{array}$$

(10)

Definition 5 A two-parameter Mittag-Leffler function is defined by the following series:

$$E_{\alpha ,\beta }(t)=\sum _{k=0}^{\mathrm{\infty }}\frac{t^k}{\mathrm{\Gamma }(\alpha k+\beta )}.$$

(11)

Observe that $E_{1,1}(t)=e^t$, $E_{1,1}(-t)=e^{-t}$.

Definition 6 The Laplace transform of a function $u(x,t)$, $t\ge 0$, denoted by $\phi (x,s)$, is defined by

$$L\{u(x,t)\}=\phi (x,s)={\int }_0^{\mathrm{\infty }}{e}^{-st}u(x,t)dt,$$

(12)

where s is the transform parameter and is assumed to be real and positive.

Note that the Laplace transform of Mittag-Leffler function $E_{\alpha ,\beta }(t)$ is

$$L(E_{\alpha ,\beta }(t))={\int }_0^{\mathrm{\infty }}{e}^{-st}{E}_{\alpha ,\beta }(t)dt=\sum _{k=0}^{\mathrm{\infty }}\frac{\mathrm{\Gamma }(k+1)}{s^{k+1}\mathrm{\Gamma }(\alpha k+\beta )}.$$

(13)

The Laplace transform of $D^{\alpha }f(t)$ can be found as follows:

$$\begin{array}{rl}L(D^{\alpha }f(t))& =L(J^{m-\alpha }{f}^{(m)}(t))\\ =L[\frac{1}{\mathrm{\Gamma }(m-\alpha )}{\int }_0^t{(t-\tau )}^{m-\alpha -1}{f}^{(m)}(\tau )d\tau ]\\ =\frac{1}{s^{m-\alpha }}L(f^{(m)}(t))\\ =\frac{1}{s^{m-\alpha }}[s^{m}L(f(t))-s^{m-1}f(0)-s^{m-2}{f}^{\prime }(0)-s^{m-3}{f}^{″}(0)-\cdots -f^{m-1}(0)].\end{array}$$

(14)

4 Description of the method

Consider the following linear fractional partial differential equation:

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+A(x)\frac{\partial u}{\partial x}+B(x)\frac{{\partial }^{2}u}{\partial x^2}+C(x)u=h(x,t),(x,t)\in [0,1]\times [0,T],$$

(15)

with the initial conditions

$$\frac{{\partial }^{k}u}{\partial t^k}(x,0)=f_k(x),k=0,1,\dots ,m-1,$$

(16)

and the boundary conditions

$$u(0,t)=g_0(t),u(1,t)=g_1(t),t\ge 0,$$

(17)

where $f_k$, $k=0,1,\dots ,m-1$, h, $g_0$, $g_1$, A and B are known functions and $T>0$ is a real number and $m-1<\alpha \le m$. Now we explain the method of solution for solving initial-boundary value problem (15)-(17).

Taking the Laplace transform of problem (15)-(17) and using (14), we obtain

$$\begin{array}{r}\frac{1}{s^{m-\alpha }}[s^m\mathrm{\Phi }(x,s)-s^{m-1}{f}_0(x)-s^{m-2}{f}_1(x)-s^{m-3}{f}_2(x)-\cdots -f_{m-1}(x)]\\ +[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]\mathrm{\Phi }(x,s)=\overline{h}(x,s),\end{array}$$

(18)

where $\mathrm{\Phi }(x,s)$ and $\overline{h}(x,s)$ denote the Laplace transform of $u(x,t)$ and $h(x,t)$, respectively, and

$$\mathrm{\Phi }(0,s)=L(g_0(t)),\mathrm{\Phi }(1,s)=L(g_1(t)).$$

(19)

Rewriting Eq. (18), we have

$$\begin{array}{rl}{s}^{\alpha }\mathrm{\Phi }(x,s)=& -[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]\mathrm{\Phi }(x,s)\\ +\frac{1}{s^{m-\alpha }}[s^{m-1}{f}_0(x)+s^{m-2}{f}_1(x)+s^{m-3}{f}_2(x)+\cdots +f_{m-1}(x)]+\overline{h}(x,s).\end{array}$$

(20)

According to HPM, we construct a homotopy for Eq. (20) as follows:

$$\begin{array}{rl}\mathrm{\Phi }(x,s)=& \frac{-p}{s^{\alpha }}[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]\mathrm{\Phi }(x,s)\\ +\frac{1}{s^m}[s^{m-1}{f}_0(x)+s^{m-2}{f}_1(x)+s^{m-3}{f}_2(x)+\cdots +f_{m-1}(x)+\frac{1}{s^{\alpha }}\overline{h}(x,s)].\end{array}$$

(21)

Then the solution of Eq. (21) can be expressed as

$$\overline{\mathrm{\Phi }}(x,s)=\sum _{j=0}^{\mathrm{\infty }}{p}^j{\mathrm{\Phi }}_j(x,s),$$

(22)

where ${\mathrm{\Phi }}_j(x,s)$, $j=0,1,2,\dots$ , are the unknown functions. Substituting (22) in (21), we get

$$\begin{array}{r}\sum _{j=0}^{\mathrm{\infty }}{p}^j{\mathrm{\Phi }}_j(x,s)\\ =\frac{-p}{s^{\alpha }}[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]\sum _{j=0}^{\mathrm{\infty }}{p}^j{\mathrm{\Phi }}_j(x,s)\\ +\frac{1}{s^m}[s^{m-1}{f}_0(x)+s^{m-2}{f}_1(x)+s^{m-3}{f}_2(x)+\cdots +f_{m-1}(x)+\frac{1}{s^{\alpha }}\overline{h}(x,s)],\end{array}$$

(23)

which, on comparing the coefficients of powers of p, yields

$$\begin{array}{r}{p}^0:{\mathrm{\Phi }}_0(x,s)=\frac{1}{s^m}[s^{m-1}{f}_0(x)+s^{m-2}{f}_1(x)+s^{m-3}{f}_2(x)+\cdots +f_{m-1}(x)]+\frac{1}{s^{\alpha }}\overline{h}(x,s),\\ p^1:{\mathrm{\Phi }}_1(x,s)=\frac{-1}{s^{\alpha }}[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]{\mathrm{\Phi }}_0(x,s),\\ p^2:{\mathrm{\Phi }}_2(x,s)=\frac{-1}{s^{\alpha }}[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]{\mathrm{\Phi }}_1(x,s),\\ ⋮\\ p^{n+1}:{\mathrm{\Phi }}_{n+1}(x,s)=\frac{-1}{s^{\alpha }}[A(x)\frac{\partial }{\partial x}+B(x)\frac{{\partial }^2}{\partial x^2}+C(x)]{\mathrm{\Phi }}_n(x,s).\end{array}$$

(24)

In the limit $p\to 1$, we note that (24) becomes the approximate solution for the problem of (15)-(17) and is given by

$$H_n(x,s)=\sum _{j=0}^n{\mathrm{\Phi }}_j(x,s).$$

(25)

Taking the inverse Laplace transform of (25), we obtain

$$u(x,t)\simeq u_n(x,t)=L^{-1}(H_n(x,s)).$$

(26)

Applying Stehfest’s algorithm [39] to $H_n(x,s)$, the solution $u(x,t)$ is found to be

$$u_n(x,t)=\frac{ln(2)}{t}\sum _{j=1}^{2p}{d}_j{H}_n(x,j\frac{ln(2)}{t}),$$

where p is a positive integer and

$$d_j={(-1)}^{j+p}\sum _{i=[\frac{j+1}{2}]}^{min(j,p)}\frac{i^p(2i)!}{(p-i)!i!(i-1)!(j-i)!(2i-j)!}.$$

Here $[r]$ denotes the integer part of the real number r.

5 Numerical results

In this section, we show the efficiency and accuracy of the new Laplace homotopy perturbation method (LHPM) by applying it to several test problems.

Example 1 Consider the following initial-boundary value problem [45].

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=\frac{1}{2}{x}^2\frac{{\partial }^{2}u}{\partial x^2},0<t\le 1,0\le x\le 1,1<\alpha \le 2,$$

(27)

$$u(x,0)=x,\frac{\partial u}{\partial t}(x,0)=x^2,u(0,t)=0,u(1,t)=1+\sum _{k=0}^{\mathrm{\infty }}\frac{t^{k\alpha +1}}{\mathrm{\Gamma }(k\alpha +2)}.$$

(28)

We know that the exact solution of this problem is

$$u(x,t)=x+x^2\sum _{k=0}^{\mathrm{\infty }}\frac{t^{k\alpha +1}}{\mathrm{\Gamma }(k\alpha +2)}.$$

(29)

By using the method developed in the previous section (24), we find that

$$\begin{array}{r}{\mathrm{\Phi }}_0(x,s)=\frac{1}{s^2}(sx+x^2),\\ {\mathrm{\Phi }}_1(x,s)=\frac{1}{s^{\alpha }}[\frac{1}{2}{x}^2\frac{{\partial }^2}{\partial x^2}{\mathrm{\Phi }}_0(x,s)]=\frac{x^2}{s^{\alpha +2}},\\ {\mathrm{\Phi }}_2(x,s)=\frac{1}{S^{\alpha }}[\frac{1}{2}{x}^2\frac{{\partial }^2}{\partial x^2}{\mathrm{\Phi }}_1(x,s)]=\frac{x^2}{s^{2\alpha +2}},\\ ⋮\\ {\mathrm{\Phi }}_{n+1}(x,s)=\frac{1}{s^{\alpha }}[\frac{1}{2}{x}^2\frac{{\partial }^2}{\partial x^2}{\mathrm{\Phi }}_n(x,s)]=\frac{x^2}{s^{(n+1)\alpha +2}}\end{array}$$

(30)

and so on. By (25), we get

$$H_n(x,s)=\frac{x}{s}+\frac{x^2}{s^2}(1+\frac{1}{s^{\alpha }}+\frac{1}{s^{2\alpha }}+\cdots +\frac{1}{s^{n\alpha }}).$$

(31)

Taking the inverse Laplace transform of (31), the approximate solution of (27)-(28) is given by

$$u_n(x,t)=L^{-1}(H_n(x,s))=x+x^2\sum _{k=0}^n\frac{t^{k\alpha +1}}{\mathrm{\Gamma }(k\alpha +2)},$$

(32)

which, on taking the limit $n\to \mathrm{\infty }$, yields

$$u(x,t)=\underset{n\to \mathrm{\infty }}{lim}{u}_n(x,t)=x+x^2\sum _{k=0}^{\mathrm{\infty }}\frac{t^{k\alpha +1}}{\mathrm{\Gamma }(k\alpha +2)}.$$

(33)

Table 1 shows the absolute errors $|u(x,t)-u_n(x,t)|$ using the LHPM with $p=8$, $\alpha =1.75,1.85,1.95$, $n=3$ for various values of x and t. Clearly, it follows from the table that the numerical solutions are in good agreement with the exact solution.

Table 1 Absolute errors $\mathbf{|}\mathit{u}\mathbf{(}\mathit{x}\mathbf{,}\mathit{t}\mathbf{)}\mathbf{-}{\mathit{u}}_{\mathit{n}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{t}\mathbf{)}\mathbf{|}$ by LHPM with $\mathit{p}\mathbf{=}\mathbf{8}$ , $\mathit{\alpha }\mathbf{=}\mathbf{1.75}\mathbf{,}\mathbf{1.85}\mathbf{,}\mathbf{1.95}$ , $\mathit{n}\mathbf{=}\mathbf{3}$ for various values of x and t for Example 1

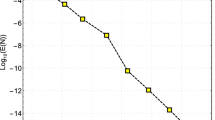
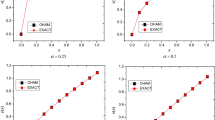
In Figure 1, we plot the logarithm of absolute errors obtained by the LHPM at $x=0.5,1$ with $n=3$, $p=8$ for various values of t. In Figure 2, we plot the numerical solution and the exact solution at $x=0.5,1$ with $n=3$, $p=8$ for various values of α and t.

Figure 1

Logarithm of absolute errors obtained by the LHPM at $\mathit{x}\mathbf{=}\mathbf{0.5}\mathbf{,}\mathbf{1}$ with $\mathit{n}\mathbf{=}\mathbf{10}$ , $\mathit{p}\mathbf{=}\mathbf{8}$ for various values of t .

Figure 2

The numerical solution and the exact solution at $\mathit{x}\mathbf{=}\mathbf{0.5}\mathbf{,}\mathbf{1}$ with $\mathit{n}\mathbf{=}\mathbf{3}$ , $\mathit{p}\mathbf{=}\mathbf{8}$ for various values of α and t .

Example 2 Let us consider the following fractional differential equation [45].

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+x\frac{\partial u}{\partial x}+\frac{{\partial }^{2}u}{\partial x^2}=2(t^{\alpha }+x^2+1),0<t\le 1,0\le x\le 1,0<\alpha \le 1,$$

(34)

with the initial condition

$$u(x,0)=x^2$$

(35)

and the boundary conditions

$$u(0,t)=2t^{2\alpha }\frac{\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(2\alpha +1)},u(1,t)=1+2t^{2\alpha }\frac{\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(2\alpha +1)}.$$

(36)

The exact solution of the given problem is given by

$$u(x,t)=x^2+2t^{2\alpha }\frac{\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(2\alpha +1)}.$$

(37)

By using the method presented in Section 4, namely (24), we obtain

$$\begin{array}{r}{\mathrm{\Phi }}_0(x,s)=\frac{x^2}{s}+\frac{2}{s^{\alpha }}[\frac{\mathrm{\Gamma }(\alpha +1)}{s^{\alpha +1}}+\frac{x^2+1}{s}],\\ {\mathrm{\Phi }}_1(x,s)=\frac{1}{s^{\alpha }}[-x\frac{\partial }{\partial x}-\frac{{\partial }^2}{\partial x^2}]{\mathrm{\Phi }}_0(x,s)=-(x^2+1)(\frac{4}{s^{2\alpha +1}}+\frac{2}{s^{\alpha +1}}),\\ {\mathrm{\Phi }}_2(x,s)=\frac{1}{s^{\alpha }}[-x\frac{\partial }{\partial x}-\frac{{\partial }^2}{\partial x^2}]{\mathrm{\Phi }}_1(x,s)=(x^2+1)(\frac{8}{s^{3\alpha +1}}+\frac{4}{s^{2\alpha +1}}),\\ ⋮\\ {\mathrm{\Phi }}_{n+1}(x,s)=\frac{1}{s^{\alpha }}[-x\frac{\partial }{\partial x}-\frac{{\partial }^2}{\partial x^2}]{\mathrm{\Phi }}_n(x,s)={(-1)}^{n+1}(x^2+1)(\frac{2^{n+2}}{s^{(n+2)\alpha +1}}+\frac{2^{n+1}}{s^{(n+1)\alpha +1}}),\end{array}$$

(38)

and so on.

As before, by using (25), we obtain

$$H_n(x,s)=\frac{2\mathrm{\Gamma }(\alpha +1)}{s^{\alpha +1}}+\frac{x^2}{s}+{(-1)}^n(1+x^2)\frac{2^{n+1}}{s^{(n+1)\alpha +1}}.$$

(39)

Taking the inverse Laplace transform of (39) and taking the limit $n\to \mathrm{\infty }$, the approximate solution for problem (34)-(36) is given by

$$u(x,t)=\underset{n\to \mathrm{\infty }}{lim}{u}_n(x,t)=x^2+2t^{2\alpha }\frac{\mathrm{\Gamma }(\alpha +1)}{\mathrm{\Gamma }(2\alpha +1)}.$$

(40)

In Table 2, we list the absolute errors using the LHPM with $p=10$, $\alpha =0.75,0.85,0.95$, $n=10$ for various values of x and t. It can easily be seen from the table that the numerical solutions are in good agreement with the exact solution.

Table 2 Absolute errors by LHPM with $\mathit{p}\mathbf{=}\mathbf{10}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.75}\mathbf{,}\mathbf{0.85}\mathbf{,}\mathbf{0.95}$ , $\mathit{n}\mathbf{=}\mathbf{10}$ for various values of x and t

In Figure 3, we plot the logarithm of absolute errors obtained by the LHPM at $x=0.5,1$ with $n=10$, $p=10$ for various values of t. In Figure 4, we plot the exact solution and the numerical solution obtained by the LHPM with $x=0.1,1$ for $n=4,6,10$, $p=10$, $\alpha =0.75$ for various values of t. As we see from Figure 4, the numerical solutions are in good agreement with the exact solution as the value of n is increased.

Figure 3

Logarithm of absolute errors obtained by the LHPM at $\mathit{x}\mathbf{=}\mathbf{0.5}\mathbf{,}\mathbf{1}$ with $\mathit{n}\mathbf{=}\mathbf{10}$ , $\mathit{p}\mathbf{=}\mathbf{10}$ for various values of t .

Figure 4

The exact solution and the numerical solution obtained by the LHPM with $\mathit{x}\mathbf{=}\mathbf{0.1}\mathbf{,}\mathbf{1}$ for $\mathit{n}\mathbf{=}\mathbf{4}\mathbf{,}\mathbf{6}\mathbf{,}\mathbf{10}$ , $\mathit{p}\mathbf{=}\mathbf{10}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.75}$ for various values of t .

Example 3 Consider the fractional differential equation [46]

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\frac{\partial u}{\partial x}=\frac{t^{1-\alpha }}{\mathrm{\Gamma }(2-\alpha )}sin(x)+tcos(x),t>0,0\le x\le 1,0<\alpha \le 1,$$

(41)

with the initial condition

$$u(x,0)=0$$

(42)

and the boundary conditions

$$u(0,t)=0,u(1,t)=tsin(1).$$

(43)

The exact solution for this problem is

$$u(x,t)=tsin(x).$$

(44)

Following the method of Section 4 (24), we find that

$$\begin{array}{r}{\mathrm{\Phi }}_0(x,s)=\frac{1}{s^{\alpha }}[\frac{sin(x)}{s^{2-\alpha }}+\frac{cos(x)}{s^2}],\\ {\mathrm{\Phi }}_1(x,s)=\frac{-1}{s^{\alpha }}\frac{\partial }{\partial x}{\mathrm{\Phi }}_0(x,s)=-\frac{1}{s^{2\alpha }}[\frac{cos(x)}{s^{2-\alpha }}-\frac{sin(x)}{s^2}],\\ {\mathrm{\Phi }}_2(x,s)=\frac{-1}{s^{\alpha }}\frac{\partial }{\partial x}{\mathrm{\Phi }}_1(x,s)=\frac{1}{s^{3\alpha }}[-\frac{sin(x)}{s^{2-\alpha }}-\frac{cos(x)}{s^2}],\\ ⋮\\ {\mathrm{\Phi }}_n(x,s)=\frac{-1}{s^{\alpha }}\frac{\partial }{\partial x}{\mathrm{\Phi }}_{n-1}(x,s)={(-1)}^n\frac{1}{s^{(n+1)\alpha }}[\frac{sin(\frac{n\pi }{2}+x)}{s^{2-\alpha }}+\frac{cos(\frac{n\pi }{2}+x)}{s^2}].\end{array}$$

(45)

By means of (25), we obtain

$$H_n(x,s)=\frac{2\mathrm{\Gamma }(\alpha +1)}{s^{\alpha +1}}+\frac{x^2}{s}+{(-1)}^n(1+x^2)\frac{2^{n+1}}{s^{(n+1)\alpha +1}}.$$

(46)

Taking the inverse Laplace transform of (46), the approximate solution of (41)-(43) is found to be

$$u_n(x,t)=L^{-1}(H_n(x,s))=\{\begin{array}{cc}\frac{sinx}{s^2}+\frac{cosx}{s^{(n+1)\alpha +2}},\hfill & n=2k,\hfill \\ sinx(\frac{1}{s^2}-\frac{1}{s^{(n+1)\alpha +2}}),\hfill & n=2k+1,\hfill \end{array}$$

(47)

which, on taking the limit $n\to \mathrm{\infty }$, gives

$$u(x,t)=\underset{n\to \mathrm{\infty }}{lim}{u}_n(x,t)=tsin(x).$$

(48)

In Table 3, we list the absolute errors using the LHPM with $p=10$, $\alpha =0.5,0.75,0.95$, $n=10$ for various values of x and t. It follows from the table that the numerical solutions are in good agreement with the exact solution.

Table 3 Absolute errors by LHPM with $\mathit{p}\mathbf{=}\mathbf{10}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.5}\mathbf{,}\mathbf{0.75}\mathbf{,}\mathbf{0.95}$ , $\mathit{n}\mathbf{=}\mathbf{10}$ for various values of x and t for Example 3

In Figure 5, we plot the logarithm of absolute errors obtained by the LHPM at $x=0.5,1$ with $n=10$, $p=10$ for various values of t. In Figure 6, we plot the exact solution and the numerical solution obtained by the LHPM with $x=0.5,1$ for $n=2,3,9$, $p=10$, $\alpha =0.25$ for various values of t. Clearly, the numerical solutions are in good agreement with the exact solution as the value of n is increased.

Figure 5

Logarithm of absolute errors obtained by the LHPM at $\mathit{x}\mathbf{=}\mathbf{0.5}\mathbf{,}\mathbf{1}$ with $\mathit{n}\mathbf{=}\mathbf{10}$ , $\mathit{p}\mathbf{=}\mathbf{10}$ for various values of t .

Figure 6

The exact solution and the numerical solution obtained by the LHPM with $\mathit{x}\mathbf{=}\mathbf{0.5}\mathbf{,}\mathbf{1}$ for $\mathit{n}\mathbf{=}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{,}\mathbf{9}$ , $\mathit{p}\mathbf{=}\mathbf{10}$ , $\mathit{\alpha }\mathbf{=}\mathbf{0.25}$ for various values of t .

Example 4 Consider the fractional differential equation

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}(x,t)+u^2(x,t)=\frac{2x{t}^{2-\alpha }}{\mathrm{\Gamma }(3-\alpha )}+x^2{t}^4,t>0,0\le x\le 1,0<\alpha \le 1,$$

(49)

with the initial condition

$$u(x,0)=0$$

(50)

and the boundary conditions

$$u(0,t)=0,u(1,t)=t^2.$$

(51)

The exact solution for this problem is

$$u(x,t)=x{t}^2.$$

(52)

Taking the Laplace transform of problem (49)-(52) and using (24), we obtain

$$\frac{1}{s^{1-\alpha }}[s^1\mathrm{\Phi }(x,s)]+\mathrm{\Omega }(x,s)=\frac{2x}{s^{3-\alpha }}+\frac{24x^2}{s^5},$$

(53)

where $\mathrm{\Phi }(x,s)$ and $\overline{h}\mathrm{\Omega }(x,s)$ denote the Laplace transform of $u(x,t)$ and $u^2(x,t)$, respectively, and

$$\mathrm{\Phi }(0,s)=0,\mathrm{\Phi }(1,s)=\frac{2}{s^3}.$$

According to HPM, we construct a homotopy for Eq. (53) as follows:

$$\mathrm{\Phi }(x,s)=\frac{1}{s^{\alpha }}(\frac{2x}{s^{3-\alpha }}-p\mathrm{\Omega }(x,s)+\frac{24x^2}{s^5}).$$

(54)

Following the method of Section 4 (24), we find that

$$\begin{array}{r}{\mathrm{\Phi }}_0(x,s)=\frac{2x}{s^3}+\frac{4!x^2}{s^{\alpha +5}},\\ {\mathrm{\Phi }}_1(x,s)=\frac{-1}{s^{\alpha }}(\frac{4!x^2}{s^5}+\frac{{(4!)}^2{x}^2\mathrm{\Gamma }(2\alpha +9)}{{\mathrm{\Gamma }}^2(\alpha +5)s^{2\alpha +9}}+\frac{48x^3\mathrm{\Gamma }(\alpha +7)}{\mathrm{\Gamma }(\alpha +5)s^{\alpha +7}}),\\ {\mathrm{\Phi }}_2(x,s)=\frac{2\times 4!x^3}{s^{2\alpha +7}\mathrm{\Gamma }(\alpha +5)}(\mathrm{\Gamma }(\alpha +7)+\frac{4!\mathrm{\Gamma }(2\alpha +9)\mathrm{\Gamma }(3\alpha +11)}{\mathrm{\Gamma }(\alpha +5)\mathrm{\Gamma }(3\alpha +9)s^{2\alpha +4}}\\ \phantom{{\mathrm{\Phi }}_2(x,s)=}+2\frac{x\mathrm{\Gamma }(\alpha +7)\mathrm{\Gamma }(2\alpha +8)}{\mathrm{\Gamma }(2\alpha +7)s^{\alpha +1}}\\ \phantom{{\mathrm{\Phi }}_2(x,s)=}+4!\frac{x\mathrm{\Gamma }(2\alpha +9)}{\mathrm{\Gamma }(\alpha +5)s^{\alpha +2}}+{(4!)}^2\frac{x^3\mathrm{\Gamma }(2\alpha +9)\mathrm{\Gamma }(4\alpha +13)}{{\mathrm{\Gamma }}^2(\alpha +5)\mathrm{\Gamma }(3\alpha +9)s^{3\alpha +6}})\end{array}$$

(55)

and so on.

By means of (25), we obtain

$$\begin{array}{rl}{H}_2(x,s)=& \frac{2x}{s^3}+\frac{2\times 4!x^3}{s^{2\alpha +7}\mathrm{\Gamma }(\alpha +5)}(\frac{4!\mathrm{\Gamma }(2\alpha +9)\mathrm{\Gamma }(3\alpha +11)}{\mathrm{\Gamma }(\alpha +5)\mathrm{\Gamma }(3\alpha +9)s^{2\alpha +4}}\\ +2\frac{x\mathrm{\Gamma }(\alpha +7)\mathrm{\Gamma }(2\alpha +8)}{\mathrm{\Gamma }(2\alpha +7)s^{\alpha +1}}+{(4!)}^2\frac{x^3\mathrm{\Gamma }(2\alpha +9)\mathrm{\Gamma }(4\alpha +13)}{{\mathrm{\Gamma }}^2(\alpha +5)\mathrm{\Gamma }(3\alpha +9)s^{3\alpha +6}}).\end{array}$$

(56)

Taking the inverse Laplace transform of (56), the approximate solution of (49)-(51) is found to be

$$\begin{array}{rl}{u}_n(x,t)=& L^{-1}(H_n(x,s))=x{t}^2+\frac{2\times 4!x^3\mathrm{\Gamma }(2\alpha +9)\mathrm{\Gamma }(3\alpha +11)}{{\mathrm{\Gamma }}^2(\alpha +5)\mathrm{\Gamma }(3\alpha +9)\mathrm{\Gamma }(3\alpha +11)}{t}^{3\alpha +10}\\ +2^2\times 4!\frac{x^4\mathrm{\Gamma }(\alpha +7)\mathrm{\Gamma }(2\alpha +8)}{\mathrm{\Gamma }(\alpha +5)\mathrm{\Gamma }(2\alpha +7)\mathrm{\Gamma }(2\alpha +8)}{t}^{2\alpha +7}\\ +2{(4!)}^2\frac{x^6\mathrm{\Gamma }(2\alpha +9)\mathrm{\Gamma }(4\alpha +13)}{{\mathrm{\Gamma }}^3(\alpha +5)\mathrm{\Gamma }(3\alpha +9)\mathrm{\Gamma }(4\alpha +13)}{t}^{4\alpha +12}.\end{array}$$

(57)

In Table 4, we list the absolute errors using the LHPM with $\alpha =0.8,0.85,0.90,0.95,0.99$, $n=2$, $x=0.5$ for various values of t. It follows from the table that the numerical solutions are in good agreement with the exact solution.

Table 4 Absolute errors by LHPM with $\mathit{\alpha }\mathbf{=}\mathbf{0.8}\mathbf{,}\mathbf{0.85}\mathbf{,}\mathbf{0.90}\mathbf{,}\mathbf{0.95}\mathbf{,}\mathbf{0.99}$ , $\mathit{n}\mathbf{=}\mathbf{2}$ , $\mathit{x}\mathbf{=}\mathbf{0.5}$ for various values of t for Example 4

6 Conclusions

In this paper, we have developed a new numerical method for solving fractional partial differential equations. This method is based on Laplace transform, the homotopy perturbation method and Stehfest’s numerical algorithm for calculating inverse Laplace transform. We demonstrate the efficiency and accuracy of the proposed method by applying it to three typical examples. It is found that the approximate solutions produced by our method are in complete agreement with the corresponding exact solutions. Moreover, in view of its simplicity, our method is applicable to a wide class of initial-boundary value problems occurring in applied sciences.