LMI approach to decentralized exponential stability of linear large-scale systems with interval non-differentiable time-varying delays

Abstract

This paper addresses decentralized exponential stability problem for a class of linear large-scale systems with time-varying delay in interconnection. The time delay is any continuous function belonging to a given interval, but not necessarily differentiable. By constructing a suitable augmented Lyapunov-Krasovskii functional combined with Leibniz-Newton’s formula, new delay-dependent sufficient conditions for the existence of decentralized exponential stability are established in terms of LMIs. Numerical examples are given to show the effectiveness of the obtained results.

1 Introduction

The theory and applications of functional differential equations form an important part of modern non-linear dynamics. Such equations are natural mathematical models for various real life phenomena where the after-effects are intrinsic features of their functioning. In recent years, functional differential equations have been used to model processes in different areas such as population dynamics and ecology, physiology and medicine, economics, and other natural sciences. Stability analysis of linear systems with time-varying delays $\dot{x}(t)=Ax(t)+Dx(t-h(t))$ is fundamental to many practical problems and has received considerable attention [1–4]. Most of the known results on this problem are derived assuming only that the time-varying delay $h(t)$ is a continuously differentiable function, satisfying some boundedness condition on its derivative: $\dot{h}(t)\le \delta <1$. In delay-dependent stability criteria, the main concern is to enlarge the feasible region of stability criteria in a given time-delay interval. Interval time-varying delay means that a time delay varies in an interval in which the lower bound is not restricted to being zero. By constructing a suitable augmented Lyapunov functional and utilizing free weight matrices, some less conservative conditions for asymptotic stability are derived in [5–10] for systems with time delay varying in an interval. However, the shortcoming of the method used in these works is that the delay function is assumed to be differential and its derivative is still bounded: $\dot{h}(t)\le \delta$.

On the other hand, there has been a considerable research interest in large-scale interconnected systems. A typical large-scale interconnected system such as a power grid consists of many subsystems and individual elements connected together to form a large, complex network capable of generating, transmitting and distributing electrical energy over a large geographical area. In general, a large-scale system can be characterized by a large number of variables representing the system, a strong interaction between subsystem variables, and a complex interaction between subsystems. The problem of decentralized control of large-scale interconnected dynamical systems has been receiving considerable attention, because there is a large number of large-scale interconnected dynamical systems in many practical control problems, e.g., transportation systems, power systems, communication systems, economic systems, social systems, and so on [11–14]. The operation of large-scale interconnected systems requires the ability to monitor and stabilize in the face of uncertainties, disturbances, failures and attacks through the utilization of internal system states. However, even with the assumption that all the state variables are available for feedback control, the task of effective controlling a large-scale interconnected system using a global (centralized) state feedback controller is still not easy as there is a necessary requirement for information transfer between the subsystems [15–18].

To the best of our knowledge, there has been no investigation on the exponential stability of large-scale systems with time-varying delays interacted between subsystems. In fact, this problem is difficult to solve; particularly, when the time-varying delays are interval, non-differentiable and the output is subjected to such time-varying delay functions. The time delay is assumed to be any continuous function belonging to a given interval, which means that the lower and upper bounds for the time-varying delay are available, but the delay function is bounded but not necessarily differentiable. This allows the time-delay to be a fast time-varying function and the lower bound is not restricted to being zero. It is clear that the application of any memoryless feedback controller to such time-delay systems would lead to closed loop systems with interval time-varying delays. The difficulties then arise when one attempts to derive exponential stability conditions. Indeed, the existing Lyapunov-Krasovskii functional and associated results in [11, 14, 15, 18–35] cannot be applied to solve the problem posed in this paper as they would either fail to cope with the non-differentiability aspects of the delays, or lead to very complex matrix inequality conditions, and any technique such as matrix computation or transformation of variables fails to extract the parameters of the memoryless feedback controllers. This has motivated our research.

In this paper, we consider a class of large-scale linear systems with interval time-varying delays in interconnections. Compared to the existing results, our result has its own advantages. (i) Stability analysis of previous papers reveals some restrictions: The time delay was proposed to be either time-invariant interconnected or the lower delay bound is restricted to being zero, or the time delay function should be differential and its derivative is bounded. In our result, the above restricted conditions are removed for the large-scale systems. In addition, the time delay is assumed to be any continuous function belonging to a given interval, which means that the lower and upper bounds for the time-varying delay are available, but the delay function is bounded but not necessarily differentiable. This allows the time-delay to be a fast time-varying function, and the lower bound is not restricted to being zero. (ii) The developed method using new inequalities for lower bounding cross terms eliminates the need for over-bounding and provides larger values of the admissible delay bound. We propose a set of new Lyapunov-Krasovskii functionals, which are mainly based on the information of the lower and upper delay bounds. (iii) The conditions will be presented in terms of the solution of LMIs that can be solved numerically in an efficient manner by using standard computational algorithms [36].

The paper is organized as follows. Section 2 presents definitions and some well-known technical propositions needed for the proof of the main results. Main result for decentralized exponential stability of large-scale systems is presented in Section 3. Numerical examples showing the effectiveness of the obtained results are given in Section 4. The paper ends with conclusions and cited references.

2 Preliminaries

The following notations are used in this paper. $R^{+}$ denotes the set of all real non-negative numbers; $R^n$ denotes the n-dimensional space with the scalar product $〈\cdot ,\cdot 〉$ and the vector norm $\parallel \cdot \parallel$; $M^{n\times r}$ denotes the space of all matrices of $(n\times r)$-dimensions; $A^T$ denotes the transpose of matrix A; A is symmetric if $A=A^T$; I denotes the identity matrix; $\lambda (A)$ denotes the set of all eigenvalues of A; ${\lambda }_{\min /\max }(A)=\min /\max \{Re\lambda ;\lambda \in \lambda (A)\}$; $C^1([a,b],R^n)$ denotes the set of all $R^n$-valued differentiable functions on $[a,b]$; $L_2([0,\mathrm{\infty }],R^r)$ stands for the set of all square-integrable $R^r$-valued functions on $[0,\mathrm{\infty }]$. $x_t:=\{x(t+s):s\in [-h,0]\}$, $\parallel x_t\parallel ={sup}_{s\in [-h,0]}\parallel x(t+s)\parallel$; $C([0,t],R^n)$ denotes the set of all $R^n$-valued continuous functions on $[0,t]$; matrix A is called semi-positive definite ($A\ge 0$) if $〈Ax,x〉\ge 0$ for all $x\in R^n$; A is positive definite ($A>0$) if $〈Ax,x〉>0$ for all $x\ne 0$; $A>B$ means $A-B>0$. ∗ denotes the symmetric term in a matrix.

Consider a class of linear large-scale systems with interval time-varying delays composed of N interconnected subsystems $i=\overline{1,N}$ of the form

$$\begin{array}{r}{\dot{x}}_i(t)=A_i{x}_i(t)+\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t)),t\in R^{+},\\ x_i(t)={\phi }_i(t),\mathrm{\forall }t\in [-h_2,0],\end{array}$$

(2.1)

where $x^T(t)=[x_1^T(t),\dots ,x_N^T(t)]$, $x_i(t)\in R^{n_i}$, is the state vector, the system matrices $A_i$, $D_{ij}$ are of appropriate dimensions.

The time delays $h_{ij}(\cdot )$ are continuous and satisfy the following condition:

$$0\le h_1\le h_{ij}(t)<h_2,t\ge 0,\mathrm{\forall }i,j=\overline{1,N},$$

and the initial function $\phi (t)=[{\phi }_1(t),\dots ,{\phi }_N{(t)}^T]$, ${\phi }_i(t)\in C^1([-h_2,0],R^{n_i})$, with the norm

$$\parallel {\phi }_i\parallel =\underset{-h\le t\le 0}{sup}\{\parallel {\phi }_i(t)\parallel ,\parallel {\dot{\phi }}_i(t)\parallel \},\parallel \phi \parallel =\sqrt{\sum _{i=1}^N{\parallel {\phi }_i\parallel }^2}.$$

Definition 2.1 Given $\alpha >0$. The zero solution of system (2.1) is α-exponentially stable if there exists a positive number $N>0$ such that every solution $x(t,\phi )$ satisfies the following condition:

$$\parallel x(t,\phi )\parallel \le N{e}^{-\alpha t}\parallel \phi \parallel ,\mathrm{\forall }t\in R^{+}.$$

We end this section with the following technical well-known propositions, which will be used in the proof of the main results.

Proposition 2.1 For any $x,y\in R^n$ and positive definite matrix $P\in R^{n\times n}$, we have

$$2x^{T}y\le y^{T}Py+x^T{P}^{-1}x.$$

Proposition 2.2 (Schur complement lemma [37])

Given constant matrices X, Y, Z with appropriate dimensions satisfying $X=X^T,Y=Y^T>0$. Then $X+Z^T{Y}^{-1}Z<0$ if and only if

$$\left(\begin{array}{cc}X& Z^T\\ Z& -Y\end{array}\right)<0\mathit{\text{or}}\left(\begin{array}{cc}-Y& Z\\ Z^T& X\end{array}\right)<0.$$

Proposition 2.3 [38]

For any constant matrix $Z=Z^T>0$ and scalar h, $\overline{h}$, $0<h<\overline{h}$ such that the following integrations are well defined, then

$$\begin{array}{c}-{\int }_{t-h}^{t}x{(s)}^{T}Zx(s)ds\le -\frac{1}{h}{({\int }_{t-h}^{t}x(s)ds)}^{T}Z({\int }_{t-h}^{t}x(s)ds),\hfill \\ -{\int }_{-\overline{h}}^{-h}{\int }_{t+\theta }^{t}x{(s)}^{T}Zx(s)dsd\theta \hfill \\ \le -\frac{2}{{\overline{h}}^2-h^2}{({\int }_{-\overline{h}}^{-h}{\int }_{t+\theta }^{t}x(s)dsd\theta )}^{T}Z({\int }_{-\overline{h}}^{-h}{\int }_{t+\theta }^{t}x(s)dsd\theta ).\hfill \end{array}$$

3 Main results

In this section, we investigate the decentralized exponential stability of linear large-scale system (2.1) with interval time-varying delays. It will be seen from the following theorem that neither free-weighting matrices nor any transformation are employed in our derivation. Before introducing the main result, the following notations of several matrix variables are defined for simplicity

$$\begin{array}{c}\begin{array}{rl}{M}_{11}^i=& A_i^T{P}_i+A_i{P}_i+2\alpha P_i\\ +2(Q_i+R_i)-2S_{i1}{A}_i-e^{2\alpha h_1}{R}_i-e^{2\alpha h_2}{R}_i\\ -\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right){(h_2-h_1)}^2{W}_i+\sum _{j\ne i,j=1}^N{P}_i{D}_{ij}{D}_{ij}^T{P}_i\\ +\sum _{j\ne i,j=1}^N{S}_{i1}{D}_{ij}{D}_{ij}^T{S}_{i1}^T+S_{i4}{A}_i{A}_i^T{S}_{i4}^T,\end{array}\hfill \\ M_{1k}^i=-S_{i4}{A}_i,\mathrm{\forall }k=\overline{2,N},\hfill \\ M_{1(N+1)}^i=2\alpha h_1{R}_i-S_{i2}{A}_i,\hfill \\ M_{1(N+2)}^i=e^{2\alpha h_2}{R}_i+S_{i3}{A}_i,\hfill \\ M_{1(N+3)}^i=S_{i1}-S_{i5}{A}_i,\hfill \\ M_{1(N+4)}^i=\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right)(h_2-h_1)W_i,\hfill \\ M_{km}^i=0,\mathrm{\forall }k\ne m,k,m=\overline{2,N},\hfill \\ M_{kk}^i=-e^{2\alpha h_2}{U}_i-e^{2\alpha h_2}{U}_i+\sum _{j\ne i,j=1}^N{S}_{i4}{D}_{ij}{D}_{ij}^T{S}_{i4}^T+7I,\mathrm{\forall }k=\overline{2,N},\hfill \\ M_{k(N+1)}^i=e^{2\alpha h_2}{U}_i,M_{k(N+2)}^i=e^{2\alpha h_2}{U}_i,M_{k(N+3)}^i=S_{i4},M_{k(N+4)}^i=0,\hfill \\ M_{(N+1)(N+1)}^i=-e^{2\alpha h_1}{Q}_i-e^{2\alpha h_1}{R}_i-e^{2\alpha h_2}{U}_i+\sum _{j\ne i,j=1}^N{S}_{i2}{D}_{ij}{D}_{ij}^T{S}_{i2}^T,\hfill \\ M_{(N+1)(N+2)}^i=0,M_{(N+1)(N+3)}^i=S_{i2},M_{(N+1)(N+4)}^i=0,\hfill \\ M_{(N+2)(N+2)}^i=-e^{2\alpha h_2}{Q}_i-e^{2\alpha h_2}{R}_i-e^{2\alpha h_2}{U}_i+\sum _{j\ne i,j=1}^N{S}_{i3}{D}_{ij}{D}_{ij}^T{S}_{i3}^T,\hfill \\ M_{(N+2)(N+3)}^i=S_{i3},M_{(N+2)(N+4)}^i=S_{i2},\hfill \\ \begin{array}{rl}{M}_{(N+3)(N+3)}^i=& (h_1^2+h_2^2)R_i+(h_2-h_1)U_i+2S_{i5}+(h_2-h_1)h_2{W}_i\\ +\sum _{j\ne i,j=1}^N{S}_{i5}{D}_{ij}{D}_{ij}^T{S}_{i5}^T,\end{array}\hfill \\ M_{(N+3)(N+4)}^i=0,M_{(N+4)(N+4)}^i=\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right)W_i,\hfill \\ {\lambda }_{i1}={\lambda }_{\min }(P_i),{\lambda }_1=\underset{i=\overline{1,N}}{min}{\lambda }_{i1},{\lambda }_2=\underset{i=\overline{1,N}}{max}{\lambda }_{i2},\hfill \\ \begin{array}{rl}{\lambda }_{i2}=& {\lambda }_{\max }(P_i)+{\alpha }^{-1}{\lambda }_{\max }(Q_i)+h_1^3{\lambda }_{\max }(R_i)\\ +{(h_2-h_1)}^3{\lambda }_{\max }(U_i)+(h_2-h_1)h_2^2{\lambda }_{\max }(W_i).\end{array}\hfill \end{array}$$

The following is the main result of the paper, which gives sufficient conditions for the decentralized exponential stability of linear large-scale system (2.1) with interval time-varying delays. Essentially, the proof is based on the construction of Lyapunov Krasovskii functions satisfying the Lyapunov stability theorem for a time-delay system [37].

Theorem 3.1 Given $\alpha >0$. System (2.1) is α-exponentially stable if there exist symmetric positive definite matrices $P_i$, $Q_i$, $R_i$, $U_i$, $W_i$, $i=\overline{1,N}$, and matrices $S_{ij}$, $i=\overline{1,N}$, $j=1,2,\dots ,5$, such that the following LMI holds:

$${\mathcal{M}}^i=\left[\begin{array}{cccc}{M}_{11}^i& M_{12}^i& \cdots & M_{1(N+4)}^i\\ \ast & M_{22}^i& \cdots & M_{2(N+4)}^i\\ \cdot & \cdot & \cdots & \cdot \\ \ast & \ast & \cdots & M_{(N+4)(N+4)}^i\end{array}\right]<0,i=\overline{1,N}.$$

(3.1)

Moreover, the solution $x(t,\phi )$ of the system satisfies

$$\parallel x(t,\phi )\parallel \le \sqrt{\frac{{\lambda }_2}{{\lambda }_1}}{e}^{-\alpha t}\parallel \phi \parallel ,\mathrm{\forall }t\in R^{+}.$$

Proof We consider the following Lyapunov-Krasovskii functional for system (2.1):

$$V(t,x_t)=\sum _{i=1}^N\sum _{j=1}^7{V}_{ij}(t,x_t),$$

where

$$\begin{array}{c}{V}_{i1}=x_i^T(t)P_i{x}_i(t),\hfill \\ V_{i2}={\int }_{t-h_1}^t{e}^{2\alpha (s-t)}{x}_i^T(s)Q_i{x}_i(s)ds,\hfill \\ V_{i3}={\int }_{t-h_2}^t{e}^{2\alpha (s-t)}{x}_i^T(s)Q_i{x}_i(s)ds,\hfill \\ V_{i4}=h_1{\int }_{-h_1}^0{\int }_{t+s}^t{e}^{2\alpha (\tau -t)}{\dot{x}}_i^T(\tau )R_i{\dot{x}}_i(\tau )d\tau ds,\hfill \\ V_{i5}=h_2{\int }_{-h_2}^0{\int }_{t+s}^t{e}^{2\alpha (\tau -t)}{\dot{x}}_i^T(\tau )R_i{\dot{x}}_i(\tau )d\tau ds,\hfill \\ V_{i6}=(h_2-h_1){\int }_{-h_2}^{-h_1}{\int }_{t+s}^t{e}^{2\alpha (\tau -t)}{\dot{x}}_i^T(\tau )U_i{\dot{x}}_i(\tau )d\tau ds,\hfill \\ V_{i7}={\int }_{-h_2}^{-h_1}{\int }_{\theta }^0{\int }_{t+s}^t{e}^{2\alpha (\tau +s-t)}{\dot{x}}_i^T(\tau )W_i{\dot{x}}_i(\tau )d\tau dsd\theta .\hfill \end{array}$$

It is easy to verify that

$$\sum _{i=1}^N{\lambda }_{i1}{\parallel x_i(t)\parallel }^2\le V(t,x_t),V(0,x_0)\le \sum _{i=1}^N{\lambda }_{i2}{\parallel {\phi }_i\parallel }^2.$$

(3.2)

Taking the derivative of V in t along the solution of system (2.1), we have

$$\begin{array}{c}{\dot{V}}_{i1}=2x_i^T(t)P_i{\dot{x}}_i(t)\hfill \\ \phantom{{\dot{V}}_{i1}}=2x_i^T(t)[A_i^T{P}_i+A_i{P}_i]x_i(t)+2x_i^T(t)P_i{D}_{ij}{x}_j(t-h_{ij}(t));\hfill \\ {\dot{V}}_{i2}=x_i^T(t)Q_i{x}_i(t)-e^{-2\alpha h_1}{x}_i^T(t-h_1)Q_i{x}_i(t-h_1)-2\alpha V_{i2};\hfill \\ {\dot{V}}_{i3}=x_i^T(t)Q_i{x}_i(t)-e^{-2\alpha h_2}{x}_i^T(t-h_2)Q_i{x}_i(t-h_2)-2\alpha V_{i3};\hfill \\ {\dot{V}}_{i4}\le h_1^2{\dot{x}}_i^T(t)R_i{\dot{x}}_i(t)-h_1{e}^{-2\alpha h_1}{\int }_{t-h_1}^t{\dot{x}}_i^T(s)R_i{\dot{x}}_i(s)ds-2\alpha V_{i4};\hfill \\ {\dot{V}}_{i5}\le h_2^2{\dot{x}}_i^T(t)R_i{\dot{x}}_i(t)-h_2{e}^{-2\alpha h_2}{\int }_{t-h_2}^t{\dot{x}}_i^T(s)R_i{\dot{x}}_i(s)ds-2\alpha V_{i5};\hfill \\ {\dot{V}}_{i6}\le {(h_2-h_1)}^2{\dot{x}}_i^T(t)U_i{\dot{x}}_i(t)\hfill \\ \phantom{{\dot{V}}_{i6}\le }-(h_2-h_1)e^{-2\alpha h_2}{\int }_{t-h_2}^{t-h_1}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds-2\alpha V_{i6};\hfill \\ {\dot{V}}_{i7}\le (h_2-h_1)h_2{\dot{x}}_i^T(t)W_i{\dot{x}}_i(t)\hfill \\ \phantom{{\dot{V}}_{i7}\le }-e^{-4\beta h_2}{\int }_{-h_2}^{-h_1}{\int }_{t+\theta }^t{\dot{x}}_i^T(s)W_i{\dot{x}}_i(s)dsd\theta -2\alpha V_{i7}.\hfill \end{array}$$

Applying Proposition 2.3 and the Leibniz-Newton formula

$${\int }_{t-h}^t{\dot{x}}_i(s)ds=x_i(t)-x_i(t-h),$$

we have

$$\begin{array}{rl}-h_i{\int }_{t-h_i}^t{\dot{x}}_i^T(s)R_i{\dot{x}}_i(s)ds& \le -{[{\int }_{t-h_i}^t{\dot{x}}_i(s)ds]}^T{R}_i[{\int }_{t-h_i}^t{\dot{x}}_i(s)ds]\\ \le -{[x_i(t)-x_i(t-h_i)]}^T{R}_i[x_i(t)-x_i(t-h_i)]\\ =-x_i^T(t)R{x}_i(t)+2x_i^T(t)R_i{x}_i(t-h_i)-x_i^T(t-h_i)R_i{x}_i(t-h_i).\end{array}$$

Note that

$${\int }_{t-h_2}^{t-h_1}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds={\int }_{t-h_2}^{t-h_{ji}(t)}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds+{\int }_{t-h_{ji}(t)}^{t-h_1}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds.$$

Using Proposition 2.3 gives

$$\begin{array}{r}[h_2-h_{ji}(t)]{\int }_{t-h_2}^{t-h_{ji}(t)}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds\\ \ge {[{\int }_{t-h_2}^{t-h_{ij}(t)}{\dot{x}}_i(s)ds]}^T{U}_i[{\int }_{t-h_2}^{t-h_{ji}(t)}{\dot{x}}_i(s)ds]\\ \ge {[x_i(t-h_{ji}(t))-x_i(t-h_2)]}^T{U}_i[x_i(t-h_{ji}(t))-x_i(t-h_2)].\end{array}$$

Since $h_2-h_{ji}(t)\le h_2-h_1$, we have

$$\begin{array}{r}[h_2-h_1]{\int }_{t-h_2}^{t-h_{ji}(t)}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds\\ \ge {[x_i(t-h_{ji}(t))-x_i(t-h_2)]}^T{U}_i[x_i(t-h_{ji}(t))-x_i(t-h_2)],\end{array}$$

then

$$\begin{array}{r}-(h_2-h_1){\int }_{t-h_2}^{t-h_{ji}(t)}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds\\ \le -{[x_i(t-h_{ji}(t))-x_i(t-h_2)]}^T{U}_i[x_i(t-h_{ji}(t))-x_i(t-h_2)].\end{array}$$

Similarly, we have

$$\begin{array}{r}-(h_2-h_1){\int }_{t-h_{ji}(t)}^{t-h_1}{\dot{x}}_i^T(s)U_i{\dot{x}}_i(s)ds\\ \le -{[x_i(t-h_1)-x_i(t-h_{ji}(t))]}^T{U}_i[x_i(t-h_1)-x_i(t-h_{ji}(t))].\end{array}$$

Note that when $h_{ji}(t)=h_1$ or $h_{ji}(t)=h_2$, we have

$${[x_i(t-h_1)-x_i(t-h_{ji}(t))]}^T=0\text{or}[x_i(t-h_{ji}(t))-x_i(t-h_2)]=0,$$

respectively. Besides, using Proposition 2.3 again, we have

$$\begin{array}{r}{e}^{-4\beta h_2}{\int }_{-h_2}^{-h_1}{\int }_{t+\theta }^t{\dot{x}}_i^T(s)W_i{\dot{x}}_i(s)dsd\theta \\ \le -e^{-4\beta h_2}\frac{2}{{\overline{h}}^2-h^2}{({\int }_{-\overline{h}}^{-h}{\int }_{t+\theta }^{t}x(s)dsd\theta )}^{T}Z({\int }_{-\overline{h}}^{-h}{\int }_{t+\theta }^{t}x(s)dsd\theta )\\ \le \frac{-2e^{-4\beta h_2}}{h_2^2-h_1^2}{((h_2-h_1)x_i(t)-{\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )}^T\\ \times W_i((h_2-h_1)x_i(t)-{\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta ).\end{array}$$

Hence,

$$\begin{array}{rl}{\dot{V}}_{i7}\le & (h_2-h_1)h_2{\dot{x}}_i^T(t)W_i{\dot{x}}_i(t)-2\alpha V_{i7}-\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}{((h_2-h_1)x_i(t)-{\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )}^T\\ \times W_i((h_2-h_1)x_i(t)-{\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta ).\end{array}$$

Therefore, we have

$$\begin{array}{rl}\dot{V}(\cdot )+2\alpha V(\cdot )\le & x_i^T(t)[A_i^T{P}_i+A_i{P}_i+2\alpha P_i+2(Q_i+R_i)]x_i(t)\\ +2x_i^T(t)P_i\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))-e^{2\alpha h_1}{x}_i^T(t-h_1)Q_i{x}_i(t-h_1)\\ -e^{2\alpha h_2}{x}_i^T(t-h_2)Q_i{x}_i(t-h_2)+{\dot{x}}_i^T(t)[(h_1^2+h_2^2)R_i+(h_2-h_1)U_i]{\dot{x}}_i(t)\\ +(h_2-h_1)h_2{\dot{x}}_i^T(t)W_i{\dot{x}}_i(t)\\ -e^{2\alpha h_1}{[x_i(t)-x_i(t-h_1)]}^T{R}_i[x_i(t)-x_i(t-h_1)]\\ -e^{2\alpha h_2}{[x_i(t)-x_i(t-h_2)]}^T{R}_i[x_i(t)-x_i(t-h_2)]\\ -e^{2\alpha h_2}\sum _{j\ne i,j=1}^N{[x_i(t-h_{ji}(t))-x_i(t-h_2)]}^T{U}_i[x_i(t-h_{ji}(t))-x_i(t-h_2)]\\ -e^{2\alpha h_2}\sum _{j\ne i,j=1}^N{[x_i(t-h_1)-x_i(t-h_{ji}(t))]}^T{U}_i[x_i(t-h_1)-x_i(t-h_{ji}(t))]\\ -\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}{((h_2-h_1)x_i(t)-{\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )}^T{W}_i(h_2-h_1)x_i(t)\\ -{\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta .\end{array}$$

(3.3)

By using the following identity relation:

$${\dot{x}}_i(t)-A_i{x}_i(t)-\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))=0,$$

we have

$$\begin{array}{r}2x_i^T(t)S_{i1}{\dot{x}}_i(t)-2x_i^T(t)S_{i1}{A}_i{x}_i(t)-2x_i^T(t)S_{i1}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))=0,\\ 2x_i^T(t-h_1)S_{i2}{\dot{x}}_i(t)-2x_i^T(t-h_1)S_{i2}{A}_i{x}_i(t)-2x_i^T(t-h_1)S_{i2}\sum _{ji,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))=0,\\ 2x_i^T(t-h_2)S_{i3}{\dot{x}}_i(t)-2x_i^T(t-h_2)S_{i3}{A}_i{x}_i(t)\\ -2x_i^T(t-h_2)S_{i3}\sum _{ji,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))=0,\\ 2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{\dot{x}}_i(t)-2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{A}_i{x}_i(t)\\ -2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))=0,\\ 2{\dot{x}}_i^T(t)S_{i5}{\dot{x}}_i(t)-2{\dot{x}}_i^T(t)S_{i5}{A}_i{x}_i(t)-2{\dot{x}}_i^T(t)S_{i5}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))=0.\end{array}$$

(3.4)

Adding all the zero items of (3.4) into (3.3), we obtain

$$\begin{array}{rl}\dot{V}(\cdot )+2\alpha V(\cdot )\le & x_i^T(t)[A_i^T{P}_i+A_i{P}_i+2\alpha P_i+2(Q_i+R_i)-2S_{i1}{A}_i\\ -e^{2\alpha h_1}{R}_i-e^{2\alpha h_2}{R}_i-\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right){(h_2-h_1)}^2{W}_i]x_i(t)\\ +2\sum _{j\ne i,j=1}^N{D}_{ij}{x}_i^T(t)[P_i-S_{i1}{D}_{ij}-S_{i4}{A}_i]x_j(t-h_{ij}(t))\\ +x_i^T(t-h_1)[-e^{2\alpha h_1}{Q}_i-e^{2\alpha h_1}{R}_i-e^{2\alpha h_2}{U}_i]x_i(t-h_1)\\ +x_i^T(t-h_2)[-e^{2\alpha h_2}{Q}_i-e^{2\alpha h_2}{R}_i-e^{2\alpha h_2}{U}_i]x_i(t-h_2)\\ +{\dot{x}}_i^T(t)[(h_1^2+h_2^2)R_i+(h_2-h_1)U_i+2S_{i5}+(h_2-h_1)h_2{W}_i]{\dot{x}}_i(t)\\ +\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))[-e^{2\alpha h_2}{U}_i-e^{2\alpha h_2}{U}_i]x_i(t-h_{ji}(t))\\ +2x_i^T(t)[e^{2\alpha h_1}{R}_i-S_{i2}{A}_i]x_i(t-h_1)+2x_i^T(t)[e^{2\alpha h_2}{R}_i+S_{i3}{A}_i]x_i(t-h_2)\\ +2e^{2\alpha h_2}\sum _{j\ne i,j=1}^N{x}_i^T(t-h_1)U_i{x}_i(t-h_{ji}(t))\\ +2e^{2\alpha h_2}\sum _{j\ne i,j=1}^N{x}_i^T(t-h_2)U_i{x}_i(t-h_{ji}(t))\\ +2x_i^T(t)[S_{i1}-S_{i5}{A}_i]{\dot{x}}_i(t)+2x_i^T(t-h_1)S_{i2}{\dot{x}}_i(t)\\ +2x_i^T(t-h_1)S_{i3}{\dot{x}}_i(t)+2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{\dot{x}}_i(t)\\ -2\sum _{j\ne i,j=1}^N{\dot{x}}_i^T(t)S_{i5}{x}_j(t-h_{ij}(t))\\ -2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{D}_{ij}{x}_j(t-h_{ij}(t))\\ -2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{A}_i{x}_i(t)-2x_i^T(t-h_1)S_{i2}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\\ -2x_i^T(t-h_2)S_{i3}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\\ -{({\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )}^T\left[\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right)W_i\right]({\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )\\ +2x_i^T(t)[\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right)(h_2-h_1)W_i]({\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta ).\end{array}$$

Applying Proposition 2.1, we obtain

$$\begin{array}{r}\begin{array}{rl}2x_i^T(t)P_i\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\le & \sum _{j\ne i,j=1}^N{x}_i^T(t)P_i{D}_{ij}{D}_{ij}^T{P}_i{x}_i(t)\\ +\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)),\end{array}\\ \begin{array}{rl}-2x_i^T(t)S_{i1}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\le & \sum _{j\ne i,j=1}^N{x}_i^T(t)S_{i1}{D}_{ij}{D}_{ij}^T{S}_{i1}^T{x}_i(t)\\ +\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)),\end{array}\\ \begin{array}{rl}-2{\dot{x}}_i^T(t)S_{i5}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\le & \sum _{j\ne i,j=1}^N{\dot{x}}_i^T(t)S_{i5}{D}_{ij}{D}_{ij}^T{S}_{i5}^T{\dot{x}}_i(t)\\ +\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)),\end{array}\\ -2x_i^T(t-h_2)S_{i3}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\le \sum _{j\ne i,j=1}^N{x}_i^T(t-h_2)S_{i3}{D}_{ij}{D}_{ij}^T{S}_{i3}^T{x}_i(t-h_2)(t)\\ \phantom{-2x_i^T(t-h_2)S_{i3}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\le }+\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)),\\ -2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\\ \le \sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{D}_{ij}{D}_{ij}^T{S}_{i4}^T{x}_i(t-h_{ji}(t))\\ +\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)),\\ \begin{array}{rl}-2x_i^T(t-h_1)S_{i2}\sum _{j\ne i,j=1}^N{D}_{ij}{x}_j(t-h_{ij}(t))\le & \sum _{j\ne i,j=1}^N{x}_i^T(t-h_1)S_{i2}{D}_{ij}{D}_{ij}^T{S}_{i2}^T{x}_i(t-h_1)\\ +\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)),\end{array}\\ \begin{array}{rl}-2x_i^T(t)S_{i4}{A}_i{x}_j(t-h_{ij}(t))\le & x_i^T(t)S_{i4}{A}_i{A}_i^T{S}_{i4}^T{x}_i(t)\\ +\sum _{j\ne i,j=1}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t)).\end{array}\end{array}$$

(3.5)

Therefore, applying inequalities (3.5) and noting that

$$\begin{array}{c}\sum _{i=1}^N\sum _{j=1,j\ne i}^N{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t))=\sum _{i=1}^N\left[\sum _{j=1,i\ne j}^N{x}_i{(t-h_{ji}(t))}^T{x}_i(t-h_{ji}(t))\right],\hfill \\ \sum _{i=1}^N\sum _{j=1,j\ne i}^N{a}_{ij}{x}_j{(t-h_{ij}(t))}^T{x}_j(t-h_{ij}(t))=\sum _{i=1}^N\left[\sum _{j=1,i\ne j}^N{a}_{ji}{x}_i{(t-h_{ji}(t))}^T{x}_i(t-h_{ji}(t))\right],\hfill \end{array}$$

we have

$$\begin{array}{r}\dot{V}(\cdot )+2\alpha V(\cdot )\\ \le \sum _{i=1}^N[x_i^T(t)[A_i^T{P}_i+A_i{P}_i+2\alpha P_i+2(Q_i+R_i)-2S_{i1}{A}_i\\ -e^{2\alpha h_1}{R}_i-e^{2\alpha h_2}{R}_i-\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right){(h_2-h_1)}^2{W}_i\\ +\sum _{j\ne i,j=1}^N{P}_i{D}_{ij}{D}_{ij}^T{P}_i+\sum _{j\ne i,j=1}^N{S}_{i1}{D}_{ij}{D}_{ij}^T{S}_{i1}^T+S_{i4}{A}_i{A}_i^T{S}_{i4}^T]x_i(t)\\ +x_i^T(t-h_1)[-e^{2\alpha h_1}{Q}_i-e^{2\alpha h_1}{R}_i-e^{2\alpha h_2}{U}_i+\sum _{j\ne i,j=1}^N{S}_{i2}{D}_{ij}{D}_{ij}^T{S}_{i2}^T]x_i(t-h_1)\\ +x_i^T(t-h_2)[-e^{2\alpha h_2}{Q}_i-e^{2\alpha h_2}{R}_i-e^{2\alpha h_2}{U}_i+\sum _{j\ne i,j=1}^N{S}_{i3}{D}_{ij}{D}_{ij}^T{S}_{i3}^T]x_i(t-h_2)\\ +{\dot{x}}_i^T(t)[(h_1^2+h_2^2)R_i+(h_2-h_1)U_i+2S_{i5}+(h_2-h_1)h_2{W}_i\\ +\sum _{j\ne i,j=1}^N{S}_{i5}{D}_{ij}{D}_{ij}^T{S}_{i5}^T]{\dot{x}}_i(t)+\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))[-e^{2\alpha h_2}{U}_i-e^{2\alpha h_2}{U}_i\\ +\sum _{j\ne i,j=1}^N{S}_{i4}{D}_{ij}{D}_{ij}^T{S}_{i4}^T+7I]x_i(t-h_{ji}(t))\\ +2x_i^T(t)[e^{2\alpha h_1}{R}_i-S_{i2}{A}_i]x_i(t-h_1)]\\ +\sum _{i=1}^N[2x_i^T(t)[e^{2\alpha h_2}{R}_i+S_{i3}{A}_i]x_i(t-h_2)+2e^{2\alpha h_2}\sum _{j\ne i,j=1}^N{x}_i^T(t-h_1)U_i{x}_i(t-h_{ji}(t))\\ +2e^{2\alpha h_2}\sum _{j\ne i,j=1}^N{x}_i^T(t-h_2)U_i{x}_i(t-h_{ji}(t))\\ +2x_i^T(t)[S_{i1}-S_{i5}{A}_i]{\dot{x}}_i(t)+2x_i^T(t-h_1)S_{i2}{\dot{x}}_i(t)\\ +2x_i^T(t-h_1)S_{i3}{\dot{x}}_i(t)+2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{\dot{x}}_i(t)\\ -2\sum _{j\ne i,j=1}^N{x}_i^T(t-h_{ji}(t))S_{i4}{A}_i{x}_i(t)\\ -{({\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )}^T\left[\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right)W_i\right]({\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )\\ +2x_i^T(t)[\left(\frac{2e^{-4\beta h_2}}{h_2^2-h_1^2}\right)(h_2-h_1)W_i]({\int }_{t-h_2}^{t-h_1}{x}_i(\theta )d\theta )]\\ =\sum _{i=1}^N{\zeta }_i^T(t){\mathcal{M}}^i{\zeta }_i(t),\end{array}$$

where ${\zeta }_i^T(t)=[x_i^T(t),x_i^T(t-h_1),x_i^T(t-h_2),{(x_i^T(t-h_{ji}))}_{j\ne i,j=1}^N,{\dot{x}}_i^T(t),{\int }_{t-h_2}^{t-h_1}{x}_i^T(\theta )d\theta ]$.

By condition (3.1), we obtain

$$\dot{V}(t,x_t)\le -2\alpha V(t,x_t),\mathrm{\forall }t\in R^{+}.$$

(3.6)

Integrating both sides of (3.6) from 0 to t, we obtain

$$V(t,x_t)\le V(\phi )e^{-2\alpha t},\mathrm{\forall }t\in R^{+}.$$

Furthermore, taking condition (3.2) into account, we have

$${\lambda }_1{\parallel x(t,\phi )\parallel }^2\le V(x_t)\le V(\phi )e^{-2\alpha t}\le {\lambda }_2{e}^{-2\alpha t}{\parallel \phi \parallel }^2,$$

then

$$\parallel x(t,\phi )\parallel \le \sqrt{\frac{{\lambda }_2}{{\lambda }_1}}{e}^{-\alpha t}\parallel \phi \parallel ,t\in R^{+}.$$

This completes the proof of the theorem. □

Remark 3.1 Theorem 3.1 provides sufficient conditions for linear large-scale system (2.1) in terms of the solutions of LMIs, which guarantees the closed-loop system to be exponentially stable with a prescribed decay rate α. The developed method using new inequalities for lower bounding cross terms eliminates the need for over-bounding and provides larger values of the admissible delay bound. Note that the time-varying delays are non-differentiable; therefore, the methods proposed in [11, 14, 15, 18–35] are not applicable to system (2.1). LMI condition (3.2) depends on parameters of the system under consideration as well as the delay bounds. The feasibility of the LMIs can be tested by the reliable and efficient Matlab LMI Control Toolbox [36].

4 Numerical examples

In this section, we give a numerical example to show the effectiveness of the proposed result.

Example 4.1 This example is a large-scale model composed of two machine subsystems as follows:

$$\begin{array}{c}{\dot{x}}_1(t)=A_1{x}_1(t)+D_{12}{x}_2(t-h_{12}(t)),t\in R^{+},\hfill \\ x_1(t)={\phi }_1(t),\mathrm{\forall }t\in [-h_2,0],\hfill \\ {\dot{x}}_2(t)=A_2{x}_2(t)+D_{21}{x}_1(t-h_{21}(t)),t\in R^{+},\hfill \\ x_2(t)={\phi }_2(t),\mathrm{\forall }t\in [-h_2,0],\hfill \end{array}$$

where the absolute rotor angle and angular velocity of the machine in each subsystem are denoted by $x_1=(x_{11},x_{12})$ and $x_2=(x_{21},x_{22})$, respectively; the i th system coefficient $A_i$; the modulus of the transfer admittance $D_{ij}$; the initial input ${\phi }_i$; the time-varying delays $h_{ij}(t)$ between the two machines in the subsystem:

$$\begin{array}{c}{h}_{12}=\{\begin{array}{cc}0.1+{sin}^{2}t\hfill & \text{if }t\in \mathcal{I}={\bigcup }_{k\ge 0}[2k\pi ,(2k+1)\pi ],\hfill \\ 0.1\hfill & \text{if }t\in R^{+}\setminus \mathcal{I},\hfill \end{array}\hfill \\ h_{21}=\{\begin{array}{cc}0.2+1.1{sin}^{2}t\hfill & \text{if }t\in \mathcal{I}={\bigcup }_{k\ge 0}[2k\pi ,(2k+1)\pi ],\hfill \\ 0.2\hfill & \text{if }t\in R^{+}\setminus \mathcal{I},\hfill \end{array}\hfill \\ A_1=\left(\begin{array}{cc}-1& 0.5\\ 1& -2\end{array}\right),D_{12}=\left(\begin{array}{cc}-0.1& 0.2\\ 0.3& -0.5\end{array}\right),\hfill \\ A_2=\left(\begin{array}{cc}-2& 0.5\\ 1& -3\end{array}\right),D_{21}=\left(\begin{array}{cc}-0.4& 0.1\\ 0.2& -0.3\end{array}\right).\hfill \end{array}$$

It is worth nothing that the delay functions $h_{12}(t)$, $h_{21}(t)$ are non-differentiable; therefore, the methods in [11, 14, 15, 18–35] are not applicable to this system. By using LMI Toolbox in Matlab [36], LMIs (3.1) is feasible with $h_1=0.1$, $h_2=1.3$, $\alpha =0.1$, and

$$\begin{array}{c}{P}_1=\left(\begin{array}{cc}0.2429& 0.0170\\ 0.0170& 0.4891\end{array}\right),P_2=\left(\begin{array}{cc}0.4872& 0.2139\\ 0.2139& 0.7821\end{array}\right),\hfill \\ Q_1=\left(\begin{array}{cc}0.7338& -0.0014\\ -0.0014& 0.7032\end{array}\right),Q_2=\left(\begin{array}{cc}0.5110& -0.0082\\ -0.0082& 0.8108\end{array}\right),\hfill \\ R_1=\left(\begin{array}{cc}0.3724& 0.0329\\ 0.0329& 0.8680\end{array}\right),R_2=\left(\begin{array}{cc}0.5001& 0.0881\\ 0.0881& 0.4892\end{array}\right),\hfill \\ U_1=\left(\begin{array}{cc}0.3486& 0.0149\\ 0.0149& 0.5664\end{array}\right),U_2=\left(\begin{array}{cc}0.7790& 0.2919\\ 0.2919& 0.5091\end{array}\right),\hfill \\ W_2=\left(\begin{array}{cc}0.3486& 0.0149\\ 0.0149& 0.5664\end{array}\right),W_2=\left(\begin{array}{cc}0.7721& 0.0128\\ 0.0128& 0.6901\end{array}\right),\hfill \\ S_{11}=\left(\begin{array}{cc}0.8136& 0.0213\\ 0.0422& 0.4275\end{array}\right),S_{21}=\left(\begin{array}{cc}0.5390& 0.0329\\ 0.0219& 0.6092\end{array}\right),\hfill \\ S_{12}=\left(\begin{array}{cc}0.3957& 0.0643\\ 0.0643& 1.3682\end{array}\right),S_{22}=\left(\begin{array}{cc}0.7230& 0.0532\\ 0.0332& 0.9011\end{array}\right),\hfill \\ S_{13}=\left(\begin{array}{cc}0.3957& 0.0643\\ 0.0643& 1.3682\end{array}\right),S_{23}=\left(\begin{array}{cc}0.5419& 0.0084\\ 0.0432& 0.8932\end{array}\right),\hfill \\ S_{14}=\left(\begin{array}{cc}0.3957& 0.0643\\ 0.0643& 1.3682\end{array}\right),S_{24}=\left(\begin{array}{cc}0.4499& 0.0772\\ 0.03490& 0.5419\end{array}\right),\hfill \\ S_{15}=\left(\begin{array}{cc}0.3957& 0.0643\\ 0.0643& 1.3682\end{array}\right),S_{25}=\left(\begin{array}{cc}0.9837& 0.04428\\ 0.0095& 0.9321\end{array}\right).\hfill \end{array}$$

According to Theorem 3.1, the system is exponentially stable. Finally, the solution $x(t,\phi )$ of the system satisfies

$$\parallel x(t,\phi )\parallel \le 19.2419e^{-0.1t}\parallel \phi \parallel ,\mathrm{\forall }t\in R^{+}.$$

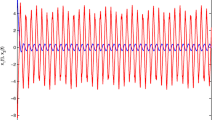
Figure 1 shows the trajectories of $x_1(t)$ and $x_2(t)$ of the closed loop system with the initial conditions ${\phi }_1(t)=[25]$, ${\phi }_2(t)=[-33]$.

Figure 1

The trajectories of a solution of the linear large-scale system.

The trajectories of a solution of the linear large-scale system are shown in Figure 1, respectively.

5 Conclusion

In this paper, the problem of the decentralized exponential stability for large-scale time-varying delay systems has been studied. The time delay is assumed to be a function belonging to a given interval, but not necessarily differentiable. By effectively combining an appropriate Lyapunov functional with the Newton-Leibniz formula and free-weighting parameter matrices, this paper has derived new delay-dependent conditions for the exponential stability in terms of linear matrix inequalities, which allow simultaneous computation of two bounds that characterize the exponential stability rate of the solution. The developed method using new inequalities for lower bounding cross terms eliminates the need for over-bounding and provides larger values of the delay bound. Numerical examples are given to show the effectiveness of the obtained result.