Abstract
This paper presents a new adaptive synchronization problem for the delayed reaction-diffusion neural networks (RDNNs) with unknown time-varying coupling strengths under stochastic perturbations. By constructing a differential-difference-type learning law and an adaptive learning control law, and using Lyapunov-Krasovskii-like composite energy functional method, a novel sufficient condition is derived to ensure adaptive asymptotical synchronization in the mean square sense for the addressed system. Finally, a numerical example is given to verify the effectiveness of the proposed method.
Similar content being viewed by others
1 Introduction
In recent decades, different types of neural networks (NNs) with time delays have been widely investigated due to their applicability in solving some image processing, signal processing automatic control engineering, fault diagnosis, telecommunications, and pattern recognition problems. The realistic applications heavily depend on the dynamical behaviors [1–7]. Thus, the analysis of the dynamical behaviors such as stability, periodic oscillation, bifurcation and chaos is a necessary step for practical design of NNs. For instance, in [1], by utilizing the Lyapunov-Krasovkii functional and combining with the linear matrix inequalities (LMIs) approach, the authors analyzed the global exponential stability of neutral-type impulsive NNs. By constructing a newly augmented Lyapunov-Krasovskii functional, [3] established less conservative stability criteria in the form of LMIs.
Control and synchronization of chaotic systems have become an important topic since the pioneering work of Pecora and Carroll in 1990 [8]. There exist many benefits of having synchronization or chaos synchronization in some engineering applications, such as secure communication, chaos generators design, chemical reactions, biological systems, information science, etc. Some papers on synchronization of chaotic systems with time delays have been published [9–11]. Since NNs can exhibit some complicated dynamics and even chaotic behavior, the synchronization of chaotic NNs has also become an important area of study. Recently, the synchronization for delayed NNs also has been reported [12–14].
When modeling real nervous systems, stochastic disturbances are probably the main resources of the performance degradations of the implemented NNs. Moreover, in real time dynamical systems, the time delays are unavoidably encountered in the implementation of NNs, and may cause undesirable dynamic network behaviors such as instability. Hence, it is of great importance to take into account the synchronization problem of stochastic delayed chaotic NNs. To date, many researchers have studied the synchronization for delayed NNs with environmental noise [15–17]. In the practical operation, diffusion effects cannot be avoided in the NNs and electric circuits when electrons are moving in a nonuniform electromagnetic fields. Therefore, it is essential to consider the state variables, which vary in time as well as in space [18–25]. In [18], by using inequality techniques and the Lyapunov functional method, the synchronization scheme is investigated for a class of delayed RDNNs. In [19], an approach combining Lyapunov stability theory with stochastic analysis and periodically intermittent control was taken to investigate synchronization problem. In [20], the authors considered the global exponential stability and synchronization of the delayed RDNNs with Dirichlet boundary conditions under the impulsive control in terms of p-norm.
As far as we know, there are two main approaches to study the complex network synchronization: one is based on the characteristics of the identical node and the coupling matrix, by Lyapunov functional theory, the stable criteria in terms of LMIs were established [26, 27]. However, if the nonlinear characteristics of the uncoupled nodes and the coupling matrix are unknown, the methods given above will fail in the synchronization of complex networks. The other is to adjust the time-varying coupling strengths to complete the synchronization, such as [28–30]. For example, [28] presented a new robust adaptive synchronization approach for the global synchronization of complex dynamical networks without time delay. In [29], the synchronization of complex topologies using couplings of time-varying strength was numerically reported and made a comparison between fixed and varying coupling strength. [30] studied the synchronization for delayed complex networks by adjusting time-varying coupling strengths. The update laws of the coupling strengths were derived to realize the synchronization based on Lassalle-Yoshizawa theorem. Recently, a new adaptive control mechanism was proposed for nonlinear system with unknown time-varying periodic parameters, the stability of the resulting closed-loop system was proven by composite energy function in [31]. The method was extended to the synchronization of two chaotic systems with unknown time-varying periodic parameters in [32] and the synchronization of complex dynamic networks with unknown time-varying periodic coupling strength in [33–36], respectively.
As mentioned above, in this paper, we consider a challenging problem, i.e., how to incorporate adaptive control techniques for time-delay systems into learning control to solve the synchronization of stochastic RDNNs with unknown time-varying parameters and unknown time-varying delays. It is still an open problem how to control a system with unknown time-varying parameters and unknown time-varying delays. Recently, on the synchronization of chaotic systems with time-varying parameters, which are expressed by ordinary differential equations, there have been a few research results [21–25]. Very recently, based on the LaSalle invariant principle of functional differential equations, a sufficient condition for the adaptive synchronization of considered system with unknown time-varying parameters was obtained in [37]. To the best of our knowledge, adaptive synchronization is seldom considered for the stochastic delayed RDNNs with unknown time-varying periodic coupling strengths. The main design difficulty is how to deal with the unknown time-varying parameters and unknown time-varying delays. Fortunately, this paper shows that this difficulty can be successfully overcome by constructing a Lyapunov-Krasovskii-like composite energy function. By applying the Weiner process and inequality techniques, an adaptive controller and an updating law are designed to ensure the states of considered system to reach the desired synchronization manifold.
Notations: Throughout the paper, is the space of scalar value Lebesgue measurable functions on Ω and is a Banach space for the -norm
Then for any , the norm is defined as
= { is continuous and with the uniform norm = }.
denotes the family of all measurable, -valued stochastic variables such that , where stands for the mathematical expectation operator with respect to the given probability measure  .
.
2 Problem statement and preliminaries
Consider the following delayed RDNNs with unknown time-varying coupling strengths:
where , is a compact set with smooth boundary ∂ Ω and in space , is a constant; denotes the state vector, associated with the n neurons at time t and in space x; represents the rate, with which the i th unit will reset its potential to the resting state in isolation when disconnected from the networks and external inputs; denotes the strength of the j th unit on the i th unit at time t and in space x; are the synaptic connection strength of the j th unit on i th unit at time t and in space x; denotes the activation function of the j th unit at time t and in space x; denotes the time-varying delay and satisfies , , , where and μ are constants; with stands for transmission diffusion operator along the i th neuron; is continuous and bounded function, , .
Remark 1 Recently, complex dynamical networks with time-varying or constant coupling strengths have attracted much attention from researchers in different areas, such as physical science, engineering, mathematics, biology, and so on [28–30]. There are many interesting collective phenomena in complex dynamical networks that can be described by coupled differential equation equations, such as self-organization, synchronization, spatiotemporal chaos and so on. Particularly, the synchronization phenomena have actively been investigated due to past physics and potential engineering application, secure communication, and so on [28–30, 34–37]. Although some methods have been developed in the field of complex networks, only a few of them are concerning time-varying coupling strengths. To the best of our knowledge, up to now, little work is reported on the synchronization of stochastic RDNNs with unknown time-varying delays and unknown time-varying coupling strengths. In this paper, using adaptive learning method on periodic coupling strengths, the synchronization of stochastic delayed RDNNs will be considered.
In order to obtain our main results, we assume the following conditions hold.
(A1) There exist positive constants such that
for all , .
(A2) In system (1), unknown time-varying coupling strengths , and satisfy the following equations:
in which , , are unknown common period time-varying nonnegative parameters, i.e., , , , , and are unknown time-invariant nonnegative parameters.
Remark 2 Since , , , clearly, , and are unknown continuous periodic functions with a known common period ω. , and are a finite unknown upper bound , and , respectively. , and are bounded, that is, there are positive constants , , , , , such that , and .
We consider model (1) as the drive system. The response system is
where is a n dimensional state vector of RDNNs; is a control input to be designed; is the noise intensity matrix and the stochastic disturbance is a Brownian motion defined on and , ; is an error signal; .
Remark 3 This type of stochastic perturbation can be regarded as a result from the occurrence of the internal error when the simulation circuits are constructed such as inaccurate design of the coupling strengths and some other important parameters [17].
Subtracting Eq. (1) from Eq. (3),we have the following error system:
where ,
Then we design controllers by
where , , , , , are estimations to , , , , , , respectively.
To prove our results, the following assumptions are necessarily in this paper.
(A3) There exist positive constants such that
for all , .
To ensure negative feedback, the time-varying periodic adaptive gains and time-invariance update law are designed as follows:
where
we can choose , , such that , and are increasing and continuous functions. ,
in which , , are positive constants.
Remark 4 The adaptation law is a difference-type pointwise integration over the period , which takes the place of the differential-type adaptation law. Due to , , , for any time instant , , we have
This means that , , can be treated as a ‘constant’ when it is sampled at any interval, which is the integer multiple of the period ω. The periodic updating law (6) in the interval of one period ω is a difference-type integrator for such a ‘constant.’
Next, we introduce the definition of asymptotic synchronization in the mean square sense for the two coupled RDNNs (1) and (3), and then present some preliminary lemmas, which are needed to prove our main results.
Definition 1 The two coupled RDNNs (1) and (3) are said to achieve asymptotic synchronization in the mean square sense, if there is a control , , such that for any given initial,
Lemma 1 [38]
Let Ω be a cube (), and let be a real-valued function belonging to , which vanish on the boundary ∂ Ω of Ω, i.e., . Then
Remark 5 Lemma 1 is a well-known result and is widely utilized in the study of partial differential equation. It plays an important role in the synchronization of stochastic delayed RDNNs with unknown time-varying coupling strengths. According to Lemma 1, the result in our future research is dependent on reaction-diffusion terms.
Lemma 2 [39]
Let and X be an positive definite matrix, then
Lemma 3 [40]
Consider system and suppose that there exist a function and class K functions , and , such that , and , then the equilibrium is stochastically asymptotically stable. Especially, if , and , are class , then, the equilibrium is globally stochastically asymptotically stable.
3 Main results
By combining the feedback control and adaptive control, and the properties of the Weiner process, we obtain the following Theorem 1.
Theorem 1 Under assumptions (A1)-(A3), if there are constants , , and Θ such that
where , , , , , , then the adaptive control mechanism (4)-(6) warrants two coupled system (1) and (3) are adaptive asymptotic synchronization in the mean square sense.
Proof Define the Lyapunov-Krasovskii-like composite energy functional as
where , , , , , , , , , . Computing along the trajectory of error system (4), one can obtain that
According to Green’s formula, Lemma 1 and the Dirichlet boundary condition, we get
By (2), (6), (7), (10), (11) and (A1), one can derive
where , , , . From (A1) and Lemma 2, we can derive
By (13), we have
Let , in which Θ is positive constant. Then it follows from (14) that
From inequality (15) and Ito’s formula, we can conclude that
According to Lemma 3 and Definition 1, it is easy to see that system (4) is globally stochastically asymptotically stable. This implies that the two coupled delayed RDNNs (1) and (3) are adaptive asymptotic synchronization in the mean square sense. This completes the proof. □
4 An illustrative example
We present a simple example here in order to illustrate the usefulness of our main results. Our aim is to examine the adaptive synchronization of a given delayed RDNNs with unknown time-varying coupling strengths.
Example 1 Consider the drive-response systems (1) and (3) with , , and , , , , , , , , , , , , , , . Then, a simple computation yields , , , , , , , , , , , , , . Choosing , , and , we have
Therefore, it can be concluded from Theorem 1 that the considered drive-response systems are adaptive asymptotic synchronization in the mean square sense.
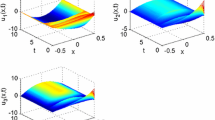
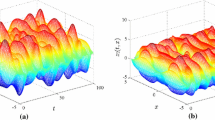
The change processes of the state variables and error variables , are shown in Figure 1 to Figure 4. By numerical simulations, we can see that the considered drive-response systems are adaptive asymptotic synchronization in the mean square sense.
5 Conclusions
In this paper, a novel adaptive learning control method is used in stochastic delayed RDNNs with unknown time-varying periodic connected strengths. By constructing Lyapunov-Krasovskii-like composite energy functional, the adaptive learning laws of parameters and the adaptive control strategy are designed to guarantee the adaptive asymptotic synchronization of considered system in the mean square sense. Finally, a simple example and simulations have been utilized to verify our theoretical result is feasible and effective.
References
Rakkiyappan R, Balasubramaniam P, Cao J: Global exponential stability results for neutral-type impulsive neural networks. Nonlinear Anal., Real World Appl. 2010, 11: 122–130. 10.1016/j.nonrwa.2008.10.050
Balasubramaniam P, Vembarasan V: Synchronization of recurrent neural networks with mixed time-delays via output coupling with delayed feedback. Nonlinear Dyn. 2012, 70: 677–691. 10.1007/s11071-012-0487-y
Kwon OM, Park JH, Lee SM, Cha EJ: Analysis on delay-dependent stability for neural networks with time-varying delays. Neurocomputing 2013, 103: 114–120.
Fang M, Park JH: Non-fragile synchronization of neural networks with time-varying delay and randomly occurring controller gain fluctuation. Appl. Math. Comput. 2013, 219: 8009–8017. 10.1016/j.amc.2013.02.030
Zhang W, Li J, Shi N: Stability analysis for stochastic Markovian jump reaction-diffusion neural networks with partially known transition probabilities and mixed time delays. Discrete Dyn. Nat. Soc. 2012., 2012: Article ID 524187 10.1155/2012/524187
Zhang W, Li J: Global exponential stability of reaction-diffusion neural networks with discrete and distributed time-varying delays. Chin. Phys. B 2011., 20(3): Article ID 030701
Zhang W, Li J, Chen M: Global exponential stability and existence of periodic solutions for delayed reaction-diffusion BAM neural networks with Dirichlet boundary conditions. Bound. Value Probl. 2013., 2013: Article ID 105 10.1186/1687-2770-2013-105
Carroll T, Pecora L: Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64: 821–824. 10.1103/PhysRevLett.64.821
He W, Cao J: Exponential synchronization of hybrid coupled networks with delayed coupling. IEEE Trans. Neural Netw. 2010, 21: 517–583.
Jeonga SC, Jib DH, Parkc Ju H, Wona SC: Adaptive synchronization for uncertain chaotic neural networks with mixed time delays using fuzzy disturbance observer. Appl. Math. Comput. 2013, 219: 5984–5995. 10.1016/j.amc.2012.12.017
Vembarasan V, Balasubramaniam P: Chaotic synchronization of Rikitake system based on T-S fuzzy control techniques. Nonlinear Dyn. 2013. 10.1007/s11071-013-0946-0
Park JH: Synchronization of cellular neural networks of neutral type via dynamic feedback controller. Chaos Solitons Fractals 2009, 42: 1299–1304. 10.1016/j.chaos.2009.03.024
Park MJ, Kwon OM, Park Ju H, Lee SM, Cha EJ: Synchronization criteria for coupled Hopfield neural networks with time-varying delays. Chin. Phys. B 2011., 20: Article ID 110504
Wu Z, Park JH, Su H, Chu J: Discontinuous Lyapunov functional approach to synchronization of time-delay neural networks using sampled-data. Nonlinear Dyn. 2012, 69: 2021–2030. 10.1007/s11071-012-0404-4
Li X, Cao J: Adaptive synchronization for delayed neural networks with stochastic perturbation. J. Franklin Inst. 2008, 345: 779–791. 10.1016/j.jfranklin.2008.04.012
Gan QT: Adaptive synchronization of Cohen-Grossberg neural networks with unknown parameters and mixed time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 3040–3049. 10.1016/j.cnsns.2011.11.012
Sun Y, Cao J, Wang Z: Exponential synchronization of stochastic perturbed chaotic delayed neural networks. Neurocomputing 2007, 70: 2477–2485. 10.1016/j.neucom.2006.09.006
Wang Y, Cao JD: Synchronization of a class of delayed neural networks with reaction-diffusion terms. Phys. Lett. A 2007, 369: 201–211. 10.1016/j.physleta.2007.04.079
Gan Q: Global exponential synchronization of generalized stochastic neural networks with mixed time delays and reaction-diffusion terms. Neurocomputing 2012, 89: 96–105.
Hu C, Jiang H, Teng Z: Impulsive control and synchronization for delayed neural networks with reaction-diffusion terms. IEEE Trans. Neural Netw. 2010, 21: 67–81.
Zhang W, Li J: Global exponential synchronization of delayed BAM neural networks with reaction-diffusion terms and the Neumann boundary conditions. Bound. Value Probl. 2012., 2012: Article ID 2 10.1186/1687-2770-2012-2
Gan Q: Exponential synchronization of stochastic Cohen-Grossberg neural networks with mixed time-varying delays and reaction-diffusion via periodically intermittent control. Neural Netw. 2012, 31: 12–21.
Zhang W, Li J, Chen M: Dynamical behaviors of impulsive stochastic reaction-diffusion neural networks with mixed time delays. Abstr. Appl. Anal. 2012., 2012: Article ID 236562 10.1155/2012/236562
Li S, Yang H, Lou X: Adaptive exponential synchronization of delayed neural networks with reaction-diffusion terms. Chaos Solitons Fractals 2009, 40: 930–939. 10.1016/j.chaos.2007.08.047
Lou X, Cui B: Asymptotic synchronization of a class of neural networks with reaction-diffusion terms and time-varying delays. Comput. Math. Appl. 2006, 52: 897–904. 10.1016/j.camwa.2006.05.013
Cao J, Chen G, Li P: Global synchronization in an array of delayed neural networks with hybrid coupling. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 2008, 38: 488–498.
Lu J, Ho DWC: Global exponential synchronization and synchronizability for general dynamical networks. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 2010, 40: 350–361.
Li Z, Jiao L, Lee JJ: Robust adaptive global synchronization of complex dynamical networks by adjusting time-varying coupling strength. Physica A 2008, 387: 1369–1380. 10.1016/j.physa.2007.10.063
Chen L, Wu L, Zhu S: Synchronization in complex networks by time-varying couplings. Eur. Phys. J. D 2008, 48: 405–409. 10.1140/epjd/e2008-00113-4
Huang L, Wang Z, Wang Y, Zuo Y: Synchronization analysis of delayed complex networks via adaptive time-varying coupling strengths. Phys. Lett. A 2009, 373: 3952–3958. 10.1016/j.physleta.2009.08.063
Xu J, Tan Y: A composite energy function based learning control approach for nonlinear systems with time-varying parametric uncertainties. IEEE Trans. Autom. Control 2002, 47: 1940–1945. 10.1109/TAC.2002.804460
Sun Y, Li J: Generalized projective synchronization of chaotic systems via adaptive learning control. Chin. Phys. B 2010., 19: Article ID 020505
Guo X, Li J: Stochastic synchronization for time-varying complex dynamical networks. Chin. Phys. B 2012., 21: Article ID 020501
Wang T, Li J, Tang S: Adaptive synchronization of nonlinearly parameterized complex dynamical networks with unknown time-varying parameters. Math. Probl. Eng. 2012., 2012: Article ID 592539 10.1155/2012/592539
Guo X, Li J: A new synchronization algorithm for delayed complex dynamical networks via adaptive control approach. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 4395–4403. 10.1016/j.cnsns.2012.03.022
Guo X, Li J: Projective synchronization of complex dynamical networks with time-varying coupling strength via hybrid feedback control. Chin. Phys. Lett. 2011., 28: Article ID 120503
Li J, Zhang W, Chen M: Synchronization of delayed reaction-diffusion neural networks via an adaptive learning control approach. Comput. Math. Appl. 2013, 65: 1775–1785. 10.1016/j.camwa.2013.03.016
Lu J: Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos Solitons Fractals 2008, 35: 116–125. 10.1016/j.chaos.2007.05.002
Liang J, Wang Z, Liu Y, Liu X: Global synchronization control of general delayed discrete-time networks with stochastic coupling and disturbances. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 2008, 38: 1073–1083.
Mao X: Stochastic Differential Equations and Applications. Horwood, Chichester; 1997.
Acknowledgements
This work is partially supported by the National Natural Science Foundation of China (60974139), Project supported by the National Science Foundation for Post-doctoral Scientists of China under Grant No. 2013M540754, the Special research projects in Shaanxi Province Department of Education under Grant No. 2013JK0578 and Doctor Introduced project of Xianyang Normal University under Grant No. 12XSYK008.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
WZ designed and performed all the steps of proof in this research and also wrote the paper. JL and MC participated in the design of the study and suggested many good ideas that made this paper possible and helped to draft the first manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, W., Li, J. & Chen, M. Adaptive synchronization of the stochastic delayed RDNNs with unknown time-varying parameters. Adv Differ Equ 2013, 253 (2013). https://doi.org/10.1186/1687-1847-2013-253
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-253