Delay-dependent optimal guaranteed cost control of stochastic neural networks with interval nondifferentiable time-varying delays

Abstract

This paper studies the problem of a guaranteed cost control for a class of stochastic delayed neural networks. The time delay is a continuous function belonging to a given interval, but it is not necessarily differentiable. A cost function is considered as a nonlinear performance measure for the closed-loop system. The stabilizing controllers to be designed must satisfy some mean square exponential stability constraints on the closed-loop poles. By constructing a set of augmented Lyapunov-Krasovskii functional, a guaranteed cost controller is designed via memory less state feedback control, and new sufficient conditions for the existence of the guaranteed cost state-feedback for the system are given in terms of linear matrix inequalities (LMIs). A numerical example is given to illustrate the effectiveness of the obtained result.

1 Introduction

Stability and control of neural networks with the time delay have attracted considerable attention in recent years [1–8]. In many practical systems, it is desirable to design neural networks, which are not only asymptotically or exponentially stable, but can also guarantee an adequate level of system performance. In the area of control, signal processing, pattern recognition and image processing, and delayed neural networks have many useful applications. Some of these applications require that the equilibrium points of the designed network be stable. In both biological and artificial neural systems, time delays due to integration and communication are ubiquitous and often become a source of instability. The time delays in electronic neural networks are usually time-varying, and sometimes vary violently with respect to time due to the finite switching speed of amplifiers and faults in the electrical circuitry. A guaranteed cost control problem [9–12] has the advantage of providing an upper bound on a given system performance index, and, thus, the system performance degradation, incurred by the uncertainties or time delays, is guaranteed to be less than this bound. The Lyapunov-Krasovskii functional technique has been among the popular and effective tools in the design of guaranteed cost controls for neural networks with time delay. Nevertheless, despite such diversity of results available, most existing works either assumed that the time delays are constant or are differentiable [13–16]. Although, in some cases, the delay-dependent guaranteed cost control for systems with time-varying delays was considered in [12, 13, 15], the approach used there cannot be applied to the systems with interval, nondifferentiable time-varying delays. To the best of our knowledge, the guaranteed cost control and state feedback stabilization for stochastic neural networks with interval, nondifferentiable time-varying delays have not been fully studied yet (see, e.g., [4–16] and the references therein), which are important in both theories and applications. This motivates our research.

In this paper, we investigate the guaranteed cost control for stochastic delayed neural networks problem. The novel features here are that the delayed neural network under consideration is with various globally Lipschitz continuous activation functions, and the time-varying delay function is interval, nondifferentiable. A nonlinear cost function is considered as a performance measure for the closed-loop system. The stabilizing controllers to be designed must satisfy some mean square exponential stability constraints on the closed-loop poles. Based on constructing a set of augmented Lyapunov-Krasovskii functional, new delay-dependent criteria for guaranteed cost control via memoryless feedback control is established in terms of LMIs, which allow simultaneous computation of two bounds that characterize the mean square exponential stability rate of the solution and can be easily determined by utilizing MATLABs LMI control toolbox.

The outline of the paper is as follows. Section 2 presents definitions and some well-known technical propositions, needed for the proof of the main result. LMI delay-dependent criteria for the guaranteed cost control and a numerical example showing the effectiveness of the result are presented in Section 3. The paper ends with the conclusions and cited references.

2 Preliminaries

The following notation will be used in this paper. ${\mathbb{R}}^{+}$ denotes the set of all real non-negative numbers; ${\mathbb{R}}^n$ denotes the n-dimensional space with the scalar product $〈x,y〉$ or $x^{T}y$ of two vectors x, y, and the vector norm $\parallel \cdot \parallel$; $M^{n\times r}$ denotes the space of all matrices of $(n\times r)$-dimensions. $A^T$ denotes the transpose of matrix A; A is symmetric if $A=A^T$; I denotes the identity matrix; $\lambda (A)$ denotes the set of all eigenvalues of A; ${\lambda }_{max}(A)=max\{Re\lambda ;\lambda \in \lambda (A)\}$. $x_t:=\{x(t+s):s\in [-h,0]\}$, $\parallel x_t\parallel ={sup}_{s\in [-h,0]}\parallel x(t+s)\parallel$; $C^1([0,t],{\mathbb{R}}^n)$ denotes the set of all ${\mathbb{R}}^n$-valued continuously differentiable functions on $[0,t]$; $L_2([0,t],{\mathbb{R}}^m)$ denotes the set of all the ${\mathbb{R}}^m$-valued square integrable functions on $[0,t]$.

Matrix A is called semi-positive definite ($A\ge 0$) if $〈Ax,x〉\ge 0$ for all $x\in {\mathbb{R}}^n$; A is positive definite ($A>0$) if $〈Ax,x〉>0$ for all $x\ne 0$; $A>B$ means $A-B>0$. The notation $diag\{\cdots \}$ stands for a block-diagonal matrix. The symmetric term in a matrix is denoted by ∗.

Consider the following stochastic neural networks with interval time-varying delay:

$$\begin{array}{r}dx(t)=[-Ax(t)+W_{0}f(x(t))+W_{1}g\left(x(t-h(t))\right)+Bu(t)]dt\\ \phantom{dx(t)=}+\sigma (t,x(t),x(t-h(t)))d\omega (t),t\ge 0,\\ x(t)=\varphi (t),t\in [-h_1,0],\end{array}$$

(2.1)

where $x(t)={[x_1(t),x_2(t),\dots ,x_n(t)]}^T\in {\mathbb{R}}^n$ is the state of the neurons, $u(\cdot )\in L_2([0,t],{\mathbb{R}}^m)$ is the control; n is the number of neurons, and

$$\begin{array}{r}f(x(t))={[f_1(x_1(t)),f_2(x_2(t)),\dots ,f_n(x_n(t))]}^T,\\ g(x(t))={[g_1(x_1(t)),g_2(x_2(t)),\dots ,g_n(x_n(t))]}^T,\end{array}$$

are the activation functions; $A=diag({\overline{a}}_1,{\overline{a}}_2,\dots ,{\overline{a}}_n)$, ${\overline{a}}_i>0$ represents the self-feedback term; $B\in R^{n\times m}$ is control input matrix; $W_0$, $W_1$ denote the connection weights, the delayed connection weights.

$\omega (t)$ is a scalar Wiener process (Brownian motion) on $(\mathrm{\Omega },\mathcal{F},\mathcal{P})$ with

$$E\{\omega (t)\}=0,E\{{\omega }^2(t)\}=1,E\{\omega (i)\omega (j)\}=0(i\ne j),$$

(2.2)

and $\sigma :R^n\times R^n\times R\to R^n$ is the continuous function, and is assumed to satisfy that

$$\begin{array}{r}{\sigma }^T(t,x(t),x(t-h(t)))\sigma (t,x(t),x(t-h(t)))\le {\rho }_1{x}^T(t)x(t)+{\rho }_2{x}^T(t-h(t))x(t-h(t)),\\ x(t),x(t-h(t))\in R^n,\end{array}$$

(2.3)

where ${\rho }_1>0$ and ${\rho }_2>0$ are known constant scalars. For simplicity, we denote $\sigma (t,x(t),x(t-h(t)))$ by σ.

The time-varying delay function $h(t)$ satisfies the condition

$$0\le h_0\le h(t)\le h_1.$$

The initial functions $\varphi (t)\in C^1([-h_1,0],R^n)$, with the norm

$$\parallel \varphi \parallel =\underset{t\in [-h_1,0]}{sup}\sqrt{{\parallel \varphi (t)\parallel }^2+{\parallel \dot{\varphi }(t)\parallel }^2}.$$

In this paper, we consider various activation functions and assume that the activation functions $f(\cdot )$, $g(\cdot )$ are Lipschitzian with the Lipschitz constants $f_i,e_i>0$:

$$\begin{array}{r}|f_i({\xi }_1)-f_i({\xi }_2)|\le f_i|{\xi }_1-{\xi }_2|,i=1,2,\dots ,n,\mathrm{\forall }{\xi }_1,{\xi }_2\in \mathbb{R},\\ |g_i({\xi }_1)-g_i({\xi }_2)|\le e_i|{\xi }_1-{\xi }_2|,i=1,2,\dots ,n,\mathrm{\forall }{\xi }_1,{\xi }_2\in \mathbb{R}.\end{array}$$

(2.4)

The performance index, associated with the system (2.1), is the following function

$$J={\int }_0^{\mathrm{\infty }}{f}^0(t,x(t),x(t-h(t)),u(t))dt,$$

(2.5)

where $f^0(t,x(t),x(t-h(t)),u(t)):R^{+}\times R^n\times R^n\times R^m\to R^{+}$ is a nonlinear cost function satisfying

$$\mathrm{\exists }{Q}_1,Q_2,R:f^0(t,x,y,u)\le 〈Q_{1}x,x〉+〈Q_{2}y,y〉+〈Ru,u〉$$

(2.6)

for all $(t,x,y,u)\in R^{+}\times R^n\times R^n\times R^m$ and $Q_1,Q_2\in R^{n\times n}$, $R\in R^{m\times m}$ are given symmetric positive definite matrices. The objective of this paper is to design a memoryless state feedback controller $u(t)=Kx(t)$ for system (2.1) and the cost function (2.5) such that the resulting closed-loop system

$$\begin{array}{rl}dx(t)=& [-(A-BK)x(t)+W_{0}f(x(t))+W_{1}g\left(x(t-h(t))\right)]dt\\ +\sigma (x(t),x(t-h(t)),t)d\omega (t)\end{array}$$

(2.7)

is mean square exponentially stable, and the closed-loop value of the cost function (2.5) is minimized.

Definition 2.1 Given $\alpha >0$. The zero solution of a closed-loop system (2.7) is α-stabilizable in the mean square if there exists a positive number $N>0$ such that every solution $x(t,\varphi )$ satisfies the following condition:

$$E\left\{\parallel x(t,\varphi )\parallel \right\}\le E\{N{e}^{-\alpha t}\parallel \varphi \parallel \},\mathrm{\forall }t\ge 0.$$

Definition 2.2 Consider the control system (2.1). If there exist a memoryless state feedback control law $u^{\ast }(t)=Kx(t)$ and a positive number $J^{\ast }$ such that the zero solution of the closed-loop system (2.7) is mean square exponentially stable and the cost function (2.5) satisfies $J\le J^{\ast }$, then the value $J^{\ast }$ is a guaranteed constant and $u^{\ast }(t)$ is a guaranteed cost control law of the system and its corresponding cost function.

We introduce the following technical well-known propositions, which will be used in the proof of our results.

Proposition 2.1 (Integral matrix inequality [17])

For any symmetric positive definite matrix $M>0$, scalar $\gamma >0$ and vector function $\omega :[0,\gamma ]\to {\mathbb{R}}^n$ such that the integrations concerned are well defined, the following inequality holds

$${({\int }_0^{\gamma }\omega (s)ds)}^{T}M({\int }_0^{\gamma }\omega (s)ds)\le \gamma ({\int }_0^{\gamma }{\omega }^T(s)M\omega (s)ds).$$

3 Design of guaranteed cost controller

In this section, we give a design of memoryless guaranteed feedback cost control for stochastic neural networks (2.1). Let us set

$$\begin{array}{c}{W}_{11}=-AP-P{A}^T-2\alpha P-B{B}^T+0.25BR{B}^T+\sum _{i=0}^1{G}_i-\sum _{i=0}^1{e}^{-2\alpha h_i}{H}_i\hfill \\ \phantom{W_{11}=}+4PF{D}_0^{-1}FP+P{Q}_{1}P+2{\rho }_{1}I,\hfill \\ W_{12}=P+AP+0.5B{B}^T,\hfill \\ W_{13}=e^{-2\alpha h_0}{H}_0+0.5B{B}^T+AP,\hfill \\ W_{14}=2e^{-2\alpha h_1}{H}_1+0.5B{B}^T+AP,\hfill \\ W_{15}=P0.5B{B}^T+AP,\hfill \\ W_{22}=\sum _{i=0}^1{W}_i{D}_i{W}_i^T+\sum _{i=0}^1{h}_i^2{H}_i+(h_1-h_0)U-2P-B{B}^T,\hfill \\ W_{23}=P,W_{24}=P,W_{25}=P,\hfill \\ W_{33}=-e^{-2\alpha h_0}{G}_0-e^{-2\alpha h_0}{H}_0-e^{-2\alpha h_1}U+\sum _{i=0}^1{W}_i{D}_i{W}_i^T,\hfill \\ W_{34}=0,W_{35}=e^{-2\alpha h_1}U,\hfill \\ W_{44}=\sum _{i=0}^1{W}_i{D}_i{W}_i^T-e^{-2\alpha h_1}U-e^{-2\alpha h_1}{G}_1-e^{-2\alpha h_1}{H}_1,\hfill \\ W_{45}=e^{-2\alpha h_1}U,\hfill \\ W_{55}=-e^{-2\alpha h_1}U+\sum _{i=0}^1{W}_i{D}_i{W}_i^T-e^{-2\alpha h_2}U+4PE{D}_1^{-1}EP+P{Q}_{2}P+2{\rho }_{2}I,\hfill \\ E=diag\{e_i,i=1,\dots ,n\},F=diag\{f_i,i=1,\dots ,n\},\hfill \\ {\lambda }_1={\lambda }_{min}\left(P^{-1}\right),\hfill \\ {\lambda }_2={\lambda }_{max}\left(P^{-1}\right)+h_0{\lambda }_{max}\left[P^{-1}\left(\sum _{i=0}^1{G}_i\right)P^{-1}\right]\hfill \\ \phantom{{\lambda }_2=}+h_1^2{\lambda }_{max}\left[P^{-1}\left(\sum _{i=0}^1{H}_i\right)P^{-1}\right]+(h_1-h_0){\lambda }_{max}\left(P^{-1}U{P}^{-1}\right).\hfill \end{array}$$

Theorem 3.1 Consider the control system (2.1) and the cost function (2.5). Given $\alpha >0$. If there exist symmetric positive definite matrices P, U, $G_0$, $G_1$, $H_0$, $H_1$, and diagonal positive definite matrices $D_i$, $i=0,1$, satisfying the following LMIs

$$\left[\begin{array}{ccccc}{W}_{11}& W_{12}& W_{13}& W_{14}& W_{15}\\ \ast & W_{22}& W_{23}& W_{24}& W_{25}\\ \ast & \ast & W_{33}& W_{34}& W_{35}\\ \ast & \ast & \ast & W_{44}& W_{45}\\ \ast & \ast & \ast & \ast & W_{55}\end{array}\right]<0,$$

(3.1)

then

$$u(t)=-\frac{1}{2}{B}^T{P}^{-1}x(t),t\ge 0$$

(3.2)

is a guaranteed cost control, and the guaranteed cost value is given by

$$J^{\ast }=E\left\{{\lambda }_2{\parallel \varphi \parallel }^2\right\}.$$

Moreover, the solution $x(t,\varphi )$ of the system satisfies

$$E\left\{\parallel x(t,\varphi )\parallel \right\}\le E\{\sqrt{\frac{{\lambda }_2}{{\lambda }_1}}{e}^{-\alpha t}\parallel \varphi \parallel \},\mathrm{\forall }t\ge 0.$$

Proof Let $Y=P^{-1}$, $y(t)=Yx(t)$. Using the feedback control (2.7), we consider the following Lyapunov-Krasovskii functional taking the mathematical expectation

$$\begin{array}{c}E\{V(t,x_t)\}=E\{\sum _{i=1}^6{V}_i(t,x_t)\},\hfill \\ E\{V_1\}=E\{x^T(t)Yx(t)\},\hfill \\ E\{V_2\}=E\{{\int }_{t-h_0}^t{e}^{2\alpha (s-t)}{x}^T(s)Y{G}_{0}Yx(s)ds\},\hfill \\ E\{V_3\}=E\{{\int }_{t-h_1}^t{e}^{2\alpha (s-t)}{x}^T(s)Y{G}_{1}Yx(s)ds\},\hfill \\ E\{V_4\}=E\{h_0{\int }_{-h_0}^0{\int }_{t+s}^t{e}^{2\alpha (\tau -t)}{\dot{x}}^T(\tau )Y{H}_{0}Y\dot{x}(\tau )d\tau ds\},\hfill \\ E\{V_5\}=E\{h_1{\int }_{-h_1}^0{\int }_{t+s}^t{e}^{2\alpha (\tau -t)}{\dot{x}}^T(\tau )Y{H}_{1}Y\dot{x}(\tau )d\tau ds\},\hfill \\ E\{V_6\}=E\{(h_1-h_0){\int }_{t-h_1}^{t-h_0}{\int }_{t+s}^t{e}^{2\alpha (\tau -t)}{\dot{x}}^T(\tau )YUY\dot{x}(\tau )d\tau ds\}.\hfill \end{array}$$

It easy to check that

$$E\left\{{\lambda }_1{\parallel x(t)\parallel }^2\right\}\le E\{V(t,x_t)\}\le E\left\{{\lambda }_2{\parallel x_t\parallel }^2\right\},\mathrm{\forall }t\ge 0.$$

(3.3)

Taking the derivative of $V_i$, $i=1,2,\dots ,6$, and taking the mathematical expectation, we have

$$\begin{array}{c}E\{\dot{V_1}\}=E\{2x^T(t)Y\dot{x}(t)\}\hfill \\ \phantom{E\{\dot{V_1}\}}=E\{y^T(t)[-P{A}^T-AP]y(t)-y^T(t)B{B}^{T}y(t)\}\hfill \\ \phantom{E\{\dot{V_1}\}=}+E\{2y^T(t)W_{0}f(\cdot )+2y^T(t)W_{1}g(\cdot )+2y^T(t)\sigma \omega (t)\};\hfill \\ E\{\dot{V_2}\}=E\left\{E\{y^T(t)G_{0}y(t)-e^{-2\alpha h_0}{y}^T(t-h_0)G_{0}y(t-h_0)-2\alpha V_2\}\right\};\hfill \\ E\{\dot{V_3}\}=E\{y^T(t)G_{1}y(t)-e^{-2\alpha h_1}{y}^T(t-h_1)G_{1}y(t-h_1)-2\alpha V_3\};\hfill \\ E\{\dot{V_4}\}=E\{h_0^2{\dot{y}}^T(t)H_0\dot{y}(t)-h_1{e}^{-2\alpha h_0}{\int }_{t-h_0}^t{\dot{x}}^T(s)H_0\dot{x}(s)ds-2\alpha V_4\};\hfill \\ E\{\dot{V_5}\}=E\{h_1^2{\dot{y}}^T(t)H_1\dot{y}(t)-h_1{e}^{-2\alpha h_1}{\int }_{t-h_1}^t{\dot{y}}^T(s)H_1\dot{y}(s)ds-2\alpha V_4\};\hfill \\ E\{\dot{V_6}\}=E\{{(h_1-h_0)}^2{\dot{y}}^T(t)U\dot{y}(t)-(h_1-h_0)e^{-2\alpha h_1}{\int }_{t-h_1}^{t-h_0}{\dot{y}}^T(s)U\dot{y}(s)ds-2\alpha V_6\}.\hfill \end{array}$$

Applying Proposition 2.1 and ${\int }_s^t\dot{y}(\tau )d\tau =y(t)-y(s)$, we have for $i,j=0,1$,

$$\begin{array}{r}-E\{h_i{\int }_{t-h_i}^t{\dot{y}}^T(s)H_j\dot{y}(s)ds\}\\ \le -E\left\{{[{\int }_{t-h_i}^t\dot{y}(s)ds]}^T{H}_j[{\int }_{t-h_i}^t\dot{y}(s)ds]\right\}\\ \le -E\left\{{[y(t)-y(t-h(t))]}^T{H}_j[y(t)-y(t-h(t))]\right\}\\ =-E\{y^T(t)H_{j}y(t)+2x^T(t)H_{j}y(t-h(t))\}\\ -E\{y^T(t-h_i)H_{j}y(t-h_i)\}.\end{array}$$

(3.4)

Note that

$$E\{{\int }_{t-h_1}^{t-h_0}{\dot{y}}^T(s)U\dot{y}(s)ds\}=E\{{\int }_{t-h_1}^{t-h(t)}{\dot{y}}^T(s)U\dot{y}(s)ds\}+E\{{\int }_{t-h(t)}^{t-h_0}{\dot{y}}^T(s)U\dot{y}(s)ds\}.$$

Applying Proposition 2.1 gives

$$\begin{array}{c}E\{[h_1-h(t)]{\int }_{t-h_1}^{t-h(t)}{\dot{y}}^T(s)U\dot{y}(s)ds\}\hfill \\ \ge E\left\{{[{\int }_{t-h_1}^{t-h(t)}\dot{y}(s)ds]}^{T}U[{\int }_{t-h_1}^{t-h(t)}\dot{y}(s)ds]\right\}\hfill \\ \ge E\left\{{[y(t-h(t))-y(t-h_1)]}^{T}U[y(t-h(t))-y(t-h_1)]\right\}.\hfill \end{array}$$

Since $h_1-h(t)\le h_1-h_0$, we have

$$\begin{array}{c}E\{[h_1-h_0]{\int }_{t-h_1}^{t-h(t)}{\dot{y}}^T(s)U\dot{y}(s)ds\}\hfill \\ \ge E\left\{{[y(t-h(t))-y(t-h_1)]}^{T}U[y(t-h(t))-y(t-h_1)]\right\},\hfill \end{array}$$

then

$$\begin{array}{c}-E\{[h_1-h_0]{\int }_{t-h_1}^{t-h(t)}{\dot{y}}^T(s)U\dot{y}(s)ds\}\hfill \\ \le -E\left\{{[y(t-h(t))-y(t-h_1)]}^{T}U[y(t-h(t))-y(t-h_1)]\right\}.\hfill \end{array}$$

Similarly, we have

$$\begin{array}{c}-E\{(h_1-h_0){\int }_{t-h(t)}^{t-h_0}{\dot{y}}^T(s)U\dot{y}(s)ds\}\hfill \\ \le -E\left\{{[y(t-h_0)-y(t-h(t))]}^{T}U[y(t-h_0)-y(t-h(t))]\right\}.\hfill \end{array}$$

Then, we have

$$\begin{array}{r}E\{\dot{V}(\cdot )+2\alpha V(\cdot )\}\\ \le E\{y^T(t)[-P{A}^T-AP]y(t)-y^T(t)B{B}^{T}y(t)+2y^T(t)W_{0}f(\cdot )\}\\ +E\{2y^T(t)W_{1}g(\cdot )+2y^T(t)\sigma \omega (t)+y^T(t)\left(\sum _{i=0}^1{G}_i\right)y(t)+2\alpha 〈Py(t),y(t)〉\}\\ +E\{{\dot{y}}^T(t)\left(\sum _{i=0}^1{h}_i^2{H}_i\right)\dot{y}(t)+(h_1-h_0){\dot{y}}^T(t)U\dot{y}(t)\}\\ -E\{\sum _{i=0}^1{e}^{-2\alpha h_i}{y}^T(t-h_i)G_{i}y(t-h_i)\}\\ -E\left\{e^{-2\alpha h_0}{[y(t)-y(t-h_0)]}^T{H}_0[y(t)-y(t-h_0)]\right\}\\ -E\left\{e^{-2\alpha h_1}{[y(t)-y(t-h_1)]}^T{H}_1[y(t)-y(t-h_1)]\right\}\\ -E\left\{e^{-2\alpha h_1}{[y(t-h(t))-y(t-h_1)]}^{T}U[y(t-h(t))-y(t-h_1)]\right\}\\ -E\left\{e^{-2\alpha h_1}{[y(t-h_0)-y(t-h(t))]}^{T}U[y(t-h_0)-y(t-h(t))]\right\}.\end{array}$$

(3.5)

Using equation (2.7)

$$P\dot{y}(t)+APy(t)-W_{0}f(\cdot )-W_{1}g(\cdot )+0.5B{B}^{T}y(t)-\sigma \omega (t)=0,$$

multiplying both sides with ${[2y(t),-2\dot{y}(t),2y(t-h_0),2y(t-h_1),2y(t-h(t)),2\sigma \omega (t)]}^T$, and taking the mathematical expectation, we have

$$\begin{array}{r}E\{2y^T(t)P\dot{y}(t)+2y^T(t)APy(t)-2y^T(t)W_{0}f(\cdot )-2y^T(t)W_{1}g(\cdot )\}\\ +E\{y^T(t)B{B}^{T}y(t)-2y^T(t)\sigma \omega (t)\}=0,\\ -E\{2{\dot{y}}^T(t)P\dot{y}(t)-2{\dot{y}}^T(t)APy(t)+2{\dot{y}}^T(t)W_{0}f(\cdot )\}\\ +E\{2{\dot{y}}^T(t)W_{1}g(\cdot )-{\dot{y}}^T(t)B{B}^{T}y(t)+2{\dot{y}}^T(t)\sigma \omega (t)\}=0,\\ E\{2y^T(t-h_0)P\dot{y}(t)+2y^T(t-h_0)APy(t)-2y^T(t-h_0)W_{0}f(\cdot )\}\\ -E\{2y^T(t-h_0)W_{1}g(\cdot )+y^T(t-h_0)B{B}^{T}y(t)-2y^T(t-h_0)\sigma \omega (t)\}=0,\\ E\{2y^T(t-h_1)P\dot{y}(t)+2y^T(t-h_1)APy(t)-2y^T(t-h_1)W_{0}f(\cdot )\}\\ -E\{2y^T(t-h_1)W_{1}g(\cdot )+y^T(t-h_1)B{B}^{T}y(t)-2y^T(t-h_1)\sigma \omega (t)\}=0,\\ E\{2y^T(t-h(t))P\dot{y}(t)+2y^T(t-h(t))APy(t)-2y^T(t-h(t))W_{0}f(\cdot )\}\\ -E\{2y^T(t-h(t))W_{1}g(\cdot )+y^T(t-h(t))B{B}^{T}y(t)-2y^T(t-h(t))\sigma \omega (t)\}=0,\\ E\{2{\omega }^T(t){\sigma }^{T}P\dot{y}(t)+2{\omega }^T(t){\sigma }^{T}APy(t)-2{\omega }^T(t){\sigma }^T{W}_{0}f(\cdot )\}\\ -E\{2{\omega }^T(t){\sigma }^T{W}_{1}g(\cdot )+{\omega }^T(t){\sigma }^{T}B{B}^{T}y(t)-2{\omega }^T(t){\sigma }^T\sigma \omega (t)\}=0.\end{array}$$

(3.6)

Adding all the zero items of (3.6) and $f^0(t,x(t),x(t-h(t)),u(t))-f^0(t,x(t),x(t-h(t)),u(t))=0$, respectively into (3.5), applying assumptions (2.2), (2.3), using the condition (2.6) for the following estimations, and taking the mathematical expectation

$$\begin{array}{c}E\left\{f^0(t,x(t),x(t-h(t)),u(t))\right\}\le E\{〈Q_{1}x(t),x(t)〉+〈Q_{2}x(t-h(t)),x(t-h(t))〉\}\hfill \\ \phantom{E\left\{f^0(t,x(t),x(t-h(t)),u(t))\right\}\le }+E\left\{〈Ru(t),u(t)〉\right\}\hfill \\ \phantom{E\left\{f^0(t,x(t),x(t-h(t)),u(t))\right\}}=E\{〈P{Q}_{1}Py(t),y(t)〉+〈P{Q}_{2}Py(t-h(t)),y(t-h(t))〉\}\hfill \\ \phantom{E\left\{f^0(t,x(t),x(t-h(t)),u(t))\right\}\le }+E\left\{0.25〈BR{B}^{T}y(t),y(t)〉\right\},\hfill \\ E\left\{2〈W_{0}f(x),y〉\right\}\le E\{〈W_0{D}_0{W}_0^{T}y,y〉+〈D_0^{-1}f(x),f(x)〉\},\hfill \\ E\left\{2〈W_{1}g(z),y〉\right\}\le E\{〈W_1{D}_1{W}_1^{T}y,y〉+〈D_1^{-1}g(z),g(z)〉\},\hfill \\ E\left\{2〈D_0^{-1}f(x),f(x)〉\right\}\le E\left\{〈F{D}_0^{-1}Fx,x〉\right\},\hfill \\ E\left\{2〈D_1^{-1}g(z),g(z)〉\right\}\le E\left\{〈E{D}_1^{-1}Ez,z〉\right\},\hfill \end{array}$$

we obtain

$$E\{\dot{V}(\cdot )+2\alpha V(\cdot )\}\le E\{{\zeta }^T(t)\mathcal{E}\zeta (t)-f^0(t,x(t),x(t-h(t)),u(t))\},$$

(3.7)

where $\zeta (t)=[y(t),\dot{y}(t),y(t-h_0),y(t-h_1),y(t-h(t))]$, and

$$\mathcal{E}=\left[\begin{array}{ccccc}{W}_{11}& W_{12}& W_{13}& W_{14}& W_{15}\\ \ast & W_{22}& W_{23}& W_{24}& W_{25}\\ \ast & \ast & W_{33}& W_{34}& W_{35}\\ \ast & \ast & \ast & W_{44}& W_{45}\\ \ast & \ast & \ast & \ast & W_{55}\end{array}\right].$$

Therefore, by condition (3.1), we obtain from (3.7) that

$$E\{\dot{V}(t,x_t)\}\le -E\{2\alpha V(t,x_t)\},\mathrm{\forall }t\ge 0.$$

(3.8)

Integrating both sides of (3.8) from 0 to t, we obtain

$$E\{V(t,x_t)\}\le E\{V(\varphi )e^{-2\alpha t}\},\mathrm{\forall }t\ge 0.$$

Furthermore, taking condition (3.3) into account, we have

$$E\left\{{\lambda }_1{\parallel x(t,\varphi )\parallel }^2\right\}\le E\{V(x_t)\}\le E\{V(\varphi )e^{-2\alpha t}\}\le E\left\{{\lambda }_2{e}^{-2\alpha t}{\parallel \varphi \parallel }^2\right\},$$

then

$$E\left\{\parallel x(t,\varphi )\parallel \right\}\le E\{\sqrt{\frac{{\lambda }_2}{{\lambda }_1}}{e}^{-\alpha t}\parallel \varphi \parallel \},t\ge 0,$$

which concludes the mean square exponential stability of the closed-loop system (2.7). To prove the optimal level of the cost function (2.5), we derive from (3.7) and (3.1) that

$$E\{\dot{V}(t,z_t)\}\le -E\left\{f^0(t,x(t),x(t-h(t)),u(t))\right\},t\ge 0.$$

(3.9)

Integration of both sides of (3.9) from 0 to t leads to

$$E\left\{{\int }_0^t{f}^0(t,x(t),x(t-h(t)),u(t))dt\right\}\le E\{V(0,z_0)-V(t,z_t)\}\le E\{V(0,z_0)\},$$

due to $E\{V(t,z_t)\}\ge 0$. Hence, letting $t\to +\mathrm{\infty }$, we have

$$J=E\left\{{\int }_0^{\mathrm{\infty }}{f}^0(t,x(t),x(t-h(t)),u(t))dt\right\}\le E\{V(0,z_0)\}\le E\left\{{\lambda }_2{\parallel \varphi \parallel }^2\right\}=J^{\ast }.$$

This completes the proof of the theorem. □

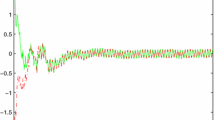
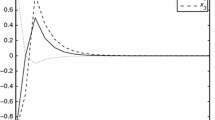
Example 3.1 Consider the stochastic neural networks with interval time-varying delays (2.1), where

$$\begin{array}{c}A=\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right],W_0=\left[\begin{array}{cc}-0.3& 0.1\\ 0.1& -0.3\end{array}\right],W_1=\left[\begin{array}{cc}-0.4& 0.3\\ 0.3& -0.9\end{array}\right],\hfill \\ B=\left[\begin{array}{c}0.5\\ 0.4\end{array}\right],E=\left[\begin{array}{cc}0.7& 0\\ 0& 0.9\end{array}\right],F=\left[\begin{array}{cc}0.7& 0\\ 0& 0.8\end{array}\right],\hfill \\ Q_1=\left[\begin{array}{cc}0.7& 0.2\\ 0.2& 0.6\end{array}\right],Q_2=\left[\begin{array}{cc}0.2& 0.3\\ 0.3& 0.3\end{array}\right],R=\left[\begin{array}{cc}0.9& 0.5\\ 0.5& 0.8\end{array}\right],\hfill \\ \{\begin{array}{cc}h(t)=0.1+2.0297{sin}^{2}t\hfill & \text{if }t\in \mathcal{I}={\bigcup }_{k\ge 0}[2k\pi ,(2k+1)\pi ],\hfill \\ h(t)=0\hfill & \text{if }t\in R^{+}\setminus \mathcal{I}.\hfill \end{array}\hfill \end{array}$$

Note that $h(t)$ is nondifferentiable, therefore, the stability criteria proposed in [5–7, 12, 15] are not applicable to this system. Given $\alpha =1.1$, ${\rho }_1=0.5$, ${\rho }_1=0.8$, $h_0=0.1$, $h_1=2.1297$, by using the Matlab LMI toolbox, we can solve for P, U, $G_0$, $G_1$, $H_0$, $H_1$, $D_0$, and $D_1$, which satisfy the condition (3.1) in Theorem 3.1. A set of solutions are

$$\begin{array}{c}P=\left[\begin{array}{cc}3.1297& 0.4831\\ 0.4831& 1.1970\end{array}\right],U=\left[\begin{array}{cc}2.0912& 0.1291\\ 0.1291& 3.0017\end{array}\right],\hfill \\ G_0=\left[\begin{array}{cc}0.1473& 0.0113\\ 0.0113& 0.8931\end{array}\right],G_1=\left[\begin{array}{cc}0.6179& 0.1197\\ 0.1197& 1.0273\end{array}\right],\hfill \\ H_0=\left[\begin{array}{cc}1.0387& 0.3970\\ 0.3970& 2.2207\end{array}\right],H_1=\left[\begin{array}{cc}0.9712& 0.0012\\ 0.0012& 0.7219\end{array}\right],\hfill \\ D_0=\left[\begin{array}{cc}0.2189& 0\\ 0& 0.2189\end{array}\right],D_1=\left[\begin{array}{cc}0.1249& 0\\ 0& 0.1249\end{array}\right].\hfill \end{array}$$

Then

$$u(t)=-1.7196x_1(t)-1.2551x_2(t),t\ge 0$$

is a guaranteed cost control law and the cost given by

$$J^{\ast }=E\left\{11.3271{\parallel \varphi \parallel }^2\right\}.$$

Moreover, the solution $x(t,\varphi )$ of the system satisfies

$$E\left\{\parallel x(t,\varphi )\parallel \right\}\le E\{0.7315e^{-1.1t}\parallel \varphi \parallel \},\mathrm{\forall }t\ge 0.$$

4 Conclusion

In this paper, the problem of guaranteed cost control for stochastic neural networks with the interval nondifferentiable time-varying delay has been studied. A nonlinear quadratic cost function is considered as a performance measure for the closed-loop system. The stabilizing controllers to be designed must satisfy some mean square exponential stability constraints on the closed-loop poles. By constructing a set of time-varying Lyapunov-Krasovskii functional, a memoryless state feedback guaranteed cost controller design has been presented and sufficient conditions for the existence of the guaranteed cost state-feedback for the system have been derived in terms of LMIs.