Exact solutions for fractional partial differential equations by a new fractional sub-equation method

Abstract

In this paper, we propose a new fractional sub-equation method for finding exact solutions of fractional partial differential equations (FPDEs) in the sense of modified Riemann-Liouville derivative, which is the fractional version of the known (G′/G) method. To illustrate the validity of this method, we apply it to the space-time fractional Fokas equation, the space-time fractional $(2+1)$-dimensional dispersive long wave equations and the space-time fractional fifth-order Sawada-Kotera equation. As a result, some new exact solutions for them are successfully established.

MSC:35Q51, 35Q53.

1 Introduction

Fractional differential equations are generalizations of classical differential equations of integer order. In recent decades, fractional differential equations have been the focus of many studies due to their frequent appearance in various applications in physics, biology, engineering, signal processing, systems identification, control theory, finance and fractional dynamics. Many articles have investigated some aspects of fractional differential equations such as the existence and uniqueness of solutions to Cauchy-type problems, the methods for explicit and numerical solutions, and the stability of solutions [1–8]. In [9], Jafari et al. applied the fractional sub-equation method to construct exact solutions of the fractional generalized reaction Duffing model and nonlinear fractional Sharma-Tasso-Olver equation. In [10], Baleanu et al. studied the existence and uniqueness of the solution for a nonlinear fractional differential equation boundary-value problem by using fixed-point methods. In [11], Nyamoradi et al. investigated the existence of solutions for the multipoint boundary value problem of a fractional order differential inclusion.

Among the investigations for fractional differential equations, research into seeking exact solutions and numerical solutions of fractional differential equations is an important topic. Many powerful and efficient methods have been proposed to obtain numerical solutions and exact solutions of fractional differential equations so far. For example, these methods include the Adomian decomposition method [12–14], the variational iterative method [15–22], the homotopy perturbation method [23–26], the differential transformation method [27], the finite difference method [28], the finite element method [29], the fractional Riccati sub-equation method [30–32] and so on. In these investigations, we note that many authors have sought exact and numerical solutions for fractional partial differential equations (FPDEs) in the sense of modified Riemann-Liouville derivative (for example, see [16, 17, 30–34]). Based on these methods, a variety of fractional differential equations have been investigated.

In this paper, we propose a new fractional sub-equation method to establish exact solutions for fractional partial differential equations (FPDEs) in the sense of modified Riemann-Liouville derivative defined by Jumarie [35], which is a fractional version of the known (G′/G) method [36–39]. This method is based on the following fractional ODE:

$$D_{\xi }^{2\alpha }G(\xi )+\lambda D_{\xi }^{\alpha }G(\xi )+\mu G(\xi )=0,$$

(1)

where $D_{\xi }^{\alpha }G(\xi )$ denotes the modified Riemann-Liouville derivative of order α for $G(\xi )$ with respect to ξ.

The rest of this paper is organized as follows. In Section 2, we present some definitions and properties of Jumarie’s modified Riemann-Liouville derivative and the expression for $\frac{D_{\xi }^{\alpha }G(\xi )}{G(\xi )}$ related to Eq. (1). In Section 3, we give the description of the fractional sub-equation method for solving FPDEs. Then in Section 4 we apply this method to establish exact solutions for the space-time fractional Fokas equation, the space-time fractional $(2+1)$-dimensional dispersive long wave equations and the space-time fractional fifth-order Sawada-Kotera equation. Some conclusions are presented at the end of the paper.

2 Jumarie’s modified Riemann-Liouville derivative and general expression for $\frac{D_{\xi }^{\alpha }G(\xi )}{G(\xi )}$

Jumarie’s modified Riemann-Liouville derivative of order α is defined by the following expression [35]:

$$D_t^{\alpha }f(t)=\{\begin{array}{ll}\frac{1}{\mathrm{\Gamma }(1-\alpha )}\frac{d}{dt}{\int }_0^t{(t-\xi )}^{-\alpha }(f(\xi )-f(0))d\xi ,& 0<\alpha <1,\\ {(f^{(n)}(t))}^{(\alpha -n)},& n\le \alpha <n+1,n\ge 1.\end{array}$$

We list some important properties for the modified Riemann-Liouville derivative as follows (see [[35], Eqs. (3.10)-(3.13)]):

$$D_t^{\alpha }{t}^r=\frac{\mathrm{\Gamma }(1+r)}{\mathrm{\Gamma }(1+r-\alpha )}{t}^{r-\alpha },$$

(2)

$$D_t^{\alpha }(f(t)g(t))=g(t)D_t^{\alpha }f(t)+f(t)D_t^{\alpha }g(t),$$

(3)

$$D_t^{\alpha }f[g(t)]=f_g^{\prime }[g(t)]D_t^{\alpha }g(t)=D_g^{\alpha }f[g(t)]{(g^{\prime }(t))}^{\alpha }.$$

(4)

In order to obtain the general solutions for Eq. (1), we suppose $G(\xi )=H(\eta )$ and a nonlinear fractional complex transformation $\eta =\frac{{\xi }^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}$. Then by Eq. (2) and the first equality in Eq. (4), Eq. (1) can be turned into the following second ordinary differential equation

$$H^{″}(\eta )+\lambda H^{\prime }(\eta )+\mu H(\eta )=0.$$

(5)

By the general solutions of Eq. (5), we have

$$\frac{H^{\prime }(\eta )}{H(\eta )}=\{\begin{array}{ll}-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2}\eta +C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2}\eta }{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2}\eta +C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2}\eta }),& {\lambda }^2-4\mu >0,\\ -\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2}\eta +C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2}\eta }{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2}\eta +C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2}\eta }),& {\lambda }^2-4\mu <0,\\ -\frac{\lambda }{2}+\frac{C_2}{C_1+C_2\eta },& {\lambda }^2-4\mu =0,\end{array}$$

(6)

where $C_1$, $C_2$ are arbitrary constants.

Since $D_{\xi }^{\alpha }G(\xi )=D_{\xi }^{\alpha }H(\eta )=H^{\prime }(\eta )D_{\xi }^{\alpha }\eta =H^{\prime }(\eta )$, we obtain

$$\frac{D_{\xi }^{\alpha }G(\xi )}{G(\xi )}=\{\begin{array}{ll}-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}),& {\lambda }^2-4\mu >0,\\ -\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}),& {\lambda }^2-4\mu <0,\\ -\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }},& {\lambda }^2-4\mu =0.\end{array}$$

(7)

3 Description of the fractional sub-equation method

In this section we describe the main steps of the fractional sub-equation method for finding exact solutions of FPDEs.

Suppose that a fractional partial differential equation, say in the independent variables $t,x_1,x_2,\dots ,x_n$, is given by

$$\begin{array}{r}P(u_1,\dots u_k,D_t^{\alpha }{u}_1,\dots ,D_t^{\alpha }{u}_k,D_{x_1}^{\alpha }{u}_1,\dots ,D_{x_1}^{\alpha }{u}_k,\dots ,\\ D_{x_n}^{\alpha }{u}_1,\dots ,D_{x_n}^{\alpha }{u}_k,D_t^{2\alpha }{u}_1,\dots ,D_t^{2\alpha }{u}_k,D_{x_1}^{2\alpha }{u}_1,\dots )=0,\end{array}$$

(8)

where $u_i=u_i(t,x_1,x_2,\dots ,x_n)$, $i=1,\dots ,k$, are unknown functions, P is a polynomial in $u_i$ and their various partial derivatives include fractional derivatives.

Step 1. Suppose that

$$u_i(t,x_1,x_2,\dots ,x_n)=U_i(\xi ),\xi =ct+k_1{x}_1+k_2{x}_2+\cdots +k_n{x}_n+{\xi }_0.$$

(9)

Then by the second equality in Eq. (4), Eq. (8) can be turned into the following fractional ordinary differential equation with respect to the variable ξ:

$$\begin{array}{r}\tilde{P}(U_1,\dots ,U_k,c^{\alpha }{D}_{\xi }^{\alpha }{U}_1,\dots ,c^{\alpha }{D}_{\xi }^{\alpha }{U}_k,k_1^{\alpha }{D}_{\xi }^{\alpha }{U}_1,\dots ,k_1^{\alpha }{D}_{\xi }^{\alpha }{U}_k,\dots ,k_n^{\alpha }{D}_{\xi }^{\alpha }{U}_1,\dots ,\\ k_n^{\alpha }{D}_{\xi }^{\alpha }{U}_k,c^{2\alpha }{D}_{\xi }^{2\alpha }{U}_1,\dots ,c^{2\alpha }{D}_{\xi }^{2\alpha }{U}_k,k_1^{2\alpha }{D}_{\xi }^{2\alpha }{U}_1,\dots )=0.\end{array}$$

(10)

Step 2. Suppose that the solution of (10) can be expressed by a polynomial in $(\frac{D_{\xi }^{\alpha }G}{G})$ as follows:

$$U_j(\xi )=\sum _{i=0}^{m_j}{a}_{j,i}{\left(\frac{D_{\xi }^{\alpha }G}{G}\right)}^i,j=1,2,\dots ,k,$$

(11)

where $G=G(\xi )$ satisfies Eq. (1), and $a_{j,i}$, $i=0,1,\dots ,m$, $j=1,2,\dots ,k$, are constants to be determined later with $a_{j,m}\ne 0$. The positive integer m can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in (10).

Step 3. Substituting (11) into (10) and using (1), collecting all terms with the same order of $(\frac{D_{\xi }^{\alpha }G}{G})$ together, the left-hand side of (10) is converted into another polynomial in $(\frac{D_{\xi }^{\alpha }G}{G})$. Equating each coefficient of this polynomial to zero yields a set of algebraic equations for $a_{j,i}$, $i=0,1,\dots ,m$, $j=1,2,\dots ,k$.

Step 4. Solving the equation system in Step 3 and using (7), we can construct a variety of exact solutions for Eq. (8).

Remark 1 If we set $\alpha =1$ in Eq. (1), then it becomes $G^{″}(\xi )+\lambda G^{\prime }(\xi )+\mu G(\xi )=0$, which is the foundation of the known (G′/G) method for solving partial differential equations (PDEs). So, in this way, the described fractional sub-equation method above is the extension of the (G′/G) method to fractional case.

Remark 2 The idea of the transformation from n independent variables to one independent variable denoted in Eq. (9) is similar to that in [[30], Eq. (12)], [[31], Eq. (8)], and [[33], Eq. (6)]. After applying this transformation to Eq. (8), by use of the second equality of Eq. (4), the original fractional partial differential equation can be transformed into another fractional ordinary differential equation in one independent variable.

4 Applications of the method

4.1 Space-time fractional Fokas equation

We consider the space-time fractional Fokas equation

$$\begin{array}{r}4\frac{{\partial }^{2\alpha }q}{\partial t^{\alpha }\partial x_1^{\alpha }}-\frac{{\partial }^{4\alpha }q}{\partial x_1^{3\alpha }\partial x_2^{\alpha }}+\frac{{\partial }^{4\alpha }q}{\partial x_2^{3\alpha }\partial x_1^{\alpha }}+12\frac{{\partial }^{\alpha }q}{\partial x_1^{\alpha }}\frac{{\partial }^{\alpha }q}{\partial x_2^{\alpha }}+12q\frac{{\partial }^{2\alpha }q}{\partial x_1^{\alpha }\partial x_2^{\alpha }}-6\frac{{\partial }^{2\alpha }q}{\partial y_1^{\alpha }\partial y_2^{\alpha }}\\ =0,0<\alpha \le 1.\end{array}$$

(12)

In [30], the authors solved Eq. (12) by a fractional Riccati sub-equation method and obtained some exact solutions for it. Now we will apply the method described in Section 3 to Eq. (12).

Suppose that $q(x,y,t)=U(\xi )$, where $\xi =ct+k_1{x}_1+k_2{x}_2+l_1{y}_1+l_2{y}_2+{\xi }_0$, $k_1$, $k_2$, $l_1$, $l_2$, c, ${\xi }_0$ are all constants with $k_1,k_2,l_1,l_2,c\ne 0$. Then by use of the second equality in Eq. (4), Eq. (12) can be turned into

$$\begin{array}{r}4c^{\alpha }{k}_1^{\alpha }{D}_{\xi }^{2\alpha }U-k_1^{3\alpha }{k}_2^{\alpha }{D}_{\xi }^{4\alpha }U+k_2^{3\alpha }{k}_1^{\alpha }{D}_{\xi }^{4\alpha }U\\ +12k_1^{\alpha }{k}_2^{\alpha }{\left(D_{\xi }^{\alpha }U\right)}^2+12k_1^{\alpha }{k}_2^{\alpha }U{D}_{\xi }^{2\alpha }U-6l_1^{\alpha }{l}_2^{\alpha }{D}_{\xi }^{2\alpha }U=0.\end{array}$$

(13)

Suppose that the solution of Eq. (13) can be expressed by

$$U(\xi )=\sum _{i=0}^m{a}_i{\left(\frac{D_{\xi }^{\alpha }G}{G}\right)}^i,$$

(14)

where $G=G(\xi )$ satisfies Eq. (1). By balancing the order between the highest order derivative term and nonlinear term in Eq. (13), we can obtain $m=2$. So, we have

$$U(\xi )=a_0+a_1\left(\frac{D_{\xi }^{\alpha }G}{G}\right)+a_2{\left(\frac{D_{\xi }^{\alpha }G}{G}\right)}^2.$$

(15)

Substituting (15) into (13) and collecting all the terms with the same power of $(\frac{D_{\xi }^{\alpha }G}{G})$ together, equating each coefficient to zero, yield a set of algebraic equations. Solving these equations yields

$$\begin{array}{c}{a}_0=\frac{k_1^{3\alpha }{k}_2^{\alpha }{\lambda }^2-k_1^{\alpha }{k}_2^{3\alpha }{\lambda }^2+8k_1^{3\alpha }{k}_2^{\alpha }\mu -8k_1^{\alpha }{k}_2^{3\alpha }\mu -4c^{\alpha }{k}_1^{\alpha }+6l_1^{\alpha }{l}_2^{\alpha }}{12k_1^{\alpha }{k}_2^{\alpha }},\hfill \\ a_1=\lambda (k_1^{2\alpha }-k_2^{2\alpha }),\hfill \\ a_2=k_1^{2\alpha }-k_2^{2\alpha }.\hfill \end{array}$$

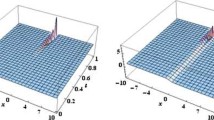
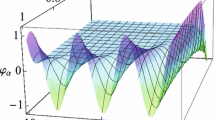
Substituting the result above into Eq. (15) and combining with (7), we can obtain the following exact solutions to Eq. (12).

When ${\lambda }^2-4\mu >0$,

$$\begin{array}{r}{q}_1(t,x_1,x_2,y_1,y_2)\\ =\frac{k_1^{3\alpha }{k}_2^{\alpha }{\lambda }^2-k_1^{\alpha }{k}_2^{3\alpha }{\lambda }^2+8k_1^{3\alpha }{k}_2^{\alpha }\mu -8k_1^{\alpha }{k}_2^{3\alpha }\mu -4c^{\alpha }{k}_1^{\alpha }+6l_1^{\alpha }{l}_2^{\alpha }}{12k_1^{\alpha }{k}_2^{\alpha }}\\ +\lambda (k_1^{2\alpha }-k_2^{2\alpha })[-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]\\ +(k_1^{2\alpha }-k_2^{2\alpha }){[-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]}^2,\end{array}$$

(16)

where $\xi =ct+k_1{x}_1+k_2{x}_2+l_1{y}_1+l_2{y}_2+{\xi }_0$.

When ${\lambda }^2-4\mu <0$,

$$\begin{array}{r}{q}_2(t,x_1,x_2,y_1,y_2)\\ =\frac{k_1^{3\alpha }{k}_2^{\alpha }{\lambda }^2-k_1^{\alpha }{k}_2^{3\alpha }{\lambda }^2+8k_1^{3\alpha }{k}_2^{\alpha }\mu -8k_1^{\alpha }{k}_2^{3\alpha }\mu -4c^{\alpha }{k}_1^{\alpha }+6l_1^{\alpha }{l}_2^{\alpha }}{12k_1^{\alpha }{k}_2^{\alpha }}\\ +\lambda (k_1^{2\alpha }-k_2^{2\alpha })[-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]\\ +(k_1^{2\alpha }-k_2^{2\alpha }){[-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]}^2,\end{array}$$

(17)

where $\xi =ct+k_1{x}_1+k_2{x}_2+l_1{y}_1+l_2{y}_2+{\xi }_0$.

When ${\lambda }^2-4\mu =0$,

$$\begin{array}{r}{q}_3(t,x_1,x_2,y_1,y_2)\\ =\frac{k_1^{3\alpha }{k}_2^{\alpha }{\lambda }^2-k_1^{\alpha }{k}_2^{3\alpha }{\lambda }^2+8k_1^{3\alpha }{k}_2^{\alpha }\mu -8k_1^{\alpha }{k}_2^{3\alpha }\mu -4c^{\alpha }{k}_1^{\alpha }+6l_1^{\alpha }{l}_2^{\alpha }}{12k_1^{\alpha }{k}_2^{\alpha }}\\ +\lambda (k_1^{2\alpha }-k_2^{2\alpha })[-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]\\ +(k_1^{2\alpha }-k_2^{2\alpha }){[-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]}^2,\end{array}$$

(18)

where $\xi =ct+k_1{x}_1+k_2{x}_2+l_1{y}_1+l_2{y}_2+{\xi }_0$.

Remark 3 As one can see, the established solutions for the space-time fractional Fokas equation above are different from the results in [30] and are new exact solutions so far to our best knowledge.

Remark 4 The method used above in solving Eq. (12) can also be used to obtain solutions to initial or boundary value problems. For example, if we add the initial value condition

$$q(0,x_1,x_2,y_1,y_2)={tan}^2\left(\frac{\sqrt{2x_1+x_2+y_1+y_2}}{\mathrm{\Gamma }(1.5)}\right),$$

then, after substituting this initial value condition to the trigonometric solutions obtained in Eq. (17) and fulfilling some basic comparison and computation, one can see that $\alpha =0.5$, $k_1=2$, $k_2=1$, $l_1=l_2=1$, ${\xi }_0=0$, $C_2=0$, $\lambda =0$, $\mu =1$, $c=\frac{41}{8}+3\sqrt{2}$. So, we obtain the solution to the initial value problem as

$$q(t,x_1,x_2,y_1,y_2)={tan}^2\left(\frac{\sqrt{2x_1+x_2+y_1+y_2+(\frac{41}{8}+3\sqrt{2})t}}{\mathrm{\Gamma }(1.5)}\right).$$

4.2 Space-time fractional $(2+1)$-dimensional dispersive long wave equations

We consider the following space-time fractional $(2+1)$-dimensional dispersive long wave equations

$$\{\begin{array}{l}\frac{{\partial }^{2\alpha }u}{\partial y^{\alpha }\partial t^{\alpha }}+\frac{{\partial }^{2\alpha }v}{\partial x^{2\alpha }}+\frac{{\partial }^{\alpha }(u\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }})}{\partial y^{\alpha }}=0,\\ \frac{{\partial }^{\alpha }v}{\partial t^{\alpha }}+\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}+\frac{{\partial }^{\alpha }(uv)}{\partial x^{\alpha }}+\frac{{\partial }^{3\alpha }u}{\partial x^{2\alpha }\partial y^{\alpha }}=0,\end{array}0<\alpha \le 1,$$

(19)

which are the known $(2+1)$-dimensional dispersive long wave equations [40–53]:

$$\{\begin{array}{l}{u}_{yt}+v_{xx}+{(u{u}_x)}_y=0,\\ v_t+u_x+{(uv)}_x+u_{xxy}=0.\end{array}$$

(20)

Some types of exact solutions for Eqs. (20) have been obtained in [40–53] by use of various methods including the Riccati sub-equation method [40, 41, 46], the nonlinear transformation method [42], the Jacobi function method [44, 45, 53], the (G′/G)-expansion method [43], the modified CK’s direct method [47], the EXP-function method [48], the Hopf-Cole transformation method [49], the modified extended Fan’s sub-equation method [50, 51], the generalized algebraic method [52]. But we notice that so far no research has been pursued for Eqs. (19). In the following, we will apply the proposed fractional sub-equation method to Eqs. (19).

To begin with, we suppose $u(x,y,t)=U(\xi )$, $v(x,y,t)=V(\xi )$, where $\xi =k_{1}x+k_{2}y+ct+{\xi }_0$, $k_1$, $k_2$, c, ${\xi }_0$ are all constants with $k_1,k_2,c\ne 0$. Then by use of the second equality in Eq. (4), Eqs. (19) can be turned into

$$\{\begin{array}{l}{c}^{\alpha }{k}_2^{\alpha }{D}_{\xi }^{2\alpha }U+k_1^{2\alpha }{D}_{\xi }^{2\alpha }V+k_1^{\alpha }{k}_2^{\alpha }(U{D}_{\xi }^{2\alpha }U+{(D_{\xi }^{\alpha }U)}^2)=0,\\ c^{\alpha }{D}_{\xi }^{\alpha }V+k_1^{\alpha }{D}_{\xi }^{\alpha }U+k_1^{\alpha }{D}_{\xi }^{\alpha }(UV)+k_1^{2\alpha }{k}_2^{\alpha }{D}_{\xi }^{3\alpha }U=0.\end{array}$$

(21)

Suppose that the solution of Eqs. (21) can be expressed by

$$\{\begin{array}{l}U(\xi )={\sum }_{i=0}^{m_1}{a}_i{(\frac{D_{\xi }^{\alpha }G}{G})}^i,\\ V(\xi )={\sum }_{i=0}^{m_2}{b}_i{(\frac{D_{\xi }^{\alpha }G}{G})}^i.\end{array}$$

(22)

Balancing the order of $D_{\xi }^{2\alpha }V$ and $U{D}_{\xi }^{2\alpha }U$, $D_{\xi }^{\alpha }(UV)$ and $D_{\xi }^{3\alpha }U$ in (21), we can obtain $m_1=1$, $m_2=2$. So, we have

$$\{\begin{array}{l}U(\xi )=a_0+a_1(\frac{D_{\xi }^{\alpha }G}{G}),\\ V(\xi )=b_0+b_1(\frac{D_{\xi }^{\alpha }G}{G})+b_2{(\frac{D_{\xi }^{\alpha }G}{G})}^2.\end{array}$$

(23)

Substituting (23) into (21), using Eq. (1) and collecting all the terms with the same power of $(\frac{D_{\xi }^{\alpha }G}{G})$ together, equating each coefficient to zero, yield a set of algebraic equations. Solving these equations yields

$$\begin{array}{c}{a}_0=\frac{\pm k_1^{2\alpha }\lambda -c^{\alpha }}{k_1^{\alpha }},a_1=\pm 2k_1^{\alpha },b_0=-2k_1^{\alpha }{k}_2^{\alpha }\mu -1,\hfill \\ b_1=-2k_1^{\alpha }{k}_2^{\alpha }\lambda ,b_2=-2k_1^{\alpha }{k}_2^{\alpha }.\hfill \end{array}$$

Substituting the result above into Eq. (23) and combining with (7), we can obtain the following exact solutions to Eqs. (19).

When ${\lambda }^2-4\mu >0$,

$$\{\begin{array}{l}{u}_1(x,y,t)=\frac{\pm k_1^{2\alpha }\lambda -c^{\alpha }}{k_1^{\alpha }}\pm 2k_1^{\alpha }[-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]\\ \phantom{u_1(x,y,t)=}-\frac{3}{2}{k}_1^{2\alpha }{[-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]}^2,\\ v_1(x,y,t)=-2k_1^{\alpha }{k}_2^{\alpha }\mu -1\\ \phantom{v_1(x,y,t)=}-2k_1^{\alpha }{k}_2^{\alpha }\lambda [-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]\\ \phantom{v_1(x,y,t)=}-2k_1^{\alpha }{k}_2^{\alpha }{[-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]}^2,\end{array}$$

(24)

where $\xi =k_{1}x+k_{2}y+ct+{\xi }_0$.

When ${\lambda }^2-4\mu <0$,

$$\{\begin{array}{l}{u}_2(x,y,t)=\frac{\pm k_1^{2\alpha }\lambda -c^{\alpha }}{k_1^{\alpha }}\pm 2k_1^{\alpha }[-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]\\ \phantom{u_2(x,y,t)=}-\frac{3}{2}{k}_1^{2\alpha }{[-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]}^2,\\ v_2(x,y,t)=-2k_1^{\alpha }{k}_2^{\alpha }\mu -1\\ \phantom{v_2(x,y,t)=}-2k_1^{\alpha }{k}_2^{\alpha }\lambda [-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]\\ \phantom{v_2(x,y,t)=}-2k_1^{\alpha }{k}_2^{\alpha }{[-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }})]}^2,\end{array}$$

(25)

where $\xi =k_{1}x+k_{2}y+ct+{\xi }_0$.

When ${\lambda }^2-4\mu =0$,

$$\{\begin{array}{l}{u}_3(x,y,t)=\frac{\pm k_1^{2\alpha }\lambda -c^{\alpha }}{k_1^{\alpha }}\pm 2k_1^{\alpha }[-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]-\frac{3}{2}{k}_1^{2\alpha }{[-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]}^2,\\ v_3(x,y,t)=-2k_1^{\alpha }{k}_2^{\alpha }\mu -1-2k_1^{\alpha }{k}_2^{\alpha }\lambda [-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]\\ \phantom{v_3(x,y,t)=}-2k_1^{\alpha }{k}_2^{\alpha }{[-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]}^2,\end{array}$$

(26)

where $\xi =k_{1}x+k_{2}y+ct+{\xi }_0$.

Remark 5 The established solutions in Eqs. (24)-(26) are new exact solutions for the space-time fractional $(2+1)$-dimensional dispersive long wave equations.

4.3 Space-time fractional fifth-order Sawada-Kotera equation

We consider the space-time fractional fifth-order Sawada-Kotera equation

$$D_t^{\alpha }u+D_x^{5\alpha }u+45u^2{D}_x^{\alpha }u+15(D_x^{\alpha }u{D}_x^{2\alpha }u+u{D}_x^{3\alpha }u)=0,0<\alpha \le 1,$$

(27)

which is the variation of the fifth-order Sawada-Kotera equation [54]

$$u_t+u_{xxxxx}+45u_x{u}^2+15(u_x{u}_{xx}+u{u}_{xxx})=0.$$

(28)

Now we apply the proposed method to Eq. (27). To begin with, we suppose $u(x,t)=U(\xi )$, where $\xi =kx+ct+{\xi }_0$, k, c, ${\xi }_0$ are all constants with $k,c\ne 0$. Then, by use of the second equality in Eq. (4), Eq. (27) can be turned into

$$c^{\alpha }{D}_{\xi }^{\alpha }U+k^{5\alpha }{D}_{\xi }^{5\alpha }U+45k^{\alpha }U{D}_{\xi }^{\alpha }U+15k^{3\alpha }(D_{\xi }^{\alpha }U{D}_{\xi }^{2\alpha }U+U{D}_{\xi }^{3\alpha }U)=0.$$

(29)

Suppose that the solution of Eq. (29) can be expressed by

$$U(\xi )=\sum _{i=0}^m{a}_i{\left(\frac{D_{\xi }^{\alpha }G}{G}\right)}^i.$$

(30)

Balancing the order of $U^{(5)}$ and $U{D}_{\xi }^{3\alpha }U$ in Eq. (30), we have $m=2$. So,

$$U(\xi )=a_0+a_1\left(\frac{D_{\xi }^{\alpha }G}{G}\right)+a_2{\left(\frac{D_{\xi }^{\alpha }G}{G}\right)}^2.$$

(31)

Substituting (31) into (29), using Eq. (1) and collecting all the terms with the same power of $(\frac{D_{\xi }^{\alpha }G}{G})$ together, equating each coefficient to zero, yield a set of algebraic equations. Solving these equations yields

$$\begin{array}{c}{a}_0=-\frac{40k^{3\alpha }\mu +5k^{3\alpha }{\lambda }^2\pm \sqrt{80k^{6\alpha }{\mu }^2-40k^{6\alpha }\mu {\lambda }^2+5k^{6\alpha }{\lambda }^4-20k^{\alpha }{c}^{\alpha }}}{30k^{\alpha }},\hfill \\ a_1=-2k^{2\alpha }\lambda ,a_2=-2k^{2\alpha }.\hfill \end{array}$$

Substituting the result above into Eq. (31) and combining with (7), we can obtain corresponding exact solutions to Eq. (27).

When ${\lambda }^2-4\mu >0$,

$$\begin{array}{rl}{u}_1(x,t)=& -\frac{40k^{3\alpha }\mu +5k^{3\alpha }{\lambda }^2\pm \sqrt{80k^{6\alpha }{\mu }^2-40k^{6\alpha }\mu {\lambda }^2+5k^{6\alpha }{\lambda }^4-20k^{\alpha }{c}^{\alpha }}}{30k^{\alpha }}\\ -2k^{2\alpha }\lambda [-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]\\ -2k^{2\alpha }{[-\frac{\lambda }{2}+\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\frac{C_{1}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cosh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sinh\frac{\sqrt{{\lambda }^2-4\mu }}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]}^2,\end{array}$$

(32)

where $\xi =kx+ct+{\xi }_0$.

When ${\lambda }^2-4\mu <0$,

$$\begin{array}{rl}{u}_2(x,t)=& -\frac{40k^{3\alpha }\mu +5k^{3\alpha }{\lambda }^2\pm \sqrt{80k^{6\alpha }{\mu }^2-40k^{6\alpha }\mu {\lambda }^2+5k^{6\alpha }{\lambda }^4-20k^{\alpha }{c}^{\alpha }}}{30k^{\alpha }}\\ -2k^{2\alpha }\lambda [-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]\\ -2k^{2\alpha }{[-\frac{\lambda }{2}+\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\frac{-C_{1}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}{C_{1}cos\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }+C_{2}sin\frac{\sqrt{4\mu -{\lambda }^2}}{2\mathrm{\Gamma }(1+\alpha )}{\xi }^{\alpha }}\right)]}^2,\end{array}$$

(33)

where $\xi =kx+ct+{\xi }_0$.

When ${\lambda }^2-4\mu =0$,

$$\begin{array}{rl}{u}_3(x,t)=& -\frac{40k^{3\alpha }\mu +5k^{3\alpha }{\lambda }^2\pm \sqrt{80k^{6\alpha }{\mu }^2-40k^{6\alpha }\mu {\lambda }^2+5k^{6\alpha }{\lambda }^4-20k^{\alpha }{c}^{\alpha }}}{30k^{\alpha }}\\ -2k^{2\alpha }\lambda [-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]\\ -2k^{2\alpha }{[-\frac{\lambda }{2}+\frac{C_2\mathrm{\Gamma }(1+\alpha )}{C_1\mathrm{\Gamma }(1+\alpha )+C_2{\xi }^{\alpha }}]}^2,\end{array}$$

(34)

where $\xi =kx+ct+{\xi }_0$.

Remark 6 The established solutions in Eqs. (32)-(34) are new exact solutions for the space-time fractional fifth-order Sawada-Kotera equation.

5 Conclusions

We have proposed a new fractional sub-equation method for solving FPDEs successfully, which is the fractional version of the known (G′/G) method. As one can see, the two nonlinear fractional complex transformations for ξ and η used here are very important. The first transformation ensures that a certain fractional partial differential equation can be turned into another fractional ordinary differential equation, the solutions of which can be expressed by a polynomial in $(\frac{D_{\xi }^{\alpha }G}{G})$, where G satisfies the fractional ODE $D_{\xi }^{2\alpha }G(\xi )+\lambda D_{\xi }^{\alpha }G(\xi )+\mu G(\xi )=0$. The general expression for $(\frac{D_{\xi }^{\alpha }G}{G})$ related to this fractional ODE can be obtained due to the second fractional complex transformations for η. Finally, we note that with this kind of nonlinear fractional complex transformations, it is worth to investigate the applications of other algebraic methods to fractional partial differential equations such as the Exp-function method, F-expansion method, Jacobi elliptic function method and so on.