Abstract
In this paper, we propose a simple and useful approach to design an observer for multiple time-delays nonlinear systems in a triangular form. By constructing a new Lyapunov-Krasovskii functional and using the differential mean-value theorem, the sufficient conditions for the existence of such an observer are derived, which guarantee that the estimation error converges asymptotically towards zero. The observer gain is independent of the time-delay. A numerical example is provided to illustrate the result.
Similar content being viewed by others
1 Introduction
Time-delay, as well as nonlinearities, is often encountered in various systems which render the control design more difficult [1]. During the past decades, a lot of significant advances have been proposed in stability analysis and feedback control for time-delay systems, e.g., [1–7] and reference therein. Among these schemes, the system states are assumed to be precisely known for the control design, which is not true in some practical cases as some commercial control systems are not equipped with enough sensors. This inspires the issue of observer design for control systems, which is an active research topic in the control community.
Different types of observers have been proposed, e.g., Luenberger observer [8], adaptive observer [9], high-gain observer [10]. The observer design problem for time-delay systems has been widely investigated in the recent years. For time-delay systems, most of the state observation methods developed in the literature concern the linear case; we refer the reader to some recent advances and their extensions [11–13]. However, the problem of state estimation of time-delay systems in the nonlinear case has been rarely studied. For an overview of recent works, see, e.g., [14–16]. In [15], a new approach to the nonlinear observer design problem in the presence of delayed output measurements was presented. The proposed nonlinear observer possesses a state-dependent gain which is computed from the solution of a system of first-order singular partial differential equations. In [18], the authors established a new method for the observer design problem for a class of Lipschitz time-delay systems. The obtained synthesis conditions are expressed in terms of linear matrix inequalities (LMIs) easily tractable and are less restrictive than those obtained in [17]. In [19], the problem of observer design for a class of multi-output nonlinear system was considered. A new state observer design methodology for linear time-varying multi-output systems was presented. Furthermore, the same methodology was extended to a class of multi-output nonlinear systems and some sufficient conditions for the existence of the proposed observer were obtained, which guaranteed that the error of state estimation converged asymptotically to zero. For further results on observation of time-delay systems, we refer the reader to [20–23] and the references therein.
In this paper, we investigate observer design for nonlinear systems written in a triangular form. Our main task is to design the observer for a class of nonlinear systems with multiple time-delays. The observer is convergent, whatever the size of the delay. The design method of observer for the class of nonlinear systems with multiple time-delays is proposed, and the gain matrix is obtained. The observer gain is independent of the time-delay. The sufficient conditions are presented, which guarantee that the estimation error converges asymptotically towards zero.
This paper is arranged as follows. In Section 2, the system description and some lemmas are given. In Section 3, we present the observer synthesis method for a class of nonlinear systems with multiple time-delays. In Section 4, we propose an illustrative example in order to show the validity of our method. Finally, some conclusions are given in Section 5.
The notation used in this paper is fairly standard. Throughout this paper, R stands for the set of real numbers. The notation (<0) means that the matrix A is symmetric and positive definite (negative definite). stands for the matrix transpose of matrix A. denotes the Euclidean norm for a vector or a matrix. denotes the infinity norm for a matrix.
2 System description
Consider the time-delays nonlinear system given in a lower-triangular form:
where is the state vector, is the bounded control input and is the system output. The delay , , are constants, and for , . The functions and , , are nonlinear and are assumed to be smooth, and

To complete the system description, the following assumptions are considered.
Assumption 1 For all , , the entries of are bounded.
Assumption 2 For all , , the entries of , , are bounded.
We set and .
The following lemmas are necessary for the proof of the main statement.
Lemma 1 Let and be the solutions of the algebraic Riccati equations (AREs):
respectively, where A and C are given in an observable canonical form as in (2), is any symmetric positive-definite matrix. Then is positive-definite for and is given by
Proof Let , where . Since is symmetric and positive-definite for all , one gets that is invertible. It is easy to verify that is stabilizable and is observable. According to ref. [24], we obtain that the matrix is the unique solution of ARE (3) which is always symmetric and positive-definite for .
Using the following properties:
we get
Pre- and post-multiplying the second ARE in (3) by , we have
Using (4), (5) can be rewritten as
By comparing the last ARE with the first ARE of (3), we conclude that
□
Lemma 2 If is a lower-triangular matrix and , then the following inequality holds for all :
where
Proof Computing the product, we have
So, it follows that
When , we have
□
Remark 1 If Assumptions 1 and 2 hold and , then there are , , , , , such that
Lemma 3 [25]
For any real vectors a, b and any matrix with appropriate dimensions, it follows that
Consider the following functional differential equation of retarded type:
where , .
Lemma 4 (Lyapunov-Krasovskii stability theorem [1])
Suppose that given in (9) maps every into a bounded set in , and that are continuous nondecreasing functions, where additionally and are positive for and . If there exists a continuous differentiable functional such that
and
then the trivial solution of (9) is uniformly stable. If for , then it is uniformly asymptotically stable. In addition, if , then it is globally uniformly asymptotically stable.
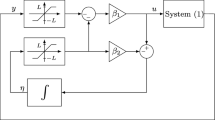
3 Observer design
Now, for the time-delay system described by (1), we propose the following state observer:
Our aim is to find the gain L such that the estimation error asymptotically converges towards zero. The estimation error dynamics is governed by
where
In the sequel, we introduce our main contribution which consists of a new feasibility condition for the observer synthesis problem of a class of nonlinear time-delays systems. The convergence analysis is performed by the use of a Lyapunov-Krasovskii functional.
For any symmetric positive-definite matrix , let be the solutions of the algebraic Riccati equations (AREs):
Theorem 1 Assume that Assumptions 1 and 2 hold and , where . Then for any
the observer error that results from (1) and (10) converges asymptotically towards zero.
Proof From Lemma 1, we known that the ARE
has the solution
where .
So, we have
For positive definite matrices , let us consider the Lyapunov-Krasovskii functional candidate:
Then we have
Using the differential mean-value theorem, we can write that
where
Let us denote
This immediately gives
Using Lemma 3, we have
This implies that
Let , we have
From (13), we have . According to Lemma 4, we deduce that the observer error converges asymptotically towards zero. This ends the proof of Theorem 1. □
Consider the following nonlinear systems:
where A, C and are given by (2), and is a lower-triangular matrix.
Remark 2 If Assumption 2 holds and , then there are , , , such that
Consider the following observer:
Our aim is to find the gain L such that the estimation error asymptotically converges towards zero. The estimation error dynamics is governed by
where
Theorem 2 Assume that Assumption 2 holds and , where . Then for any
the observer error that results from (16) and (17) converges asymptotically towards zero.
Proof From Lemma 1, we known that the ARE
has the solution
where .
So, we have
For positive definite matrices , let us consider the Lyapunov-Krasovskii functional candidate
Then we have
Using the differential mean-value theorem, we can write that
where
Let us denote
This immediately gives
Using Lemma 3, we have
This implies that
Let , we have
From (19), we have . This ends the proof of Theorem 2. □
Remark 3 In (16), the nonlinear term is the function of and , . But it does not contain . If , then (1) can be written as
When , , (16) becomes (22). So, (22) is the special case of (16).
Consider the following time-delay system:
where A and C are defined as in (2). and , , are real and lower-triangular matrices and is an input-injection vector of dimension n.
From Lemma 2, we have
where
Consider the following observer:
The estimation error is . The estimation error dynamics is governed by
Corollary 1 Consider the nonlinear system (23). Assume that , where . Then for any
the estimation error that results from (23) and (26) converges asymptotically towards zero.
Proof The matrices A and can be seen as the matrix Jacobian. Therefore, the proof becomes straightforward as it was developed before. □
Remark 4 Those results obtained can be extended to multiple time-delays nonlinear systems in upper-triangular form.
Remark 5 In [26], the sufficient conditions which guarantee that the estimation error converges asymptotically towards zero are given in terms of a linear matrix inequality. Comparing with [26], our results are less conservative and more convenient to use.
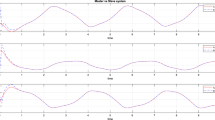
4 Numerical example
Let us consider the time delay system
where
Take
Solving the following equation:
we get
It is easy to obtain that , . Let , . It is easy to verify that (19) holds.
We get
The observer is given by
According to Theorem 2, the estimation error converges asymptotically towards zero.
5 Conclusion
The main purpose of this paper is to offer a systematic algorithm for designing an observer for a class of nonlinear systems with multiple time-delays. By using an improved Lyapunov-Krasovskii functional and the differential mean-value theorem, we present the sufficient conditions for the existence of the observer, which guarantee that the estimation error converges asymptotically towards zero. The new design plays an important role in obtaining a nonrestrictive synthesis condition and rendering our approach application to a broader class of systems, namely the class of nonlinear time-delay systems in a lower-triangular form. The proposed design is valid whatever the size of the delay. Finally, the efficiency of the proposed method is shown by a numerical example.
References
Gu K, Chen J, Kharitonov VL: Stability of Time-Delay Systems. Birkhäuser, Boston; 2003.
Dong Y, Wang X, Mei S, Li W: Exponential stabilization of nonlinear uncertain systems with time-varying delay. J. Eng. Math. 2012, 77: 225-237. 10.1007/s10665-012-9554-0
Ge SS, Tee KP: Approximation-based control of nonlinear MIMO time-delay systems. Automatica 2007, 34: 31-43.
Dong Y, Liu J: Exponential stabilization of uncertain nonlinear time-delay systems. Adv. Differ. Equ. 2012, 2012: 1-11. doi:10.1186/1687-1847-2012-180 10.1186/1687-1847-2012-1
Diblik J, Khusainov DY, Růžičková M: Controllability of linear discrete systems with constant coefficients and pure delay. SIAM J. Control Optim. 2008, 47(3):1140-1149. doi:10.1137/070689085 10.1137/070689085
Diblik J, Khusainov DY, Lukáčová J, Růžičková M: Control of oscillating systems with a single delay. Adv. Differ. Equ. 2010., 2010: Article ID 108218. doi:10.1155/2010/108218
Baštinec J, Diblík J, Khusainov DY, Ryvolová A: Exponential stability and estimation of solutions of linear differential systems of neutral type with constant coefficients. Bound. Value Probl. 2010., 2010: Article ID 956121. doi:10.1155/2010/956121
Shim H, Son YI, Seo JH: Semi-global observer for multi-output nonlinear systems. Syst. Control Lett. 2001, 42: 233-244. 10.1016/S0167-6911(00)00098-0
Dong Y, Mei S: Adaptive observer for a class of nonlinear systems. Acta Autom. Sin. 2007, 33: 1081-1084.
Tornambe A: High-gain observers for non-linear systems. Int. J. Syst. Sci. 1992, 23: 1475-1489. 10.1080/00207729208949400
Boutayeb M, Darouach M: Observers for discrete-time systems with multiple delays. IEEE Trans. Autom. Control 2001, 46: 746-750. 10.1109/9.920794
Boutayeb M: Observers design for linear time-delay systems. Syst. Control Lett. 2001, 44: 103-109. 10.1016/S0167-6911(01)00129-3
Darouach M: Linear functional observers for systems with delays in state variables: the discrete-time case. IEEE Trans. Autom. Control 2005, 50: 228-233.
Trinh H, Aldeen M, Nahavandi S: An observer design procedure for a class of nonlinear time-delay systems. Comput. Electr. Eng. 2004, 30: 61-71. 10.1016/S0045-7906(03)00037-5
Kazantzis N, Wright RA: Nonlinear observer design in the presence of delayed output measurements. Syst. Control Lett. 2005, 54: 877-886. 10.1016/j.sysconle.2004.12.005
Dong Y, Liu J, Mei S: Observer design for a class of nonlinear discrete-time systems with time-delay. Kybernetika 2013, 49: 342-359.
Aggoune W, Boutayeb M, Darouach M: Observers design for a class of nonlinear systems with time-varying delay. CDC’1999 1999, 2912-2913.
Zemouche A, Boutayeb M, Bara GI: On observers design for nonlinear time-delay systems. 2006 American Control Conference ACC’06 2006.
Dong Y, Mei S: State observers for a class of multi-output nonlinear dynamic systems. Nonlinear Anal., Theory Methods Appl. 2011, 74: 4738-4745. 10.1016/j.na.2011.04.042
Ibrir S, Xie WF, Su C-Y: Observer design for discrete-time systems subject to time-delay nonlinearities. Int. J. Syst. Sci. 2006, 37: 629-641. 10.1080/00207720600774289
Boutayeb M: Observer design for linear time-delay systems. Syst. Control Lett. 2001, 44: 103-109. 10.1016/S0167-6911(01)00129-3
Wang Z, Goodall DP, Burnham KJ: On designing observers for time-delay systems with nonlinear disturbances. Int. J. Control 2002, 75: 803-811. 10.1080/00207170210126245
Germani A, Manes C, Pepe P: A new approach to state observation of nonlinear systems with delayed output. IEEE Trans. Autom. Control 2002, 47: 96-101. 10.1109/9.981726
Ni M: Existence condition on solutions to the algebraic Riccati equation. Acta Autom. Sin. 2008, 34: 85-87.
Wu H, Mizukami K: Exponential stability of a class of nonlinear dynamics systems with uncertainties. Syst. Control Lett. 1993, 21: 307-313. 10.1016/0167-6911(93)90073-F
Zemouche A, Boutayeb M, Bara GI:Observers for a class of Lipschitz systems with extension to performance analysis. Syst. Control Lett. 2008, 57: 18-27. 10.1016/j.sysconle.2007.06.012
Acknowledgements
This work was supported by the Natural Science Foundation of Tianjin under Grant 11JCYBJC06800.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
YD carried out the main part of this manuscript. FY participated in the discussion and gave the example. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dong, Y., Yang, F. Stability analysis and observer design for a class of nonlinear systems with multiple time-delays. Adv Differ Equ 2013, 147 (2013). https://doi.org/10.1186/1687-1847-2013-147
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-147