Abstract
In this study, we consider a biological resource management predator-prey model with impulsive releasing and harvesting at different moments. First, we prove that all solutions of the investigated system are uniformly ultimately bounded. Second, the conditions of the globally asymptotic stability predator-extinction boundary periodic solution are obtained. Third, the permanence condition of the investigated system is also obtained. Finally, the numerical simulation verifies our results. These results provide reliable tactic basis for the biological resource management in practice.
Similar content being viewed by others
1 Introduction
Biological resources are renewable resources. Economic and biological aspects of renewable resources management have been considered by Clark [1]. In recent years, the optimal management of renewable resources, which has direct relationship to sustainable development, has been studied extensively by many authors [2–4]. Especially, the predator-prey models with harvesting (or dispersal and competition) are investigated by many articles [5–8]. In general, the exploitation of population should be determined by the economic and biological value of the population. It is the purpose of this article to analyze the exploitation of the predator-prey model with impulsive releasing and harvesting at different moments.
Impulsive delay differential equations are suitable for the mathematical simulation of the evolutionary process. The application of impulsive delay differential equations to population dynamics is an interesting topic since it is reasonable and correct in modelling the evolution of population, such as pest management [9]. Moreover, impulsive delay differential equations are used in various fields of applied sciences too, for example physics, ecology, pest control and so on. According to the nature of biological resource management, Jiao et al. [10] introduced the stocking on prey at fixed moments, and considering the following impulsive delay differential equation
The biological meanings of the parameters in (1.1) can be seen in [10]. Jiao and Chen [10] consider the mature predator population is harvested continuously. In fact, the population with economic value are harvested discontinuously. It will be arisen at fixed moments or state-dependent moments, that is to say, the releasing population and harvesting population should be occurred at differential moments in [10]. In this article, in order to model the fact of the biological resource management, we investigate a differential equation with two impulses for the biological resource management.
2 The model
It is well known that the basic Lotka-Volterra predator-prey model can be written as
where x1(t) and x2(t) are densities of the prey population and the predator population, respectively, r > 0 is the intrinsic growth rate of prey, a > 0 is the coefficient of intraspecific competition, b > 0 is the per-capita rate of predation of the predator, d > 0 is the death rate of predator, c > 0 denotes the product of the per-capita rate of predation and the rate of conversing prey into predator. If rc < ad is satisfied, the predator x2(t) will go extinct and the prey will tend to r/a, that is to say, system (2.1) has boundary equilibrium r/a, 0). If rc > ad is satisfied, system (2.1) has globally asymptotically stable unique positive equilibrium (d/c, rc - ad/cb).
System (2.1) is an organic growth model, that is to say, there is no intervention management on system (2.1). Obviously, the dynamical behaviors of system (2.1) is very simple. As a matter of fact, the mankind more and more devote themselves to investigate and empolder the ecosystem with the development of society. Bases on the ideology, we develop (2.1) by introducing releasing the prey and harvesting the predator and prey at different fixed moments, that is, we consider the following impulsive differential equation
where x(t) denotes the density of the predator population at time t. y(t) denotes the density of the prey population Y at time t. a > 0 denotes the intrinsic growth rate of the prey population X. b > 0 denotes the coefficient of the intraspecific competition in prey population X. β > 0 denotes the per-capita rate predation of the predator population Y. k > 0 denotes product of the per-capita rate and the rate of conversing prey population X into predator population Y. d > 0 denotes the death rate of the predator population Y. 0 < μ1 < 1 denotes the harvesting rate of prey population X at t = (n + l)τ, n ∈ Z+. 0 < μ2 < 1 denotes the harvesting rate of predator population Y at t = (n + l)τ, n ∈ Z+. μ > 0 denotes the released amount of prey population X at t = (n + 1)τ, n ∈ Z+. Δx(t) = x(t+) - x(t), where x(t+) represents the density of prey population X immediately after the impulsive releasing (or harvesting) at time t, while x(t) represents the density of prey population X before the impulsive releasing (or harvesting) at time t. Δy(t) = y(t+) - y(t), where y(t+) represents the density of predator population Y immediately after the impulsive harvesting at time t, while y(t) represents the density of predator population Y before the impulsive harvesting at time t. 0 < l < 1, and τ denotes the period of impulsive effect.
3 The lemmas
Before discussing main results, we will give some definitions, notations and lemmas. Let R+ = [0, ∞), . Denote f = (f1, f2) the map defined by the right hand of system (2.2). Let , then V is said to belong to class V0, if
(i) V is continuous in and , for each , and exists.
(ii) V is locally Lipschitzian in z.
Definition 3.1. V ∈ V0, then for and , the upper right derivative of V(t, z) with respect to the impulsive differential system (2.2) is defined as
The solution of system (2.2), denote by z(t) = (x(t), y(t))T, is a piecewise continuous function , z(t) is continuous on and . Obviously, the global existence and uniqueness of solutions of (2.2) is guaranteed by the smoothness properties of f, which denotes the mapping defined by right-side of system (2.2) (see Lakshmikantham [4]).
Before we have the main results. We need give some lemmas which will be used in the next. Since (dx(t)/dt = 0) whenever x(t) = 0, dy(t)/dt = 0 whenever y(t) = 0, t = nτ, x(nτ+) = (1 - μ1)x(nτ), y(nτ+) = (1 - μ2)y(nτ), and t = (n + l)τ, x((n + l)τ+) = x((n + l)τ) + μ, μ ≥ 0. We can easily have
Lemma 3.2. Suppose z(t) is a solution of system (2.2) with z(0+) ≥ 0, then z(t) ≥ 0 for t ≥ 0. and further z(t) > 0 t ≥ 0 for z(0+) > 0.
Now, we show that all solutions of (2.3) are uniformly ultimately bounded.
Lemma 3.3. There exists a constant M > 0 such that x(t) ≤ M, y(t) ≤ M for each solution (x(t), y(t)) of (2.2) with all t large enough.
Proof. Define V(t) = kx(t) + y(t). When t ≠ nτ and t ≠ (n + l)τ, we have
where M0 = k(a + d)2/4b. When t = nτ, V(nτ+) = kx(nτ+) + y(nτ+) = (1 - μ1)kx(nτ) + (1-μ2)y(nτ) ≤ kx(nτ) + y(nτ) = V(nτ). When t = (n + l)τ, V((n + l)τ+) = kx((n + l)τ+) + y((n + l)τ+) = kx((n + l)τ)+μ + y((n + l)τ) = V((n + l)τ) + μ. From ([[6], Lemma 2.2, p. 23]), for t ∈ (nτ, (n + l)τ] and ((n + l)τ, (n + 1)τ], we have
So V(t) is uniformly ultimately bounded. Hence, by the definition of V(t), there exists a constant M > 0 such that x(t) ≤ M, y(t) ≤ M for t large enough. The proof is complete.
If y(t) = 0, we obtain the subsystem of system (2.2)
It is easy to solve the first equation of system (3.1) between pulses
By considering the last two equations of system (3.1), we obtain the following stroboscopic map of system (3.1):
Taking A = (1 - μ1)aeaτ> 0 and B = bealτ[1 + (1 - μ1) (ea(1-l)τ- 1)] > 0, we can rewrite (3.3) as
Referring to [11], we can easily prove that (3.4) has unique positive fixed point
which can be easily proved to be globally asymptotically stable.
Then, we can derive the following lemma:
Lemma 3.4. System (3.1) has a positive periodic solution . For every solution x(t) of system (3.1), we have x(t) → as t → ∞, where
4 The dynamics
In this article, we will prove that the predator-extinction periodic solution is globally asymptotically stable and system (2.2) is permanent.
4.1 The extinction
From above discussion, we know that (2.2) has a predator-extinction periodic solution . Then we have following theorem.
Theorem 4.1. If
and
hold, then predator-extinction periodic solution of (2.2) is globally asymptotically stable. Where x* is defined as (3.5):
Proof. First, we prove the local stability. Define , y(t) = y(t), we have the following linearly similar system of system (2.2):
It is easy to obtain the fundamental solution matrix
There is no need to calculate the exact form of (*) as it is not required in the following analysis. The linearization of the third and fourth equations of (2.2) is
The linearization of the fifth and sixth equations of (2.2) is
The stability of the periodic solution is determined by the eigenvalues of
which are
According to the Floquet theory [6], if | λ2 |< 1, i.e. (4.1) holds, then is locally stable.
The following study is to prove the global attraction, choose ε > 0 such that
From the first equation of (2.2), we notice that dx(t)/dt ≤ x(t)(a - bx(t)), so we consider following impulsive differential equation
From Lemma 3.4 and comparison theorem of impulsive equation (see [[6], Theorem 3.1.1]), we have x(t) ≤ z(t) and as t → ∞, that is
for all t large enough, for convenience, we may assume (4.2) hold for all t ≥ 0. From (2.2) and (4.5), we get.
So y((n + l + 1)τ+) ≤ y((n + l)τ+)(1 - μ2) exp , hence y((n + l)τ+) ≤ y(lτ+) ρn and y((n + l)τ+) → 0 as n → ∞. Since 0 < y(t) ≤ y((n + l)τ+)(1 - μ1) for (n + l)τ < t ≤ (n + l + 1)τ, therefore y(t) → 0 as t → ∞.
Next we prove that as t → ∞. For ε > 0, there must exist a t0 > 0 such that 0 < y(t) < ε for all t ≥ t0. Without loss of generality, we assume that 0 < y(t) < ε for all t ≥ 0, then, for the first equation of system (2.2), we have
then, we have z1(t) ≤ x(t) ≤ z2(t), and , , as t → ∞. While z1(t) and z2(t) are the solutions of
and
respectively. And
where
and A1 = (1-μ1)(a - βε)e(a-βε)τ> 0 and B1 = be(a - βε)lτ[1 + (1 - μ1)(e(a - βε)(1-l)τ- 1)] > 0.
Therefore, for any ε1 > 0. there exists a t1, t > t1 such that
Let ε → 0, so we have
for t large enough, which implies as t → ∞. This completes the proof.
4.2 The permanence
The following study is to investigate the permanence of system (2.2). Before starting this study, we should give the following definition.
Definition 4.2. System (2.2) is said to be permanent if there are constants m, M > 0 (independent of initial value) and a finite time T0 such that for all solutions (x(t), y(t)) with all initial values x(0+) > 0, y(0+) > 0, m ≤ x(t) ≤ M, m ≤ y(t) ≤ M holds for all t ≥ T0. Here T0 may depends on the initial values (x(0+), (y(0+)).
Theorem 4.3. If
holds, then, system (2.2) is permanent. Where x* is defined as (3.5).
Proof. Let (x(t), y(t)) be a solution of (2.2) with x(0) > 0, y(0) > 0. By Lemma 3.3, we have proved there exists a constant M > 0 (βM < a) such that x(t) ≤ M, y(t) ≤ M for t large enough. We may assume x(t) ≤ M, y(t) ≤ M for t ≥ 0.
In this view, for the first equation of system (2.2), we have
then, we obtain the following comparative impulsive differential equation
Analyzing (4.14) with similarity as (4.8), we have , and
where
and A2 = (1 - μ1)(a - βM)e(a - βM)τ> 0 and B2 = be(a-βM)lτ[1 + (1 - μ1)(e(a - βM)(1-l)τ- 1)] > 0. Following comparative theory of impulsive differential equation [6], we know there exists a ε2 such that - ε2 for all t large enough, and ε2 > 0. So x(t) > [n* + (1 - μ1)(a - βM)e(a-βM)lτ/(a - βM) + b(e(a - βM)lτ- 1)] - ε2 = m2 for t large enough. Thus, we only need to find m1 > 0 such that y(t) ≥ m1 for t large enough. We will do it in the following two steps.
-
(1)
By the condition of Theorem 2, we can select m3 > 0, ε1 > 0 small enough such that , and
where z* is defined as (4.20). We will prove that y(t) < m3 cannot hold for t ≥ 0.
Otherwise,
By Lemma 3.4, we have x(t) ≥ z(t) and , t → ∞, where z(t) is the solution of
and
where
and and .
Therefore, there exists a T1 > 0 such that
and
for t ≥ T1. Let N1 ∈ N and N1τ > T1, integrating (4.21) on ((n + l - 1)τ, (n + l)τ), n ≥ N1, we have
then, y((N1 + k + l)τ) ≥ (1 - μ2)ky((N1 + l)τ)ekσ → ∞, as k → ∞, which is a contradiction to the boundedness of y(t). Hence there exists a t1 > 0 such that y(t) ≥ m3.
-
(2)
If y(t) ≥ m3 for t ≥ t1, then our aim is obtained. Hence, we only need to consider those solutions which leave region and reenter it again. Let , there are two possible cases for t*.
Case 1. t* = (n + l - 1)τ, n1 ∈ Z + , then x(t) ≥ m3 for t ∈ [t1, t*) and y(t*) = m3, and y(t*+) = y(t*) ≤ m3. Select n2, n3 ∈ N, such that
where σ1 = kβm2 - d < 0, Let T = n1τ + n2τ. We claim that there must be a t2 ∈ [t*, t* + T] such that y(t2) > m3, otherwise, consider (4.21) with z(t*+) = y(t*+). We have
and n1 + 1 ≤ n ≤ n2 + n3, then
and , (n1 + n2 - 1)τ ≤ t ≤ t* + T, which implies (4.22) holds for t* + n2τ ≤ t ≤ t* + T. As in step 1, we have
The second equation of system (2.1) gives
Integrating (4.23) on [t*, t* + n2τ], we have
thus we have
which is a contradiction. Let , thus for , we have for . So we have y(t) ≥ m1. The same arguments can be continued since . Hence for all .
Case 2. t ≠ (n + l - 1)τ, n ∈ Z+, then y(t) ≥ m3 for t ∈ [t1, t*), and y(t*) = m3. Suppose , then there are two possible cases for .
Case 2(a). y(t) ≤ m3 for all . Similar to case 1., we can prove that there must be a such that . Here we omit it.
Let , then y(t) ≤ m3 for and . For , we have
Let , so y(t) ≥ m1 for . For , the same arguments can be continued since y(t) ≥ m1.
Case 2(b). There exists a such that y(t) > m3. Let , then y(t) ≤ m3 for and . For , (4.23) holds true, integrating (4.23) on , we derive
Since for , the same arguments can be continued. Hence y(t) ≥ m3 for t ≥ t1. This completes the proof.
5 Discussion
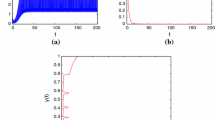
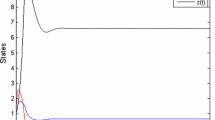
In this article, according to the fact of biological resource management, we proposed and investigated a predator-prey model with impulsive releasing prey population and impulsive harvesting predator population and prey population at different fixed moment. We analyze that the predator-extinction periodic solution of this system is globally asymptotic stability. If it is assumed that x(0) = 2, y(0) = 2, a = 2, b = 1, d = 1, β = 0.6, k = 0.9, μ1 = 0.2, μ2 = 0.6, μ = 3, l = 0.25, τ = 1, obviously, the condition of predator-extinction are satisfied, then the predator-extinction periodic solution of system (2.1) is globally asymptotically stable (the numerical simulation can be seen in Figures 1, 2, and 3). We also obtain the condition of the permanence of system (2.2). If it is assumed that x(0) = 2, y(0) = 2, a = 2, b = 1, d = 1, β = 0.6, k = 0.9, μ1 = 0.2, μ2 = 0.4, μ = 3, l = 0.25, τ = 1, obviously, the permanent condition of system (2.2) is satisfied, then, system (2.1) is permanent (the numerical simulation can also be seen in Figures 4, 5, and 6). From results of the numerical simulation, we know that there exists an impulsive harvesting predator population threshold , which satisfies . If , the predator-extinction periodic solution of system (2.2) is globally asymptotically stable. If , system (2.2) is permanent.
From Theorems 4.1 and 4.3, we can easily guess that there must exist an impulsive harvesting predator population threshold . If , the predator-extinction periodic solution of system (2.2) is globally asymptotically stable. If , system (2.2) is permanent. The same discussion can be applied to parameters μ1 and τ. These results show that the impulsive effect plays an important role for the permanence of system (2.2). Our results provide reliable tactic basis for the practically biological resource management.
References
Clark CW: Mathematical Bioeconomics. Wiley, New York; 1990.
Goh BS: Management and Analysis of Biological Populations. Elsevier, Amsterdam; 1980.
Wang WD, Chen LS: A predator-prey system with stage structure for predator. Comput Math Appl 1997, 33(8):83–91. 10.1016/S0898-1221(97)00056-4
Lakshmikantham V, Bainov DD, Simeonov P: Theory of Impulsive Differential Equations. World Scientific, Singapore; 1989.
Song XY, Chen LS: Optimal harvesting and stability for a predator-prey system with stage structure. Acta Math Appl (English series) 2002, 18(3):423–430. 10.1007/s102550200042
Bainov D, Simeonov P: Impulsive Differential Equations: Periodic Solutions and Applications. In Pitman Mongraphs and Surveys in Pure and Applied Mathematics. Volume 66. Wiley, New York; 1993.
Meng X, Jiao J, Chen L: Global dynamics behaviors for a nonautonomous Lotka- Volterra almost periodic dispersal system with delays. Nonlinear Anal Theory Methods Appl 2008, 68: 3633–3645. 10.1016/j.na.2007.04.006
Jiao J, Chen L: A pest management SI model with biological and chemical control concern. Appl Math Comput 2006, 183: 1018–1026. 10.1016/j.amc.2006.06.070
Meng X, Chen L: Permanence and global stability in an impulsive Lotka-Volterra N -species competitive system with both discrete delays and continuous delays. Int J Biomath 2008, 1: 179–196. 10.1142/S1793524508000151
Jiao J, Chen L: A stage-structured holling mass defence predator-prey model with impulsive perturbations on predators. Appl Math Comput 2007, 189: 1448–1458. 10.1016/j.amc.2006.12.043
Meng X, Jiao J, Chen L: The dynamics of an age structured predator-prey model with disturbing pulse and time delays. Nonlinear Anal Real World Appl 2008, 9: 547–561. 10.1016/j.nonrwa.2006.12.001
Acknowledgements
The authors were grateful to the associate editor, Professor Leonid Berezansky, and the referees for their helpful suggestions that are beneficial to our original article. This study was supported by the Development Project of Nature Science Research of Guizhou Province Department (No. 2010027), the National Natural Science Foundation of China (10961008), and the Science Technology Foundation of Guizhou(2010J2130).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
JJ carried out the main part of this article, LC corrected the manuscript. SC brought forward some suggestion on this article. All authors have read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiao, J., Chen, L. & Cai, S. Dynamical analysis of a biological resource management model with impulsive releasing and harvesting. Adv Differ Equ 2012, 9 (2012). https://doi.org/10.1186/1687-1847-2012-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-9