Abstract
In this paper, we propose a new technique for solving space-time fractional telegraph equations. This method is based on perturbation theory and the Laplace transformation. Fractional Taylor series and fractional initial conditions have been introduced. However, all the previous works avoid the term of fractional initial conditions in the space-time telegraph equations. The results of introducing fractional order initial conditions and the Laplace transform for the studied cases show the high accuracy, simplicity and efficiency of the approach.
Similar content being viewed by others
1 Introduction
Telegraph equations are hyperbolic partial differential equations that are applicable in several fields such as wave propagation [1], signal analysis [2], random walk theory [3], etc. In recent years, there has been a great deal of interest in fractional differential equations [4, 5]. Time-fractional telegraph equations have been studied by Orsingher and Zhao [6] and Orsingher and Beghin [7]. Telegraph equations apply to high-frequency transmission lines such as telegraph wires and radio frequency conductors. They are also applicable to designing high-voltage transmission lines.
In this paper, we consider two different types of telegraph equations. The first one is the space-fractional telegraph equation
subject to the initial and boundary conditions
and the second equation is the classical time-fractional telegraph equation
subject to the initial conditions
where u can be considered as a function depending on distance (x) and time (t), a and b are constants depending on a given problem and f, φ, ϕ, ψ are known continuous functions. The second equation has been solved by Das et al. [8] using the homotopy analysis method.
The aim of this paper is to introduce a new method for fractional space-time telegraph equations. This new technique is a combined form of the perturbation method [9–14] with the Laplace transform. This method is called the perturbation Laplace method (PLM). Moreover, we have introduced fractional order initial conditions for space-time telegraph equations. Point to be noted regarding fractional differential equations is that one should use fractional Taylor series. To make the calculation easy and simple, for the first time, we have used the Laplace transform to solve the systems of equations formed after applying homotopy perturbation instead of applying an inverse operator. Through the Laplace transform of fractional order term, it is easy to judge that one must use fractional order initial conditions. It is easy to judge, by applying the Laplace transformation, that it is essential to use a fractional order initial condition to analyze any physical phenomenon which has been expressed in terms of fractional differential equations. To the best of authors’ knowledge, in the literature on space-fractional telegraph equations [15], there is no closed form solution for different values of α except for the standard case, i.e., for . The elegance of this article can be attributed to its endeavor of finding the solution in a simple way by considering only the PLM. Two examples which show that only a few iterations are needed to obtain accurate approximate solutions are solved.
2 Fractional calculus theory
We give some basic definitions and properties of the fractional calculus theory proposed by Jumarie [16] which are used further in this paper.
Definition 1 Let , , denote a continuous (but not necessarily differentiable) function. Then its fractional derivative of order α, , is defined by the following expression:
For positive α, we define

and
With this definition, the Laplace transform of the fractional derivative is defined as follows:
Proposition 1 (On the decomposition of fractional derivatives)
Let α be such that . There are two different ways to obtain (see [16]). One can calculate to obtain the Laplace transform
Proposition 2 Assume that the continuous function , has a fractional derivative of order kα for any positive integer k and any α, . Then the following equality holds:
On making and the substitution , we obtain the fractional Maclaurin series
3 Perturbative Laplace method
In order to elucidate the solution procedure of the perturbative Laplace method (PLM), we consider the following fractional differential equation:

where ,  is generally the linear differential operator with respect to the variable x and , are continuous functions. In view of HPM [9–15], we can construct a homotopy for Eq. (2) as follows:
is generally the linear differential operator with respect to the variable x and , are continuous functions. In view of HPM [9–15], we can construct a homotopy for Eq. (2) as follows:

or

where is an embedding parameter. If , Eq. (3) and Eq. (4) become
and when , both Eq. (3) and Eq. (4) turn out to be the original fractional differential equation (2).
The homotopy perturbation method [9–15] admits a solution in the form
Setting in the solution of Eq. (6), we get
Invoking Eq. (6) into Eq. (4) and collecting the terms with the same powers of p, we can obtain a series of equations of the following form:

By using the definition given in Eq. (1), we get
Solving Eq. (9) for respectively, by using the fractional initial value conditions, we get
Substituting successive iterations in Eq. (7) will give the required result.
4 Space-time fractional telegraph equations
Example 1 Let us consider the space-fractional telegraph equation
subject to the initial and boundary conditions
In order to illustrate the efficiency of our method, we replace the fractional order α, , by the order 2α, , in Eq. (11)
subject to the initial and boundary conditions
Using the procedure in Section 2, we can write Eq. (12) in the form of recurrence equations as follows:

In view of Eq. (9), Eq. (13) can be written in the following form:

Solving Eq. (14) for , we get the following form:

Equation (15) in the most refined form can be written as

The solution in a series form can be expressed as
where denotes the Mittag-Leffler function.
Example 2 We consider the nonhomogeneous fractional time telegraph equation
subject to the initial conditions
with
and for the fractional initial condition
subject to the initial conditions
with
By applying the aforesaid method, we can write Eq. (18) in the form of recurrence equations as follows:
By using Eq. (9), we can write Eq. (19) in the following form:

Proceeding as before, we obtain
Equation (20) can also be written as

and so on. In this way, the rest of components of the homotopy perturbation series can be obtained. Finally, we obtain the series solution as
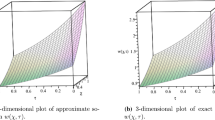
Figure 1 shows the approximate solution of Eq. (18) for different values of α using the perturbative Laplace method. The numerical result of the probability density function for different fractional Brownian motions , and also for standard motion , is calculated for , with respect to the variable t. The three-dimensional variation of vs. x and t at and is shown in Figure 2. It is seen from the figures that increases with increasing t but decreases with increasing α, which assures the exponential decay of regular Brownian motion.
5 Conclusion
In this paper, we have introduced a combination of perturbation and Laplace methods for space-time fractional problem which we called the PLM. We described the method and used it in some fractional telegraph equations in order to show its applicability and validity. We achieved accurate approximations by using only a few numbers of iterations, which reveals efficiency of the new method. The solution very rapidly converges by utilizing the perturbation Laplace method. The PLM is also valid for other fractional differential equations, and this paper can be used as a standard paradigm for other applications.
References
Weston VH, He S:Wave splitting of the telegraph equation in and its application to inverse scattering. Inverse Probl. 1993, 9: 789–812. 10.1088/0266-5611/9/6/013
Jordan PM, Puri A: Digital signal propagation in dispersive media. J. Appl. Phys. 1999, 85: 1273–1282. 10.1063/1.369258
Banasiak J, Mika R: Singular perturbed telegraph equations with applications in random walk theory. J. Appl. Math. Stoch. Anal. 1998, 11: 9–28. 10.1155/S1048953398000021
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York; 1974.
Podlubny I: Fractional Differential Equations. Academic Press, New York; 1999.
Orsingher E, Zhao X: The space-fractional telegraph equation and the related fractional telegraph process. Chin. Ann. Math., Ser. B 2003, 24: 45–56. 10.1142/S0252959903000050
Orsingher E, Beghin L: Time-fractional telegraph equations and telegraph processes with Brownian time. Probab. Theory Relat. Fields 2004, 128: 141–160. 10.1007/s00440-003-0309-8
Das S, Vishal K, Gupta PK, Yildirim A: An approximate analytical solution of time-fractional telegraph equation. Appl. Math. Comput. 2011, 217: 7405–7411. 10.1016/j.amc.2011.02.030
He JH: Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178(3–4):257–262. 10.1016/S0045-7825(99)00018-3
Xu L: He’s homotopy perturbation method for a boundary layer equation in unbounded domain. Comput. Math. Appl. 2007, 54: 1067–1070. 10.1016/j.camwa.2006.12.052
Turkyilmazoglu M: Convergence of the homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2011, 12: 9–14.
Hetmaniok E, Nowak I, Slota D, Witula R: Application of the homotopy perturbation method for the solution of inverse heat conduction problem. Int. Commun. Heat Mass Transf. 2012, 39: 30–35. 10.1016/j.icheatmasstransfer.2011.09.005
Gupta PK, Singh M: Homotopy perturbation method for fractional Fornberg-Whitham equation. Comput. Math. Appl. 2011, 61: 250–254. 10.1016/j.camwa.2010.10.045
Golbabai A, Sayevand K: Analytical modelling of fractional advection-dispersion equation defined in a bounded space domain. Math. Comput. Model. 2011, 53: 1708–1718. 10.1016/j.mcm.2010.12.046
Momani S: Analytic and approximate solutions of the space- and time-fractional telegraph equations. Appl. Math. Comput. 2005, 170: 1126–1134. 10.1016/j.amc.2005.01.009
Jumarie G: Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions. Appl. Math. Lett. 2009, 22: 378–385. 10.1016/j.aml.2008.06.003
Acknowledgements
The second author is supported by Grant P201/11/0768 of the Czech Grant Agency (Prague). The fourth author is supported by Grant FEKT-S-11-2-921 of the Faculty of Electrical Engineering and Communication, Brno University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have made the same contribution. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Khan, Y., Diblík, J., Faraz, N. et al. An efficient new perturbative Laplace method for space-time fractional telegraph equations. Adv Differ Equ 2012, 204 (2012). https://doi.org/10.1186/1687-1847-2012-204
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-204