Abstract
In this work, we study qualitative properties of the solutions of the following class of nonlinear third order difference equations
First we study the relation of attractivity and stability of equilibrium point of this equation and some related equations. Further more we prove the existence of Neimark-Sacker and period doubling (flip) bifurcation for this system by analysing the characteristic equation, and investigate the direction of this bifurcations by using normal form theory. Finally some numerical simulations are carried out to support the analytical results.
Similar content being viewed by others
1 Introduction
We consider the third order difference equation
where , is a continuous real function with , for and , , are given real numbers (initial conditions).
Particular cases of (1.1) have been appeared in mathematical models of macroeconomics, see [1, 2]. Equations of the form considered and studied extensively by [3–6].
In this work we study various properties of (1.1). In Section 2 we study attractivity, stability and attractive region of (1.1) and its related equations. Further more we study bifurcations of (1.1). In Section 3 we prove the existence of Neimark-Sacker and period doubling (flip) bifurcation for this system by analysing the characteristic equation, and then in Section 4 we investigate the direction of this bifurcations by using normal form theory. Finally in Section 5 we give numerical simulations to support our theoretical analysis.
2 Attractivity
In this section we study global attractivity and stability of the equilibrium point of (1.1). Equation (1.1) can be transformed to another form which has equivalent properties. Let
Then (1.1) reduced to
which has the unique equilibrium .
At first we show the following result.
Theorem 2.1 The equilibrium point is global attractive (respectively asymptotically stable) in (1.1) if and only if is global attractive (respectively asymptotically stable) in (2.2).
Proof Equation (1.1) can be written as:
Hence we see that:

Using induction we have that, if n is even then:
And if n is odd then:
Now if n is even, let and if n is odd, we prove that .
We distinguish two cases.
Case 1. (). In this case
Case 2. (). In this case by using Stolz Theorem and since n is even, we have that:
Using continuity of f we see that if then (and by a similar argument ), which implies that . □
By using weak contractions introduced in [6] we obtain the following sufficient conditions for attractivity of solutions of (1.1).
Proposition 2.2
-
(1)
If for all t and , then origin is globally attracting in (1.1).
-
(2)
If for all t and , then every positive solution of (1.1) converges to zero.
Proof For the proof of (1), define and notice that
since , it follows that F is a weak contraction on the entire space and therefore by [6], the origin is globally attracting.
-
(2)
For notice that:
Now since , it follows that F is a weak contraction on , and since is invariant under , [6] implies that the origin is exponentially stable relative to , hence every positive solution of (1.1) converges to zero. □
Now we study stability properties. Let be a solution of (1.1). We define the vector , where
Using this notation the delay Equation (1.1) transformed to the following 3D system:
where which has the unique equilibrium point .
Now we study the relation of the stability properties of the delay Equation (1.1) to those of the associated nondelay equation:
First we prove the following lemma which will be used in the next results.
Lemma 2.3 Let be a solution of the system (2.7). Then for , the following statements are true:
For odd :
And for even :
Furthermore for :
Proof From (2.6) we have that for :


Now by using these relations and induction we see that, if n is odd then:
And if n is even then:
Furthers more:
By using this relation we have that, if is odd then:
And if is even then:
□
Theorem 2.4 Assume that f satisfies:
for all . If the equilibrium point of (2.8) is stable, then the equilibrium point of (1.1) is also stable.
Proof It is sufficient to prove the stability of the equilibrium of (2.7) because of the equivalence of (1.1) and (2.7). Let be arbitrary. Since the equilibrium point of (2.8) is stable, there exists such that implies for all . Choose , since , we have that
Now for :
which implies that:
for all . Therefore, for :
And hence
Now implies that for . Hence
and from the previous lemma, if is odd then:
and if is even then:
Therefore, for arbitrary , there exists , such that implies that for , and hence the equilibrium point of (2.7) is stable. □
Theorem 2.5 Assume that (2.17) holds. If there exists such that is a subset of the attractive region of the equilibrium point of (2.8), then is also contained in the attractive region of the equilibrium point of (1.1).
Proof Let be arbitrary. Since is a subset of attractive region of (2.8), there exists such that implies that for . Assume that , then we have . So there exists such that for , which implies that:
for all . Let . If is odd we have:
provided that . If is even we have:
Now:
The continuity of f implies there exists such that and . Now if is odd we have for :
Now choose such that:
holds for .
If is even we have:
Now choose such that:
holds for . We consider , Then implies that for . Hence is also subset of attractive region of the equilibrium of (1.1). □
3 Existence of bifurcations
Now we study bifurcations of (1.1), for this aim we suppose that . First we prove the existence of bifurcations. Dynamics of system (1.1) described by the mapping:
The Jacobian matrix of g at O is:
in which . The characteristic equation of H is:
By the Jury’s conditions, the necessary and sufficient conditions for all eigenvalues of the characteristic equation lying inside the unit circle are:
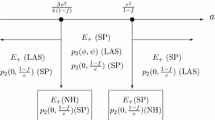
We consider the following curves, which are the boundary curves of the region of asymptotic stability shown in Figure 1:
On , , respectively which is impossible. We show in the following theorem occurrence of bifurcations on the boundary curves , .
Theorem 3.1 For system (3.1) the following conditions holds:
-
(1)
Flip bifurcation occurs when .
-
(2)
Neimark-Sacker bifurcation occurs when .
Proof First, we show the existence of the flip bifurcation. Because , we have the characteristic equation:
which has eigenvalues , . So is an eigenvector of H with corresponding eigenvalue , and 1 is not the eigenvalue. A straight forward calculation shows that:
in which . Now:
and:
Therefore by [7], Th.1.4.5], flip bifurcation occurs.
Now we show the existence of Neimark-Sacker bifurcation. If is a root of Equation (3.2), separating the real and imaginary parts, we have the following:
squaring and adding both equations, we have:
so we get:
In the case that we have . By substitution of into , we have:
Therefore, Equation (3.2) has a unique pair of complex roots:
On the other hand, means . Because and , we get and hence , which refers . Thus , for . On the other hand we have:
Assume that , that is, or . In previous discussion, we obtain , hence . If , then from and , we see that , which corresponds to that is impossible on . So we have that, . Therefore, by the generic Neimark-Sacker bifurcation theorem [7, 8], Neimark-Sacker bifurcation occurs, that is, the system (3.1) has a unique closed invariant curve bifurcating from the equilibrium . □
4 Direction of the bifurcations
In the previous section, we have shown that system (3.1) undergoes a flip (period-doubling) bifurcation when and a Neimark-Sacker bifurcation when at equilibrium point . In this section, by using the normal form method for discrete systems, as studied by Sacker, Kuznetsov and Wiggins, we shall study the direction of the two bifurcations and stability of the bifurcating invariant curves. We can write system as:
where is a smooth function and its Taylor expansion is:
where:
in which:
for , and . At the beginning, we study the direction of period-doubling bifurcation and the stability of period-doubling cycle. Let be the eigenvector of H with respect to eigenvalue −1, that is, ; be the adjoint eigenvector of that is, where is the transposed matrix, and , where is the standard scalar product in . So we have:
Following the algorithms given in Kuznetsov [8], the critical normal form coefficient , that determines the nondegeneracy of the period-doubling bifurcation and the stability of period-doubling cycle, is given by the following formula:
From the above relations we have:
and therefore:
Applying the general theory for the direction of flip bifurcation and stability of period doubling cycle (see Wiggins [9] or Kuznetsov [8]), we derive the following result:
Theorem 4.1 For system (3.1) flip bifurcation occurs in when , and if , the flip bifurcation is supercritical and if , the flip bifurcation is subcritical.
Now, we are going to study the direction of the Neimark-Sacker bifurcation and the stability of the bifurcating invariant curve in . In the above section, we see that H has simple eigenvalues on the unit circle:
Let α be a complex eigenvector corresponding to and β be a complex eigenvector of the transposed matrix corresponding , i.e. , . By computation we obtain the following eigenvectors:
Normalize α with respect to β such that:
where means the standard scalar product in  defined by , we have:
defined by , we have:

Following the algorithms given in Kuznetsov [8], the critical normal form coefficient , that determines the nondegeneracy of the Neimark-Sacker bifurcation and allows us to predict the stability of bifurcating invariant curve, is given by the following formula:
Furthermore in this case we have:

Which yields the following formula for :
in which:

From the theory of the direction of Neimark-Sacker bifurcation and the stability of the bifurcating invariant curve (see Sacker [10, 11], Wiggins [9] or Kuznetsov [8]), we have:
Theorem 4.2 For system (3.1), if hold, then (respectively >0) implies that a unique and stable (respectively, unstable) closed invariant curve bifurcates from , and the Neimark-Sacker bifurcation in is supercritical (respectively, subcritical).
5 Numerical simulations
In this section, we give numerical simulations to illustrate our theoretical analysis.
Example 1 Let and . In this case , and , therefore by Theorem 4.1 flip bifurcation occurs. Figures 2, 3 and 4 show bifurcation diagram.
Example 2 Let and . In this case , , and , therefore by Theorem 4.2 Neimark-Sacker bifurcation occurs. Figures 5, 6 and 7 show orbits of system when , and , respectively.
References
Eckaus RS: The stability of dynamic models. Rev. Econ. Stat. 1957, 39: 172–182. 10.2307/1928534
Hicks JR: A Contribution to the Theory of the Trade Cycle. Clarendon, Oxford; 1965.
Dai B, Zhang N: Stability and global attractivity for a class of nonlinear delay difference equations. Discrete Dyn. Nat. Soc. 2005, 3: 227–234.
Li S, Zhang W: Bifurcations in a second-order difference equation from macroeconomics. J. Differ. Equ. Appl. 2007, 2: 365–374.
Sedaghat H: A class of nonlinear second-order difference equations from macroeconomics. Nonlinear Anal. 1997, 29: 593–603. 10.1016/S0362-546X(96)00054-5
Sedaghat H: Nonlinear Difference Equations: Theory with Applications to Social Science Models. Kluwer Academic, Dordrecht; 2003.
Stuart AM, Humphries AR: Dynamical Systems and Numerical Analysis. Cambridge University Press, Cambridge; 1998.
Kuznetsov YA: Elements of Applied Bifurcation Theory. Springer, New York; 1998.
Wiggins S: Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York; 1990.
Sacker, RJ: On invariant surfaces and bifurcation of periodic solutions of ordinary differential equations. Technical report IMM-NYU 333, New York University (1964)
Sacker RJ, Von Bremen HF: Bifurcation of maps and cycling in genetic systems. Fields Inst. Commun. 2004, 42: 305–311.
Acknowledgements
The authors would like to thank the referees for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors carried out the proof. All authors conceived of the study, and participated in its design and coordination. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Memarbashi, R., Ghasemabadi, A. Regarding the dynamics of a third order nonlinear difference equation. Adv Differ Equ 2012, 107 (2012). https://doi.org/10.1186/1687-1847-2012-107
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-107