Introduction

Rhythmic processes are common and very important to life: cyclic behaviors are found in heart beating, breath, and circadian rhythms [1]. The biological systems are always exposed to external perturbations, which may produce alterations on these rhythms as a consequence of coupling synchronization of the autonomous oscillators with perturbations. Coupling of therapeutic perturbations, such as drugs and radiation, on biological systems result in biological rhythms, which is known as chronotherapy. Cancer [2, 3], rheumatoid arthritis [4], and asthma [5, 6] are a number of the diseases under study in this field because of their relation with circadian cycles. Mathematical models and numerical simulations are necessary to understand the functions of biological rhythms, to comprehend the transition from simple to complex behaviors, and to delineate their conditions [7]. Chaotic behavior is a usual phenomenon in these systems, which is the main focus of this article.

Chaos theory as a new branch of physics and mathematics has provided a new way of viewing the universe and is an important tool to understand the behavior of the processes in the world. Chaotic behaviors have been observed in different areas of science and engineering such as mechanics, electronics, physics, medicine, ecology, biology, economy, and so on. To avoid troubles arising from unusual behaviors of a chaotic system, chaos control has gained increasing attention in recent years. An important objective of a chaos controller is to suppress the chaotic oscillations completely or to reduce them toward regular oscillations [8]. Many control techniques such as open-loop control, adaptive control, and fuzzy control methods have been implemented for controlling the chaotic systems [9–11].

Generally, one can classify the main problems in chaos control into three cases: stabilization, chaotification, and synchronization. The stabilization problem of the unstable periodic solution (orbit) arises in the suppression of noise and vibrations of various constructions, elimination of harmonics in the communication systems, electronic devices, and so on. These problems are distinguished for the fact that the controlled plant is strongly oscillatory, that is, the eigenvalues of the matrix of the linearized system are close to the imaginary axis. The harmful vibrations can be either regular (quasiperiodic) or chaotic. The problems of suppressing the chaotic oscillations by reducing them to the regular oscillations or suppressing them completely can be formalized as stabilization techniques. The second class includes the control problems of excitation or generation of chaotic oscillations. These problems are also called the chaotification or anticontrol.

The third important class of the control objectives corresponds to the problems of synchronization or, more precisely, controllable synchronization as opposed to auto-synchronization. Synchronization has important applications in vibration technology (synchronization of vibrational exciters [12]), communications (synchronization of the receiver and transmitter signals) [13], biology and biotechnology, and so on.

As an important problem, it has been found that a model for the mechanism of circadian rhythms in Neurospora (three-variable model) develops non-autonomous chaos when it is perturbed with a periodic forcing, and its dynamical behavior depends on the forcing waveform (square wave to sine wave) [14]. Instead, in a ten-equation model of the circadian rhythm in Drosophila, autonomous chaos occurs in a restricted domain of parameter values, but this chaos can be suppressed by a sinusoidal or square wave forcing cycle [15].

The subject of fractional calculus has gained considerable popularity and importance during the past three decades or so, mainly due to its applications in numerous seemingly diverse and widespread fields of science and engineering. Applications including modeling of damping behavior of viscoelastic materials, cell diffusion processes, transmission of signals through strong magnetic fields, and finance systems are some examples [16–18]. Moreover, fractional order dynamic systems have been studied in the design and implementation of control systems [19]. Studies have shown that a fractional order controller can provide better performances than an integer order one and leads to more robust control performance [20]. Usefulness of fractional order controllers has been reported in many practical applications [21].

Recently numerous works have been reported on the fractional order Rossler control and synchronization. For instance [22–25] have considered the fractional order Rossler system. However, their control and synchronization methodologies had two important limitations: considering the commensurate fractional order system, and controlling via multiple input. In this article, at first we study the dynamics of the fractional order version of the well-known Rossler system. In contrast to [23, 24, 26], in this article, we want to control a chaotic fractional order system via a single actuating input, which is more suitable for implementation. The capability of the proposed control methodology is justified using a reliable numerical simulation. Synchronization of two chaotic fractional order Rossler systems is considered. The simulation is carried out in the time domain technique instead of the frequency based methods since the latter are not reliable in simulating chaotic fractional systems.

This article is organized as follows. 'Basic tools of fractional order systems' section summarizes some basic concepts in fractional calculus theory. The well-known Rössler system is illustrated in 'Fractional order Rössler system' section. 'Control and synchronization of Rössler system' section is devoted to control and synchronization of the Rossler system via an active control methodology. Finally, the article is concluded in 'Conclusion' section.

Basic tools of fractional order systems

Definitions and theorems

In this subsection, some mathematical backgrounds are presented.

Definition 1 [27]

The fractional order integral operator of a Lebesgue integrable function x(t) is defined as follows:

(1)

in which is the Gamma function.

Definition 2 [28]

The left fractional order derivative operator in the sense of Riemann-Liouville (LRL) is defined as follows:

(2)

Remark 1 [28]

For fractional derivative and integral RL operators we have:

(3)

where L is Laplace transform operator. As one can see RL differentiation of a constant is not zero; also its Laplace transform needs fractional derivatives of the function in initial time. For overcoming these imperfections the following definition is presented:

Definition 3 [28]

The left fractional order derivative operator in the sense of Caputo is defined as follows:

(4)

Remark 2 [29]

For fractional Caputo derivative operator, we have:

(5)

Usually a dynamical system with fractional order could be described by:

(6)

where are vector state, nonlinear vector field, and differentiation order vector, respectively. If q 1 = q 2 = ··· = q n Equation (6) refers to commensurate fractional order dynamical system [29]; otherwise it is an incommensurate one. Moreover, the sum orders of all the involved derivatives in Equation 6, i.e., is called the effective dimension of Equation (6) [30].

Theorem 1 [30]

The following commensurate order system:

(7)

with and is asymptotically stable if and only if is satisfied for all eigenvalues λ of A. Moreover, this system is stable if and only if is satisfied for all eigenvalues λ of A with those critical eigenvalues satisfying have geometric multiplicity of one.

Theorem 2 [31]

Consider the following linear fractional order system:

(8)

with and and q = (q 1 q 2 ··· q n )T, 0 < q i ≤ 1 with . Let M be the lowest common multiple of the denominators d i 's. The zero solution of system (8) is globally asymptotically stable in the Lyapunov sense if all roots λ's of the equation:

(9)

satisfy .

Numerical solution of fractional differential equations

Numerical methods used for solving ODEs have to be modified for solving fractional differential equations (FDE). A modification of Adams-Bashforth-Moulton algorithm is proposed in [32–34] to solve FDEs.

Consider for q ∈ (m - 1,m] the initial value problem:

(10)

This equation is equivalent to the Volterra integral equation given by [35]:

(11)

Consider the uniform grid {t n = nh: n = 0,1, ···, N} for some integer N and . Let x h (t n ) be an approximation to x(t n ). Assuming to have approximations x h (t j ), j = 1,2, ···, n and we want to obtain x h (t n +1) by means of the equation:

(12)

where

(13)

The preliminary approximation is called predictor and is given by:

(14)

where

(15)

The error in this method is:

(16)

where p = min(2,1+q).

Fractional order Rössler system

The Rössler system [36] is a three dimensional nonlinear system that can exhibit chaotic behavior. The attractor of the Rössler system belongs to the 1-scroll chaotic attractor family. The fractional order Rössler system is defined by the following equations [37]:

(17)

The equilibria of this system are:

(18)

The Jacobian of this system at the equilibrium Q: (x 1*,x 2*,x 3*) is:

(19)

The eigenvalues of the Jacobian matrix (19) associated with the two above equilibria are:

(20)

Since Q 1 is a saddle point of index 2, if chaos occurs in this system, the 1-scroll attractor will encircle this equilibrium.

Assume that a three dimensional chaotic system displays a chaotic attractor. For every scroll existing in the chaotic attractor, this system has a saddle point of index 2 encircled by its respective scroll. Suppose that Ω is the set of equilibrium points of the system surrounded by scrolls. We know that system with q = (q 1,q 2,q 3)T and system have the same equilibrium points.

Hence, a necessary condition for fractional order system to exhibit the chaotic attractor similar to its integer order counterpart is the instability of all the equilibrium points in Ω; otherwise, one of these equilibrium points becomes asymptotically stable and attracts the nearby trajectories. According to (9), this necessary condition is mathematically equivalent to [38]:

(21)

where λ i 's are the roots of:

(22)

We consider three cases for fractional differentiation orders:

(23)

For order (q 1,q 2,q 3) = (0.7,0.2,0.9) (22) reduces to:

(24)

Finding the roots of Equation 24, one can verify that:

(25)

Since the necessary condition for chaoticity is not satisfied, one cannot deduce any result about chaos occurrence in the fractional Rössler system with this order. However, (25) implies that there are some initial conditions for which the Rössler system has no chaotic attractor. An example is illustrated in Figure 1 using x(0) = (0,0,0).

Figure 1
figure 1

Simulation results for system (17) when ( q 1 , q 2 , q 3 ) = (0.7,0.2,0.9).

Full size image

Now consider (q 1,q 2,q 3) = (0.9,0.8,0.7) as order of the fractional Rössler system. Similar to the previous case we have:

(26)

Thus:

(27)

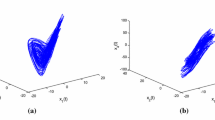
This shows only that the fractional Rössler system satisfies the necessary condition. Simulations in Figure 2 using x(0) = (0,0,0) clarify the chaotic behavior.

Figure 2
figure 2

Simulation results for system (17) when ( q 1 , q 2 , q 3 ) = (0.9,0.8,0.7).

Full size image

As the final case, we examine (q 1,q 2,q 3) = (1,1,1) which indicates the integer order Rössler system which is known as a chaotic system. To check the necessary condition of chaos in this case, one can see that from (22):

(28)

which is consistent with those of classical case [37].

Control and synchronization of Rössler system

Active control methodology

In this section, an active control law is applied to the incommensurate fractional chaotic Rössler system using only one actuating input. In this technique, controller output signal is directly exerted to the fractional chaotic system. The controlled system is described by:

(29)

For the sake of suitable stabilization, we first use the following transformation:

(30)

Applying this control law to (29) yields:

(31)

Let' us select a state feedback structure for v(x) as follows:

(32)

Now, the design process reduces to choosing three parameters k 1,k 2,k 3 such that (29) is asymptotically stable. The dynamics (31) reduces to:

(33)

Using standard methods in linear control systems one can find a proper gain k 1,k 2,k 3 such that the desired poles of (33) are located in stability region of the fractional order system. Here we consider the desired poles to be at -1, -2, -3. Thus the final controller is:

(34)

Note that all three desired poles satisfy the stability conditions in Theorem 2. Indeed:

(35)

Therefore:

(36)

This shows the stability of (33). In the following simulations (Figure 3) we examine the designed controller for the order (q 1,q 2,q 3) = (0.9,0.8,0.7) which previously shown in (27) that this order produces a chaotic behavior. Note that the control signal is applied on t = 500. It can be seen that the linearizing state feedback has stabilized the chaotic system.

Figure 3
figure 3

Simulation results for the controlled system (29) when ( q 1 , q 2 , q 3 ) = (0.9,0.8,0.7).

Full size image

Active synchronization of Rössler system

In this section, we are designing a controllable synchronization scheme in which a particular dynamical system, i.e., chaotic incommensurate fractional Rössler system, acts as master and a different dynamical system acts as a slave. As told previously the main goal is to synchronize the slave with the master using an active controller.

Now we consider two chaotic incommensurate fractional order Rössler system:

(37)

and

(38)

Note that the initial conditions are different and we want to synchronize the signals in spite of discrepancy between the initial conditions. So let us define the errors as:

(39)

Therefore, the error states can be written as:

(40)

Also note that here we used only one actuating signal. Based on active controller structure one can choose the control law as:

(41)

So using (41), the error state (40) reduces to:

(42)

Substituting v = -k 1 e 1 - k 2 e 2 - k 3 e 3 into (42) yields:

(43)

Choosing k 1 = -44.3269, k 2 = -56.2959, k 3 = 11.63 the poles of (43) will be: -2, -4, -5.

Now let us determine the characteristic equations:

(44)

Thus:

(45)

Based on Theorem 2, one can see that all these poles lie in the stability region. This indicates that the proposed controller can asymptotically synchronize foregoing systems.

Figure 4 shows the simulation result of synchronization of the chaotic systems with initial conditions: x 0 = (0.2, 0, 2) and x 0 ' = (0, 2.5,0). Note that the synchronization scheme is activated on t = 500.

Figure 4
figure 4

Numerical simulation for the synchronized systems (40) when ( q 1 , q 2 , q 3 ) = (0.9,0.8,0.7).

Full size image

Conclusions

In this article, we proposed an active control for controlling the chaotic fractional order Rössler system. Moreover, based on the same methodology, i.e., active control, a synchronization scheme was presented. The method was applied to an incommensurate fractional order Rössler system, for which the existence of chaotic behavior was analytically explored. Using some known facts from nonlinear analysis, we have derived the necessary conditions for fractional orders in the Rossler system for exhibiting chaos. The proposed control law has two main features: simplicity for practical implementation and the use of single actuating signal for control. Simulations show the effectiveness of the proposed control.