Abstract
In this paper, we prove the demiclosed principle for total asymptoticallynonexpansive nonself mappings in hyperbolic spaces. Then we obtain convergencetheorems of the mixed Agarwal-O’Regan-Sahu type iteration for totalasymptotically nonexpansive nonself mappings. Our results extend some results inthe literature.
MSC: 47H09, 49M05.
Similar content being viewed by others
1 Introduction
One of the fundamental and celebrated results in the theory of nonexpansive mappingsis Browder’s demiclosed principle[1] which states that if X is a uniformly convex Banach space,C is a nonempty closed convex subset of X, and if is a nonexpansive nonself mapping, then
is a nonexpansive nonself mapping, then is demiclosed at 0, that is, for any sequence
is demiclosed at 0, that is, for any sequence in C if
in C if  weakly and
weakly and  , then
, then  (where I is the identity mapping inX). Later, Chidume et al.[2] proved the demiclosed principle for asymptotically nonexpansive nonselfmappings in uniformly convex Banach spaces. Recently, Chang et al.[3] proved the demiclosed principle for total asymptotically nonexpansivenonself mappings in CAT(0) spaces. It is well known that the demiclosed principleplays an important role in studying the asymptotic behavior for nonexpansivemappings. The purpose of this paper is to extend Chang’s result from CAT(0)spaces to the general setup of uniformly convex hyperbolic spaces. We also apply ourresult to approximate common fixed points of total asymptotically nonexpansivenonself mappings in hyperbolic spaces, using the mixed Agarwal-O’Regan-Sahutype iterative scheme [4]. Our results extend and improve the corresponding results of Chang etal.[3], Nanjaras and Panyanak [5], Chang et al.[6], Zhao et al.[7], Khan et al.[8] and many other recent results.
(where I is the identity mapping inX). Later, Chidume et al.[2] proved the demiclosed principle for asymptotically nonexpansive nonselfmappings in uniformly convex Banach spaces. Recently, Chang et al.[3] proved the demiclosed principle for total asymptotically nonexpansivenonself mappings in CAT(0) spaces. It is well known that the demiclosed principleplays an important role in studying the asymptotic behavior for nonexpansivemappings. The purpose of this paper is to extend Chang’s result from CAT(0)spaces to the general setup of uniformly convex hyperbolic spaces. We also apply ourresult to approximate common fixed points of total asymptotically nonexpansivenonself mappings in hyperbolic spaces, using the mixed Agarwal-O’Regan-Sahutype iterative scheme [4]. Our results extend and improve the corresponding results of Chang etal.[3], Nanjaras and Panyanak [5], Chang et al.[6], Zhao et al.[7], Khan et al.[8] and many other recent results.
In this paper, we work in the setting of hyperbolic spaces introduced by Kohlenbach [9]. Concretely,  is called a hyperbolic space if
is called a hyperbolic space if is a metric space and
is a metric space and  a function satisfying
a function satisfying
-
(I)
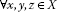 ,
, 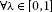 ,
, 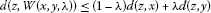 ;
; -
(II)
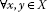 ,
, 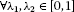 ,
, 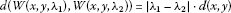 ;
; -
(III)
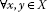 ,
, 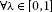 ,
, 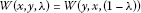 ;
; -
(IV)
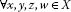 ,
, 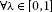 ,
, 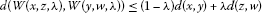 .
.
If a space satisfies only (I), it coincides with the convex metric space introducedby Takahashi [10]. The concept of hyperbolic spaces in [9] is more restrictive than the hyperbolic type introduced by Goebel andKirk [11] since (I)-(III) together are equivalent to  being a space of hyperbolic type in [11]. But it is slightly more general than the hyperbolic space defined inReich and Shafrir [12] (see [9]). This class of metric spaces in [9] covers all normed linear spaces, ℝ-trees in the sense of Tits, theHilbert ball with the hyperbolic metric (see [13]), Cartesian products of Hilbert balls, Hadamard manifolds (see [12, 14]), and CAT(0) spaces in the sense of Gromov (see [15]). A thorough discussion of hyperbolic spaces and a detailed treatment ofexamples can be found in [9] (see also [11–13]).
being a space of hyperbolic type in [11]. But it is slightly more general than the hyperbolic space defined inReich and Shafrir [12] (see [9]). This class of metric spaces in [9] covers all normed linear spaces, ℝ-trees in the sense of Tits, theHilbert ball with the hyperbolic metric (see [13]), Cartesian products of Hilbert balls, Hadamard manifolds (see [12, 14]), and CAT(0) spaces in the sense of Gromov (see [15]). A thorough discussion of hyperbolic spaces and a detailed treatment ofexamples can be found in [9] (see also [11–13]).
A hyperbolic space is uniformly convex[16] if for  ,
,  , and
, and  there exists a
there exists a  such that
such that

provided that  ,
,  , and
, and  .
.
A map  is called modulus of uniform convexity if
is called modulus of uniform convexity if for given
for given  . The function η is monotone ifit decreases with r (for a fixed ϵ), that is,
. The function η is monotone ifit decreases with r (for a fixed ϵ), that is,

A subset C of a hyperbolic space X is convex if for all
for all  and
and  .
.
Let  be a metric space and let C be a nonemptysubset of X. C is said to be a retract of X, ifthere exists a continuous map
be a metric space and let C be a nonemptysubset of X. C is said to be a retract of X, ifthere exists a continuous map  such that
such that  ,
,  . A map
. A map  is said to be a retraction, if
is said to be a retraction, if . If P is a retraction, then
. If P is a retraction, then for all y in the range of P. Recallthat a nonself mapping
for all y in the range of P. Recallthat a nonself mapping  is said to be a
is said to be a  -total asymptotically nonexpansive nonselfmapping if there exist nonnegative sequences
-total asymptotically nonexpansive nonselfmapping if there exist nonnegative sequences  ,
,  with
with  ,
,  , and a strictly increasing continuous function
, and a strictly increasing continuous function with
with  such that
such that

where P is a nonexpansive retraction of X onto C. It iswell known that each nonexpansive mapping is an asymptotically nonexpansive mappingand each asymptotically nonexpansive mapping is a  -total asymptotically nonexpansive mapping.
-total asymptotically nonexpansive mapping.
 is said to be uniformlyL-Lipschitzian if there exists a constant
is said to be uniformlyL-Lipschitzian if there exists a constant  such that
such that

2 Preliminaries
We now give the concept of △-convergence and collect some of its properties.Let  be a bounded sequence in a hyperbolic spaceX. For
be a bounded sequence in a hyperbolic spaceX. For  , we define
, we define

The asymptotic radius of
of is given by
is given by

The asymptotic radius of
of with respect to
with respect to is given by
is given by

The asymptotic center of
of is the set
is the set

The asymptotic center of
of with respect to
with respect to is the set
is the set

Recall that a sequence  in X is said to △-converge to
in X is said to △-converge to if x is the unique asymptotic center of
if x is the unique asymptotic center of for every subsequence
for every subsequence  of
of  . In this case we call x the△-limit of
. In this case we call x the△-limit of .
.
Let be a complete uniformly convex hyperbolic space with monotone modulus of uniformconvexity andCa nonempty closed convex subset ofX. Then every bounded sequence
be a complete uniformly convex hyperbolic space with monotone modulus of uniformconvexity andCa nonempty closed convex subset ofX. Then every bounded sequence inXhas a unique asymptotic center with respect toC.
inXhas a unique asymptotic center with respect toC.
Lemma 2[17]
Let be a uniformly convex hyperbolic space with monotone modulus of uniformconvexityη. Let
be a uniformly convex hyperbolic space with monotone modulus of uniformconvexityη. Let and
and be a sequence in
be a sequence in for some
for some . If
. If and
and are sequences inXsuch that
are sequences inXsuch that ,
,  , and
, and for some
for some . Then
. Then

Lemma 3[3]
Let ,
,  , and
, and be sequences of nonnegative numbers such that
be sequences of nonnegative numbers such that

If and
and , then
, then exists.
exists.
3 Main results
We shall prove that a total asymptotically nonexpansive nonself mapping in a completeuniformly convex hyperbolic space X with monotone modulus of uniformconvexity is demiclosed. We need the following notation:

where C is a closed convex subset which contains the bounded sequence and
and  .
.
Theorem 1 (Demiclosed principle for total asymptotically nonexpansive nonselfmappings in hyperbolic spaces)
Let be a complete uniformly convex hyperbolic space with monotone modulus of uniformconvexityη. LetCbe a nonempty closed and convex subset ofX. Let
be a complete uniformly convex hyperbolic space with monotone modulus of uniformconvexityη. LetCbe a nonempty closed and convex subset ofX. Let be a uniformlyL-Lipschitzian and
be a uniformlyL-Lipschitzian and -total asymptotically nonexpansive nonselfmapping. Pis a nonexpansive retraction ofXontoC. Let
-total asymptotically nonexpansive nonselfmapping. Pis a nonexpansive retraction ofXontoC. Let be a bounded approximate fixed point sequence, i.e.,
be a bounded approximate fixed point sequence, i.e., and
and . Then we have
. Then we have .
.
Proof By the definition,  if and only if
if and only if  . By Lemma 1, we have
. By Lemma 1, we have  . Since
. Since  , by induction we can prove that
, by induction we can prove that

In fact, it is obvious that the conclusion is true for  . Suppose the conclusion holds for
. Suppose the conclusion holds for , now we prove that it is also true for
, now we prove that it is also true for . Indeed, since T is uniformlyL-Lipschitzian, we have
. Indeed, since T is uniformlyL-Lipschitzian, we have

Equation (2) is proved. Hence for each  and
and  , from (2) we have
, from (2) we have

Taking  ,
,  in (3), then by (1) we get
in (3), then by (1) we get

Letting  and taking superior limit on the both sides, we have
and taking superior limit on the both sides, we have

Assume that  . Then
. Then  does not converge to p, so we can find
does not converge to p, so we can find , for any
, for any  , that there exists
, that there exists  such that
such that  . We can assume
. We can assume  . Then
. Then  and there exist
and there exist  such that
such that

By the definition of Φ and (4), for the above θ, there exists such that
such that

For M, there exists  such that
such that

Since X is uniformly convex and η is monotone, applying (5)we have

Since  , we have got a contradiction with
, we have got a contradiction with . It follows that
. It follows that  and the proof is completed. □
and the proof is completed. □
Theorem 2LetCbe a nonempty closed and convex subset of a complete uniformly convex hyperbolicspaceXwith monotone modulus of uniform convexityη. Let ,
,  , be uniformlyL-Lipschitzian and
, be uniformlyL-Lipschitzian and -total asymptotically nonexpansive nonselfmappings. For arbitrarily chosen
-total asymptotically nonexpansive nonselfmappings. For arbitrarily chosen ,
,  is defined as follows:
is defined as follows:

wherePis a nonexpansive retraction ofXontoC. Assume that and the following conditions are satisfied:
and the following conditions are satisfied:
-
(i)
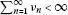 and
and ;
; -
(ii)
there exist constants
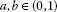 such that
such that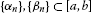 ;
; -
(iii)
there exists a constant
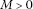 such that
such that ,
, 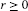 ,
,
then the sequence defined by (6) △-converges to a point in ℱ.
defined by (6) △-converges to a point in ℱ.
Proof We divide our proof into three steps.
Step 1. In the sequel, we shall show that

In fact, by conditions (1), (I), and (iii), we get

and

Combining (8) and (9), we have

where  ,
,  . Furthermore, using the condition (i), we have
. Furthermore, using the condition (i), we have

Consequently, a combination of (10), (11), and Lemma 3 shows that (7) isproved.
Step 2. We claim that

In fact, it follows from (7) that  exists for each given
exists for each given  . Without loss of generality, we assume that
. Without loss of generality, we assume that

By (8) and (13), we have

Noting

by (14) we have

Besides, by (10) we get

which yields

Now by (13), (15), (16), and Lemma 2, we have

Using the same method, we also have

By virtue of (18), we get

Combining (17) and (19), we obtain

Moreover, it follows from (17) that

Now by (18), (20), and (21), for each  , we get
, we get

Therefore, (12) holds.
Step 3. Now we are in a position to prove the △-convergence of . Since
. Since  is bounded, by Lemma 1, it has a uniqueasymptotic center
is bounded, by Lemma 1, it has a uniqueasymptotic center  . Let
. Let  be any subsequence of
be any subsequence of  with
with  . Since
. Since  , it follow from Theorem 1 that
, it follow from Theorem 1 that . By the uniqueness of asymptotic centers, we get
. By the uniqueness of asymptotic centers, we get . It implies that
. It implies that  is the unique asymptotic center of
is the unique asymptotic center of for each subsequence
for each subsequence  of
of  , that is,
, that is,  △-converges to
△-converges to  . The proof is completed. □
. The proof is completed. □
Example 1 Let ℝ be the real line with the usual norm and let
and let  . Define two mappings
. Define two mappings  by
by

and

It is proved in [[19], Example 3.1] that both  and
and  are asymptotically nonexpansive mappings with
are asymptotically nonexpansive mappings with ,
,  . Therefore, they are total asymptoticallynonexpansive mappings with
. Therefore, they are total asymptoticallynonexpansive mappings with  ,
,  ,
,  ,
,  . Additionally, they are uniformlyL-Lipschitzian mappings with
. Additionally, they are uniformlyL-Lipschitzian mappings with  .
.  and
and  . Let
. Let

Therefore, the conditions of Theorem 2 are fulfilled.
Example 2 Let ℝ be the real line with the usual norm and let
and let  . Define two mappings
. Define two mappings  by
by

It is proved in [[20], Example 1] that both  and
and  are total asymptotically nonexpansive mappings with
are total asymptotically nonexpansive mappings with ,
,  ,
,  . Moreover, they are uniformly L-Lipschitzianmappings with
. Moreover, they are uniformly L-Lipschitzianmappings with  .
.  and
and  . Let
. Let  ,
,  be the same as in (22). Therefore, the conditions ofTheorem 2 are fulfilled.
be the same as in (22). Therefore, the conditions ofTheorem 2 are fulfilled.
Theorem 3Under the assumptions of Theorem 2, if one of and
and is demi-compact, then the sequence defined by (6)converges strongly (i.e., in the metrictopology) to a common fixed point in ℱ.
is demi-compact, then the sequence defined by (6)converges strongly (i.e., in the metrictopology) to a common fixed point in ℱ.
Proof By (12) and the assumption that one of  and
and  is demi-compact, there exists a subsequence
is demi-compact, there exists a subsequence such that
such that  converges strongly to some point
converges strongly to some point . Then by the continuity of
. Then by the continuity of  and
and  , we get
, we get

which implies that  . It follows from (7) that
. It follows from (7) that  exists and thus
exists and thus  . The proof is completed. □
. The proof is completed. □
Theorem 4Under the assumptions of Theorem 2, if there exists anondecreasing function with
with ,
,  ,
,  such that
such that

then the sequence defined by (6) converges strongly(i.e., in the metric topology) to a common fixedpoint in ℱ.
Proof By (12) and (23) we obtain  . Since f is nondecreasing with
. Since f is nondecreasing with ,
,  ,
,  , we have
, we have

Now we prove that  is a Cauchy sequence in C. In fact, itfollows from (10) that, for any
is a Cauchy sequence in C. In fact, itfollows from (10) that, for any  ,
,

where  and
and  . Then, for any
. Then, for any  and any positive integers n, m, weget
and any positive integers n, m, weget

Since for each  ,
,  , we obtain
, we obtain

where  . It follows from (24) that
. It follows from (24) that

Thus  is a Cauchy sequence in C. C iscomplete for it is a closed subset in a complete hyperbolic space. Without loss ofgenerality, we can assume that
is a Cauchy sequence in C. C iscomplete for it is a closed subset in a complete hyperbolic space. Without loss ofgenerality, we can assume that  converges strongly to some point
converges strongly to some point . It is easy to prove that ℱ is closed. Itfollows from (24) that
. It is easy to prove that ℱ is closed. Itfollows from (24) that  . The proof is completed. □
. The proof is completed. □
References
Browder FE: Semicontractive and semiaccretive nonlinear mappings in Banach spaces.Bull. Am. Math. Soc. 1968, 74:660–665. 10.1090/S0002-9904-1968-11983-4
Chidume CE, Ofoedu EU, Zegeye H: Strong and weak convergence theorems for asymptotically nonexpansivemappings.J. Math. Anal. Appl. 2003, 280:364–374. 10.1016/S0022-247X(03)00061-1
Chang SS, Wang L, Joesph Lee HW, Chan CK: Strong and △-convergence for mixed type total asymptoticallynonexpansive mappings in CAT(0) spaces.Fixed Point Theory Appl. 2013., 2013: Article ID 122 10.1186/1687-1812-2013-122
Agarwal RP, O’Regan D, Sahu DR: Iterative construction of fixed points of nearly asymptotically nonexpansivemappings.J. Nonlinear Convex Anal. 2007, 8:61–79.
Nanjaras B, Panyanak B: Demiclosed principle for asymptotically nonexpansive mappings in CAT(0)spaces.Fixed Point Theory Appl. 2010., 2010: Article ID 268780 10.1155/2010/268780
Chang SS, Wang L, Joseph Lee HW, Chan CK, Yang L: Demiclosed principle and △-convergence theorems for totalasymptotically nonexpansive mappings in CAT(0) spaces.Appl. Math. Comput. 2012, 219:2611–2617. 10.1016/j.amc.2012.08.095
Zhao LC, Chang SS, Kim JK: Mixed type iteration for total asymptotically nonexpansive mappings inhyperbolic spaces.Fixed Point Theory Appl. 2013., 2013: Article ID 353 10.1186/1687-1812-2013-353
Khan AR, Fukhar-ud-din H, Kalsoom A, Lee BS: Convergence of a general algorithm of asymptotically nonexpansive maps inuniformly convex hyperbolic spaces.Appl. Math. Comput. 2014, 238:547–556.
Kohlenbach U: Some logical metatheorems with applications in functional analysis.Trans. Am. Math. Soc. 2005, 357:89–128. 10.1090/S0002-9947-04-03515-9
Takahashi W: A convexity in metric spaces and nonexpansive mappings.Kodai Math. Semin. Rep. 1970, 22:142–149. 10.2996/kmj/1138846111
Goebel K, Kirk WA: Iteration processes for nonexpansive mappings. Contemporary Mathematics 21. In Topological Methods in Nonlinear Functional Analysis. Edited by: Singh SP, Thomeier S, Watson B. Am. Math. Soc., Provindence; 1983:115–123.
Reich S, Shafrir I: Nonexpansive iterations in hyperbolic spaces.Nonlinear Anal., Theory Methods Appl. 1990, 15:537–558. 10.1016/0362-546X(90)90058-O
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. Dekker, New York; 1984.
Reich S, Zaslavski AJ: Generic aspects of metric fixed point theory. In Handbook of Metric Fixed Point Theory. Edited by: Kirk WA, Sims B. Kluwer Academic, Dordrecht; 2001:557–576.
Bridson M, Haefliger A: Metric Spaces of Non-Positive Curvature. Springer, Berlin; 1999.
Shimizu T, Takahashi W: Fixed points of multivalued mappings in certain convex metric spaces.Topol. Methods Nonlinear Anal. 1996, 8:197–203.
Khan AR, Fukhar-ud-din H, Khan MAA: An implicit algorithm for two finite families of nonexpansive maps inhyperbolic spaces.Fixed Point Theory Appl. 2012., 2012: Article ID 54 10.1186/1687-1812-2012-54
Leustean L: Nonexpansive iterations in uniformly convexW-hyperbolic spaces. Contemporary Mathematics 513. In Nonlinear Analysis and Optimization I: Nonlinear Analysis. Edited by: Leizarowitz A, Mordukhovich BS, Shafrir I, Zaslavski A. Am. Math. Soc., Providence; 2010:193–209.
Guo WP, Cho YJ, Guo W: Convergence theorems for mixed type asymptotically nonexpansive mappings.Fixed Point Theory Appl. 2012., 2012: Article ID 224 10.1186/1687-1812-2012-224
Kiziltunc H, Yolacan E: Strong convergence theorems for two total asymptotically nonexpansive nonselfmappings in Banach spaces.Fixed Point Theory Appl. 2013., 2013: Article ID 90 10.1186/1687-1812-2013-90
Acknowledgements
Supported by General Project of Educational Department in Sichuan (No. 13ZB0182)and National Natural Science Foundation of China (No. 11426190).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wan, LL. Demiclosed principle and convergence theorems for total asymptoticallynonexpansive nonself mappings in hyperbolic spaces. Fixed Point Theory Appl 2015, 4 (2015). https://doi.org/10.1186/1687-1812-2015-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2015-4



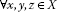 ,
, 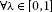 ,
, 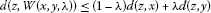 ;
;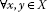 ,
, 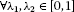 ,
, 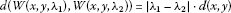 ;
;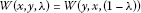 ;
;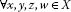 ,
, 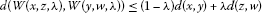 .
.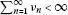 and
and ;
;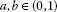 such that
such that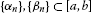 ;
;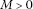 such that
such that ,
, 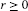 ,
,