Acceleration of the Halpern algorithm to search for a fixed point of a nonexpansive mapping

Abstract

This paper presents an algorithm to accelerate the Halpern fixed point algorithm in a real Hilbert space. To this goal, we first apply the Halpern algorithm to the smooth convex minimization problem, which is an example of a fixed point problem for a nonexpansive mapping, and indicate that the Halpern algorithm is based on the steepest descent method for solving the minimization problem. Next, we formulate a novel fixed point algorithm using the ideas of conjugate gradient methods that can accelerate the steepest descent method. We show that, under certain assumptions, our algorithm strongly converges to a fixed point of a nonexpansive mapping. We numerically compare our algorithm with the Halpern algorithm and show that it dramatically reduces the running time and iterations needed to find a fixed point compared with that algorithm.

MSC:47H10, 65K05, 90C25.

1 Introduction

Fixed point problems for nonexpansive mappings [[1], Chapter 4], [[2], Chapter 3], [[3], Chapter 1], [[4], Chapter 3] have been investigated in many practical applications, and they include convex feasibility problems [5], [[1], Example 5.21], convex optimization problems [[1], Corollary 17.5], problems of finding the zeros of monotone operators [[1], Proposition 23.38], and monotone variational inequalities [[1], Subchapter 25.5].

Fixed point problems can be solved by using useful fixed point algorithms, such as the Krasnosel’skiĭ-Mann algorithm [[1], Subchapter 5.2], [[6], Subchapter 1.2], [7, 8], the Halpern algorithm [[6], Subchapter 1.2], [9, 10], and the hybrid method [11]. Meanwhile, to make practical systems and networks (see, e.g., [12–15] and references therein) stable and reliable, the fixed point has to be found at a faster pace. That is, we need a new algorithm that approximates the fixed point faster than the conventional ones. In this paper, we focus on the Halpern algorithm and present an algorithm to accelerate the search for a fixed point of a nonexpansive mapping.

To achieve the main objective of this paper, we first apply the Halpern algorithm to the smooth convex minimization problem, which is an example of a fixed point problem for a nonexpansive mapping, and indicate that the Halpern algorithm is based on the steepest descent method [[16], Subchapter 3.3] for solving the minimization problem.

A number of iterative methods [[16], Chapters 5-19] have been proposed to accelerate the steepest descent method. In particular, conjugate gradient methods [[16], Chapter 5] have been widely used as an efficient accelerated version of most gradient methods. Here, we focus on the conjugate gradient methods and devise an algorithm blending the conjugate gradient methods with the Halpern algorithm.

Our main contribution is to propose a novel algorithm for finding a fixed point of a nonexpansive mapping, for which we use the ideas of accelerated conjugate gradient methods for optimization over the fixed point set [17, 18], and prove that the algorithm converges to some fixed point in the sense of the strong topology of a real Hilbert space. To demonstrate the effectiveness and fast convergence of our algorithm, we numerically compare our algorithm with the Halpern algorithm. Numerical results show that it dramatically reduces the running time and iterations needed to find a fixed point compared with that algorithm.

This paper is organized as follows. Section 2 gives the mathematical preliminaries. Section 3 devises the acceleration algorithm for solving fixed point problems and presents its convergence analysis. Section 4 applies the proposed and conventional algorithms to a concrete fixed point problem and provides numerical examples comparing them.

2 Mathematical preliminaries

Let H be a real Hilbert space with the inner product $〈\cdot ,\cdot 〉$ and its induced norm $\parallel \cdot \parallel$, and let ℕ be the set of all positive integers including zero.

2.1 Fixed point problem

Suppose that $C\subset H$ is nonempty, closed, and convex. A mapping $T:C\to C$ is said to be nonexpansive [[1], Definition 4.1(ii)], [[2], (3.2)], [[3], Subchapter 1.1], [[4], Subchapter 3.1] if

$$\parallel T(x)-T(y)\parallel \le \parallel x-y\parallel (x,y\in C).$$

The fixed point set of $T:C\to C$ is denoted by

$$Fix(T):=\{x\in C:T(x)=x\}.$$

The metric projection onto C [[1], Subchapter 4.2, Chapter 28] is denoted by $P_C$. It is defined by $P_C(x)\in C$ and $\parallel x-P_C(x)\parallel ={inf}_{y\in C}\parallel x-y\parallel$ ($x\in H$). $P_C$ is nonexpansive with $Fix(P_C)=C$ [[1], Proposition 4.8, (4.8)].

Proposition 2.1 Suppose that $C\subset H$ is nonempty, closed, and convex, $T:C\to C$ is nonexpansive, and $x\in H$. Then

• (i) [[1], Corollary 4.15], [[2], Lemma 3.4], [[3], Proposition 5.3], [[4], Theorem 3.1.6] $Fix(T)$ is closed and convex.

• (ii) [[1], Theorem 3.14] $\hat{x}=P_C(x)$ if and only if $〈x-\hat{x},y-\hat{x}〉\le 0$ ($y\in C$).

Proposition 2.1(i) guarantees that if $Fix(T)\ne \mathrm{\varnothing }$, $P_{Fix(T)}(x)$ exists for all $x\in H$.

This paper discusses the following fixed point problem.

Problem 2.1 Suppose that $T:H\to H$ is nonexpansive with $Fix(T)\ne \mathrm{\varnothing }$. Then

$$\text{find }{x}^{\star }\in H\text{ such that }T\left(x^{\star }\right)=x^{\star }.$$

2.2 The Halpern algorithm and our algorithm

The Halpern algorithm generates the sequence ${(x_n)}_{n\in \mathbb{N}}$ [[6], Subchapter 1.2] [9, 10] as follows: given $x_0\in H$ and ${({\alpha }_n)}_{n\in \mathbb{N}}$ satisfying ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{n=0}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$, and ${\sum }_{n=0}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$,

$$x_{n+1}:={\alpha }_n{x}_0+(1-{\alpha }_n)T(x_n)(n\in \mathbb{N}).$$

(1)

Algorithm (1) strongly converges to $P_{Fix(T)}(x_0)$ ($\in Fix(T)$) [[6], Theorem 6.17], [9, 10].

Here, we shall discuss Problem 2.1 when $Fix(T)$ is the set of all minimizers of a convex, continuously Fréchet differentiable functional f over H and see that algorithm (1) is based on the steepest descent method [[16], Subchapter 3.3] to minimize f over H. Suppose that the gradient of f, denoted by ∇f, is Lipschitz continuous with a constant $L>0$ and define $T^f:H\to H$ by

$$T^f:=I-\alpha \mathrm{\nabla }f,$$

(2)

where $\alpha \in (0,2/L]$ and $I:H\to H$ stands for the identity mapping. Accordingly, $T^f$ satisfies the nonexpansivity condition (see, e.g., [[12], Proposition 2.3]) and

$$Fix\left(T^f\right)=\underset{x\in H}{argmin}f(x):=\{x^{\star }\in H:f\left(x^{\star }\right)=\underset{x\in H}{min}f(x)\}.$$

Therefore, algorithm (1) with $T:=T^f$ can be expressed as follows.

$$\{\begin{array}{c}{d}_{n+1}^f:=-\mathrm{\nabla }f(x_n),\hfill \\ y_n:=T^f(x_n)=x_n-\alpha \mathrm{\nabla }f(x_n)=x_n+\alpha d_{n+1}^f,\hfill \\ x_{n+1}:={\alpha }_n{x}_0+(1-{\alpha }_n)y_n(n\in \mathbb{N}).\hfill \end{array}$$

(3)

This implies that algorithm (3) uses the steepest descent direction [[16], Subchapter 3.3] $d_{n+1}^{f,\mathrm{SDD}}:=-\mathrm{\nabla }f(x_n)$ of f at $x_n$, and hence algorithm (3) is based on the steepest descent method.

Meanwhile, conjugate gradient methods [[16], Chapter 5] are popular acceleration methods of the steepest descent method. The conjugate gradient direction of f at $x_n$ ($n\in \mathbb{N}$) is $d_{n+1}^{f,\mathrm{CGD}}:=-\mathrm{\nabla }f(x_n)+{\beta }_n{d}_n^{f,\mathrm{CGD}}$, where $d_0^{f,\mathrm{CGD}}:=-\mathrm{\nabla }f(x_0)$ and ${({\beta }_n)}_{n\in \mathbb{N}}\subset (0,\mathrm{\infty })$, which, together with (2), implies that

$$d_{n+1}^{f,\mathrm{CGD}}=\frac{1}{\alpha }(T^f(x_n)-x_n)+{\beta }_n{d}_n^{f,\mathrm{CGD}}.$$

(4)

Therefore, by replacing $d_{n+1}^f:=-\mathrm{\nabla }f(x_n)$ in algorithm (3) with $d_{n+1}^{f,\mathrm{CGD}}$ defined by (4), we can formulate a novel algorithm for solving Problem 2.1.

Before presenting the algorithm, we provide the following lemmas which are used to prove the main theorem.

Proposition 2.2 [[6], Lemmas 1.2 and 1.3]

Let ${(a_n)}_{n\in \mathbb{N}},{(b_n)}_{n\in \mathbb{N}},{(c_n)}_{n\in \mathbb{N}},{({\alpha }_n)}_{n\in \mathbb{N}}\subset (0,\mathrm{\infty })$ be sequences with $a_{n+1}\le (1-{\alpha }_n)a_n+{\alpha }_n{b}_n+c_n$ ($n\in \mathbb{N}$). Suppose that ${\sum }_{n=0}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$, ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{b}_n\le 0$, and ${\sum }_{n=0}^{\mathrm{\infty }}{c}_n<\mathrm{\infty }$. Then ${lim}_{n\to \mathrm{\infty }}{a}_n=0$.

Proposition 2.3 [[19], Lemma 1]

Suppose that ${(x_n)}_{n\in \mathbb{N}}\subset H$ weakly converges to $x\in H$ and $y\ne x$. Then ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}\parallel x_n-x\parallel <{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}\parallel x_n-y\parallel$.

3 Acceleration of the Halpern algorithm

We present the following algorithm.

Algorithm 3.1

Step 0. Choose $\mu \in (0,1]$, $\alpha >0$, and $x_0\in H$ arbitrarily, and set ${({\alpha }_n)}_{n\in \mathbb{N}}\subset (0,1)$, ${({\beta }_n)}_{n\in \mathbb{N}}\subset [0,\mathrm{\infty })$. Compute $d_0:=(T(x_0)-x_0)/\alpha$.

Step 1. Given $x_n,d_n\in H$, compute $d_{n+1}\in H$ by

$$d_{n+1}:=\frac{1}{\alpha }(T(x_n)-x_n)+{\beta }_n{d}_n.$$

Compute $x_{n+1}\in H$ as follows.

$$\{\begin{array}{c}{y}_n:=x_n+\alpha d_{n+1},\hfill \\ x_{n+1}:=\mu {\alpha }_n{x}_0+(1-\mu {\alpha }_n)y_n.\hfill \end{array}$$

Put $n:=n+1$, and go to Step 1.

We can check that Algorithm 3.1 coincides with the Halpern algorithm (1) when ${\beta }_n:=0$ ($n\in \mathbb{N}$) and $\mu :=1$.

This section makes the following assumptions.

Assumption 3.1 The sequences ${({\alpha }_n)}_{n\in \mathbb{N}}$ and ${({\beta }_n)}_{n\in \mathbb{N}}$ satisfy^a

$$\begin{array}{r}(\mathrm{C}1)\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n=0,(\mathrm{C}2)\sum _{n=0}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty },(\mathrm{C}3)\sum _{n=0}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty },\\ (\mathrm{C}4){\beta }_n\le {\alpha }_n^2(n\in \mathbb{N}).\end{array}$$

Moreover, ${(x_n)}_{n\in \mathbb{N}}$ in Algorithm 3.1 satisfies

$$(\mathrm{C}5){(T(x_n)-x_n)}_{n\in \mathbb{N}}\text{ is bounded}.$$

Let us do a convergence analysis of Algorithm 3.1.

Theorem 3.1 Under Assumption  3.1, the sequence ${(x_n)}_{n\in \mathbb{N}}$ generated by Algorithm  3.1 strongly converges to $P_{Fix(T)}(x_0)$.

Algorithm 3.1 when ${\beta }_n:=0$ ($n\in \mathbb{N}$) is the Halpern algorithm defined by

$$x_{n+1}:=\mu {\alpha }_n{x}_0+(1-\mu {\alpha }_n)T(x_n)(n\in \mathbb{N}).$$

Hence, the nonexpansivity of T ensures that, for all $x\in Fix(T)$ and for all $n\in \mathbb{N}$,

$$\begin{array}{rl}\parallel x_{n+1}-x\parallel & =\parallel \mu {\alpha }_n(x_0-x)+(1-\mu {\alpha }_n)(T(x_n)-x)\parallel \\ \le \mu {\alpha }_n\parallel x_0-x\parallel +(1-\mu {\alpha }_n)\parallel T(x_n)-x\parallel \\ \le \mu {\alpha }_n\parallel x_0-x\parallel +(1-\mu {\alpha }_n)\parallel x_n-x\parallel .\end{array}$$

(5)

Suppose that $n:=0$. From (5), we have $\parallel x_1-x\parallel \le \mu {\alpha }_0\parallel x_0-x\parallel +(1-\mu {\alpha }_0)\parallel x_0-x\parallel =\parallel x_0-x\parallel$. Assume that $\parallel x_m-x\parallel \le \parallel x_0-x\parallel$ for some $m\in \mathbb{N}$. Then (5) implies that $\parallel x_{m+1}-x\parallel \le \mu {\alpha }_m\parallel x_0-x\parallel +(1-\mu {\alpha }_m)\parallel x_m-x\parallel \le \mu {\alpha }_m\parallel x_0-x\parallel +(1-\mu {\alpha }_m)\parallel x_0-x\parallel =\parallel x_0-x\parallel$. Hence, induction guarantees that

$$\parallel x_n-x\parallel \le \parallel x_0-x\parallel (n\in \mathbb{N}).$$

Therefore, we find that ${(x_n)}_{n\in \mathbb{N}}$ is bounded. Moreover, since the nonexpansivity of T ensures that ${(T(x_n))}_{n\in \mathbb{N}}$ is also bounded, (C5) holds. Accordingly, Theorem 3.1 says that if ${({\alpha }_n)}_{n\in \mathbb{N}}$ satisfies (C1)-(C3), Algorithm 3.1 when ${\beta }_n:=0$ ($n\in \mathbb{N}$) (i.e., the Halpern algorithm) strongly converges to $P_{Fix(T)}(x_0)$. This means that Theorem 3.1 is a generalization of the convergence analysis of the Halpern algorithm.

3.1 Proof of Theorem 3.1

We first show the following lemma.

Lemma 3.1 Suppose that Assumption  3.1 holds. Then ${(d_n)}_{n\in \mathbb{N}}$, ${(x_n)}_{n\in \mathbb{N}}$, and ${(y_n)}_{n\in \mathbb{N}}$ are bounded.

Proof We have from (C1) and (C4) that ${lim}_{n\to \mathrm{\infty }}{\beta }_n=0$. Accordingly, there exists $n_0\in \mathbb{N}$ such that ${\beta }_n\le 1/2$ for all $n\ge n_0$. Define $M_1:=max\{\parallel d_{n_0}\parallel ,(2/\alpha ){sup}_{n\in \mathbb{N}}\parallel T(x_n)-x_n\parallel \}$. Then (C5) implies that $M_1<\mathrm{\infty }$. Assume that $\parallel d_n\parallel \le M_1$ for some $n\ge n_0$. The triangle inequality ensures that

$$\parallel d_{n+1}\parallel =\parallel \frac{1}{\alpha }(T(x_n)-x_n)+{\beta }_n{d}_n\parallel \le \frac{1}{\alpha }\parallel T(x_n)-x_n\parallel +{\beta }_n\parallel d_n\parallel \le M_1,$$

which means that $\parallel d_n\parallel \le M_1$ for all $n\ge n_0$, i.e., ${(d_n)}_{n\in \mathbb{N}}$ is bounded.

The definition of $y_n$ ($n\in \mathbb{N}$) implies that

$$\begin{array}{rl}{y}_n& =x_n+\alpha (\frac{1}{\alpha }(T(x_n)-x_n)+{\beta }_n{d}_n)\\ =T(x_n)+\alpha {\beta }_n{d}_n.\end{array}$$

(6)

The nonexpansivity of T and (6) imply that, for all $x\in Fix(T)$ and for all $n\ge n_0$,

$$\begin{array}{rl}\parallel y_n-x\parallel & =\parallel T(x_n)+\alpha {\beta }_n{d}_n-x\parallel \\ \le \parallel T(x_n)-T(x)\parallel +\alpha {\beta }_n\parallel d_n\parallel \\ \le \parallel x_n-x\parallel +\alpha M_1{\beta }_n.\end{array}$$

Therefore, we find that, for all $x\in Fix(T)$ and for all $n\ge n_0$,

$$\begin{array}{rl}\parallel x_{n+1}-x\parallel & =\parallel \mu {\alpha }_n(x_0-x)+(1-\mu {\alpha }_n)(y_n-x)\parallel \\ \le \mu {\alpha }_n\parallel x_0-x\parallel +(1-\mu {\alpha }_n)\parallel y_n-x\parallel \\ \le \mu {\alpha }_n\parallel x_0-x\parallel +(1-\mu {\alpha }_n)\{\parallel x_n-x\parallel +\alpha M_1{\beta }_n\}\\ \le (1-\mu {\alpha }_n)\parallel x_n-x\parallel +\mu {\alpha }_n\parallel x_0-x\parallel +\alpha M_1{\beta }_n,\end{array}$$

which, together with (C4) and ${\alpha }_n<1$ ($n\in \mathbb{N}$), means that, for all $x\in Fix(T)$ and for all $n\ge n_0$,

$$\parallel x_{n+1}-x\parallel \le (1-\mu {\alpha }_n)\parallel x_n-x\parallel +\mu {\alpha }_n(\parallel x_0-x\parallel +\frac{\alpha M_1}{\mu }).$$

Induction guarantees that, for all $x\in Fix(T)$ and for all $n\ge n_0$,

$$\parallel x_n-x\parallel \le \parallel x_0-x\parallel +\frac{\alpha M_1}{\mu }.$$

Therefore, ${(x_n)}_{n\in \mathbb{N}}$ is bounded.

The definition of $y_n$ ($n\in \mathbb{N}$) and the boundedness of ${(x_n)}_{n\in \mathbb{N}}$ and ${(d_n)}_{n\in \mathbb{N}}$ imply that ${(y_n)}_{n\in \mathbb{N}}$ is also bounded. This completes the proof. □

Lemma 3.2 Suppose that Assumption  3.1 holds. Then

• (i) ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-x_n\parallel =0$.

• (ii) ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T(x_n)\parallel =0$.

• (iii) ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}〈x_0-x^{\star },y_n-x^{\star }〉\le 0$, where $x^{\star }:=P_{Fix(T)}(x_0)$.

Proof (i) Equation (6), the triangle inequality, and the nonexpansivity of T imply that, for all $n\in \mathbb{N}$,

$$\begin{array}{rl}\parallel y_{n+1}-y_n\parallel & =\parallel T(x_{n+1})-T(x_n)+\alpha ({\beta }_{n+1}{d}_{n+1}-{\beta }_n{d}_n)\parallel \\ \le \parallel T(x_{n+1})-T(x_n)\parallel +\alpha \parallel {\beta }_{n+1}{d}_{n+1}-{\beta }_n{d}_n\parallel \\ \le \parallel x_{n+1}-x_n\parallel +\alpha ({\beta }_{n+1}\parallel d_{n+1}\parallel +{\beta }_n\parallel d_n\parallel ),\end{array}$$

which, together with $\parallel d_n\parallel \le M_1$ ($n\ge n_0$) and (C4), implies that, for all $n\ge n_0$,

$$\parallel y_{n+1}-y_n\parallel \le \parallel x_{n+1}-x_n\parallel +\alpha M_1({\alpha }_{n+1}^2+{\alpha }_n^2).$$

(7)

On the other hand, from ${\alpha }_n\le |{\alpha }_{n+1}-{\alpha }_n|+{\alpha }_{n+1}$ and ${\alpha }_n<1$ ($n\in \mathbb{N}$), we have that, for all $n\in \mathbb{N}$,

$$\begin{array}{rl}{\alpha }_{n+1}^2+{\alpha }_n^2& \le {\alpha }_{n+1}^2+{\alpha }_n(|{\alpha }_{n+1}-{\alpha }_n|+{\alpha }_{n+1})\\ \le ({\alpha }_{n+1}+{\alpha }_n){\alpha }_{n+1}+|{\alpha }_{n+1}-{\alpha }_n|.\end{array}$$

(8)

We also find that, for all $n\in \mathbb{N}\mathrm{\setminus }\{0\}$,

$$\begin{array}{rl}\parallel x_{n+1}-x_n\parallel =& \parallel \mu {\alpha }_n{x}_0+(1-\mu {\alpha }_n)y_n-(\mu {\alpha }_{n-1}{x}_0+(1-\mu {\alpha }_{n-1})y_{n-1})\parallel \\ =& \parallel \mu ({\alpha }_n-{\alpha }_{n-1})x_0+(1-\mu {\alpha }_n)(y_n-y_{n-1})\\ +\mu ({\alpha }_{n-1}-{\alpha }_n)y_{n-1}\parallel \\ \le & \mu |{\alpha }_n-{\alpha }_{n-1}|(\parallel x_0\parallel +\parallel y_{n-1}\parallel )+(1-\mu {\alpha }_n)\parallel y_n-y_{n-1}\parallel \\ \le & (1-\mu {\alpha }_n)\parallel y_n-y_{n-1}\parallel +M_2|{\alpha }_n-{\alpha }_{n-1}|,\end{array}$$

where $M_2:={sup}_{n\in \mathbb{N}}\mu (\parallel x_0\parallel +\parallel y_n\parallel )<\mathrm{\infty }$. Hence, (7) and (8) ensure that, for all $n\ge n_0$,

$$\begin{array}{rl}\parallel x_{n+1}-x_n\parallel \le & (1-\mu {\alpha }_n)\parallel x_n-x_{n-1}\parallel +\alpha M_1(({\alpha }_n+{\alpha }_{n-1}){\alpha }_n+|{\alpha }_n-{\alpha }_{n-1}|)\\ +M_2|{\alpha }_n-{\alpha }_{n-1}|\\ =& (1-\mu {\alpha }_n)\parallel x_n-x_{n-1}\parallel +(\alpha M_1+M_2)|{\alpha }_n-{\alpha }_{n-1}|\\ +\frac{\alpha M_1}{\mu }({\alpha }_n+{\alpha }_{n-1})\mu {\alpha }_n.\end{array}$$

Proposition 2.2, (C1), (C2), and (C3) lead us to

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =0.$$

(9)

(ii) From $\parallel x_{n+1}-y_n\parallel =\mu {\alpha }_n\parallel x_0-y_n\parallel \le M_2{\alpha }_n$ ($n\in \mathbb{N}$), (C1) means that ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-y_n\parallel =0$. Since the triangle inequality ensures that $\parallel y_n-x_n\parallel \le \parallel y_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel$ ($n\in \mathbb{N}$), we find from (9) that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel d_{n+1}\parallel =\frac{1}{\alpha }\underset{n\to \mathrm{\infty }}{lim}\parallel y_n-x_n\parallel =0.$$

(10)

From the definition of $d_{n+1}$ ($n\in \mathbb{N}$), we have, for all $n\ge n_0$,

$$0\le \frac{1}{\alpha }\parallel T(x_n)-x_n\parallel \le \parallel d_{n+1}\parallel +{\beta }_n\parallel d_n\parallel \le \parallel d_{n+1}\parallel +M_1{\beta }_n.$$

Since Equation (10) and ${lim}_{n\to \mathrm{\infty }}{\beta }_n=0$ guarantee that the right-hand side of the above inequality converges to 0, we find that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel T(x_n)-x_n\parallel =0.$$

(11)

• (iii) From the limit superior of ${(〈x_0-x^{\star },y_n-x^{\star }〉)}_{n\in \mathbb{N}}$, there exists ${(y_{n_k})}_{k\in \mathbb{N}}$ ($\subset {(y_n)}_{n\in \mathbb{N}}$) such that

  $$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈x_0-x^{\star },y_n-x^{\star }〉=\underset{k\to \mathrm{\infty }}{lim}〈x_0-x^{\star },y_{n_k}-x^{\star }〉.$$

  (12)

Moreover, since ${(y_{n_k})}_{k\in \mathbb{N}}$ is bounded, there exists ${(y_{n_{k_i}})}_{i\in \mathbb{N}}$ ($\subset {(y_{n_k})}_{k\in \mathbb{N}}$) which weakly converges to some point $\hat{y}$ (∈H). Equation (10) guarantees that ${(x_{n_{k_i}})}_{i\in \mathbb{N}}$ weakly converges to $\hat{y}$.

We shall show that $\hat{y}\in Fix(T)$. Assume that $\hat{y}\notin Fix(T)$, i.e., $\hat{y}\ne T(\hat{y})$. Proposition 2.3, (11), and the nonexpansivity of T ensure that

$$\begin{array}{rl}\underset{i\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_{k_i}}-\hat{y}\parallel & <\underset{i\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_{k_i}}-T(\hat{y})\parallel \\ =\underset{i\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_{k_i}}-T(x_{n_{k_i}})+T(x_{n_{k_i}})-T(\hat{y})\parallel \\ =\underset{i\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel T(x_{n_{k_i}})-T(\hat{y})\parallel \\ \le \underset{i\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_{k_i}}-\hat{y}\parallel .\end{array}$$

This is a contradiction. Hence, $\hat{y}\in Fix(T)$. Hence, (12) and Proposition 2.1(ii) guarantee that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈x_0-x^{\star },y_n-x^{\star }〉=\underset{i\to \mathrm{\infty }}{lim}〈x_0-x^{\star },y_{n_{k_i}}-x^{\star }〉=〈x_0-x^{\star },\hat{y}-x^{\star }〉\le 0.$$

This completes the proof. □

Now, we are in a position to prove Theorem 3.1.

Proof of Theorem 3.1 The inequality ${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2〈y,x+y〉$ ($x,y\in H$), (6), and the nonexpansivity of T imply that, for all $n\in \mathbb{N}$,

$$\begin{array}{rl}{\parallel y_n-x^{\star }\parallel }^2& ={\parallel T(x_n)-x^{\star }+\alpha {\beta }_n{d}_n\parallel }^2\\ \le {\parallel T(x_n)-T\left(x^{\star }\right)\parallel }^2+2\alpha {\beta }_n〈y_n-x^{\star },d_n〉\\ \le {\parallel x_n-x^{\star }\parallel }^2+M_3{\alpha }_n^2,\end{array}$$

where ${\beta }_n\le {\alpha }_n^2$ ($n\in \mathbb{N}$) and $M_3:={sup}_{n\in \mathbb{N}}2\alpha |〈y_n-x^{\star },d_n〉|<\mathrm{\infty }$. We thus have that, for all $n\in \mathbb{N}$,

$$\begin{array}{rl}{\parallel x_{n+1}-x^{\star }\parallel }^2=& {\parallel \mu {\alpha }_n(x_0-x^{\star })+(1-\mu {\alpha }_n)(y_n-x^{\star })\parallel }^2\\ =& {\mu }^2{\alpha }_n^2{\parallel x_0-x^{\star }\parallel }^2+{(1-\mu {\alpha }_n)}^2{\parallel y_n-x^{\star }\parallel }^2\\ +2\mu {\alpha }_n(1-\mu {\alpha }_n)〈x_0-x^{\star },y_n-x^{\star }〉\\ \le & {\mu }^2{\alpha }_n^2{\parallel x_0-x^{\star }\parallel }^2+{(1-\mu {\alpha }_n)}^2\{{\parallel x_n-x^{\star }\parallel }^2+M_3{\alpha }_n^2\}\\ +2\mu {\alpha }_n(1-\mu {\alpha }_n)〈x_0-x^{\star },y_n-x^{\star }〉\\ \le & (1-\mu {\alpha }_n){\parallel x_n-x^{\star }\parallel }^2+\{\mu {\alpha }_n{\parallel x_0-x^{\star }\parallel }^2+\frac{M_3{\alpha }_n}{\mu }\}\mu {\alpha }_n\\ +\{2(1-\mu {\alpha }_n)〈x_0-x^{\star },y_n-x^{\star }〉\}\mu {\alpha }_n.\end{array}$$

Proposition 2.2, (C1), (C2), and Lemma 3.2(iii) lead one to deduce that

$$\underset{n\to \mathrm{\infty }}{lim}{\parallel x_{n+1}-x^{\star }\parallel }^2=0.$$

This guarantees that ${(x_n)}_{n\in \mathbb{N}}$ generated by Algorithm 3.1 strongly converges to $x^{\star }:=P_{Fix(T)}(x_0)$. □

Suppose that $Fix(T)$ is bounded. Then we can set a bounded, closed convex set C ($\supset Fix(T)$) such that $P_C$ can be computed within a finite number of arithmetic operations (e.g., C is a closed ball with a large enough radius). Hence, we can compute

$$x_{n+1}:=P_C(\mu {\alpha }_n{x}_0+(1-\mu {\alpha }_n)y_n)$$

(13)

instead of $x_{n+1}$ in Algorithm 3.1. From ${(x_n)}_{n\in \mathbb{N}}\subset C$, the boundedness of C means that ${(x_n)}_{n\in \mathbb{N}}$ is bounded. The nonexpansivity of T guarantees that $\parallel T(x_n)-T(x)\parallel \le \parallel x_n-x\parallel$ ($x\in Fix(T)$), which means that ${(T(x_n))}_{n\in \mathbb{N}}$ is bounded. Therefore, (C5) holds. We can prove that Algorithm 3.1 with (13) strongly converges to a point in $Fix(T)$ by referring to the proof of Theorem 3.1.

Let us consider the case where $Fix(T)$ is unbounded. In this case, we cannot choose a bounded C satisfying $Fix(T)\subset C$. Although we can execute Algorithm 3.1, we need to verify the boundedness of ${(T(x_n)-x_n)}_{n\in \mathbb{N}}$. Instead, we can apply the Halpern algorithm (1) to this case without any problem. However, the Halpern algorithm would converge slowly because it is based on the steepest descent method (see Section 1). Hence, in this case, it would be desirable to execute not only the Halpern algorithm but also Algorithm 3.1.

4 Numerical examples and conclusion

Let us apply the Halpern algorithm (1) and Algorithm 3.1 to the following convex feasibility problem [5], [[1], Example 5.21].

Problem 4.1 Given a nonempty, closed convex set $C_i\subset {\mathbb{R}}^N$ ($i=0,1,\dots ,m$),

$$\text{find }{x}^{\star }\in C:=\bigcap _{i=0}^m{C}_i,$$

where one assumes that $C\ne \mathrm{\varnothing }$.

Define a mapping $T:{\mathbb{R}}^N\to {\mathbb{R}}^N$ by

$$T:=P_0\left(\frac{1}{m}\sum _{i=1}^m{P}_i\right),$$

(14)

where $P_i:=P_{C_i}$ ($i=0,1,\dots ,m$) stands for the metric projection onto $C_i$. Since $P_i$ ($i=0,1,\dots ,m$) is nonexpansive, T defined by (14) is also nonexpansive. Moreover, we find that

$$Fix(T)=Fix(P_0)\cap \bigcap _{i=1}^{m}Fix(P_i)=C_0\cap \bigcap _{i=1}^m{C}_i=C.$$

Therefore, Problem 4.1 coincides with Problem 2.1 with T defined by (14).

The experiment used an Apple Macbook Air with a 1.30GHz Intel(R) Core(TM) i5-4250U CPU and 4GB DDR3 memory. The Halpern algorithm (1) and Algorithm 3.1 were written in Java. The operating system of the computer was Mac OSX version 10.8.5.

We set $\alpha :=1$, $\mu :=1/{10}^5$, ${\alpha }_n:=1/(n+1)$ ($n\in \mathbb{N}$), and ${\beta }_n:=1/{(n+1)}^2$ ($n\in \mathbb{N}$) in Algorithm 3.1 and compared Algorithm 3.1 with the Halpern algorithm (1) with ${\alpha }_n:=\mu /(n+1)$ ($n\in \mathbb{N}$). In the experiment, we set $C_i$ ($i=0,1,\dots ,m$) as a closed ball with center $c_i\in {\mathbb{R}}^N$ and radius $r_i>0$. Thus, $P_i$ ($i=0,1,\dots ,m$) can be computed with

$$P_i(x):=c_i+\frac{r_i}{\parallel c_i-x\parallel }(x-c_i)\text{if }\parallel c_i-x\parallel >r_i,$$

or $P_i(x):=x$ if $\parallel c_i-x\parallel \le r_i$.

We set $N:=100$, $m:=3$, $r_i:=1$ ($i=0,1,2,3$), and $c_0:=0$. The experiment used random vectors $c_i\in {(-1/\sqrt{N},1/\sqrt{N})}^N$ ($i=1,2,3$) generated by the java.util.Random class so as to satisfy $C\ne \mathrm{\varnothing }$. We also used the java.util.Random class to set a random initial point in ${(-16,16)}^N$.

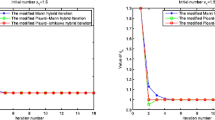
Figure 1 describes the behaviors of $\parallel T(x_n)-x_n\parallel$ for the Halpern algorithm (1) and Algorithm 3.1 (proposed). The x-axis and y-axis represent the elapsed time and value of $\parallel T(x_n)-x_n\parallel$. The results show that compared with the Halpern algorithm, Algorithm 3.1 dramatically reduces the time required to satisfy $\parallel T(x_n)-x_n\parallel <{10}^{-6}$. We found that the Halpern algorithm took 850 iterations to satisfy $\parallel T(x_n)-x_n\parallel <{10}^{-6}$, whereas Algorithm 3.1 took only six.

Figure 1

Behavior of $\mathbf{\parallel }\mathit{T}\mathbf{(}{\mathit{x}}_{\mathit{n}}\mathbf{)}\mathbf{-}{\mathit{x}}_{\mathit{n}}\mathbf{\parallel }$ for the Halpern algorithm and Algorithm  3.1 (proposed). (The Halpern algorithm took 850 iterations to satisfy $\parallel T(x_n)-x_n\parallel <{10}^{-6}$, whereas Algorithm 3.1 took only six.)

This paper presented an algorithm to accelerate the Halpern algorithm for finding a fixed point of a nonexpansive mapping on a real Hilbert space and its convergence analysis. The convergence analysis guarantees that the proposed algorithm strongly converges to a fixed point of a nonexpansive mapping under certain assumptions. We numerically compared the abilities of the proposed and Halpern algorithms in solving a concrete fixed point problem. The results showed that the proposed algorithm performs better than the Halpern algorithm.

Endnote

Examples of ${({\alpha }_n)}_{n\in \mathbb{N}}$ and ${({\beta }_n)}_{n\in \mathbb{N}}$ satisfying (C1)-(C4) are ${\alpha }_n:=1/{(n+1)}^a$ and ${\beta }_n:=1/{(n+1)}^{2a}$ ($n\in \mathbb{N}$), where $a\in (0,1]$.