Abstract
In this paper, we use the notion of a mixed weakly monotone pair of maps of Gordji et al. (Fixed Point Theory Appl. 2012:95, 2012) to state a coupled common fixed point theorem for maps on partially ordered S-metric spaces. This result generalizes the main results of Gordji et al. (Fixed Point Theory Appl. 2012:95, 2012), Bhaskar, Lakshmikantham (Nonlinear Anal. 65(7):1379-1393, 2006), Kadelburg et al. (Comput. Math. Appl. 59:3148-3159, 2010) into the structure of S-metric spaces.
Similar content being viewed by others
1 Introduction and preliminaries
There are many generalized metric spaces such as 2-metric spaces [1], G-metric spaces [2], -metric spaces [3], partial metric spaces [4] and cone metric spaces [5]. These notions have been investigated by many authors and various versions of fixed point theorems have been stated in [6–23] recently. In [24], Sedghi, Shobe and Aliouche have introduced the notion of an S-metric space and proved that this notion is a generalization of a G-metric space and a -metric space. Also, they have proved some properties of S-metric spaces and some fixed point theorems for a self-map on an S-metric space. An interesting work that naturally rises is to transport certain results in metric spaces and known generalized metric spaces to S-metric spaces. In this way, some results have been obtained in [24–26].
In [27], Gordji et al. have introduced the concept of a mixed weakly monotone pair of maps and proved some coupled common fixed point theorems for a contractive-type maps with the mixed weakly monotone property in partially ordered metric spaces. These results give rise to stating coupled common fixed point theorems for maps with the mixed weakly monotone property in partially ordered S-metric spaces.
In this paper, we use the notion of a mixed weakly monotone pair of maps to state a coupled common fixed point theorem for maps on partially ordered S-metric spaces. This result generalizes the main results of [6, 27, 28] into the structure of S-metric spaces.
First we recall some notions, lemmas and examples which will be useful later.
Definition 1.1 [[24], Definition 2.1]
Let X be a nonempty set. An S-metric on X is a function that satisfies the following conditions for all :
-
1.
if and only if .
-
2.
.
The pair is called an S-metric space.
The following is an intuitive geometric example for S-metric spaces.
Example 1.2 [[24], Example 2.4]
Let and d be an ordinary metric on X. Put
for all , that is, S is the perimeter of the triangle given by x, y, z. Then S is an S-metric on X.
Lemma 1.3 [[24], Lemma 2.5]
Let be an S-metric space. Then for all .
The following lemma is a direct consequence of Definition 1.1 and Lemma 1.3.
Lemma 1.4 [[25], Lemma 1.6]
Let be an S-metric space. Then
and
for all .
Definition 1.5 [[24], Definition 2.8]
Let be an S-metric space.
-
1.
A sequence is said to converge to if as . That is, for each , there exists such that for all we have . We write for brevity.
-
2.
A sequence is called a Cauchy sequence if as . That is, for each , there exists such that for all we have .
-
3.
The S-metric space is said to be complete if every Cauchy sequence is a convergent sequence.
From [[24], Examples on p.260] we have the following.Example 1.6
-
1.
Let ℝ be a real line. Then
for all is an S-metric on ℝ. This S-metric is called the usual S-metric on ℝ. Furthermore, the usual S-metric space ℝ is complete.
-
2.
Let Y be a nonempty subset of ℝ. Then
for all is an S-metric on Y. Furthermore, if Y is a closed subset of the usual metric space ℝ, then the S-metric space Y is complete.
Lemma 1.7 [[24], Lemma 2.12]
Let be an S-metric space. If and , then .
Definition 1.8 [24]
Let be an S-metric space. For and , we define the open ball and the closed ball with center x and radius r as follows:

The topology induced by the S-metric or the S-metric topology is the topology generated by the base of all open balls in X.
Lemma 1.9 Let be a sequence in X. Then in the S-metric space if and only if in the S-metric topological space X.
Proof It is a direct consequence of Definition 1.5(1) and Definition 1.8. □
The following lemma shows that every metric space is an S-metric space.
Lemma 1.10 Let be a metric space. Then we have
-
1.
for all is an S-metric on X.
-
2.
in if and only if in .
-
3.
is Cauchy in if and only if is Cauchy in .
-
4.
is complete if and only if is complete.
Proof
-
1.
See [[24], Example (3), p.260].
-
2.
in if and only if , if and only if
that is, in .
-
3.
is Cauchy in if and only if as , if and only if
as , that is, is Cauchy in .
-
4.
It is a direct consequence of (2) and (3).
□
The following example proves that the inverse implication of Lemma 1.10 does not hold.
Example 1.11 Let and for all . By [[24], Example (1), p.260], is an S-metric space. We will prove that there does not exist any metric d such that for all . Indeed, suppose to the contrary that there exists a metric d with for all . Then and for all . It is a contradiction.
Lemma 1.12 [[27], p.7]
Let be a metric space. Then is a metric space with the metric given by
for all .
Lemma 1.13 Let be an S-metric space. Then is an S-metric space with the S-metric D given by
for all .
Proof For all , we have and
if and only if , , that is, ; and

By the above, D is an S-metric on . □
Remark 1.14 Let be a metric space. By using Lemma 1.13 with , we get
for all .
Lemma 1.15 [[17], p.4]
Let be a partially ordered set. Then is a partially ordered set with the partial order ⪯ defined by
Remark 1.16 Let X be a subset of ℝ with the usual order. For each , put and , then and . Therefore, for each , there exists that is comparable to and .
Definition 1.17 [[27], Definition 1.5]
Let be a partially ordered set and be two maps. We say that a pair has the mixed weakly monotone property on X if, for all , we have
and
Example 1.18 [[27], Example 1.6]
Let be two functions given by
Then the pair has the mixed weakly monotone property.
Example 1.19 [[27], Example 1.7]
Let be two functions given by
Then f and g have the mixed monotone property but the pair does not have the mixed weakly monotone property.
Remark 1.20 [[27], Remark 2.5]
Let be a partially ordered set; be a map with the mixed monotone property on X. Then for all , the pair has the mixed weakly monotone property on X.
2 Main results
Theorem 2.1 Let be a partially ordered S-metric space; be two maps such that
-
1.
X is complete;
-
2.
The pair has the mixed weakly monotone property on X; or for some ;
-
3.
There exist satisfying and
 (2.1)
(2.1)
for all with and where D is defined as in Lemma 1.13;
-
4.
f or g is continuous or X has the following property:
-
(a)
If is an increasing sequence with , then for all ;
-
(b)
If is an decreasing sequence with , then for all .
Then f and g have a coupled common fixed point in X.
Proof First we note that the roles of f and g can be interchanged in the assumptions. We need only prove the case and , the case and is proved similarly by interchanging the roles of f and g.
Step 1. We construct two Cauchy sequences in X.
Put , . Since has the mixed weakly monotone property, we have
and
Put , . Then we have
and
Continuously, for all , we put
that satisfy
We will prove that and are two Cauchy sequences. For all , it follows from (2.1) that

By using (2.2) we get
That is,

Analogously to (2.4), we have

It follows from (2.4) and (2.5) that

For all , by interchanging the roles of f and g and using (2.1) again, we have

By using (2.2) we get
That is,

Analogously to (2.7), we have

It follows from (2.7) and (2.8) that

For all , (2.6) and (2.9) combine to give

Now we have

and

For all with , by using Lemma 1.4 and (2.11), (2.12), we have

Similarly, we have

and

and

Hence, for all with , it follows that
Since , taking the limit as , we get
It implies that
Therefore, and are two Cauchy sequences in X. Since X is complete, there exist such that and in X as .
Step 2. We prove that is a coupled common fixed point of f and g. We consider the following two cases.
Case 2.1. f is continuous. We have
and
Now using (2.1) we have

Therefore,

That is,
Since , we get . That is, and . Therefore, is a coupled common fixed point of f and g.
Case 2.2. g is continuous. We can also prove that is a coupled common fixed point of f and g similarly as in Case 2.1.
Case 2.3. X satisfies two assumptions (a) and (b). Then by (2.3) we get and for all . By using Lemma 1.4 and Lemma 1.13, we have

By interchanging the roles of f and g and using (2.1), we have

Again, by using (2.1), we have

It follows from (2.13), (2.14) and (2.15) that

By using Lemma 1.7 and taking the limit as in (2.16), we have

It implies that

Since , we have , that is, and . Similarly, one can show that and . This proves that is a coupled common fixed point of f and g. □
From Theorem 2.1, we have following corollaries.
Corollary 2.2 [[27], Theorems 2.1 and 2.2]
Let be a partially ordered metric space; be two maps such that
-
1.
X is complete;
-
2.
The pair has the mixed weakly monotone property on X; , or , for some ;
-
3.
There exist satisfying and
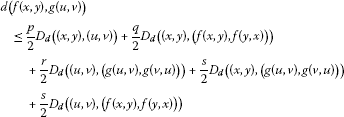 (2.19)
(2.19)
for all with and , where is defined as in Lemma 1.12;
-
4.
f or g is continuous or X has the following property:
-
(a)
If is an increasing sequence with , then for all ;
-
(b)
If is an decreasing sequence with , then for all .
Then f and g have a coupled common fixed point in X.
Proof It is a direct consequence of Lemma 1.10, Remark 1.14 and Theorem 2.1. □
For similar results of the following for maps on metric spaces and cone metric spaces, the readers may refer to [[6], Theorems 2.1, 2.2, 2.4 and 2.6] and [[28], Theorem 3.1].
Corollary 2.3 Let be a partially ordered S-metric space and be a map such that
-
1.
X is complete;
-
2.
f has the mixed monotone property on X; and for some ;
-
3.
There exist satisfying and
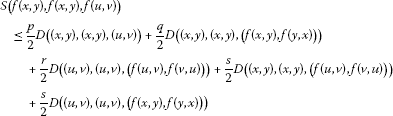 (2.20)
(2.20)
for all with and ;
-
4.
f is continuous or X has the following property:
-
(a)
If is an increasing sequence with , then for all ;
-
(b)
If is an decreasing sequence with , then for all .
Then f has a coupled fixed point in X.
Proof By choosing in Theorem 2.1 and using Remark 1.20, we get the conclusion. □
Corollary 2.4 Let be a partially ordered S-metric space and be a map such that
-
1.
X is complete;
-
2.
f has the mixed monotone property on X; and for some ;
-
3.
There exists satisfying
(2.21)
for all with and ;
-
4.
f is continuous or X has the following property:
-
(a)
If is an increasing sequence with , then for all ;
-
(b)
If is an decreasing sequence with , then for all .
Then f has a coupled fixed point in X.
Proof By choosing and , in Theorem 2.1 and using Remark 1.20, we get the conclusion. □
Corollary 2.5 Assume that X is a totally ordered set in addition to the hypotheses of Theorem 2.1; in particular, Corollary 2.3, Corollary 2.4. Then f and g have a unique coupled common fixed point and .
Proof By Theorem 2.1, f and g have a coupled common fixed point . Let be another coupled common fixed point of f and g. Without loss of generality, we may assume that . Then by (2.1) and Lemma 1.3, we have

Since , we have . Then and . This proves that the coupled common fixed point of f and g is unique.
Moreover, by using (2.1) and Lemma 1.3 again, we get
Since , we get , that is, . □
Finally, we give an example to demonstrate the validity of the above results.
Example 2.6 Let with the S-metric as in Example 1.6 and the usual order ≤. Then X is a totally ordered, complete S-metric space. For all , put
Then the pair has the mixed weakly monotone property and
Then the contraction (2.1) is satisfied with and . Note that other assumptions of Corollary 2.5 are also satisfied and is the unique common fixed point of f and g.
References
Gähler S: Über die uniformisierbarkeit 2-metrischer Räume. Math. Nachr. 1965, 28: 235–244.
Mustafa Z, Sims B: A new approach to generalized metric spaces. J. Nonlinear Convex Anal. 2006, 7(2):289–297.
Sedghi S, Shobe N, Zhou H: A common fixed point theorem in -metric spaces. Fixed Point Theory Appl. 2007., 2007: Article ID 27906
Bukatin M, Kopperman R, Matthews S, Pajoohesh H: Partial metric spaces. Am. Math. Mon. 2009, 116: 708–718. 10.4169/193009709X460831
Huang LG, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 2007, 332: 1468–1476. 10.1016/j.jmaa.2005.03.087
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. 2006, 65(7):1379–1393. 10.1016/j.na.2005.10.017
Sintunavarat W, Radenović S, Golubović Z, Kumam P: Coupled fixed point theorems for F -invariant set and applications. Appl. Math. Inf. Sci. 2013, 7(1):247–255.
Abbas M, Nazir T, Radenović S: Common coupled fixed points of generalized contractive mappings in partially ordered metric spaces. Positivity 2013. doi:10.1007/s11117–012–0219-z
Kadelburg Z, Nashine HK, Radenović S: Coupled fixed point results under -cone metric and w -cone-distance. Bull. Math. Anal. Appl. 2012, 2(2):51–63.
Kadelburg Z, Radenović S: Common coupled fixed point results in partially ordered Gmetric spaces. Adv. Fixed Point Theory 2012, 2: 29–36.
Radenović S, Pantelić S, Salimi P, Vujaković J: A note on some tripled coincidence point results in G -metric spaces. Int. J. Math. Sci. Eng. App. 2012, 6(VI):23–28.
Rajić, VČ, Radenović, S: A note on tripled fixed point of w-compatible mappings in -cone metric spaces. Thai J. Math. (2013, accepted paper)
Nashine HK, Kadelburg Z, Radenović S: Coupled common fixed point theorems for -compatible mappings in ordered cone metric spaces. Appl. Math. Comput. 2012, 218: 5422–5432. 10.1016/j.amc.2011.11.029
Jleli M, Rajić VČ, Samet B, Vetro C: Fixed point theorems on ordered metric spaces and applications to nonlinear elastic beam equations. J. Fixed Point Theory Appl. 2012. doi:10.1007/s11784–012–0081–4
Golubović Z, Kadelburg Z, Radenović S: Coupled coincidence points of mappings in ordered partial metric spaces. Abstr. Appl. Anal. 2012., 2012: Article ID 192581
Dorić D, Kadelburg Z, Radenović S: Coupled fixed point results for mappings without mixed monotone property. Appl. Math. Lett. 2012, 25: 1803–1808. 10.1016/j.aml.2012.02.022
Ding HS, Li L, Radenovic S: Coupled coincidence point theorems for generalized nonlinear contraction in partially ordered metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 96
Altun I, Acar O: Fixed point theorems for weak contractions in the sense of Berinde on partial metric spaces. Topol. Appl. 2012, 159: 2642–2648. 10.1016/j.topol.2012.04.004
Aydi H, Karapinar E: A Meir-Keeler common type fixed point theorem on partial metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 26
Berinde V: Generalized coupled fixed point theorems for mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 2011., 74: Article ID 18
Berinde V, Vetro F: Common fixed points of mappings satisfying implicit contractive conditions. Fixed Point Theory Appl. 2012., 2012: Article ID 105
Choudhurya BS, Kundu A: A coupled coincidence point result in partially ordered metric spaces for compatible mappings. Nonlinear Anal. 2010, 73: 2524–2531. 10.1016/j.na.2010.06.025
Lakshmikantham V, Ćirić L: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal. 2009, 70(12):4341–4349. 10.1016/j.na.2008.09.020
Sedghi S, Shobe N, Aliouche A: A generalization of fixed point theorem in S -metric spaces. Mat. Vesn. 2012, 64(3):258–266.
An, TV, Dung, NV: Two fixed point theorems in S-metric spaces. Preprint (2012)
Sedghi, S, Dung, NV: Fixed point theorems on S-metric spaces. Mat. Vesnik (2012, accepted paper)
Gordji ME, Ramezani M, Cho YJ, Akbartabar E: Coupled common fixed point theorems for mixed weakly monotone mappings in partially ordered metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 95
Kadelburg Z, Pavlović M, Radenović S: Common fixed point theorems for ordered contractions and quasicontractions in ordered cone metric spaces. Comput. Math. Appl. 2010, 59: 3148–3159. 10.1016/j.camwa.2010.02.039
Acknowledgements
The author would like to thank the referees for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dung, N.V. On coupled common fixed points for mixed weakly monotone maps in partially ordered S-metric spaces. Fixed Point Theory Appl 2013, 48 (2013). https://doi.org/10.1186/1687-1812-2013-48
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-48