Iterative approximation of common element of solution sets of various nonlinear operator problems

Abstract

In this paper, we prove strong convergence theorem for finding a common element of the set of fixed point of a finite family of nonexpansive mappings and a finite family of ${\kappa }_i$-strictly pseudocontractive mappings and the set of a finite family of the set of solution of equilibrium problems by using the new mapping generated by a finite family of nonexpansive mappings and a finite family of ${\kappa }_i$-strictly pseudocontractive mappings and a sequences of positive real numbers. Furthermore, by using our main result, we obtain two interesting theorems involving variational inequality problems and variational inclusion problems. In the last section, we give numerical examples to support our main results.

1 Introduction

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. A self mapping $f:C\to C$ is a contraction on C if there exists a constant $k\in [0,1)$ such that $\parallel f(x)-f(y)\parallel \le k\parallel x-y\parallel$, $\mathrm{\forall }x,y\in C$. Let $T:C\to C$ be a mapping, a point $x\in C$ is called a fixed point of T if and only if $Tx=x$. In this paper, we use $F(T)$ to denote the set of fixed point of T. Recall the following definitions.

Definition 1.1 A mapping $T:C\to C$ is called nonexpansive if and only if for all $x,y\in C$,

$$\parallel Tx-Ty\parallel \le \parallel x-y\parallel .$$

Definition 1.2 A mapping $T:C\to C$ is called κ-strictly pseudocontractive [1] if and only if there exists a constant $\kappa \in [0,1)$ such that for all $x,y\in C$,

$${\parallel Tx-Ty\parallel }^2\le {\parallel x-y\parallel }^2+\kappa {\parallel (I-T)x-(I-T)y\parallel }^2.$$

(1.1)

For such case, T is also said to be a κ-strictly pseudo contraction.

Note that the class of κ-strict pseudo-contractions strictly includes the class of nonexpansive mappings, that is T is nonexpansive if and only if T is 0-strict pseudo-contractive.

Let $F:C\times C\to \mathbb{R}$ be a bifunction. The equilibrium problem for F is to determine its equilibrium points, i.e., the set

$$\mathit{EP}(F)=\{x\in C:F(x,y)\ge 0,\mathrm{\forall }y\in C\}.$$

(1.2)

Given $T:C\to H$, let $F(x,y)=〈Tx,y-x〉$ for all $x,y\in C$. Then $z\in \mathit{EP}(F)$ if and only if $〈Tz,y-z〉\ge 0$ for all $y\in C$, that is, z is a solution of the variational inequality.

Equilibrium problems, which were introduced in [2] in 1994, have had a great impact and influence in the development of several branches of pure and applied sciences. Numerous problems in physics, minimization problems, Nash equilibria in noncooperative games, optimization and economics reduce to find a solution of $\mathit{EP}(F)$ (see, for example, [2–4]). Some methods have been proposed to solve the equilibrium problem (see, for example, [5–7]).

In 2007, Takahashi and Takahashi [8] proved the following theorem.

Theorem 1.1 Let C be a nonempty closed convex subset of H. Let F be a bifunction from $C\times C$ to ℝ satisfying

• (A1) $F(x,x)=0$, $\mathrm{\forall }x\in C$;

• (A2) F is monotone, i.e., $F(x,y)+F(y,x)\le 0$, $\mathrm{\forall }x,y\in C$;

• (A3) $\mathrm{\forall }x,y,z\in C$,

  $$\underset{t\to 0^{+}}{lim}F(tz+(1-t)x,y)\le F(x,y);$$

• (A4) $\mathrm{\forall }x\in C$, $y\mapsto F(x,y)$ is convex and lower semicontinuous;

and let S be a nonexpansive mapping of C into H such that $F(S)\cap \mathit{EP}(G)\ne \mathrm{\varnothing }$. Let f be a contraction of H into itself, and let $\{x_n\}$ and $\{u_n\}$ be sequences generated by $x_1\in H$ and

$$\begin{array}{c}F(u_n,y)+\frac{1}{r_n}〈y-u_n,u_n-x_n〉\ge 0,\mathrm{\forall }y\in C,\hfill \\ x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)S{u}_n\hfill \end{array}$$

for all $n\in N$, where $\{{\alpha }_n\}\subset [0,1]$ and $\{r_n\}\subset (0,1)$ satisfy (C1)-(C3) as follows:

• (C1) ${\alpha }_n\to 0$;

• (C2) ${\sum }_{n=0}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (C3) either ${\sum }_{n=0}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$ or ${lim}_{n\to \mathrm{\infty }}\frac{{\alpha }_{n+1}}{{\alpha }_n}=1$,

and ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{r}_n>0$ and ${\sum }_{n=1}^{\mathrm{\infty }}|r_{n+1}-r_n|<\mathrm{\infty }$.

Then $\{x_n\}$ and $\{u_n\}$ converge strongly to $z\in F(S)\cap \mathit{EP}(F)$, where $z=P_{F(S)\cap \mathit{EP}(F)}f(z)$.

In 2010, Kangtunyakarn and Suantai [9] proved the strong convergence theorem by using the S-mapping generated by a finite family of strictly pseudocontractive mappings and a finite family of real number as follows.

Theorem 1.2 Let H be a Hilbert space, let f be an α-contraction on H, and let A be a strongly positive linear bounded self-adjoint operator with coefficient $\overline{\gamma }>0$. Assume that $0<\gamma <\frac{\overline{\gamma }}{\alpha }$. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strictly pseudo contraction of H into itself for some ${\kappa }_i\in [0,1)$ and $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$ with ${\bigcap }_{i=1}^{N}F(T_i)\ne \mathrm{\varnothing }$. Let $S_n$ be the S-mappings generated by $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$, where ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j})\in I\times I\times I$, $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$ and $\kappa <a\le {\alpha }_1^{n,j},{\alpha }_3^{n,j}\le b<1$ for all $j=1,2,\dots ,N-1$, $\kappa <c\le {\alpha }_1^{n,N}\le 1$, $\kappa \le {\alpha }_3^{n,N}\le d<1$, $\kappa \le {\alpha }_2^{n,j}\le e<1$ for all $j=1,2,\dots ,N$. For a point $u\in H$ and $x_1\in H$, let $\{x_n\}$ and $\{y_n\}$ be the sequences defined iteratively by

$$\{\begin{array}{c}{y}_n={\beta }_n{x}_n+(1-{\beta }_n)S_n{x}_n,\hfill \\ x_{n+1}={\alpha }_n\gamma (a_{n}u+(1-a_n)f(x_n))+(I-{\alpha }_{n}A)y_n,n\ge 1,\hfill \end{array}$$

(1.3)

where $\{{\beta }_n\}$, $\{{\alpha }_n\}$ and $\{a_n\}$ are sequences in $[0,1]$. Assume that the following conditions hold:

• (i) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$ and ${lim}_{n\to \mathrm{\infty }}{a}_n=0$;

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|<\mathrm{\infty }$ for all $j\in \{1,2,3,\dots ,N\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\beta }_{n+1}-{\beta }_n|<\mathrm{\infty }$ and ${\sum }_{n=1}^{\mathrm{\infty }}|a_{n+1}-a_n|<\mathrm{\infty }$;

• (iii) $0\le \kappa \le {\beta }_n<\theta <1$ for all $n\ge 1$ for some $\theta \in (0,1)$.

Then both $\{x_n\}$ and $\{y_n\}$ strongly converge to $q\in {\bigcap }_{i=1}^{N}F(T_i)$, which solves the following variational inequality

$$〈\gamma f(q)-Aq,p-q〉\le 0,\mathrm{\forall }p\in \bigcap _{i=1}^{N}F(T_i).$$

Question Can we prove a strong convergence theorem for finding a common solution of the set of fixed point of a finite family of nonexpansive mappings and a finite family of strictly pseudocontractive mappings and a finite family of the set of solution of equilibrium problems?

Let C be a nonempty closed convex subset of Hilbert space H. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself, and let ${\{S_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself. For each $n\in \mathbb{N}$ and $j=1,2,\dots ,N$, let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j})\in I\times I\times I$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$. We define the mapping $S_n^A:C\to C$ as follows:

$$\begin{array}{c}{U}_{n,0}=I,\hfill \\ U_{n,1}=S_1({\alpha }_1^{n,1}{T}_1{U}_{n,0}+{\alpha }_2^{n,1}{U}_{n,0}+{\alpha }_3^{n,1}I),\hfill \\ U_{n,2}=S_2({\alpha }_1^{n,2}{T}_2{U}_{n,1}+{\alpha }_2^{n,2}{U}_{n,1}+{\alpha }_3^{n,2}I),\hfill \\ U_{n,3}=S_3({\alpha }_1^{n,3}{T}_3{U}_{n,2}+{\alpha }_2^{n,3}{U}_{n,2}+{\alpha }_3^{n,3}I),\hfill \\ ⋮\hfill \\ U_{n,N-1}=S_{N-1}({\alpha }_1^{n,N-1}{T}_{N-1}{U}_{n,N-2}+{\alpha }_2^{n,N-1}{U}_{n,N-2}+{\alpha }_3^{n,N-1}I),\hfill \\ S_n^A=U_{n,N}=S_N({\alpha }_1^{n,N}{T}_N{U}_{n,N-1}+{\alpha }_2^{n,N}{U}_{n,N-1}+{\alpha }_3^{n,N}I).\hfill \end{array}$$

(1.4)

In Lemma 2.8, under suitable conditions of the real sequences $\{{\alpha }_1^{n,j}\}$, $\{{\alpha }_2^{n,j}\}$ and $\{{\alpha }_3^{n,j}\}$ for every $j=1,2,\dots ,N$, we show that $F(S_n^A)={\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)$ and $S_n^A$ is a nonexpansive mapping.

In this paper, motivated by the ongoing research and Theorems 1.1 and 1.2, we prove strong convergence theorem for finding a common solution of the set of fixed point of a finite family of nonexpansive mappings and a finite family of strictly pseudocontractive mappings and a finite family of the set of solution of equilibrium problems by using the mapping defined by (1.4). Furthermore, in the last section, we prove two interesting theorems involving a finite family of the set of solutions of variational inequality problem and variational inclusion problem. In the last section, we give numerical examples to support our main results.

2 Preliminaries

In this section, we need the following lemmas to prove our main result. Let C be a closed convex subset of a real Hilbert space H, let $P_C$ be the metric projection of H onto C, i.e., for $x\in H$, $P_{C}x$ satisfies the property

$$\parallel x-P_{C}x\parallel =\underset{y\in C}{min}\parallel x-y\parallel .$$

The following characterizes the projection $P_C$.

Lemma 2.1 (See [10])

Given $x\in H$ and $y\in C$. Then $P_{C}x=y$ if and only if the following inequality holds

$$〈x-y,y-z〉\ge 0,\mathrm{\forall }z\in C.$$

Lemma 2.2 (See [11])

Let $\{s_n\}$ be a sequence of nonnegative real numbers satisfying

$$s_{n+1}=(1-{\alpha }_n)s_n+{\alpha }_n{\beta }_n,\mathrm{\forall }n\ge 0,$$

where $\{{\alpha }_n\}$, $\{{\beta }_n\}$ satisfy the conditions

$$\begin{array}{c}(1)\{{\alpha }_n\}\subset [0,1],\sum _{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty };\hfill \\ (2)\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{\beta }_n\le 0\mathit{\text{or}}\sum _{n=1}^{\mathrm{\infty }}|{\alpha }_n{\beta }_n|<\mathrm{\infty }.\hfill \end{array}$$

Then ${lim}_{n\to \mathrm{\infty }}{s}_n=0$.

Lemma 2.3 (See [12])

Let $\{s_n\}$ be a sequence of nonnegative real numbers satisfying

$$s_{n+1}=(1-{\alpha }_n)s_n+{\delta }_n,\mathrm{\forall }n\ge 0,$$

where $\{{\alpha }_n\}$ is a sequence in $(0,1)$ and $\{{\delta }_n\}$ is a sequence such that

$$\begin{array}{c}(1)\sum _{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty };\hfill \\ (2)\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{{\delta }_n}{{\alpha }_n}\le 0\mathit{\text{or}}\sum _{n=1}^{\mathrm{\infty }}|{\delta }_n|<\mathrm{\infty }.\hfill \end{array}$$

Then ${lim}_{n\to \mathrm{\infty }}{s}_n=0$.

Lemma 2.4 (See [13])

Let C be a nonempty closed convex subset of a real Hilbert space H, and let $S:C\to C$ be a self-mapping of C. If S is a κ-strict pseudo-contraction mapping, then S satisfies the Lipschitz condition

$$\parallel Sx-Sy\parallel \le \frac{1+\kappa }{1-\kappa }\parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

For solving the equilibrium problem for a bifunction $F:C\times C\to \mathbb{R}$, let us assume that F satisfies the following conditions:

• (A1) $F(x,x)=0$, $\mathrm{\forall }x\in C$;

• (A2) F is monotone, i.e., $F(x,y)+F(y,x)\le 0$, $\mathrm{\forall }x,y\in C$;

• (A3) $\mathrm{\forall }x,y,z\in C$,

  $$\underset{t\to 0^{+}}{lim}F(tz+(1-t)x,y)\le F(x,y);$$

• (A4) $\mathrm{\forall }x\in C$, $y\mapsto F(x,y)$ is convex and lower semicontinuous.

The following lemma appears implicitly in [2].

Lemma 2.5 (See [2])

Let C be a nonempty closed convex subset of H, and let F be a bifunction of $C\times C$ into ℝ satisfying (A1)-(A4). Let $r>0$ and $x\in H$. Then there exists $z\in C$ such that

$$F(z,y)+\frac{1}{r}〈y-z,z-x〉$$

(2.1)

for all $y\in C$.

Lemma 2.6 (See [14])

Assume that $F:C\times C\to \mathbb{R}$ satisfies (A1)-(A4). For $r>0$ and $x\in H$, define a mapping $T_r:H\to C$ as follows:

$$T_r(x)=\{z\in C:F(z,y)+\frac{1}{r}〈y-z,z-x〉\ge 0,\mathrm{\forall }y\in C\}$$

for all $z\in H$. Then the following hold:

• (1) $T_r$ is single-valued;

• (2) $T_r$ is firmly nonexpansive, i.e.,

  $${\parallel T_r(x)-T_r(y)\parallel }^2\le 〈T_r(x)-T_r(y),x-y〉,\mathrm{\forall }x,y\in H;$$

• (3) $F(T_r)=\mathit{EP}(F)$;

• (4) $\mathit{EP}(F)$ is closed and convex.

Lemma 2.7 (See [15])

Let E be a uniformly convex Banach space, C be a nonempty closed convex subset of E, and $S:C\to C$ be a nonexpansive mapping. Then $I-S$ is demi-closed at zero.

Definition 2.1 Let C be a nonempty convex subset of real Hilbert space. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself, and let ${\{S_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself. For each $j=1,2,\dots ,N$, let ${\alpha }_j=({\alpha }_1^j,{\alpha }_2^j,{\alpha }_3^j)\in I\times I\times I$, where $I\in [0,1]$ and ${\alpha }_1^j+{\alpha }_2^j+{\alpha }_3^j=1$. We define the mapping $S^A:C\to C$ as follows:

$$\begin{array}{c}{U}_0=I,\hfill \\ U_1=S_1({\alpha }_1^1{T}_1{U}_0+{\alpha }_2^1{U}_0+{\alpha }_3^{1}I),\hfill \\ U_2=S_2({\alpha }_1^2{T}_2{U}_1+{\alpha }_2^2{U}_1+{\alpha }_3^{2}I),\hfill \\ U_3=S_3({\alpha }_1^3{T}_3{U}_2+{\alpha }_2^3{U}_2+{\alpha }_3^{3}I),\hfill \\ ⋮\hfill \\ U_{N-1}=S_{N-1}({\alpha }_1^{N-1}{T}_{N-1}{U}_{N-2}+{\alpha }_2^{N-1}{U}_{N-2}+{\alpha }_3^{N-1}I),\hfill \\ S^A=U_N=S_N({\alpha }_1^N{T}_N{U}_{N-1}+{\alpha }_2^N{U}_{N-1}+{\alpha }_3^{N}I).\hfill \end{array}$$

This mapping is called the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N$.

Lemma 2.8 Let C be a nonempty closed convex subset of a real Hilbert space. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself, and let ${\{S_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself with ${\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\ne \mathrm{\varnothing }$ and $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$, and let ${\alpha }_j=({\alpha }_1^j,{\alpha }_2^j,{\alpha }_3^j)\in I\times I\times I$, $j=1,2,3,\dots ,N$, where $I=[0,1]$, ${\alpha }_1^j+{\alpha }_2^j+{\alpha }_3^j=1$, ${\alpha }_1^j,{\alpha }_3^j\in (\kappa ,1)$ for all $j=1,2,\dots ,N-1$ and ${\alpha }_1^N\in (\kappa ,1]$, ${\alpha }_3^N\in [\kappa ,1)$, ${\alpha }_2^j\in (\kappa ,1)$ for all $j=1,2,\dots ,N$. Let $S^A$ be the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N$. Then $F(S^A)={\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)$, and $S^A$ is a nonexpansive mapping.

Proof It is easy to see that ${\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\subseteq F(S^A)$. Let $x_0\in F(S^A)$ and $x^{\ast }\in {\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)$. Then we have

$$\begin{array}{rcl}{\parallel S^A{x}_0-x^{\ast }\parallel }^2& =& {\parallel S_N({\alpha }_1^N{T}_N{U}_{N-1}{x}_0+{\alpha }_2^N{U}_{N-1}{x}_0+{\alpha }_3^N{x}_0)-x^{\ast }\parallel }^2\\ \le & {\parallel {\alpha }_1^N{T}_N{U}_{N-1}{x}_0+{\alpha }_2^N{U}_{N-1}{x}_0+{\alpha }_3^N{x}_0-x^{\ast }\parallel }^2\\ =& {\parallel {\alpha }_1^N(T_N{U}_{N-1}{x}_0-x^{\ast })+{\alpha }_2^N(U_{N-1}{x}_0-x^{\ast })+{\alpha }_3^N(x_0-x^{\ast })\parallel }^2\\ =& {\alpha }_1^N{\parallel T_N{U}_{N-1}{x}_0-x^{\ast }\parallel }^2+{\alpha }_2^N{\parallel U_{N-1}{x}_0-x^{\ast }\parallel }^2+{\alpha }_3^N{\parallel x_0-x^{\ast }\parallel }^2\\ -{\alpha }_1^N{\alpha }_2^N{\parallel T_N{U}_{N-1}{x}_0-U_{N-1}{x}_0\parallel }^2-{\alpha }_1^N{\alpha }_3^N{\parallel T_N{U}_{N-1}{x}_0-x_0\parallel }^2\\ -{\alpha }_2^N{\alpha }_3^N{\parallel U_{N-1}{x}_0-x_0\parallel }^2\\ \le & {\alpha }_1^N({\parallel U_{N-1}{x}_0-x^{\ast }\parallel }^2+\kappa {\parallel (I-T_N)U_{N-1}{x}_0-(I-T_N)x^{\ast }\parallel }^2)\\ +{\alpha }_2^N{\parallel U_{N-1}{x}_0-x^{\ast }\parallel }^2+{\alpha }_3^N{\parallel x_0-x^{\ast }\parallel }^2-{\alpha }_1^N{\alpha }_2^N{\parallel T_N{U}_{N-1}{x}_0-U_{N-1}{x}_0\parallel }^2\\ -{\alpha }_1^N{\alpha }_3^N{\parallel T_N{U}_{N-1}{x}_0-x_0\parallel }^2-{\alpha }_2^N{\alpha }_3^N{\parallel U_{N-1}{x}_0-x_0\parallel }^2\\ =& (1-{\alpha }_3^N){\parallel U_{N-1}{x}_0-x^{\ast }\parallel }^2+{\alpha }_1^N(\kappa -{\alpha }_2^N){\parallel (I-T_N)U_{N-1}{x}_0\parallel }^2\\ +(1-(1-{\alpha }_3^N)){\parallel x_0-x^{\ast }\parallel }^2-{\alpha }_1^N{\alpha }_3^N{\parallel T_N{U}_{N-1}{x}_0-x_0\parallel }^2\\ -{\alpha }_2^N{\alpha }_3^N{\parallel U_{N-1}{x}_0-x_0\parallel }^2\\ \le & (1-{\alpha }_3^N){\parallel U_{N-1}{x}_0-x^{\ast }\parallel }^2+{\alpha }_1^N(\kappa -{\alpha }_2^N){\parallel (I-T_N)U_{N-1}{x}_0\parallel }^2\\ +(1-(1-{\alpha }_3^N)){\parallel x_0-x^{\ast }\parallel }^2-{\alpha }_2^N{\alpha }_3^N{\parallel U_{N-1}{x}_0-x_0\parallel }^2\\ \le & \prod _{j=N-1}^N(1-{\alpha }_3^j){\parallel U_{N-2}{x}_0-x^{\ast }\parallel }^2\\ +(1-{\alpha }_3^N){\alpha }_1^{N-1}(\kappa -{\alpha }_2^{N-1}){\parallel (I-T_{N-1})U_{N-2}{x}_0\parallel }^2\\ -(1-{\alpha }_3^N){\alpha }_2^{N-1}{\alpha }_3^{N-1}{\parallel U_{N-2}{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=N-1}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & \prod _{j=N-1}^N(1-{\alpha }_3^j){\parallel U_{N-2}{x}_0-x^{\ast }\parallel }^2+(1-\prod _{j=N-1}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & \prod _{j=N-2}^N(1-{\alpha }_3^j){\parallel U_{N-3}{x}_0-x^{\ast }\parallel }^2\\ +\prod _{j=N-1}^N(1-{\alpha }_3^j){\alpha }_1^{N-2}(\kappa -{\alpha }_2^{N-2}){\parallel (I-T_{N-2})U_{N-3}{x}_0\parallel }^2\\ -\prod _{j=N-1}^N(1-{\alpha }_3^j){\alpha }_2^{N-2}{\alpha }_3^{N-2}{\parallel U_{N-3}{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=N-2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & \prod _{j=N-2}^N(1-{\alpha }_3^j){\parallel U_{N-3}{x}_0-x^{\ast }\parallel }^2+(1-\prod _{j=N-2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ ⋮\\ \le & \prod _{j=3}^N(1-{\alpha }_3^j){\parallel U_2{x}_0-x^{\ast }\parallel }^2\\ +\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_1^3(\kappa -{\alpha }_2^3){\parallel (I-T_3)U_2{x}_0\parallel }^2\\ -\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_2^3{\alpha }_3^3{\parallel U_2{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=3}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\end{array}$$

(2.2)

$$\begin{array}{rc}\le & \prod _{j=3}^N(1-{\alpha }_3^j){\parallel U_2{x}_0-x^{\ast }\parallel }^2+(1-\prod _{j=3}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & \prod _{j=2}^N(1-{\alpha }_3^j){\parallel U_1{x}_0-x^{\ast }\parallel }^2+\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_1^2(\kappa -{\alpha }_2^2){\parallel (I-T_2)U_1{x}_0\parallel }^2\\ -\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_2^2{\alpha }_3^2{\parallel U_1{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\end{array}$$

(2.3)

$$\begin{array}{rc}\le & \prod _{j=2}^N(1-{\alpha }_3^j){\parallel U_1{x}_0-x^{\ast }\parallel }^2+(1-\prod _{j=2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & \prod _{j=1}^N(1-{\alpha }_3^j){\parallel U_0{x}_0-x^{\ast }\parallel }^2\\ +\prod _{j=2}^N(1-{\alpha }_3^j){\alpha }_1^1(\kappa -{\alpha }_2^1){\parallel (I-T_1)U_0{x}_0\parallel }^2\\ -\prod _{j=2}^N(1-{\alpha }_3^j){\alpha }_2^1{\alpha }_3^1{\parallel U_0{x}_0-x_0\parallel }^2+(1-\prod _{j=1}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & {\parallel x_0-x^{\ast }\parallel }^2+\prod _{j=2}^N(1-{\alpha }_3^j){\alpha }_1^1(\kappa -{\alpha }_2^1){\parallel (I-T_1)x_0\parallel }^2.\end{array}$$

(2.4)

By (2.4), we have

$$\prod _{j=2}^N(1-{\alpha }_3^j){\alpha }_1^1({\alpha }_2^1-\kappa ){\parallel (I-T_1)x_0\parallel }^2\le {\parallel x_0-x^{\ast }\parallel }^2-{\parallel x_0-x^{\ast }\parallel }^2=0,$$

which implies that $T_1{x}_0=x_0$, that is, $x_0\in F(T_1)$. It implies that

$$U_1{x}_0=S_1({\alpha }_1^1{T}_1{U}_0{x}_0+{\alpha }_2^1{U}_0{x}_0+{\alpha }_3^1{x}_0)=S_1{x}_0.$$

(2.5)

By (2.3) and (2.5), we have

$$\begin{array}{rcl}{\parallel S^A{x}_0-x^{\ast }\parallel }^2& \le & \prod _{j=2}^N(1-{\alpha }_3^j){\parallel S_1{x}_0-x^{\ast }\parallel }^2\\ +\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_1^2(\kappa -{\alpha }_2^2){\parallel (I-T_2)U_1{x}_0\parallel }^2\\ -\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_2^2{\alpha }_3^2{\parallel U_1{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & {\parallel x_0-x^{\ast }\parallel }^2-\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_2^2{\alpha }_3^2{\parallel U_1{x}_0-x_0\parallel }^2.\end{array}$$

(2.6)

By (2.6), we have

$$\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_2^2{\alpha }_3^2{\parallel U_1{x}_0-x_0\parallel }^2\le 0.$$

It implies that

$$x_0=U_1{x}_0.$$

(2.7)

By (2.5) and (2.7), we have $x_0\in F(S_1)$. Hence, we have

$$x_0\in F(S_1)\cap F(T_1).$$

(2.8)

Since $x_0=U_1{x}_0$ and (2.3), we have

$$\begin{array}{rcl}{\parallel S^A{x}_0-x^{\ast }\parallel }^2& \le & \prod _{j=2}^N(1-{\alpha }_3^j){\parallel U_1{x}_0-x^{\ast }\parallel }^2\\ +\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_1^2(\kappa -{\alpha }_2^2){\parallel (I-T_2)U_1{x}_0\parallel }^2\\ -\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_2^2{\alpha }_3^2{\parallel U_1{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ =& \prod _{j=2}^N(1-{\alpha }_3^j){\parallel x_0-x^{\ast }\parallel }^2\\ +\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_1^2(\kappa -{\alpha }_2^2){\parallel (I-T_2)x_0\parallel }^2\\ +(1-\prod _{j=2}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2.\end{array}$$

It follows that

$$\prod _{j=3}^N(1-{\alpha }_3^j){\alpha }_1^2({\alpha }_2^2-\kappa ){\parallel (I-T_2)x_0\parallel }^2\le 0,$$

which implies that $x_0=T_2{x}_0$, that is, $x_0\in F(T_2)$. Since $x_0=U_1{x}_0=T_2{x}_0$, we have

$$U_2{x}_0=S_2({\alpha }_1^2{T}_2{U}_1{x}_0+{\alpha }_2^2{U}_1{x}_0+{\alpha }_3^2{x}_0)=S_2{x}_0.$$

(2.9)

By (2.2), we have

$$\begin{array}{rcl}{\parallel S^A{x}_0-x^{\ast }\parallel }^2& \le & \prod _{j=3}^N(1-{\alpha }_3^j){\parallel U_2{x}_0-x^{\ast }\parallel }^2\\ +\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_1^3(\kappa -{\alpha }_2^3){\parallel (I-T_3)U_2{x}_0\parallel }^2\\ -\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_2^3{\alpha }_3^3{\parallel U_2{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=3}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & \prod _{j=3}^N(1-{\alpha }_3^j){\parallel S_2{x}_0-x^{\ast }\parallel }^2\\ -\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_2^3{\alpha }_3^3{\parallel U_2{x}_0-x_0\parallel }^2\\ +(1-\prod _{j=3}^N(1-{\alpha }_3^j)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & {\parallel x_0-x^{\ast }\parallel }^2-\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_2^3{\alpha }_3^3{\parallel U_2{x}_0-x_0\parallel }^2.\end{array}$$

It follows that

$$\prod _{j=4}^N(1-{\alpha }_3^j){\alpha }_2^3{\alpha }_3^3{\parallel U_2{x}_0-x_0\parallel }^2\le 0.$$

It implies that

$$x_0=U_2{x}_0.$$

(2.10)

By (2.9) and (2.10), we have $x_0\in F(S_2)$. Hence, we have

$$x_0\in F(S_2)\cap F(T_2).$$

(2.11)

By continuing in this way, we can show that $x_0\in F(S_i)\cap F(T_i)$ and $x_0=U_i{x}_0$ for all $i=1,2,\dots ,N-1$. Finally, we shall show that $x_0\in F(S_N)\cap F(T_N)$. Since

$$\begin{array}{rcl}{\parallel S^A{x}_0-x^{\ast }\parallel }^2& \le & (1-{\alpha }_3^N){\parallel U_{N-1}{x}_0-x^{\ast }\parallel }^2\\ +{\alpha }_1^N(\kappa -{\alpha }_2^N){\parallel (I-T_N)U_{N-1}{x}_0\parallel }^2\\ +(1-(1-{\alpha }_3^N)){\parallel x_0-x^{\ast }\parallel }^2\\ =& (1-{\alpha }_3^N){\parallel S_{N-1}{x}_0-x^{\ast }\parallel }^2+{\alpha }_1^N(\kappa -{\alpha }_2^N){\parallel (I-T_N)x_0\parallel }^2\\ +(1-(1-{\alpha }_3^N)){\parallel x_0-x^{\ast }\parallel }^2\\ \le & {\parallel x_0-x^{\ast }\parallel }^2+{\alpha }_1^N(\kappa -{\alpha }_2^N){\parallel (I-T_N)x_0\parallel }^2.\end{array}$$

It implies that

$${\alpha }_1^N({\alpha }_2^N-\kappa ){\parallel (I-T_N)x_0\parallel }^2\le 0,$$

which implies that $x_0=T_N{x}_0$, that is, $x_0\in F(T_N)$. It implies that

$$x_0=S^A{x}_0=S_N({\alpha }_1^N{T}_N{U}_{N-1}{x}_0+{\alpha }_2^N{U}_{N-1}{x}_0+{\alpha }_3^N{x}_0)=S_N{x}_0.$$

(2.12)

Then we have $x_0\in F(S_N)\cap F(T_N)$. Hence $F(S^A)\subseteq {\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)$.

Applying (2.4), we have that the mapping $S^A$ is a nonexpansive. □

Lemma 2.9 Let C be a nonempty closed convex subset of a real Hilbert space. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself, and let ${\{S_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself with $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$, and let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}),{\alpha }_j=({\alpha }_1^j,{\alpha }_2^j,{\alpha }_3^j)\in I\times I\times I$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$ and ${\alpha }_1^j+{\alpha }_2^j+{\alpha }_3^j=1$ such that ${\alpha }_i^{n,j}\to {\alpha }_i^j\in [0,1]$ as $n\to \mathrm{\infty }$ for $i=1,3$ and $j=1,2,3,\dots ,N$. Moreover, for every $n\in \mathbb{N}$, let $S^A$ and $S_n^A$ be the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N$ and $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$, respectively. Then ${lim}_{n\to \mathrm{\infty }}\parallel S_n^A{x}_n-S^A{x}_n\parallel =0$ for every bounded sequence $\{x_n\}$ in C.

Proof Let $\{x_n\}$ be a bounded sequence in C, $U_k$ and $U_{n,k}$ be generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N$ and $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$, respectively. For each $n\in \mathbb{N}$, we have

$$\begin{array}{rcl}\parallel U_{n,1}{x}_n-U_1{x}_n\parallel & =& \parallel S_1({\alpha }_1^{n,1}{T}_1{x}_n+(1-{\alpha }_1^{n,1})x_n)-S_1({\alpha }_1^1{T}_1{x}_n+(1-{\alpha }_1^1)x_n)\parallel \\ \le & \parallel {\alpha }_1^{n,1}{T}_1{x}_n+(1-{\alpha }_1^{n,1})x_n-{\alpha }_1^1{T}_1{x}_n-(1-{\alpha }_1^1)x_n\parallel \\ =& |{\alpha }_1^{n,1}-{\alpha }_1^1|\parallel T_1{x}_n-x_n\parallel ,\end{array}$$

(2.13)

and for $k\in \{2,3,\dots ,N\}$, by using Lemma 2.4, we obtain

$$\begin{array}{rcl}\parallel U_{n,k}{x}_n-U_k{x}_n\parallel & =& \parallel S_k({\alpha }_1^{n,k}{T}_k{U}_{n,k-1}{x}_n+{\alpha }_2^{n,k}{U}_{n,k-1}{x}_n+{\alpha }_3^{n,k}{x}_n)\\ -S_k({\alpha }_1^k{T}_k{U}_{k-1}{x}_n+{\alpha }_2^k{U}_{k-1}{x}_n+{\alpha }_3^k{x}_n)\parallel \\ \le & \parallel {\alpha }_1^{n,k}{T}_k{U}_{n,k-1}{x}_n+{\alpha }_2^{n,k}{U}_{n,k-1}{x}_n+{\alpha }_3^{n,k}{x}_n\\ -{\alpha }_1^k{T}_k{U}_{k-1}{x}_n-{\alpha }_2^k{U}_{k-1}{x}_n-{\alpha }_3^k{x}_n\parallel \\ =& \parallel {\alpha }_1^{n,k}(T_k{U}_{n,k-1}{x}_n-T_k{U}_{k-1}{x}_n)+({\alpha }_1^{n,k}-{\alpha }_1^k)T_k{U}_{k-1}{x}_n\\ +({\alpha }_3^{n,k}-{\alpha }_3^k)x_n+{\alpha }_2^{n,k}(U_{n,k-1}{x}_n-U_{k-1}{x}_n)\\ +({\alpha }_2^{n,k}-{\alpha }_2^k)U_{k-1}{x}_n\parallel \\ \le & {\alpha }_1^{n,k}\parallel T_k{U}_{n,k-1}{x}_n-T_k{U}_{k-1}{x}_n\parallel +|{\alpha }_1^{n,k}-{\alpha }_1^k|\parallel T_k{U}_{k-1}{x}_n\parallel \\ +|{\alpha }_3^{n,k}-{\alpha }_3^k|\parallel x_n\parallel +{\alpha }_2^{n,k}\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel \\ +|{\alpha }_2^{n,k}-{\alpha }_2^k|\parallel U_{k-1}{x}_n\parallel \\ =& {\alpha }_1^{n,k}\parallel T_k{U}_{n,k-1}{x}_n-T_k{U}_{k-1}{x}_n\parallel +|{\alpha }_1^{n,k}-{\alpha }_1^k|\parallel T_k{U}_{k-1}{x}_n\parallel \\ +{\alpha }_2^{n,k}\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel +|1-{\alpha }_1^{n,k}-{\alpha }_3^{n,k}-1\\ +{\alpha }_1^k+{\alpha }_3^k|\parallel U_{k-1}{x}_n\parallel +|{\alpha }_3^{n,k}-{\alpha }_3^k|\parallel x_n\parallel \\ \le & {\alpha }_1^{n,k}\frac{1+\kappa }{1-\kappa }\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel \\ +|{\alpha }_1^{n,k}-{\alpha }_1^k|\parallel T_k{U}_{k-1}{x}_n\parallel +{\alpha }_2^{n,k}\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel \\ +(|{\alpha }_1^k-{\alpha }_1^{n,k}|+|{\alpha }_3^{n,k}-{\alpha }_3^k|)\parallel U_{k-1}{x}_n\parallel +|{\alpha }_3^{n,k}-{\alpha }_3^k|\parallel x_n\parallel \\ \le & \frac{1+\kappa }{1-\kappa }\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel +|{\alpha }_1^{n,k}-{\alpha }_1^k|\parallel T_k{U}_{k-1}{x}_n\parallel \\ +\frac{1-\kappa }{1-\kappa }\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel +(|{\alpha }_1^k-{\alpha }_1^{n,k}|\\ +|{\alpha }_3^{n,k}-{\alpha }_3^k|)\parallel U_{k-1}{x}_n\parallel +|{\alpha }_3^{n,k}-{\alpha }_3^k|\parallel x_n\parallel \\ \le & \frac{2}{1-\kappa }\parallel U_{n,k-1}{x}_n-U_{k-1}{x}_n\parallel +|{\alpha }_1^{n,k}-{\alpha }_1^k|(\parallel T_k{U}_{k-1}{x}_n\parallel +\parallel U_{k-1}{x}_n\parallel )\\ +|{\alpha }_3^{n,k}-{\alpha }_3^k|(\parallel U_{k-1}{x}_n\parallel +\parallel x_n\parallel ).\end{array}$$

(2.14)

By (2.13) and (2.14), we have

$$\begin{array}{rcl}\parallel S_n^A{x}_n-S^A{x}_n\parallel & =& \parallel U_{n,N}{x}_n-U_N{x}_n\parallel \\ \le & \frac{2}{1-\kappa }\parallel U_{n,N-1}{x}_n-U_{N-1}{x}_n\parallel +|{\alpha }_1^{n,N}-{\alpha }_1^N|(\parallel T_N{U}_{N-1}{x}_n\parallel \\ +\parallel U_{N-1}{x}_n\parallel )+|{\alpha }_3^{n,N}-{\alpha }_3^N|(\parallel U_{N-1}{x}_n\parallel +\parallel x_n\parallel )\\ \le & \frac{2}{1-\kappa }(\frac{2}{1-\kappa }\parallel U_{n,N-2}{x}_n-U_{N-2}{x}_n\parallel \\ +|{\alpha }_1^{n,N-1}-{\alpha }_1^{N-1}|(\parallel T_{N-1}{U}_{N-2}{x}_n\parallel +\parallel U_{N-2}{x}_n\parallel )\\ +|{\alpha }_3^{n,N-1}-{\alpha }_3^{N-1}|(\parallel U_{N-2}{x}_n\parallel +\parallel x_n\parallel ))\\ +|{\alpha }_1^{n,N}-{\alpha }_1^N|(\parallel T_N{U}_{N-1}{x}_n\parallel +\parallel U_{N-1}{x}_n\parallel )\\ +|{\alpha }_3^{n,N}-{\alpha }_3^N|(\parallel U_{N-1}{x}_n\parallel +\parallel x_n\parallel )\\ =& {\left(\frac{2}{1-\kappa }\right)}^2\parallel U_{n,N-2}{x}_n-U_{N-2}{x}_n\parallel \\ +\sum _{j=N-1}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_1^{n,j}-{\alpha }_1^j|(\parallel T_j{U}_{j-1}{x}_n\parallel +\parallel U_{j-1}{x}_n\parallel )\\ +\sum _{j=N-1}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_3^{n,j}-{\alpha }_3^j|(\parallel U_{j-1}{x}_n\parallel +\parallel x_n\parallel )\\ \le & \cdots \\ \le & {\left(\frac{2}{1-\kappa }\right)}^{N-1}\parallel U_{n,1}{x}_n-U_1{x}_n\parallel \\ +\sum _{j=2}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_1^{n,j}-{\alpha }_1^j|(\parallel T_j{U}_{j-1}{x}_n\parallel +\parallel U_{j-1}{x}_n\parallel )\\ +\sum _{j=2}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_3^{n,j}-{\alpha }_3^j|(\parallel U_{j-1}{x}_n\parallel +\parallel x_n\parallel )\\ =& {\left(\frac{2}{1-\kappa }\right)}^{N-1}|{\alpha }_1^{n,1}-{\alpha }_1^1|\parallel T_1{x}_n-x_n\parallel \\ +\sum _{j=2}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_1^{n,j}-{\alpha }_1^j|(\parallel T_j{U}_{j-1}{x}_n\parallel +\parallel U_{j-1}{x}_n\parallel )\\ +\sum _{j=2}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_3^{n,j}-{\alpha }_3^j|(\parallel U_{j-1}{x}_n\parallel +\parallel x_n\parallel ).\end{array}$$

(2.15)

This together with the assumption ${\alpha }_i^{n,j}\to {\alpha }_i^j$ as $n\to \mathrm{\infty }$ ($i=1,3$, $j=1,2,\dots ,N$), we can conclude that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel S_n^A{x}_n-S^A{x}_n\parallel =0.$$

 □

Lemma 2.10 Let C be a nonempty closed convex subset of a real Hilbert space. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself, and let ${\{S_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself with $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$, and let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}),{\alpha }_j=({\alpha }_1^j,{\alpha }_2^j,{\alpha }_3^j)\in I\times I\times I$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$ and ${\alpha }_1^j+{\alpha }_2^j+{\alpha }_3^j=1$ such that ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|<\mathrm{\infty }$ for all $j\in \{1,2,3,\dots ,N\}$. For every $n\in \mathbb{N}$, let $S_n^A$ be the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$. Then ${\sum }_{n=1}^{\mathrm{\infty }}\parallel S_{n+1}^A{z}_n-S_n^A{z}_n\parallel <\mathrm{\infty }$ for every bounded sequence $\{z_n\}$ in C.

Proof Let $\{z_n\}$ be a bounded sequence in C. For each $n\in \mathbb{N}$ and the definition of $S^A$, we have

$$\begin{array}{rcl}\parallel U_{n+1,1}{z}_n-U_{n,1}{z}_n\parallel & =& \parallel S_1({\alpha }_1^{n+1,1}{T}_1{z}_n+(1-{\alpha }_1^{n+1,1})z_n)-S_1({\alpha }_1^{n,1}{T}_1{z}_n+(1-{\alpha }_1^{n,1})z_n)\parallel \\ \le & \parallel {\alpha }_1^{n+1,1}{T}_1{z}_n+(1-{\alpha }_1^{n+1,1})z_n-{\alpha }_1^{n,1}{T}_1{z}_n-(1-{\alpha }_1^{n,1})z_n\parallel \\ =& |{\alpha }_1^{n+1,1}-{\alpha }_1^{n,1}|\parallel T_1{z}_n-z_n\parallel .\end{array}$$

(2.16)

For $k\in \{2,3,\dots ,N\}$, and using the same method as (2.14) in Lemma 2.9, we have

$$\begin{array}{rcl}\parallel U_{n+1,k}{z}_n-U_{n,k}{z}_n\parallel & \le & \frac{2}{1-\kappa }\parallel U_{n+1,k-1}{z}_n-U_{n,k-1}{z}_n\parallel +|{\alpha }_1^{n+1,k}-{\alpha }_1^{n,k}|(\parallel T_k{U}_{n,k-1}{z}_n\parallel \\ +\parallel U_{n,k-1}{z}_n\parallel )+|{\alpha }_3^{n+1,k}-{\alpha }_3^{n,k}|(\parallel U_{n,k-1}{z}_n\parallel +\parallel z_n\parallel ).\end{array}$$

(2.17)

From (2.16), (2.17), and using the same method as (2.15) in Lemma 2.9, we have

$$\begin{array}{rcl}\parallel S_{n+1}^A{z}_n-S_n^A{z}_n\parallel & \le & {\left(\frac{2}{1-\kappa }\right)}^{N-1}|{\alpha }_1^{n+1,1}-{\alpha }_1^{n,1}|\parallel T_1{z}_n-z_n\parallel \\ +\sum _{j=2}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|(\parallel T_j{U}_{n,j-1}{z}_n\parallel +\parallel U_{n,j-1}{z}_n\parallel )\\ +\sum _{j=2}^N{\left(\frac{2}{1-\kappa }\right)}^{N-j}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|(\parallel U_{n,j-1}{z}_n\parallel +\parallel z_n\parallel ).\end{array}$$

It implies that

$$\sum _{n=1}^{\mathrm{\infty }}\parallel S_{n+1}^A{z}_n-S_n^A{z}_n\parallel <\mathrm{\infty }.$$

 □

3 Main result

Theorem 3.1 Let C be a nonempty closed convex subset of Hilbert spaces H, and let f be an α-contraction on H. Let $F_i$ be a bifunction from $C\times C$ into ℝ, for every $i=1,2,\dots ,N$ satisfying (A1)-(A4). Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself, and let ${\{S_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself with $\mathbb{F}\equiv {\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\cap {\bigcap }_{i=1}^N\mathit{EP}(F_i)\ne \mathrm{\varnothing }$ and $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$, and let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j})\in I\times I\times I$, $j=1,2,3,\dots ,N$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$, ${\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}\in [a,b]\subset (\kappa ,1)$ for all $j=1,2,\dots ,N$. Let $S_n^A$ be the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$. Let $\{x_n\}$ and $\{z_n\}$ be the sequences generated by $x_1\in C$ and

$$\{\begin{array}{c}{F}_i(u_n^i,y)+\frac{1}{r_n^i}〈y-u_n^i,u_n^i-x_n〉\ge 0,\mathrm{\forall }y\in C\mathit{\text{ and }}i=1,2,\dots ,N,\hfill \\ z_n={\sum }_{i=1}^N{\delta }_n^i{u}_n^i,\hfill \\ x_{n+1}={\alpha }_{n}f(z_n)+(1-{\alpha }_n)S_n^A{z}_n,\mathrm{\forall }n\ge 1,\hfill \end{array}$$

(3.1)

where $\{{\alpha }_n\}$ is a sequence in $[0,1]$. Assume that the following conditions hold:

• (i) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|<\mathrm{\infty }$, for all $j\in \{1,2,3,\dots ,N\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$;

• (iii) ${\sum }_{i=1}^N{\delta }_n^i=1$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\delta }_{n+1}^i-{\delta }_n^i|<\mathrm{\infty }$ and ${lim}_{n\to \mathrm{\infty }}{\delta }_n^i={\delta }_i\in (\kappa ,1)$, for every $i=1,2,\dots ,N$;

• (iv) $\kappa <\theta \le r_n^i\le \eta$, for every $i=1,2,\dots ,N$ and ${\sum }_{n=1}^{\mathrm{\infty }}|r_{n+1}^i-r_n^i|<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ converges strongly to $x^{\ast }=P_{\mathbb{F}}f(x^{\ast })$.

Proof Let $p\in \mathbb{F}$, we have $p\in {\bigcap }_{i=1}^N\mathit{EP}(F_i)$ from Lemma 2.6, we obtain $p\in {\bigcap }_{i=1}^{N}F(T_{r_n^i})$. Since

$$F_i(u_n^i,y)+\frac{1}{r_n^i}〈y-u_n^i,u_n^i-x_n〉\ge 0,\mathrm{\forall }y\in C\text{ and }i=1,2,\dots ,N.$$

(3.2)

Again from Lemma 2.6, we have $u_n^i=T_{r_n^i}{x}_n$ for every $i=1,2,\dots ,N$. By definition of $x_n$, we have

$$\begin{array}{rcl}\parallel x_{n+1}-p\parallel & \le & {\alpha }_n\parallel f(z_n)-p\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_n-p\parallel \\ \le & {\alpha }_n\parallel f(z_n)-f(p)\parallel +{\alpha }_n\parallel f(p)-p\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_n-p\parallel \\ \le & {\alpha }_n\alpha \parallel z_n-p\parallel +{\alpha }_n\parallel f(p)-p\parallel +(1-{\alpha }_n)\parallel z_n-p\parallel \\ =& {\alpha }_n\parallel f(p)-p\parallel +(1-{\alpha }_n(1-\alpha ))\parallel z_n-p\parallel \\ =& {\alpha }_n\parallel f(p)-p\parallel +(1-{\alpha }_n(1-\alpha ))\parallel \sum _{i=1}^N{\delta }_n^i(u_n^i-p)\parallel \\ \le & {\alpha }_n\parallel f(p)-p\parallel +(1-{\alpha }_n(1-\alpha ))\sum _{i=1}^N{\delta }_n^i\parallel u_n^i-p\parallel \\ \le & {\alpha }_n\parallel f(p)-p\parallel +(1-{\alpha }_n(1-\alpha ))\parallel x_n-p\parallel .\end{array}$$

(3.3)

Put $K=max\{\parallel x_1-p\parallel ,\frac{\parallel f(p)-p\parallel }{1-\alpha }\}$. By (3.3), we can show by induction that $\parallel x_n-p\parallel \le K$, $\mathrm{\forall }n\in \mathbb{N}$. This implies that $\{x_n\}$ is bounded, and so are $\{u_n^i\}$, for every $i=1,2,\dots ,N$ and $\{z_n\}$.

Next, we will show that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =0.$$

(3.4)

By nonexpansiveness of $x_n$, we have

$$\begin{array}{rcl}\parallel x_{n+1}-x_n\parallel & =& \parallel {\alpha }_{n}f(z_n)+(1-{\alpha }_n)S_n^A{z}_n-{\alpha }_{n-1}f(z_{n-1})-(1-{\alpha }_{n-1})S_{n-1}^A{z}_{n-1}\parallel \\ =& \parallel {\alpha }_n(f(z_n)-f(z_{n-1}))+({\alpha }_n-{\alpha }_{n-1})f(z_{n-1})+(1-{\alpha }_n)(S_n^A{z}_n-S_{n-1}^A{z}_{n-1})\\ +({\alpha }_{n-1}-{\alpha }_n)S_{n-1}^A{z}_{n-1}\parallel \\ \le & {\alpha }_n\parallel f(z_n)-f(z_{n-1})\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_n-S_{n-1}^A{z}_{n-1}\parallel \\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ \le & {\alpha }_n\alpha \parallel z_n-z_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel \\ +(1-{\alpha }_n)(\parallel S_n^A{z}_n-S_n^A{z}_{n-1}\parallel +\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel )\\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ \le & (1-{\alpha }_n(1-\alpha ))\parallel z_n-z_{n-1}\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel \\ +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ =& (1-{\alpha }_n(1-\alpha ))\left(\parallel \sum _{i=1}^N{\delta }_n^i{u}_n^i-\sum _{i=1}^N{\delta }_{n-1}^i{u}_{n-1}^i\parallel \right)+|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel \\ +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ =& (1-{\alpha }_n(1-\alpha ))\left(\parallel \sum _{i=1}^N{\delta }_n^i(u_n^i-u_{n-1}^i)+\sum _{i=1}^N({\delta }_n^i-{\delta }_{n-1}^i)u_{n-1}^i\parallel \right)\\ +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel \\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ \le & (1-{\alpha }_n(1-\alpha ))(\sum _{i=1}^N{\delta }_n^i\parallel u_n^i-u_{n-1}^i\parallel +\sum _{i=1}^N|{\delta }_n^i-{\delta }_{n-1}^i|\parallel u_{n-1}^i\parallel )\\ +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel \\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel .\end{array}$$

(3.5)

From Lemma 2.10, we have

$$\sum _{n=1}^{\mathrm{\infty }}\parallel S_{n+1}^A{z}_n-S_n^A{z}_n\parallel <\mathrm{\infty }.$$

(3.6)

Since $u_n^i=T_{r_n^i}{x}_n$ for every $i=1,2,\dots ,N$. By definition of $T_{r_n^i}$, we have

$$F(T_{r_n^i}{x}_n,y)+\frac{1}{r_n^i}〈y-T_{r_n^i}{x}_n,T_{r_n^i}{x}_n-x_n〉\ge 0,\mathrm{\forall }y\in C,$$

(3.7)

similarly,

$$F(T_{r_{n+1}^i}{x}_{n+1},y)+\frac{1}{r_{n+1}^i}〈y-T_{r_{n+1}^i}{x}_{n+1},T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}〉\ge 0,\mathrm{\forall }y\in C.$$

(3.8)

From (3.7) and (3.8), we obtain

$$F(T_{r_n^i}{x}_n,T_{r_{n+1}^i}{x}_{n+1})+\frac{1}{r_n^i}〈T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n,T_{r_n^i}{x}_n-x_n〉\ge 0$$

(3.9)

and

$$F(T_{r_{n+1}^i}{x}_{n+1},T_{r_n^i}{x}_n)+\frac{1}{r_{n+1}^i}〈T_{r_n^i}{x}_n-T_{r_{n+1}^i}{x}_{n+1},T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}〉\ge 0.$$

(3.10)

By (3.9) and (3.10), we have

$$\frac{1}{r_n^i}〈T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n,T_{r_n^i}{x}_n-x_n〉+\frac{1}{r_{n+1}^i}〈T_{r_n^i}{x}_n-T_{r_{n+1}^i}{x}_{n+1},T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}〉\ge 0.$$

It follows that

$$〈T_{r_n^i}{x}_n-T_{r_{n+1}^i}{x}_{n+1},\frac{T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}}{r_{n+1}^i}-\frac{T_{r_n^i}{x}_n-x_n}{r_n^i}〉\ge 0.$$

This implies that

$$0\le 〈T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n,T_{r_n^i}{x}_n-T_{r_{n+1}^i}{x}_{n+1}+T_{r_{n+1}^i}{x}_{n+1}-x_n-\frac{r_n^i}{r_{n+1}^i}(T_{r_{n+1}^i}{x}_{n+1}-x_{n+1})〉.$$

It follows that

$$\begin{array}{c}{\parallel T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n\parallel }^2\hfill \\ \le 〈T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n,T_{r_{n+1}^i}{x}_{n+1}-x_n-\frac{r_n^i}{r_{n+1}^i}(T_{r_{n+1}^i}{x}_{n+1}-x_{n+1})〉\hfill \\ =〈T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n,x_{n+1}-x_n+(1-\frac{r_n^i}{r_{n+1}^i})(T_{r_{n+1}^i}{x}_{n+1}-x_{n+1})〉\hfill \\ \le \parallel T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n\parallel \parallel x_{n+1}-x_n+(1-\frac{r_n^i}{r_{n+1}^i})(T_{r_{n+1}^i}{x}_{n+1}-x_{n+1})\parallel \hfill \\ \le \parallel T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n\parallel (\parallel x_{n+1}-x_n\parallel +|1-\frac{r_n^i}{r_{n+1}^i}|\parallel T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}\parallel )\hfill \\ =\parallel T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n\parallel (\parallel x_{n+1}-x_n\parallel +\frac{1}{r_{n+1}^i}|r_{n+1}^i-r_n^i|\parallel T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}\parallel )\hfill \\ \le \parallel T_{r_{n+1}^i}{x}_{n+1}-T_{r_n^i}{x}_n\parallel (\parallel x_{n+1}-x_n\parallel +\frac{1}{a}|r_{n+1}^i-r_n^i|\parallel T_{r_{n+1}^i}{x}_{n+1}-x_{n+1}\parallel ).\hfill \end{array}$$

It follows that

$$\parallel u_{n+1}^i-u_n^i\parallel \le \parallel x_{n+1}-x_n\parallel +\frac{1}{a}|r_{n+1}^i-r_n^i|\parallel u_{n+1}^i-x_{n+1}\parallel$$

(3.11)

for every $i=1,2,\dots ,N$.

Substitute (3.11) into (3.5), we have

$$\begin{array}{rcl}\parallel x_{n+1}-x_n\parallel & \le & (1-{\alpha }_n(1-\alpha ))(\sum _{i=1}^N{\delta }_n^i\parallel u_n^i-u_{n-1}^i\parallel +\sum _{i=1}^N|{\delta }_n^i-{\delta }_{n-1}^i|\parallel u_{n-1}^i\parallel )\\ +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel \\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ \le & (1-{\alpha }_n(1-\alpha ))(\sum _{i=1}^N{\delta }_n^i(\parallel x_{n+1}-x_n\parallel +\frac{1}{a}|r_{n+1}^i-r_n^i|\parallel u_{n+1}^i-x_{n+1}\parallel )\\ +\sum _{i=1}^N|{\delta }_n^i-{\delta }_{n-1}^i|\parallel u_{n-1}^i\parallel )\\ +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel \\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ =& (1-{\alpha }_n(1-\alpha ))(\parallel x_{n+1}-x_n\parallel +\sum _{i=1}^N{\delta }_n^i\frac{1}{a}|r_{n+1}^i-r_n^i|\parallel u_{n+1}^i-x_{n+1}\parallel \\ +\sum _{i=1}^N|{\delta }_n^i-{\delta }_{n-1}^i|\parallel u_{n-1}^i\parallel )\\ +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel +(1-{\alpha }_n)\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel \\ +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel \\ \le & (1-{\alpha }_n(1-\alpha ))\parallel x_{n+1}-x_n\parallel +\sum _{i=1}^N{\delta }_n^i\frac{1}{a}|r_{n+1}^i-r_n^i|\parallel u_{n+1}^i-x_{n+1}\parallel \\ +\sum _{i=1}^N|{\delta }_n^i-{\delta }_{n-1}^i|\parallel u_{n-1}^i\parallel +|{\alpha }_n-{\alpha }_{n-1}|\parallel f(z_{n-1})\parallel \\ +\parallel S_n^A{z}_{n-1}-S_{n-1}^A{z}_{n-1}\parallel +|{\alpha }_{n-1}-{\alpha }_n|\parallel S_{n-1}^A{z}_{n-1}\parallel .\end{array}$$

(3.12)

By (3.12), (3.6), conditions (iii), (iv) and Lemma 2.3, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =0.$$

(3.13)

From (3.11), (3.13) and condition (iv), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel u_{n+1}^i-u_n^i\parallel =0,\mathrm{\forall }i=1,2,\dots ,N.$$

(3.14)

Let $p\in \mathbb{F}$. From $u_n^i=T_{r_n^i}{x}_n$ for every $i=1,2,\dots ,N$, we have

$$\begin{array}{rcl}{\parallel u_n^i-p\parallel }^2& =& {\parallel T_{r_n^i}{x}_n-T_{r_n^i}p\parallel }^2\\ \le & 〈T_{r_n^i}{x}_n-T_{r_n^i}p,x_n-p〉\\ =& \frac{1}{2}({\parallel u_n^i-p\parallel }^2+{\parallel x_n-p\parallel }^2-{\parallel u_n^i-x_n\parallel }^2).\end{array}$$

It implies that

$${\parallel u_n^i-p\parallel }^2\le {\parallel x_n-p\parallel }^2-{\parallel u_n^i-x_n\parallel }^2.$$

(3.15)

By definition of $\{x_n\}$ and (3.15), we have

$$\begin{array}{rcl}{\parallel x_{n+1}-p\parallel }^2& \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+(1-{\alpha }_n){\parallel S_n^A{z}_n-p\parallel }^2\\ \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+(1-{\alpha }_n){\parallel z_n-p\parallel }^2\\ =& {\alpha }_n{\parallel f(z_n)-p\parallel }^2+(1-{\alpha }_n){\parallel \sum _{i=1}^N{\delta }_n^i(u_n^i-p)\parallel }^2\\ \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+(1-{\alpha }_n)\sum _{i=1}^N{\delta }_n^i{\parallel u_n^i-p\parallel }^2\\ \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+(1-{\alpha }_n)\sum _{i=1}^N{\delta }_n^i({\parallel x_n-p\parallel }^2-{\parallel u_n^i-x_n\parallel }^2)\\ \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+{\parallel x_n-p\parallel }^2-(1-{\alpha }_n)\sum _{i=1}^N{\delta }_n^i{\parallel u_n^i-x_n\parallel }^2.\end{array}$$

It implies that

$$\begin{array}{rcl}(1-{\alpha }_n)\sum _{i=1}^N{\delta }_n^i{\parallel u_n^i-x_n\parallel }^2& \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+{\parallel x_n-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2\\ \le & {\alpha }_n{\parallel f(z_n)-p\parallel }^2+(\parallel x_n-p\parallel \\ +\parallel x_{n+1}-p\parallel )\parallel x_{n+1}-x_n\parallel .\end{array}$$

(3.16)

From conditions (i), (iii) and (3.13), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel u_n^i-x_n\parallel =0,\mathrm{\forall }i=1,2,\dots ,N.$$

(3.17)

Since

$$x_{n+1}-S_n^A{z}_n={\alpha }_n(f(z_n)-S_n^A{z}_n),$$

from condition (i), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-S_n^A{z}_n\parallel =0.$$

(3.18)

From the definition of $z_n$, we have

$$\begin{array}{rcl}\parallel z_n-x_n\parallel & =& \parallel \sum _{i=1}^N{\delta }_n^i(u_n^i-x_n)\parallel \\ \le & \sum _{i=1}^N{\delta }_n^i\parallel u_n^i-x_n\parallel .\end{array}$$

From condition (iii) and (3.17), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-x_n\parallel =0.$$

(3.19)

Since

$$\parallel z_n-S_n^A{z}_n\parallel \le \parallel z_n-x_n\parallel +\parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-S_n^A{z}_n\parallel ,$$

by (3.13), (3.18) and (3.19), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-S_n^A{z}_n\parallel =0.$$

(3.20)

Next, we show that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈f(z)-z,x_n-z〉\le 0,$$

(3.21)

where $z=P_{\mathbb{F}}f(z)$. To show this inequality, take a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈f(z)-z,x_n-z〉=\underset{k\to \mathrm{\infty }}{lim}〈f(z)-z,x_{n_k}-z〉.$$

(3.22)

Without loss of generality, we may assume that a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ converges weakly to some $q\in H$. From (3.19), we have that $\{z_{n_k}\}$ converges weakly to q.

Since $\kappa <a\le {\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}\le b<1$ for all $j=1,2,\dots ,N$. Without loss of generality, we may assume that

$$\begin{array}{c}{\alpha }_1^{n_k,j}\to {\alpha }_1^j\in (\kappa ,1),{\alpha }_3^{n_k,j}\to {\alpha }_3^j\in (\kappa ,1)\text{and}{\alpha }_2^{n_k,j}\to {\alpha }_2^j\in (\kappa ,1)\text{as }k\to \mathrm{\infty },\hfill \\ \mathrm{\forall }j=1,2,\dots ,N.\hfill \end{array}$$

Let $S^A$ be the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\beta }_1,{\beta }_2,\dots ,{\beta }_N$, where ${\beta }_j=({\alpha }_1^j,{\alpha }_2^j,{\alpha }_3^j)$, $\mathrm{\forall }j=1,2,\dots ,N$. By Lemma 2.8, $S^A$ is a nonexpansive mapping, and $F(S^A)={\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)$.

By Lemma 2.9, we have

$$\underset{k\to \mathrm{\infty }}{lim}\parallel S_{n_k}^A{z}_{n_k}-S^A{z}_{n_k}\parallel =0.$$

(3.23)

Since

$$\parallel z_{n_k}-S^A{z}_{n_k}\parallel \le \parallel z_{n_k}-S_{n_k}^A{z}_{n_k}\parallel +\parallel S_{n_k}^A{z}_{n_k}-S^A{z}_{n_k}\parallel ,$$

by (3.20), (3.23), we have

$$\underset{k\to \mathrm{\infty }}{lim}\parallel z_{n_k}-S^A{z}_{n_k}\parallel =0.$$

(3.24)

Since $\{z_{n_k}\}$ converges weakly to q as $k\to \mathrm{\infty }$ (3.24) and Lemma 2.7, we have

$$q\in F\left(S^A\right)=\bigcap _{i=1}^{N}F(S_i)\cap \bigcap _{i=1}^{N}F(T_i).$$

(3.25)

Next, we show that $q\in {\bigcap }_{i=1}^N\mathit{EP}(F_i)$. To show this, we may assume that

$$\underset{k\to \mathrm{\infty }}{lim}{r}_{n_k}^i=r^i\in [\theta ,\eta ],\mathrm{\forall }i=1,2,\dots ,N.$$

By Lemmas 2.5 and 2.6, for every $i=1,2,\dots ,N$, we define $T_{r^i}:H\to C$ by

$$T_{r^i}(x)=\{z\in C:F_i(z,y)+\frac{1}{r^i}〈y-z,z-x〉\ge 0,\mathrm{\forall }y\in C\},\mathrm{\forall }x\in H\text{ and }i=1,2,\dots ,N.$$

Then we have

$$F_i(T_{r^i}{x}_n,y)+\frac{1}{r^i}〈y-T_{r^i}{x}_n,T_{r^i}{x}_n-x_n〉\ge 0,\mathrm{\forall }y\in C\text{ and }i=1,2,\dots ,N.$$

From (3.1) and $u_n^i=T_{r_n^i}{x}_n$, we have

$$F_i(T_{r_n^i}{x}_n,y)+\frac{1}{r_n^i}〈y-T_{r_n^i}{x}_n,T_{r_n^i}{x}_n-x_n〉\ge 0,\mathrm{\forall }y\in C\text{ and }i=1,2,\dots ,N.$$

It implies that

$$F_i(T_{r^i}{x}_{n_k},T_{r_{n_k}^i}{x}_{n_k})+\frac{1}{r^i}〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},T_{r^i}{x}_{n_k}-x_{n_k}〉\ge 0,\mathrm{\forall }i=1,2,\dots ,N$$

and

$$F_i(T_{r_{n_k}^i}{x}_{n_k},T_{r^i}{x}_{n_k})+\frac{1}{r_{n_k}^i}〈T_{r^i}{x}_{n_k}-T_{r_{n_k}^i}{x}_{n_k},T_{r_{n_k}^i}{x}_{n_k}-x_{n_k}〉\ge 0,\mathrm{\forall }i=1,2,\dots ,N.$$

By (A2), we have

$$\frac{1}{r^i}〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},T_{r^i}{x}_{n_k}-x_{n_k}〉+\frac{1}{r_{n_k}^i}〈T_{r^i}{x}_{n_k}-T_{r_{n_k}^i}{x}_{n_k},T_{r_{n_k}^i}{x}_{n_k}-x_{n_k}〉\ge 0.$$

It implies that

$$〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},\frac{T_{r^i}{x}_{n_k}-x_{n_k}}{r^i}-\frac{T_{r_{n_k}^i}{x}_{n_k}-x_{n_k}}{r_{n_k}^i}〉\ge 0.$$

It follows that

$$〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},T_{r^i}{x}_{n_k}-x_{n_k}-\frac{r^i}{r_{n_k}^i}(T_{r_{n_k}^i}{x}_{n_k}-x_{n_k})〉\ge 0.$$

Then

$$\begin{array}{rcl}0& \le & 〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},T_{r^i}{x}_{n_k}-T_{r_{n_k}^i}{x}_{n_k}+T_{r_{n_k}^i}{x}_{n_k}-x_{n_k}-\frac{r^i}{r_{n_k}^i}(T_{r_{n_k}^i}{x}_{n_k}-x_{n_k})〉\\ =& 〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},T_{r^i}{x}_{n_k}-T_{r_{n_k}^i}{x}_{n_k}+(1-\frac{r^i}{r_{n_k}^i})(T_{r_{n_k}^i}{x}_{n_k}-x_{n_k})〉.\end{array}$$

It follows that

$$\begin{array}{rcl}{\parallel T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k}\parallel }^2& \le & 〈T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k},(1-\frac{r^i}{r_{n_k}^i})(T_{r_{n_k}^i}{x}_{n_k}-x_{n_k})〉\\ \le & \parallel T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k}\parallel |1-\frac{r^i}{r_{n_k}^i}|\parallel T_{r_{n_k}^i}{x}_{n_k}-x_{n_k}\parallel .\end{array}$$

It implies that

$$\parallel T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k}\parallel \le \frac{1}{a}|r_{n_k}^i-r^i|\parallel T_{r_{n_k}^i}{x}_{n_k}-x_{n_k}\parallel .$$

From ${lim}_{k\to \mathrm{\infty }}{r}_{n_k}^i=r^i$ and (3.17), we have

$$\underset{k\to \mathrm{\infty }}{lim}\parallel T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k}\parallel =0,\mathrm{\forall }i=1,2,\dots ,N.$$

(3.26)

For every $i=1,2,\dots ,N$, we have

$$\begin{array}{rcl}\parallel x_{n_k}-T_{r^i}{x}_{n_k}\parallel & \le & \parallel x_{n_k}-T_{r_{n_k}^i}{x}_{n_k}\parallel +\parallel T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k}\parallel \\ =& \parallel x_{n_k}-u_{n_k}^i\parallel +\parallel T_{r_{n_k}^i}{x}_{n_k}-T_{r^i}{x}_{n_k}\parallel ,\end{array}$$

by (3.17) and (3.26), we have

$$\underset{k\to \mathrm{\infty }}{lim}\parallel x_{n_k}-T_{r^i}{x}_{n_k}\parallel =0,\mathrm{\forall }i=1,2,\dots ,N.$$

(3.27)

Since a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ converges weakly to q as $k\to \mathrm{\infty }$, from (3.27) and Lemma 2.7, we have

$$q\in F(T_{r^i}),\mathrm{\forall }i=1,2,\dots ,N.$$

Then

$$q\in \bigcap _{i=1}^{N}F(T_{r^i}).$$

(3.28)

From Lemma 2.6, we have $\mathit{EP}(F_i)=F(T_{r^i})$, $\mathrm{\forall }i=1,2,\dots ,N$. From (3.28), we have

$$q\in \bigcap _{i=1}^{N}F(T_{r^i})=\bigcap _{i=1}^N\mathit{EP}(F_i).$$

(3.29)

By (3.25) and (3.29), we have

$$q\in \mathbb{F}.$$

(3.30)

Since $x_{n_k}\rightharpoonup q$ as $k\to \mathrm{\infty }$ and $q\in \mathbb{F}$ and (3.22), we have

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈f(z)-z,x_n-z〉=\underset{k\to \mathrm{\infty }}{lim}〈f(z)-z,x_{n_k}-z〉=〈f(z)-z,q-z〉\le 0.$$

Finally, we show that $\{x_n\}$ converges strongly to $z=P_{\mathbb{F}}f(z)$. Putting $z=P_{\mathbb{F}}f(z)$, by nonexpansiveness of $S^A$, we have

$$\begin{array}{rcl}{\parallel x_{n+1}-z\parallel }^2& =& {\parallel {\alpha }_n(f(z_n)-z)+(1-{\alpha }_n)(S_n^A{z}_n-z)\parallel }^2\\ \le & {(1-{\alpha }_n)}^2{\parallel S_n^A{z}_n-z\parallel }^2+2{\alpha }_n〈f(z_n)-z,x_{n+1}-z〉\\ =& {(1-{\alpha }_n)}^2{\parallel S_n^A{z}_n-z\parallel }^2+2{\alpha }_n〈f(z_n)-f(z),x_{n+1}-z〉\\ +2{\alpha }_n〈f(z)-z,x_{n+1}-z〉\\ \le & (1-2{\alpha }_n+{\alpha }_n^2){\parallel z_n-z\parallel }^2+2{\alpha }_n\alpha \parallel z_n-z\parallel \parallel x_{n+1}-z\parallel \\ +2{\alpha }_n〈f(z)-z,x_{n+1}-z〉\\ \le & (1-2{\alpha }_n+{\alpha }_n^2){\parallel z_n-z\parallel }^2+{\alpha }_n\alpha {\parallel z_n-z\parallel }^2+{\alpha }_n\alpha {\parallel x_{n+1}-z\parallel }^2\\ +2{\alpha }_n〈f(z)-z,x_{n+1}-z〉\\ \le & (1-2{\alpha }_n+{\alpha }_n\alpha ){\parallel x_n-z\parallel }^2+{\alpha }_n^2{\parallel x_n-z\parallel }^2+{\alpha }_n\alpha {\parallel x_{n+1}-z\parallel }^2\\ +2{\alpha }_n〈f(z)-z,x_{n+1}-z〉\\ =& (1-{\alpha }_n\alpha -2{\alpha }_n(1-\alpha )){\parallel x_n-z\parallel }^2+{\alpha }_n^2{\parallel x_n-z\parallel }^2+{\alpha }_n\alpha {\parallel x_{n+1}-z\parallel }^2\\ +2{\alpha }_n〈f(z)-z,x_{n+1}-z〉.\end{array}$$

It implies that

$$\begin{array}{rcl}{\parallel x_{n+1}-z\parallel }^2& \le & (1-\frac{2{\alpha }_n(1-\alpha )}{1-{\alpha }_n\alpha }){\parallel x_n-z\parallel }^2+\frac{{\alpha }_n^2}{1-{\alpha }_n\alpha }{\parallel x_n-z\parallel }^2\\ +\frac{2{\alpha }_n}{1-{\alpha }_n\alpha }〈f(z)-z,x_{n+1}-z〉.\end{array}$$

This implies that by condition (i), (3.21) and Lemma 2.2, we have that the sequence $\{x_n\}$ converges strongly to $z=P_{\mathbb{F}}f(z)$. By (3.19), we have

$$\parallel z_n-z\parallel \le \parallel z_n-x_n\parallel +\parallel x_n-z\parallel \to 0\text{as }n\to \mathrm{\infty }.$$

This completes the proof. □

4 Applications

In this section, we apply our main result to prove strong convergence theorems involving variational inclusion problems and variational inequality problems. To prove these results, we need definition and lemmas as follows.

A set-valued mapping $M:H\to 2^H$ is called monotone if for all $x,y\in H$, $f\in Mx$ and $g\in My$ imply that $〈x-y,f-g〉\ge 0$. A monotone mapping $M:H\to 2^H$ is maximal if the graph $Graph(M)$ of M is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping M is maximal if and only if for $(x,f)\in H\times H$, $〈x-y,f-g〉\ge 0$ for every $(y,g)\in Graph(M)$ implies that $f\in Mx$.

Next, we consider the following so-called variational inclusion problem: Find a $u\in H$ such that

$$\theta \in Bu+Mu,$$

(4.1)

where $B:H\to H$, $M:H\to 2^H$ are two nonlinear mappings, and θ is zero vector in H (see, for instance, [16–21]). The set of the solution of (4.1) is denoted by $\mathit{VI}(H,B,M)$.

Definition 4.1 (See [16])

Let $M:H\to 2^H$ be a multi-valued maximal monotone mapping, then the single-valued mapping $J_{M,\lambda }:H\to H$ defined by

$$J_{M,\lambda }(u)={(I+\lambda M)}^{-1}(u),\mathrm{\forall }u\in H,$$

is called the resolvent operator associated with M, where λ is any positive number, and I is an identity mapping.

Lemma 4.1 (See [16])

$u\in H$ is a solution of variational inclusion (4.1) if and only if $u=J_{M,\lambda }(u-\lambda Bu)$, $\mathrm{\forall }\lambda >0$, i.e.,

$$\mathit{VI}(H,B,M)=F(J_{M,\lambda }(I-\lambda B)),\mathrm{\forall }\lambda >0.$$

Further, if $\lambda \in (0,2\alpha ]$, then $\mathit{VI}(H,B,M)$ is a closed convex subset in H.

Lemma 4.2 (See [6])

The resolvent operator $J_{M,\lambda }$ associated with M is single-valued, nonexpansive for all $\lambda >0$ and 1-inverse-strongly monotone.

A mapping A of C into H is called α-inverse strongly monotone, see [22], if there exists a positive real number α such that

$$〈x-y,Ax-Ay〉\ge \alpha {\parallel Ax-Ay\parallel }^2$$

for all $x,y\in C$. The variational inequality problem is to find $u\in C$ such that

$$〈Au,v-u〉\ge 0$$

(4.2)

for all $v\in C$. The set of solutions of the variational inequality is denoted by $\mathit{VI}(C,A)$. We need the following lemma to prove a strong convergence theorem in this section.

Lemma 4.3 (See [23])

Let C be a closed convex subset of Hilbert space H. Let $A_i:C\to H$ be mappings, and let $G_i:C\to C$ be defined by $G_i(y)=P_C(I-{\lambda }_i{A}_i)y$ with ${\lambda }_i>0$, $\mathrm{\forall }i=1,2,\dots ,N$. Then $x^{\ast }\in {\bigcap }_{i=1}^N\mathit{VI}(C,A_i)$ if and only if $x^{\ast }\in {\bigcap }_{i=1}^{N}F(G_i)$.

Theorem 4.4 Let C be a nonempty closed convex subset of Hilbert spaces H, and let f be an α-contraction on H. For every $i=1,2,\dots ,N$, let $F_i$ be a bifunction from $C\times C$ into ℝ satisfying (A1)-(A4), let $A_i:C\to H$ be an ${\alpha }_i$-inverse strongly monotone, and let $G_i:C\to C$ be a mapping defined by $G_i(y)=P_C(I-{\lambda }_i{A}_i)y$, $\mathrm{\forall }y\in C$ with ${\lambda }_i\in (0,1]\subset (0,2{\alpha }_i)$. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of C into itself with $\mathbb{F}\equiv {\bigcap }_{i=1}^N\mathit{VI}(C,A_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\cap {\bigcap }_{i=1}^N\mathit{EP}(F_i)\ne \mathrm{\varnothing }$ and $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$, and let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j})\in I\times I\times I$, $j=1,2,3,\dots ,N$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$, ${\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}\in [a,b]\subset (\kappa ,1)$ for all $j=1,2,\dots ,N$. Let $S_n^A$ be the $S^A$-mapping generated by $G_1,G_2,\dots ,G_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$. Let $\{x_n\}$ and $\{z_n\}$ be the sequences generated by $x_1\in C$ and

$$\{\begin{array}{c}{F}_i(u_n^i,y)+\frac{1}{r_n^i}〈y-u_n^i,u_n^i-x_n〉\ge 0,\mathrm{\forall }y\in C\mathit{\text{ and }}i=1,2,\dots ,N,\hfill \\ z_n={\sum }_{i=1}^N{\delta }_n^i{u}_n^i,\hfill \\ x_{n+1}={\alpha }_{n}f(z_n)+(1-{\alpha }_n)S_n^A{z}_n,\mathrm{\forall }n\ge 1,\hfill \end{array}$$

(4.3)

where $\{{\alpha }_n\}$ is a sequence in $[0,1]$. Assume that the following conditions hold:

• (i) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|<\mathrm{\infty }$ for all $j\in \{1,2,3,\dots ,N\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$;

• (iii) ${\sum }_{i=1}^N{\delta }_n^i=1$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\delta }_{n+1}^i-{\delta }_n^i|<\mathrm{\infty }$ and ${lim}_{n\to \mathrm{\infty }}{\delta }_n^i={\delta }_i\in (\kappa ,1)$ for every $i=1,2,\dots ,N$;

• (iv) $\kappa <\theta \le r_n^i\le \eta$ for every $i=1,2,\dots ,N$ and ${\sum }_{n=1}^{\mathrm{\infty }}|r_{n+1}^i-r_n^i|<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ converges strongly to $x^{\ast }=P_{\mathbb{F}}f(x^{\ast })$.

Proof First, we show that $(I-{\lambda }_i{A}_i)$ is a nonexpansive mapping for every $i=1,2,\dots ,N$. For $x,y\in C$, we have

$$\begin{array}{rcl}{\parallel (I-{\lambda }_i{A}_i)x-(I-{\lambda }_i{A}_i)y\parallel }^2& =& {\parallel x-y-{\lambda }_i(A_{i}x-A_{i}y)\parallel }^2\\ =& {\parallel x-y\parallel }^2-2{\lambda }_i〈x-y,A_{i}x-A_{i}y〉+{\lambda }_i^2{\parallel A_{i}x-A_{i}y\parallel }^2\\ \le & {\parallel x-y\parallel }^2-2{\alpha }_i{\lambda }_i{\parallel A_{i}x-A_{i}y\parallel }^2+{\lambda }_i^2{\parallel A_{i}x-A_{i}y\parallel }^2\\ =& {\parallel x-y\parallel }^2+{\lambda }_i({\lambda }_i-2{\alpha }_i){\parallel A_{i}x-A_{i}y\parallel }^2\\ \le & {\parallel x-y\parallel }^2.\end{array}$$

(4.4)

Thus, $(I-{\lambda }_i{A}_i)$ is a nonexpansive mapping, and so is $G_i$ for all $i=1,2,\dots ,N$. Then we obtain the desired result from Lemma 4.3 and Theorem 3.1. □

Corollary 4.5 Let C be a nonempty closed convex subset of Hilbert spaces H, and let f be an α-contraction on H. For every $i=1,2,\dots ,N$, let $F_i$ be a bifunction from $C\times C$ into ℝ, satisfying (A1)-(A4), let $A_i:C\to H$ be an ${\alpha }_i$-inverse strongly monotone, and let $G_i:C\to C$ be a mapping defined by $G_i(y)=P_C(I-{\lambda }_i{A}_i)y$, $\mathrm{\forall }y\in C$ with ${\lambda }_i\in (0,1]\subset (0,2{\alpha }_i)$. Let ${\{T_i\}}_{i=1}^N$ be a finite family of nonexpansive mappings of C into itself with $\mathbb{F}\equiv {\bigcap }_{i=1}^N\mathit{VI}(C,A_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\cap {\bigcap }_{i=1}^N\mathit{EP}(F_i)\ne \mathrm{\varnothing }$, and let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j})\in I\times I\times I$, $j=1,2,3,\dots ,N$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$, ${\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}\in [a,b]\subset (0,1)$ for all $j=1,2,\dots ,N$. Let $S_n^A$ be the $S^A$-mapping generated by $G_1,G_2,\dots ,G_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$. Let $\{x_n\}$ and $\{z_n\}$ be the sequences generated by $x_1\in C$ and

$$\{\begin{array}{c}{F}_i(u_n^i,y)+\frac{1}{r_n^i}〈y-u_n^i,u_n^i-x_n〉\ge 0,\mathrm{\forall }y\in C\mathit{\text{ and }}i=1,2,\dots ,N,\hfill \\ z_n={\sum }_{i=1}^N{\delta }_n^i{u}_n^i,\hfill \\ x_{n+1}={\alpha }_{n}f(z_n)+(1-{\alpha }_n)S_n^A{z}_n,\mathrm{\forall }n\ge 1,\hfill \end{array}$$

(4.5)

where $\{{\alpha }_n\}$ is a sequence in $[0,1]$. Assume that the following conditions hold:

• (i) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|<\mathrm{\infty }$ for all $j\in \{1,2,3,\dots ,N\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$;

• (iii) ${\sum }_{i=1}^N{\delta }_n^i=1$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\delta }_{n+1}^i-{\delta }_n^i|<\mathrm{\infty }$ and ${lim}_{n\to \mathrm{\infty }}{\delta }_n^i={\delta }_i\in (0,1)$ for every $i=1,2,\dots ,N$;

• (iv) $0<\theta \le r_n^i\le \eta$ for every $i=1,2,\dots ,N$ and ${\sum }_{n=1}^{\mathrm{\infty }}|r_{n+1}^i-r_n^i|<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ converges strongly to $x^{\ast }=P_{\mathbb{F}}f(x^{\ast })$.

Proof Since ${\{T_i\}}_{i=1}^N$ is a finite family of nonexpansive mappings, we have that ${\{T_i\}}_{i=1}^N$ is a finite family of ${\kappa }_i$-strict pseudo-contractive mappings. From Theorem 4.4, we can draw the desired conclusion. □

Theorem 4.6 Let C be a nonempty closed convex subset of Hilbert spaces H, and let f be an α-contraction on H. For every $i=1,2,\dots ,N$, let $F_i$ be a bifunction from $C\times C$ into ℝ satisfying (A1)-(A4). Let $M_i:H\to 2^H$ be maximal monotone mappings for every $i=1,2,\dots ,N$, and let $B_i:H\to H$ be a ${\delta }_i$-inverse strongly monotone mapping for every $i=1,2,\dots ,N$. Let $G_i:H\to H$ be a mapping defined by $J_{M_i,\eta }(I-\eta B_i)x=G_{i}x$ for every $x\in H$ with $\eta \in (0,2{\delta }_i)$ $i=1,2,\dots ,N$. Let ${\{T_i\}}_{i=1}^N$ be a finite family of ${\kappa }_i$-strict pseudo-contractions of H into itself with $\mathbb{F}\equiv {\bigcap }_{i=1}^{N}V(H,B_i,M_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\cap {\bigcap }_{i=1}^N\mathit{EP}(F_i)\ne \mathrm{\varnothing }$ and $\kappa =max\{{\kappa }_i:i=1,2,\dots ,N\}$, and let ${\alpha }_j^{(n)}=({\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j})\in I\times I\times I$, $j=1,2,3,\dots ,N$, where $I=[0,1]$, ${\alpha }_1^{n,j}+{\alpha }_2^{n,j}+{\alpha }_3^{n,j}=1$, ${\alpha }_1^{n,j},{\alpha }_2^{n,j},{\alpha }_3^{n,j}\in [a,b]\subset (\kappa ,1)$ for all $j=1,2,\dots ,N$. Let $S_n^A$ be the $S^A$-mapping generated by $G_1,G_2,\dots ,G_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$. Let $\{x_n\}$ and $\{z_n\}$ be the sequences generated by $x_1\in H$ and

$$\{\begin{array}{c}{F}_i(u_n^i,y)+\frac{1}{r_n^i}〈y-u_n^i,u_n^i-x_n〉\ge 0,\mathrm{\forall }y\in C\mathit{\text{ and }}i=1,2,\dots ,N,\hfill \\ z_n={\sum }_{i=1}^N{\delta }_n^i{u}_n^i,\hfill \\ x_{n+1}={\alpha }_{n}f(z_n)+(1-{\alpha }_n)S_n^A{z}_n,\mathrm{\forall }n\ge 1,\hfill \end{array}$$

(4.6)

where $\{{\alpha }_n\}$ is a sequence in $[0,1]$. Assume that the following conditions hold:

• (i) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_1^{n+1,j}-{\alpha }_1^{n,j}|<\mathrm{\infty }$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_3^{n+1,j}-{\alpha }_3^{n,j}|<\mathrm{\infty }$ for all $j\in \{1,2,3,\dots ,N\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$;

• (iii) ${\sum }_{i=1}^N{\delta }_n^i=1$, ${\sum }_{n=1}^{\mathrm{\infty }}|{\delta }_{n+1}^i-{\delta }_n^i|<\mathrm{\infty }$ and ${lim}_{n\to \mathrm{\infty }}{\delta }_n^i={\delta }_i\in (\kappa ,1)$, for every $i=1,2,\dots ,N$;

• (iv) $\kappa <\theta \le r_n^i\le \eta$, for every $i=1,2,\dots ,N$ and ${\sum }_{n=1}^{\mathrm{\infty }}|r_{n+1}^i-r_n^i|<\mathrm{\infty }$.

Then the sequence $\{x_n\}$ converges strongly to $x^{\ast }=P_{\mathbb{F}}f(x^{\ast })$.

Proof By using the same method as (4.4), we have that $I-\eta B_i$ is a nonexpansive mapping for every $i=1,2,\dots ,N$. By Lemma 4.2, we have $J_{M_i,\eta }(I-\eta B_i)=G_i$ is a nonexpansive mapping for every $i=1,2,\dots ,N$. Then we obtain the desired result from Theorem 3.1. □

5 Example and numerical results

In the last section, we give numerical examples to support our main results.

Example 5.1 Let ℝ be the set of real numbers. For every $i=1,2,\dots ,N$, let the mappings $F_i:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$, $T_i:\mathbb{R}\to \mathbb{R}$, $S_i:\mathbb{R}\to \mathbb{R}$, $f:\mathbb{R}\to \mathbb{R}$ defined by

$$\begin{array}{c}{F}_i(x,y)=i(4y^2+xy-5x^2),\hfill \\ T_{i}x={(-1)}^{2i+1}\frac{3}{2}x,\hfill \\ S_{i}x=\frac{2i}{2i+1}x,\hfill \\ fx=\frac{1}{3}x\hfill \end{array}$$

for every $x,y\in \mathbb{R}$.

Suppose that $S_n^A$ is the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$, where ${\alpha }_j^{(n)}=({\alpha }_1^{(n,j)},{\alpha }_2^{(n,j)},{\alpha }_3^{(n,j)})$ and ${\alpha }_1^{(n,j)}={\alpha }_2^{(n,j)}={\alpha }_3^{(n,j)}=\frac{1}{3}$ for every $n\ge 1$ and $j=1,2,\dots ,N$. Let the sequences $\{x_n\}$ and $\{z_n\}$ be generated by (3.1), where ${\alpha }_n=\frac{1}{5n}$, ${\delta }_n^i=(\frac{1^n}{2^i}+\frac{1^n}{N\times 2^N})$ and $r_n^i=\frac{in}{n+1}$ for every $n\ge 1$ and $i=1,2,\dots ,N$. Then the sequences $\{x_n\}$ and $\{z_n\}$ converge strongly to 0.

Solution. For every $i=1,2,\dots ,N$. It is easy to see that $S_i$ is nonexpansive and $T_i$ is $\frac{1}{5}$-strictly pseudo contractive mappings with $\{0\}={\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)$.

Since $S_n^A$ is the $S^A$-mapping generated by $S_1,S_2,\dots ,S_N$, $T_1,T_2,\dots ,T_N$ and ${\alpha }_1^{(n)},{\alpha }_2^{(n)},\dots ,{\alpha }_N^{(n)}$, where ${\alpha }_j^{(n)}=({\alpha }_1^{(n,j)}{\alpha }_2^{(n,j)},{\alpha }_3^{(n,j)})$ and ${\alpha }_1^{(n,j)}={\alpha }_2^{(n,j)}={\alpha }_3^{(n,j)}=\frac{1}{3}$ for every $n\ge 1$ and $j=1,2,\dots ,N$, then we have

$$\begin{array}{c}{U}_{n,0}x=x,\hfill \\ U_{n,1}x=\frac{2}{3}(\frac{1}{3}\times \frac{-3}{2}{U}_{n,0}+\frac{1}{3}\times U_{n,0}+\frac{1}{3})x,\hfill \\ U_{n,2}x=\frac{4}{5}(\frac{1}{3}\times \frac{-3}{2}{U}_{n,1}+\frac{1}{3}\times U_{n,1}+\frac{1}{3})x,\hfill \\ U_{n,3}x=\frac{6}{7}(\frac{1}{3}\times \frac{-3}{2}{U}_{n,2}+\frac{1}{3}\times U_{n,2}+\frac{1}{3})x,\hfill \\ ⋮\hfill \\ U_{n,N-1}x=\frac{2(N-1)}{2(N-1)+1}(\frac{1}{3}\times \frac{-3}{2}{U}_{n,N-2}+\frac{1}{3}\times U_{n,N-2}+\frac{1}{3})x,\hfill \\ S_n^{A}x=U_{n,N}x=\frac{2N}{2N+1}(\frac{1}{3}\times \frac{-3}{2}{U}_{n,N-1}+\frac{1}{3}\times U_{n,N-1}+\frac{1}{3})x\hfill \end{array}$$

for every $x\in \mathbb{R}$. From Lemma 2.8, we have $\{0\}={\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)=F(S_n^A)$. For every $n\ge 1$ and $i=1,2,\dots ,N$, we can see that ${\sum }_{i=1}^N{\delta }_n^i={\sum }_{i=1}^N(\frac{1^n}{2^i}+\frac{1^n}{N\times 2^N})=1$. From definition of $F_i$, we have ${\bigcap }_{i=1}^N\mathit{EP}(F_i)=\{0\}$. Then $\{0\}={\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\cap {\bigcap }_{i=1}^N\mathit{EP}(F_i)=\mathbb{F}$.

For every $n\ge 1$ and $i=1,2,\dots ,N$, the mappings $F_i$, $T_i$, $S_i$ and ${\alpha }_n$, $r_n^i$, ${\delta }_n^i$ satisfy conditions in Theorem 3.1. Then from Theorem 3.1, we have the sequences $\{x_n\}$ and $\{z_n\}$ converge to 0.

Next, we give numerical results to support this example. Let $r>0$ and $z\in \mathbb{R}$. For every $y\in \mathbb{R}$ and $i=1,2,\dots ,N$, and from Lemma 2.5, there exist $x\in \mathbb{R}$ such that

$$\begin{array}{c}{F}_i(x,y)+\frac{1}{r}〈y-x,x-z〉\ge 0\hfill \\ \iff i(4y^2+xy-5x^2)+\frac{1}{r}〈y-x,x-z〉\ge 0\hfill \\ \iff 4ir{y}^2+irxy-5ir{x}^2+(y-x)(x-z)\ge 0\hfill \\ \iff 4ir{y}^2+irxy-5ir{x}^2+xy-x^2-zy+zx\ge 0\hfill \\ \iff 4ir{y}^2+(rix+x-z)y-(5ir{x}^2+x^2-zx)\ge 0.\hfill \end{array}$$

Put $G(y)=4ir{y}^2+(rix+x-z)y-(5ir{x}^2+x^2-zx)$. Then G is a quadratic function of y with coefficient $a=4ir$, $b=rix+x-z$, $c=-(5ir{x}^2+x^2-zx)$. Next, we compute the discriminant Δ of G as follows:

$$\begin{array}{rcl}\mathrm{\Delta }& =& b^2-4ac\\ =& {(rix+x-z)}^2+4(4ir)(5ir{x}^2+x^2-zx)\\ =& {(rix+x)}^2-2z(rix+x)+z^2+80i^2{r}^2{x}^2+16ir{x}^2-16irzx\\ =& 81i^2{r}^2{x}^2+18ir{x}^2+x^2-18irzx-2zx+z^2\\ =& z^2+(81i^2{r}^2+18ir+1)x^2-2zx(9ir+1)\\ =& {(z-x(9ir+1))}^2.\end{array}$$

Since $G(y)\ge 0$ for all $y\in \mathbb{R}$. If it has most one solution in ℝ, so $\mathrm{\Delta }\le 0$. It implies that $z=x(9ir+1)$. Then we have

$$x=T_{r}z=\frac{z}{i(9r)+1}$$

(5.1)

for all $r>0$ and $i=1,2,\dots ,N$. From (3.1) and (5.1), we have

$$u_n^i=T_{r_n^i}{x}_n=\frac{x_n}{i(9r_n^i)+1}$$

(5.2)

for every $n\ge 1$ and $i=1,2,\dots ,N$. Since ${\alpha }_n=\frac{1}{5n}$, ${\delta }_n^i=(\frac{1^n}{2^i}+\frac{1^n}{N\times 2^N})$, $r_n^i=\frac{in}{n+1}$ and (5.2), we can rewrite (3.1) as follows:

$$\{\begin{array}{c}{z}_n={\sum }_{i=1}^N(\frac{1^n}{2^i}+\frac{1^n}{N\times 2^N})\frac{x_n}{i(9\frac{in}{n+1})+1},\hfill \\ x_{n+1}=\frac{1}{5n}f(z_n)+(1-\frac{1}{5n})S_n^A{z}_n,\mathrm{\forall }n\ge 1\hfill \end{array}$$

(5.3)

for every $n\ge 1$ and $i=1,2,\dots ,N$.

Put $N=8$ and initial points $x_1=700$, $x_1=-500$ in (5.3) we have the following results respectively.

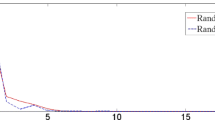
The numerical results for initial points $x_1=700$ and $x_1=-500$ were shown in Tables 1 (Figure 1(b)) and 2 (Figure 1(a)), respectively. We observe that the sequences $\{x_n\}$ and $\{z_n\}$ converge to $0\in {\bigcap }_{i=1}^{N}F(S_i)\cap {\bigcap }_{i=1}^{N}F(T_i)\cap {\bigcap }_{i=1}^N\mathit{EP}(F_i)$.

Figure 1

The convergence comparison with different initial values (a) ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{500}$ and (b) ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{700}$ .

Table 1 The values of $\mathbf{\{}{\mathit{z}}_{\mathit{n}}\mathbf{\}}$ and $\mathbf{\{}{\mathit{x}}_{\mathit{n}}\mathbf{\}}$ with initial points ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{700}$ , $\mathit{n}\mathbf{=}\mathbf{8}$ and $\mathit{N}\mathbf{=}\mathbf{8}$

Table 2 The values of $\mathbf{\{}{\mathit{z}}_{\mathit{n}}\mathbf{\}}$ and $\mathbf{\{}{\mathit{x}}_{\mathit{n}}\mathbf{\}}$ with initial points ${\mathit{x}}_{\mathbf{1}}\mathbf{=}\mathbf{-}\mathbf{500}$ , $\mathit{n}\mathbf{=}\mathbf{8}$ and $\mathit{N}\mathbf{=}\mathbf{8}$