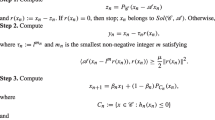A new general iterative algorithm with Meir-Keeler contractions for variational inequality problems in q-uniformly smooth Banach spaces

Abstract

In this paper, we generalize the iterative scheme and extend the space studied in (Fixed Point Theory and Applications 2012:46, 2012). Further, we prove some strong convergence theorems of the new iterative scheme for variational inequality problems in q-uniformly smooth Banach spaces under very mild conditions. Our results improve and extend corresponding ones announced by many others.

MSC:47H09, 47H10.

1 Introduction

Throughout this paper, we denote by X and $X^{\ast }$ a real Banach space and the dual space of X, respectively. Let C be a nonempty closed convex subset of X.

The duality mapping $J:X\to 2^{X^{\ast }}$ is defined by $J(x)=\{x^{\ast }\in X^{\ast }:〈x,x^{\ast }〉={\parallel x\parallel }^2,\parallel x^{\ast }\parallel =\parallel x\parallel \}$, $\mathrm{\forall }x\in X$. It is well known that if X is smooth, then J is single-valued, which is denoted by j. Let $q>1$ be a real number. The generalized duality mapping $J_q:X\to 2^{X^{\ast }}$ is defined by

$$J_q(x)=\{x^{\ast }\in X^{\ast }:〈x,x^{\ast }〉={\parallel x\parallel }^q,\parallel x^{\ast }\parallel ={\parallel x\parallel }^{q-1}\},$$

for all $x\in X$, where $〈\cdot ,\cdot 〉$ denotes the generalized duality pairing between X and $X^{\ast }$. In particular, $J=J_2$ is called the normalized duality mapping and $J_q(x)={\parallel x\parallel }^{q-2}{J}_2(x)$ for $x\ne 0$. It is well known that if X is smooth, then $J_q$ is single-valued, which is denoted by $j_q$.

Recall that a mapping $f:C\to C$ is a contraction on C if there exists a constant $\alpha \in (0,1)$ such that

$$\parallel f(x)-f(y)\parallel \le \alpha \parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

(1.1)

A mapping $W:C\to C$ is said to be nonexpansive if

$$\parallel W(x)-W(y)\parallel \le \parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

(1.2)

A mapping $F:E\to C$ is said to be L-Lipschitzian if there exists a positive constant L such that

$$\parallel F(x)-F(y)\parallel \le L\parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

(1.3)

A mapping $F:E\to C$ is said to be η-strongly accretive if there exist $j_q(x-y)\in J_q(x-y)$ and $\eta >0$ such that

$$〈Fx-Fy,j_q(x-y)〉\ge \eta {\parallel x-y\parallel }^q,\mathrm{\forall }x,y\in C.$$

(1.4)

Without loss of generality, we can assume that $\eta \in (0,1]$ and $L\in [1,\mathrm{\infty })$.

Recall that if C and D are nonempty subsets of a Banach space X such that C is nonempty closed convex and $D\subset C$, then a mapping $P:C\to D$ is sunny [1] provided $P(x+t(x-P(x)))=P(x)$ for all $x\in C$ and $t\ge 0$, whenever $x+t(x-P(x))\in C$. A mapping $P:C\to D$ is called a retraction if $Px=x$ for all $x\in D$. Furthermore, P is a sunny nonexpansive retraction from C onto D if P is a retraction from C onto D which is also sunny and nonexpansive. A subset D of C is called a sunny nonexpansive retraction of C if there exists a sunny nonexpansive retraction from C onto D.

Let $\{B_n\}$ be a family of mappings from a subset C of a Banach space X into itself with ${\bigcap }_{n=1}^{\mathrm{\infty }}F(B_n)\ne \mathrm{\varnothing }$. We say that $\{B_n\}$ satisfies the AKTT-condition if for each bounded subset D of C,

$$\sum _{n=1}^{\mathrm{\infty }}\underset{\omega \in D}{sup}\parallel B_{n+1}\omega -B_n\omega \parallel <\mathrm{\infty }.$$

Proposition 1.1 (Banach [2])

Let $(X,d)$ be a complete metric space, and let f be a contraction on X, then f has a unique fixed point.

Proposition 1.2 (Meir and Keeler [3])

Let $(X,d)$ be a complete metric space, and let ϕ be a Meir-Keeler contraction (MKC, for short) on X, that is, for every $\epsilon >0$, there exists $\delta >0$ such that $d(x,y)<\epsilon +\delta$ implies $d(\varphi (x),\varphi (y))<\epsilon$ for all $x,y\in X$. Then ϕ has a unique fixed point.

This proposition is one of generalizations of Proposition 1.1, because the contractions are Meir-Keeler contractions.

Proposition 1.3 [4]

Let C be a closed convex subset of a smooth Banach space X. Let $\tilde{C}$ be a nonempty subset of C. Let $Q_C:C\to \tilde{C}$ be a retraction, and let J be the normalized duality mapping on X. Then the following are equivalent:

• (i) $Q_C$ is sunny and nonexpansive.

• (ii) ${\parallel Q_{C}x-Q_{C}y\parallel }^2\le 〈x-y,J(Q_{C}x-Q_{C}y)〉$, $\mathrm{\forall }x,y\in C$.

• (iii) $〈x-Q_{C}x,J(y-Q_{C}x)〉\le 0$, $\mathrm{\forall }x\in C,y\in \tilde{C}$.

Variational inequality theory has emerged as a great important tool in studying a wide class of unilateral, free, obstacle, moving and equilibrium problems arising in several branches of pure and applied sciences in a unified and general framework. This field is dynamics and it is experiencing an explosive growth in both theory and applications. Several numerical methods have been developed for solving variational inequalities and related optimization problems; see [4–7] and the references therein.

Let C be a nonempty closed convex subset of a real Hilbert space H. Recall that the classical variational inequality is to find an $x^{\ast }$ such that

$$〈F{x}^{\ast },x-x^{\ast }〉\ge 0,\mathrm{\forall }x\in C,$$

(1.5)

where $F:C\to C$ is a nonlinear mapping. The set of solutions of (1.5) is denoted by $VI(F,C)$.

In 2008, Yao et al. [8] modified Mann’s iterative scheme by using the viscosity approximation method which was introduced by Moudafi [1]. More precisely, they introduced and studied the following iterative algorithm:

$$\{\begin{array}{l}{x}_0=x\in C,\\ y_n={\beta }_n{x}_n+(1-{\beta }_n)T{x}_n,\\ x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)y_n,n\ge 0,\end{array}$$

(1.6)

where T is a nonexpansive mapping of K into itself and f is a contraction on K. They obtained a strong convergence theorem under some mild restrictions on the parameters.

Zhou [9] and Qin et al. [10] modified normal Mann’s iterative process (1.6) for k-strictly pseudo-contractions to have strong convergence in Hilbert spaces. Qin et al. [10] introduced the following iterative algorithm scheme:

$$\{\begin{array}{l}{x}_1=x\in K,\\ y_n=P_K[{\beta }_n{x}_n+(1-{\beta }_n)T{x}_n],\\ x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_{n}A)y_n,n\ge 1,\end{array}$$

(1.7)

where T is a k-strictly pseudo-contraction, f is a contraction and A is a strong positive linear bounded operator, $P_K$ is the metric projection. They proved, under certain appropriate assumptions on the sequences $\{{\alpha }_n\}$ and $\{{\beta }_n\}$, that $\{x_n\}$ defined by (1.7) converges strongly to a fixed point of the k-strictly pseudo-contraction, which solves some variational inequality.

Very recently, Song et al. [11] introduced the following iteration process:

$$\{\begin{array}{l}{x}_1=x\in C,\\ y_n=P_C[{\beta }_n{x}_n+(1-{\beta }_n){\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}{T}_i{x}_n],\\ x_{n+1}={\alpha }_n\varphi (x_n)+{\gamma }_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n,n\ge 1,\end{array}$$

(1.8)

where $T_i$ is a $k_i$-strictly pseudo-contraction, ϕ is an MKC contraction and $F:C\to C$ is an L-Lipschitzian and η-strongly monotone mapping in a Hilbert space, $P_C$ is the metric projection. Under certain appropriate assumptions on the sequences $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{\gamma }_n\}$ and $\{{\mu }_i^n\}$, the sequence $\{x_n\}$ defined by (1.8) converges strongly to a common fixed point of an infinite family of $k_i$-strictly pseudo-contractions, which solves some variational inequality.

Question 1 Can the space in Song [11] be extended from a Hilbert space to a q-uniformly smooth Banach space?

Question 2 Can the projection $P_C$ in Song [11] be changed to the sunny nonexpansive retraction $Q_C$ and be put to other place of the iteration process?

Question 3 Can we extend the iterative scheme of algorithm (1.8) to a more general iterative scheme?

Question 4 Can we remove the very strict condition $C+C\subset C$ which is necessary in Lemma 3.1 and Theorem 3.2 of Song [11]?

The purpose of this paper is to give affirmative answers to these questions mentioned above. In this paper we study a new general iterative scheme as follows:

$$\{\begin{array}{l}{x}_1=x\in C,\\ y_n={\beta }_n{x}_n+(1-{\beta }_n){\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}{T}_i{x}_n,\\ x_{n+1}=Q_C[{\alpha }_n\gamma \varphi (x_n)+{\gamma }_n(\alpha I+(1-\alpha ){\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}{T}_i)x_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n],\\ n\ge 1,\end{array}$$

(1.9)

where $T_i$ is a ${\lambda }_i$-strictly pseudo-contraction, ϕ is an MKC contraction, $Q_C$ is the sunny nonexpansive retraction and $F:X\to C$ is an L-Lipschitzian and η-strongly accretive mapping in a q-uniformly smooth Banach space. Under some suitable assumptions on the sequences $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{\gamma }_n\}$ and $\{{\mu }_i^{(n)}\}$, the sequence $\{x_n\}$ defined by (1.9) converges strongly to a common fixed point of an infinite family of ${\lambda }_i$-strictly pseudo-contractions, which solves some variational inequality.

2 Preliminaries

In this section, we first recall some notations. T is said to be a λ-strict pseudo-contraction in the terminology of Browder and Petryshyn [12] if there exists a constant $\lambda \in [0,1)$ such that

$$〈Tx-Ty,j_q(x-y)〉\le {\parallel x-y\parallel }^q-\lambda {\parallel (I-T)x-(I-T)y\parallel }^q$$

(2.1)

for every $x,y\in C$ and for some $j_q(x-y)\in J_q(x-y)$. It is clear that (2.1) is equivalent to the following:

$$〈(I-T)x-(I-T)y,j_q(x-y)〉\ge \lambda {\parallel (I-T)x-(I-T)y\parallel }^q.$$

(2.2)

A Banach space X is said to be strictly convex if whenever x and y are not collinear, then $\parallel x+y\parallel <\parallel x\parallel +\parallel y\parallel$.

Then the modulus of convexity of X is defined by

$${\delta }_X(ϵ)=inf\{1-\frac{1}{2}\parallel x+y\parallel :\parallel x\parallel ,\parallel y\parallel \le 1,\parallel x-y\parallel \ge ϵ\}$$

for all $ϵ\in [0,2]$. X is said to be uniformly convex if ${\delta }_X(0)=0$ and ${\delta }_X(ϵ)>0$ for all $0<ϵ\le 2$, and if ${\delta }_X(ϵ)\ge c{ϵ}^p$ with $p\ge 2$, then X is said to be p-uniformly convex. A Hilbert space H is 2-uniformly convex, while $L^p$ is $max\{p,2\}$-uniformly convex for every $p>1$. Let ${\rho }_X:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ be the modulus of smoothness of X defined by

$${\rho }_X(t)=sup\{\frac{1}{2}(\parallel x+y\parallel +\parallel x-y\parallel )-1:x\in S(X),\parallel y\parallel \le t\}.$$

A Banach space X is said to be uniformly smooth if $\frac{{\rho }_X(t)}{t}\to 0$ as $t\to 0$. A Banach space X is said to be q-uniformly smooth if there exists a fixed constant $c>0$ such that ${\rho }_X(t)\le c{t}^q$ with $q>1$. A typical example of uniformly smooth Banach spaces is $L^p$, where $p>1$. More precisely, $L^p$ is $min\{p,2\}$-uniformly smooth for every $p>1$.

The norm of a Banach space X is said to be Gâteaux differentiable if the limit

$$\underset{t\to 0}{lim}\frac{\parallel x+ty\parallel -\parallel x\parallel }{t}$$

(2.3)

exists for all x, y on the unit sphere $S(X)=\{x\in X:\parallel x\parallel =1\}$. If, for each $y\in S(X)$, the limit (2.3) is uniformly attained for $x\in S(X)$, then the norm of X is said to be uniformly Gâteaux differentiable. The norm of X is said to be Fréchet differentiable if, for each $x\in S(X)$, the limit (2.3) is attained uniformly for $y\in S(X)$.

In order to prove our main results, we need the following lemmas.

Lemma 2.1 [13]

Let ϕ be an MKC on a convex subset C of a Banach space X. Then, for each $\epsilon >0$, there exists $r\in (0,1)$ such that

$$\parallel x-y\parallel \ge \epsilon \mathit{\text{ implies }}\parallel \varphi x-\varphi y\parallel \le r\parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

Lemma 2.2 [14]

Let X be a real q-uniformly smooth Banach space, then there exists a constant $C_q>0$ such that

$${\parallel x+y\parallel }^q\le {\parallel x\parallel }^q+q〈y,J_q(x)〉+C_q{\parallel y\parallel }^q\mathit{\text{for all }}x,y\in X.$$

Lemma 2.3 [15]

Let $\{{\alpha }_n\}$ be a sequence of nonnegative numbers satisfying the property

$${\alpha }_{n+1}\le (1-{\gamma }_n){\alpha }_n+b_n+{\gamma }_n{c}_n,n\ge 0,$$

where $\{{\gamma }_n\}$, $\{b_n\}$, $\{c_n\}$ satisfy the restrictions:

• (i) ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\gamma }_n=0$, ${\sum }_{n=0}^{\mathrm{\infty }}{\gamma }_n=\mathrm{\infty }$;

• (ii) $b_n\ge 0$, ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n<\mathrm{\infty }$;

• (iii) ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{c}_n\le 0$. Then ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$.

Lemma 2.4 [16]

Let C be a nonempty convex subset of a real q-uniformly smooth Banach space X, and let $T:C\to C$ be a λ-strict pseudo-contraction. For $\alpha \in (0,1)$, we define $T_{\alpha }x=(1-\alpha )x+\alpha Tx$. Then, as $\alpha \in (0,\mu ]$, $\mu =min\{1,{(\frac{q\lambda }{C_q})}^{\frac{1}{q}}\}$, $T_{\alpha }:C\to C$ is nonexpansive such that $F(T_{\alpha })=F(T)$.

Lemma 2.5 [17]

Let $q>1$, then the following inequality holds:

$$ab\le \frac{1}{q}{a}^q+\frac{q-1}{q}{b}^{\frac{q}{q-1}}$$

for arbitrary positive real numbers a, b.

Lemma 2.6 Let F be an L-Lipschitzian and η-strongly accretive operator on a nonempty closed convex subset C of a real q-uniformly smooth Banach space X with $0<\eta q\le 1$ and $0<t<{(\frac{q\eta }{C_q{L}^q})}^{\frac{1}{q-1}}$. Then $G=(I-tF):C\to X$ is a contraction with contraction coefficient ${\tau }_t=1-\frac{1}{q}(qt\eta -C_q{L}^q{t}^q)$.

Proof From the definition of η-strongly accretive and L-Lipschitzian operator, we have

$$\begin{array}{rl}{\parallel Gx-Gy\parallel }^q& ={\parallel x-y-t(Fx-Fy)\parallel }^q\\ \le {\parallel x-y\parallel }^q-qt〈Fx-Fy,j_q(x-y)〉+C_q{t}^q{\parallel Fx-Fy\parallel }^q\\ \le {\parallel x-y\parallel }^q-qt\eta {\parallel x-y\parallel }^q+C_q{L}^q{t}^q{\parallel x-y\parallel }^q\\ =[1-(qt\eta -C_q{L}^q{t}^q)]{\parallel x-y\parallel }^q.\end{array}$$

Therefore, we have

$$\begin{array}{rl}\parallel Gx-Gy\parallel & \le {[1-(qt\eta -C_q{L}^q{t}^q)]}^{\frac{1}{q}}\parallel x-y\parallel \\ \le [1-\frac{1}{q}(qt\eta -C_q{L}^q{t}^q)]\parallel x-y\parallel \end{array}$$

for all $x,y\in C$. From $0<\eta q\le 1$ and $0<t<{(\frac{q\eta }{C_q{L}^q})}^{\frac{1}{q-1}}$, we have $0<1-\frac{1}{q}(qt\eta -C_q{L}^q{t}^q)<1$ and

$$\parallel Gx-Gy\parallel \le {\tau }_t\parallel x-y\parallel ,$$

where ${\tau }_t=1-\frac{1}{q}(qt\eta -C_q{L}^q{t}^q)\in (0,1)$. Hence, G is a contraction with contraction coefficient ${\tau }_t$. This completes the proof. □

Lemma 2.7 ([18], Demiclosedness principle)

Let C be a nonempty closed convex subset of a reflexive Banach space X which satisfies Opial’s condition, and suppose that $T:C\to X$ is nonexpansive. Then the mapping $I-T$ is demiclosed at zero, that is, $x_n\rightharpoonup x$, $x_n-T{x}_n\to 0$ implies $x=Tx$.

Lemma 2.8 Let C be a closed convex subset of a smooth Banach space X. Let $\tilde{C}$ be a nonempty subset of C. Let $Q_C:C\to \tilde{C}$ be a retraction, and let j, $j_q$ be the normalized duality mapping and generalized duality mapping on X, respectively. Then the following are equivalent:

• (i) $Q_C$ is sunny and nonexpansive.

• (ii) ${\parallel Q_{C}x-Q_{C}y\parallel }^2\le 〈x-y,j(Q_{C}x-Q_{C}y)〉$, $\mathrm{\forall }x,y\in C$.

• (iii) $〈x-Q_{C}x,j(y-Q_{C}x)〉\le 0$, $\mathrm{\forall }x\in C,y\in \tilde{C}$.

• (iv) $〈x-Q_{C}x,j_q(y-Q_{C}x)〉\le 0$, $\mathrm{\forall }x\in C,y\in \tilde{C}$.

Proof From Proposition 1.3, we have (i) ⇔ (ii) ⇔ (iii). We need only to prove (iii) ⇔ (iv).

Indeed, if $y-Q_{C}x\ne 0$, it follows from the fact $j_q(x)={\parallel x\parallel }^{q-2}j(x)$ that $〈x-Q_{C}x,j(y-Q_{C}x)〉\le 0\iff 〈x-Q_{C}x,j_q(y-Q_{C}x)〉\le 0$, $\mathrm{\forall }x\in C,y\in \tilde{C}$.

If $y-Q_{C}x=0$, then $〈x-Q_{C}x,j(y-Q_{C}x)〉=〈x-Q_{C}x,j_q(y-Q_{C}x)〉=0$, $\mathrm{\forall }x\in C,y\in \tilde{C}$. This completes the proof. □

Lemma 2.9 [19]

Suppose that $\{B_n\}$ satisfies the AKTT-condition, then for each bounded subset D of C:

• (i) $\{B_n\}$ converges strongly to some point in C for each $x\in C$;

• (ii) Furthermore, if the mapping $B:C\to C$ is defined by $Bx={lim}_{n\to \mathrm{\infty }}{B}_{n}x$ for all $x\in D$, then ${lim}_{n\to \mathrm{\infty }}{sup}_{\omega \in D}\parallel B\omega -B_n\omega \parallel =0$.

Lemma 2.10 Let C be a closed convex subset of a reflexive Banach space X which admits a weakly sequentially continuous duality mapping $j_q$ from X to $X^{\ast }$. Let $S:C\to C$ be a nonexpansive mapping with $F(S)\ne \mathrm{\varnothing }$ and ϕ be an MKC on C. Suppose that $F:C\to X$ is an η-strongly accretive and L-Lipschitzian mapping with coefficient and $\eta >\gamma >0$. Then the sequence $\{x_t\}$ defined by $x_t=Q_C[t\gamma \varphi (x_t)+(1-tF)S{x}_t]$ converges strongly as $t\to 0$ to a fixed point $\tilde{x}$ of S, which solves the variational inequality

$$〈(F-\gamma \varphi )\tilde{x},j_q(\tilde{x}-z)〉\le 0,\mathrm{\forall }z\in F(S).$$

(2.4)

Proof The definition of $\{x_t\}$ is a good definition. Indeed, from the definition of MKC, we can see that an MKC is also a nonexpansive mapping. Consider a mapping $L_t$ on C defined by

$$L_{t}x=Q_C[t\gamma \varphi (x)+(I-tF)Sx],x\in C.$$

It is easy to see that $L_t$ is a contraction when $0<t<{(\frac{q(\eta -\gamma )}{C_q{L}^q})}^{\frac{1}{q-1}}$. Indeed, by Lemmas 2.1 and 2.5, we have

$$\begin{array}{rl}\parallel L_{t}x-L_{t}y\parallel & =\parallel Q_C[t\gamma \varphi (x)+(I-tF)Sx]-Q_C[t\gamma \varphi (y)+(I-tF)Sy]\parallel \\ \le \parallel t\gamma \varphi (x)+(I-tF)Sx-t\gamma \varphi (y)-(I-tF)Sy\parallel \\ \le t\gamma \parallel \varphi (x)-\varphi (y)\parallel +\parallel (I-tF)Sx-(I-tF)Sy\parallel \\ \le t\gamma \parallel \varphi (x)-\varphi (y)\parallel +{\tau }_t\parallel Sx-Sy\parallel \\ \le t\gamma \parallel x-y\parallel +{\tau }_t\parallel x-y\parallel \\ \le {\theta }_t\parallel x-y\parallel ,\end{array}$$

where ${\theta }_t=t\gamma +{\tau }_t\in (0,1)$. Hence $L_t$ has a unique fixed point, denoted by $x_t$, which uniquely solves the fixed point equation

$$x_t=Q_C[t\gamma \varphi (x_t)+(I-tF)S{x}_t].$$

(2.5)

Next we show the uniqueness of a solution of the variational inequality (2.4). Suppose that $\tilde{x}\in F(S)$ and $\hat{x}\in F(S)$ are solutions to (2.4), then, without loss of generality, we may assume that there is a number ε such that $\parallel \hat{x}-\tilde{x}\parallel \ge \epsilon$. Then, by Lemma 2.1, there is a number $r\in (0,1)$ such that $\parallel \varphi \hat{x}-\varphi \tilde{x}\parallel \le r\parallel \hat{x}-\tilde{x}\parallel$. From (2.4) we have

$$〈(F-\gamma \varphi )\tilde{x},j_q(\tilde{x}-\hat{x})〉\le 0,$$

(2.6)

$$〈(F-\gamma \varphi )\hat{x},j_q(\hat{x}-\tilde{x})〉\le 0.$$

(2.7)

Adding up (2.6) and (2.7), we obtain

$$〈(F-\gamma \varphi )\hat{x}-(F-\gamma \varphi )\tilde{x},j_q(\hat{x}-\tilde{x})〉\le 0.$$

(2.8)

Meanwhile, we notice that

$$\begin{array}{rl}〈(F-\gamma \varphi )\hat{x}-(F-\gamma \varphi )\tilde{x},j_q(\hat{x}-\tilde{x})〉& =〈F\hat{x}-F\tilde{x},j_q(\hat{x}-\tilde{x})〉-\gamma 〈\varphi (\hat{x})-\varphi (\tilde{x}),j_q(\hat{x}-\tilde{x})〉\\ \ge \eta {\parallel \hat{x}-\tilde{x}\parallel }^q-\gamma \parallel \varphi (\hat{x})-\varphi (\tilde{x})\parallel {\parallel \hat{x}-\tilde{x}\parallel }^{q-1}\\ \ge \eta {\parallel \hat{x}-\tilde{x}\parallel }^q-\gamma r\parallel \hat{x}-\tilde{x}\parallel {\parallel \hat{x}-\tilde{x}\parallel }^{q-1}\\ \ge \eta {\parallel \hat{x}-\tilde{x}\parallel }^q-\gamma r{\parallel \hat{x}-\tilde{x}\parallel }^q\\ =(\eta -\gamma r){\parallel \hat{x}-\tilde{x}\parallel }^q\\ \ge (\eta -\gamma r)\epsilon \\ >0.\end{array}$$

Thus $\hat{x}=\tilde{x}$ and the uniqueness is proved. Below, we use $\tilde{x}$ to denote the unique solution of (2.3).

First, we prove that $\{x_t\}$ is bounded.

Assume that $0<t<\frac{\eta -\gamma }{L^2}$ for $\mathrm{\forall }z\in F(S)$, fixed ${\epsilon }^{\prime }$ for each t.

Case 1. $(\parallel x_t-z\parallel <{\epsilon }^{\prime })$. In this case, we can see easily that $\{x_t\}$ is bounded.

Case 2. $(\parallel x_t-z\parallel \ge {\epsilon }^{\prime })$. In this case, by Lemma 2.1, there is a number $r^{\prime }\in (0,1)$ such that $\parallel \varphi (x_t)-\varphi (p)\parallel <r^{\prime }\parallel x_t-p\parallel$, then we have

$$\begin{array}{rl}\parallel x_t-z\parallel & =\parallel Q_C[t\gamma \varphi (x_t)+(I-tF)S{x}_t]-z\parallel \\ =\parallel t\gamma \varphi (x_t)+(I-tF)S{x}_t-z\parallel \\ =\parallel t(\gamma \varphi (x_t)-Fz)+(I-tF)S{x}_t-(I-tF)z\parallel \\ \le t\parallel \gamma \varphi (x_t)-p\parallel +{\tau }_t\parallel x_t-z\parallel \\ \le t\parallel \gamma \varphi (x_t)-\gamma \varphi (z)\parallel +t\parallel \gamma \varphi (z)-Fz\parallel +{\tau }_t\parallel x_t-z\parallel \\ \le t\gamma r^{\prime }\parallel x_t-z\parallel +t\parallel \varphi (z)-Fz\parallel +{\tau }_t\parallel x_t-z\parallel ,\end{array}$$

which implies $\parallel x_t-z\parallel \le \frac{2\parallel \gamma \varphi (z)-z\parallel }{\eta -\gamma }$. Thus $\{x_t\}$ is bounded.

Then, we prove that $x_t\to \tilde{x}$ ($\tilde{x}\in F(S)$) as $t\to 0$.

Since X is reflexive and $\{x_t\}$ is bounded, there exists a subsequence $\{x_{t_n}\}$ of $\{x_t\}$ such that $x_{t_n}\rightharpoonup x^{\ast }$. Setting $y_t=t\gamma \varphi (x_t)+(I-tF)S{x}_t$, we obtain $x_t=Q_C{y}_t$.

We claim $\parallel x_{t_n}-x^{\ast }\parallel \to 0$.

It follows from Lemma 2.8 that

$$〈y_t-Q_C{y}_t,j_q(x^{\ast }-Q_C{y}_t)〉\le 0,$$

(2.9)

then we have

$$\begin{array}{rl}{\parallel x_{t_m}-x^{\ast }\parallel }^q& =〈Q_C{y}_{t_m}-y_{t_m},j_q(x_{t_m}-x^{\ast })〉+〈y_{t_m}-x^{\ast },j_q(x_{t_m}-x^{\ast })〉\\ \le 〈y_{t_m}-x^{\ast },j_q(x_{t_m}-x^{\ast })〉\\ =〈(I-t_{m}F)S{x}_{t_m}-(I-t_{m}F)x^{\ast },j_q(x_{t_m}-x^{\ast })〉+t_m〈\gamma \varphi x_{t_m}-F{x}^{\ast },j_q(x_{t_m}-x^{\ast })〉\\ \le {\tau }_m{\parallel x_{t_m}-x^{\ast }\parallel }^q+t_m〈\gamma \varphi x_{t_m}-F{x}^{\ast },j_q(x_{t_m}-x^{\ast })〉,\end{array}$$

which implies that

$${\parallel x_{t_m}-x^{\ast }\parallel }^q\le \frac{t_m}{1-{\tau }_m}〈\gamma \varphi x_{t_m}-F{x}^{\ast },j_q(x_{t_m}-x^{\ast })〉.$$

(2.10)

Since $t_m\to 0$ as $m\to \mathrm{\infty }$, by (2.10) we obtain that $x_{t_m}\to x^{\ast }$. Hence, we have $x_{t_n}\to x^{\ast }$.

Now, we prove that $x^{\ast }$ solves the variational inequality (2.4).

Since

$$x_t=Q_C{y}_t=Q_C{y}_t-y_t+t\gamma \varphi (x_t)+(I-tF)S{x}_t,$$

(2.11)

we get that

$$(F-\gamma \varphi )x_t=\frac{1}{t}(Q_C{y}_t-y_t)-\frac{1}{t}(I-S)x_t+(F{x}_t-FS{x}_t).$$

(2.12)

Notice that

$$\begin{array}{rl}〈(I-S)x_t-(I-S)z,j_q(x_t-z)〉& =〈x_t-z,j_q(x_t-z)〉-〈S{x}_t-Sz,j_q(x_t-z)〉\\ \ge {\parallel x_t-z\parallel }^q-\parallel S{x}_t-Sz\parallel {\parallel x_t-z\parallel }^{q-1}\\ \ge {\parallel x_t-z\parallel }^q-{\parallel x_t-z\parallel }^q\\ =0.\end{array}$$

Then, for $z\in F(S)$,

$$\begin{array}{rcl}〈(F-\gamma \varphi )x_t,j_q(x_t-z)〉& =& \frac{1}{t}〈Q_C{y}_t-y_t,j_q(x_t-z)〉-\frac{1}{t}〈(I-S)x_t,j_q(x_t-z)〉\\ +〈F{x}_t-FS{x}_t,j_q(x_t-z)〉\\ =& \frac{1}{t}〈Q_C{y}_t-y_t,j_q(x_t-z)〉-\frac{1}{t}〈(I-S)x_t-(I-S)z,j_q(x_t-z)〉\\ +〈F{x}_t-FS{x}_t,j_q(x_t-z)〉\\ \le & 〈F{x}_t-F(S{x}_t),j_q(x_t-z)〉\\ \le & M\parallel x_t-S{x}_t\parallel ,\end{array}$$

(2.13)

where $M={sup}_{n\ge 0}\{L{\parallel x_t-z\parallel }^{q-1}\}<\mathrm{\infty }$. Notice

$$x_t-S{x}_t=t[\gamma \varphi (x_t)-FS{x}_t].$$

Thus, we have

$$x_t-S{x}_t\to 0\text{as }t\to 0.$$

Now replacing t in (2.13) with $t_n$ and letting $n\to \mathrm{\infty }$, notice that $(I-S)x_{t_n}\to (I-S)x^{\ast }=0$ for $x^{\ast }\in F(S)$, we obtain $〈(F-\gamma \varphi )x^{\ast },j_q(x^{\ast }-z)〉\le 0$, i.e., $x^{\ast }\in F(S)$ is a solution of (2.4). Hence $\tilde{x}=x^{\ast }$ by uniqueness. Thus, we have shown that every cluster point of $\{x_t\}$ (at $t\to 0$) equals $\tilde{x}$, therefore $x_t\to \tilde{x}$ as $t\to 0$. □

Lemma 2.11 Let X be a q-uniformly smooth Banach space, and let C be a nonempty convex subset of X. Assume that $T_i:C\to C$ is a countable family of ${\lambda }_i$-strict pseudo-contractions for some $0\le {\lambda }_i<1$ and $inf\{{\lambda }_i:i\in \mathbb{N}\}>0$ such that $\mathfrak{F}:={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$. Assume that $\{{\mu }_i\}$ is a positive sequence such that ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i=1$. Then ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i{T}_i:C\to C$ is a λ-strict pseudo-contraction with $\lambda =inf\{{\lambda }_i:i\in \mathbb{N}\}$ and $F({\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i{T}_i)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$.

Proof Let $H_{n}x={\mu }_1{T}_{1}x+{\mu }_2{T}_{2}x+\cdots +{\mu }_n{T}_{n}x$, where ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i=1$. Then $H_n:C\to X$ is a λ-strict pseudo-contraction with $\lambda =min\{{\lambda }_i:1\le i\le n\}$.

Step 1. We firstly prove the case of $n=2$.

$$\begin{array}{rl}〈(& I-H_2)x-(I-H_2)y,j_q(x-y)〉\\ =〈{\mu }_1(I-T_1)x+{\mu }_2(I-T_2)x-{\mu }_1(I-T_1)y-{\mu }_2(I-T_2)y,j_q(x-y)〉\\ ={\mu }_1〈(I-T_1)x-(I-T_1)y,j_q(x-y)〉+{\mu }_2〈(I-T_2)x-(I-T_2)y,j_q(x-y)〉\\ \ge {\mu }_1{\lambda }_1{\parallel (I-T_1)x-(I-T_1)y\parallel }^q+{\mu }_2{\lambda }_2{\parallel (I-T_2)x-(I-T_2)y\parallel }^q\\ \ge \lambda [{\mu }_1{\parallel (I-T_1)x-(I-T_1)y\parallel }^q+{\mu }_2{\parallel (I-T_2)x-(I-T_2)y\parallel }^q]\\ =\lambda {\parallel (I-H_2)x-(I-H_2)y\parallel }^q,\end{array}$$

where $\lambda =min\{{\lambda }_i:i=1,2\}$, which shows that $H_2:C\to C$ is a λ-strict pseudo-contraction.

Using the same means, our proof method can easily carry over to the general finite case.

Step 2. We prove the infinite case. From the definition of λ-strict pseudo-contraction, we have

$$〈(I-T_n)x-(I-T_n)y,j_q(x-y)〉\ge \lambda {\parallel (I-T_n)x-(I-T_n)y\parallel }^q,$$

(2.14)

then we obtain

$$\parallel (I-T_n)x-(I-T_n)y\parallel \le {\left(\frac{1}{\lambda }\right)}^{\frac{1}{q-1}}\parallel x-y\parallel .$$

(2.15)

Taking $p\in F(T_n)$, it follows from (2.15) that

$$\parallel (I-T_n)x\parallel =\parallel (I-T_n)x-(I-T_n)p\parallel \le {\left(\frac{1}{\lambda }\right)}^{\frac{1}{q-1}}\parallel x-p\parallel .$$

(2.16)

Thus, for $\mathrm{\forall }x\in X$, if ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$ with ${\mu }_i>0$ and ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i=1$, then ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i{T}_i$ strongly converges.

Let

$$Hx=\sum _{i=1}^{\mathrm{\infty }}{\mu }_i{T}_{i}x,$$

then we obtain

$$Hx=\sum _{i=1}^{\mathrm{\infty }}{\mu }_i{T}_{i}x=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n{\mu }_i{T}_{i}x=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i{T}_{i}x.$$

Therefore

$$\begin{array}{rl}〈(& I-H)x-(I-H)y,j_q(x-y)〉\\ =\underset{n\to \mathrm{\infty }}{lim}〈(I-\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i{T}_i)x+(I-\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i{T}_i)y,j_q(x-y)〉\\ =\underset{n\to \mathrm{\infty }}{lim}\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i〈(I-T_i)x-(I-T_i)y,j_q(x-y)〉\\ \ge \underset{n\to \mathrm{\infty }}{lim}\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i\lambda {\parallel (I-T_i)x-(I-T_i)y\parallel }^q\\ \ge \lambda \underset{n\to \mathrm{\infty }}{lim}{\parallel (I-\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i{T}_i)x-(I-\frac{1}{{\sum }_{i=1}^n{\mu }_i}\sum _{i=1}^n{\mu }_i{T}_i)y\parallel }^q\\ =\lambda {\parallel (I-H)x-(I-H)y\parallel }^q.\end{array}$$

Thus, H is a λ-strict pseudo-contraction.

Step 3. We prove $F({\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i{T}_i)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$.

Let $x={\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i{T}_{i}x$, then, for $p\in {\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$, we obtain

$$\begin{array}{rl}{\parallel x-p\parallel }^q& =〈x-p,j_q(x-p)〉\\ =〈\sum _{i=1}^{\mathrm{\infty }}{\mu }_i{T}_{i}x-p,j_q(x-p)〉\\ =\sum _{i=1}^{\mathrm{\infty }}{\mu }_i〈T_{i}x-p,j_q(x-p)〉\\ \le {\parallel x-p\parallel }^q-\lambda \sum _{i=1}^{\mathrm{\infty }}{\mu }_i{\parallel x-T_{i}x\parallel }^q,\end{array}$$

where $\lambda =inf\{{\lambda }_i:i\in \mathbb{N}\}$. Thus, we obtain $x=T_{i}x$, it follows that $x\in {\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. □

3 Main results

Lemma 3.1 Let C be a nonempty closed convex subset of a q-uniformly smooth Banach space X. Let $Q_C$ be the sunny nonexpansive retraction from X onto C, and let ϕ be an MKC on C. Let $F:C\to X$ be η-strongly accretive and L-Lipschitzian with $0<\gamma <\eta$, and let $T_i:C\to C$ be a ${\lambda }_i$-strictly pseudo-contractive non-self-mapping such that $\mathfrak{F}:={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$. Assume $\lambda =inf\{{\lambda }_i:i\in \mathbb{N}\}>0$. Let $\{x_n\}$ be a sequence of C generated by (1.9). We assume that the following parameters are satisfied:

• (i) $0<{\alpha }_n<1$, ${\sum }_{i=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$, ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{i=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$;

• (ii) $0<1-{(\frac{q\lambda }{C_q})}^{\frac{1}{q}}\le {\beta }_n<1$, ${\sum }_{i=1}^{\mathrm{\infty }}|{\beta }_{n+1}-{\beta }_n|<\mathrm{\infty }$;

• (iii) ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}=1$, ${\sum }_{n=1}^{\mathrm{\infty }}{\sum }_{i=1}^{\mathrm{\infty }}|{\mu }_i^{(n+1)}-{\mu }_i^{(n)}|<\mathrm{\infty }$;

• (iv) $0<{\gamma }_n<a<1$, ${\sum }_{i=1}^{\mathrm{\infty }}|{\gamma }_{n+1}-{\gamma }_n|<\mathrm{\infty }$, ${\alpha }_{n+1}{\beta }_{n}L+\alpha {\gamma }_{n+1}+{\beta }_n>{\alpha }_{n+1}L+{\beta }_n{\gamma }_{n+1}$;

• (v) $1-b\le \alpha <1$, $b:=min\{1,{(\frac{q\lambda }{C_q})}^{\frac{1}{q}}\}$.

Then ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-x_n\parallel =0$.

Proof Let $B_n={\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}{T}_i$, by Lemma 2.11 we obtain that for each $n\ge 0$, $B_n$ is a λ-strict pseudo-contraction on C and $F(B_n)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. Further, we can get that

$$\sum _{n=1}^{\mathrm{\infty }}\parallel B_{n+1}x-B_{n}x\parallel =\sum _{n=1}^{\mathrm{\infty }}\sum _{i=1}^{\mathrm{\infty }}|{\mu }_i^{(n+1)}-{\mu }_i^{(n)}|\parallel T_{i}x\parallel <\mathrm{\infty },$$

thus ${\{B_n\}}_{n=1}^{\mathrm{\infty }}$ satisfies the AKTT-condition. Let $W_n=\alpha I+(1-\alpha ){\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}{T}_i$, where $\alpha \in [1-b,1)$, $b:=min\{1,{(\frac{q\lambda }{C_q})}^{\frac{1}{q}}\}$. From Lemma 2.4 and Lemma 2.11 we have that $W_n$ is a nonexpansive mapping and $F(W_n)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)=\mathfrak{F}$, then the iterative algorithm (1.9) can be rewritten as follows:

$$\{\begin{array}{l}{x}_1=x\in C,\\ y_n={\beta }_n{x}_n+(1-{\beta }_n)B_n{x}_n,\\ x_{n+1}=Q_C[{\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n],n\ge 1.\end{array}$$

(3.1)

We divide the rest of the proof into two parts.

Step 1. We will prove that the sequence $\{x_n\}$ is bounded.

Letting

$$L_{n}x={\beta }_{n}x+(1-{\beta }_n)B_{n}x,$$

from Lemma 2.4 and condition (ii), we get that $L_n:C\to C$ is nonexpansive. Taking a point $p\in {\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$, we have $L_{n}p=p$ and $p\in F(W_n)$. Therefore, we obtain

$$\parallel y_n-p\parallel =\parallel L_n{x}_n-p\parallel \le \parallel x_n-p\parallel .$$

From the definition of MKC and Lemma 2.1, for any $\epsilon >0$, there is a number $r_{\epsilon }\in (0,1)$, if $\parallel x_n-p\parallel <\epsilon$, then $\parallel \varphi (x_n)-\varphi (p)\parallel <\epsilon$; if $\parallel x_n-p\parallel \ge \epsilon$, then $\parallel \varphi (x_n)-\varphi (p)\parallel \le r_{\epsilon }\parallel x_n-p\parallel$. It follows from (3.1) and Lemma 2.5 that

$$\begin{array}{r}\parallel x_{n+1}-p\parallel \\ =\parallel Q_C[{\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n]-p\parallel \\ \le \parallel {\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n-p\parallel \\ =\parallel {\alpha }_n(\gamma \varphi (x_n)-Fp)+{\gamma }_n(W_n{x}_n-p)+[(1-{\gamma }_n)I-{\alpha }_{n}F]y_n-[(1-{\gamma }_n)I-{\alpha }_{n}F]p\parallel \\ \le [1-{\gamma }_n-({\alpha }_n\eta -\frac{C_q{L}^q{\alpha }_n^q}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-p\parallel +{\gamma }_n\parallel x_n-p\parallel +{\alpha }_n\parallel \gamma \varphi (x_n)-Fp\parallel \\ \le [1-({\alpha }_n\eta -\frac{C_q{L}^q{\alpha }_n^q}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-p\parallel +{\alpha }_n\gamma max\{r\parallel x_n-p\parallel ,\epsilon \}+{\alpha }_n\parallel \gamma \varphi (p)-Fp\parallel \\ =max\{[1-({\alpha }_n\eta -\frac{C_q{L}^q{\alpha }_n^q}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-p\parallel +{\alpha }_n\gamma r\parallel x_n-p\parallel +{\alpha }_n\parallel \gamma \varphi (p)-Fp\parallel ,\\ [1-({\alpha }_n\eta -\frac{C_q{L}^q{\alpha }_n^q}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-p\parallel +{\alpha }_n\gamma \epsilon +{\alpha }_n\parallel \gamma \varphi (p)-Fp\parallel \}\\ =max\{[1-({\alpha }_n\eta -\frac{C_q{L}^q{\alpha }_n^q}{q{(1-{\gamma }_n)}^{q-1}}-{\alpha }_n\gamma r)]\parallel x_n-p\parallel +{\alpha }_n\parallel \gamma \varphi (p)-Fp\parallel ,\\ [1-({\alpha }_n\eta -\frac{C_q{L}^q{\alpha }_n^q}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-p\parallel +{\alpha }_n\gamma \epsilon +{\alpha }_n\parallel \gamma \varphi (p)-Fp\parallel \}.\end{array}$$

By induction, we obtain

$$\begin{array}{r}\parallel x_{n+1}-p\parallel \\ \le max\{[1-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r)]\parallel x_n-p\parallel \\ +{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r)\frac{\parallel \gamma \varphi (p)-Fp\parallel }{\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r},\\ [1-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-p\parallel \\ +{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}})\frac{\gamma \epsilon +\parallel \gamma \varphi (p)-Fp\parallel }{\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}}\}.\end{array}$$

Hence, we obtain

$$\parallel x_n-p\parallel \le max\{\parallel x_0-p\parallel ,M\},n\ge 0,$$

where M is a constant such that

$$M=max\{\underset{n\ge 0}{sup}\left\{\frac{\parallel \gamma \varphi (p)-Fp\parallel }{\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r}\right\},sup\left\{\frac{\gamma \epsilon +\parallel \gamma \varphi (p)-Fp\parallel }{\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}}\right\}\},$$

which implies that $\{x_n\}$ is bounded, so are $\{y_n\}$ and $\{L_n{x}_n\}$.

Step 2. We claim that $\parallel x_{n+1}-x_n\parallel \to 0$ as $n\to \mathrm{\infty }$.

From (3.1) we have

$$\begin{array}{r}\parallel x_{n+2}-x_{n+1}\parallel \\ =\parallel Q_C[{\alpha }_{n+1}\gamma \varphi (x_{n+1})+{\gamma }_{n+1}{W}_{n+1}{x}_{n+1}+((1-{\gamma }_{n+1})I-{\alpha }_{n+1}F)L_{n+1}{x}_{n+1}]\\ -Q_C[{\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)L_n{x}_n]\parallel \\ \le \parallel {\alpha }_{n+1}\gamma \varphi (x_{n+1})+{\gamma }_{n+1}{W}_{n+1}{x}_{n+1}+((1-{\gamma }_{n+1})I-{\alpha }_{n+1}F)L_{n+1}{x}_{n+1}\\ -{\alpha }_n\gamma \varphi (x_n)-{\gamma }_n{W}_n{x}_n-((1-{\gamma }_n)I-{\alpha }_{n}F)L_n{x}_n\parallel \\ =\parallel ((1-{\gamma }_{n+1})I-{\alpha }_{n+1}F)L_{n+1}{x}_{n+1}-((1-{\gamma }_n)I-{\alpha }_{n}F)L_n{x}_n\\ +({\alpha }_{n+1}\gamma \varphi (x_{n+1})-{\alpha }_n\gamma \varphi (x_n))+({\gamma }_{n+1}{W}_{n+1}{x}_{n+1}-{\gamma }_n{W}_n{x}_n)\parallel \\ \le \parallel ((1-{\gamma }_{n+1})I-{\alpha }_{n+1}F)L_{n+1}{x}_{n+1}-((1-{\gamma }_{n+1})I-{\alpha }_{n+1}F)L_{n+1}{x}_n\parallel \\ +\parallel ((1-{\gamma }_{n+1})I-{\alpha }_{n+1}F)L_{n+1}{x}_n-((1-{\gamma }_n)I-{\alpha }_{n}F)L_n{x}_n\parallel \\ +\parallel {\alpha }_{n+1}\gamma \varphi (x_{n+1})-{\alpha }_n\gamma \varphi (x_n)\parallel +\parallel {\gamma }_{n+1}{W}_{n+1}{x}_{n+1}-{\gamma }_n{W}_n{x}_n\parallel \\ \le (1-{\gamma }_{n+1}-{\alpha }_{n+1}(\eta -\frac{C_q{L}^q{\alpha }_{n+1}^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}))\parallel x_{n+1}-x_n\parallel \\ +(1-{\gamma }_{n+1})\parallel L_{n+1}{x}_n-L_n{x}_n\parallel +|{\gamma }_{n+1}-{\gamma }_n|\parallel L_n{x}_n\parallel \\ +{\alpha }_{n+1}\parallel F{L}_{n+1}{x}_n-F{L}_n{x}_n\parallel +|{\alpha }_{n+1}-{\alpha }_n|\parallel F{L}_n{x}_n\parallel +\parallel {\alpha }_{n+1}\gamma \varphi (x_{n+1})-{\alpha }_{n+1}\gamma \varphi (x_n)\parallel \\ +\parallel {\alpha }_{n+1}\gamma \varphi (x_n)-{\alpha }_n\gamma \varphi (x_n)\parallel +\parallel {\gamma }_{n+1}{W}_{n+1}{x}_{n+1}-{\gamma }_{n+1}{W}_{n+1}{x}_n\parallel \\ +\parallel {\gamma }_{n+1}{W}_{n+1}{x}_n-{\gamma }_n{W}_n{x}_n\parallel \\ \le (1-{\gamma }_{n+1}-{\alpha }_{n+1}(\eta -\frac{C_q{L}^q{\alpha }_{n+1}^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}))\parallel x_{n+1}-x_n\parallel \\ +(1-{\gamma }_{n+1})\parallel L_{n+1}{x}_n-L_n{x}_n\parallel +|{\gamma }_{n+1}-{\gamma }_n|\parallel L_n{x}_n\parallel \\ +{\alpha }_{n+1}\parallel F{L}_{n+1}{x}_n-F{L}_n{x}_n\parallel +|{\alpha }_{n+1}-{\alpha }_n|\parallel F{L}_n{x}_n\parallel +{\alpha }_{n+1}\gamma \parallel x_{n+1}-x_n\parallel \\ +|{\alpha }_{n+1}-{\alpha }_n|\parallel \gamma \varphi (x_n)\parallel +{\gamma }_{n+1}\parallel x_{n+1}-x_n\parallel \\ +{\gamma }_{n+1}\parallel W_{n+1}{x}_n-W_n{x}_n\parallel +|{\gamma }_{n+1}-{\gamma }_n|\parallel W_n{x}_n\parallel \\ \le (1-{\alpha }_{n+1}(\eta -\frac{C_q{L}^q{\alpha }_{n+1}^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma ))\parallel x_{n+1}-x_n\parallel \\ +(1-{\gamma }_{n+1})\parallel L_{n+1}{x}_n-L_n{x}_n\parallel +{\gamma }_{n+1}\parallel W_{n+1}{x}_n-W_n{x}_n\parallel \\ +|{\gamma }_{n+1}-{\gamma }_n|(\parallel L_n{x}_n\parallel +\parallel W_n{x}_n\parallel )+{\alpha }_{n+1}L\parallel L_{n+1}{x}_n-L_n{x}_n\parallel \\ +|{\alpha }_{n+1}-{\alpha }_n|(\parallel F{L}_n{x}_n\parallel +\parallel \gamma \varphi (x_n)\parallel )\\ =(1-{\alpha }_{n+1}(\eta -\frac{C_q{L}^q{\alpha }_{n+1}^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma ))\parallel x_{n+1}-x_n\parallel \\ +|{\alpha }_{n+1}-{\alpha }_n|(\parallel F{L}_n{x}_n\parallel +\parallel \gamma \varphi (x_n)\parallel )\\ +|{\gamma }_{n+1}-{\gamma }_n|(\parallel L_n{x}_n\parallel +\parallel W_n{x}_n\parallel )+(1+{\alpha }_{n+1}L-{\gamma }_{n+1})\parallel L_{n+1}{x}_n-L_n{x}_n\parallel \\ +{\gamma }_{n+1}\parallel W_{n+1}{x}_n-W_n{x}_n\parallel .\end{array}$$

(3.2)

Next, we estimate $\parallel L_{n+1}{x}_n-L_n{x}_n\parallel$ and $\parallel W_{n+1}{x}_n-W_n{x}_n\parallel$. Notice that

$$\begin{array}{c}\parallel L_{n+1}{x}_n-L_n{x}_n\parallel =\parallel [{\beta }_{n+1}{x}_n+(1-{\beta }_{n+1})B_{n+1}{x}_n]-[{\beta }_n{x}_n+(1-{\beta }_n)B_n{x}_n]\parallel \hfill \\ \phantom{\parallel L_{n+1}{x}_n-L_n{x}_n\parallel }\le |{\beta }_{n+1}-{\beta }_n|\parallel x_n-B_{n+1}{x}_n\parallel +(1-{\beta }_n)\parallel B_{n+1}{x}_n-B_n{x}_n\parallel ,\hfill \end{array}$$

(3.3)

$$\begin{array}{c}\parallel W_{n+1}{x}_n-W_n{x}_n\parallel =\parallel \alpha x_n+B_{n+1}{x}_n-\alpha x_n+(1-\alpha )B_n{x}_n\parallel \hfill \\ \phantom{\parallel W_{n+1}{x}_n-W_n{x}_n\parallel }=(1-\alpha )\parallel B_{n+1}{x}_n-B_n{x}_n\parallel .\hfill \end{array}$$

(3.4)

Substituting (3.3) and (3.4) into (3.2) and using condition (iv), we have

$$\begin{array}{rcl}\parallel x_{n+2}-x_{n+1}\parallel & \le & (1-{\alpha }_{n+1}(\eta -\frac{C_q{L}^q{\alpha }_{n+1}^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma ))\parallel x_{n+1}-x_n\parallel +M_1(|{\alpha }_{n+1}-{\alpha }_n|\\ +(1+{\alpha }_{n+1}L-{\gamma }_{n+1})|{\beta }_{n+1}-{\beta }_n|+|{\gamma }_{n+1}-{\gamma }_n|)\\ +[1-({\alpha }_{n+1}{\beta }_{n}L+\alpha {\gamma }_{n+1}+{\beta }_n-{\alpha }_{n+1}L-{\beta }_n{\gamma }_{n+1})]\parallel B_{n+1}{x}_n-B_n{x}_n\parallel \\ \le & (1-{\alpha }_{n+1}(\eta -\frac{C_q{L}^q{\alpha }_{n+1}^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma ))\parallel x_{n+1}-x_n\parallel +M_1(|{\alpha }_{n+1}-{\alpha }_n|\\ +(1+{\alpha }_{n+1}L-{\gamma }_{n+1})|{\beta }_{n+1}-{\beta }_n|+|{\gamma }_{n+1}-{\gamma }_n|)+\parallel B_{n+1}{x}_n-B_n{x}_n\parallel ,\end{array}$$

(3.5)

where $M_1$ is an appropriate constant such that

$$M_1\ge \parallel x_n-B_{n+1}{x}_n\parallel +\parallel F{L}_n{x}_n\parallel +\parallel L_n{x}_n\parallel +\gamma \parallel \varphi (x_n)\parallel +\parallel W_n{x}_n\parallel \text{for all }n.$$

Since $\{B_n\}$ satisfies the AKTT-condition, we get that

$$\sum _{i=1}^{\mathrm{\infty }}\parallel B_{n+1}{x}_n-B_n{x}_n\parallel <\mathrm{\infty }.$$

Noticing conditions (i), (iii) and (iv) and applying Lemma 2.3 to (3.5), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =0.$$

(3.6)

This completes the proof. □

Lemma 3.2 Let C be a nonempty closed convex subset of a q-uniformly smooth Banach space X. Let $Q_C$ be the sunny nonexpansive retraction from X onto C, and let ϕ be an MKC on C. Let $F:C\to X$ be η-strongly accretive and L-Lipschitzian with $0<\gamma <\eta$, and let $T_i:C\to C$ be a ${\lambda }_i$-strictly pseudo-contractive non-self-mapping such that $\mathfrak{F}:={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$. Assume $\lambda =inf\{{\lambda }_i:i\in \mathbb{N}\}>0$. Let $\{x_n\}$ be a sequence of C generated by (1.9). We assume that the parameters $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{\mu }_i^{(n)}\}$ and $\{{\gamma }_n\}$ satisfy the conditions (i), (ii), (iii), (iv), (v) in Lemma  3.1 and (vi) ${lim}_{n\to \mathrm{\infty }}{\beta }_n=\alpha$. Then $\{x_n\}$ converges strongly to $\tilde{x}\in \mathfrak{F}$, which solves the following variational inequality:

$$〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(p-\tilde{x})〉\le 0,\mathrm{\forall }p\in \bigcap _{i=1}^{\mathrm{\infty }}F(T_i).$$

Proof The proof of the lemma will be split into three parts.

Step 1. We will prove that ${lim}_{n\to \mathrm{\infty }}\parallel T{x}_n-x_n\parallel =0$, where $T:C\to C$ is defined by $Tx=\alpha x+(1-\alpha )Bx$ and $Bx={lim}_{n\to \mathrm{\infty }}{B}_{n}x$. From (3.1) we have

$$\begin{array}{rl}\parallel L_n{x}_n-x_{n+1}\parallel & =\parallel Q_C[{\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)L_n{x}_n]-L_n{x}_n\parallel \\ \le \parallel {\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)L_n{x}_n-L_n{x}_n\parallel \\ =\parallel {\alpha }_n\gamma \varphi (x_n)-{\alpha }_{n}F{L}_n{x}_n+{\gamma }_n{W}_n{x}_n-{\gamma }_n{L}_n{x}_n\parallel \\ \le {\alpha }_n\parallel \gamma \varphi (x_n)-F{L}_n{x}_n\parallel +{\gamma }_n\parallel W_n{x}_n-L_n{x}_n\parallel \\ ={\alpha }_n\parallel \gamma \varphi (x_n)-F{L}_n{x}_n\parallel +{\gamma }_n\parallel \alpha x_n+(1-\alpha )B_n{x}_n-{\beta }_n{x}_n-(1-{\beta }_n)B_n{x}_n\parallel \\ ={\alpha }_n\parallel \gamma \varphi (x_n)-F{L}_n{x}_n\parallel +{\gamma }_n|{\beta }_n-\alpha |\parallel x_n-B_n{x}_n\parallel .\end{array}$$

Using conditions (i) and (vi), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel L_n{x}_n-x_{n+1}\parallel =0.$$

(3.7)

Since ${\{B_n\}}_{n=1}^{\mathrm{\infty }}$ satisfies the AKTT-condition, from Lemma 2.9 we can obtain ${lim}_{n\to \mathrm{\infty }}\parallel B_{n}x-Bx\parallel =0$. Furthermore, notice that

$$\begin{array}{rl}〈Bx-By,j_q(x-y)〉& =\underset{n\to \mathrm{\infty }}{lim}〈B_{n}x-B_{n}y,j_q(x-y)〉\\ \le \underset{n\to \mathrm{\infty }}{lim}[{\parallel B_{n}x-B_{n}y\parallel }^q-\lambda {\parallel (I-B_n)x-(I-B_n)y\parallel }^q]\\ ={\parallel Bx-By\parallel }^q-\lambda {\parallel (I-B)x-(I-B)y\parallel }^q,\end{array}$$

therefore, we deduce that $B:C\to C$ is a λ-strict pseudo-contraction. Applying Lemma 2.4, we obtain that T is nonexpansive with $F(T)=F(B)$. Notice that

$$\begin{array}{r}\parallel T{x}_n-x_n\parallel \\ \le \parallel L_n{x}_n-T{x}_n\parallel +\parallel L_n{x}_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel \\ =\parallel {\beta }_n{x}_n+(1-{\beta }_n)B_n{x}_n-\alpha x_n-(1-\alpha )B{x}_n\parallel +\parallel L_n{x}_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel \\ =\parallel ({\beta }_n-\alpha )(x_n-B_n{x}_n)+(1-\alpha )(B_n{x}_n-B{x}_n)\parallel +\parallel L_n{x}_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel \\ \le |{\beta }_n-\alpha |\parallel x_n-B_n{x}_n\parallel +(1-\alpha )\parallel B_n{x}_n-B{x}_n\parallel +\parallel L_n{x}_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel .\end{array}$$

Using (3.6), (3.7) and (vi), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel T{x}_n-x_n\parallel =0.$$

(3.8)

Step 2. We will show that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_n-\tilde{x})〉\le 0,$$

(3.9)

where $\tilde{x}={lim}_{t\to 0}{x}_t$ with $x_t$ being the fixed point of the contraction

$$x\mapsto Q_C[t\gamma \varphi (x)+(1-tF)Tx].$$

From the above, we know that $\tilde{x}\in \mathfrak{F}=F(T)$, then we take a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ and assume that $x_{n_k}\rightharpoonup \omega$, where $\omega \in F(T)$. Since the Banach space X has a weakly sequentially continuous generalized duality mapping $j_q:X\to X^{\ast }$, by using Lemma 2.7, 2.10 and (3.8), we have

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_n-\tilde{x})〉& =\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}sup}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_k}-\tilde{x})〉\\ =〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(\omega -\tilde{x})〉\\ \le 0.\end{array}$$

Step 3. We will prove that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-\tilde{x}\parallel =0$.

By contradiction, there is a number ${\epsilon }_0$ such that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel x_n-\tilde{x}\parallel \ge {\epsilon }_0.$$

First, let

$$z_n={\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n.$$

(3.10)

Now, we will obtain the contradiction from two cases.

Case 1. Fix ${\epsilon }_1$ (${\epsilon }_1<{\epsilon }_0$), if for some $n>N\in \mathbb{N}$ such that $\parallel x_n-\tilde{x}\parallel \ge {\epsilon }_0-{\epsilon }_1$, and for the other $n>N\in \mathbb{N}$ such that $\parallel x_n-\tilde{x}\parallel <{\epsilon }_0-{\epsilon }_1$.

Let

$$M_n=\frac{q〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉}{{({\epsilon }_0-{\epsilon }_1)}^q}.$$

From (3.9) we know ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{M}_n\le 0$, thus there are two numbers h and N. When $n>N$, we have $M_n\le h$, where $h=min\{\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}}-\gamma \}$. We extract a number $n_0>N$ satisfying $\parallel x_{n_0}-\tilde{x}\parallel <{\epsilon }_0-{\epsilon }_1$, then from Lemma 2.5 and (3.10), we have

$$\begin{array}{r}{\parallel x_{n_0+1}-\tilde{x}\parallel }^q\\ =〈Q_C{z}_{n_0}-z_{n_0},j_q(x_{n_0+1}-\tilde{x})〉+〈z_{n_0}-\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ \le 〈z_{n_0}-\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ =〈{\alpha }_{n_0}\gamma \varphi (x_{n_0})+{\gamma }_{n_0}{W}_{n_0}{x}_{n_0}+((1-{\gamma }_{n_0})I-{\alpha }_{n_0}F)y_{n_0}-\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ =〈[(1-{\gamma }_{n_0})I-{\alpha }_{n_0}F]y_{n_0}-[(1-{\gamma }_{n_0})I-{\alpha }_{n_0}F]\tilde{x}\\ +{\alpha }_{n_0}[\gamma \varphi (x_{n_0})-F\tilde{x}]+{\gamma }_{n_0}(W_{n_0}{x}_{n_0}-\tilde{x}),j_q(x_{n_0+1}-\tilde{x})〉\\ =〈[(1-{\gamma }_{n_0})I-{\alpha }_{n_0}F]y_{n_0}-[(1-{\gamma }_{n_0})I-{\alpha }_{n_0}F]\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ +〈{\alpha }_{n_0}[\gamma \varphi (x_{n_0})-\gamma \varphi (\tilde{x})],j_q(x_{n_0+1}-\tilde{x})〉\\ +{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉+{\gamma }_{n_0}〈W_{n_0}{x}_{n_0}-\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ \le \parallel [(1-{\gamma }_{n_0})I-{\alpha }_{n_0}F]y_{n_0}-[(1-{\gamma }_{n_0})I-{\alpha }_{n_0}F]\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}\gamma \parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉+{\gamma }_{n_0}\parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ \le [1-{\gamma }_{n_0}-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}})]\parallel y_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}\gamma \parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉+{\gamma }_{n_0}\parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ \le [1-{\gamma }_{n_0}-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}})]\parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}\gamma \parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉+{\gamma }_{n_0}\parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ =[1-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}}-\gamma )]\parallel x_{n_0}-\tilde{x}\parallel {\parallel x_{n_0+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ \le \frac{1}{q}[1-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}}-\gamma )]{\parallel x_{n_0}-\tilde{x}\parallel }^q\\ +\frac{q-1}{q}{\parallel x_{n_0+1}-\tilde{x}\parallel }^q+{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ \le \frac{1}{q}[1-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}}-\gamma )]{({\epsilon }_0-{\epsilon }_1)}^q+\frac{q-1}{q}{\parallel x_{n_0+1}-\tilde{x}\parallel }^q\\ +{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉,\end{array}$$

which implies that

$$\begin{array}{rl}{\parallel x_{n_0+1}-\tilde{x}\parallel }^q& <[1-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}}-\gamma )]{({\epsilon }_0-{\epsilon }_1)}^q\\ +q{\alpha }_{n_0}〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n_0+1}-\tilde{x})〉\\ =[1-{\alpha }_{n_0}(\eta -\frac{C_q{L}^q{\alpha }_{n_0}^{q-1}}{q{(1-{\gamma }_{n_0})}^{q-1}}-\gamma -M_{n_0})]{({\epsilon }_0-{\epsilon }_1)}^q\\ \le {({\epsilon }_0-{\epsilon }_1)}^q.\end{array}$$

Hence, we have

$$\parallel x_{n_0+1}-\tilde{x}\parallel <{\epsilon }_0-{\epsilon }_1.$$

In the same way, we obtain

$$\parallel x_n-\tilde{x}\parallel <{\epsilon }_0-{\epsilon }_1,\mathrm{\forall }n\ge n_0.$$

It contradicts ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}\parallel x_n-\tilde{x}\parallel \ge {\epsilon }_0$.

Case 2. Fix ${\epsilon }_1$ (${\epsilon }_1<{\epsilon }_0$), if $\parallel x_n-\tilde{x}\parallel \ge {\epsilon }_0-{\epsilon }_1$ for all $n>N\in \mathbb{N}$. In this case, from Lemma 2.1 there exists a number $r\in (0,1)$ such that

$$\parallel \varphi (x_n)-\varphi (\tilde{x})\parallel \le r\parallel x_n-\tilde{x}\parallel ,n\ge N.$$

From (3.10) we have

$$\begin{array}{r}{\parallel x_{n+1}-\tilde{x}\parallel }^q\\ =〈Q_C{z}_n-z_n,j_q(x_{n+1}-\tilde{x})〉+〈z_n-\tilde{x},j_q(x_{n+1}-\tilde{x})〉\\ \le 〈z_n-\tilde{x},j_q(x_{n+1}-\tilde{x})〉\\ =〈{\alpha }_n\gamma \varphi (x_n)+{\gamma }_n{W}_n{x}_n+((1-{\gamma }_n)I-{\alpha }_{n}F)y_n-\tilde{x},j_q(x_{n+1}-\tilde{x})〉\\ =〈[(1-{\gamma }_n)I-{\alpha }_{n}F]y_n-[(1-{\gamma }_n)I-{\alpha }_{n}F]\tilde{x}\\ +{\alpha }_n[\gamma \varphi (x_n)-F\tilde{x}]+{\gamma }_n(W_n{x}_n-\tilde{x}),j_q(x_{n+1}-\tilde{x})〉\\ =〈[(1-{\gamma }_n)I-{\alpha }_{n}F]y_n-[(1-{\gamma }_n)I-{\alpha }_{n}F]\tilde{x},j_q(x_{n+1}-\tilde{x})〉\\ +〈{\alpha }_n[\gamma \varphi (x_n)-\gamma \varphi (\tilde{x})],j_q(x_{n+1}-\tilde{x})〉\\ +{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉+{\gamma }_n〈W_n{x}_n-\tilde{x},j_q(x_{n+1}-\tilde{x})〉\\ \le \parallel [(1-{\gamma }_n)I-{\alpha }_{n}F]y_n-[(1-{\gamma }_n)I-{\alpha }_{n}F]\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n\gamma r\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉+{\gamma }_n\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ \le [1-{\gamma }_n-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}})]\parallel y_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n\gamma r\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉+{\gamma }_n\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ \le [1-{\gamma }_n-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}})]\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n\gamma r\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉+{\gamma }_n\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ =[1-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r)]\parallel x_n-\tilde{x}\parallel {\parallel x_{n+1}-\tilde{x}\parallel }^{q-1}\\ +{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉\\ \le \frac{1}{q}[1-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r)]{\parallel x_n-\tilde{x}\parallel }^q\\ +\frac{q-1}{q}{\parallel x_{n+1}-\tilde{x}\parallel }^q+{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉,\end{array}$$

which implies that

$$\begin{array}{rcl}{\parallel x_{n+1}-\tilde{x}\parallel }^q& <& [1-{\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r)]{\parallel x_n-\tilde{x}\parallel }^q\\ +q{\alpha }_n〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉.\end{array}$$

(3.11)

Put $a_n={\alpha }_n(\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r)$ and $c_n=\frac{q〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(x_{n+1}-\tilde{x})〉}{\eta -\frac{C_q{L}^q{\alpha }_n^{q-1}}{q{(1-{\gamma }_n)}^{q-1}}-\gamma r}$. Applying Lemma 2.3 to (3.11), we obtain $x_n\to \tilde{x}$ as $n\to \mathrm{\infty }$, which contradicts $\parallel x_n-\tilde{x}\parallel \ge {\epsilon }_0-{\epsilon }_1$. Thus ${lim}_{n\to \mathrm{\infty }}\parallel x_n-\tilde{x}\parallel =0$. This completes the proof. □

Theorem 3.1 Let C be a nonempty closed subset of a q-uniformly smooth Banach space X. Let $Q_C$ be the sunny nonexpansive retraction from X onto C, and let ϕ be an MKC on C. Let $F:C\to X$ be an η-strongly accretive L-Lipschitzian and linear mapping with $0<\gamma <\eta$, and let $T_i:C\to C$ be a ${\lambda }_i$-strictly pseudo-contractive non-self-mapping such that $\mathfrak{F}:={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$. Assume $\lambda =inf\{{\lambda }_i:i\in \mathbb{N}\}>0$. Let $\{x_n\}$ be a sequence of C generated by (1.9). We assume that the following parameters are satisfied:

• (i) $0<{\alpha }_n<1$, ${\sum }_{i=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$, ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${\sum }_{i=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty }$;

• (ii) $0<1-{(\frac{q\lambda }{C_q})}^{\frac{1}{q}}\le {\beta }_n<1$, ${\sum }_{i=1}^{\mathrm{\infty }}|{\beta }_{n+1}-{\beta }_n|<\mathrm{\infty }$;

• (iii) ${\sum }_{i=1}^{\mathrm{\infty }}{\mu }_i^{(n)}=1$, ${\sum }_{n=1}^{\mathrm{\infty }}{\sum }_{i=1}^{\mathrm{\infty }}|{\mu }_i^{(n+1)}-{\mu }_i^{(n)}|<\mathrm{\infty }$;

• (iv) $0<{\gamma }_n<a<1$, ${\sum }_{i=1}^{\mathrm{\infty }}|{\gamma }_{n+1}-{\gamma }_n|<\mathrm{\infty }$, ${\alpha }_{n+1}{\beta }_{n}L+\alpha {\gamma }_{n+1}+{\beta }_n>{\alpha }_{n+1}L+{\beta }_n{\gamma }_{n+1}$;

• (v) $1-b\le \alpha <1$, $b:=min\{1,{(\frac{q\lambda }{C_q})}^{\frac{1}{q}}\}$;

• (vi) ${lim}_{n\to \mathrm{\infty }}{\beta }_n=\alpha$.

Then $\{x_n\}$ generated by (3.1) converges strongly to $\tilde{x}\in \mathfrak{F}$, which solves the following variational inequality:

$$〈\gamma \varphi (\tilde{x})-F\tilde{x},j_q(p-\tilde{x})〉\le 0,\mathrm{\forall }p\in \bigcap _{i=1}^{\mathrm{\infty }}F(T_i).$$

Proof Combining the proof of Lemma 3.1 with Lemma 3.2, we can obtain the conclusion. □

Remark 3.1 Compared with Theorem 3.2 of Song [11], our results are different from those in the following aspects:

• (i) Theorem 3.1 improves and extends Theorem 3.2 of Song [11]. Especially, our results extend the above results from a Hilbert space to a more general q-uniformly smooth and uniformly convex Banach space.

• (ii) We change the metric projection $P_C$ in Song [11] into the sunny nonexpansive retraction $Q_C$ and put it to the other place of the iteration process so that our iteration process is better defined.

• (iii) We generalize the iteration process so that our iteration process is more general.

• (iv) We remove the very strict condition $C+C\subset C$ in Lemma 3.1 and Theorem 3.2 of Song [11], and it is worth stressing that the strict condition is also very necessary in Qin et al. [10] and Cai et al. [20].