A new iterative method for equilibrium problems and fixed point problems for infinite family of nonself strictly pseudocontractive mappings

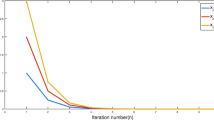
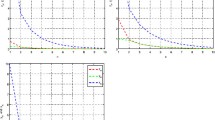
Abstract

The purpose of this paper is to present an iterative method for finding a common element of the set of solutions for an equilibrium problem and the set of common fixed points for a countably infinite family of nonself ${\lambda }_i$-strictly pseudocontractive mappings ${\{T_i\}}_{i=1}^{\mathrm{\infty }}$ from a closed convex subset C into a Hilbert space H.

MSC:47H17, 47H20.

1 Introduction and preliminaries

Let H be a real Hilbert space with the inner product $〈\cdot ,\cdot 〉$ and the norm $\parallel \cdot \parallel$, respectively. Let C be a nonempty closed convex subset of H, and let $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ be a bifunction. The equilibrium problem for G is to find $u^{\ast }\in C$ such that

$$G(u^{\ast },v)\ge 0,\mathrm{\forall }v\in C.$$

(1.1)

The set of solutions of (1.1) is denoted by $EP(G)$. The equilibrium problem (1.1) includes as special cases numerous problems in physics, optimization, economics, transportation, and engineering.

Assume that the bifunction G satisfies the following standard properties.

Assumption A Let $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ be a bifunction satisfying conditions (A1)-(A4).

• (A1) $G(u,u)=0$, $\mathrm{\forall }u\in C$;

• (A2) $G(u,v)+G(v,u)\le 0$, $\mathrm{\forall }(u,v)\in C\times C$;

• (A3) For each $u\in C$, $G(u,\cdot ):C\to (-\mathrm{\infty },+\mathrm{\infty })$ is lower semicontinuous and convex;

• (A4) ${lim\hspace{0.17em}sup}_{t\to +0}G((1-t)u+tz,v)\le G(u,v)$, $\mathrm{\forall }(u,z,v)\in C\times C\times C$.

Recall that a mapping T in H is said to be λ-strictly pseudocontractive in the terminology of Browder and Petryshyn [1], if there exists a constant $0\le \lambda <1$ such that

$${\parallel Tx-Ty\parallel }^2\le {\parallel x-y\parallel }^2+\lambda {\parallel (I-T)x-(I-T)y\parallel }^2$$

for all $x,y\in D(T)$, the domain of T, where I is the identity operator in H. Clearly, when $\lambda =0$, T is nonexpansive, i.e.,

$$\parallel T(x)-T(y)\parallel \le \parallel x-y\parallel .$$

It means that the class of λ-strictly pseudocontractive mappings strictly includes the class of nonexpansive mappings.

A single-valued mapping A in H is said to be monotone, if

$$〈A(x)-A(y),x-y〉\ge 0,\mathrm{\forall }x,y\in D(A),$$

and λ-inverse strongly monotone, if there exists a positive constant λ such that

$$〈A(x)-A(y),x-y〉\ge \lambda {\parallel A(x)-A(y)\parallel }^2,\mathrm{\forall }x,y\in D(A).$$

Therefore, any λ-inverse strongly monotone mapping is monotone and Lipschitz continuous with the Lipschitz constant $L_A=1/\lambda$. It is well known [2] that if T is a nonexpansive mapping, then $I-T$ is $(1/2)$-inverse strongly monotone. It is easy to verify that if T is λ-strictly pseudocontractive, then it is $(1-\lambda )/2$-inverse strongly monotone. Hence, $I-T$ is Lipschitz continuous with the Lipschitz constant $L=2/(1-\lambda )$.

Let ${\{T_i\}}_{i=1}^{\mathrm{\infty }}$ be a countably infinite family of nonself ${\lambda }_i$-strictly pseudocontractive mappings from C into H with the set of fixed points $F(T_i)$ (i.e., $F(T_i)=\{x\in C:x=T_{i}x\}$). Set $\mathcal{F}:={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. Assume that

$$\mathcal{S}:=\mathcal{F}\cap EP(G)\ne \mathrm{\varnothing }.$$

The problem studied in this paper is to find an element

$$u^{\ast }\in \mathcal{S}.$$

(1.2)

If $T_i\equiv I$, $i\ge 1$, then problem (1.2) is reduced to (1.1) and shown in [3] and [4] to cover monotone inclusion problems, saddle point problems, variational inequality problems, minimization problems, the Nash equilibria in noncooperative games, vector equilibrium problems, as well as certain fixed point problems (see also [5]). For finding approximative solutions of (1.1), there exist several approaches: the regularization approach [6–10], the gap-function approach [8, 11–13], and iterative procedure approach [14–30].

In the case that $G\equiv 0$ and $T_i=I$, $i>1$, (1.2) is a problem of finding a fixed point for a λ-strictly pseudocontractive mapping in C (see [31]).

In the case that $G\equiv 0$ and $T_i=I$, $i>N>1$, (1.2) is a problem of finding a common fixed point for a finite family of ${\lambda }_i$-strictly pseudocontractive mappings $T_i$ in C studied in [32], where the following algorithm is constructed:

Let $x_0\in C$ and $\{{\alpha }_n\}$, $\{{\beta }_n\}$, $\{{\gamma }_n\}$ be three sequences in $[0,1]$ satisfying ${\alpha }_n+{\beta }_n+{\gamma }_n=1$ for all $n\ge 1$, and let $\{u_n\}$ be a sequence in C. Then the sequence $\{x_n\}$ generated by

$$x_n={\alpha }_n{x}_{n-1}+{\beta }_n{T}_n{x}_n+{\gamma }_n{u}_n,$$

(1.3)

where $T_n=T_{nmodN}$, is called the implicit iteration process with mean errors for a finite family of strictly pseudocontractive mappings ${\{T_i\}}_{i=1}^N$. The sequence $\{x_n\}$ converges weakly to a common fixed point of the maps ${\{T_i\}}_{i=1}^N$.

If $T_i=I$, $i>1$, then (1.2) is a problem of finding a fixed point for a λ-strictly pseudocontractive mapping in C, which is an equilibrium point for G (see [33]).

Theorem 1.1 [33]

Let C be a nonempty closed convex subset of a Hilbert space H. Let G be a bifunction from $C\times C$ to $(-\mathrm{\infty },+\mathrm{\infty })$ satisfying (A1)-(A4), and let S be a nonexpansive mapping of C into H such that

$$F(S)\cap EP(G)\ne \mathrm{\varnothing }.$$

Let f be a contraction of H into itself, and let $\{x_n\}$ and $\{u_n\}$ be sequences generated by $x_1\in H$ and

$$\{\begin{array}{c}G(u_n,y)+\frac{1}{r_n}〈y-u_n,u_n-x_n〉\ge 0,\mathrm{\forall }y\in C,\hfill \\ x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)S{u}_n\hfill \end{array}$$

for all $n\ge 0$, where $\{{\alpha }_n\}\subset [0,1]$ and $\{r_n\}\subset (0,\mathrm{\infty })$ satisfy

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n=0,\sum _{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty },\sum _{n=1}^{\mathrm{\infty }}|{\alpha }_{n+1}-{\alpha }_n|<\mathrm{\infty },\\ \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}{r}_n>0,\sum _{n=1}^{\mathrm{\infty }}|r_{n+1}-r_n|<\mathrm{\infty }.\end{array}$$

Then $\{x_n\}$ and $\{u_n\}$ converge strongly to $z\in F(S)\cap EP(G)$, where $z=P_{F(S)\cap EP(G)}f(z)$.

If $T_i=I$, $i>N>1$, then (1.2) is a problem of finding a common fixed point for a finite family of ${\lambda }_i$-strictly pseudocontractive mapping $T_i$ from C into H, which is an equilibrium point for G. We have constructed regularization algorithms (see [10, 19, 29]). First algorithm is defined as follows. The regularization solution $u_{\alpha }$ is an element being a solution for the single equilibrium problem

$$\{\begin{array}{cc}{G}_{\alpha }(u_{\alpha },v)\ge 0\hfill & \mathrm{\forall }v\in C,u_{\alpha }\in C,\hfill \\ G_{\alpha }(u,v):={\sum }_{i=0}^N{\alpha }^{{\mu }_i}{G}_i(u,v)+\alpha 〈u,v-u〉,\hfill & \alpha >0,\hfill \\ G_0(u,v)=G(u,v),G_i(u,v)=〈A_i(u),v-u〉,\hfill & i=1,\dots ,N,\hfill \\ {\mu }_0=0<{\mu }_i<{\mu }_{i+1}<1,\hfill & i=2,\dots ,N-1,\hfill \end{array}$$

(1.4)

where α is the regularization parameter.

Theorem 1.2 [19]

For each $\alpha >0$, problem (1.4) has a unique solution $u_{\alpha }$ such that

• (i) ${lim}_{\alpha \to +0}{u}_{\alpha }=u^{\ast }$, $u^{\ast }\in \mathcal{S}$.

• (ii) $\parallel u^{\ast }\parallel \le \parallel y\parallel$, $\mathrm{\forall }y\in \mathcal{S}$.

• (iii) $\parallel u_{\alpha }-u_{\beta }\parallel \le (\parallel u^{\ast }\parallel +dN)\frac{|\alpha -\beta |}{\alpha }$, $\alpha ,\beta >0$, where d is a positive constant.

In the second algorithm, the regularization solution is defined on the base of the inertial proximal point algorithm proposed by Alvarez and Attouch [34], where the sequence $\{z_n\}$ is defined by an equilibrium problem

$$\begin{array}{r}{\tilde{c}}_n(\sum _{i=0}^N{\alpha }_n^{{\mu }_i}{F}_i(z_{n+1},v)+{\alpha }_n〈z_{n+1},v-z_{n+1}〉)+〈z_{n+1}-z_n,v-z_{n+1}〉\\ -{\gamma }_n〈z_n-z_{n-1},v-z_{n+1}〉\ge 0\mathrm{\forall }v\in C,z_0,z_1\in C,\end{array}$$

and $\{{\tilde{c}}_n\}$ and $\{{\gamma }_n\}$ are the sequences of positive numbers.

Theorem 1.3 [19]

Assume that the parameters ${\tilde{c}}_n$, ${\gamma }_n$ and ${\alpha }_n$ are chosen such that

• (i) $0<c_0<{\tilde{c}}_n$, $0\le {\gamma }_n<{\gamma }_0$,

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n=+\mathrm{\infty }$, $b_n={\tilde{c}}_n{\alpha }_n/(1+{\tilde{c}}_n{\alpha }_n)$,

• (iii) ${\sum }_{n=1}^{\mathrm{\infty }}{\gamma }_n{b}_n^{-1}\parallel z_n-z_{n-1}\parallel <+\mathrm{\infty }$,

• (iv) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$, ${lim}_{n\to \mathrm{\infty }}\frac{|{\alpha }_n-{\alpha }_{n+1}|}{{\alpha }_n{b}_n}=0$.

Then the sequence $\{z_n\}$ converges strongly to the element $u^{\ast }$, as $n\to +\mathrm{\infty }$.

In the case that $G\equiv 0$, Maingé [35] considered the following iteration method:

$$x_{n+1}={\alpha }_{n}D{x}_n+\sum _{i\ge 1}{w}_{i,n}{T}_i{x}_n,n\ge 0,$$

(1.5)

where $D:C\to C$ is a given contraction with constant $\rho \in [0,1)$, $x_0\in C$ is a starting point, $\{{\alpha }_n\}\subset (0,1)$, $w_{i,n}\ge 0$ for all $i\ge 1$ and ${\sum }_{i\ge 1}{w}_{i,n}=1-{\alpha }_n$ with the following conditions:

• C1. ${\sum }_{n=0}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$.

• C2. For all $i\in {\mathcal{N}}_I:=\{i:T_i\ne I\}$,

  • (a) $\frac{1}{w_{i,n}}|1-\frac{{\alpha }_{n-1}}{{\alpha }_n}|\to 0$, or ${\sum }_n\frac{1}{w_{i,n}}|{\alpha }_n-{\alpha }_{n-1}|<\mathrm{\infty }$,

  • (b) $\frac{1}{{\alpha }_n}|\frac{1}{w_{i,n}}-\frac{1}{w_{i,n-1}}|\to 0$, or ${\sum }_n|\frac{1}{w_{i,n}}-\frac{1}{w_{i,n-1}}|<\mathrm{\infty }$,

  • (c) $\frac{1}{w_{i,n}{\alpha }_n}{\sum }_{k\ge 0}|w_{k,n}-w_{k,n-1}|\to 0$, or ${\sum }_n\frac{1}{w_{i,n}}{\sum }_{k\ge 0}|w_{k,n}-w_{k,n-1}|<\mathrm{\infty }$.

• C3. $\frac{{\alpha }_n}{w_{i,n}}\to 0$ for all $i\in {\mathcal{N}}_I$.

Then the sequence $\{x_n\}$ given by (1.5) converges strongly to $\overline{x}$ the unique fixed point of $P_{\mathcal{F}}oD$, where $P_{\mathcal{F}}$ is the metric projection from H onto ℱ.

For solving (1.2), Ceng and Yao [36] proposed the following algorithm:

Let $x_1\in H$ be an arbitrary element and

$$\{\begin{array}{c}G(u_n,v)+\frac{1}{r_n}〈u_n-x_n,v-u_n〉,\mathrm{\forall }v\in C,\hfill \\ y_n=(1-{\gamma }_n)x_n+{\gamma }_n{W}_n{u}_n,\hfill \\ x_{n+1}=(1-{\alpha }_n-{\beta }_n)x_n+{\alpha }_{n}f(y_n)+{\beta }_n{W}_n{y}_n,\hfill \end{array}$$

(1.6)

where $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are three sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n\le 1$, and the mapping $W_n$ is defined by

$$\{\begin{array}{c}{U}_{n,n+1}=I,\hfill \\ U_{n,n}={\lambda }_n{T}_n{U}_{n,n+1}+(1-{\lambda }_n)I,\hfill \\ U_{n,n-1}={\lambda }_{n-1}{T}_{n-1}{U}_{n,n}+(1-{\lambda }_{n-1})I,\hfill \\ \cdots \hfill \\ U_{n,k}={\lambda }_k{T}_n{U}_{n,k+1}+(1-{\lambda }_k)I,\hfill \\ U_{n,k-1}={\lambda }_{k-1}{T}_{k-1}{U}_{n,k}+(1-{\lambda }_{k-1})I,\hfill \\ \cdots \hfill \\ U_{n,2}={\lambda }_2{T}_2{U}_{n,3}+(1-{\lambda }_2)I,\hfill \\ W_n=U_{n,1}={\lambda }_1{T}_1{U}_{n,2}+(1-{\lambda }_1)I.\hfill \end{array}$$

Theorem 1.4 [36]

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ be a bifunction satisfying (A1)-(A4), and let ${\{T_i\}}_{i=1}^{\mathrm{\infty }}$ be a sequence of nonexpansive self-mappings on C such that

$$\mathcal{S}=\bigcap _{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)\ne \mathrm{\varnothing }.$$

Suppose that $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_n\}$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n\le 1$, and $\{r_n\}\subset (0,\mathrm{\infty })$ is a real sequence. Suppose that the following conditions are satisfied:

• (i) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\sum }_{n=0}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

• (ii) $0<lim{inf}_{n\to \mathrm{\infty }}{\beta }_n\le lim{sup}_{n\to \mathrm{\infty }}{\beta }_n<1$;

• (iii) $0<lim{inf}_{n\to \mathrm{\infty }}{\gamma }_n\le lim{sup}_{n\to \mathrm{\infty }}{\gamma }_n<1$ and ${lim}_{n\to \mathrm{\infty }}|{\gamma }_{n+1}-{\gamma }_n|=0$;

• (iv) $0<lim{inf}_{n\to \mathrm{\infty }}{r}_n$ and ${lim}_{n\to \mathrm{\infty }}|r_{n+1}-r_n|=0$.

Let f be a contraction of C into itself and given $x_0\in C$. Then the sequences $\{x_n\}$ and $\{u_n\}$ generated by (1.6), where $\{{\lambda }_n\}$ is a sequence in $(0,b]$ for some $b\in (0,1)$, converge strongly to $x^{\ast }\in {\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)$, where $x^{\ast }=P_{{\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)}f(x^{\ast })$.

2 Main results

In this section, for solving problem (1.2), we present a new iterative method.

Let $z_0$ be an arbitrary element in a Hilbert space H, the sequence of iterations $\{z_n\}$ is defined by finding $u_n\in C$ such that

$$\{\begin{array}{c}G(u_n,y)+〈u_n-z_n,y-u_n〉\ge 0,\mathrm{\forall }y\in C,\hfill \\ z_{n+1}=P_C(z_n-{\beta }_n[z_n-u_n+{\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i(z_n)+{\alpha }_n{z}_n])\hfill \\ \phantom{z_{n+1}}=P_C(z_n-{\beta }_n[{\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i(z_n)+(1+{\alpha }_n)z_n-u_n]),n\ge 0,\hfill \end{array}$$

(2.1)

where $P_C$ is the metric projection of H onto C, and $\{{\alpha }_n\}$, $\{{\beta }_n\}$, and $\{{\gamma }_i\}$ are three sequences of positive numbers such that

$$\sum _{i=1}^{\mathrm{\infty }}{\gamma }_i\frac{2}{1-{\lambda }_i}=\gamma <\mathrm{\infty }.$$

(2.2)

Also, we construct a regularization solution $u_{\alpha }$ for (1.2) by solving the following variational inequality problem: find $u_{\alpha }\in C$ such that

$$\{\begin{array}{cc}〈A_0(u_{\alpha })+{\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i(u_{\alpha })+\alpha u_{\alpha },v-u_{\alpha }〉\ge 0,\hfill & \mathrm{\forall }v\in C,\hfill \\ A_i=I-T_i,\hfill & i\ge 0,\hfill \end{array}$$

(2.3)

where $T_0(x)=\{z\in C:G(z,v)+〈z-x,v-z〉\ge 0\mathrm{\forall }v\in C\}$, $\{{\gamma }_i\}$ is a sequence of positive numbers satisfying $(2,2)$, and α is a small regularization parameter tending to zero.

We need the following important lemmas for the proof of our main results.

Lemma 2.1 [7]

Let C be a nonempty closed convex subset of a Hilbert space H, and let G be a bifunction of $C\times C$ into $(-\mathrm{\infty },+\mathrm{\infty })$ satisfying (A1)-(A4). Let $r>0$ and $x\in H$. Then there exists $z\in C$ such that

$$G(z,v)+\frac{1}{r}〈z-x,v-z〉\ge 0,\mathrm{\forall }v\in C.$$

Lemma 2.2 [7]

Assume that $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ satisfies conditions (A1)-(A4). For $r>0$ and $x\in H$, define a mapping $T_r:H\to C$ as follows:

$$T_r(x)=\{z\in C:G(z,v)+\frac{1}{r}〈z-x,v-z〉\ge 0\mathrm{\forall }v\in C\}.$$

(2.4)

Then the following statements hold:

• (i) $T_r$ is single-valued;

• (ii) $T_r$ is firmly nonexpansive, i.e., for any $x,y\in H$,

  $${\parallel T_r(x)-T_r(y)\parallel }^2\le 〈T_r(x)-T_r(y),x-y〉;$$

• (iii) $F(T_r)=EP(G)$;

• (iv) $EP(G)$ is closed and convex.

It is easy to see that $T_r$ is a nonexpansive mapping.

Lemma 2.3 [37]

Let $\{a_n\}$, $\{b_n\}$, and $\{c_n\}$ be the sequences of positive numbers satisfying the conditions:

• (i) $a_{n+1}\le (1-b_n)a_n+c_n$, $b_n<1$,

• (ii) ${\sum }_{n=0}^{\mathrm{\infty }}{b}_n=+\mathrm{\infty }$, ${lim}_{n\to +\mathrm{\infty }}\frac{c_n}{b_n}=0$.

Then ${lim}_{n\to +\mathrm{\infty }}{a}_n=0$.

Lemma 2.4 [38, 39]

Assume that T is a λ-strictly pseudocontractive mapping of a closed convex subset C of a Hilbert space H. Then $I-T$ is demiclosed at zero; that is, whenever $\{x_n\}$ is a sequence in C weakly converging to some $x\in C$, and the sequence $\{(I-T)(x_n)\}$ strongly converges to zero, it follows that $(I-T)(x)=0$.

Now, we are in a position to introduce and prove the main results.

Theorem 2.5 Let C be a nonempty closed convex subset of a real Hilbert space H. Let $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ be a bifunction satisfying (A1)-(A4), and let ${\{T_i\}}_{i=1}^{\mathrm{\infty }}$ be a sequence of nonself ${\lambda }_i$-strictly pseudocontractive mappings from C into H such that

$$\mathcal{S}=\bigcap _{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)\ne \mathrm{\varnothing }.$$

Assume that $\{{\gamma }_i\}$ satisfies condition (2.2). Then for each $\alpha >0$, problem (2.3) has a unique solution $u_{\alpha }$ such that

• (i) ${lim}_{\alpha \to 0}{u}_{\alpha }=u^{\ast }$, $u^{\ast }\in \mathcal{S}$ and $\parallel u^{\ast }\parallel \le \parallel y\parallel$, $\mathrm{\forall }y\in \mathcal{S}$,

• (ii) $\parallel u_{\alpha }-u_{\beta }\parallel \le \frac{|\alpha -\beta |}{\alpha }\parallel u^{\ast }\parallel$.

Proof First, we prove that problem (2.3) has a unique solution. Set

$$A:=\sum _{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i.$$

Let $x^{\ast }$ be a common fixed point of ${\{T_i\}}_{i\ge 1}$. Since

$${\gamma }_i\parallel A_i(x)\parallel \le {\gamma }_i\parallel A_i(x)-A_i\left(x^{\ast }\right)\parallel +{\gamma }_i\parallel A_i\left(x^{\ast }\right)\parallel \le {\gamma }_i\frac{2}{1-{\lambda }_i}\parallel x-x^{\ast }\parallel$$

and ${\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i\frac{2}{1-{\lambda }_i}=\gamma <+\mathrm{\infty }$, the mapping A is well defined, and ${\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i(x)$ converges absolutely for each $x\in C$. It is easy to see that A is Lipschitz continuous with the Lipschitz constant $L_A=\gamma$ and monotone.

Set

$$G_i(u,v)=〈{\gamma }_i{A}_i(u),v-u〉,i\ge 1$$

and

$$G_0(u,v)=〈A_0(u),v-u〉.$$

Then, problem (2.3) is equivalent to that: find $u_{\alpha }\in C$ such that

$$G_{\alpha }(u_{\alpha },v)\ge 0,\mathrm{\forall }v\in C,$$

(2.5)

where

$$G_{\alpha }(u,v)=\tilde{G}(u,v)+\alpha 〈u,v-u〉$$

and

$$\tilde{G}(u,v)=\sum _{i=0}^{\mathrm{\infty }}{G}_i(u,v)=〈A_0(u)+A(u),v-u〉.$$

It is not difficult to verify that for each $i\ge 0$, $G_i(u,v)$ is a bifunction. Therefore, $\tilde{G}(u,v)(u,v)$ also is a bifunction, i.e., $\tilde{G}(u,v)(u,v)$ satisfies Assumption A. By using Lemma 2.2 with $(1/r)=\alpha >0$ and $x=0$, we can conclude that problem (2.5) (consequently (2.3)) has a unique solution $u_{\alpha }$ for each $\alpha >0$.

(i) Next, we prove that

$$\parallel u_{\alpha }\parallel \le \parallel y\parallel ,\mathrm{\forall }y\in \mathcal{S}.$$

(2.6)

Since $y\in \mathcal{S}$, we have $A_i(y)=0$, $i\ge 0$. Thus,

$$\sum _{i=0}^{\mathrm{\infty }}〈{\gamma }_i{A}_i(u_{\alpha }),y-u_{\alpha }〉+\alpha 〈u_{\alpha },y-u_{\alpha }〉\ge 0,\mathrm{\forall }y\in \mathcal{S}.$$

(2.7)

Since

$$〈{\gamma }_i{A}_i(u_{\alpha }),u_{\alpha }-y〉\ge 0,\mathrm{\forall }y\in \mathcal{S},i\ge 0,$$

from (2.7), follows (2.6). Then, there exists a subsequence $\{u_{{\alpha }_k}\}$ of $\{u_{\alpha }\}$ that converges weakly to some element $u^{\ast }\in H$. Now, we have to prove that $u^{\ast }\in \mathcal{S}$. The $(1-{\lambda }_l)/2$-inverse strongly monotone property of $A_l$ implies that

$$\begin{array}{rl}0& \le {\gamma }_l\frac{1-{\lambda }_l}{2}{\parallel A_l(u_{{\alpha }_k})\parallel }^2\\ \le 〈{\gamma }_l{A}_l(u_{{\alpha }_k}),u_{{\alpha }_k}-y〉\\ \le \sum _{i=1}^{\mathrm{\infty }}〈{\gamma }_i{A}_i(u_{{\alpha }_k}),u_{{\alpha }_k}-y〉\\ \le -{\alpha }_k〈u_{{\alpha }_k},u_{{\alpha }_k}-y〉\\ \le {\alpha }_k〈y,y-u_{{\alpha }_k}〉.\end{array}$$

Therefore,

$$\underset{k\to \mathrm{\infty }}{lim}\parallel A_l(u_{{\alpha }_k})\parallel =0.$$

By virtue of Lemma 2.4, we have $u^{\ast }\in F(T_l)$. Since the closed convex set $\mathcal{S}$ has only one element with the minimal norm, using (2.6) and the weak convergence of $\{u_{\alpha }\}$, we can conclude that all the sequence $\{u_{\alpha }\}$ converges strongly to $u^{\ast }$ as $\alpha \to 0$.

(ii) By virtue of (2.4), (2.5) and the monotone property of $A_i$, we obtain

$$\alpha 〈u_{\alpha },u_{\beta }-u_{\alpha }〉+\beta 〈u_{\beta },u_{\alpha }-u_{\beta }〉\ge 0$$

or

$$\parallel u_{\alpha }-u_{\beta }\parallel \le \frac{|\alpha -\beta |}{\alpha }\parallel u_{\beta }\parallel \le \frac{|\alpha -\beta |}{\alpha }\parallel u^{\ast }\parallel$$

for each $\alpha ,\beta >0$. This completes the proof. □

Remark Obviously, if $u_{{\alpha }_k}\to \tilde{u}$, where $u_{{\alpha }_k}$ is the solution of (2.4) with $\alpha ={\alpha }_k\to 0$, as $k\to +\mathrm{\infty }$, then $\mathcal{S}\ne \mathrm{\varnothing }$.

Theorem 2.6 Let C be a nonempty closed convex subset of a real Hilbert space H. Let $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ be a bifunction satisfying (A1)-(A4), and let ${\{T_i\}}_{i=1}^{\mathrm{\infty }}$ be a sequence of nonself ${\lambda }_i$-strictly pseudocontractive mappings from C into H such that

$$\mathcal{S}=\bigcap _{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)\ne \mathrm{\varnothing }.$$

Assume that $\{{\gamma }_i\}$ satisfies condition (2.2), and ${\alpha }_n$, ${\beta }_n$ satisfy the following conditions:

$$\begin{array}{r}{\alpha }_n,{\beta }_n>0,\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n=0,\underset{n\to \mathrm{\infty }}{lim}\frac{|{\alpha }_n-{\alpha }_{n+1}|}{{\alpha }_n^2{\beta }_n}=0,\\ \sum _{n=0}^{\mathrm{\infty }}{\alpha }_n{\beta }_n=\mathrm{\infty },{\overline{lim}}_{n\to \mathrm{\infty }}{\beta }_n\frac{{(2+\gamma +{\alpha }_n)}^2}{{\alpha }_n}<1.\end{array}$$

Then the sequence $\{z_n\}$ given by (2.1) converges strongly to $u^{\ast }\in \mathcal{S}$, that is,

$$\underset{n\to \mathrm{\infty }}{lim}{z}_n=u^{\ast }\in \mathcal{S}.$$

Proof Clearly, iteration $\{z_n\}$ in (2.1) has the form

$$z_{n+1}=P_C(z_n-{\beta }_n[\sum _{i=0}^{\mathrm{\infty }}{\gamma }_i{A}_i(z_n)+{\alpha }_n{z}_n]),z_0\in C,n\ge 0,$$

(2.8)

where ${\gamma }_0=1$.

Let $u_n$ be the solution of (2.3) when $\alpha ={\alpha }_n$. Then

$$u_n=P_C(u_n-{\beta }_n[\sum _{i=0}^{\mathrm{\infty }}{\gamma }_i{A}_i(u_n)+{\alpha }_n{u}_n]).$$

(2.9)

Set ${\mathrm{\Delta }}_n=\parallel z_n-u_n\parallel$. Obviously,

$${\mathrm{\Delta }}_{n+1}=\parallel z_{n+1}-u_{n+1}\parallel \le \parallel z_{n+1}-u_n\parallel +\parallel u_{n+1}-u_n\parallel .$$

From the nonexpansive property of $P_C$, the monotone and Lipschitz continuous properties of $A_i$, $i\ge 0$, (2.8), and (2.9), we have

$$\parallel z_{n+1}-u_n\parallel \le \parallel z_n-u_n-{\beta }_n[\sum _{i=0}^{\mathrm{\infty }}{\gamma }_i(A_i(z_n)-A_i(u_n))+{\alpha }_n(z_n-u_n)]\parallel ,$$

and

$$\begin{array}{r}{\parallel z_n-u_n-{\beta }_n[\sum _{i=0}^{\mathrm{\infty }}{\gamma }_i(A_i(z_n)-A_i(u_n))+{\alpha }_n(z_n-u_n)]\parallel }^2\\ ={\parallel z_n-u_n\parallel }^2+{\beta }_n^2{\parallel [\sum _{i=1}^{\mathrm{\infty }}{\gamma }_i(A_i(z_n)-A_i(u_n))+{\alpha }_n(z_n-u_n)]\parallel }^2\\ -2{\beta }_n〈\sum _{i=0}^{\mathrm{\infty }}{\gamma }_i(A_i(z_n)-A_i(u_n))+{\alpha }_n(z_n-u_n),z_n-u_n〉\\ \le {\parallel z_n-u_n\parallel }^2[1-2{\beta }_n{\alpha }_n+{\beta }_n^2{(2+\sum _{i=1}^{\mathrm{\infty }}{\gamma }_i\frac{2}{1-{\lambda }_i}+{\alpha }_n)}^2].\end{array}$$

Thus,

$$\begin{array}{rl}\parallel z_{n+1}-u_n\parallel & \le {\mathrm{\Delta }}_n{(1-2{\beta }_n{\alpha }_n+{\beta }_n^2{(2+\gamma +{\alpha }_n)}^2)}^{1/2}\\ \le {\mathrm{\Delta }}_n{(1-{\beta }_n{\alpha }_n)}^{1/2}\\ \le {\mathrm{\Delta }}_n(1-\frac{1}{2}{\beta }_n{\alpha }_n).\end{array}$$

Set

$$\begin{array}{rl}{b}_n& =\frac{1}{2}{\alpha }_n{\beta }_n,\\ c_n& =\frac{{\alpha }_n-{\alpha }_{n+1}}{{\alpha }_n}\parallel u^{\ast }\parallel .\end{array}$$

It is not difficult to check that $b_n$ and $c_n$ satisfy the conditions in Lemma 2.3 for sufficiently large n. Hence, ${lim}_{n\to +\mathrm{\infty }}{\mathrm{\Delta }}_n^2=0$. Since ${lim}_{n\to \mathrm{\infty }}{u}_n=u^{\ast }$, we have

$$\underset{n\to \mathrm{\infty }}{lim}{z}_n=u^{\ast }\in \mathcal{S}.$$

This completes the proof. □

Remark The sequences ${\alpha }_n={(1+n)}^{-p}$, $0<p<1/2$, and ${\beta }_n={\gamma }_0{\alpha }_n$ with

$$0<{\gamma }_0<\frac{1}{{(2+\gamma +{\alpha }_0)}^2}$$

satisfy all the necessary conditions in Theorem 2.6.

3 Application

In this section, we show that algorithm (2.1) can be applied to find an element

$$u^{\ast }\in \mathcal{S}\cap VI(C,A^0),$$

(3.1)

where $VI(C,A^0)$ is the set of solutions of the following variational inequality problem:

$$〈A^0(u),v-u〉\ge 0,\mathrm{\forall }v\in C,u\in C,$$

(3.2)

involving a monotone hemicontinuous mapping $A^0$. If $A^0$ is a λ-inverse strongly monotone mapping, and ${\{T_i\}}_{i\ge 1}$ is a countably infinite family of nonexpansive self mappings in C, then problem (3.1) is recently studied in [40] and [41].

Let $A^0$ be a monotone hemicontinuous mapping. Then it is easy to see that $G^0(u,v):=〈A^0(u),v-u〉$ is a bifunction, i.e., $G^0(u,v)$ satisfies Assumption A. Using Lemma 2.2, we construct a nonexpansive mapping $T^0:H\to C$ such that

$$T^0(x):=\{z\in C:G^0(z,v)+〈z-x,v-z〉\ge 0\mathrm{\forall }v\in C\}.$$

Then, $F(T^0)=VI(C,A^0)$. So, $T^0$ as $T_0$ are nonexpansive. Consequently, both mappings $T^0$ and $T_0$ are $(1/2)$-strictly pseudocontractive. Thus, the mapping $I-T^0$ is also Lipschitz continuous with the Lipschitz constant $L=2$. Then, algorithm (2.1) has the form:

Let $z_0$ be an arbitrary element in a Hilbert space H, the sequence of iteration $\{z_n\}$ is defined by

$$\{\begin{array}{c}{u}_n\in C:G(u_n,y)+〈u_n-z_n,y-u_n〉\ge 0,\mathrm{\forall }y\in C,\hfill \\ u_n^0\in C:G^0(u_n^0,y)+〈u_n^0-z_n,y-u_n^0〉\ge 0,\mathrm{\forall }y\in C,\hfill \\ z_{n+1}=P_C(z_n-{\beta }_n[z_n-u_n+z_n-u_n^0+{\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i(z_n)+{\alpha }_n{z}_n])\hfill \\ \phantom{z_{n+1}}=P_C(z_n-{\beta }_n[{\sum }_{i=1}^{\mathrm{\infty }}{\gamma }_i{A}_i(z_n)+(2+{\alpha }_n)z_n-u_n-u_n^0]),n\ge 0.\hfill \end{array}$$

(3.3)

Theorem 3.1 Let C be a nonempty closed convex subset of a real Hilbert space H. Let $G:C\times C\to (-\mathrm{\infty },+\mathrm{\infty })$ be a bifunction satisfying (A1)-(A4), let ${\{T_i\}}_{i=1}^{\mathrm{\infty }}$ be a sequence of nonself ${\lambda }_i$-strictly pseudocontractive mappings from C into H, and let $A^0$ be a hemicontinuous monotone mapping from C into H such that

$$\bigcap _{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)\cap VI(C,A^0)\ne \mathrm{\varnothing }.$$

Assume that $\{{\gamma }_i\}$ satisfies condition (2.2), and ${\alpha }_n$, ${\beta }_n$ satisfy the following conditions:

$$\begin{array}{r}{\alpha }_n,{\beta }_n>0,\underset{n\to \mathrm{\infty }}{lim}{\alpha }_n=0,\underset{n\to \mathrm{\infty }}{lim}\frac{|{\alpha }_n-{\alpha }_{n+1}|}{{\alpha }_n^2{\beta }_n}=0,\\ \sum _{n=0}^{\mathrm{\infty }}{\alpha }_n{\beta }_n=\mathrm{\infty },{\overline{lim}}_{n\to \mathrm{\infty }}{\beta }_n\frac{{(4+\gamma +{\alpha }_n)}^2}{{\alpha }_n}<1.\end{array}$$

Then

$$\underset{n\to \mathrm{\infty }}{lim}{z}_n=u^{\ast }\in \bigcap _{i=1}^{\mathrm{\infty }}F(T_i)\cap EP(G)\cap VI(C,A^0),$$

where $\{z_n\}$ is defined by (3.3).