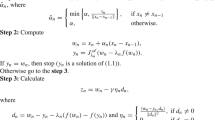Perturbed Ishikawa-hybrid quasi-proximal point algorithm with accretive mappings for a fuzzy system

Abstract

A new class of fuzzy general nonlinear set-valued mixed quasi-variational inclusions frameworks for a perturbed Ishikawa-hybrid quasi-proximal point algorithm using the notion of $(A,\eta )$-accretive is developed. Convergence analysis for the algorithm of solving a fuzzy nonlinear set-valued inclusions problem and existence analysis of a solution for the problem is explored along with some results on the resolvent operator corresponding to an $(A,\eta )$-accretive mapping due to Lan et al. The result that the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ generated by the perturbed Ishikawa-hybrid quasi-proximal point algorithm converges linearly to a solution of the fuzzy general nonlinear set-valued mixed quasi-variational inclusions with the convergence rate ε is proved.

MSC:49J40, 47H06.

1 Introduction

The set-valued inclusions problem, which was introduced and discussed by Bella [1], Huang et al. [2] and Jeong [3], is a useful extension of the mathematics analysis. And the variational inclusion (inequality) is an important context in the set-valued inclusions problem. It provides us with a unified, natural, novel, innovative and general technique to study a wide class of problems arising in different branches of mathematical and engineering sciences. Various variational inclusions have been intensively studied in recent years. Ding [4], Verma [5], Huang [6], Fang and Huang [7], Lan et al. [8], Fang et al. [9], Zhang et al. [10] introduced the concepts of η-subdifferential operators, maximal η-monotone operators, H-monotone operators, A-monotone operators, $(H,\eta )$-monotone operators, $(A,\eta )$-accretive mappings, $(G,\eta )$-monotone operators and defined resolvent operators associated with them, respectively. Moreover, by using the resolvent operator technique, many authors constructed some approximation algorithms for some nonlinear variational inclusions in Hilbert spaces or Banach spaces. In 2008, Li [11] studied the existence of solutions and the stability of a perturbed Ishikawa iterative algorithm for nonlinear mixed quasi-variational inclusions involving $(A,\eta )$-accretive mappings in Banach spaces by using the resolvent operator technique.

On the other hand, in many scientific and engineering applications, the fuzzy set concept and the variational inequalities with fuzzy mappings play an important role. The fuzziness appears when we need to perform, on manifold, calculations with imprecision variables. The concept of fuzzy sets was introduced initially by Zadeh [12] in 1965. Since then, to use this concept in topology and analysis, many authors have expansively developed the theory of fuzzy sets and application [13, 14]. Various concepts of fuzzy metrics on an ordinary set were considered in [15, 16], and many authors studied fixed point theory for ordinary mappings in such fuzzy metric spaces [17–21]. A number of metrics are used on the subspaces of fuzzy sets. The sendograph metric [22, 23] and the d1-metric induced by the Hausdorff metric [24, 25] were studied most frequently. Some attention was also given to Lp-type metrics [26, 27]. These results have a very important application in quantum particle physics, particularly in connection with both string and e1-theory, which were given and studied by El-Naschie [28, 29].

From 1989, Chang and Zhu [30] introduced and investigated a class of variational inequalities for fuzzy mappings. Afterwards, Chang and Huang [31], Ding and Jong [32], Jin [33], Li [34] and others studied several kinds of variational inequalities (inclusions) for fuzzy mappings.

Recently, Verma has developed a hybrid version of the Eckstein-Bertsekas [35] proximal point algorithm, introduced the algorithm based on the $(A,\eta )$-maximal monotonicity framework [36] and studied convergence of the algorithm. The author showed the general nonlinear set-valued inclusions problem based on an $(A,\eta )$-accretive framework and suggested and discussed an Ishikawa-hybrid proximal point algorithm for solving the inclusions problem. On the other hand, from 1989, the generalized nonlinear quasi-variational inequalities (inclusions) with fuzzy mappings have been studied widely by a number of authors, who have more and more achievements [17–37], and we refer to [1–56] and references contained therein.

Inspired and motivated by recent research work in this field, in this paper, a fuzzy general nonlinear set-valued mixed quasi-variational inclusions framework for a perturbed Ishikawa-hybrid quasi-proximal point algorithm using the notion of $(A,\eta )$-accretive is developed. Convergence analysis for the algorithm of solving a fuzzy nonlinear set-valued inclusions problem and existence analysis of a solution for the problem are explored along with some results on the resolvent operator corresponding to an $(A,\eta )$-accretive mapping due to Lan et al. [8]. The result that the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ generated by the perturbed Ishikawa-hybrid quasi-proximal point algorithm converges linearly to a solution of the fuzzy general nonlinear set-valued mixed quasi-variational inclusions with the convergence rate ε is proved.

2 Preliminaries

Let X be a real Banach space with the dual space $X^{\ast }$, $〈\cdot ,\cdot 〉$ be the dual pair between X and $X^{\ast }$, $2^X$ denote the family of all the nonempty subsets of X, and $CB(X)$ denote the family of all nonempty closed bounded subsets of X. The generalized duality mapping $J_q:X\to 2^{X^{\ast }}$ is defined by

$$J_q(x)=\{f^{\ast }\in X^{\ast }:〈x,f^{\ast }〉={\parallel x\parallel }^q,\parallel f^{\ast }\parallel ={\parallel x\parallel }^{q-1}\},\mathrm{\forall }x\in X,$$

where $q>1$ is a constant.

The modulus of smoothness of X is the function ${\rho }_X:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ defined by

$${\rho }_X(t)=sup\{\frac{1}{2}(\parallel x+y\parallel +\parallel x-y\parallel )-1:\parallel x\parallel \le 1,\parallel y\parallel \le t\}.$$

A Banach space X is called uniformly smooth if

$$\underset{t\to 0}{lim}\frac{{\rho }_X(t)}{t}=0.$$

X is called q-uniformly smooth if there exists a constant $c>0$ such that

$${\rho }_X(t)\le c{t}^q(q>1).$$

Remark 2.1 In particular, $J_2$ is the usual normalized duality mapping, and $J_q(x)={\parallel x\parallel }^{q-2}{J}_2(x)$ (for all $x\ne 0$). If $X^{\ast }$ is strictly convex [41], or X is a uniformly smooth Banach space, then $J_q$ is single-valued. In what follows, we always denote the single-valued generalized duality mapping by $J_q$ in a real uniformly smooth Banach space X unless otherwise stated.

Let us recall the following results and concepts.

Definition 2.2 A single-valued mapping $\eta :X\times X\to X$ is said to be τ-Lipschitz continuous if there exists a constant $\tau >0$ such that

$$\parallel \eta (x,y)\parallel \le \tau \parallel x-y\parallel ,\mathrm{\forall }x,y\in X.$$

Definition 2.3 A single-valued mapping $A:X\to X$ is said to be

• (i) accretive if

  $$〈A(x_1)-A(x_2),J_q(x_1-x_2)〉\ge 0,\mathrm{\forall }{x}_1,x_2\in X;$$

• (ii) strictly accretive if A is accretive and $〈A(x_1)-A(x_2),J_q(x_1-x_2)〉=0$ if and only if $x_1=x_2$ $\mathrm{\forall }{x}_1,x_2\in X$;

• (iii) r-strongly η-accretive if there exists a constant $r>0$ such that

  $$〈A(x_1)-A(x_2),J_q(\eta (x_1,x_2))〉\ge r{\parallel x_1-x_2\parallel }^q,\mathrm{\forall }{x}_1,x_2\in X;$$

• (iv) α-Lipschitz continuous if there exists a constant $\alpha >0$ such that

  $$\parallel A(x_1)-A(x_2)\parallel \le \alpha \parallel x_1-x_2\parallel ,\mathrm{\forall }{x}_1,x_2\in X.$$

• (v) A single-valued mapping $F:X\times X\to X$ is said to be $(\mu ,\nu )$-Lipschitz continuous if there exist constants $\mu ,\nu >0$ such that

  $$\parallel F(x_1,y_1)-F(x_2,y_2)\parallel \le \mu \parallel x_1-x_2\parallel +\nu \parallel y_1-y_2\parallel \mathrm{\forall }{x}_i,y_i\in X,i=1,2.$$

• (vi) Let $A,g:X\to X$ be single-valued mappings, $S:X\to 2^X$ be a set-valued mapping. g is said to be $(\psi ,\kappa )$-S-relaxed cocoercive with respect to A mapping, if there exist two constants $\psi ,\kappa >0$ such that for any $x_i\in X$, the following holds:

  $$\begin{array}{r}〈A(u_1)-A(u_2),J_q(g(x_1)-g(x_2))〉\\ \ge \psi {\parallel x_1-x_2\parallel }^q-\kappa {\parallel A(u_1)-A(u_2)\parallel }^q,\mathrm{\forall }{u}_i\in S(x_i),i=1,2.\end{array}$$

Definition 2.4 Let $A:X\to X$ and $\eta :X\times X\to X$ be single-valued mappings. A set-valued mapping $G:X\to 2^X$ is said to be:

• (i) accretive if

  $$〈u_1-u_2,J_q(x_1-x_2)〉\ge 0,\mathrm{\forall }{x}_1,x_2\in X,u_1\in G(x_1),u_2\in G(x_2);$$

• (ii) η-accretive if

  $$〈u_1-u_2,J_q(\eta (x_1,x_2))〉\ge 0,\mathrm{\forall }{x}_1,x_2\in X,u_1\in G(x_1),u_2\in G(x_2);$$

• (iii) r-strongly accretive if there exists a constant $r>0$ such that

  $$〈y_1-y_2,J_q(x_1-x_2)〉\ge r{\parallel x_1-x_2\parallel }^q,\mathrm{\forall }{x}_i\in X,y_i\in G(x_i)(i=1,2);$$

• (iv) m-relaxed η-accretive if there exists a constant $m>0$ such that

  $$〈u_1-u_2,J_q(\eta (x_1,x_2))〉\ge -m{\parallel x_1-x_2\parallel }^q,\mathrm{\forall }{x}_1,x_2\in X,u_1\in G(x_1),u_2\in G(x_2).$$

• (v) A-accretive if M is accretive and $(A+\rho G)(X)=X$ for all $\rho >0$;

• (vi) $(A,\eta )$-accretive if M is m-relaxed η-accretive and $(A+\rho G)(X)=X$ for all $\rho >0$.

• (vii) h-Lipschitz continuous with constants ξ if

  $$\mathbf{h}(G(x_1),G(x_2))\le \xi \parallel x_1-x_2\parallel ,\mathrm{\forall }{x}_1,x_2\in X,$$

where $\mathbf{h}(\cdot ,\cdot )$ is the Hausdorff metric in $CB(X)$.

Based on the literature [8], we can define the resolvent operator $R_{\rho ,G}^{A,\eta }$ as follows.

Definition 2.5 ([8])

Let $\eta :X\times X\to X$ be a single-valued mapping, $A:X\to X$ be a strictly η-accretive single-valued mapping and $G:X\times X\to 2^X$ be an $(A,\eta )$-accretive mapping. The resolvent operator $R_{\rho ,G}^{A,\eta }:X\to X$ is defined by

$$R_{\rho ,G}^{A,\eta }(x)={(A+\rho G)}^{-1}(x)\text{for all }x\in X,$$

where $\rho >0$ is a constant.

Remark 2.6 The $(A,\eta )$-accretive mappings are more general than the $(H,\eta )$-monotone mappings and m-accretive mappings in a Banach space or a Hilbert space, and the resolvent operators associated with $(A,\eta )$-accretive mappings include as special cases the corresponding resolvent operators associated with $(H,\eta )$-monotone operators, m-accretive mappings, A-monotone operators, η-subdifferential operators [3–11, 30–34].

Lemma 2.7 ([8])

Let $\eta :X\times X\to X$ be a τ-Lipschitz continuous mapping, $A:X\to X$ be an r-strongly η-accretive mapping, and $G:X\times X\to 2^X$ be an $(A,\eta )$-accretive mapping. Then the generalized resolvent operator $R_{\rho ,G}^{A,\eta }:X\to X$ is ${\tau }^{q-1}/(r-m\rho )$-Lipschitz continuous, that is,

$$\parallel R_{\rho ,G}^{A,\eta }(x)-R_{\rho ,G}^{A,\eta }(y)\parallel \le \frac{{\tau }^{q-1}}{r-m\rho }\parallel x-y\parallel \mathit{\text{for all }}x,y\in X,$$

where $\rho \in (0,r/m)$.

In the study of characteristic inequalities in q-uniformly smooth Banach spaces, Xu [38] proved the following result.

Lemma 2.8 ([38])

Let X be a real uniformly smooth Banach space. Then X is q-uniformly smooth if and only if there exists a constant $c_q>0$ such that for all $x,y\in X$,

$${\parallel x+y\parallel }^q\le {\parallel x\parallel }^q+q〈y,J_q(x)〉+c_q{\parallel y\parallel }^q.$$

3 Fuzzy general nonlinear set-valued mixed quasi variational inclusions with $(A,\eta )$-accretive mappings

Let X be a real q-uniformly smooth Banach space with the dual space $X^{\ast }$, $〈\cdot ,\cdot 〉$ be the dual pair between X and $X^{\ast }$, $2^X$ denote the family of all the nonempty subsets of X, and $CB(X)$ denote the family of all nonempty closed bounded subsets of X.

Let $\mathcal{F}(X)$ be a collection of all fuzzy sets over X. A mapping $\hat{F}:X\to \mathcal{F}(X)$ is called a fuzzy mapping. For each $x\in X$, $\hat{F}(x)$ (denote it by ${\hat{F}}_x$ in the sequel) is a fuzzy set on X and ${\hat{F}}_x(y)$ is the membership function of y in ${\hat{F}}_x$. For $\hat{B}\in \mathcal{F}(X)$, $q\in [0,1]$, the set ${(\hat{B})}_q=\{x\in X:\hat{B}(x)\ge q\}$ is called a q-cut set of $\hat{B}$.

Let $C=\{1,2,3,4\}$ for any $k\in C$, $\widehat{S_k}:X\to \mathcal{F}(X)$ be a fuzzy mapping satisfying the condition $(\ast )$:

there exists a function $a_k:X\to [0,1]$ such that for all $x\in X$, ${({\hat{S}}_x)}_{a_k(x)}\in CB(X)$, where $CB(X)$ denotes the family of all nonempty bounded closed subsets of X.

By using the fuzzy mapping $\widehat{S_k}$, we can define a set-valued mapping $S_k:X\to CB(X)$ by $S_k(x)={({\hat{S}}_x)}_{a_k(x)}$ for each $x\in X$, and $S_k$ is called the set-valued mapping induced by the fuzzy mapping $\widehat{S_k}$ for any $k\in C$ in the sequel, respectively.

Let $A,f,g:X\to X$; $\eta ,F:X\times X\to X$ be single-valued mappings. Let $G:X\times X\to 2^X$ be a set-valued $(A,\eta )$-accretive mapping and $range(S_3)\cap domG(\cdot ,t)\ne \mathrm{\varnothing }$ for each $t\in X$. We consider the fuzzy general nonlinear set-valued mixed quasi-variational inclusions with $(A,\eta )$-accretive mappings (FGNSVMQVI):

Find $x\in X$ and $b^k\in X$ ($k\in C$) such that ${\hat{S}}_{kx}(b^k)\ge a_k(x)$ and

$$0\in F(b^1,f\left(b^2\right))+G(b^3,b^4)+g(x),$$

(3.1)

where problem (3.1) is called fuzzy general nonlinear set-valued mixed quasi-variational inclusions with $(A,\eta )$-accretive mappings.

If for any $k\in C$, $S_k:X\to CB(X)$ is a set-valued mapping, we can define the fuzzy mapping ${\hat{S}}_{kx}(u)\ge a_k(x):X\to \mathcal{F}(X)$ by $x\mapsto {\chi }_{S_k(x)}$, where ${\chi }_{S_k(x)}$ is the characteristic function of $\widehat{S_k}$. Taking $a_k(x)=1$ ($k\in C$) for all $x\in X$, problem (3.1) is equivalent to the following problem:

Find $x\in X$ and $b^k\in S_k(x)$ ($k\in C$) such that

$$0\in F(b^1,f\left(b^2\right))+G(b^3,b^4)+g(x),$$

(3.2)

which is called a new class of general nonlinear set-valued mixed quasi-variational inclusions with $(A,\eta )$-accretive mappings (GNSVMQVI).

Remark 3.1

• (1) A special case of problem (3.1) is the following:

  • (i) If X is a Hilbert space, an $(A,\eta )$-accretive mapping $\widehat{S_1}=\hat{S}$, $\widehat{S_2}=\hat{T}$, $\widehat{S_3}=g$, $\widehat{S_4}=\hat{G}$, $a_1(x)=a(x)$, $a_2(x)=b(x)$, $a_3(x)=c(x)$, and $F(\cdot ,\cdot )=N(\cdot ,\cdot )$ and $M(\cdot ,\cdot )=G(\cdot ,\cdot )$, then problem (3.1) becomes problem (2.1) in [53], which was studied by Li [53].

  • (ii) For a suitable choice of A, f, g, η, F, G, $\widehat{S_k}$ ($k\in C$) and the space X, a number of known classes of fuzzy variational inclusions and fuzzy variational inequalities in [30–32, 37] can be obtained as special cases of the fuzzy general nonlinear set-valued mixed quasi-variational inclusions (3.1).

• (2) A special case of problem (3.2) is the following:

  • (i) Comparing problem (2.2) in [55] and letting $g(x)=-u$ be a constant in X, $S_1(x)=S_3(x)=S_4(x)=Q(x)$ be single-valued mappings, $S_2(x)=x$ and $f=g$ and $F=N$, $G(\cdot )=M(\cdot ,\cdot )$, then we can see that $GNSVMQVI$ (3.2) becomes problem (2.2) in [55] as follows:

    For any $u\in X$, find $x\in X$ and $y=Q(x)$ such that

    $$u\in N(y,g(x))+M(y).$$

    (3.3)

  • (ii) If $X=X^{\ast }$ is a Hilbert space, $F=0$ is the zero operator in X, $S_1(x)=S_3(x)=S_4(x)=f(x)=Q(x)=I$ are the identity operators in X, $g=0$, and $G(\cdot ,\cdot )=M(\cdot )$, then problem (3.2) becomes the parametric usual variational inclusion $0\in M(x)$ with an $(A,\eta )$-maximal monotone mapping M, which was studied by Verma [36].

  • (iii) If X is a real Banach space, $Q=I$ is the identity operator in X, and $u=0$, then problem (3.3) becomes the parametric usual variational inclusion $u\in N(x,g(x))+M(x)$ with an $(A,\eta )$-accretive mapping, which was studied by Li [54].

Furthermore, these types of fuzzy variational inclusions and variational inclusions can enable us to study many important nonlinear problems arising in mechanics, physics, optimization and control, nonlinear programming, economics, finance, regional, structural, transportation, elasticity and applied sciences in a general and unified framework.

4 The existence of solutions

Now, we study the existence of solutions for problem (3.1).

Lemma 4.1 Let X be a Banach space. Let $S_k$ be the set-valued mapping induced by the fuzzy mapping $\widehat{S_k}$ for any $k\in \{1,2,3,4\}$, let $\eta :X\times X\to X$ be a τ-Lipschitz continuous mapping, $A:X\to X$ be an r-strongly η-accretive mapping, $F:X\times X\to X$ be a single-valued mapping, and $G(\cdot ,t):X\times X\to 2^X$ be an $(A,\eta )$-accretive mapping for any $t\in X$. Then the following statements are mutually equivalent:

• (i) $(x,b^1,b^2,b^3,b^4)\in X^5$ is a solution of problem (3.1), where $\widehat{S_k(x)}(b^k)\ge a_k(x)$, that is, $b^k\in S_k(x)$ ($1\le k\le 4$).

• (ii) For $(x,b^1,b^2,b^3,b^4)\in X^5$ and any $1>\lambda >0$, the following relation holds:

  $$b^3=R_{\rho ,G(b^3,b^4)}^{A,\eta }\left((A\left(b^3\right)-\rho F(b^1,f\left(b^2\right))-\rho g(x))\right),$$

  (4.1)

  where $\widehat{S_k(x)}(b^k)\ge a_k(x)$, that is, $b^k\in S_k(x)$ ($1\le k\le 4$).

• (iii) For $(x,b^1,b^2,b^3,b^4)\in X^5$ and any $1>\lambda >0$, the following relation holds:

  $$x=(1-\lambda )x+\lambda (x-b^3+R_{\rho ,G(b^3,b^4)}^{A,\eta }(A\left(b^3\right)-\rho F(b^1,f\left(b^2\right))-\rho g(x))),$$

  (4.2)

  where $\rho >0$ is a constant, and $\widehat{S_k(x)}(b^k)\ge a_k(x)$, that is, $b^k\in S_k(x)$ ($1\le k\le 4$).

Proof This directly follows from the definition of $R_{\rho ,G(\cdot ,b^4)}^{A,\eta }$. □

Theorem 4.2 Let X be a q-uniformly smooth Banach space. Let $A,f,g:X\to X$; $\eta ,N:X\times X\to X$ be single-valued mappings, and let η be a τ-Lipschitz continuous mapping, A be an r-strongly η-accretive and α-Lipschitz continuous mapping, f be a χ-Lipschitz continuous mapping, and g be a φ-Lipschitz continuous and $(\psi ,\kappa )$-$S_3$-relaxed cocoercive with respect to A mapping, respectively. For $k\in \{1,2,3,4\}$, let $\widehat{S_k}:X\to \mathcal{F}(X)$ be a fuzzy mapping satisfying condition $(\ast )$ and $S_k:X\to CB(X)$ be a set-valued mapping induced by the fuzzy mapping $\widehat{S_k}$, and suppose that $S_k$ is D-Lipschitz continuous with constants ${\xi }_k$ and that $S_3$ is γ-strongly accretive. Let $F:X\times X\to X$ be $(\mu ,\nu )$-Lipschitz continuous. Let $G(\cdot ,t):X\to 2^X$ be a set-valued $(A,\eta )$-accretive mapping for any $t\in X$ and $range(S_3)\cap domG(\cdot ,t)\ne \mathrm{\varnothing }$, and for any $x,y,z\in X$,

$$\parallel R_{\rho ,G(x,\cdot )}^{A,\eta }(z)-R_{\rho ,G(y,\cdot )}^{A,\eta }(z)\parallel \le \delta \parallel x-y\parallel .$$

(4.3)

If there exists a constant $\rho >0$ such that the following condition holds:

$$\begin{array}{r}(1-{(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}-\delta {\xi }_3^q)(r-m\rho ){\tau }^{q-1}\\ <\rho (\mu {\xi }_1+\nu \chi {\xi }_2)+{({\alpha }^q{\xi }_3^q+c_q{\rho }^q{\phi }^q-q\rho \psi +\rho \kappa {\alpha }^q{\xi }_1^q)}^{\frac{1}{q}},\end{array}$$

(4.4)

where $c_q>0$ is the same as in Lemma  2.8, and $\rho \in (0,\frac{r}{m})$, then problem (3.1) has a solution $(x^{\ast },b^{1\ast },b^{2\ast },b^{3\ast },b^{4\ast })\in X^5$, which $b^{k\ast }\in S_k(x^{\ast })$ ($1\le k\le 4$).

Proof For $1>\lambda >0$, define a mapping $H:X\to X$ as follows:

$$\begin{array}{rl}H(x)=& (1-\lambda )x+\lambda (x-b^3\\ +R_{\rho ,G(b^3,b^4)}^{A,\eta }(A\left(b^3\right)-\rho F(b^1,f\left(b^2\right))-\rho g(x)))(\mathrm{\forall }x\in X).\end{array}$$

(4.5)

For elements $x_i\in X$, if for $k\in \{1,2,3,4\}$, letting $\widehat{S_{k{x}_i}}(b_i^k)\ge a_k(x_i)$ or $b_i^k\in S_k(x_i)$ and

$$t_i=A\left(b_i^3\right)-\rho F(b_i^1,f\left(b_i^2\right))-\rho g(x_i)(i=1,2),$$

then by (4.1), (4.2), (4.4), Lemma 2.7 and Lemma 2.8, we have

$$\begin{array}{r}\parallel H(x_1)-H(x_2)\parallel \\ =\parallel (1-\lambda )x_1+\lambda (x_1-b_1^3+R_{\rho ,G(b_1^3,b_1^4)}^{A,\eta }(t_1))-(1-\lambda )x_2-\lambda (x_2-b_2^3+R_{\rho ,G(b_2^3,b_2^4)}^{A,\eta }(t_2))\parallel \\ \le (1-\lambda )\parallel x_1-x_2\parallel +\lambda \parallel x_1-x_2-(b_1^3-b_2^3)\parallel +\lambda \parallel R_{\rho ,G(b_1^3,b_1^4)}^{A,\eta }(t_1)-R_{\rho ,G(b_2^3,b_2^4)}^{A,\eta }(t_2)\parallel \\ \le (1-\lambda )\parallel x_1-x_2\parallel +\lambda \parallel x_1-x_2-(b_1^3-b_2^3)\parallel \\ +(\parallel R_{\rho ,G(b_1^3,b_1^4)}^{A,\eta }(t_1)-R_{\rho ,G(b_1^3,b_2^4)}^{A,\eta }(t_1)\parallel +\parallel R_{\rho ,G(b_1^3,b_2^4)}^{A,\eta }(t_1)-R_{\rho ,G(b_2^3,b_2^4)}^{A,\eta }(t_2)\parallel )\\ \le (1-\lambda )\parallel x_1-x_2\parallel +\lambda \parallel x_1-x_2-(b_1^3-b_2^3)\parallel +\delta \parallel b_1^3-b_2^3\parallel +\frac{{\tau }^{q-1}}{r-m\rho }\parallel t_1-t_2\parallel ,\end{array}$$

(4.6)

where

$$\begin{array}{rcl}\parallel t_1-t_2\parallel & =& \parallel A\left(b_1^3\right)-A\left(b_2^3\right)-\rho (F(b_1^1,f\left(b_1^2\right))-F(b_2^1,f\left(b_2^2\right)))-\rho (g(x_1)-g(x_2))\parallel \\ \le & \parallel A\left(b_1^3\right)-A\left(b_2^3\right)-\rho (g(x_1)-g(x_2))\parallel +\rho \parallel F(b_1^1,f\left(b_1^2\right))-F(b_2^1,f\left(b_2^2\right))\parallel .\end{array}$$

Since g is φ-Lipschitz continuous and $(\psi ,\kappa )$-$S_3$-relaxed cocoercive with respect to A and A is α-Lipschitz continuous, we obtain

$$\begin{array}{r}{\parallel A\left(b_1^3\right)-A\left(b_2^3\right)-\rho (g(x_1)-g(x_2))\parallel }^q\\ \le {\parallel A\left(b_1^3\right)-A\left(b_2^3\right)\parallel }^q+c_q{\rho }^q{\parallel g(x_1)-g(x_2)\parallel }^q-q\rho 〈A\left(b_1^3\right)-A\left(b_2^3\right),J_q(g(x_1)-g(x_2))〉\\ \le {\alpha }^q{\xi }_3^q{\parallel x_1-x_2\parallel }^q+c_q{\rho }^q{\phi }^q{\parallel x_1-x_2\parallel }^q-q\rho \psi {\parallel x_1-x_2\parallel }^q+\rho \kappa {\parallel A\left(b_1^3\right)-A\left(b_2^3\right)\parallel }^q\\ \le {\alpha }^q{\xi }_3^q{\parallel x_1-x_2\parallel }^q+c_q{\rho }^q{\phi }^q{\parallel x_1-x_2\parallel }^q-q\rho \psi {\parallel x_1-x_2\parallel }^q+\rho \kappa {\alpha }^q{\xi }_3^q{\parallel x_1-x_2\parallel }^q\\ \le ({\alpha }^q{\xi }_3^q+c_q{\rho }^q{\phi }^q-q\rho \psi +\rho \kappa {\alpha }^q{\xi }_1^q){\parallel x_1-x_2\parallel }^q.\end{array}$$

(4.7)

Since $F(\cdot ,\cdot )$ is $(\mu ,\nu )$-Lipschitz continuous and f is χ-Lipschitz continuous, the following holds:

$$\begin{array}{r}\parallel F(b_1^1,f\left(b_1^2\right))-F(b_2^1,f\left(b_2^2\right))\parallel \\ \le \mu \parallel b_1^1-b_2^1\parallel +\nu \parallel f\left(b_1^2\right)-\left(b_2^2\right)\parallel \le (\mu {\xi }_1+\nu \chi {\xi }_2)\parallel x_1-x_2\parallel .\end{array}$$

(4.8)

By using γ-strong accretion of $S_3$, we obtain

$$\begin{array}{rl}{\parallel x_1-x_2-(b_1^3-b_2^3)\parallel }^q& \le {\parallel x_1-x_2\parallel }^q+c_q{\parallel b_1^3-b_2^3\parallel }^q-q〈b_1^3-b_2^3,J_q(x_1-x_2)〉\\ \le (1+c_q{\xi }_3^q-q\gamma ){\parallel x_1-x_2\parallel }^q.\end{array}$$

(4.9)

Combining(4.5), (4.6), (4.7) and (4.8), we can get

$$\parallel H(x_1)-H(x_2)\parallel \le [(1-\lambda )+\lambda \theta ]\parallel x_1-x_2\parallel ,$$

(4.10)

where

$$\begin{array}{rl}\theta =& {(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}+\delta {\xi }_3^q\\ +\frac{{\tau }^{q-1}}{r-m\rho }[\rho (\mu {\xi }_1+\nu \chi {\xi }_2)+{({\alpha }^q{\xi }_3^q+c_q{\rho }^q{\phi }^q-q\rho \psi +\rho \kappa {\alpha }^q{\xi }_1^q)}^{\frac{1}{q}}].\end{array}$$

It follows from (4.3) and (4.9) that H has a fixed point in X, i.e., there exists a point $x^{\ast }\in X$ such that

$$x^{\ast }=(1-\lambda )x^{\ast }+\lambda (x^{\ast }-b^{3\ast }+R_{\rho ,G(b^{3\ast },b^{4\ast })}^{A,\eta }(A\left(b^{3\ast }\right)-\rho F(b^{1\ast },b^{2\ast })+\rho g\left(x^{\ast }\right))),$$

where $b^{k\ast }\in S_k(x^{\ast })$ ($1\le k\le 4$). This completes the proof. □

5 Perturbed Ishikawa-hybrid quasi-proximal point algorithm and solvability of problem (3.1)

Based on Lemma 4.1, we develop a perturbed Ishikawa-hybrid quasi-proximal point algorithm for finding iterative sequence solving problem (3.1) as follows.

Algorithm 5.1 Let X be a q-uniformly smooth Banach space, let $\widehat{S_k}:X\to \mathcal{F}(x)$ be a fuzzy mapping satisfying condition $(\ast )$ and $S_k:X\to CB(X)$ be the set-valued mapping induced by the fuzzy mapping $\widehat{S_k}$ ($1\le k\le 4$). Let $A,f,g:X\to X$, $\eta ,F:X\times X\to X$ be single-valued mappings, and let $G:X\times X\to 2^X$ be such that for each fixed $t\in X$, $G(\cdot ,t):X\to 2^X$ is an $(A,\eta )$-accretive mapping and $range(S_3)\cap domG(\cdot ,t)\ne \mathrm{\varnothing }$. Let ${\{u_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{v_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{p_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{s_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{l_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{t_n\}}_{n=0}^{\mathrm{\infty }}$ and ${\{{\rho }_n\}}_{n=0}^{\mathrm{\infty }}$ be five nonnegative sequences such that

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{p}_n=\underset{n\to \mathrm{\infty }}{lim}{s}_n=\underset{n\to \mathrm{\infty }}{lim}{l}_n=\underset{n\to \mathrm{\infty }}{lim}{t}_n=0,\\ u=\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{u}_n<1,v=\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{v}_n<1,{\rho }_n\uparrow \rho \le \mathrm{\infty }.\end{array}$$

Step 1: For an arbitrarily initial point $x_0\in X$, we choose suitable $b_{x_0}^k\in S_k(x_0)$ ($1\le k\le 4$), $z_0\in X$, $b_{z_0}^3\in S_3(z_0)$ and $b_{w_0}^3\in S_3(w_0)$, letting

$$\{\begin{array}{l}{y}_0=(1-v_0)x_0+v_0{z}_0+l_0{e}_0,\\ \parallel z_0-[x_0-b_{x_0}^3+R_{{\rho }_0,G(b_{x_0}^3,b_{x_0}^4)}^{A,\eta }(A(b_{x_0}^3)-{\rho }_{0}F(b_{x_0}^1,b_{x_0}^2)+{\rho }_{0}g(x_0))]\parallel \\ \le p_0\parallel z_0-x_0-(b_{z_0}^3-b_{x_0}^3)\parallel ,\\ x_1=(1-u_0)x_0+u_0{w}_0+t_0{h}_0,\\ \parallel w_0-[y_0-b_{y_0}^3+R_{{\rho }_0,G(b_{y_0}^3,b_{y_0}^4)}^{A,\eta }(A(b_{y_0}^3)-{\rho }_{0}F(b_{y_0}^1,b_{y_0}^2)+{\rho }_{0}g(x_0))]\parallel \\ \le s_0\parallel w_0-y_0-(b_{w_0}^3-b_{y_0}^3)\parallel ,\end{array}$$

where $b_{y_0}^k\in S_k(y_0)$ ($1\le k\le 4$), and $e_0,h_0\in X$ are errors to take into account a possible inexact computation of the proximal point.

Step 2: The sequences $\{x_n\}$ and $\{y_n\}$ are generated by an iterative procedure

$$\{\begin{array}{l}{y}_n=(1-v_n)x_n+v_n{z}_n+l_n{e}_n;\\ \parallel z_n-[x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A(b_{x_n}^3)-\rho F(b_{x_n}^1,b_{x_n}^2)+{\rho }_{n}g(x_n))]\parallel \\ \le p_n\parallel z_n-x_n-(b_{z_n}^3-b_{x_n}^3)\parallel ,\\ x_{n+1}=(1-u_n)x_n+u_n{w}_n+t_n{h}_n,\\ \parallel w_n-[y_n-b_{y_n}^3+R_{{\rho }_n,G(b_{y_n}^3,b_{y_n}^4)}^{A,\eta }(A(b_{y_n}^3)-\rho F(b_{y_n}^1,b_{y_n}^2)+{\rho }_{n}g(y_n))]\parallel \\ \le s_n\parallel w_n-y_n-(b_{w_n}^3-b_{y_n}^3)\parallel ,\end{array}$$

(5.1)

where $b_{x_n}^k\in S_k$ and $b_{y_n}^k\in S_k$ ($1\le k\le 4$), and $e_n,h_n\in X$ are errors to take into account a possible inexact computation of the proximal point and

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel e_n\parallel =\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel h_n\parallel <+\mathrm{\infty }.$$

By using Nadler [39], we can choose suitable $b_n^k\in S_k(x_n)$ such that

$$\parallel b_{n-1}^k-b_n^k\parallel \le (1+\frac{1}{n_1})\mathbf{h}(S_k(x_{n-1}),S_k(x_n)),$$

(5.2)

where $\mathbf{h}(\cdot ,\cdot )$ is the Hausdorff metric in $CB(X)$, $n=1,2,\dots$ .

Remark 5.2 For a suitable choice of the mappings A, η, f, g, F, G, $\widehat{S_k}$, $a_k$, space X, and nonnegative sequences ${\{u_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{v_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{p_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{s_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{l_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{t_n\}}_{n=0}^{\mathrm{\infty }}$ and ${\{{\rho }_n\}}_{n=0}^{\mathrm{\infty }}$, Algorithm 5.1 can be degenerated to a number of algorithms involving many known algorithms which are due to classes of variational inequalities and variational inclusions [10, 11, 30–34, 45, 47, 50, 56].

Theorem 5.3 Let X be a q-uniformly smooth Banach space. Let $A,f,g:X\to X$; $\eta ,N:X\times X\to X$ be single-valued mappings, and η be a τ-Lipschitz continuous mapping, A be an r-strongly η-accretive and α-Lipschitz continuous mapping, f be a χ-Lipschitz continuous mapping, and g be a φ-Lipschitz continuous and $(\psi ,\kappa )$-$S_3$-relaxed cocoercive with respect to A mapping, respectively. For $k\in \{1,2,3,4\}$, let $\widehat{S_k}:X\to \mathcal{F}(X)$ be a fuzzy mapping satisfying condition $(\ast )$ and $S_k:X\to CB(X)$ be a set-valued mapping induced by the fuzzy mapping $\widehat{S_k}$, and suppose that $S_k$ is h-Lipschitz continuous with constants ${\xi }_k$ and that $S_3$ is γ-strongly accretive. Let $F:X\times X\to X$ be $(\mu ,\nu )$-Lipschitz continuous. Let $G(\cdot ,t):X\to 2^X$ be a set-valued $(A,\eta )$-accretive mapping for any $t\in X$ and $range(S_3)\cap domG(\cdot ,t)\ne \mathrm{\varnothing }$, and for any $x,y,z\in X$,

$$\parallel R_{\rho ,G(x,\cdot )}^{A,\eta }(z)-R_{\rho ,G(y,\cdot )}^{A,\eta }(z)\parallel \le \delta \parallel x-y\parallel .$$

(5.3)

If nonnegative sequences ${\{u_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{v_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{p_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{s_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{l_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{t_n\}}_{n=0}^{\mathrm{\infty }}$ and ${\{{\rho }_n\}}_{n=0}^{\mathrm{\infty }}$ are the same as in Algorithm 5.1 and ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{v}_n=v<\frac{1-3\theta }{\theta (1-\theta )}$, where

$$\begin{array}{rl}\theta =& {(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}+\delta {\xi }_3^q\\ +\frac{{\tau }^{q-1}}{r-m\rho }[\rho (\mu {\xi }_1+\nu \chi {\xi }_2)+{({\alpha }^q{\xi }_3^q+c_q{\rho }^q{\phi }^q-q\rho \psi +\rho \kappa {\alpha }^q{\xi }_1^q)}^{\frac{1}{q}}],\end{array}$$

then the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ generated by perturbed Ishikawa-hybrid quasi-proximal point Algorithm 5.1 converges linearly to $x^{\ast }$ as

$$\begin{array}{r}(\frac{1}{3}-{(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}-\delta {\xi }_3^q)(r-m\rho ){\tau }^{q-1}\\ <\rho (\mu {\xi }_1+\nu \chi {\xi }_2)+{({\alpha }^q{\xi }_3^q+c_q{\rho }^q{\phi }^q-q\rho \psi +\rho \kappa {\alpha }^q{\xi }_1^q)}^{\frac{1}{q}},\end{array}$$

(5.4)

where $c_q>0$ is the same as in Lemma  2.8, $\rho \in (0,\frac{r}{m})$, and the convergence rate is $\epsilon =1-u(1-\theta (3+v\theta -v))$, and problem (3.1) has a solution $(x^{\ast },b^{1\ast },b^{2\ast },b^{3\ast },b^{4\ast })\in X^5$, where $b^{k\ast }\in S_k(x^{\ast })$ ($1\le k\le 4$).

Proof Suppose that the sequence $\{x_n\}$ is the sequence generated by perturbed Ishikawa-hybrid quasi-proximal point Algorithm 5.1, and that $(x^{\ast },b^{1\ast },b^{2\ast },b^{3\ast },b^{4\ast })\in X^5$ is a solution of problem (3.1). From Lemma 4.1 and condition ${\alpha }_n\in [0,1)$, we can get

$$x^{\ast }=(1-u_n)x^{\ast }+u_n(x^{\ast }-b^{3\ast }+R_{{\rho }_n,G(b^{3\ast },b^{4\ast })}^{A,\eta }(A\left(b^{3\ast }\right)-{\rho }_{n}F(b^{1\ast },f\left(b^{2\ast }\right))-{\rho }_{n}g\left(x^{\ast }\right))),$$

where $b^{k\ast }\in S_k(x^{\ast })$ ($1\le k\le 4$).

For all $n\ge 0$ and $b^{k\ast }\in S_k(x^{\ast })$ ($1\le k\le 4$), set

$$c_{n+1}=(1-u_n)x_n+u_n(x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)-{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n))).$$

By using (4.9), we find the estimation

$$\begin{array}{r}\parallel c_{n+1}-x^{\ast }\parallel \\ \le (1-u_n)\parallel x_n-x^{\ast }\parallel +u_n\parallel x^{\ast }-x_n-(b^{3\ast }-b_{x_n}^3)\parallel \\ +u_n\parallel R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)-{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n))\\ -R_{{\rho }_n,G(b^{3\ast },b^{4\ast })}^{A,\eta }(A\left(b^{3\ast }\right)-{\rho }_{n}F(b^{1\ast },f\left(b^{2\ast }\right))-{\rho }_{n}g\left(x^{\ast }\right))\parallel \\ \le [(1-u_n)+u_n{\theta }_n]\parallel x_n-x^{\ast }\parallel ,\end{array}$$

(5.5)

where

$$\begin{array}{rcl}{\theta }_n& =& {(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}+\delta {\xi }_3^q+{(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}\\ +\frac{{\tau }^{q-1}}{r-m{\rho }_n}[{\rho }_n(\mu {\xi }_1+\nu \chi {\xi }_2)+{({\alpha }^q{\xi }_3^q+c_q{\rho }_n^q{\phi }^q-q{\rho }_n\psi +{\rho }_n\kappa {\alpha }^q{\xi }_1^q)}^{\frac{1}{q}}].\end{array}$$

Since $x_{n+1}=(1-u_n)x_n+u_n{w}_n+t_n{h}_n$, (5.1) and (4.8)-(4.9) so that $x_{n+1}-x_n=u_n(w_n-x_n)+t_n{h}_n$ and

$$\begin{array}{r}\parallel x_{n+1}-c_{n+1}\parallel \\ \le \parallel (1-u_n)x_n+u_n{w}_n+t_n{h}_n\\ -[(1-u_n)x_n+u_n(x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)\\ -{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n)\left)\right)]\parallel \\ \le u_n\parallel [y_n-b_{y_n}^3+R_{{\rho }_n,G(b_{y_n}^3,b_{y_n}^4)}^{A,\eta }(A\left(b_{y_n}^3\right)-{\rho }_{n}F(b_{y_n}^1,f\left(b_{y_n}^2\right))-{\rho }_{n}g(y_n))]\\ -[(1-u_n)x_n+u_n(x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)\\ -{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n)\left)\right)]\parallel \\ +u_n\parallel w_n-[y_n-b_{y_n}^3+R_{{\rho }_n,G(b_{y_n}^3,b_{y_n}^4)}^{A,\eta }(A\left(b_{y_n}^3\right)\\ -{\rho }_{n}F(b_{y_n}^1,f\left(b_{y_n}^2\right))-{\rho }_{n}g(y_n)\left)\right]\parallel +t_n\parallel h_n\parallel \\ \le u_n{s}_n\parallel w_n-y_n-(b_{w_n}^3-b_{y_n}^3)\parallel +u_n{\theta }_n\parallel x_n-y_n\parallel +t_n\parallel h_n\parallel \\ \le u_n{s}_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}\parallel w_n-y_n\parallel +u_n{\theta }_n\parallel x_n-y_n\parallel +t_n\parallel h_n\parallel .\end{array}$$

Next, we calculate

$$\begin{array}{r}\parallel x_{n+1}-x^{\ast }\parallel \\ \le \parallel c_{n+1}-x^{\ast }\parallel +\parallel x_{n+1}-c_{n+1}\parallel \\ \le \parallel c_{n+1}-x^{\ast }\parallel +u_n{s}_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}\parallel w_n-y_n\parallel +u_n{\theta }_n\parallel x_n-y_n\parallel +t_n\parallel h_n\parallel \\ \le \parallel c_{n+1}-x^{\ast }\parallel +u_n{s}_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}(\parallel w_n-x_n\parallel +\parallel y_n-x_n\parallel )\\ +u_n{\theta }_n\parallel x_n-y_n\parallel +t_n\parallel h_n\parallel \\ \le \parallel c_{n+1}-x^{\ast }\parallel +s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}{u}_n\parallel w_n-x_n\parallel \\ +u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)\parallel y_n-x_n\parallel +t_n\parallel h_n\parallel \\ \le [(1-u_n)+u_n{\theta }_n]\parallel x_n-x^{\ast }\parallel +s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}(\parallel x_{n+1}-x_n\parallel +t_n\parallel h_n\parallel )\\ +u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)\parallel y_n-x_n\parallel +t_n\parallel h_n\parallel \\ \le [(1-u_n)+u_n{\theta }_n]\parallel x_n-x^{\ast }\parallel +s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}\parallel x_{n+1}-x_n\parallel \\ +u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)\parallel y_n-x_n\parallel \\ +(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+1)t_n\parallel h_n\parallel \\ \le [(1-u_n)+u_n{\theta }_n]\parallel x_n-x^{\ast }\parallel +s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}(\parallel x_{n+1}-x^{\ast }\parallel +\parallel x^{\ast }-x_n\parallel )\\ +u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)(\parallel y_n-x^{\ast }\parallel +\parallel x^{\ast }-x_n\parallel )\\ +(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+1)t_n\parallel h_n\parallel \\ \le [(1-u_n)+u_n{\theta }_n+s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)]\parallel x_n-x^{\ast }\parallel \\ +s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}\parallel x_{n+1}-x^{\ast }\parallel +u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)\parallel y_n-x^{\ast }\parallel \\ +(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+1)t_n\parallel h_n\parallel .\end{array}$$

(5.6)

This implies that

$$\begin{array}{r}\parallel x_{n+1}-x^{\ast }\parallel \\ \le \frac{u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)}{1-s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\parallel y_n-x^{\ast }\parallel +\frac{(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+1)t_n}{1-s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\parallel h_n\parallel \\ +\frac{[(1-u_n)+u_n{\theta }_n+s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)]}{1-s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\\ \times \parallel x_n-x^{\ast }\parallel .\end{array}$$

(5.7)

Let

$$x^{\ast }=(1-v_n)x^{\ast }+v_n(x^{\ast }-b^{3\ast }+R_{{\rho }_n,G(b^{3\ast },b^{4\ast })}^{A,\eta }(A\left(b^{3\ast }\right)-{\rho }_{n}F(b^{1\ast },f\left(b^{2\ast }\right))-{\rho }_{n}g\left(x^{\ast }\right))).$$

For all $n\ge 0$, set

$$d_n=(1-v_n)x_n+v_n(x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)-{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n))).$$

For the same reason,

$$\parallel d_n-x^{\ast }\parallel \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel ,$$

(5.8)

and by using $y_n=(1-v_n)x_n+v_n{z}_n+l_n{e}_n$ in (5.1), the following holds:

$$\begin{array}{r}\parallel y_n-x^{\ast }\parallel \\ \le \parallel d_n-x^{\ast }\parallel +\parallel y_n-d_n\parallel \\ \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel +[(1-v_n)x_n+v_n{z}_n+l_n{e}_n\\ -((1-v_n)x_n+v_n(x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)\\ -{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n)\left)\right)\left)\right]\\ \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel +l_n\parallel e_n\parallel \\ +v_n\parallel z_n-(x_n-b_{x_n}^3+R_{{\rho }_n,G(b_{x_n}^3,b_{x_n}^4)}^{A,\eta }(A\left(b_{x_n}^3\right)-{\rho }_{n}F(b_{x_n}^1,f\left(b_{x_n}^2\right))-{\rho }_{n}g(x_n)))\parallel \\ \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel +l_n\parallel e_n\parallel +v_n{p}_n\parallel z_n-x_n-(b_{z_n}^3-b_{x_n}^3)\parallel \\ \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel +l_n\parallel e_n\parallel +v_n{p}_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}\parallel z_n-x_n\parallel \\ \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel +l_n\parallel e_n\parallel \\ +p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}(\parallel y_n-x_n\parallel +l_n\parallel e_n\parallel )\\ \le ((1-v_n)+v_n{\theta }_n)\parallel x_n-x^{\ast }\parallel +p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}(\parallel y_n-x^{\ast }\parallel +\parallel x^{\ast }-x_n\parallel )\\ +(1+p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}})l_n\parallel e_n\parallel .\end{array}$$

(5.9)

Furthermore,

$$\begin{array}{rcl}\parallel y_n-x^{\ast }\parallel & \le & \frac{(1-v_n)+v_n{\theta }_n+p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}{1-p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\parallel x_n-x^{\ast }\parallel \\ +\frac{(1+p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}})l_n}{1-p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}{l}_n\parallel e_n\parallel .\end{array}$$

(5.10)

Combining (5.7)-(5.10), we have

$$\begin{array}{r}\parallel x_{n+1}-x^{\ast }\parallel \\ \le [\frac{u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)}{1-s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\times \frac{(1-v_n)+v_n{\theta }_n+p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}{1-p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\\ +\frac{[(1-u_n)+u_n{\theta }_n+s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+u_n(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+{\theta }_n)]}{1-s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}]\parallel x_n-x^{\ast }\parallel \\ \times \frac{(s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}+1)t_n}{1-s_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}\parallel h_n\parallel \\ +\frac{(1+p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}})l_n}{1-p_n{(1+c_q{\xi }_3^q-q\gamma )}^{\frac{1}{q}}}{l}_n\parallel e_n\parallel .\end{array}$$

(5.11)

By (5.4) and the conditions

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{p}_n=\underset{n\to \mathrm{\infty }}{lim}{s}_n=\underset{n\to \mathrm{\infty }}{lim}{l}_n=\underset{n\to \mathrm{\infty }}{lim}{t}_n=0,\\ u=\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{u}_n<1,v=\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{v}_n<\frac{1-3\theta }{\theta (1-\theta )},{\rho }_n\uparrow \rho \le \mathrm{\infty },\\ \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel e_n\parallel =\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\parallel h_n\parallel <+\mathrm{\infty },\end{array}$$

we can see

$$\begin{array}{rcl}\parallel x_{n+1}-x^{\ast }\parallel & \le & [u\theta (1-v(1-\theta ))+(1-u(1-2\theta ))]\parallel x_n-x^{\ast }\parallel \\ =& \epsilon \parallel x_n-x^{\ast }\parallel ,\end{array}$$

where $\epsilon =1-u(1-\theta (3+v\theta -v))\in (0,1)$ for $v<\frac{1-3\theta }{\theta (1-\theta )}$; and

$$\begin{array}{rcl}\theta & =& \underset{n\to \mathrm{\infty }}{lim}{\theta }_n\\ =& {(1+c_q{\chi }^q-q\gamma )}^{\frac{1}{q}}+\delta {\xi }_3^q\\ +\frac{{\tau }^{q-1}}{r-m\rho }[\rho (\mu {\xi }_1+\nu \chi {\xi }_2)+{({\alpha }^q{\xi }_3^q+c_q{\rho }^q{\phi }^q-q\rho \psi +\rho \kappa {\alpha }^q{\xi }_1^q)}^{\frac{1}{q}}],\end{array}$$

and the convergence rate is ε.

Therefore, the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ generated by Algorithm 5.1 converges linearly to a solution $x^{\ast }$ with convergence rate ε in a Banach space.

Let $x_n\to x^{\ast }$ as $n\to \mathrm{\infty }$. For any $k\in \{1,2,3,4\}$, by the h-Lipschitz continuity of $S_k(x)$ ($1\le k\le 4$) with constants ${\xi }_k$, we obtain

$$\parallel b_{n+1}^k-b_n^k\parallel \le (1+n^{-1})D(S_k(x_{n+1}),S_k(x_n))\le {\xi }_k(1+n^{-1})\parallel x_{n+1}-x_n\parallel .$$

It follows that ${\{b_n^k\}}_{n=1}^{\mathrm{\infty }}$ are also Cauchy sequences in X. We can assume that $b_n^k\to b^{k\ast }$. Note that $b_n^k\in S_k(x_n)$, we have

$$\begin{array}{rcl}d(b^{k\ast },S\left(x^{\ast }\right))& \le & \parallel b^{k\ast }-b_n^k\parallel +d(b_n^k,S\left(x^{\ast }\right))\\ \le & \parallel b^{k\ast }-b_n^k\parallel +D(S(x_n),S\left(x^{\ast }\right))\\ \le & \parallel b^{k\ast }-b_n^k\parallel +{\xi }_k\parallel x_n-x^{\ast }\parallel \to 0(n\to \mathrm{\infty }).\end{array}$$

Hence $d(b^{k\ast },S_k(x^{\ast }))=0$ and therefore $b^{k\ast }\in S_k(x^{\ast })$.

By the Lipschitz continuity of $S_k$ and Lemma 2.7, condition (5.4), we have

$$x^{\ast }=(1-\lambda )x^{\ast }+\lambda (x^{\ast }-b^{3\ast }+R_{{\rho }_n,G(b^{3\ast },b^{4\ast })}^{A,\eta }(A\left(b^{3\ast }\right)-{\rho }_{n}F(b^{1\ast },f\left(b^{2\ast }\right))-{\rho }_{n}g\left(x^{\ast }\right)))$$

for any $0<\lambda <1$. By Lemma 4.1, we know that problem (3.1) has a solution $(x^{\ast },b^{1\ast },b^{2\ast },b^{3\ast },b^{4\ast })\in X^5$, where $b^{k\ast }\in S_k(x^{\ast })$ ($1\le k\le 4$). This completes the proof. □

Remark 5.4 For a suitable choice of the mappings A, η, f, g, F, G, $\widehat{S_k}$ ($1\le k\le 4$), we can obtain several known results [1, 3–11, 30–34, 45, 47, 56] as special cases of Theorem 5.3.