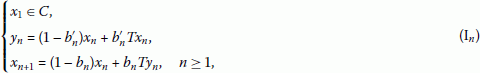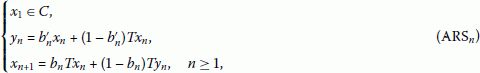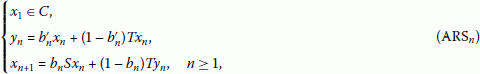Iteration scheme for common fixed points of hemicontractive and nonexpansive operators in Banach spaces

Abstract

The purpose of this paper is to characterize the conditions for the convergence of the iterative scheme in the sense of Agarwal et al. (J. Nonlinear Convex. Anal. 8(1): 61-79, 2007), associated with nonexpansive and ϕ-hemicontractive mappings in a nonempty convex subset of an arbitrary Banach space.

Dedication

Dedicated to Professor Wataru Takahashi on the occasion of his seventieth birthday

1 Preliminaries

Let K be a nonempty subset of an arbitrary Banach space X, and let $X^{\ast }$ be its dual space. Let $T:X\to X$ be an operator. The symbols $D(T)$ and $R(T)$ stand for the domain and the range of T, respectively. We denote $F(T)$ by the set of fixed points of a single-valued mapping $T:K\to K$. We denote by J the normalized duality mapping from X to $2^{X^{\ast }}$ defined by

$$J(x)=\{f^{\ast }\in X^{\ast }:〈x,f^{\ast }〉={\parallel x\parallel }^2={\parallel f^{\ast }\parallel }^2\}.$$

Let $T:D(T)\subseteq X\to X$ be an operator.

Definition 1 T is called L-Lipschitzian if there exists $L\ge 0$ such that

$$\parallel Tx-Ty\parallel ⩽L\parallel x-y\parallel$$

for all $x,y\in D(T)$. If $L=1$, then T is called non-expansive, and if $0⩽L<1$, T is called contraction.

Definition 2 [1–3]

• (i) T is said to be strongly pseudocontractive if there exists a $t>1$ such that for each $x,y\in D(T)$, there exists $j(x-y)\in J(x-y)$ satisfying

  $$Re〈Tx-Ty,j(x-y)〉\le \frac{1}{t}{\parallel x-y\parallel }^2.$$

• (ii) T is said to be strictly hemicontractive if $F(T)\ne \mathrm{\varnothing }$ and if there exists a $t>1$ such that for each $x\in D(T)$ and $q\in F(T)$, there exists $j(x-y)\in J(x-y)$ satisfying

  $$Re〈Tx-q,j(x-q)〉\le \frac{1}{t}{\parallel x-q\parallel }^2.$$

• (iii) T is said to be ϕ-strongly pseudocontractive if there exists a strictly increasing function $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $\varphi (0)=0$ such that for each $x,y\in D(T)$, there exists $j(x-y)\in J(x-y)$ satisfying

  $$Re〈Tx-Ty,j(x-y)〉\le {\parallel x-y\parallel }^2-\varphi (\parallel x-y\parallel )\parallel x-y\parallel .$$

• (iv) T is said to be ϕ-hemicontractive if $F(T)\ne \mathrm{\varnothing }$ and if there exists a strictly increasing function $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $\varphi (0)=0$ such that for each $x\in D(T)$ and $q\in F(T)$, there exists $j(x-y)\in J(x-y)$ satisfying

  $$Re〈Tx-q,j(x-q)〉\le {\parallel x-q\parallel }^2-\varphi (\parallel x-q\parallel )\parallel x-q\parallel .$$

Clearly, each strictly hemicontractive operator is ϕ-hemicontractive.

For a nonempty convex subset K of a normed space $X,S:K\to K$ and $T:K\to K$,

• (a) the Mann iteration scheme [4] is defined by the following sequence $\{x_n\}$:

  

  where $\{b_n\}$ is a sequence in $[0,1]$;

• (b) the sequence $\{x_n\}$ defined by

  

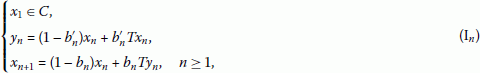
  where $\{b_n\}$, $\{b_n^{\prime }\}$ are sequences in $[0,1]$ is known as the Ishikawa [2] iteration scheme;

• (c) the sequence $\{x_n\}$ defined by

  

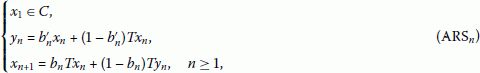
  where $\{b_n\}$, $\{b_n^{\prime }\}$ are sequences in $[0,1]$, is known as the Agarwal-O’Regan-Sahu [5] iteration scheme;

• (d) the sequence $\{x_n\}$ defined by

  

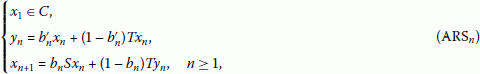
  where $\{b_n\}$, $\{b_n^{\prime }\}$ are sequences in $[0,1]$, is known as the modified Agarwal-O’Regan-Sahu iteration scheme.

Chidume [1] established that the Mann iteration sequence converges strongly to the unique fixed point of T in case T is a Lipschitz strongly pseudo-contractive mapping from a bounded closed convex subset of $L_p$ (or $l_p$) into itself. Afterwards, several authors generalized this result of Chidume in various directions [3, 6–12].

The purpose of this paper is to characterize conditions for the convergence of the iterative scheme in the sense of Agarwal et al. [5] associated with nonexpansive and ϕ-hemicontractive mappings in a nonempty convex subset of an arbitrary Banach space. Our results improve and generalize most results in recent literature [1, 3, 5, 6, 8, 9, 11, 12].

2 Main result

The following result is now well known.

Lemma 3 [13]

For all $x,y\in X$ and $j(x+y)\in J(x+y)$,

$${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2Re〈y,j(x+y)〉.$$

Now, we prove our main result.

Theorem 4 Let K be a nonempty closed and convex subset of an arbitrary Banach space X, let $S:K\to K$ be nonexpansive, and let $T:K\to K$ be a uniformly continuous ϕ-hemicontractive mapping such that S and T have the common fixed point. Suppose that ${\{b_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{b_n^{\prime }\}}_{n=1}^{\mathrm{\infty }}$ are sequences in $[0,1]$ satisfying conditions

• (i) ${lim}_{n\to \mathrm{\infty }}(1-b_n)={lim}_{n\to \mathrm{\infty }}{b}_n^{\prime }=0$,

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}(1-b_n)=\mathrm{\infty }$.

For any $x_1\in K$, define the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ inductively as follows:

$$\{\begin{array}{c}{y}_n=b_n^{\prime }{x}_n+(1-b_n^{\prime })T{x}_n,\hfill \\ x_{n+1}=b_{n}S{x}_n+(1-b_n)T{y}_n,n\ge 1.\hfill \end{array}$$

(2.1)

Then the following conditions are equivalent:

• (a) ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to the common fixed point q of S and T.

• (b) ${\{S{x}_n\}}_{n=1}^{\mathrm{\infty }}$, ${\{T{x}_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{T{y}_n\}}_{n=1}^{\mathrm{\infty }}$ are bounded.

Proof First, we prove that (a) implies (b).

Since T is ϕ-hemicontractive, it follows that $F(T)$ is a singleton. Let $F(S)\cap F(T)=\{q\}$ for some $q\in K$.

Suppose that ${lim}_{n\to \mathrm{\infty }}{x}_n=q$. Then the continuity of S and T yields that

$$\underset{n\to \mathrm{\infty }}{lim}S{x}_n=q=\underset{n\to \mathrm{\infty }}{lim}T{x}_n$$

and

$$\underset{n\to \mathrm{\infty }}{lim}{y}_n=\underset{n\to \mathrm{\infty }}{lim}[b_n^{\prime }{x}_n+(1-b_n^{\prime })T{x}_n]=q.$$

Thus, ${lim}_{n\to \mathrm{\infty }}T{y}_n=q$. Therefore, ${\{S{x}_n\}}_{n=1}^{\mathrm{\infty }}$, ${\{T{x}_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{T{y}_n\}}_{n=1}^{\mathrm{\infty }}$ are bounded.

Second, we need to show that (b) implies (a). Suppose that ${\{S{x}_n\}}_{n=1}^{\mathrm{\infty }}$, ${\{T{x}_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{T{y}_n\}}_{n=1}^{\mathrm{\infty }}$ are bounded.

Put

$$M_1=\parallel x_1-q\parallel +\underset{n\ge 1}{sup}\parallel S{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel T{y}_n-q\parallel .$$

It is clear that $\parallel x_1-q\parallel \le M_1$. Let $\parallel x_n-q\parallel \le M_1$. Next, we will prove that $\parallel x_{n+1}-q\parallel \le M_1$.

Note that

$$\begin{array}{rcl}\parallel x_{n+1}-q\parallel & =& \parallel b_{n}S{x}_n+(1-b_n)T{y}_n-q\parallel \\ =& \parallel b_n(S{x}_n-q)+(1-b_n)(T{y}_n-q)\parallel \\ \le & b_n\parallel S{x}_n-q\parallel +(1-b_n)\parallel T{y}_n-q\parallel \\ \le & (b_n+(1-b_n))M_1\\ =& M_1.\end{array}$$

Thus, we can conclude that the sequence ${\{x_n-q\}}_{n\ge 1}$ is bounded, and hence, there is a constant $M>0$ satisfying

$$M=\underset{n\ge 1}{sup}\parallel x_n-q\parallel +\underset{n\ge 1}{sup}\parallel S{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel T{y}_n-q\parallel .$$

(2.2)

Let $w_n=\parallel T{y}_n-T{x}_{n+1}\parallel$ for each $n\ge 1$. The uniform continuity of T ensures that

$$\underset{n\to \mathrm{\infty }}{lim}{w}_n=0,$$

(2.3)

because

$$\begin{array}{rl}\parallel y_n-x_{n+1}\parallel & =\parallel b_n^{\prime }(x_n-T{x}_n)+(1-b_n)(S{x}_n-T{y}_n)\parallel \\ \le b_n^{\prime }\parallel x_n-T{x}_n\parallel +(1-b_n)\parallel S{x}_n-T{y}_n\parallel \\ \le 2M(b_n^{\prime }+(1-b_n))\\ \to 0\text{as }n\to \mathrm{\infty }.\end{array}$$

By virtue of Lemma 3 and (2.1), we infer that

$$\begin{array}{rl}{\parallel x_{n+1}-q\parallel }^2=& {\parallel b_{n}S{x}_n+(1-b_n)T{y}_n-q\parallel }^2\\ =& {\parallel b_n(S{x}_n-q)+(1-b_n)(T{y}_n-q)\parallel }^2\\ \le & b_n^2{\parallel S{x}_n-q\parallel }^2+2(1-b_n)Re〈T{y}_n-q,j(x_{n+1}-q)〉\\ \le & b_n^2{\parallel x_n-q\parallel }^2+2(1-b_n)Re〈T{y}_n-T{x}_{n+1},j(x_{n+1}-q)〉\\ +2(1-b_n)Re〈T{x}_{n+1}-q,j(x_{n+1}-q)〉\\ \le & b_n^2{\parallel x_n-q\parallel }^2+2(1-b_n)\parallel T{y}_n-T{x}_{n+1}\parallel \parallel x_{n+1}-q\parallel \\ +2(1-b_n){\parallel x_{n+1}-q\parallel }^2-2(1-b_n)\varphi (\parallel x_{n+1}-q\parallel )\parallel x_{n+1}-q\parallel \\ \le & b_n^2{\parallel x_n-q\parallel }^2+2M(1-b_n)w_n+2(1-b_n){\parallel x_{n+1}-q\parallel }^2\\ -2(1-b_n)\varphi (\parallel x_{n+1}-q\parallel )\parallel x_{n+1}-q\parallel .\end{array}$$

(2.4)

The real function $f:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$, $f(t)=t^2$ is increasing and convex. For all $a\in [0,1]$ and $t_1,t_2>0$, we have

$${((1-a)t_1+a{t}_2)}^2\le (1-a)t_1^2+a{t}_2^2.$$

Hence,

$$\begin{array}{rcl}{\parallel x_{n+1}-q\parallel }^2& =& {\parallel b_{n}S{x}_n+(1-b_n)T{y}_n-q\parallel }^2\\ =& {\parallel b_n(S{x}_n-q)+(1-b_n)(T{y}_n-q)\parallel }^2\\ \le & b_n{\parallel S{x}_n-q\parallel }^2+(1-b_n){\parallel T{y}_n-q\parallel }^2\\ \le & b_n{\parallel x_n-q\parallel }^2+(1-b_n)M^2,\end{array}$$

(2.5)

where the second inequality holds by the convexity of ${\parallel \cdot \parallel }^2$.

By substituting (2.5) in (2.4), we get

$$\begin{array}{rcl}{\parallel x_{n+1}-q\parallel }^2& \le & (b_n^2+2b_n(1-b_n)){\parallel x_n-q\parallel }^2\\ +2M(1-b_n)(w_n+M(1-b_n))\\ -2(1-b_n)\varphi (\parallel x_{n+1}-q\parallel )\parallel x_{n+1}-q\parallel \\ =& (1-{(1-b_n)}^2){\parallel x_n-q\parallel }^2+2M(1-b_n)(w_n+M(1-b_n))\\ -2(1-b_n)\varphi (\parallel x_{n+1}-q\parallel )\parallel x_{n+1}-q\parallel \\ \le & {\parallel x_n-q\parallel }^2+2M(1-b_n)(w_n+M(1-b_n))\\ -2(1-b_n)\varphi (\parallel x_{n+1}-q\parallel )\parallel x_{n+1}-q\parallel \\ =& {\parallel x_n-q\parallel }^2+(1-b_n)l_n-2(1-b_n)\varphi (\parallel x_{n+1}-q\parallel )\parallel x_{n+1}-q\parallel ,\end{array}$$

(2.6)

where

$$l_n=2M(w_n+M(1-b_n))\to 0,$$

(2.7)

as $n\to \mathrm{\infty }$.

Let $\delta =inf\{\parallel x_{n+1}-q\parallel :n\ge 0\}$. We claim that $\delta =0$. Otherwise, $\delta >0$. Thus, (2.7) implies that there exists a positive integer $N_1$ such that $l_n<\varphi (\delta )\delta$ for each $n\ge N_1$. In view of (2.6), we conclude that

$${\parallel x_{n+1}-q\parallel }^2\le {\parallel x_n-q\parallel }^2-\varphi (\delta )\delta (1-b_n),n\ge N_1,$$

which implies that

$$\varphi (\delta )\delta \sum _{n=N_1}^{\mathrm{\infty }}(1-b_n)\le {\parallel x_{N_1}-q\parallel }^2,$$

(2.8)

which contradicts (ii). Therefore, $\delta =0$. Thus, there exists a subsequence ${\{x_{n_i+1}\}}_{n=1}^{\mathrm{\infty }}$ of ${\{x_{n+1}\}}_{n=1}^{\mathrm{\infty }}$ such that

$$\underset{i\to \mathrm{\infty }}{lim}{x}_{n_i+1}=q.$$

(2.9)

Let $ϵ>0$ be a fixed number. By virtue of (2.7) and (2.9), we can select a positive integer $i_0>N_1$ such that

$$\parallel x_{n_{i_0}+1}-q\parallel <ϵ,l_n<\varphi (ϵ)ϵ,n\ge n_{i_0}.$$

(2.10)

Let $p=n_{i_0}$. By induction, we show that

$$\parallel x_{p+m}-q\parallel <ϵ,m\ge 1.$$

(2.11)

Observe that (2.6) means that (2.11) is true for $m=1$. Suppose that (2.11) is true for some $m\ge 1$. If $\parallel x_{p+m+1}-q\parallel \ge ϵ$, by (2.6) and (2.10), we know that

$$\begin{array}{rcl}{ϵ}^2& \le & {\parallel x_{p+m+1}-q\parallel }^2\\ \le & {\parallel x_{p+m}-q\parallel }^2+(1-b_{p+m})l_{p+m}\\ -2(1-b_{p+m})\varphi (\parallel x_{p+m+1}-q\parallel )\parallel x_{p+m+1}-q\parallel \\ <& {ϵ}^2+(1-b_{p+m})\varphi (ϵ)ϵ-2(1-b_{p+m})\varphi (ϵ)ϵ\\ =& {ϵ}^2-(1-b_{p+m})\varphi (ϵ)ϵ<{ϵ}^2,\end{array}$$

which is impossible. Hence, $\parallel x_{p+m+1}-q\parallel <ϵ$. That is, (2.11) holds for all $m\ge 1$. Thus, (2.11) ensures that ${lim}_{n\to \mathrm{\infty }}{x}_n=q$. This completes the proof. □

Taking $S=I$ in Theorem 4, we get the following.

Corollary 5 Let K be a nonempty closed and convex subset of an arbitrary Banach space X, and let $T:K\to K$ be a uniformly continuous ϕ-hemicontractive mapping. Suppose that ${\{b_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{b_n^{\prime }\}}_{n=1}^{\mathrm{\infty }}$ are sequences in $[0,1]$ satisfying conditions (i)-(ii) of Theorem  4. For any $x_1\in K$, define the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ inductively as follows:

$$\{\begin{array}{c}{y}_n=b_n^{\prime }{x}_n+(1-b_n^{\prime })T{x}_n,\hfill \\ x_{n+1}=b_n{x}_n+(1-b_n)T{y}_n,n\ge 1.\hfill \end{array}$$

Then the following conditions are equivalent:

• (a) ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to the unique fixed point q of T.

• (b) ${\{T{x}_n\}}_{n=1}^{\mathrm{\infty }}$ is bounded.

Remark 6

• 1. All the results can also be proved for the same iterative scheme with error terms.

• 2. The known results for strongly pseudocontractive mappings are weakened by the ϕ-hemicontractive mappings.

• 3. Our results hold in arbitrary Banach spaces, where as other known results are restricted for $L_p$ (or $l_p$) spaces and q-uniformly smooth Banach spaces.

• 4. Theorem 4 is more general in comparison to the results of Agarwal et al. [5] in the context of the class of ϕ-hemicontractive mappings. Theorem 4 extends convergence results coercing ϕ-hemicontractive mappings in the literature in the framework of Agarwal-O’Regan-Sahu iteration process (see also [14–21]).

3 Applications

Theorem 7 Let X be an arbitrary real Banach space, $S:X\to X$ be nonexpansive, and let $T:X\to X$ be uniformly continuous ϕ-strongly accretive operators, respectively. Suppose that ${\{b_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{b_n^{\prime }\}}_{n=1}^{\mathrm{\infty }}$ are sequences in $[0,1]$ satisfying conditions (i)-(ii) of Theorem  4. For any $x_1\in X$, define the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ inductively as follows:

$$\{\begin{array}{c}{y}_n=b_n^{\prime }{x}_n+(1-b_n^{\prime })(f+(I-T)x_n),\hfill \\ x_{n+1}=b_n(f+(I-S)x_n)+(1-b_n)(f+(I-T)y_n),n\ge 1,\hfill \end{array}$$

where $f\in X$, and I is the identity operator. Then the following conditions are equivalent:

• (a) ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to the solution of the system $Sx=f=Tx$.

• (b) ${\{(I-S)x_n\}}_{n=1}^{\mathrm{\infty }}$, ${\{(I-T)x_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{(I-T)y_n\}}_{n=1}^{\mathrm{\infty }}$ are bounded.

Proof Suppose that $x^{\ast }$ is the solution of the system $Sx=f=Tx$. Define $G,G^{\prime }:X\to X$ by $Gx=f+(I-S)x$ and $G^{\prime }x=f+(I-T)x$, respectively. Since S and T are nonexpansive and uniformly continuous ϕ-strongly accretive operators, respectively, so are G and $G^{\prime }$, then $x^{\ast }$ is the common fixed point of G and $G^{\prime }$. Thus, Theorem 7 follows from Theorem 4. □

Example 8 Let $X=\mathbb{R}$ be the reals with the usual norm and $K=[0,1]$. Define $S:K\to K$ by

$$Sx=sinx\text{for all }x\in K$$

and $T:K\to K$ by

$$Tx=x-tanx\text{for all }x\in K.$$

By the mean value theorem, we have

$$|T(x)-T(y)|\le \underset{c\in (0,1)}{sup}|T^{\prime }(c)||x-y|\text{for all }x,y\in K.$$

Noticing that $T^{\prime }(c)=1-{sec}^2(c)$ and $1<{sup}_{c\in (0,1)}|T^{\prime }(c)|=2.4255$. Hence,

$$|T(x)-T(y)|\le L|x-y|\text{for all }x,y\in K,$$

where $L=2.4255$. It is easy to verify that T is ϕ-hemicontractive mapping with $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ defined by $\varphi (t)=tan(t)$ for all $t\in [0,\mathrm{\infty })$. Moreover, 0 is the common fixed point of S and T. Let ${\{b_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{b_n^{\prime }\}}_{n=1}^{\mathrm{\infty }}$ be sequences in $[0,1]$ defined by

$$b_n=1-\frac{1}{n}\text{and}{b}_n^{\prime }=\frac{1}{n},n\ge 1.$$

Then ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ defined by (2.1) in Theorem 4 converges to 0, which is the common fixed point of S and T.