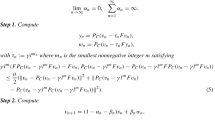Abstract
Korpelevich’s extragradient method has been studied and extended extensively due to its applicability to the whole class of monotone variational inequalities. In the present paper, we propose a variant extragradient-type method for solving monotone variational inequalities. Convergence analysis of the method is presented under reasonable assumptions on the problem data.
MSC:47H05, 47J05, 47J25.
Similar content being viewed by others
1 Introduction
Let H be a real Hilbert space with the inner product and its induced norm . Let C be a nonempty, closed and convex subset of H and let be a nonlinear operator. The variational inequality problem for A and C, denoted by , is the problem of finding a point satisfying
We denote the solution set of this problem by . Under the monotonicity assumption, the solution set of is always closed and convex.
The variational inequality problem is a fundamental problem in variational analysis and, in particular, in optimization theory. There are several iterative methods for solving it. See, e.g., [1–38]. The basic idea consists of extending the projected gradient method for constrained optimization, i.e., for the problem of minimizing subject to . For , compute the sequence in the following manner:
where is the stepsize and is the metric projection onto C. See [1] for convergence properties of this method for the case in which f is convex and is a differentiable function, which are related to the results in this article. An immediate extension of the method (2) to is the iterative procedure given by
Convergence results for this method require some monotonicity properties of A. Note that for the method given by (3) there is no chance of relaxing the assumption on A to plain monotonicity. The typical example consists of taking and A, a rotation with a angle. A is monotone and the unique solution of is . However, it is easy to check that for all and all , therefore the sequence generated by (3) moves away from the solution, independently of the choice of the stepsize .
To overcome this weakness of the method defined by (3), Korpelevich [20] proposed a modification of the method, called the extragradient algorithm. It generates iterates using the following formulae:
where is a fixed number. The difference in (4) is that A is evaluated twice and the projection is computed twice at each iteration, but the benefit is significant, because the resulting algorithm is applicable to the whole class of monotone variational inequalities. However, we note that Korpelevich assumed that A is Lipschitz continuous and that an estimate of the Lipschitz constant is available. When A is not Lipschitz continuous, or it is Lipschitz but the constant is not known, the fixed parameter λ must be replaced by stepsizes computed through an Armijo-type search, as in the following method, presented in [39] (see also [18] for another related approach).
Let , and . Given define
If , then stop. Otherwise, let
and
Define
It is proved that if A is maximal monotone, point-to-point and uniformly continuous on bounded sets, and if is nonempty, then strongly converges to .
We now know that the difficult implementation of these methods is in computational respect. First, we note that in order to get , we have to compute , which may be time-consuming. At the same time, we observe that (6) involves two half-spaces and . If the sets C, and are simple enough, then , and are easily executed. But may be complicated, so that the projection is not easily executed. This might seriously affect the efficiency of the method.
The literature on the is vast and Korpelevich’s method has received great attention from many authors, who improved it in various ways; see, e.g., [33, 39–44] and references therein. It is known that Korpelevich’s method (4) has only weak convergence in the infinite-dimensional Hilbert spaces (please refer to a recent result of Censor et al. [40] and [41]). So, to obtain strong convergence, the original method was modified by several authors. For example, in [4, 43] it was proved that some very interesting Korpelevich-type algorithms strongly converge to a solution of . Very recently, Yao et al. [33] suggested modified Korpelevich’s method which converges strongly to the minimum norm solution of variational inequality (1) in infinite-dimensional Hilbert spaces.
Motivated by the works given above, in the present paper, we propose a variant extragradient-type method for solving monotone variational inequalities. Strong convergence analysis of the method is presented under reasonable assumptions on the problem data in the infinite-dimensional Hilbert spaces.
2 Preliminaries
In this section, we present some definitions and results that are needed for the convergence analysis of the proposed method. Let C be a closed convex subset of a real Hilbert space H.
A mapping is said to be Lipschitz if there exists a positive real number such that
for all . In the case , F is called L-contractive. A mapping is called α-inverse-strongly-monotone if there exists a positive real number α such that
The following result is well known.
Proposition 1 [45]
Let C be a bounded closed convex subset of a real Hilbert space H and let A be an α-inverse strongly monotone operator of C into H. Then is nonempty.
For any , there exists a unique such that
We denote by , where is called the metric projection of H onto C. The following is a useful characterization of projections.
Proposition 2 Given . We have
which is equivalent to
Consequently, we deduce immediately that is nonexpansive, that is,
for all .
It is well known that is nonexpansive.
Lemma 1 [45]
Let C be a nonempty closed convex subset of a real Hilbert space H. Let the mapping be α-inverse strongly monotone and be a constant. Then we have
In particular, if , then is nonexpansive.
Lemma 2 [46]
Let and be bounded sequences in a Banach space X and let be a sequence in with .
Suppose that
-
(1)
for all ;
-
(2)
.
Then .
Lemma 3 [47]
Assume that is a sequence of nonnegative real numbers, which satisfies
where is a sequence in and is a sequence such that
-
(1)
;
-
(2)
or .
Then .
3 Algorithm and its convergence analysis
In this section, we present the formal statement of our proposal for the algorithm.
Variant extragradient-type method
Let C be a nonempty, closed and convex subset of a real Hilbert space H. Let be an α-inverse-strongly-monotone mapping and let be a ρ-contractive mapping. Consider the sequences , , and .
-
1.
Initialization:
-
2.
Iterative step: Given , define
(7)
Remark 1 Note that algorithm (7) includes Korpelevich’s method (4) as a special case.
Next, we shall perform a study on the convergence analysis of the proposed algorithm (7).
Theorem 1 Suppose that . Assume that the algorithm parameters , , and satisfy the following conditions:
-
(C1)
and ;
-
(C2)
and ;
-
(C3)
, and .
Then the sequence generated by (7) converges strongly to , which solves the following variational inequality:
We shall prove our main result in several steps, included into the propositions given bellow.
Proposition 3 The sequences and are bounded. Therefore, the sequences , and are all bounded.
Proof From conditions (C1) and (C2), since and , we have , for n large enough. Without loss of generality, we may assume that, for all , . So, .
Consider any . By the property of the metric projection, we know for any . Hence,
Thus, by (7) and (8), we have
Since , from Lemma 1, we know that is nonexpansive. From (9), we get
By (C3), we obtain . So, is also nonexpansive. Therefore,
By induction, we get
Then is bounded, and so are , , and . Therefore, the proof is complete. □
Proposition 4 The following two properties hold:
Proof Let . From the property of the metric projection, we known that S is nonexpansive. Therefore, we can rewrite in (7) as
where
It follows that
So,
Again, by using the nonexpansivity of and S, we have
Next, we estimate .
By (7), we have
So, we deduce
Since and , we derive that
At the same time, note that , , and are bounded. Therefore,
By Lemma 2, we obtain
Hence,
From (9), (10), Lemma 1 and the convexity of the norm, we deduce
Therefore, we have
Since , and , we deduce
By the property (ii) of the metric projection , we have
where is some constant satisfying
It follows that
and hence
which implies that
Since , and , we derive
and this concludes the proof. □
Proposition 5 , where .
Proof In order to show that , we choose a subsequence of such that
As is bounded, we deduce that a subsequence of converges weakly to z.
Next, we show that . The following proofs are similar to the one in [45]. Since the involved algorithms are not different, we still give the details. Now, we define a mapping T by the formula
Then T is maximal monotone.
Let . Since and , we have . On the other hand, from , we obtain
that is,
Therefore, we have
Noting that , and A is Lipschitz continuous, we obtain . Since T is maximal monotone, we have and hence . Therefore,
The proof of this proposition is now complete. □
Finally, by using Propositions 3-5, we prove Theorem 1.
Proof By the property of the metric projection , we have
Hence,
Therefore,
We apply Lemma 3 to the last inequality to deduce that .
The proof of our main result is completed. □
Remark 2 Our algorithm (7) includes Korpelevich’s method (4) as a special case. However, it is well known that Korpelevich’s algorithm (4) has only weak convergence in the setting of infinite-dimensional Hilbert spaces. But our algorithm (7) has strong convergence in the setting of infinite-dimensional Hilbert spaces.
If we take , then we have the following algorithm:
-
1.
Initialization:
-
2.
Iterative step: Given , define
(11)
Corollary 1 Suppose that . Assume that the algorithm parameters , , and satisfy the following conditions:
-
(C1)
and ;
-
(C2)
and ;
-
(C3)
, and .
Then the sequence generated by (11) converges strongly to the minimum norm element in .
Proof It is clear that algorithm (11) is a special case of algorithm (7). So, from Theorem 1, we have that the sequence defined by (11) converges strongly to , which solves
Applying the characterization of the metric projection, we can deduce from (12) that
This indicates that is the minimum-norm element in . This completes the proof. □
Remark 3 Corollary 1 includes the main result in [1] as a special case.
References
Alber YI, Iusem AN: Extension of subgradient techniques for nonsmooth optimization in Banach spaces. Set-Valued Anal. 2001, 9: 315–335. 10.1023/A:1012665832688
Bao TQ, Khanh PQ: A projection-type algorithm for pseudomonotone non-Lipschitzian multivalued variational inequalities. Nonconvex Optim. Appl. 2005, 77: 113–129. 10.1007/0-387-23639-2_6
Bauschke HH: The approximation of fixed points of composition of nonexpansive mapping in Hilbert space. J. Math. Anal. Appl. 1996, 202: 150–159. 10.1006/jmaa.1996.0308
Bello Cruz JY, Iusem AN: A strongly convergent direct method for monotone variational inequalities in Hilbert space. Numer. Funct. Anal. Optim. 2009, 30: 23–36. 10.1080/01630560902735223
Bello Cruz JY, Iusem AN: Convergence of direct methods for paramonotone variational inequalities. Comput. Optim. Appl. 2010, 46: 247–263. 10.1007/s10589-009-9246-5
Bnouhachem A, Noor MA, Hao Z: Some new extragradient iterative methods for variational inequalities. Nonlinear Anal. 2009, 70: 1321–1329. 10.1016/j.na.2008.02.014
Bruck RE: On the weak convergence of an ergodic iteration for the solution of variational inequalities for monotone operators in Hilbert space. J. Math. Anal. Appl. 1977, 61: 159–164. 10.1016/0022-247X(77)90152-4
Cegielski A, Zalas R: Methods for variational inequality problem over the intersection of fixed point sets of quasi-nonexpansive operators. Numer. Funct. Anal. Optim. 2013, 34: 255–283. 10.1080/01630563.2012.716807
Censor Y, Gibali A, Reich S: Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space. Optim. Methods Softw. 2011, 26: 827–845. 10.1080/10556788.2010.551536
Censor Y, Gibali A, Reich S: Algorithms for the split variational inequality problem. Numer. Algorithms 2012, 59: 301–323. 10.1007/s11075-011-9490-5
Facchinei F, Pang JS: Finite-Dimensional Variational Inequalities and Complementarity Problems, vols. I and II. Springer, New York; 2003.
Glowinski R: Numerical Methods for Nonlinear Variational Problems. Springer, New York; 1984.
He BS: A new method for a class of variational inequalities. Math. Program. 1994, 66: 137–144. 10.1007/BF01581141
He BS, Yang ZH, Yuan XM: An approximate proximal-extragradient type method for monotone variational inequalities. J. Math. Anal. Appl. 2004, 300: 362–374. 10.1016/j.jmaa.2004.04.068
Hirstoaga SA: Iterative selection methods for common fixed point problems. J. Math. Anal. Appl. 2006, 324: 1020–1035. 10.1016/j.jmaa.2005.12.064
Iiduka H, Takahashi W: Weak convergence of a projection algorithm for variational inequalities in a Banach space. J. Math. Anal. Appl. 2008, 339: 668–679. 10.1016/j.jmaa.2007.07.019
Iusem AN: An iterative algorithm for the variational inequality problem. Comput. Appl. Math. 1994, 13: 103–114.
Khobotov EN: Modification of the extra-gradient method for solving variational inequalities and certain optimization problems. U.S.S.R. Comput. Math. Math. Phys. 1989, 27: 120–127.
Kinderlehrer D, Stampacchia G: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York; 1980.
Korpelevich GM: An extragradient method for finding saddle points and for other problems. Èkon. Mat. Metody 1976, 12: 747–756.
Lions JL, Stampacchia G: Variational inequalities. Commun. Pure Appl. Math. 1967, 20: 493–517. 10.1002/cpa.3160200302
Lu X, Xu HK, Yin X: Hybrid methods for a class of monotone variational inequalities. Nonlinear Anal. 2009, 71: 1032–1041. 10.1016/j.na.2008.11.067
Sabharwal A, Potter LC: Convexly constrained linear inverse problems: iterative least-squares and regularization. IEEE Trans. Signal Process. 1998, 46: 2345–2352. 10.1109/78.709518
Solodov MV, Svaiter BF: A new projection method for variational inequality problems. SIAM J. Control Optim. 1999, 37: 765–776. 10.1137/S0363012997317475
Solodov MV, Tseng P: Modified projection-type methods for monotone variational inequalities. SIAM J. Control Optim. 1996, 34: 1814–1830. 10.1137/S0363012994268655
Verma RU: General convergence analysis for two-step projection methods and applications to variational problems. Appl. Math. Lett. 2005, 18: 1286–1292. 10.1016/j.aml.2005.02.026
Xu HK, Kim TH: Convergence of hybrid steepest-descent methods for variational inequalities. J. Optim. Theory Appl. 2003, 119: 185–201.
Yamada I, Ogura N: Hybrid steepest descent method for the variational inequality problem over the fixed point set of certain quasi-nonexpansive mappings. Numer. Funct. Anal. Optim. 2004, 25: 619–655.
Yao JC: Variational inequalities with generalized monotone operators. Math. Oper. Res. 1994, 19: 691–705. 10.1287/moor.19.3.691
Yao Y, Chen R, Xu HK: Schemes for finding minimum-norm solutions of variational inequalities. Nonlinear Anal. 2010, 72: 3447–3456. 10.1016/j.na.2009.12.029
Yao Y, Liou YC, Kang SM: Two-step projection methods for a system of variational inequality problems in Banach spaces. J. Glob. Optim. 2013, 55(4):801–811. 10.1007/s10898-011-9804-0
Yao Y, Liou YC, Shahzad N: Construction of iterative methods for variational inequality and fixed point problems. Numer. Funct. Anal. Optim. 2012, 33: 1250–1267. 10.1080/01630563.2012.660796
Yao Y, Marino G, Muglia L: A modified Korpelevich’s method convergent to the minimum norm solution of a variational inequality. Optimization 2012. 10.1080/02331934.2012.674947
Yao Y, Noor MA, Liou YC, Kang SM: Iterative algorithms for general multi-valued variational inequalities. Abstr. Appl. Anal. 2012., 2012: Article ID 768272
Yao Y, Noor MA: On viscosity iterative methods for variational inequalities. J. Math. Anal. Appl. 2007, 325: 776–787. 10.1016/j.jmaa.2006.01.091
Zeng LC, Hadjisavvas N, Wong NC: Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems. J. Glob. Optim. 2010, 46: 635–646. 10.1007/s10898-009-9454-7
Zeng LC, Teboulle M, Yao JC: Weak convergence of an iterative method for pseudomonotone variational inequalities and fixed point problems. J. Optim. Theory Appl. 2010, 146: 19–31. 10.1007/s10957-010-9650-0
Zhu D, Marcotte P: New classes of generalized monotonicity. J. Optim. Theory Appl. 1995, 87: 457–471. 10.1007/BF02192574
Iusem AN, Svaiter BF: A variant of Korpelevich’s method for variational inequalities with a new search strategy. Optimization 1997, 42: 309–321. 10.1080/02331939708844365
Censor Y, Gibali A, Reich S: Extensions of Korpelevich’s extragradient method for the variational inequality problem in Euclidean space. Optimization 2010. 10.1080/02331934.2010.539689
Censor Y, Gibali A, Reich S: The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 2011, 148: 318–335. 10.1007/s10957-010-9757-3
Iusem AN, Lucambio Peŕez LR: An extragradient-type algorithm for non-smooth variational inequalities. Optimization 2000, 48: 309–332. 10.1080/02331930008844508
Mashreghi J, Nasri M: Forcing strong convergence of Korpelevich’s method in Banach spaces with its applications in game theory. Nonlinear Anal. 2010, 72: 2086–2099. 10.1016/j.na.2009.10.009
Noor MA: New extragradient-type methods for general variational inequalities. J. Math. Anal. Appl. 2003, 277: 379–394. 10.1016/S0022-247X(03)00023-4
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. J. Optim. Theory Appl. 2003, 118: 417–428. 10.1023/A:1025407607560
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory Appl. 2005, 2005: 103–123.
Xu HK: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66: 240–256. 10.1112/S0024610702003332
Acknowledgements
Yonghong Yao was supported in part by NSFC 11071279 and NSFC 71161001-G0105. Yeong-Cheng Liou was partially supported by NSC 100-2221-E-230-012.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yao, Y., Postolache, M. & Liou, YC. Variant extragradient-type method for monotone variational inequalities. Fixed Point Theory Appl 2013, 185 (2013). https://doi.org/10.1186/1687-1812-2013-185
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-185