The variational iteration method for fuzzy fractional differential equations with uncertainty

Abstract

In this paper the variational iteration method is used to solve the fractional differential equations with a fuzzy initial condition. We consider a differential equation of fractional order with uncertainty and present the concept of solution. We compared the results with their exact solutions in order to demonstrate the validity and applicability of the method.

1 Introduction

With the rapid development of linear and nonlinear science, many different methods such as the variational iteration method (VIM) [1] were proposed to solve fuzzy differential equations.

Fuzzy initial value problems for fractional differential equations have been considered by some authors recently [2, 3]. To study some dynamical processes, it is necessary to take into account imprecision, randomness or uncertainty. The uncertainty can be modeled by incorporating it into the dynamical system and considering fuzzy differential equations. Some recent contributions on the theory of differential equations with uncertainty can be seen in [4].

Let $q\in (0,1]$, $T>0$ and E be the set of fuzzy real numbers [4, 5].

We consider a differential equation with uncertainty of the type

$$D^{q}u(t)=f(t,u(t)),t\in (0,T],$$

(1)

where $f:[0,T]\times \mathbb{R}\to \mathbb{R}$ is continuous. We will consider this equation with some adequate initial condition for a given $u_0\in E$:

• If $f:[0,T]\times \mathbb{R}\to \mathbb{R}$ and $u_0\in \mathbb{R}$, then (1) reduces to a fractional differential equation.

• If $q=1$, then (1) is just a first-order fuzzy differential equation.

Here we combine both types of differential equations, of fractional order and with uncertainty, to consider a new type of dynamical system: fuzzy differential equations of fractional order [3]. The objective of the present paper is to extend the application of the variational iteration method, to provide approximate solutions for fuzzy initial value problems of differential equations of fractional order, and to make comparison with that obtained by an exact fuzzy solution.

2 Preliminaries

In this section the most basic notations used in fuzzy calculus are introduced. We start with defining a fuzzy number.

Definition 1 A fuzzy number (or an interval) u in parametric form is a pair $(\underline{u},\overline{u})$ of functions $\underline{u}(r)$, $\overline{u}(r)$, $0\le r\le 1$, which satisfy the following requirements [2]:

• 1. $\underline{u}(r)$ is a bounded non-decreasing left continuous function in $(0,1]$ and right continuous at 0.

• 2. $\overline{u}(r)$ is a bounded non-decreasing left continuous function in $(0,1]$ and right continuous at 0.

• 3. $\underline{u}(r)\le \overline{u}(r)$, $0\le r\le 1$.

Definition 2 The Riemann-Liouville fractional derivative of order $0<q<1$ of a continuous function $f:{\mathbb{R}}^{+}\to \mathbb{R}$ is given by

$$D^{q}f(t)=\frac{1}{\mathrm{\Gamma }(1-q)}\frac{d}{dt}{\int }_0^t{(t-s)}^{-q}f(s)ds,$$

provided the right-hand side is pointwisely defined on ${\mathbb{R}}^{+}$.

3 Fuzzy fractional differential equations with uncertainty

Consider the following fuzzy fractional differential equation:

$$D^{q}u(t)=f(t,u(t)),$$

(2)

where $0<q<1$ and $f:[0,T]\times E\to E$ is a continuous function on $[0,T]\times E$.

A fuzzy function $u\in C((0,T],E)\cap L^1((0,T),E)$ is a solution of fuzzy fractional differential equation (2) if $D^{q}u$ is continuous on $(0,T]$; and assume that there exits $\mu >0$ such that the nonlinearity f is of the form

$$D^{q}u(t)=\mu u(t)+g(t,u(t)),t\in (0,T],$$

(3)

where

$$D^{q}u(t)=\frac{1}{\mathrm{\Gamma }(1-q)}\frac{d}{dt}{\int }_0^t{(t-s)}^{-q}u(s)ds,$$

is the usual Riemann-Liouville fractional derivative of order q of the function $u:(0,T]\to \mathbb{R}$ and $g:[0,T]\times E\to E$ is continuous.

Also, we can associate the following initial condition to fuzzy fractional differential equation (2):

$$\underset{t\to 0^{+}}{lim}{t}^{1-q}u(t)=u_0\in E.$$

Lemma

• (i) If there exists ${lim}_{t\to 0^{+}}{t}^{1-q}u(t)=v$, then there also exists ${lim}_{t\to 0^{+}}{t}^{1-q}u(t)=\mathrm{\Gamma }(q)v$.

• (ii) If there exists ${lim}_{t\to 0^{+}}{t}^{1-q}u(t)=w$, then ${lim}_{t\to 0^{+}}{t}^{1-q}u(t)=\frac{w}{\mathrm{\Gamma }(q)}$.

Proof (i) If there exists ${lim}_{t\to 0^{+}}{t}^{1-q}u(t)=v$, then for each $\epsilon >0$, we can choose $\delta =\delta (\epsilon )$ such that

$$d(t^{1-q}u(t),v)<\frac{\epsilon }{\mathrm{\Gamma }(q)}$$

for $|t|<\delta$. Since $I^{1-q}{t}^{1-q}=\mathrm{\Gamma }(q)$, we have

$$\begin{array}{rcl}d(D^{1-q}u(t),\mathrm{\Gamma }(q)v)& =& d(D^{1-q}u(t),D^{1-q}{t}^{q-1}v)\\ =& \frac{1}{\mathrm{\Gamma }(1-q)}d({\int }_0^t{(t-s)}^{-q}u(s)ds,{\int }_0^t{(t-s)}^{-q}{s}^{q-1}ds)\\ \le & \frac{1}{\mathrm{\Gamma }(1-q)}{\int }_0^t{(t-s)}^{-q}{s}^{q-1}d(s^{q-1}u(s),v)ds<\epsilon \end{array}$$

which proves (i). Assertion (ii) is obvious [6]. □

Hence, we define a solution of this Eq. (3) as a function $u:[0,T]\to E$ such that

$$u(t)=u_0\mathrm{\Gamma }(q)t^{q-1}{E}_{q,q}\left(\mu t^q\right)+{\int }_0^t{(t-s)}^{q-1}{E}_{q,q}\left(\mu {(t-s)}^q\right)g(s,u(s))ds,$$

where $E_{\alpha ,\beta }$ is the classical Mittag-Leffler function

$$E_{\alpha ,\beta }(z)=\sum _{k=0}^{\mathrm{\infty }}\frac{z^k}{\mathrm{\Gamma }(\alpha k+\beta )}(\alpha >0,\beta >0).$$

Example 1

Consider the fractional differential equation

$$D^{q}u(t)=0,t\in (0,T].$$

The general solution of this equation [7] is

$$u(t)=c{e}^{q-1},c\in \mathbb{R}.$$

Imposing the initial condition

$$\underset{t\to 0^{+}}{lim}{t}^{1-q}u(t)=u_0,$$

we then have

$$u(t)=u_0{t}^{q-1}.$$

In the fuzzy case, the solution is also

$$u(t)=u_0{t}^{q-1}.$$

Now, let $\mu >0$ and $0<q\le 1$ and consider the equation

$$D^{q}u(t)=\mu u(t),t\in (0,T].$$

The solution is given by the following expression:

$$u(t)=\mathrm{\Gamma }(q)t^{q-1}{E}_{q,q}\left(\mu t^q\right)u_0.$$

4 Analysis of the variational iteration method

We consider the fractional differential equation

$$D^{q}u(t)=\mu u(t)+g(t,u(t)),t\in (0,T]$$

(4)

with the fuzzy initial condition

$$\underset{t\to 0^{+}}{lim}{t}^{1-q}u(t)=u_0,$$

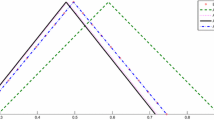
where $t\in (0,1]$, $0<q\le 1$, and $u_0\in E$ is a fuzzy triangular number,

$${[u_0]}^{\alpha }=[{\underline{u}}_0(t,\alpha ),{\overline{u}}_0(t,\alpha )]\text{for }\alpha \in (0,1].$$

According to the variational iteration method [1], we construct a correction functional for (4) which reads

where $\underline{\lambda }$ and $\overline{\lambda }$ are general Lagrange multipliers, which can be identified optimally via the variational, and ${\underline{\tilde{u}}}_n$ and ${\overline{\tilde{u}}}_n$ are restricted variations that are $\delta {\underline{\tilde{u}}}_n=0$ and $\delta {\tilde{\overline{u}}}_n=0$.

Therefore, we first determine the Lagrange multipliers $\underline{\lambda }$ and $\overline{\lambda }$ that will be identified via integration by parts. Respectively, the successive approximations ${\underline{u}}_{n+1}(t;\alpha )\ge 0$ and ${\overline{u}}_{n+1}(t;\alpha )\ge 0$ of the solutions $\underline{u}(t;\alpha )$ and $\overline{u}(t;\alpha )$ will be readily obtained upon using the Lagrange multiplier obtained by using any selective functions ${\underline{u}}_0(t;\alpha )$ and ${\overline{u}}_0(t;\alpha )$. Consequently, the solutions are obtained by taking the limits:

$$\underline{u}(t;\alpha )=\underset{n\to \mathrm{\infty }}{lim}{\underline{u}}_n(t;\alpha ),\overline{u}(t;\alpha )=\underset{n\to \mathrm{\infty }}{lim}{\overline{u}}_n(t;\alpha ).$$

(5)

Example 2

Consider the crisp differential equation

$$D^{q}u(t)=-u(t)$$

(6)

with the fuzzy initial condition

$$\underset{t\to 0^{+}}{lim}{t}^{1-q}u(t)=(1\mid 2\mid 3),$$

(7)

where $t\in (0,1]$, $0<q\le 1$, and $u_0=(1\mid 2\mid 3)\in E$ is a fuzzy triangular number, ${[u_0]}^{\alpha }=[1+\alpha ,3-\alpha ]$ for $\alpha \in (0,1]$.

If we put ${[u(t)]}^{\alpha }=[{\underline{u}}^{\alpha }(t),{\overline{u}}^{\alpha }(t)]$, then ${[D^{q}u(t)]}^{\alpha }=[D^q{\underline{u}}^{\alpha }(t),D^q{\overline{u}}^{\alpha }(t)]$. We obtain the system

$$\begin{array}{c}{D}^q{\underline{u}}^{\alpha }(t)=-{\overline{u}}^{\alpha }(t),\underset{t\to 0^{+}}{lim}{t}^{1-q}{\underline{u}}^{\alpha }(t)=1+\alpha ,\hfill \\ D^q{\overline{u}}^{\alpha }(t)=-{\underline{u}}^{\alpha }(t),\underset{t\to 0^{+}}{lim}{t}^{1-q}{\overline{u}}^{\alpha }(t)=3-\alpha ,\hfill \end{array}$$

or

$$D^{q}y(t)=Ay(t),\underset{t\to 0^{+}}{lim}{t}^{1-q}y(t)=c,$$

(8)

where

$$y(t)=\left[\begin{array}{c}{\underline{u}}^{\alpha }(t)\\ {\overline{u}}^{\alpha }(t)\end{array}\right],A=\left[\begin{array}{cc}0& -1\\ -1& 0\end{array}\right],c=\left[\begin{array}{c}1+\alpha \\ 3-\alpha \end{array}\right].$$

Using the same method as that in [8], we obtain the solution of (8). It is given by

$$y(t)=t^{q-1}{E}_{q,q}\left(A{t}^q\right)c=t^{q-1}{E}_{q,q}\left(A{t}^q\right)\left[\begin{array}{c}1+\alpha \\ 3-\alpha \end{array}\right],$$

where

$$\begin{array}{rcl}{E}_{q,q}\left(A{t}^q\right)& =& \sum _{k=0}^{\mathrm{\infty }}\frac{{(A{t}^q)}^k}{\mathrm{\Gamma }(q(k+1))}=\sum _{k=0}^{\mathrm{\infty }}\frac{{(t^q)}^k}{\mathrm{\Gamma }(q(k+1))}{\left(\left[\begin{array}{cc}0& -1\\ -1& 0\end{array}\right]\right)}^k\\ =& \sum _{n=0}^{\mathrm{\infty }}\frac{{(t^q)}^{2n}}{\mathrm{\Gamma }(q(2n+1))}{\left(\left[\begin{array}{cc}0& -1\\ -1& 0\end{array}\right]\right)}^{2n}+\sum _{n=0}^{\mathrm{\infty }}\frac{{(t^q)}^{2n+1}}{\mathrm{\Gamma }(q(2n+2))}{\left(\left[\begin{array}{cc}0& -1\\ -1& 0\end{array}\right]\right)}^{2n+1}\\ =& \sum _{n=0}^{\mathrm{\infty }}\frac{{(t^q)}^{2n}}{\mathrm{\Gamma }(q(2n+1))}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]+\sum _{n=0}^{\mathrm{\infty }}\frac{{(t^q)}^{2n+1}}{\mathrm{\Gamma }(q(2n+2))}\left[\begin{array}{cc}0& -1\\ -1& 0\end{array}\right].\end{array}$$

Then we obtain

$$\begin{array}{c}{\underline{u}}^{\alpha }(t)=\underline{u}(t;\alpha )=\sum _{n=0}^{\mathrm{\infty }}\frac{t^{(2n+1)q-1}}{\mathrm{\Gamma }(q(2n+1))}(1+\alpha )-\sum _{n=0}^{\mathrm{\infty }}\frac{t^{(2n+2)q-1}}{\mathrm{\Gamma }(q(2n+2))}(3-\alpha ),\hfill \\ {\overline{u}}^{\alpha }(t)=\overline{u}(t;\alpha )=\sum _{n=0}^{\mathrm{\infty }}\frac{t^{(2n+1)q-1}}{\mathrm{\Gamma }(q(2n+1))}(3-\alpha )-\sum _{n=0}^{\mathrm{\infty }}\frac{t^{(2n+2)q-1}}{\mathrm{\Gamma }(q(2n+2))}(1+\alpha ).\hfill \end{array}$$

It easy to see that $[{\underline{u}}^{\alpha }(t),{\overline{u}}^{\alpha }(t)]$ define the α-level intervals of a fuzzy number. So, ${[u(t)]}^{\alpha }$ are the α-level intervals of the fuzzy solution of (6)-(7), [2].

To apply the VIM, first we rewrite Eq. (6) in the form

$$L[\underline{u}(t)]+N[\underline{u}(t)]=0,L[\overline{u}(t)]+N[\overline{u}(t)]=0,$$

(9)

where the notations $L[\underline{u}(t)]=\frac{{\partial }^q\underline{u}}{\partial t^q}$, $L[\overline{u}(t)]=\frac{{\partial }^q\overline{u}}{\partial t^q}$ and $N[\underline{u}(t)]=\underline{u}(t)$, $N[\overline{u}(t)]=\overline{u}(t)$ symbolize the linear and nonlinear terms, [1], respectively. The correction functionals for Eqs. (9) read

$$\begin{array}{r}{\underline{u}}_{n+1}(t;\alpha )={\underline{u}}_n(t;\alpha )t^{q-1}\\ \phantom{{\underline{u}}_{n+1}(t;\alpha )=}+\frac{1}{\mathrm{\Gamma }(q)}{\int }_0^t{(t-\xi )}^{q-1}\underline{\lambda }(\xi ;\alpha )(\frac{{\partial }^q{\underline{u}}_n}{\partial {\xi }^q}(\xi ;\alpha )+N[{\underline{\tilde{u}}}_n(\xi ;\alpha )])d\xi ,\\ {\overline{u}}_{n+1}(t;\alpha )={\overline{u}}_n(t;\alpha )t^{q-1}\\ \phantom{{\overline{u}}_{n+1}(t;\alpha )=}+\frac{1}{\mathrm{\Gamma }(q)}{\int }_0^t{(t-\xi )}^{q-1}\overline{\lambda }(\xi ;\alpha )(\frac{{\partial }^q{\overline{u}}_n}{\partial {\xi }^q}(\xi ;\alpha )+N[{\tilde{\overline{u}}}_n(\xi ;\alpha )])d\xi .\end{array}$$

(10)

Taking the variation with respect to the independent variables ${\underline{u}}_n$ and ${\overline{u}}_n$, and noticing that $\delta N[\underline{\tilde{u}}(0)]=0$, $\delta N[\tilde{\overline{u}}(0)]=0$,

$$\begin{array}{r}\delta {\underline{u}}_{n+1}(t;\alpha )=\delta {\underline{u}}_n(t;\alpha )t^{q-1}+\frac{1}{\mathrm{\Gamma }(q)}\delta {\int }_0^t{(t-\xi )}^{q-1}\underline{\lambda }(\xi ;\alpha )(\frac{{\partial }^q{\underline{u}}_n}{\partial {\xi }^q}(\xi ;\alpha ))d\xi ,\\ \delta {\overline{u}}_{n+1}(t;\alpha )={\overline{\delta u}}_n(t;\alpha )t^{q-1}+\frac{1}{\mathrm{\Gamma }(q)}\delta {\int }_0^t{(t-\xi )}^{q-1}\overline{\lambda }(\xi ;\alpha )(\frac{{\partial }^q{\overline{u}}_n}{\partial {\xi }^q}(\xi ;\alpha ))d\xi ,\end{array}$$

(11)

for $q\in (0,1]$, we obtain for Eq. (9) the following stationary conditions:

$$\begin{array}{r}1+\underline{\lambda }(\xi ;\alpha ){|}_{t=\xi }=0,1+\overline{\lambda }(\xi ;\alpha ){|}_{t=\xi }=0,\\ \frac{{\partial }^q\underline{\lambda }(\xi ;\alpha )}{\partial {\xi }^q}{|}_{t=\xi }=0,\frac{{\partial }^q\overline{\lambda }(\xi ;\alpha )}{\partial {\xi }^q}{|}_{t=\xi }=0.\end{array}$$

(12)

The general Lagrange multipliers, therefore, can be identified

$$\underline{\lambda }(\xi ;\alpha )=-1,\overline{\lambda }(\xi ;\alpha )=-1.$$

(13)

As a result, we obtain the following iteration formula:

$$\begin{array}{r}{\underline{u}}_{n+1}(t;\alpha )={\underline{u}}_n(t;\alpha )t^{q-1}-\frac{1}{\mathrm{\Gamma }(q)}{\int }_0^t{(t-\xi )}^{q-1}(\frac{{\partial }^q{\underline{u}}_n}{\partial {\xi }^q}(\xi ;\alpha )+{\underline{u}}_n(\xi ;\alpha ))d\xi ,\\ {\overline{u}}_{n+1}(t;\alpha )={\overline{u}}_n(t;\alpha )t^{q-1}-\frac{1}{\mathrm{\Gamma }(q)}{\int }_0^t{(t-\xi )}^{q-1}(\frac{{\partial }^q{\overline{u}}_n}{\partial {\xi }^q}(\xi ;\alpha )+{\overline{u}}_n(\xi ;\alpha ))d\xi .\end{array}$$

(14)

As a result, we obtain the following iterative formula:

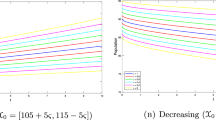
and so on. The n th approximate solution of the variational iteration method converges to the exact series solution [9]. So, we approximate the solutions $\underline{u}(t;\alpha )={lim}_{n\to \mathrm{\infty }}{\underline{u}}_n(t;\alpha )$, $\overline{u}(t;\alpha )={lim}_{n\to \mathrm{\infty }}{\overline{u}}_n(t;\alpha )$.

5 Conclusion

The results of the study reveal that the proposed method with fractional Riemann-Liouville derivatives is efficient, accurate, and convenient for solving the fuzzy fractional differential equations.