Abstract
This paper studies the bit error rate (BER) performance of an adaptive decode-and-forward (DF) relaying scheme for a cooperative wireless network operating on independent and identically distributed (i.i.d.) or independent and non-identically distributed (i.n.d.) Rayleigh fading channels. The considered network is with one source, K relays, and one destination in which binary frequency-shift keying modulation is employed to facilitate noncoherent communications. A relay decodes and retransmits the received signal to the destination only if its decision variable is larger than the corresponding threshold. Depending on the availability of the information of whether a particular relay retransmits or remains silent, the destination combines the received signals from all the relays and the received signal from the source or only the received signals from the retransmitting relays and the received signal from the source to detect the transmitted information. The average end-to-end BERs are determined in closed-form expressions. The thresholds employed at the relays are investigated to minimize the end-to-end BERs. Analytical and simulation results are provided to validate our theoretical analysis. The obtained results show that the studied scheme improves the BER performance significantly compared to the previous proposed piecewise-linear (PL) scheme. In addition, the information of whether a particular relay retransmits or remains silent at the destination does not really improve the BER performance of the network.
Similar content being viewed by others
1 Introduction
Spatial diversity is a well-known technique to mitigate the fading effects in a wireless channel [1]. However, in some wireless applications, such as ad-hoc networks, implementing multiple transmit and/or receive antennas to provide spatial diversity might not be possible due to the size and cost limitations. Cooperative (or relay) diversity is attractive for such networks, i.e., networks with mobile terminals having single-antenna transceivers, since it is able to achieve spatial diversity. The basic idea is that a source node transmits information to the destination not only through a direct link but also through the relay links [2–9]. Cooperative protocols have been classified into three main groups: amplify-and-forward (AF), decode-and-forward (DF), and compress-and-forward (CF) [2, 10]. With DF, relays decode the source’s messages, re-encode, and retransmit to the destination. However, it is not simple to provide cooperative diversity with the DF protocol. This is due to possible retransmission of erroneously decoded bits of the message by the relays [2, 5, 6, 11].
In recent years, much more research works have focused on noncoherent cooperative networks, i.e., the networks in which channel state information (CSI) is assumed to be unknown at the receivers (relays and destination) [12–16]. It is due to the fact that true values of the CSIs cannot actually be obtained in realistic systems. Differential phase-shift keying (DPSK), a popular candidate in noncoherent communications, has been studied for both AF and DF protocols in [12–15]. However, with the DF protocol in [13], the authors considered an ideal case that the relay is able to know exactly whether each decoded symbol is correct or not. The works in [14, 15] examine a very simple cooperative system with one source, one relay, and one destination node. A framework of noncoherent cooperative diversity for the DF protocol employing frequency-shift keying modulation, another popular modulation scheme in noncoherent communications, has been studied in [16]. The maximum likelihood (ML) demodulation was proposed to detect the signals at the destination. A suboptimal piecewise linear (PL) scheme was also proposed in [16] to eliminate the nonlinearity of the ML scheme. However, it should be mentioned that the closed-form BER approximations for both ML and PL schemes in [16] are not available for networks with more than one relays. Furthermore the BER performance with either ML or PL demodulation can still be limited by the error propagation phenomenon [8].
To address the issue of error propagation in noncoherent cooperative networks in [16], the work in [17] employs two different thresholds: one threshold is used at the relays to select retransmitting relays and the other threshold is used at the destination for detection. By utilizing the maximal ratio combining (MRC), the destination combines the signals from the retransmitting relays and the signal from the source to make the final decision. The results show that the proposed scheme can significantly improve the error performance. Unfortunately, the closed-form BER expressions are only available for the single-relay and two-relay networks [17]. As such, the optimal threshold values could not be found easily for networks with more than two relays. To overcome this limitation, reference [18] employs the selection combining, i.e., select a received signal with the largest decision variable, for the detection of the transmitted information. With this detection scheme, the average end-to-end BER is analytically determined in a closed-form expression with arbitrary number of relays. The scheme still significantly improves the BER performance compared to either ML or PL schemes. However, the work in [18] assumes that there is no direct link between the source and destination and the network operates on independent and identically distributed (i.i.d.) Rayleigh fading channels. Also, the theoretical analysis of the diversity order is not provided.
This work is concerned with a general network, i.e., a multiple-relay network operated on either i.i.d. or non-identically distributed (i.n.d.) Rayleigh fading channels. In particular, after receiving the signal in the first phase from the source, relay i decodes and retransmits if its decision variable is larger than the corresponding threshold, θ r,i th. Otherwise, it remains silent. Two scenarios are considered: (i) the information of whether a particular relay decodes and retransmits or remains silent in the second phase is unavailable at the destination (scenario 1), (ii) the information of whether a particular relay decodes and retransmits or remains silent in the second phase is available at the destination. The destination combines the signals from all the relays and the signal from the source (scenario 1) or only the signals from the retransmitting relays and the signal from the source (scenario 2) to detect the transmitted information. The average BERs of the proposed schemes are computed in closed-form expressions. Using the derived BERs, the optimal threshold values are determined to minimize the average BERs of the networks. Furthermore, approximate thresholds that achieve a full-diversity order are derived. Numerical results verify that our obtained BER expressions are accurate. Moreover, our proposed scheme provides a superior performance under different channel conditions compared to the previous proposed piecewise-linear (PL) scheme in [16]. Since the information of whether a particular relay retransmits or remains silent does not really improve the BER performance of the network; the relays do not need to send such information to the destination to reduce the complexity of the network.
The remainder of this paper is organized as follows: Section 2 describes the system model; Section 3 presents the BER computation for scenario 1; the BER computation for scenario 2 is derived in Section 4; the optimal and approximate threshold values are discussed in Section 5; analytical and simulation results are presented in Section 6; finally, Section 7 concludes the paper.
2 System model
Consider a wireless network as illustrated in Figure 1, where K relays help one source node to communicate with its destination. Every node has only one antenna and operates in a half-duplex mode (i.e., a node cannot transmit and receive simultaneously). The K relays communicate with the destination over orthogonal channels and the DF protocol is employed at each relay. The source, relays, and destination are denoted and indexed by node 0, node i, i=1,…,K, and node K+1, respectively.
Signal transmission from the source to destination is completed in two phases as follows: in the first phase, the source broadcasts a BFSK signal. In the baseband model, the received signals at node i are written as
where h0,i and n0,i,k are the fading channel coefficients between node 0 and node i and the noise component at node i, i=1,…,K+1, respectively. E0 is the average transmitted symbol energy of the source. In (1) and (2), the third subscript k∈{0,1} denotes the two frequency subbands used in BFSK signalling. Furthermore, the source symbol x0=0 if the first frequency subband is used and x0=1 if the second frequency subband is used.
For the DF protocol, node i decodes the signal received from the source and retransmits a BFSK signal to the destination. If node i transmits in the second phase, the baseband received signals at the destination are given by
where E i is the average transmitted symbol energy sent by node i and ni,K+1,k is the noise component at the destination in the second phase. Note that if the i th relay makes a correct detection, then x i =x0. Otherwise x i ≠x0.
The channel between any two nodes is assumed to be Rayleigh flat fading, modeled as1, where i,j refer to transmit and receive nodes, respectively. The noise components at the relays and destination are modeled as i.i.d. random variables. The instantaneous received SNR for the transmission from node i to node j is γi,j=E i |hi,j|2/N0 and the average SNR is . With Rayleigh fading, the probability distribution function (pdf) of γi,j is .
2.1 ML and PL schemes
A study [16] discusses a framework for ML detection in noncoherent cooperative communications in which the relays always decode and retransmit the received signals. After receiving K+1 signals from the source and relays and assuming that the destination knows all the average SNRs of the relay-destination links, the ML detector for a noncoherent DF cooperative network can be shown to be [16]
and ε i is the average probability of error at node i which is also assumed to be available at the destination. When the conventional envelope detector is used to detect BFSK signal at the i th relay, one has . Therefore, requiring to know all ε i at the destination is equivalent to requiring the knowledge of all the average SNRs of source-relay links.
Though being optimal, the nonlinear behavior of (7) makes the implementation of the ML detector as well as its BER analysis very difficult. Therefore, a piecewise linear approximation to f(t i ) is proposed in [16] to overcome these disadvantages. The approximation is as follows:
where T i = ln[(1−ε i )/ε i ] and ε i <1/2. The above approximation is shown in [16] to be very tight. Due to the linear behavior of the PL scheme, it is more amenable to practical implementation. Moreover, the error performances of the ML and PL schemes are very close. Therefore, the PL scheme shall be used as a benchmark to analyze the BER performance of our proposed scheme.
2.2 Previous adaptive relaying scheme
The proposed scheme in [17] is summarized as follows: after receiving the signal from the source, node i decodes and retransmits a BFSK signal if the magnitude of the energy difference in two subbands θ0,i=||y0,i,0|2−|y0,i,1|2| satisfies θ0,i>θ r,i th2. If node i transmits in the second phase, the received signals at the destination in the two subbands are given as in (3) and (4). Otherwise, node i remains silent. In this case, the outputs in the two subbands are
Then the destination compares the magnitude of the energy difference in the two subbands of each relay-destination link, i.e., θi,K+1=||yi,K+1,0|2−|yi,K+1,1|2| for i=1,…,K, with the threshold to decide a retransmitting relay. If , the destination marks the i th relay as a retransmitting relay. Otherwise it marks it as a silent relay.
Finally, the destination combines the signals from the retransmitting relays and the signal from the source to decode. Based on the available information at the destination, the optimum detector is of the following form [16]:
where δ i =1 if node i is marked as a retransmitting relay, and δ i =0 otherwise.
It is worth to mention again that the closed-form BER expressions were only available for the single-relay and two-relay networks for this scheme. As such, the important task of optimizing the threshold values has to rely on numerical search for networks with more than two relays.
2.3 Proposed scheme
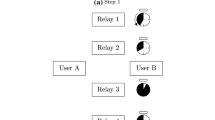
The proposed scheme is illustrated in Figure 2. Different from the work in [17], this work does not assume that all the relays have the same average SNRs to the source and to the destination, i.e., i.i.d. Rayleigh fading channels. Therefore, K thresholds {θ r,1th,θ r,2th,…,θ r,K th} are employed. Similar to [17], if node i transmits in the second phase, the outputs in the two subbands are given as in (3) and (4). Otherwise, the outputs in the two subbands are as in (9) and (10).
As mentioned earlier, this paper studies two different scenarios: (scenario 1) the information of whether a particular relay retransmits or remains silent in the second phase is unavailable at the destination. In this scenario, the destination combines the received signals from all the relays and the received signal from the source to detect the transmitted information, i.e., the detector is written as (11) where δ0=δ1=⋯=δ K =1, scenario 2) this scenario assumes that the destination knows exactly whether a particular relay transmits or remains silent in the second phase. Hence, the detector is also as (11) where δ i =1 if node i is a retransmitting relay, and δ i =0 otherwise. It is noted that the detector in [17] employs a threshold to mark whether a particular relay is a retransmitting relay or not. It is clear that the performance of the detector in [17] is always worse than the performance of the detector in scenario 1, but better than the performance of the detector in scenario 2. However, the complexity is inverse. On the other hand, the advantage of the detection in this study over the study in [17] is that it allows a closed-form BER expression for a general network with K relays.
In the next sections, we derive the average BERs for two scenarios under i.i.d. and i.n.d. Rayleigh fading channels. Using the derived BERs, the optimal thresholds are numerically found in Section 5.
3 BER analysis for scenario 1
Recall that scenario 1 assumes that the information of whether a particular relay retransmits or remains silent in the second phase is unavailable at the destination. The detector is as (11) where δ0=δ1=⋯=δ K =1. To compute the average BER expression, the detector can be rewritten as
We adopt the convention that i.i.d. fading channels means that all the relays have the same average SNRs to the source and to the destination, i.e., and . Otherwise, the term ‘i.n.d. fading channels’ is used. In what follows, the average BERs for scenario 1 under i.i.d. and i.n.d. Rayleigh fading channels are derived.
3.1 i.n.d. fading channels
We assume that the set of K relays are divided into three disjoint subsets ΩC,ΩI, and ΩS where ΩC,ΩI, and ΩS are the sets of relays that forward a correct bit, an incorrect bit, and remain silent in the second phase, respectively. The probability of occurrence of {ΩC,ΩI,ΩS} can be computed as [17, 18]
where is the probability that the magnitude of the energy difference in the two subbands at node i is smaller than the corresponding threshold, i.e., θ0,i<θ r,i th. It is given as [17, 18]
On the other hand, is the probability of error at node i, i=1,…,K, given that the magnitude of the energy difference in the two subbands is larger than the threshold, i.e., θ0,i>θ r,i th. It is computed as [17, 18]
The average BER of the network is equal to
where the conditioned BER given {ΩC,ΩI,ΩS} is found as (see Appendix Appendix 1: conditional probability of error for case 1 of scenario 1)
where
3.2 i.i.d. fading channels
Since all the relays are assumed to have the same average SNRs to the source and to the destination, i.e., and , all the relays employ the same threshold, i.e., θ r,1th=⋯=θ r,K th=θ rth. Similar to the previous section, three disjoint subsets ΩC,ΩI, and ΩS are divided. Assume that |ΩC|=M,|ΩI|=N, and |ΩS|=L where |Ω| denotes the cardinality of the set Ω. Clearly, K=M+N+L. Using the moment-generating function (MGF) technique as in Appendix Appendix 1: conditional probability of error for case 1 of scenario 1, the average BER of the network in this case can be computed as
where the probability of occurrence of {M,N,L} is
Meanwhile, the conditional BER given {M,N,L} can be determined as
To summarize, the final expressions of the average BERs of the proposed adaptive relaying scheme for scenario 1 under i.n.d. and i.i.d. fading channels can be analytically computed by substituting all the related expressions into (16) and (24). Based on the average BERs, the optimal threshold values shall be chosen to minimize the average BER.
4 BER analysis for scenario 2
In this section, we derive the average BER for a K-relay network in which the destination exactly knows the information of whether a particular relay transmits or remains silent in the second phase. Similar to scenario 1, two different cases are considered: (i) the transmission is over i.n.d. Rayleigh fading channels, (ii) the transmission is over i.i.d. Rayleigh fading channels. The detector in (11) is rewritten as
where δ i =1 if node i is a retransmitting relay, and δ i =0 otherwise.
4.1 i.n.d. fading channels
With three disjoint subsets ΩC,ΩI, and ΩS defined in the previous section, the subset ΩS is known at the destination in this scenario. It is clear that the destination does not combine the received signals from the relays that belongs to the subset ΩS. Therefore, the conditioned BER given {ΩC,ΩI,ΩS} can be found by eliminating the subset ΩS in (17). Similarly, A1,B j ,C j ,D1,E j , and F j are defined as in (18) to (23) but eliminating the subset ΩS (see Appendix Appendix 2: conditional probability of error for case 1 of scenario 2). Meanwhile, the probability of occurrence of {ΩC,ΩI,ΩS} and the average BER of the network are computed as (13) and (16), respectively.
4.2 i.i.d. fading channels
Similar to Section 3.2, the average BER of the network and the probability of occurrence of {M,N,L} are given in (24) and (25), respectively. Meanwhile, the conditioned BER given {M,N,L} can be found by removing the L component in (26) (see Appendix Appendix 3: conditional probability of error for case 2 of scenario 2).
5 Optimal and approximate thresholds
The choice of the thresholds can strongly affect the BER performance. If the thresholds are either too large (relays rarely retransmit, i.e., the system degenerates to the source-destination channel) or too small (relays always retransmit, i.e., the retransmission of erroneously decoded bits makes the error performance worse), the performance of the network resembles that of a point-to-point system because in either case, the diversity order of the system is equal to one. Hence, one is interested in finding the optimal thresholds for the proposed relaying scheme. With the closed-form BERs obtained in the previous sections, the optimization problem for the i.n.d. fading channel case can be set up as follows:
Meanwhile, the optimization problem for the i.i.d. fading channel case can be set up:
The above optimization problems can be solved by some optimization techniques such as the Lagrange method [19] since the average BER expressions have been set up. However, the exponential terms in the final BER expressions render closed-form solutions intractable. Therefore, the optimization problem in (34) or (35) is simply solved by using the MATLAB Optimization Toolbox command ‘fmincon’ designed to find the minimum of a given constrained nonlinear multivariable function. It should be noted that the average BERs formulated in the previous sections only require information on the average SNRs of the source-destination, source-relay, and relay-destination links. The optimization problems can therefore be solved off-line for typical sets of average SNRs and the obtained optimal threshold values are stored in a look-up table.
It is clear from (34) and (35) that a closed-form solution for optimal threshold values is very difficult, if not impossible, to find. Therefore, in what follows, we propose an approximate threshold θ rth,∗ and prove that by using those thresholds, the system can achieve the maximum diversity order of (K+1) for both scenarios.
Theorem 1
With or without the information of whether a relay retransmits in the second phase at the destination, the threshold θ rth,∗=Q logc γ where γ=E0/N0 is sufficient for achieving a full diversity order of K+1 for any Q≥K and a positive constant c.
Proof
Appendix Appendix 4: proof of theorem 1 □
6 Simulation results
In this section, simulation results are provided to verify the analytical results derived in Sections 3 and 4. Furthermore, the performances with optimal thresholds are provided to illustrate the advantages of the proposed scheme compared to other existing schemes. In all simulations, the noise components at the destination and relays are modeled as i.i.d. random variables.
Figures 3 and 4 plot the average BERs at the destination for two scenarios and under different channel conditions. Specifically, the thresholds are arbitrarily chosen as {θ r,1th=θ r,2th=θ r,3th=2} for the three-relay network with scenario 1 in Figure 3, while they are set as {θ r,1th=θ r,2th=2} for the two-relay network with scenario 2 in Figure 4. The channel variance of the network is denoted by σ2 where . In both networks, the transmitted powers are set to be the same for the source and relays. The two figures clearly show that analytical results (shown in lines) and simulation results (shown as marker symbols) are identical, hence verifying our analysis in Sections 3 and 4.
Next, Figures 5 and 6 present the comparative performances of the PL scheme, the two-threshold schemes in [17], and the proposed scheme with scenarios 1 and 2, for the case of i.i.d. Rayleigh fading in a two-relay network. It should also be noted that the channel variances of all communication links are set to be σ2=[2 2 0.5 1 1], i.e., the relays are nearby the source, for Figure 5 and σ2=[2 2 1 20 20], i.e., the relays are close to the destination, for Figure 6. The figures show that our proposed scheme outperforms the PL scheme. Since the relays in the PL scheme always decode and forward the received signals, they can induce error propagation, hence limiting the BER performance of the system. Meanwhile, the relays in our proposed schemes are designed to be adaptive, i.e., decode and forward the received signals only when the received signals are reliable, hence limiting the error propagation. The figures also confirm that the performance of the detector in [17] is in-between the performances of the detectors of scenario 1 and scenario 2. When the relays place nearby the source as in Figure 5, i.e., the source-relay links are strong, the relays likely decodes and forwards the received signals. Hence, the BER performance of the proposed scheme of scenario 1 achieves that of the two-threshold scheme. However, the performance of scenario 1 is a little bit worse than that of the two-threshold scheme as illustrated in Figure 6 when the relays are close to the destination, i.e, the source-relay links are poor. In this case, the relays likely remain silent in the second phase. It is also clear that the BER performance of scenario 2 is the best since the information of retransmitting relays is available at the destination. The figures also show that BER difference between scenario 1 and scenario 2 is not much since the detector of scenario 1 only adds noise components from silent relays to the final decision form. It also explains why the BERs of two scenarios have the same slope as observed in Figures 5 and 6.
Finally, Figure 7 illustrates the usefulness of the proposed scheme where three-relay and four-relay networks are considered. It is seen from Figure 7 that the proposed scheme yields a much better BER performance than the PL scheme, especially at the high SNR region.
7 Conclusion
The paper studied the BER performance of an adaptive decode-and-forward relaying scheme in noncoherent cooperative networks with K+2 nodes. BFSK is used to modulate the signals at both the source and the relays. The channels between any two nodes are Rayleigh fading. The studied scheme employs thresholds to select retransmitting relays. A relay decodes and retransmits if its decision variable is larger than the corresponding threshold. Otherwise it remains silent. The average BERs for K-relay networks with i.i.d. and i.n.d. Rayleigh fading channels are derived for two different scenarios. Optimal thresholds are chosen to minimize the average BER. The full diversity are verified with approximate thresholds. Simulation results were provided to corroborate the analysis. Performance comparison reveals that the proposed scheme improves the error performance significantly compared to the previous proposed PL scheme.
Appendices
Appendix 1: conditional probability of error for case 1 of scenario 1
We first review pdf and MGF of some related random variables. When the transmitted bit at node i is ‘0’, the pdfs of two random variables Zi,K+1,0 and Zi,K+1,1, defined as and , are given, respectively, by [17]
So the MGFs3 of Zi,K+1,0 and Zi,K+1,1 are derived, respectively, as
Recall that ΩC,ΩI, and ΩS are the sets of relays that forward a correct bit, an incorrect bit, and remain silent in the second phase, respectively. The MGFs of X and Y in (12) are expressed, respectively, as4
Using partial fractions, (40) and (41) can be rewritten as
where A1,B j ,C j ,D1,E j , and F j are defined in (18) to (23).
Taking the inverse Laplace transform of M X (s) and M Y (s), the pdfs of X and Y are, respectively, as
Thus, the conditioned BER given {ΩC,ΩI,ΩS} can be computed as
By performing the integrals in (46), the conditioned BER given {ΩC,ΩI,ΩS} is found as in (17).
Appendix 2: conditional probability of error for case 1 of scenario 2
Similar to Appendix Appendix 1: conditional probability of error for case 1 of scenario 1, the conditioned BER given {ΩC,ΩI,ΩS} for case 1 of scenario 2 is found as
where
Appendix 3: conditional probability of error for case 2 of scenario 2
The conditioned BER given {M,N,L} for this case is found as
where
Appendix 4: proof of theorem 1
To simplify our derivation, we consider the i.i.d. case for both scenarios. Generalization of the analysis to the networks with arbitrary qualities of source-relay and relay-destination links is straightforward and thus omitted. In what follows, the events that no relay retransmits and at least one relay retransmits in the second phase are parameterized by Θ=1 and Θ=2, respectively. The average BER of the network with a given threshold θ rth can be written as
where P(ε,Θ=i) is the average BER at the destination in the case Θ=i.
We verify Theorem 1 for scenario 2 first. Obviously P(ε,Θ=1) can be calculated as follows:
Since θ rth=Q logc γ and
one has5
On the other hand, P(ε,Θ=2) can be written as
where PΘ=2(ε|i) and PΘ=2(i) denote the conditioned BER and case probability for the case that there are i relays that transmit in the second phase. One has
Furthermore, PΘ=2(ε|i) can be written as
where PΘ=2,i(ε|k) and PΘ=2,i(k) denote the conditioned BER and case probability for the case that in i retransmitting relays, k relays decode the signal correctly. PΘ=2(ε|i) can be upper-bound as
Note that PΘ=2,i(ε|k=i) is the probability of error when all i retransmitting relays decode the signal correctly, thus
and
In summary, the average BER of the network is upper bounded on
where Q≥K.
When approaches infinity, one can ignore the term logγ. Thus, the diversity order of (K+1) can be achieved when Q≥K, and the proof is complete with scenario 2. Now, we continue with scenario 1. The derivation of P(ε,Θ=2) in scenario 1 is similar to that in scenario 2, i.e., . Hence, we need to prove that when γ→∞,P(ε,Θ=1) has a diversity order of K+1 for scenario 1.
Recall that the case Θ=1 happens when no relay retransmits in the second phase. Therefore, the conditional BER given Θ=1 can be computed by applying (26) with M=N=0 and L=K. We thus obtain
When , one verifies that then , so
Similarly, the probability of occurrence Θ=1 can be computed by applying (13) and becomes
Hence, , so the theorem is proved.
References
Tse D, Viswanath P: Fundamentals of Wireless Communications. Cambridge: Cambridge University Press; 2005.
Laneman J, Wornell G: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Trans. Inform. Theory 2003, 49: 2415-2425. 10.1109/TIT.2003.817829
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity, Part I: System description. IEEE Trans. Commun 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity, Part II: Implementation aspects and performance analysis. IEEE Trans. Commun 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Bletsas A, Khisti A, Reed D, Lippman A: A simple cooperative diversity method based on network path selection. IEEE J. Select. Areas Commun 2006, 24: 659-672.
Bletsas A, Shin H, Win M: Cooperative communications with outage-optimal opportunistic relaying. IEEE Trans. Wireless Commun 2007, 6: 3450-3460.
Michalopoulos D, Karagiannidis G: Performance analysis of single relay selection in Rayleigh fading. IEEE Trans. Wireless Commun 2008, 7: 3718-3724.
Onat F, Adinoyi A, Fan Y, Yanikomeroglu H, Thompson J, Marsland I: Threshold selection for SNR-based selective digital relaying in cooperative wireless networks. IEEE Trans. Wireless Commun 2008, 7: 4226-4237.
Onat F, Fan Y, Yanikomeroglu H, Thompson J: Asymptotic BER analysis of threshold digital relaying schemes in cooperative wireless systems. IEEE Trans. Wireless Commun 2008, 7: 4938-4947.
Hi J, Hu R: Slepian-Wolf cooperation: a practical and effcient compress-and-forward relay scheme. In Allerton Conf. Commun. Contr. and Comp. St. Louis; November 2005.
Laneman J, Tse D, Wornell G: Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inform. Theory 2004, 50: 3062-3080. 10.1109/TIT.2004.838089
Himsoon T, Su W, Liu K: Differential transmission for amplify-and-forward cooperative communications. IEEE Signal Process. Lett 2005, 12: 597-600.
Himsoon T, Siriwongpairat W, Su W, Liu K: Differential modulation with threshold-based decision combining for cooperative communications. IEEE Trans. Signal Process 2007, 55: 3905-3923.
Zhao Q, Li H: Differential modulation for cooperative wireless systems. IEEE Trans. Signal Process 2007, 55: 2273-2283.
Zhao Q, Li H, Wang P: Performance of cooperative relay with binary modulation in Nakagami- m fading channels. IEEE Trans. Veh. Technol 2008, 57: 3310-3315.
Chen D, Laneman J: Modulation and demodulation for cooperative diversity in wireless systems. IEEE Trans. Wireless Commun 2006, 5: 1785-1794.
Nguyen HX, Nguyen HH: Adaptive relaying in noncoherent cooperative networks. IEEE Trans. Signal Process 2010, 58: 3938-3945.
Nguyen HX, Nguyen HH: Selection combining for noncoherent decode-and-forward relay networks. EURASIP J. Wireless Commun. Network 2011, 2011(1):106. 10.1186/1687-1499-2011-106
Bertsekas DP: Constrained Optimization and Lagrange Multiplier Methods. Belmont: Athena Scientific; 1996.
Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.04-2012.33.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Nguyen, H.X., Tran, N.N. & Nguyen, H.T. Performance analysis of adaptive decode-and-forward relaying in noncoherent cooperative networks. J Wireless Com Network 2013, 281 (2013). https://doi.org/10.1186/1687-1499-2013-281
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2013-281