Abstract
In this paper, we present a novel hybrid automatic repeat request (HARQ) scheme for cooperative communication systems, called cooperative partial retransmission (CPR). The method is based on the retransmission of only a fraction of the original code word by the cooperating nodes. Based on the outage analysis, we derive the theoretical throughput expressions that are compared to numerical simulations using LDPC codes, showing that CPR outperforms regular cooperative HARQ techniques. Additionally, we show that the CPR throughput, even using a single relay, may be considerably larger than the throughput of a regular cooperative HARQ scheme using multiple relays. Finally, the energy consumption analysis of the schemes shows that CPR consumes less energy than regular cooperative HARQ, mainly due to the shorter retransmissions.
Similar content being viewed by others
1. Introduction
The demand for constant evolution of the wireless communication systems poses many challenges, as that of circumventing the effect of the channel fading, inherent to the wireless medium [1]. Spatial diversity, through the use of multiple antennas, has proved to be very efficient to combat the effects of fading in wireless systems [2]. However, to achieve the expected gains, the antennas must be properly spaced, which may be impractical in small-sized devices. Cooperative communication [3–10] emerged as an alternative to the use of multiple antennas. Probably, the two most known cooperative protocols are the amplify-and-forward (AF) and the decode-and-forward (DF) [3]. Later, the association of error correcting codes with AF and DF protocols showed to considerably increase the performance [6–11], giving rise to what is called coded cooperation. Convolutional codes [6, 8], turbo codes [7, 8] and LDPC codes [9–11] are some important coding techniques that were associated with the relay channel.
Coded cooperation can be roughly divided into two classes [8, 9]: repetition coding (RC), which uses the same encoder for source and relay, and parallel coding (PC), in which source and relay encoders are built to send different parities. PC is shown to outperform RC, specially when turbo codes or irregular LDPC codes are used [8, 9]. However, in PC, the codes need to be specifically designed for the relay channel, while the complexity at both the relay and destination increases. Recently, in [12], partial repetition coding (PR) was proposed to be used under the selective DF protocol. In PR, source and relay operate with the same encoder, similar to RC, but the relay forwards only a fraction of the original message, with a proper power allocation between source and relay. Theoretical results in [12] showed that PR performs quite close to PC, which makes PR very interesting from the practical point of view, since it has a lower complexity at both the relay and destination.
Another group of recent works demonstrates the advantages of using automatic repeat request (ARQ) [13] or Hybrid ARQ (HARQ) [14] techniques in cooperative communication systems [15–18]. A pioneering work in this area is that in [15], while in [16] novel protocols for a cooperative system with multiple relays were presented. In [17], the authors have shown that the performance of the cooperative protocols is always better than that of the non-cooperative ARQ protocols. Moreover, in [18], two different concepts, post-cooperative ARQ and pre-cooperative ARQ, are introduced and analyzed. Post-cooperative ARQ is a fixed relaying protocol [3], in which both source and relay participate at each ARQ round. On the other hand, pre-cooperative ARQ is an incremental relaying protocol [3], in which the cooperation occurs only if needed, reducing the loss in spectral efficiency inherent to the cooperative systems.
Based on these recent results, in this paper, we assume a cooperative communication system where the delivery of packets should be guaranteed and that a feedback channel is available. Then, we propose a novel Hybrid ARQ cooperative scheme, referred to as cooperative partial retransmission (CPR), in which the relay retransmits only a fraction of the original message when the destination requests a retransmission. The system operates under the incremental DF (IDF) cooperative protocol using Type-I HARQ with chase combining (CC) [19]. The option for Type-I HARQ with chase combining is supported by some recent results [20–22], which demonstrate that Type-I HARQ may perform very close to Type-II HARQ (incremental redundancy--IR) with a considerably smaller computational complexity. Note that by retransmitting only a fraction of the original code word by the relay does not imply in any complexity increase at the receiver, since the received code words (partial or not) pass through the same decoder, characterizing a particular case for Repetition Coding. On the other hand, when IR is employed, the code rate changes at each retransmission, and as a consequence, the decoder is more complex in order to support different code rates, which in fact characterizes a particular case for Parallel Coding. Moreover, the proposed CPR scheme can also be used with IR, however, due to the same complexity constraints cited before, we consider this implementation out of the scope of this paper.
A. Main contributions
Based on the outage analysis, we derive closed-form expressions for the throughput and energy consumption of the proposed CPR scheme, which is compared to the performance of the non-cooperative and regular cooperative Pre-HARQ [18]. The proposed scheme is based on the partial retransmissions of the source original code word at the relay and differs from that of [12] mainly by considering the use of HARQ and by exploring scenarios where multiple relays are available. In addition, to validate the analysis, simulation results using LDPC codes are carried out. Our theoretical and simulation results agree very well. Moreover, we also show that the proposed scheme, operating with a single relay, can achieve a higher throughput than the regular cooperative Pre-HARQ scheme with multiple relays. If multiple relays are also available with CPR, the throughput gains are even greater. Finally, an energy consumption analysis is carried out, showing that, besides obtaining a larger throughput, the proposed scheme also consumes less energy than Pre-HARQ.
B. Organization
The rest of this paper is organized as follows. In Section 2, we present the outage analysis of the proposed CPR scheme, as well as for the Pre-HARQ and direct transmission, in order to compare the system throughput of these three schemes. Section 3 deals with the energy consumption of the cooperative schemes. Simulation results are shown in Section 4, and Section 5 concludes the paper.
2. Outage analysis
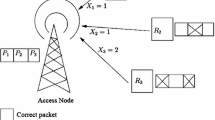
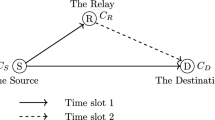
Consider a system with three cooperating terminals, source, relay, and destination, disposed according to Figure 1. A normalized unity distance has been assumed between source and destination, with the relay at an intermediate distance δ from the source. The relay-destination distance is (1 - δ). The channel noise is considered to be AWGN with variance N0/2 per dimension. A long-term quasi-static Rayleigh fading channel [23] is considered, which means that channel coefficients are constant during the retransmissions, changing only for a new block of data. We assume perfect CSI at the receivers.a Due to delay constraints, the system operates within a truncated HARQ assumption, in which only a finite number M of retransmissions is allowed. Moreover, motivated by their practical feasibility, we assume half-duplex nodes operating in an orthogonal fashion.
In the following, we characterize the system in terms of the outage probability and throughput. Sections 2-A and 2-B describe two known transmission schemes for the above scenario: the direct transmission and the regular cooperative Pre-HARQ transmission, respectively. These schemes will serve as a benchmark to the proposed scheme, which is presented in Section 2-C.
A. Direct transmission
In the direct transmission, the received signal at the destination is:

where P is the transmit power, hsd represents the Rayleigh fading coefficient of the S-D link, X is the message to be transmitted representing the information bits u, and wsd is additive noise.
An outage in the direct transmission occurs when Isd < R, where Isd is the mutual information in the S-D link and R is the information transmission rate. Supposing real Gaussian inputs and unitary bandwidth, the mutual information can be written as [24]:

where N is the noise power and E b is the received energy per information bit, such that P = RE b .
The outage probability in the S-D link is then:

where  is the probability of event ϕ.
is the probability of event ϕ.
We assume that an error free feedback channel between the destination and the other nodes is available. Therefore, after the first source transmission, the destination estimates û from the received code word ysd, detects possible errors, and responds with an ACK/NACK depending on the error verification. If an ACK is received, then the source proceeds with the transmission of the next packet. Instead, in case of a NACK, the retransmission process begins. After each retransmission, the destination applies chase combining, or equivalently maximal ratio combining (MRC), among the received packets. The mutual information in this case, in long-term quasi-static fading and after m retransmissions, is:

where the term (m + 1) is due to the chase combining of each retransmission at the destination, which in fact is seen as an SNR accumulation [21]. The associated outage probability is:

Since we consider the existence of a feedback channel and message retransmission, an important performance metric is the system throughput, which is the effective spectral efficiency seen by the receiver. Based on the outage probability of each transmission,  , we define the throughput of the direct communication scheme for at most M retransmissions as:
, we define the throughput of the direct communication scheme for at most M retransmissions as:

The first line in Equation 6 represents the case when the transmission from the source was already correctly decoded by the destination, then no retransmissions are necessary. In this case, the throughput will be R, with probability  . The following lines represent the contribution of each HARQ round. For instance, considering the first retransmission, the throughput expression must take into account that an error already occurred in the first transmission, which happens with probability
. The following lines represent the contribution of each HARQ round. For instance, considering the first retransmission, the throughput expression must take into account that an error already occurred in the first transmission, which happens with probability  . Moreover, since we consider slow-fading, the occurrence of a successful retransmission is not independent of an outage in the first transmission, so that a retransmitted packet is correctly decoded with probability:
. Moreover, since we consider slow-fading, the occurrence of a successful retransmission is not independent of an outage in the first transmission, so that a retransmitted packet is correctly decoded with probability:  . Finally, for the next retransmissions, the same idea is applied, but the number of terms increases since all the previous erroneous transmissions must be taken into account.
. Finally, for the next retransmissions, the same idea is applied, but the number of terms increases since all the previous erroneous transmissions must be taken into account.
However,

since Idir(m) ≥ Idir(m - 1) ≥ ⋯ ≥ I dir (0).
Moreover, the conditional probability:

Thus, a closed-form expression for the throughput of the direct transmission is given by:

B. Regular cooperative Pre-HARQ
In the orthogonal cooperative transmission, the communication is carried out in two different time slots. In the first time slot, the transmission from the source is received at both the relay and destination. At the destination, the received packet is described in Equation 1 and the mutual information in Equation 2. At the relay, the received packet is:

where γsr = δ-α, such that α is the path loss exponent, hsr is the channel fading, and wsr is the additive noise vector at the relay.
The mutual information in the S-R link is:

while the outage probability is:

Similar to the direct transmission, after the first source transmission, the destination estimates û from the received code word ysd, detects possible errors, and responds with an ACK/NACK using the feedback channel. However, in the case of an NACK, the retransmission process may involve the relay. According to the pre-cooperative ARQ strategy in [18], the retransmissions come from the node with the best node-destination channel condition, be it either the source or the relay. Since in our topology, the relay is usually with a better channel condition with respect to the destination, due to the shorter distance in the R-D link than in the S-D link, we assume that all the retransmissions come from the relay, unless when the relay was not able to decode the source message.
In case of a relay retransmission, the signal received at the destination is:

where γrd = (1 - δ)-α, hrd is the channel fading coefficient, and wrd is additive noise.
After chase combining of m retransmissions coming from the relay, the mutual information in the regular cooperative scheme equals:

The outage probability is:

The overall outage probability of the Pre-HARQ scheme can then be written as:

Finally, the throughput of the regular cooperative Pre-HARQ for a maximum of M retransmissions is:

1) Pre-HARQ with multiple relays: Now assume that instead of a single relay, a set of K ∈ ℤ+ relays is available. Thus, we define the set of relay-destination links as  , where
, where  is the fading coefficient between the i th relay and the destination. In the case of multiple relays, a controlling protocol must be implemented to coordinate which node will retransmit. As we consider the decode-and-forward protocol, this decision of the best node must take into account all the relay-destination links among those relays which were capable of correctly receiving the source message. Therefore, we define the subset
is the fading coefficient between the i th relay and the destination. In the case of multiple relays, a controlling protocol must be implemented to coordinate which node will retransmit. As we consider the decode-and-forward protocol, this decision of the best node must take into account all the relay-destination links among those relays which were capable of correctly receiving the source message. Therefore, we define the subset  , where
, where  is the mutual information between the source and the i th relay.
is the mutual information between the source and the i th relay.
For the sake of simplicity, we assume that all the relays are approximately at the same distance δ from the source, such that  . Therefore, we can assume that the outage probability between the source and any of the K relays is given by Equation 11. In the case of a relay retransmission, we assume perfect relay selection. Then, the mutual information in this case is given by:
. Therefore, we can assume that the outage probability between the source and any of the K relays is given by Equation 11. In the case of a relay retransmission, we assume perfect relay selection. Then, the mutual information in this case is given by:

such that the outage probability is given by  .
.
Then, the throughput of Pre-HARQ with K relays for a maximum of M retransmissions can be generalized to:

C. Cooperative partial retransmission
The proposed CPR scheme is based on the partial retransmission of the original packet. The packet sent by the source is divided into L ∈ ℤ+ equal length sub-packets for retransmission. The sub-packets can be constructed in practice by puncturing the originally transmitted code word. The method is based on a scheme proposed by the authors for the non-cooperative AWGN channel [25].
The proposed scheme can be summarized as:
-
1)
In the first transmission, the source operates as usual, transmitting the whole packet;
-
2)
If a retransmission is required, then the relay sends only the first fraction of symbols pertaining to that packet. If the relay was not able to decode the source message, then the source retransmits as usual, the entire packet;
-
3)
If more retransmissions are required, the relay sends the next fraction. If the L th fraction of symbols was already sent, the method repeats from step 2.
Note that, in the above method, the length of the retransmitted fractions is constant. Since the retransmissions from the relay are always shorter than in the regular cooperative scheme, it is reasonable to expect that this would reflect in an improved throughput. In addition, it is also reasonable to expect a lower energy consumption due to the shorter retransmissions. Moreover, the received fractions are always combined with the previously received symbols, just as in the other methods.
The mutual information after chase combining of m partial retransmissions coming from the relay is:

where the function ⌊ϕ⌋ returns the largest integer not larger than ϕ. The outage probability associated with the above mutual information is:

The solution for the outage probability is particular for any given L and m, as it involves a sum of multiple random variables. As an example, next we particularize the solution for m = L = 4:

which we compare to Pre-HARQ in Section 2-D. More details about  can be found in the Appendix.
can be found in the Appendix.
The overall outage probability of the proposed CPR scheme is:

while the throughput for the maximum of M retransmissions is:

1) CPR with multiple relays: Similar to Pre-HARQ, the mutual information of the partial cooperation is:

while the outage probability is given by  , and the throughput of CPR with K relays for a maximum of M retransmissions is:
, and the throughput of CPR with K relays for a maximum of M retransmissions is:

D. Performance comparison
Figure 2 compares the outage probabilities of the direct transmission, Pre-HARQ, and the proposed CPR scheme with L = 4, given by Equations 3, 15, and 22. We assumed unitary transmit power (P = 1 W), the relay is exactly in the midpoint between the source and the destination (δ = 0.5) in the cooperative schemes, the path loss exponent is α = 4 (dense urban area), the information transmission rate is  , and the number of retransmissions in this case is m = 4. For all the transmission schemes, we plot the theoretical expressions and the simulation results, obtained via the Monte Carlo method, which show the accuracy of the theoretical analysis. From the figure, we can notice that the outage probability of the proposed CPR scheme is worse than that of Pre-HARQ for L = 4 and m = 4. However, as the relay retransmits packets which are shorter, a positive impact in throughput is expected.
, and the number of retransmissions in this case is m = 4. For all the transmission schemes, we plot the theoretical expressions and the simulation results, obtained via the Monte Carlo method, which show the accuracy of the theoretical analysis. From the figure, we can notice that the outage probability of the proposed CPR scheme is worse than that of Pre-HARQ for L = 4 and m = 4. However, as the relay retransmits packets which are shorter, a positive impact in throughput is expected.
The throughput performance of the presented schemes is shown in Figure 3 for a maximum of M = 4 retransmissions.b From the figure, we can see that CPR outperforms considerably the regular Pre-HARQ, achieving a higher throughput in the medium and high SNR regions, which are the regions of interest for communication. Only in the low SNR region, and by a very small margin, the proposed CPR scheme is outperformed by Pre-HARQ. Moreover, we can also notice that the throughput performance increases with L. When comparing the proposed scheme with Pre-HARQ, up to 2.1 dB of throughput gain is achieved when L = 2, up to 2.8 dB when L = 3, and up to 3.3 dB when L = 4. However, by increasing L, other issues must be taken into account. By retransmitting a fraction which is very small, the number of required retransmissions could increase and consequently compromise the energy efficiency of the scheme. The issue of the energy consumption for each of the above cooperative schemes will be handled in the next section.
Figure 4 extends these results to the case when multiple relays are available for the cooperative schemes. We compare the performance of the direct transmission, CPR with L = 4 and Pre-HARQ, both with K = 1, 2, and 4 relays. In the case of multiple relays, all relays were assumed to be at the midpoint between the source and the destination.c From the figure, we can see that the proposed CPR scheme with a single relay already outperforms considerably the regular Pre-HARQ in the high SNR region, even when K = 4 relays are available in the latter. The introduction of multiple relays in Pre-HARQ increases the system performance only in the low SNR region, which was already noted in [26]. This is due to the fact that in the low SNR region, the source-destination link is very noisy, and more relays provide alternative paths with a higher reliability. On the other hand, while the SNR increases, the number of retransmissions requests is low, then the throughput performance of Pre-HARQ is not affected by increasing the number of relays. When multiple relays are also available in CPR, we can notice similar throughput increase in the low to medium SNR region, presenting a large advantage when compared to Pre-HARQ with the same number of relays. The throughput gain when K = 4 relays are available can be up to 6 dB when comparing CPR with Pre-HARQ. However, due to its simplicity and to its practical feasibility, next we consider only the case of K = 1 relay.
3. Energy consumption analysis
Retransmitting only a fraction of the original message at a time could require a higher number of retransmissions for the proposed CPR scheme than for the regular Pre-HARQ. For instance, suppose that a given packet, in a given channel condition, had two retransmission requests with Pre-HARQ. Its instantaneous throughput is then  . Now suppose that two retransmission requests for the same packet, with the same channel conditions, were not enough for CPR with L = 2, and a third retransmission was required. Then,
. Now suppose that two retransmission requests for the same packet, with the same channel conditions, were not enough for CPR with L = 2, and a third retransmission was required. Then,  . Thus, even using more retransmissions, the CPR throughput is larger than that of Pre-HARQ. Since the number of transmissions is larger, but on the other hand the retransmitted packets are shorter, then the CPR energy consumption becomes interesting to be investigated.
. Thus, even using more retransmissions, the CPR throughput is larger than that of Pre-HARQ. Since the number of transmissions is larger, but on the other hand the retransmitted packets are shorter, then the CPR energy consumption becomes interesting to be investigated.
In order to scrutinize this issue, it is important to define the energy consumption of the Pre-HARQ and CPR schemes. For simplicity, we analyze the energy consumption only for the case of a single relay. Nevertheless, the extension to multiple relays is straightforward. The energy consumption of Pre-HARQ is:

where Es is the energy consumed by the source and Epre the energy consumed by the relay for each transmission in the Pre-HARQ scheme.d Since no power allocation optimization is carried out in this paper, we assume that Epre = Es.
In the case of CPR:

where ECPR(L) is the energy consumed by each relay transmission in the proposed CPR scheme. Since each retransmission in CPR is 1/L of the original code word, the average consumed energy of CPR is ECPR(L) = Epre/L.
Figure 5 shows the energy consumption of the Pre-HARQ and CPR,  and
and  , when L ∈ {2, 3, 4}. From the figure, we can notice that the energy consumption of CPR is lower than that of Pre-HARQ and decreasing with L. For instance, when Eb/N0 is at 0 dB, CPR with L = 2 consumes 17% less energy than Pre-HARQ, 22% less when L = 3, and 25% less energy when L = 4. On other words, the energy consumption can be reduced in one quarter when the relays retransmit only a fraction of the original code word. The relative energy savings achieved for the CPR scheme with L ∈ {2, 3, 4} when compared to Pre-HARQ are shown in Figure 6. From the figure, we can see that the proposed scheme presents energy savings in the whole SNR range, specially in middle SNR, and that CPR with L = 4 presents the largest savings.
, when L ∈ {2, 3, 4}. From the figure, we can notice that the energy consumption of CPR is lower than that of Pre-HARQ and decreasing with L. For instance, when Eb/N0 is at 0 dB, CPR with L = 2 consumes 17% less energy than Pre-HARQ, 22% less when L = 3, and 25% less energy when L = 4. On other words, the energy consumption can be reduced in one quarter when the relays retransmit only a fraction of the original code word. The relative energy savings achieved for the CPR scheme with L ∈ {2, 3, 4} when compared to Pre-HARQ are shown in Figure 6. From the figure, we can see that the proposed scheme presents energy savings in the whole SNR range, specially in middle SNR, and that CPR with L = 4 presents the largest savings.
4. LDPC Implementation
In this section, we investigate the performance of a practical CPR scheme using LDPC codes. A block of k equally probable and independent binary symbols, u = [u0, u1, ..., uk-1], generated by the source, is encoded by a systematic LDPC encoder with rate R = k/n, resulting in a block of n encoded symbols, v = [v0, v1, ..., vn-1]. This encoded block v is BPSK modulated, generating a set of symbols x = [x0, x1, ..., xn-1], which are simultaneously transmitted to the relay and destination nodes. The received signals at the destination and at the relay are given by Equations 1 and 9, respectively. In case of error after the first source transmission, the CPR method and the Pre-HARQ scheme operate exactly as described in Section 2.
In our simulations, for each E b /N0 value, 1000 blocks of 288 information bits are sent. The IEEE 802.16e R = 1/2 LDPC code is used [27]. The decoding is made by a sum-product algorithm with maximum number of iterations equal to 50. The relay has been positioned at a distance δ = 0.5 from the source and the path loss exponent is α = 4. The maximum number of retransmissions has been fixed at M = 4, and the number of constant length fractions considered were L ∈ {2, 3, 4}.
The simulated throughput is defined as:

where NW is the number of simulated code words for each E b /N0 value, and NRTX(i) is the number of required retransmissions for the correct decoding of the i th code word. In the case that code word i has not been correctly decoded within the maximum number of retransmissions, then we consider that NRTX(i) → ∞. Note that for the regular Pre-HARQ scheme, where the retransmissions include the entire code word, L = 1 in Equation 28.
The simulation results for the direct transmission, Pre-HARQ, and CPR with L = 4 are shown in Figure 7 and are compared to the theoretical results of Section 2. The theoretical curves serve as capacity bounds to the LDPC based implementation. From the figure, we can observe that the simulated curves are at some distance from the theoretical ones, which is reasonable, since the LDPC code was not specifically designed to the underlying channel, the block length is relatively short, and the theoretical results assume Gaussian inputs. Many works deal with the optimization of HARQ retransmissions using irregular LDPC codes [28–31]. For instance, by proper designing the LDPC code and by ordering the best fractions to be retransmitted at each round may reduce the gap to the theoretical estimation. However, this is out of the scope of this paper. The most important information in Figure 7 is that the behavior predicted by the theoretical analysis was confirmed by the simulations, with the proposed CPR scheme considerably outperforming Pre-HARQ and the direct transmission. Moreover, the agreement between the theoretical and simulated results for L = 2 and L = 3 is as good as that for L = 4, and they are not shown in Figure 7 for the sake of an easier visualization. Additionally, as predicted by the theoretical results, the simulated CPR with L = 4 outperforms CPR with L = 3 and L = 2, but by a small margin, and they all outperform Pre-HARQ.
5. Final comments
We presented a novel HARQ cooperative technique, the CPR scheme. Such strategy is based on the relay retransmission of only a fraction of the original packet at a time. The rationale behind this strategy is that fractions received and chase combined with the previous ones may already help the destination in successfully decoding the entire packet and thus increase the throughput and reduce the energy consumption. Based on the outage analysis of the proposed scheme, we derived the expressions for the throughput, which are compared to numerical results obtained using LDPC codes. Our results show that the proposed scheme considerably outperforms the regular cooperative Pre-HARQ method in terms of throughput, while also consuming less energy. Moreover, we showed that CPR with a single relay can even outperform Pre-HARQ using multiple relays.
Appendix CPR outage probability
Consider the mutual information of the CPR scheme for the particular case of L = 4 and m = 4, so that:

We define  and
and  as continuous random variables with negative exponential distributions whose means are given by
as continuous random variables with negative exponential distributions whose means are given by  and
and  . Note that S2 > S1.
. Note that S2 > S1.
Then, we can rewrite (29) as:

since  for any given 0 ≤ l ≤ 3. The outage probability is
for any given 0 ≤ l ≤ 3. The outage probability is  .
.
Let us define two new random variables:  and
and  . Then, writing
. Then, writing  and
and  , where u1 and u2 define the one-to-one transformation between
, where u1 and u2 define the one-to-one transformation between  and
and  , we can calculate the joint probability density function (pdf) of
, we can calculate the joint probability density function (pdf) of  and
and  as:
as:

where  is the joint pdf of
is the joint pdf of  and
and  , and J is the Jacobian of the transformation, given by:
, and J is the Jacobian of the transformation, given by:

As  and
and  are independent variables, we can define the joint pdf:
are independent variables, we can define the joint pdf:

Therefore, the joint pdf of  and
and  is:
is:

Finally, to obtain the pdf of  we must solve the marginal distribution of
we must solve the marginal distribution of  with respect to
with respect to  :
:

Then:

This procedure can be carried out for any given L and m. However, when m/L is not an integer, the integral in (35) does not converge and a closed-form expression can not be obtained. Nevertheless, in such cases, (35) can still be evaluated numerically by any integration method.
Endnotes
aWe assume that CSI is available due to the slow-fading characteristic of the wireless medium, and this information can be obtained in practice by relatively short training sequences through pilot symbols, as described in [32, 33]. bSupposing the existence of a practical delay constraint, the number of retransmissions was limited to M = 4. However, considering larger values for M did not reflect in any qualitative change into the conclusions. cIt is easy to notice that the best position for the relay operating under the DF protocol is the midpoint between the source and the destination. Therefore, the assumption that the relays are collocated leads to the best performance which can be achieved by the system. Any other configuration for the relay positioning will result in a decrease in throughput for both schemes, thus leading to similar qualitative results. dIn the case of somewhat long distances between transmitter and receiver (hundreds of meters), the energy used for transmission is much larger than the energy consumed by the nodes circuitry and baseband processing [34]. Therefore, we have considered only the power required for transmitting in the energy consumption model in this paper. The circuitry consumption would be relevant only in short distance communication scenarios.
References
Rappaport TS: Wireless Communications: Principles and Practice. 2nd edition. Prentice-Hall; 2002.
Alamouti S: A simple transmit diversity technique for wireless communications. IEEE J Sel Areas Commun 1998, 16(8):1451-1458. 10.1109/49.730453
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Trans Inf Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Nosratinia A, Hunter TE, Hedayat A: Cooperative communication in wireless networks. IEEE Commun Mag 2004, 42(10):74-80. 10.1109/MCOM.2004.1341264
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity--part I: system description. IEEE Trans Commun 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Oruç O, Aygolu U: M-PSK cooperative trellis codes for coordinate interleaved coded cooperation. EURASIP J Wirel Commun Netw 2009, 2009: 11.
Zhao B, Valenti MC: Distributed turbo coded diversity for relay channel. IEE Electron Lett 2003, 39(10):786-787. 10.1049/el:20030526
Zhang Z, Duman TM: Capacity-approaching turbo coding and iterative decoding for relay channels. IEEE Trans Commun 2005, 53(11):1895-1905. 10.1109/TCOMM.2005.858654
Hu J, Duman TM: Low density parity check codes over wireless relay channels. IEEE Trans Wirel Commun 2007, 6(9):3384-3394.
Karkooti M, Cavallaro JR: Cooperative communication using scalable, medium block-length LDPC codes. Proc IEEE Wireless Communications and Networking Conference 2008, 88-93.
Duyck D, Capirone D, Boutros JJ, Moeneclaey M: Analysis and construction of full-diversity joint network-LDPC codes for cooperative communications. EURASIP J Wirel Commun Netw 2010, 2010: 16.
Khormuji M, Larsson E: Cooperative transmission based on decode-and-forward relaying with partial repetition coding. IEEE Trans Wirel Commun 2009, 8(4):1716-1725.
Wicker SB: Error Control Systems for Digital Communication and Storage. 1st edition. Prentice-Hall, Englewood Cliffs; 1994.
Lott C, Milenkovic O, Soljanin E: Hybrid ARQ: theory, state of the art and future directions. Proc IEEE Information Theory Workshop on Information Theory for Wireless Networks 2007, 1-5.
Zhao B, Valenti MC: Practical relay networks: a generalization of hybrid-ARQ. IEEE J Sel Areas Commun 2005, 23(1):7-18.
Krikidis I: Distributed truncated ARQ protocol for cooperative diversity networks. IET Commun 2007, 1(6):1212-1217. 10.1049/iet-com:20070034
Yu G, Zhang Z, Qiu P: Efficient ARQ protocols for exploiting cooperative relaying in wireless sensor networks. Elsevier Comput Commun 2007, 30(14-15):2765-2773.
Zhang C, Wang W, Wei G: Design of ARQ protocols for two-user cooperative diversity systems in wireless networks. Elsevier Comput Commun 2009, 32(6):1111-1117.
Chase D: Code combining--a maximum-likelihood decoding approach for combining an arbitrary number of noisy packets. IEEE Trans Commun 1985, 33(5):385-393. 10.1109/TCOM.1985.1096314
Frenger P, Parkvall S, Dahlman E: Performance comparison of HARQ with chase combining and incremental redundancy for HSDPA. Proc IEEE 54th Vehicular Technology Conference 2001, 3: 1829-1833.
Cheng J-F: Coding performance of hybrid ARQ schemes. IEEE Trans Commun 2006, 54(6):1017-1029. 10.1109/TCOMM.2006.876846
Lee J, Lou H-L, Toumpakaris D, Jang E, Cioffi J: Transceiver design for MIMO wireless systems incorporating hybrid ARQ. IEEE Commun Mag 2009, 47(1):32-40.
Tabet T, Dusad S, Knopp R: Diversity-multiplexing-delay tradeoff in half-duplex ARQ relay channels. IEEE Trans Inf Theory 2007, 53(10):3797-3805.
Cover TM, Thomas JA: Elements of Information Theory. 2nd edition. Wiley; 1991.
Degraf Uchôa A, Souza R, Pellenz M: Novel hybrid ARQ scheme using LDPC codes and partial retransmissions. Proc IEEE Latin-American Conference on Communications 2009, 1-6.
Stanojev I, Simeone O, Bar-Ness Y, You C: Performance of multi-relay collaborative hybrid-ARQ protocols over fading channels. IEEE Commun Lett 2006, 10(7):522-524.
IEEE Standard for Local and metropolitan area networks Part 16: Air Interface for Broadband Wireless Access Systems, IEEE Std 802.16e Std., May 2009.
Cao Y, Gu J, Qi L, Yang D: Degree distribution based HARQ for irregular LDPC. IEE Electron Lett 2006, 42(6):363-364. 10.1049/el:20063676
Li X, Cao Y, Yang D: An improved degree distribution based HARQ for LDPC. Proc International Conference on Wireless Communications, Networking and Mobile Computing 2006, 1-4.
Inaba Y, Saito T, Ohtsuki T: WLC16-2: Reliability-based hybrid ARQ (RB-HARQ) schemes using low-density parity-check (LDPC) codes. IEEE Global Telecommunications Conference (GLOBECOM), December 2006 1-5.
Huang F, Yi X, Wang T: Reliability-based selective repeat hybrid ARQ protocol on low density parity check codes. 16th International Conference on Artificial Reality and Telexistence (ICAT), December 2006 576-579.
Cavers J: An analysis of pilot symbol assisted modulation for rayleigh fading channels [mobile radio]. IEEE Trans Veh Technol 1991, 40(4):686-693. 10.1109/25.108378
Haykin S, Moher M: Modern Wireless Communication. Prentice-Hall, Inc.: Upper Saddle River, NJ; 2004.
Cui S, Goldsmith A, Bahai A: Energy-constrained modulation optimization. IEEE Trans Wirel Commun 2005, 4(5):2349-2360.
Acknowledgements
This work was partially supported by CNPq and CAPES (Brazil) under grants 147375/2010-0 and 472357/2010-7. This paper was presented, in part, at the 21st Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC 2010).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
de Oliveira Brante, G.G., Souza, R.D. & Pellenz, M.E. Cooperative partial retransmission scheme in incremental decode-and-forward relaying. J Wireless Com Network 2011, 57 (2011). https://doi.org/10.1186/1687-1499-2011-57
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-57