Abstract
Background
The Hospital Anxiety and Depression Scale (HADS) is commonly used to assess symptoms of anxiety and depression in motor neurone disease (MND). The measure has never been specifically validated for use within this population, despite questions raised about the scale's validity. This study seeks to analyse the construct validity of the HADS in MND by fitting its data to the Rasch model.
Methods
The scale was administered to 298 patients with MND. Scale assessment included model fit, differential item functioning (DIF), unidimensionality, local dependency and category threshold analysis.
Results
Rasch analyses were carried out on the HADS total score as well as depression and anxiety subscales (HADS-T, D and A respectively). After removing one item from both of the seven item scales, it was possible to produce modified HADS-A and HADS-D scales which fit the Rasch model. An 11-item higher-order HADS-T total scale was found to fit the Rasch model following the removal of one further item.
Conclusion
Our results suggest that a modified HADS-A and HADS-D are unidimensional, free of DIF and have good fit to the Rasch model in this population. As such they are suitable for use in MND clinics or research. The use of the modified HADS-T as a higher-order measure of psychological distress was supported by our data. Revised cut-off points are given for the modified HADS-A and HADS-D subscales.
Similar content being viewed by others
Introduction
The Hospital Anxiety and Depression Scale (HADS) [1] is a reliable and potentially valid [2, 3] measure for detecting depression and anxiety. The scale was designed to exclude measurement of somatic symptoms in medical outpatients; making it potentially suitable for use with motor neurone disease (MND) patients.
Due to the scale's apparent suitability, the HADS has been widely used in MND research for assessing states of anxiety and depression [4–7]. However, questions have been raised as to the suitability of the HADS depression subscale with MND patients as two previous studies [6, 7] have omitted item D8 "I feel as though I am slowed down", on the reasonable assumption that responses to this item would be confounded by physical impairment. Whilst this change had clinical and face validity, in neither study was it accompanied by appropriate statistical or psychometric analysis to justify the alteration.
The Rasch model [8], a modern psychometric approach, ensures that the fundamental scaling properties of an instrument are assessed alongside traditional psychometric assessments of reliability and construct validity. The model operationalises the formal axioms of measurement [9] (order, unidimensionality and additivity), so allowing interval level data to be obtained from questionnaires. Rasch validation of the HADS has been proven useful in other clinical settings, such as rehabilitation [10] and Parkinson's disease [11].
The current study is a modern psychometric assessment of the HADS anxiety (HADS-A) and depression (HADS-D) subscales to assess the dimensionality, item suitability, reliability, scaling assumptions and internal consistency of the scales for use with MND patients. The analysis included evaluation of differential item functioning (DIF) by gender and age. In addition, the HADS total score (HADS-T) was investigated as a potentially valid measure of psychological distress in this population.
Methods
Main data collection
The psychometric and scaling properties of the HADS were assessed among 298 patients recruited from five regional MND care centres in the United Kingdom: The Walton Centre for Neurology and Neurosurgery in Liverpool, Preston Royal Hospital, Oxford John Radcliffe Hospital, Salford Hope Hospital, and Sheffield Royal Hallamshire Hospital. Participants all had a diagnosis of MND from a neurologist with expertise in MND. Patients were unselected for age, sex, and disease presentation or disability status. Questionnaires were either handed out during a routine clinic appointment or sent to the patients' home over a period of twelve months, along with a newsletter describing the research activities of their local care centre. Where patients were unable to complete the questionnaires by themselves a nurse or caregiver was allowed to act as a scribe. Informed consent was given by each participant.
Ethical permission was granted for this study from relevant hospital committees in the U.K. (Hammersmith 05/Q0401/7 and Tayside 07/S1402/64), and local research governance committees at all participating sites.
Rasch Analysis
To evaluate the scaling properties and construct validity of the HADS, the Rasch measurement model was used [8]. Rasch analysis is a probabilistic mathematic modelling technique used to assess properties of outcome measures. Where data are shown to accord with model expectations, the internal construct validity of the scale is supported, and a transformation of ordinal data to interval scaling is possible [12].
For Rasch analysis, sample sizes requirements are influenced by scale targeting. For a scale that is well targeted (i.e. 40-60% endorsement rates for dichotomous items), a sample size of 108 will give accurate estimates of person and item locations (99% confidence of locations being within 0.5 logits). A sample size of 243 will provide accurate estimations of items and person locations irrespective of scale targeting [13].
Analyses used to assess whether the scale conformed to Rasch model expectations are briefly explained below. A comprehensive review with a more detailed explanation of the Rasch analytical process may be found elsewhere [10].
Rasch Unidimensional Measurement Model 2020 (RUMM2020) software (Version 4.1, Build 194) was used for the Rasch analyses presented in this study [14].
1) Fit to the Rasch model
Rasch model fit is primarily indicated by a non-significant fit statistics, indicating that the scale does not deviate from model expectations. For example, both summary and individual item chi-square statistics should be non-significant, after adjusting for multiple testing. In addition, both person and item fit are assessed by their residual mean values. This examines the differences between the observed data and what is expected by the model for each person and each item estimate. At the summary level perfect fit is represented by a mean of zero and a SD of ± 1, while at the individual level for persons and items, a residual value between ± 2.5 is appropriate.
2) Item difficulty and person ability
Estimates of a location on a common metric are provided for both persons (ability) and items (difficulty). In the context of the health sciences, 'ability' may be understood to represent the amount the person has of a given symptom, trait or feeling and difficulty may be understood to represent the magnitude of the symptom, trait or feeling represented by the item. For example, an item that reflected the sentiment that life was no longer worth living would be expected to represent a high level of depression when affirmed.
When data from a patient reported outcome scale is analysed through the Rasch model, both the items and persons are calibrated on the same metric that is measured in logits, or log-odds units. This allows for a comparison of the match between patients and items, showing whether or not the scale is well targeted. In the case of dichotomous items measuring depression, a patient with a logit value of zero on the depression scale would have a 50% chance of affirming an item whose level of depression (difficulty) was also at zero logits. A person with a level of depression at +2 logits (high depression) would have an 88% chance of affirming the item located at zero logits, whereas a person at -2 logits (low depression) would only have a 12% chance of affirming that item.
3) Item category thresholds
The Rasch model allows for the analysis of the way in which response categories are understood by respondents. For example, in the case of a Likert style response as used in the HADS, some respondents may have difficulty differentiating between "Never" or "Very Rarely". In instances where there is too little discrimination between two response categories on an item, collapsing the categories into one response option can improve scale fit to the Rasch model.
Furthermore, where the same rating scale structure across items in not supported (i.e. where the distances between category thresholds vary across items) the unrestricted 'partial credit' Rasch polytomous model is used with conditional pair-wise parameter estimation [15].
4) Local dependency
An assumption of the Rasch model is the local independence of items. A good example of this is where two stair climbing items are included in the same scale. If you can climb several flights of stairs unaided, you must be able to climb one flight of stairs. Such items are said to be locally dependent, and are not providing the same information as two independent items. This has the effect of spuriously inflating reliability, as well as affecting the parameter estimates of the Rasch model. This can be identified through the magnitude of residual item correlations, where items with residual correlations above 0.3 are considered to be locally dependent. The problem can be accommodated through the use of testlets, where the locally dependent items are simply added together into one 'super' item [16].
5) Differential item functioning (DIF) [17]
Differential item functioning (DIF) occurs when different demographic or other contextual groups within the sample (e.g. males and females) respond in a different way to a certain question when they have the same level of the underlying attribute. Two types of DIF can be identified; uniform and non-uniform. Uniform DIF would occur, for example, when males respond consistently higher than females on an item, given the same level of depression. Non-uniform DIF would occur, for example, if females selected a higher response option to an item at lower levels of depression, compared to males, but a lower option at higher levels of depression. Differential item functioning is detected using analysis of variance (ANOVA, 5% alpha).
DIF was assessed for 3 contextual factors (called person factors within the Rasch analysis) including Location (Liverpool/Salford/Oxford/Sheffield/Preston), Age (Quartile split between participants, grouped < 55, 55-62,63-70, > 71) and Gender.
6) Person separation index
The Person separation index (PSI) reflects the extent to which items can distinguish between distinct levels of functioning (where 0.7 is considered a minimal value for research use; 0.85 for clinical use) [18]. Where the distribution is normal, the PSI is equivalent to Cronbach's alpha.
7) Unidimensionality
Finally, independent t-tests are employed to assess the final scale for unidimensionality. Two estimates are derived from subsets of items identified by a principal component analysis of the residuals, and the latent estimate of each person (and its standard error) calculated independently for each test. These estimates are then compared and the number of significant t-tests outside the ± 1.96 range indicates whether the scale is unidimensional or not. Generally, where less than 5% of the t-tests are significant this is indicative of a unidimensional scale (or the lower bound of the binomial confidence interval overlaps 5%) [19].
Results
Summary demographic information and questionnaire response by centre is displayed in Table 1. This sample is broadly representative of the U.K. population of patients with MND [6, 7].
HADS-Depression
Initial fit to the Rasch model for the HADS-D subscale was poor (χ2(28) = 59.76 p < 0.01 - see Table 2 HADS-D Initial). Analysis of individual item fit statistics revealed that one item, item D8 "I feel as though I am slowed down" displayed a different level of fit to the other items. Whilst it appeared to have good fit statistics, all other items in the scale displayed classical misfit. Thus item D8 (Slowed down) was quantitatively different. This is an example of 'reverse fit indication' and the removal of item D8 (Slowed down) meant that the remaining 6 HADS-D items provided good fit to the Rasch model, χ2(24) = 39.90 p = 0.02 - see Table 2 HADS-D Final). Scale fit was marginally improved by collapsing disordered response categories for items D2 "I look forward with enjoyment to things" and D14 "I can enjoy a good book or radio or TV programme". Mild misfit was present for item D12 (Enjoyment) though this did not cause misfit to the Rasch model at the scale level and therefore the item was not removed. Analysis of variance tests revealed that all of the modified HADS-D scale items were free from DIF for location, age and sex.
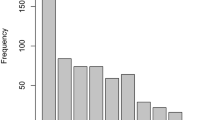
The modified HADS-D exhibited a person separation index of 0.79, which is slightly lower than the suggested value of 0.85 for the scale to distinguish between distinct groups in a clinical setting [18]. But the fit statistic is likely to be affected by the skewed distribution shown in Figure 1.
Individual item statistics for the final HADS-D subscale, along with scoring structure, are given in Table 3.
HADS-Anxiety
Initial fit of the anxiety scale to the Rasch model was poor (see Table 2 HADS-A Initial). Item A11"I feel restless as though I have to be on the move" displayed a high fit residual (4.18) and poor fit to the Rasch model (χ2(4) = 52.27 p < 0.01). Mild local dependency was shown between items A3 "I get a sort of frightened feeling as if something awful is about to happen" and A5 "Worrying thoughts go through my mind" (r = 0.33; p < 0.05). This local dependency was accommodated when the two items were collapsed into a testlet and, for this analysis, they would be considered as a single item. Removing item A11 improved fit to the Rasch model, with the six item solution (which included a pair of grouped items as above) providing acceptable fit statistics (see Table 2 HADS-A Final). Individual item fit statistics for the final HADS-A subscale are given in Table 4. All items in the HADS-A subscale were shown to be free from DIF for age, sex and location.
HADS-Total
The viability of a HADS-T measure was explored by evaluating the scaling and psychometric properties of the 12 items remaining from the HADS-D and HADS-A subscales. Initial fit using the 12 items from the modified HADS-A and HADS-D subscales was unacceptable (χ2(48) = 113.92 p < 0.01, see Table 2 HADS-T Initial). Items D2 and D14 were rescored in the same manner as the HADS-D analysis. Following rescoring items D2 and D14, item D10 appeared to misfit the Rasch model. Removal of item D10 significantly improved fit to the Rasch model. Mild local dependency was present between items from the HADS-A and HADS-D subscales. Items from the HADS-A and HADS-D subscale were made into testlets to reduce the effect of the local dependency. Following this acceptable model fit was achieved (χ2(8) = 12.76, p = 0.12, see Table 2 HADS A Final). Unidimensionality was deemed acceptable with 7.37% (4-10%) of t-tests significant. Person separation index of 0.76 (α Cronbach's 0.78) was below the acceptable level for distinguishing between groups in a clinical context, and could not be explained by any floor effect as per the HADS-D analysis. Figure 2 shows that the HADS-T has a good spread of thresholds, indicating an excellent variation in item 'difficulty'. Item Fit statistics for the HADS-T are given in Table 5. Analysis of variance tests showed that the HADS-T measure of psychological distress was free from DIF by age, sex or location.
Modified cut-off points
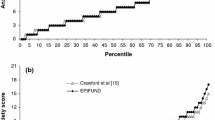
Rasch analysis allows for the transformation of scores between the raw questionnaire scores and post-Rasch estimates. Table 6 shows the relationship between cut-off points suggested by Zigmond and Snaith [1] on their original scale and on the revised scale. Cut off points were originally suggested as 11 or greater for case levels of depression or anxiety, 8-10 for borderline cases and scores of 7 or lower representing non-cases. An example of the process whereby new cut-off points are ascertained for the HADS-A is given in Figure 3. A scale score of 11 (probable anxiety) on the original scale equates to a person location of 0.26 logits on the latent estimate of anxiety. Equating this person location to the revised scale gives a new cut-off point of 9.
For the HADS-T total score of mood disorder, equating tests suggest cut-off points of 17 for 'possible' mood disorder and 21 for 'probable' mood disorder (10).
Table 6 shows that the original HADS-D was slightly overestimating the prevalence of probable (together) depression, which could be driven by the inclusion of the item D8 (slowed down) in the original scale to which 88% of respondents scored highly. Likewise equating scores for the HADS-A subscale revealed that possible and probable levels of anxiety were being overestimated by the original scale due to the inclusion of item A11 "I feel restless as if I have to be on the move". The revised scale also increases the level of 'probable' anxiety while the 'possible' levels fall sharply.
Discussion
The HADS is commonly used in MND clinics and has been used in a number of past studies in MND [4–7]. Rasch analysis of the scale makes an important contribution to current understanding of the measurement properties of the HADS in MND.
The results of our study indicate that the standard 7-item measure of depression should be modified for use in MND due to the confounding effect of item D8 "I feel slowed down" causing overestimation of possible cases of depression in this population. Following the removal of item D8 the HADS-D subscale showed good fit to the Rasch model, including acceptable dimensionality. The removal of this item mirrors alterations made to the HADS-D subscale by other researchers working in MND [6, 7] who felt the item confounded with the high levels of impairment frequently witnessed in the disease. Reliability for the depression subscale in the current study was below the recommended threshold for clinical use [18], and may have been affected by the large floor effect in our sample. A floor effect may be expected when administering a depression scale to a population that have been shown to have a low incidence of depression [20]. Analysis of the person-item distribution for the depression subscale reveals scale information to be maximised around the clinical cut off points, indicating that the floor effect does not impact upon the usefulness of the modified HADS.
In the current study problems were also evident in the original HADS-A, where one item "I feel restless as if I have to be on the move" was found to misfit the Rasch model. The removal of this item yielded a reliable 6-item solution satisfying Rasch model expectations, including the assumption of unidimensionality. The level of reliability of this modified scale makes it suitable for estimation of anxiety states both in clinic or when used in research. It was also shown to be free from item bias by gender, age or location. With the revised cut points for the modified HADS-A, it was shown that the original anxiety subscale overestimate anxiety states.
Previous research has identified that the HADS-D and HADS-A subscales are highly correlated and have suggested that a HADS-T measure could be a single higher order factor corresponding to psychological distress or negative affectivity [3, 21]. This has been statistically supported by some studies [10, 22–24]. Likewise the current study gave support to the use of a modified HADS-T total score as a measure of psychological distress in this population. The low person separation index demonstrated by this scale suggests that it is suitable as a summary scale for research, rather than for clinical use. This may have been as a result of the narrower operational range of the scale caused by removing the effects of local dependency in the data through the testlet design.
The performance of the HADS has been called into question following Rasch analysis in other conditions. In patients with cancer, the HADS requires some modification (removal of items D5, D7 and A6) in order to satisfy the demands of the Rasch model [25]. Likewise, the anxiety item A6 "I feel restless as if I have to be on the move" was also found to misfit the Rasch model when the HADS was tested in a population of 296 musculoskeletal outpatients [10]. In Parkinson's disease the original depression subscale was deemed unsuitable for use and could not be successfully modified to fit the Rasch model [11]. Conversely, in a Chinese sample of stroke patients, the depression subscale of the HADS displayed adequate fit to the Rasch model [26]. The variability of the results of Rasch analyses across a range of diseases suggests that the performance of the HADS may vary by diagnostic group and reinforces the need for clinicians and researchers to formally test the psychometric properties of the instruments they intend to use on different diagnostic groups [27].
For clinical guidance, revised cut-off values are required to indicate clinical case status for depression and anxiety for the new Rasch validated modified scales that have been suggested. Such values are provided for the original scales. We provide these for the new scales by simple mathematical equivalence, accounting for the reduced number of items. While revised values have not been subject to validation by clinical diagnostic interview, the suggested prevalence of case-level depression in our sample (11.1%) is similar to the pooled prevalence estimate of 9.7% (range 9-11) taken from three studies in MND that used DSM-IV criteria for diagnosis of current major depressive episode (MDE) [28–30]. The current study may have been improved by validating the revised cut-off values by clinical diagnostic interview.
These findings support the use of the modified HADS-D and HADS-A for use with patients with MND within clinics and research, and support the modified HADS-T for research use where necessary. All three measures displayed internal construct validity and had no gender or age related item bias.
Conflicts of Interest
The authors declare that they have no competing interests.
References
Zigmond AS, Snaith RP: The Hospital Anxiety and Depression Scale. Acta Psych Scand 1983,67(6):361–370. 10.1111/j.1600-0447.1983.tb09716.x
Bjelland I, Dahl AA, Haug TT, Neckelmann D: The validity of the Hospital Anxiety and Depression Scale: An updated literature review. J Psychosom Res 2002, 52: 69–77. 10.1016/S0022-3999(01)00296-3
Crawford JR, Henry JD, Crombie C, Taylor EP: Normative data for the HADS from a large non-clinical sample. Br J Clin Psychol 2001,40(4):429–434. 10.1348/014466501163904
Goldstein LH, Atkins L, Landau S, Brown RG, Leigh PN: Longitudinal predictors of psychological distress and self-esteem in people with ALS. Neurology 2006,67(9):1652–1658. 10.1212/01.wnl.0000242886.91786.47
Wicks P, Abrahams S, Masi D, Hejda-Forde S, Leigh PN, Goldstein LH: Prevalence of depression in a 12-month consecutive sample of patients with ALS. Eur J Neurol 2007,14(9):993–1001. 10.1111/j.1468-1331.2007.01843.x
Goldstein LH, Atkins L, Leigh PN: Correlates of quality of life in people with motor neuron disease (MND). Amyotroph Lat Sclerosis 2002,3(3):123–129. 10.1080/146608202760834120
Abrahams S, Goldstein LH, Al-Chalabi A, Pickering A, Morris RG, Passingham RE, Brooks DJ, Leigh PN: Relation between cognitive dysfunction and pseudobulbar palsy in amyotrophic lateral sclerosis. J Neurol Neurosurg Psychiatry 1997, 62: 464–472. 10.1136/jnnp.62.5.464
Rasch G: Probabilistic models for some intelligence and attainment tests. Chicago: The University of Chicago Press; 1960.
Karabatsos G: The Rasch model, additive conjoint measurement, and new models of probabilistic measurement theory. J Appl Meas 2001,2(4):389–423.
Pallant JF, Tennant A: An introduction to the Rasch measurement model: An example using the Hospital Anxiety and Depression Scale (HADS). Br J Clin Psychol 2007,46(1):1–18. 10.1348/014466506X96931
Forjaz MJ, Rodriguez-Blázquez C, Martinez-Martin P: Rasch Analysis of the Hospital Anxiety and Depression Scale in Parkinson's Disease. Movement Disord 2009,24(4):526–532. 10.1002/mds.22409
Perline R, Wright BD, Wainer H: The Rasch model as additive conjoint measurement. Appl Psych Meas 1979,3(2):237–256. 10.1177/014662167900300213
Linacre JM: Sample size and item calibration stability. Rasch Meas Trans 1994, 7: 28.
Andrich D, Lyne A, Sheridan B, Luo G: Rasch unitary measurement model 2020 (RUMM2020). RUMM Laboratory Pty: Perth, Australia;
Choppin B: A fully conditional estimation procedure for Rasch model parameters. University of California: Centre for the Study of Evaluation; 1982.
Wainer H, Kiely G: Item clusters and computerized adaptive testing: A case for testlets. J Educ Measurement 1987, 24: 185–202. 10.1111/j.1745-3984.1987.tb00274.x
Holland P, Wainer H: Differential Item Functioning. Philadelphia, PA: Lawrence Erlbaum; 1995.
Fisher W: Reliability Statistics. Rasch Meas Trans 1992, 6: 238.
Tennant A, Pallant JF: Unidimensionality matters (a tale of two Smiths?). Rasch Meas Trans 2006, 20: 1048–1051.
Ferentinos P, Paparrigopoulos T, Rentzos M, Zouvelou V, Alexakis T, Evdokimidis I: Prevalence of major depression in ALS: Comparison of a semi-structured interview and four self-report measures. Amyotrop Lat Scler 2011,12(4):297–303. 10.3109/17482968.2011.556744
Smith AB, Selby PJ, Velikova G, Stark DP, Gould A, Cull A: Factor analysis of the Hospital Anxiety and Depression Scale from a large cancer population. Psychol Psychother Theor Res Pract 2002,75(2):165–176. 10.1348/147608302169625
Martinus J, Leentjen AF, Visser M, Stiggelbout AM, van Hilten JJ: Evaluation of the hospital anxiety and depression scale in patients with Parkinson's disease. Clin Neuropharmacol 2002,25(6):318–324. 10.1097/00002826-200211000-00008
Razavi D, Robaye E: Screening for adjustment disorders and major depressive disorders in cancer in-patients. Br J Psychiatry 1990, 156: 79–83. 10.1192/bjp.156.1.79
Martin CR, Tweed AE, Metcalfe MS: A psychometric evaluation of the hospital anxiety and depression scale in patients diagnosed with end-stage renal disease. Br J Clin Psychol 2004,43(1):51–64. 10.1348/014466504772812968
Smith AB, Wright EP, Rush R, Stark DP, Velikova G, Selby PJ: Rasch analysis of the dimensional structure of the Hospital Anxiety and Depression Scale. Psychooncology 2006,15(9):817–827. 10.1002/pon.1015
Tang WK, Wong E, Chiu HFK, Ungvari GS: Rasch analysis of the scoring scheme of the HADS Depression subscale in Chinese stroke patients. Psychiatry Res 2007,150(1):97–103. 10.1016/j.psychres.2006.01.015
Lamberts S, Pallant JF, Girgis A: Rasch analysis of the Hospital Anxiety and Depression Scale among caregivers of cancer survivors: implications for use in psycho-oncology. Psychooncology 2010, in press.
Johnston WS, McFarland BH, Tolle SW, Lee MA: Attitudes of patients with amyotrophic lateral sclerosis and their caregivers towards assisted suicide. N Engl J Med 1998, 339: 967–973. 10.1056/NEJM199810013391406
Wagner GJ, del Bene M: Resilience and distress among amyotrophic lateral sclerosis patients and caregivers. Psychosom Med 2000,62(2):271–279.
del Bene, Tider T, Rowland LP, et al.: Prevalence of depressive disorders and change over time in late-stage ALS. Neurology 2005,65(1):62–67. 10.1212/01.wnl.0000167187.14501.0c
Acknowledgements and funding
Research nurses involved in the study: Robert Addison-Jones, Pauline Callagher, Samantha Holden, Hannah Hollinger, Elizabeth Johnson, Rachael Marsden,. Dave Watling and the Walton Centre Clinical Trials Unit staff. This research was supported by The Walton Centre Neurological Disability Fund and the Motor Neurone Disease Association U.K. We would particularly like to thank the patients and carers who graciously gave of their time to participate in the study.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
CJG collected data, conducted analyses and is the primary author of this paper.
EWT assisted in study design and authoring of the paper. Co-grant holder.
RJM provided expert review and assisted in study design and editing.
JE, JDM, PJS and KT facilitated data collection in the MND care centres they run.
AT provided expert statistical advice regarding Rasch analysis.
CAY assisted in study design, authoring, collection of data and editing. Primary grant holder.
All authors read and approved the final version of this manuscript.
John D Mitchell contributed equally to this work.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gibbons, C.J., Mills, R.J., Thornton, E.W. et al. Rasch analysis of the Hospital Anxiety and Depression Scale (HADS) for use in motor neurone disease. Health Qual Life Outcomes 9, 82 (2011). https://doi.org/10.1186/1477-7525-9-82
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1477-7525-9-82