Abstract
Background
A warm and humid climate triggers several water-associated diseases such as malaria. Climate- or weather-driven malaria models, therefore, allow for a better understanding of malaria transmission dynamics. The Liverpool Malaria Model (LMM) is a mathematical-biological model of malaria parasite dynamics using daily temperature and precipitation data. In this study, the parameter settings of the LMM are refined and a new mathematical formulation of key processes related to the growth and size of the vector population are developed.
Methods
One of the most comprehensive studies to date in terms of gathering entomological and parasitological information from the literature was undertaken for the development of a new version of an existing malaria model. The knowledge was needed to allow the justification of new settings of various model parameters and motivated changes of the mathematical formulation of the LMM.
Results
The first part of the present study developed an improved set of parameter settings and mathematical formulation of the LMM. Important modules of the original LMM version were enhanced in order to achieve a higher biological and physical accuracy. The oviposition as well as the survival of immature mosquitoes were adjusted to field conditions via the application of a fuzzy distribution model. Key model parameters, including the mature age of mosquitoes, the survival probability of adult mosquitoes, the human blood index, the mosquito-to-human (human-to-mosquito) transmission efficiency, the human infectious age, the recovery rate, as well as the gametocyte prevalence, were reassessed by means of entomological and parasitological observations. This paper also revealed that various malaria variables lack information from field studies to be set properly in a malaria modelling approach.
Conclusions
Due to the multitude of model parameters and the uncertainty involved in the setting of parameters, an extensive literature survey was carried out, in order to produce a refined set of settings of various model parameters. This approach limits the degrees of freedom of the parameter space of the model, simplifying the final calibration of undetermined parameters (see the second part of this study). In addition, new mathematical formulations of important processes have improved the model in terms of the growth of the vector population.
Similar content being viewed by others
Background
A warm and humid climate triggers several water-associated diseases, such as malaria [1]. Vector-borne diseases are highly sensitive to global warming and associated changes in precipitation [2]. Malaria is strongly influenced by warm and moist tropical atmospheric conditions [3]. Temperatures in Africa lie above the threshold for parasite development and the rainy seasons lead to a rapid increase of the mosquito population.
At the beginning of the 20th century, Ross was the pioneer who developed the first mathematical model of malaria transmission [4]. Since Ross' work, numerous mathematical malaria models have been developed. One of the most accepted models of malaria transmission dynamics and immunity to date is that of the Garki project [5]. The development of malaria models is hampered when key parameter values are uncertain. For example, so far no general value or satisfying functional relation has been found for the adult mosquito survival probability observed in nature. Most older malaria models further leave out the generation of a variable size of the mosquito population.
Meteorological variables turn out to be useful explanatory variables for the simulation of malaria [6]. Various biological processes depend on temperature, rainfall, and humidity conditions [7]. Climate- or weather-driven malaria models, therefore, allow for a better understanding of the dynamics of malaria transmission. More recently, the construction of dynamic vector models enabled the simulation of a time-dependent mosquito population [8, 9].
Hoshen and Morse [10] introduced a weather-driven mathematical biological model of malaria parasite dynamics, known as the Liverpool Malaria Model (LMM; see Figure 1 for an illustrative outline of the newly developed LMM version). The LMM comprises weather-dependent within-vector stages as well as weather-independent within-host stages. On a daily basis, the size and behaviour of the total mosquito population and malaria prevalence within human hosts are simulated. The LMM entails the combination of many separate sub-models, each with its own parameterization (see Table 1). The LMM can be used for the understanding of the process of malaria transmission, for mapping purposes, the seasonal forecasting of malaria [11, 12], as well as the assessment of the impact of climate change on the disease [13].
Components of the LMM. Illustration of various components of the LMM version of 2010. Blue and red arrows depict the rainfall and temperature dependence of various parts of the model, respectively. The fuzzy logic approach of the oviposition as well as the immature mosquito survival are displayed by pink arrows. Note that abbreviations of model parameters are explained in Table 1.
A prerequisite for realistic simulations using malaria models is an optimal set of parameter settings. At the present time, numerous malaria models, including the LMM, are partly based on fairly qualitative assumptions. An optimal set of parameter settings has often not been explored and the models are usually not extensively validated against entomological and parasitological field observations. In the case of the LMM, biological processes were handled somewhat heuristically [10]. The present study aimed to define an optimal parameter setting based on the literature and an improved mathematical formulation of the LMM (this paper), as well as an extensive validation and calibration of the LMM against field studies using quality checked meteorological data as input (second paper [14]). According to Hoshen and Morse [10], the application of the LMM is limited to epidemic malaria areas, as the inclusion of immunity was not part of the model structure. However, it will be shown that the LMM can also be used for endemic malaria areas, where large parts of the population exhibit immunity to infection and disease. The present study illustrates that the refined version of the LMM simulates realistic transmission rates for epidemic as well as endemic malaria areas.
The present study was conducted under the umbrella of the IMPETUS project (Integrated Approach to the Efficient Management of Scarce Water Resources in West Africa) [15] and is probably one of the most comprehensive studies to date in terms of gathering knowledge from the literature. Due to the extensiveness of the study, it is split into two parts. In the first part of this study (this paper), changes of the mathematical formulation, which were introduced to better simulate known physical relationships, are described. Further, in this paper the LMM parameter settings are reassessed by means of an extensive literature survey. In the second part [14], meteorological data and malaria observations from West Africa are used for the final calibration of model parameters that lack data from the literature. It will be demonstrated that the calibration by means of field data, results in realistic simulations of disease transmission.
Methods
Literature review of entomological and parasitological malaria variables
In terms of malaria modelling, entomological and parasitological data are of particular interest since malaria models have to undergo some form of validation procedure. Information regarding different malaria variables was required for the refinement of the LMM parameter settings. Numerous published malaria observations were extracted from the literature such as from review articles. Data were gathered for the gametocyte prevalence, which is the percentage of humans with gametocytes in their blood. Articles were reviewed in terms of the mosquito survival probability. Horizontal (controlled conditions) and vertical (field conditions) life tables from various studies furnished data for the daily survival probability of aquatic stages of mosquitoes. Furthermore, data were provided by the literature observing the gonotrophic cycle, the number of eggs per female mosquito, the duration of the immature mosquito stages, the duration until asexual and sexual parasites appear in the blood circulation, and the preference towards humans by Anopheles females. In addition, values for the transmission efficiencies of the malaria parasite between the human and mosquito hosts were searched for in the literature.
Changes of the set of parameter settings
The LMM consists of a number of parameters that have to be set for the simulation of the malaria transmission cycle. In the first part of this study, the parameter settings and mathematical formulation of the LMM is reviewed and refined according to the gathered literature data. Sub-modules of the LMM are modified in order to handle specific model problems. For example, in the current version of the model, too many infective mosquito bites are generated in humid areas such as the equatorial tropics (see Figure Six in [14]). In order to refine the model parameter settings and mathematical formulations, the following strategy was applied: (i) Model parameters lacking numerous literature references such as those related to the gonotrophic or sporogonic cycle were not changed. (ii) Parameters exhibiting various values in the literature were reassessed if possible (bold values and formulations in Table 1). As a result of an extensive literature survey, entomological and parasitological malaria data were gathered. (iii) In the second part of this study [14], uncertain model parameters and those parameters that lack literature references are calibrated.
The strategy was to set as many parameters as possible, in order to simplify the final calibration of the model by means of entomological and parasitological observations from West Africa. The selected procedure significantly reduces the degrees of freedom of the parameter space, and the literature survey ensures a refined setting of individual model parameters.
LMM simulations reveal that various model parameters exert the same effects on the model behaviour [13]. In terms of malaria transmission, for example, the human blood index (a) can be compensated by a lower value of the number of produced eggs per female mosquito (#E p ). For this reason, the final calibration (see [14]) will compensate some uncertain assessments of predefined model parameters.
Changes of LMM modules
The simulation of some key processes is changed in the new LMM version of 2010 (henceforth called LMM2010) to achieve a higher biological and physical accuracy. For example, the process of oviposition, the immature survival probability, as well as the mosquito survival schemes are reviewed. In the original LMM version of 2004 (henceforth called LMM2004), some detailed aspects of parasitological processes as well as age-dependencies of the malaria disease in humans are not included. Some of these aspects are newly introduced in the model.
Results
The LMM simulates the spread of malaria at a daily time resolution, using daily mean temperature (T) and 10-day accumulated precipitation (RΣ10d). For a thorough mathematical formulation of the LMM2004 version the reader is referred to Hoshen and Morse [10]. In this paper, the mathematical formulations of important processes are refined, and parameters of the LMM are reviewed and changed if necessary.
Review of the LMM set of parameter settings and mathematical formulation
Oviposition
A realistic simulation of the size of the mosquito population is a prerequisite for the simulation of malaria transmission in the human population [8, 16–18]. Ovipositioning is dependent on open water bodies that are mostly created by precipitation events. In the LMM2004 version, the number of laid eggs is roughly assumed to be proportional to both the number of ovipositing mosquitoes and to the 10-day accumulated rainfall (RΣ10d). The constant of proportionality is the so-called rainfall laying multiplier (R • ), which couples RΣ10dwith the number of ovipositioning female mosquitoes.
Observations show that the number of produced eggs per female mosquito (#E p ; i.e. the number of eggs/mature oocytes that are found by dissection and/or the oviposition of females) depends on the body size of female mosquitoes [19] as well as on the age of the females [20]. As shown (see Additional file 1) #E p ranges between 5 and 290 eggs [19–21]. For this reason, the LMM2010 version takes into account a realistic number of eggs per Anopheles female (i.e. accounted by #E p and is determined in the second part of this study [14]). However, due to environmental conditions, not all produced eggs are (successfully) oviposited [22, 23].
In the LMM2010, in terms of the deposition of eggs as well as the immature survival a fuzzy logic approach is used: The availability of suitable mosquito habitats is not a simple linear function of rainfall [24]. Certain rainfall regimes will be more suitable, and probably no further breeding sites are provided with increasing rainfall amounts. Various studies have noted that breeding places are washed out by strong rainfall events [24–26]. In fact, rainfall significantly affects larvae by flushing them out of their aquatic habitat and killing them [23]. For these reasons, the LMM2010 uses a simple fuzzy distribution model comparable to Craig et al.[27], which applies RΣ10das input. The general concept is the following: (i) none or a small amount of eggs are oviposited during dry conditions; (ii) more moist conditions lead to a higher proportion of deposited eggs; and (iii) breeding places are washed out by excessive rainfall. The fuzzy logic approach, therefore, differentiates between dry unsuitable conditions (threshold U1), a most suitable condition (S), and again unsuitable conditions due to very high rainfall (threshold U2). Obviously, U1 is set to zero since female mosquitoes are not able to produce progeny without water supply. This fuzzy distribution model might reflect a more physically correct relationship of the egg laying process than the construction with R • used in the LMM2004.
The fuzzy distribution model computes fractions between zero (conditions unsuitable, U1 and U2) and one (condition most suitable, S). The fuzzy suitability (f) of RΣ10dis computed by means of a sigmoidal fuzzy membership curve (see also Figure 2):
Fuzzy distribution model. Illustration of the fuzzy function with regard to the influence of the 10-day accumulated rainfall (RΣ10d) on the number of oviposited eggs per female mosquito (#E o ) as well as the daily immature mosquito survival probability (η d ). The green vertical line at 10 mm (= S) depicts the most suitable rainfall conditions and separates different scales of the abscissa. Pink and blue lines depict two different settings of the fuzzy distribution model. According to these adjustments rainfall condition are unsuitable for RΣ10dvalues of 0 mm (= U1) and above of 500 or 1000 mm (= U2), respectively.
The final number of oviposited eggs per female mosquito (#E o ), which forms the basis of the modelled immature mosquito population, is simply determined by the multiplication of the #E p with the respective value of the fuzzy function (Eq. 1), that is:
Due to the protective effect of houses or the usage of mosquito nets, only a limited number of mosquitoes are able to come into contact with humans. Humans, therefore, can only be exposed to a certain number of biting mosquitoes. Environmental conditions also have an impact on the growth of the mosquito population. Due to the limited flight range of mosquitoes of less than seven kilometres [28] only a limited number of breeding sites are available for Anopheles females. Provided that there are a large number of fertile mosquitoes, the larval densities will increase under such circumstances and will hence produce higher larval mortalities [29–32]. Takken et al.[19] showed that high larval densities lead to a higher mortality and a slower gonotrophic development of adult mosquitoes due to reduced body sizes and, therefore, small nutritional resources.
All the environmental and physical causes, outlined above, are combined in another model parameter limiting the number of fertile mosquitoes. The cap on the number of fertile mosquitoes (CAP) simply restricts the size of the mosquito population to a certain level. Without the application of CAP the growth of the mosquito population is often unrealistically large. Note that the size of the number of fertile mosquitoes is also limited in the LMM2004, where CAP has been set to 10,000. However, CAP will be calibrated to a much lower value in the LMM2010 in the second part of this study [14].
Mosquito Mature Age (MMA)
Immature mosquitoes undergo the egg, larval, and pupal stages until they mature to adult mosquitoes. In the LMM2004, the Mosquito Mature Age (MMA; i.e. the time between the egg stage and adult emergence) is fixed at 15 days. However, field studies in Kenya and Mali showed (see Additional file 2) that on average the time between oviposition and eclosion is about 12 days [33–37]. On this account MMA is reduced from 15 to 12 days in the LMM2010.
Survival of immature mosquitoes
The life cycle of mosquitoes comprises the egg, larval, pupal, and adult stages. The egg, larval, and pupal stages are entirely aquatic and, therefore, mostly depend on weather conditions. Besides climatic conditions, competition due to overcrowding, water quality, food supply, cannibalism, predators, parasites, as well as pathogens are limiting factors for aquatic stages of mosquitoes [23, 32, 34, 38, 39]. In the LMM2004, the daily survival probability of immature mosquitoes (η d ) is only subject to RΣ10dand is calculated as follows:
Therefore, also under small precipitation amounts, a large fraction of larvae outlives the maturation period of 15 days (i.e. the mature age of mosquitoes of the LMM2004). For example, 27.1 and 49.8% of the larvae become adults in the model at a constant RΣ10dvalue of 10 and 20 mm, respectively. However, age distributions from so-called vertical life tables from field studies (see Additional file 2) reveal that a much smaller fraction (2-15%) of deposited eggs emerge to adults [33–35, 37, 40, 41]. By contrast, most laboratory studies prove by means of so-called horizontal life tables (see Additional file 3) that under controlled conditions more than 90% of eggs, larvae, and pupae survive one day [29–32, 36]. The higher laboratory survival is because under controlled conditions various natural factors are eliminated.
In the LMM2010, the calculation of the survival of immature mosquitoes is separated into two parts. In a first step, it is assumed that survival is independent of hydrological conditions. The rainfall-independent daily survival probability of immature mosquitoes (ηd,¬R) is set to 82.5%. This is due to the fact that in general less than 10% of the immature mosquitoes reach the adult stage under field conditions (see Additional file 2) and because the MMA is fixed to twelve days (0.82512 ≈ 0.099). In a second step, the dependence on the hydrological stage is included. For simplicity, the same parameters are used as for the fuzzy logic approach of the oviposition (U1, S, and U2; Table 1). The survival probability of immature mosquitoes is realized by the multiplication of ηd,¬Rwith the fuzzy value:
As a consequence, in the LMM2010 the η d can reach at maximum 82.5% and no more than 10% of the oviposited eggs emerge to adults (i.e. about 5.4% and 0.7% for f = 0.95 and f = 0.8, respectively; f: value of the fuzzy distribution model). This modelling approach again reflects a more physically correct relationship than the original η d equation (see Eq. 3). Note that Pascual et al.[9] used a comparable approach in their model. Larval mortality was simulated as a function of accumulated days with no rain to represent desiccation of breeding sites. What is not considered is the fact that mosquito larvae can benefit from drought conditions such as when streams dry up due the occurrence of numerous pools [42–44]. Also the existence of permanent breeding sites provided by, for example, large ponds, lakes, and rivers is neglected in both versions of the model.
Survival probability of adult mosquitoes (pd)
The age structure of Anopheles females and survival rate exerts a strong influence on the reproduction rate of the mosquito population and the spread of the malaria parasite. Hence, the vector survivorship is of paramount ecological importance for the distribution of malaria [45–49]. The daily survival probability of female mosquitoes (p d ) depends on characteristics of mosquito species, activities of individuals, climatic conditions, the incidence of parasites, predators [50], and the mosquito age [51]. Most of these factors are elusive to observe and are only indirectly taken into account in malaria models. The LMM only considers the weather impact on the vector survivorship. However, there is only limited information available from entomological field campaigns in terms of the dependence of the adult mosquito survival on temperatures. With regard to climate the survival is affected by temperature and the relative humidity [52, 53]. At daily mean temperatures of about 5°C or even lower malaria vectors seem to disappear [27]. The entomological study of Kirby and Lindsay [54] clearly showed that extremely high temperatures above 40°C are often fatal to mosquitoes. Note that for simplicity the LMM uses an exponential model of mortality. Most observed p d values range between about 80 and 95% (see Additional file 4).
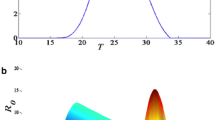
Various daily mosquito survival probability schemes (p d -scheme) were developed with regard to malaria modelling. In the LMM, four different p d -schemes are implemented, these are: the so-called Lindsay-Birley, the Martens I, the Martens II, and the Bayoh scheme (Figure 3). Initially, the LMM was set by the Lindsay-Birley scheme [10, 55]. However, it is not clear whether vector survival per gonotrophic cycle is constant [10]. This p d -scheme is furthermore unrealistic at very high temperatures. Experiments performed by Kirby and Lindsay [54] showed that 50% of Anopheles arabiensis and Anopheles gambiae s.s. are killed at 40°C within at least two hours. In contrast, above 40°C the Lindsay-Birley scheme shows unrealistic high survivorships (cf. Figure 3).
Mosquito survival schemes. Illustration of different schemes regarding the daily mosquito survival (p d ) against the daily mean temperature (T): the Lindsay-Birley (humid (dry) conditions in dashed purple (orange)), the Martens I (red line; derived from [57–59]), the Martens II (green line; given by [27] and [59]), and the Bayoh scheme (blue line; derived from [61]). Crosses (+) denote p d values with regard to different temperature and humidity conditions (see text). In addition, the data basis of the two Martens schemes is inserted as dots (•).
The literature [27, 56] refers to studies published by Martens [57–59]. Martens [59] states (see also [57, 58]): Relying on data reported by Boyd [50], Horsfall [60], and Clements and Paterson [46], a daily survival probability of 0.82, 0.90, and 0.04 at temperatures of 9, 20, and 40°C is assumed, respectively, expressed as:
The so-called Martens I scheme was obviously generated as a polynomial connecting the quoted three data points in the T-p d -diagram (Figure 3) and is based on the following equation:
The formula (Eq. 5) provided by Martens [59] is not used in the LMM2004. However, in the LMM2010 this formula is introduced and forms the so-called Martens II scheme. The main difference between the Martens I and II schemes is the earlier and smoother decrease of p d at temperatures above 25°C in the Martens I scheme.
Taking into account the uncertainty of the so far introduced p d -schemes, further data are needed. Bayoh [61] observed the survival and mortality rates of Anopheles gambiae s.s. in environmental chambers at combinations of temperatures from 0-45°C at 5°C intervals and relative humidities of 40%, 60%, 80%, and 100%. Using the data from these experiments and assuming an exponential model of mortality it is possible to derive p d values. The identified probabilities did not vary considerably with regard to different humidities. For this reason, the probabilities were averaged at each temperature. Finally, the average was used to define a polynomial regarding Anopheles gambiae s.s. survivorship in the laboratory, the so-called Bayoh scheme (Figure 3):
As previously discussed, vector survival is higher in captivity than in the wild and hence p d is generally higher in the Bayoh scheme than in both Martens schemes. It is interesting to note that the Bayoh scheme reveals only a slight decrease of p d between 25 and 35°C. For this reason, the Bayoh scheme agrees better with the Martens II than with the Martens I scheme. On account of these facts the Martens II scheme is utilized for the LMM2010 version.
Various studies point out the importance of the atmospheric humidity on the longevity of adult vectors [58, 62–66]. Relative humidities above 60% seem to be preferred by most vector species. However, it is noted that the crucial factor for the physiology of Anopheles females might be the absolute saturation deficit rather than the relative humidity [67]. The usual dryness of the atmosphere in arid or semi-arid areas such as the Sahel militates against the longevity of mosquitoes and thus reducing malaria transmission [68]. In Niger, for example, Anopheles populations seem to drop steeply around October, when shifts in the prevailing winds drastically reduce humidity. Favourable microclimates become gradually scarcer as the Harmattan conditions establish and the dry season progresses (A. Kiszewsky, personal communication, 2006). In El Salvador, Weidhaas et al.[40] calculated lower adult survival rates for Anopheles albimanus during the dry than during the rainy season. Daily survival was 65-70% and 73-91%, respectively. However, the authors note that the occurrence of breeding outside the study area and the immigration of mosquitoes might be in part responsible for the higher calculated rainy season survival. On account of the possible influence of humidity on vector survival a shift of the dry season mosquito survival probability (pd↓) is introduced in the LMM2010 version and is set in the second part of this study [14]. To simplify matters, pd↓is applied when the 10-day rainfall amount(RΣ10d) is lower than the 10-day accumulated precipitation threshold (R _) that distinguishes between dry and humid weather conditions [10].
Sporogonic cycle
The sporogonic cycle or extrinsic incubation denotes the development of the malaria parasite within the mosquito vector. The development of sporozoites is temperature dependent [7, 69]. There is an uncertainty about the value of the sporogonic temperature threshold (T s ; note that T s refers to the daily average temperature). Lindsay and Birley [63] concluded that the parasite development ceases below temperatures between 14.5 and 16°C for Plasmodium vivax and between 16 and 19°C for Plasmodium falciparum. It is not surprising that the T s data given in the literature are inconsistent. Various publications agree that the T s is located within a certain range [57, 58, 62, 63, 70]. On the other hand a temperature threshold of 18°C is referred to in various publications [1, 10, 71–73], whereas others quote a value of 16°C or even lower [27, 43, 56, 59, 65, 74–81].
The setting of the threshold is particularly important when malaria is modelled in areas with temperatures in the range of T s (e.g., in highlands of East Africa). For temperatures well above T s the length of the sporogonic cycle is much less dependent upon the setting of the lower threshold temperature. Regarding the sporogonic cycle the LMM2004 was set at a threshold of 18°C [10]. However, modelled temperatures or data from weather stations are unlikely to record conditions in the microhabitats where vectors spend most of their time [53, 82]. For example, indoor temperatures in the Usambara mountains (northeast Tanzania) have found to be 2.6°C higher than outdoor air temperatures [83, 84]. By resting in more climatically stable and warmer houses, vectors may avoid cold temperatures and thus the restrictions concerning the progress of the parasite development [64, 70, 85]. Therefore, the effect of altitude might be partly compensated when mosquitoes stay in heated houses [86]. For this reason, the use of 16°C as a temperature threshold for parasite development is used for the LMM2010.
Human blood index (a)
The rate of malaria transmission directly depends on the degree of the host-vector-pathogen contact. Anopheles mosquitoes with a high preference for human blood are considered important vectors of malaria [87]. This fact is expressed in the so-called human blood index (a) that is the proportion of blood meals of a mosquito population obtained from humans rather than animals, for example, cattle.
The assessment of a is a difficult task as it is dependent on the feeding preference of each species, the accessibility of different potential hosts, as well as on the mosquito sampling technique. The calculation of a is most often performed by captures of indoor resting mosquitoes (endophilic females) excluding exophilic mosquitoes feeding on humans [88]. By contrast, a is best estimated by applying the unweighted mean of a part-sample collected from human dwellings and one from other types of resting-place [89]. Kiszewski et al.[81] and Moffet et al.[90] presented median and mean values of a from four and ten African Anopheles vectors, respectively. The major malaria vectors in Africa Anopheles arabiensis, Anopheles gambiae s.s., and Anopheles funestus show fairly high values of a. Except for the mean value of a of Anopheles arabiensis all the median and mean values of these vectors are consistently higher than 80% for these three vectors. For this reason, the LMM2004 value of a of 50% seems to be an underestimation. Due to the fact that the endophily of major African vectors probably was overestimated [88, 91] the value for LMM2010 is approximated by 80%.
Mosquito-to-human transmission efficiency (b)
Not every biting infectious mosquito is able to pass malaria infection by injecting parasites into humans. Unfortunately, the mosquito-to-human transmission efficiency (b; i.e. the proportion of sporozoite-positive mosquito bites infecting susceptible people; see Additional file 5) is a largely undefined parameter [92]. For this reason, this factor is commonly ignored in most malaria models [93]. However, the proportion of actually infective Anophelines is a crucial parameter in the epidemiology and simulation of malaria.
One infectious bite is generally thought to infect about half of immunologically-naive people and this level seems to decrease with the level of endemicity and is age dependent [94]. This transmission efficiency is a function of the exposure history, reflecting effects of immunity [95]. The study of Rickman et al.[96] showed that three (two) out of five non-immune subjects developed malaria parasitaemia after the exposure to one (two) infected mosquito(es) (that means b = 33%). In addition, a total of 44.1% of 68 experimentally infected Anopheles gambiae and 49.2% of 63 infectious Anopheles stephensi transmitted sporozoites in vitro into a sucrose solution [97]. By contrast, surveys of infants revealed fairly low b values. For example, Pull and Grab [98] estimated the value of b as between 1.5 and 2.6%. Indeed, such studies generally ignore superinfection and the fact that adults are bitten more often than children or infants [99]. Superinfection also explains the strong variation of b in children in an urban area of Senegal, where age-corrected Human Biting Rate (HBR) values were used for the analysis of b[91]. The low observed Entomological Inoculation Rate (EIR) values in March led to comparatively high computed b values of about 46%. By contrast, the stronger transmission in June resulted in the calculation of b of only about 8% [91]. In this context it should be noted that there is no reason for the seasonal variation of b. In conclusion, the value of b seems to be generally lower than 50% - the value of the LMM2004 - for most African populations. For this reason, b is approximated as 30% in the LMM2010 version.
Human Infectious Age (HIA)
The transmission of the malaria parasite from humans to mosquitoes is made possible by male and female gametocytes. The duration after infection until mature gametocytes appear in the blood is termed here as the Human Infectious Age (HIA). The duration in days after that a human becomes infectious starting from the mosquito bite is longer than the so-called prepatent period (n p ; i.e. the time needed for the detection of asexual parasites in the blood after the infection of humans). This is due to the time needed for gametocytogenesis (n mf ; i.e. the time needed for the production of male and female gametocytes), which is also called sequestration time, as well as the final maturation period of gametocytes (n m ). Therefore, HIA is computed via HIA = n p + n mf + n m .
Asexual parasites are usually detected by blood slides, which are examined under a microscope. According to microscope detection n p lasts one week or slightly longer (e.g., [100]: eight days). Schneider et al.[101] compared the microscope with the QuanTitative-Nucleic Acid Sequence-Based Amplification (QT-NASBA) detection method. They found that the microscope detection is delayed by one to two days (n p : 8.3 versus 6.0-7.0 days). This is in agreement with the findings of Murphy et al.[102], who cultured asexual parasites from blood taken 6.5-7.0 days after exposure. By contrast, Rickman et al.[96] found a prolonged n p of 14.0-16.5 days from patients without antimalarial immunity. Moreover, a study comparing the Panama, McLendon, and Santee Cooper strain of Plasmodium falciparum revealed mean n p values of 10.3, 13.0 and 9.8 days, respectively [103].
The duration for gametocytogenesis (n mf ) is derived in vitro or from the delay in vivo between the onset of symptoms (e.g., fever) or the detection of asexual parasites and the detection of male and female gametocytes [104]. The values reported in the literature generally range between 7 and 15 days ([105]: about ten days for non-immune subjects; [106]: about twelve days for immune adults; [107]: nine to twelve days; [108]: 7-15 days). Diebner et al.[109] and Eichner et al.[104] more recently estimated the sequestration time from fitting a model to malaria therapy data. According to their studies the time needed for the transition of asexual blood stages of Plasmodium falciparum to mature gametocytes amounts to four to twelve days (mean 7.4 days). It is also shown that sequestration time depends on presence of the parasite strain (geometric mean: 4.9 days for Santee Cooper strain (South Carolina, 1946); 6.2 days for El Limon strain (Panama, 1948); 8.7 days for McLendon strain (South Carolina, 1940)). Eichner et al.[104] concluded that in the former literature the time for sequestration was probably overestimated by the time needed to reach a certain level of gametocytaemia that can be detected by microscopy. However, gametocytes of Plasmodium falciparum do not infect mosquitoes when the mature forms first appear in the blood. The time needed for n m is about one to four days, when these forms of the malaria parasite finally become capacitated [68, 110, 111].
In summary, due to the length of n p (about six to ten days), n mf (four to twelve days), and n m (one to four days) HIA lasts altogether about 11-26 days. For this reason, HIA is approximated as 20 days in the LMM2010, which is five days longer than the LMM2004 value of 15 days (cf. Table 1).
Recovery rate (r)
A low recovery rate (r) of malaria infection is a crucial factor for transmission of malaria. Recovery is affected by the genetic multiplicity of the malaria parasite and is a function of the exposure history, reflecting effects of immunity. Parasite clearance is, therefore, closely related to the age of an individual as well as to the transmission intensity. The former fact was found in data from longitudinal studies from 16 villages in the West African savannah [112]. Daily recovery rates were 0.0045 in infants (< 1 year), fell to a minimum of 0.0016 in young children (1-4 years), and increased again to 0.0194 in the oldest adult age group (≥43 years). The dependence of r on the transmission intensity was found at 30 sites along coastal Kenya. Gu et al.[95] showed that the daily parasite clearance was lower than 0.005 day-1 at one or less infectious bites per year and higher at intensities of ten or more.
The mathematical formulation of the LMM does not account for an individual immune status. As a result, r is independent from transmission intensity or age of an individual in the model, only one single setting of the recovery rate is possible. For this reason, the applied clearance rate represents an age or transmission intensity average. Due to the fact that the LMM2004 does not include superinfection, parasite clearance is related to the elimination of single parasite clones [10]. The recovery rate was originally set to 0.0284 day-1 enabling about 90% of the infected population to clear their infection after 80 days ((1 - r)80 ≈ 0.10). However, estimates from simple infections of Plasmodium falciparum induced in immunologically naive patients for malaria therapy often revealed longer persistence. Patterns of recrudescence survived partly longer than 150 days [100]. In order to partly take into account superinfection, the parasite clearance is significantly decreased in the LMM2010 and is set to 0.005 day-1. In fact, the value of 0.005 day-1 was previously assessed by Macdonald and Gockel [113] and was applied in various malaria models [95, 114]. Note that the reduction of the r value is essential when the LMM is extended to endemic malaria areas.
Gametocyte prevalence (sPR)
The presence of male and female gametocytes in the blood of a human host, the so-called sexual Parasite Ratio (sPR; i.e. gametocytaemia), is a necessary condition for malaria transmission. Gametocytaemia is generally lower than the parasite ratio (PR). Only one annual mean sPR value was found to be higher than 40%, which has been detected by the Reverse Transcriptase-Polymerase Chain Reaction (RT-PCR) (see Additional file 6). In most studies using microscopy less than 15% of the population were detected as gametocyte carriers. In contrast, the majority of studies revealed asexual parasite ratios above 30%.
There is a problem of enumerating gametocytes patterns. Gametocytes are prone to be missed by standard microscopy examination [111, 115]. For example, RT-PCR revealed in comparison with microscopy a 40% higher sPR[116]. Ouedraogo et al.[117] recently found that the QT-NASBA technique provided about 3.3 fold higher estimates of sPR than microscopy. This clearly demonstrates that studies based on the detection of gametocytes by microscopy are rather insensitive and inaccurate in the quantification of gametocytes in blood smears.
Sexual and asexual parasite ratios are generally higher in children than in adults. That is due to the fact that adults better control asexual and sexual parasite densities, and are, therefore, more likely to carry gametocytes at the borderline level of detection [115]. Young children are unlikely to be able to control malaria infections, and likely more parasites turn into gametocytes. In Kenya, Bousema et al.[118] found a decrease in the mean duration of gametocyte carriage with increasing age for asymptomatic children.
The fact that not all infected humans actually carry male and female gametocytes is accounted for in the LMM2010 version. Note that this detailed aspect is not included in the LMM2004. A fraction of gametocyte carriers (GF) is introduced into the model. This fraction stands for the proportion of the population that: (i) is infected by the malaria parasite; (ii) has already passed the human infectious age (HIA); and (iii) is exhibiting a sufficiently high density of gametocytes. These humans are, therefore, the infectors of the human population. Due to the problem of enumerating gametocytes patterns, the GF is set to the comparatively high value of 0.5 in the LMM2010.
Human-to-mosquito transmission efficiency (c)
Not all Anopheles females feeding on gametocyte-infected hosts get infected. Most malaria transmission models have not used direct field estimates of the human-to-mosquito transmission efficiency (c; i.e. the proportion of mosquito bites on infectious humans, which infect susceptible mosquitoes) that is usually termed parameter c in the literature [119].
One factor reducing the infectivity of gametocytes to mosquitoes is transmission-blocking immunity: a specific immunity acquired in humans. Immune factors, ingested with the blood meal, inhibit or block the development of the free sexual stages: gamete, zygote, and ookinete, which have common antigens with gametocytes [120].
The infectiousness of mosquitoes can be determined by using blood from gametocyte carriers. It is either measured by direct skin feeding or by membrane feeding [121]. However, the best method for estimating infectiousness of a human population is to feed laboratory-reared Anopheles on a representative population sample without regard to the presence of gametocytes [122]. Obviously, not all Anophelines feeding on gametocyte-infected hosts become infected. Human-to-mosquito transmission efficiencies are generally lower than 40%, and for the majority of trials infectiousness is higher than 20% (see Additional file 7). Muirhead-Thomson [123] observed that the 'best infectors' infected only about 30% of mosquitoes feeding on them. On the other hand, cryptic gametocytaemia can result in mosquito infections [124]. In the LMM2010 version, c is approximated as 20% in contrast to 50% of the LMM2004, which is located amidst the observed measurements. This means, in combination with the value of GF, that a fraction of 10% of females feeding on gametocyte-infected hosts becomes infected with the parasite in the model.
Issues regarding the age-dependence of malaria
Entomological and parasitological studies clearly identified the age-dependence of malaria in areas of year-round and seasonal malaria transmission. The increase of functional immunity from child- to adulthood leads to an age-dependence of various malaria parameters (these are: PR, sPR, r, b, as well as c). The values differ considerably between children than in adults.
Some individuals are more likely to be bitten than others. Port et al.[99] found that the proportions of feeds upon an individual human are associated with the body surface of the host. Their results from The Gambia revealed a child-to-adult conversion factor of 3.57. Such a heterogeneous biting pattern was also found in a village close to Brazzaville (Congo). Number of bites increased regularly in infants (age: <2 years), children (2-10 years), adolescents (10-20 years), and adults, in proportions of 1:1.93:2.53:3.00 [125] implying a child-to-adult conversion factor of 1.43. Note that averaged proportions of adolescents and adults were used (1.93·1.43 ≈ 2.765 = )
The parameter settings in the present study refer to observations from children, since data values (e.g., that of PR) are mostly available for this population group. This in turn implies that the model output (e.g., PR, HBR, EIR) is again related to that of children. Due to the lack of an age-dependence of the LMM it is assumed that children between 2-10 years (groupC) and the rest of the population (groupR; these are infants, adolescents, and adults) equally contribute to the infectious reservoir of malaria. On that condition an isolated simulation of the malaria transmission based on groupC, groupR, or that of the whole population always results in the same infection level of the mosquito population and after age-adjustment also in the same HBR and EIR values. The LMM simulation is, therefore, henceforth orientated on groupC. For this reason, the host-vector contact is lowered in the LMM2010 version by the adult-child conversion rate (ca→c). Due to findings of Port et al.[99] and Carnevale et al.[125]c a→c is approximated as 0.5, which means that HBR and EIR values for children between 2-10 years are about two times lower than that for adults. This in turn implies that simulated HBR and EIR values must be doubled when they are compared to field observations.
Discussion
The aim of the first part of the present study was the development of a refined parameter setting and mathematical formulation of the LMM (cf. the various components of the LMM2010 outlined by flow charts in Figures 4 and 5). For this reason, key model parameters as well as some modules of the original LMM were reviewed. It was found that the knowledge gathered by entomological and parasitological field research enabled the final setting of most model parameters. Various parameters were, therefore, reassessed by means of an extensive literature survey. The setting of numerous model parameters furthermore reduces the degrees of freedom of the model, which simplifies the final calibration of the model in the second part of this study [14]. In addition, important malaria processes such as the vector survival during aquatic stages were changed in the model to achieve a higher biological and physical accuracy (Figure 4).
Flow chart of the simulation of the mosquito population. Flow chart of various components of the LMM version of 2010 regarding the simulation of the mosquito population. The gonotrophic cycle as well as the development of immature mosquitoes within the aquatic stages are illustrated. Individual states of immature and mature mosquitoes are indicated by black rectangles. The orange rhombi denote decisions within the model as well as implemented functions. Green and red arrows represent a positive and negative affirmation, respectively. The impact of the model drivers is indicated via blue triangles and blue arrows (T: daily mean temperature; RΣ10d: 10-day accumulated rainfall). Note that abbreviations of model parameters are explained in Table 1.
Flow chart of the malaria parasite transmission between humans and mosquitoes. Flow chart of various components of the LMM version of 2010 in terms of the modelling of the malaria parasite transmission between the human and mosquito populations. The sporogonic cycle of infected female mosquitoes is furthermore displayed. Individual states of humans and mosquitoes are indicated by black rectangles. The orange rhombi denote decisions within the model as well as implemented functions. Green and red arrows represent a positive and negative affirmation, respectively. The impact of model drivers is indicated via blue triangles and blue arrows (T: daily mean temperature; RΣ10d: 10-day accumulated rainfall; tr im : trickle of the number of added infectious mosquitoes). Note that abbreviations of model parameters are explained in Table 1.
Most model parameters were set based on data and knowledge currently available in the literature. However, various model parameters lack a precise setting due to variable observed values, which are probably a result of different environmental conditions. As in other malaria models (e.g, [8, 18]), various model parameters were set by a consensus literature value and a parameter range is indicated for most parameters (see Table 1). Comparable with previous studies (e.g., [5, 18]), the remaining undetermined parameters will be calibrated by means of field observations [14]. As mentioned earlier, the final calibration (see [14]) will largely compensate potential inaccurate assessments of the predefined model parameters. Some newly inserted (these are S, U2, #E p , and pd↓; see Table 1 for their explanation) and one old parameter (i.e. CAP) of the LMM2010 were not set due to the lack of (precise) information in the literature. In the second part of this study [14], such parameters are calibrated by means of entomological and parasitological data from West Africa.
One of the most important aspects of malaria transmission is the size of the mosquito population, which strongly depends upon breeding conditions. The relationship between rainfall and larval breeding was treated in a very simple approach in the original version of the LMM. In the current model version, ovipositioning and immature mosquito survival is controlled by the fuzzy distribution model (Figure 4). As will be shown in the second part of this study [14] the fuzzy logic approach seems to be more realistic than the former linear rainfall relationship with regard to the oviposition. In addition, the survival through the aquatic stages was adjusted to the field conditions. In contrast to the LMM2004, the fuzzy distribution model ensures that only a reasonable fraction of oviposited eggs emerge to adults. Note that the fuzzy distribution model is based on qualitative arguments, however, the assumptions seem to be reasonable. Unfortunately, the settings of the required model parameters are not available from the literature. This would require case studies under different rainfall conditions as such from Paaijmans et al.[23]. In the second part of this study, parameter values of the fuzzy distribution model will be calibrated [14].
There are further possible future extensions of the LMM. For instance, a necessity for an improvement of the LMM concerns the dependence of immature development on water temperatures [126]. This would require the incorporation of meteorological variables such as potential evaporation, cloud cover, or sunshine duration [8] as well as information on their relation to water temperatures. The presented adult mosquito survival schemes are not fully satisfactory. Therefore, the incorporation of upcoming new information would be essential for future refinements of the LMM.
Ideally a more complete understanding of the complex ecology of malaria will require integration of research efforts across diverse areas [127]. The present formulation of the LMM actually misses various aspects of malaria. For example, the immune status of the human population as well as age-dependencies are neglected (cf. Figure 5). This would require the inclusion of the exposure history of individuals, which is not possible under the current mathematical formulation of the LMM. This issue of the LMM might be overcome by running the Garki model (see [5]) with EIR data from the LMM provided that the LMM2010 produces reasonable EIR values. The last fact will be shown by the second part of this study [14]. The hybrid LMM-Garki model was utilised by Ermert [13] and enables the simulation of realistic transmission rates between humans and mosquitoes (via the LMM2010) and provides a reasonable pattern of malaria exposure within the human population (via the Garki model).
Conclusions
One of the most comprehensive studies to date in terms of gathering information from the malaria literature was undertaken for the development of a new version of an existing malaria model (Figures 4 and 5). An extensive literature survey with regard to entomological and parasitological malaria variables (see the seven Additional files) provided valuable information for a refined setting of most of the model parameters. This approach limits the degrees of freedom of the parameter space of the model simplifying the final calibration of undetermined parameters. In addition, the simulation of some key processes was changed in order to reflect a more physically correct relationship. For example, the oviposition as well as the survival of immature mosquitoes is now steered via a fuzzy distribution model. In the second part of this study [14], undetermined model parameters will be calibrated and the model simulations are validated by means of entomological and parasitological observations from West Africa.
Abbreviations
- LMM:
-
Liverpool Malaria Model
- LMM2004:
-
Liverpool Malaria Model version of 2004
- LMM2010:
-
Liverpool Malaria Model version of 2010
- QT-NASBA:
-
QuanTitative-Nucleic Acid Sequence-Based Amplification
- RT-PCR:
-
Reverse Transcriptase-Polymerase Chain Reaction. List of symbols: EIR: Entomological Inoculation Rate
- F :
-
fuzzy suitability
- groupC :
-
children between 2-10 years
- groupR :
-
rest of the population (excluding group C)
- HBR :
-
Human Biting Rate
- n m :
-
maturation period of gametocytes
- n mf :
-
time needed for gametocytogenesis
- n p :
-
prepatent period
- PR :
-
Parasite Ratio
- R Σ10d :
-
10-day accumulated rainfall
- sPR :
-
sexual Parasite Ratio
- T :
-
daily mean temperature.
References
Githeko AK, Lindsay SW, Confalonieri UE, Patz JA: Climate change and vector-borne diseases: a regional analysis. Bull World Health Org. 2000, 78: 1136-1147.
Martens WJM, Jetten TH, Focks DA: Sensitivity of malaria, schistomiasis and dengue to global warming. Clim Change. 1997, 35: 145-156. 10.1023/A:1005365413932.
Patz JA, Strzepec K, Lele S, Hedden M, Green S, Noden B, Hay SI, Kalkstein L, Beier JC: Predicting key malaria transmission factors, biting and entomological inoculation rates, using modelled soil moisture in Kenja. Trop Med Int Health. 1998, 3: 818-827. 10.1046/j.1365-3156.1998.00309.x.
Ross R: The prevention of malaria. 1911, London, United Kingdom: John Murray, 2
Dietz K, Molineaux L, Thomas A: A malaria model tested in the African savannah. Bull World Health Org. 1974, 50: 347-357.
Chalvet-Monfray K, Sabatier P, Bicout DJ: Downscaling modeling of the aggressiveness of mosquitoes vectors of diseases. Ecol Model. 2007, 204: 540-546. 10.1016/j.ecolmodel.2007.01.024.
Detinova TS: Age-grouping methods in Diptera of medical importance with special reference to some vectors of malaria. No. 47 in Monograph Series, WHO. 1962
Depinay JMO, Mbogo CM, Killeen G, Knols B, Beier J, Carlson J, Dushoff J, Billingsley P, Mwambi H, Githure J, Toure AM, McKenzie FE: A simulation model of African Anopheles ecology and population dynamics for the analysis of malaria transmission. Malar J. 2004, 3: 29-10.1186/1475-2875-3-29.
Pascual M, Ahumada JA, Chaves LF, Rodó X, Bouma M: Malaria resurgence in the East African highlands: temperature trends revisited. Proc Natl Acad Sci USA. 2006, 103: 5829-5834. 10.1073/pnas.0508929103.
Hoshen MB, Morse AP: A weather-driven model of malaria transmission. Malar J. 2004, 3: 32-10.1186/1475-2875-3-32.
Jones AE: Seasonal ensemble prediction of malaria in Africa. PhD thesis. 2007, University of Liverpool, Liverpool, United Kingdom
Jones AE, Morse AP: Application and validation of a seasonal ensemble prediction system using a dynamic malaria model. J Clim. 2010, 23: 4202-4215. 10.1175/2010JCLI3208.1.
Ermert V: Risk assessment with regard to the occurrence of malaria in Africa under the influence of observed and projected climate change. PhD thesis. 2010, University of Cologne, Cologne, Germany, [http://kups.ub.uni-koeln.de/volltexte/2010/3109/]
Ermert V, Fink AH, Jones AE, Morse AP: A new version of the Liverpool Malaria Model. II. Calibration and validation for West Africa. 2011, [in the Malar J],
Speth P, Christoph M, Diekkrüger B, Bollig M, Fink AH, Goldbach H, Heckelei T, Menz G, Reichert B, Rössler M: Impacts of global change on the hydrological cycle in West and Northwest Africa. 2010, Heidelberg, Germany: Springer, [http://www.springer.com/978-3-642-12956-8]
Ross R: Studies on malaria. 1928, London, United Kingdom: John Murray
McKenzie FE, Killeen GF, Beier JC, Bossert WH: Seasonality, parasite diversity, and local extinctions in Plasmodium falciparum malaria. Ecology. 2001, 82: 2673-2681.
Ahumada JA, Lapointe D, Samuel MD: Modeling the population dynamics of Culex quinquefasciatus (Diptera: Culicidae), along an Elevational Gradient in Hawaii. J Med Entomol. 2004, 41: 1157-70. 10.1603/0022-2585-41.6.1157.
Takken W, Klowden MJ, Chambers GM: Effect of body size on host seeking and blood meal utilization in Anopheles gambiae sensu stricto (Diptera: Culicidae): the disadvantage of being small. J Med Entomol. 1998, 35: 639-645.
Lyimo EO, Takken W: Effects of adult body size on fecundity and the pre-gravid rate of Anopheles gambiae females in Tanzania. Med Vet Entomol. 1993, 7: 328-332. 10.1111/j.1365-2915.1993.tb00700.x.
Hogg JC, Thompson MC, Hurd H: Comparative fecundity and associated factors for two sibling species of the Anopheles gambiae complex occuring sympatrically in The Gambia. Med Vet Entomol. 1996, 10: 385-391. 10.1111/j.1365-2915.1996.tb00761.x.
Koenraadt CJM, Paaijmans KP, Githeko AK, Knols BGJ, Takken W: Egg hatching, larval movement and larval survival of the malaria vector Anopheles gambiae in desiccating habitats. Malar J. 2003, 2: 20-10.1186/1475-2875-2-20.
Paaijmans KP, Wandago MO, Githeko AK, Takken W: Unexpected high losses of Anopheles gambiae larvae due to rainfall. PLoS One. 2007, 2: e1146-10.1371/journal.pone.0001146.
Shaman J, Day JF: Achieving operational hydrologic monitoring of mosquitoborne disease. Emerg Infect Dis. 2005, 11: 1343-1350.
Gimnig JE, Ombok M, Kamau L, Hawley WA: Characteristics of larval anopheline (Diptera: Culicidae) habitats in Western Kenya. J Med Entomol. 2001, 38: 282-288. 10.1603/0022-2585-38.2.282.
Drakeley CJ, Carneiro I, Reyburn H, Malima R, Lusingu JPA, Cox J, Theander TG, Nkya WMMM, Lemnge MM, Riley EM: Altitude-dependent and -independent variations in Plasmodium falciparum prevalence in Northeastern Tanzania. J Infect Dis. 2005, 191: 1589-1598. 10.1086/429669.
Craig MH, Snow RW, le Sueur D: A climate-based distribution model of malaria transmission in sub-Saharan Africa. Parasitol Today. 1999, 15: 105-111. 10.1016/S0169-4758(99)01396-4.
Gillies MT: Studies on the dispersion and survival of Anopheles gambiae Giles in East Africa, by means of marking and release experiments. Bull Entomol Res. 1961, 52: 99-127. 10.1017/S0007485300055309.
Lyimo EO, Takken W, Koella J: Effect of rearing temperature and larval density on larval survival, age at pupation and adult size of Anopheles gambiae. Entomol Exp Appl. 1992, 63: 265-271.
Schneider P, Takken W, McCall PJ: Interspecific competition between sibling species larvae of Anopheles arabiensis and An. gambiae. Med Vet Entomol. 2000, 14: 165-170. 10.1046/j.1365-2915.2000.00204.x.
Gimnig JE, Ombok M, Otieno S, Kaufman MG, Vulule JM, Walker ED: Density-dependent development of Anopheles gambiae (Diptera: Culicidae) larvae in artificial habitats. J Med Entomol. 2002, 39: 162-172. 10.1603/0022-2585-39.1.162.
Munga S, Minakawa N, Zhou G, Mushinzimana E, Barrack OOJ, Githeko AK, Yan G: Association between land cover and habitat productivity of malaria vectors in western Kenyan highlands. Am J Trop Med Hyg. 2006, 74: 69-75.
Service MW: Studies on sampling larval populations of the Anopheles gambiae complex. Bull World Health Org. 1971, 45: 169-180.
Service MW: Mortalities of the larvae of the Anopheles gambiae Giles complex and detection of predators by the precipitin test. Bull Entomol Res. 1973, 62: 359-369. 10.1017/S0007485300003862.
Service MW: Mortalities of the immature stages of species B of the Anopheles gambiae complex in Kenya: comparison between rice fields and temporary pools, identification of predators, and effects of insecticidal spraying. J Med Entomol. 1977, 13: 535-545.
Edillo FE, Touré YT, Lanzaro GC, Dolo G, Taylor CE: Survivorship and distribution of immature Anopheles gambiae s.l. (Diptera: Culicidae) in Banambani village, Mali. J Med Entomol. 2004, 41: 333-339. 10.1603/0022-2585-41.3.333.
Mwangangi JM, Muturi EJ, Shililu J, Muriu SM, Jacob B, Kabiru EW, Mbogo CM, Githure J, Novak R: Survival of immature Anopheles arabiensis (Diptera: Culicidae) in aquatic habitats in Mwea rice irrigation scheme, Central Kenya. Malar J. 2006, 5: 114-10.1186/1475-2875-5-114.
Koenraadt CJM, Takken W: Cannibalism and predation among larvae of the Anopheles gambiae complex. Med Vet Entomol. 2003, 17: 61-66. 10.1046/j.1365-2915.2003.00409.x.
Bayoh MN, Lindsay SW: Temperature-related duration of aquatic stages of the Afrotropical malaria vector mosquito Anopheles gambiae in the laboratory. Med Vet Entomol. 2004, 18: 174-179. 10.1111/j.0269-283X.2004.00495.x.
Weidhaas DE, Breeland SG, Lofgren CS, Dame DA, Kaiser R: Release of chemosterilized males for the control of Anopheles Albimanus in El Salvador. IV. Dynamics of the test population. Am J Trop Med Hyg. 1974, 23: 298-308.
Aniedu I, Mutinga MJ, Mutero CM: Vertical estimates of survivorship of larvae and pupae of Anopheles gambiae Giles complex in Baringo district, Kenya. Insect Science and its Application. 1993, 14: 39-48.
Wijesundera MdS: Malaria outbreaks in new foci in Sri Lanka. Parasitol Today. 1988, 4: 147-150. 10.1016/0169-4758(88)90193-7.
Reiter P: From Shakespeare to Defoe: malaria in England in the Little Ice age. Emerg Infect Dis. 2000, 6: 1-11. 10.3201/eid0604.000431.
Shaman J, Day JF: Reproductive phase locking of mosquito populations in response to rainfall frequency. PLoS One. 2007, 3: e331-10.1371/journal.pone.0000331.
Service MW: Mosquito ecology: field sampling methods. 1976, London, United Kingdom: Elsevier Applied Science
Clements AN, Paterson GD: The analysis of mortality and survival rates in wild populations of mosquitoes. J Appl Ecol. 1981, 18: 373-399. 10.2307/2402401.
Lee HI, Lee JS, Shin EH, Lee WJ, Kim YY, Lee KR: Malaria transmission potential by Anopheles sinensis in the Republic of Korea. Korean J Parasitol. 2001, 39: 185-192. 10.3347/kjp.2001.39.2.185.
McKenzie FE, Baird JK, Beier JC, Lal AA, Bossert WH: A biologic basis for integrated malaria control. Am J Trop Med Hyg. 2002, 67: 571-577.
Scholte EJ, Njiru BN, Smallegang RC, Takken W, Knols BGJ: Infection of malaria (Anopheles gambiae s.s.) and filariasis (Culex quinquefasciatus) vectors with the entomopathogenic fungus Metarhizium anisopliae. Malar J. 2003, 2: 29-10.1186/1475-2875-2-29.
Boyd MF: Malariology. 1949, Philadelphia, USA: WB Saunders Co, 1:
Samarawickrema WA: A study of the age-composition of natural populations of Culex pipiens fatigans Wiedemann in relation to the transmission of filariasis due to Wuchereria bancrofti (Cobbold) in Ceylon. Bull World Health Org. 1967, 37: 117-137.
Macdonald G: Epidemiological basis of malaria control. Bull World Health Org. 1956, 15: 613-626.
Hay SI, Tucker CJ, Rogers DJ, Packer MJ: Remotely sensed surrogates of meteorological data for the study of the distribution and abundance of arthropod vectors of disease. Ann Trop Med Parasitol. 1996, 90: 1-19.
Kirby MJSWL: Responses of adult mosquitoes of two sibling species, Anopheles arabiensis and A. gambiae s.s. (Diptera: Culicidae), to high temperatures. Bull Entomol Res. 2004, 94: 441-448. 10.1079/BER2004316.
Hoshen MB, Morse AP: A model structure for estimating malaria risk. Environmental change and malaria risk - global and local implications, no. 9 in UR Frontis Series. Edited by: Takken W, Martens P, Bogers RJ. 2005, Wageningen, Netherlands: Springer, 41-50.
Hay SI, Omumbo JA, Craig MH, Snow RW: Earth observation, geographic information systems and Plasmodium falciparum malaria in sub-Saharan Africa. Adv Parasitol. 2000, 47: 173-215. full_text.
Martens WJM, Jetten TH, Rottmans J, Niessen LW: Climate change and vector-borne diseases: a global modelling perspective. Glob Environ Change. 1995, 5: 195-209. 10.1016/0959-3780(95)00051-O.
Martens WJM, Niessen LW, Rotmans J, Jetten TH, McMichael AJ: Potential impact of global climate change on malaria risk. Environ Health Perspect. 1995, 103: 458-464. 10.2307/3432584.
Martens WJM: Health impacts of climate change and ozone depletion: an eco-epidemiological modelling approach. PhD thesis. 1997, Maastricht University, Maastricht, Netherlands
Horsfall WR: Mosquitoes: their bionomics and relation to disease. 1955, New York, USA: Ronald Press
Bayoh MN: Studies on the development and survival of Anopheles gambiae sensu stricto at various temperatures and relative humidities. PhD thesis. 2001, University of Durham
Kovats S, Haines A: The potential health impacts of climate change: an overview. Med War. 1995, 11: 168-178.
Lindsay SW, Birley MH: Climate change and malaria transmission. Ann Trop Med Parasitol. 1996, 90: 573-588.
Reiter P: Climate change and mosquito-borne disease. Environ Health Perspect. 2001, 109: 141-161. 10.2307/3434853.
Sachs J, Malaney P: The economic and social burden of malaria. Nature. 2002, 415: 680-685. 10.1038/415680a.
van Lieshout M, Kovats RS, Livermore MTJ, Martens P: Climate change and malaria: analysis of the SRES climate and socio-economic scenarios. Glob Environ Change. 2004, 14: 87-99. 10.1016/j.gloenvcha.2003.10.009.
Wernsdorfer WH, McGregor SI: Malaria - principles and practice of malariology. 1988, Edinburgh, London, Melbourne, and New York: Churchill Livingstone
Macdonald G: The epidemiology and control of malaria. 1957, London, United Kingdom: Oxford University Press
Snow RW, Omumbo JA, Lowe B, Molyneux CS, Obiero JO, Palmer A, Weber MW, Pinder M, Nahlen B, Obonyo C, Newbold C, Gupta S, Marsh K: Relation between severe malaria morbidity in children and level of Plasmodium falciparum transmission in Africa. Lancet. 1997, 349: 1650-1654. 10.1016/S0140-6736(97)02038-2.
Epstein PR, Diaz HF, Elias S, Grabherr G, Graham NE, Martens WJM, Moseley-Thompson E, Susskind J: Biological and physical signs of climate change: focus on mosquito-borne diseases. Bulletin of the American Meteorological Society. 1998, 79: 409-417. 10.1175/1520-0477(1998)079<0409:BAPSOC>2.0.CO;2.
Bouma MJ, Sondrop HE, van der Kaay HJ: Health and climate change. Lancet. 1994, 343: 302-10.1016/S0140-6736(94)91152-5.
Patz JA, Lindsay SW: New challenges, new tools: the impact of climate change on infectious diseases. Curr Opin Microbiol. 1999, 2: 445-451. 10.1016/S1369-5274(99)80078-2.
Patz JA, Reisen WK: Immunology, climate change and vector-borne disease. Trends Immunol. 2001, 22: 171-172. 10.1016/S1471-4906(01)01867-1.
Patz JA, Epstein PR, Burke TA, Balbus JM: Global climate change and emerging infectious diseases. J Am Med Assoc. 1996, 275: 217-223. 10.1001/jama.275.3.217.
Charlwood JD, Smith T, Billingsley PF, Takken W, Lyimo EOK, Meuwissen JHET: Survival and infection probabilities of anthropophagic anophelines from an area of high prevalence of Plasmodium falciparum in humans. Bull Entomol Res. 1997, 87: 445-453. 10.1017/S0007485300041304.
Martens P: How will climate change affect human health?. Am Sci. 1999, 87: 534-541.
Martens P, Kovats RS, Nijhof S, de Vries P, Livermore MTJ, Bradley DJ, Cox J, McMichael AJ: Climate change and future populations at risk of malaria. Glob Environ Change. 1999, 9: S98-S107. 10.1016/S0959-3780(99)00020-5.
Snow RW, Craig M, Deichmann U, Marsh K: Estimating mortality, morbidity and disability due to malaria among Africa's non-pregnant population. Bull World Health Org. 1999, 77: 624-640.
Ikemoto T, Takai K: A new linearized formula for the law of total effective temperature and the evaluation of line-fitting methods with both variables subject to error. Environ Entomol. 2000, 29: 671-682. 10.1603/0046-225X-29.4.671.
Hay SI, Guerra CA, Tatem AJ, Noor AM, Snow RW: The global distribution and population at risk of malaria: past, present, and future. Lancet Infect Dis. 2004, 4: 327-336. 10.1016/S1473-3099(04)01043-6.
Kiszewski A, Mellinger A, Spielman A, Malaney P, Sachs SE, Sachs J: A global index representing the stability of malaria transmission. Am J Trop Med Hyg. 2004, 70: 486-498.
Kovats RS, Campbell-Lendrum DH, McMichael AJ, Woodward A, Cox JS: Early effects of climate change: do they include changes in vector-borne disease?. Philos Trans R Soc Lond B Biol Sci. 2001, 356: 1057-1068. 10.1098/rstb.2001.0894.
Bôdker R: Malaria in the Usambara Mountains, Tanzania. PhD thesis. 2000, Danish Bilharziasis Laboratory, University of Copenhagen, Copenhagen, Denmark
Balls MJ, Bødker R, Thomas CJ, Kisinza W, Msangeni HA, Lindsay SW: Effect of topography on the risk of malaria infection in the Usambara Mountains, Tanzania. Trans R Soc Trop Med Hyg. 2004, 98: 400-408. 10.1016/j.trstmh.2003.11.005.
Koenraadt CJM, Paaijmans KP, Schneider P, Githeko AK, Takken W: Low larval vector survival explains unstable malaria in the western Kenya highlands. Trop Med Int Health. 2006, 11: 1195-1205. 10.1111/j.1365-3156.2006.01675.x.
Malakooti MA, Biomndo K, Shanks GD: Reemergence of epidemic malaria in the highlands of Western Kenya. Emerg Infect Dis. 1998, 4: 671-676. 10.3201/eid0404.980422.
Muriu SM, Muturi EJ, Shililu JI, Mbogo CM, Mwangangi JM, Jacob BG, Irungu LW, Mukabana RW, Githure JI, Novak RJ: Host choice and multiple blood feeding behaviour of malaria vectors and other anophelines in Mwea rice scheme, Kenya. Malar J. 2008, 7: 43-10.1186/1475-2875-7-43.
Diatta M, Spiegel A, Lochouarn L, Fontenille D: Similar feeding preferences of Anopheles gambiae and A. arabiensis in Senegal. Trans R Soc Trop Med Hyg. 1998, 92: 270-272. 10.1016/S0035-9203(98)91005-7.
Garrett-Jones C: The human blood index of malaria vectors in relation to epidemiological assessment. Bull World Health Org. 1964, 30: 241-261.
Moffett A, Shackelford N, Sarkar S: Malaria in Africa: vector niche models and relative risk maps. PLoS One. 2007, 2: e824-10.1371/journal.pone.0000824.
Vercruysse J, Jancloes M, van de Velden L: Epidemiology of seasonal falciparum malaria in an urban area of Senegal. Bull World Health Org. 1983, 61: 821-831.
Nájera JA: A critical review of the field application of a mathematical model of malaria eradication. Bull World Health Org. 1974, 50: 449-457.
Nedelman J: Inoculation and recovery rates in the malaria model of Dietz, Molineaux, and Thomas. Math Biosci. 1984, 69: 209-233. 10.1016/0025-5564(84)90086-5.
Filion GJP, Paul REL, Robert V: Transmission and immunity: the importance of heterogeneity in the fight against malaria. Trends Parasitol. 2006, 22: 345-348. 10.1016/j.pt.2006.06.005.
Gu W, Mbogo CM, Githure JI, Regens JL, Killeen GF, Swalm CM, Yan G, Beier JC: Low recovery rates stabilize malaria endemicity in areas of low transmission in coastal Kenya. Acta Trop. 2003, 86: 71-81. 10.1016/S0001-706X(03)00020-2.
Rickman L, Jones TR, Long GW, Paparello S, Schneider I, Paul CF, Beaudoin RL, Hoffman SL: Plasmodium falciparum-infected Anopheles stephensi inconsistently transmit malaria to humans. Am J Trop Med Hyg. 1990, 43: 441-445.
Beier JC, Davis JR, Vaughan JA, Noden BH, Beier MS: Quantitation of Plasmodium falciparum sporozoites transmitted in vitro by experimentally infected Anopheles gambiae and Anopheles stephensi. Am J Trop Med Hyg. 1991, 44: 564-570.
Pull JH, Grab B: A simple epidemiological model for evaluating the malaria inoculation rate and the risk of infection in infants. Bull World Health Org. 1974, 51: 507-516.
Port GR, Boreham PFL, Bryan JH: The relationship of host size to feeding by mosquitoes of the Anopheles gambiae Giles complex (Diptera: Culicidae). Bull Entomol Res. 1980, 70: 133-144. 10.1017/S0007485300009834.
Collins WE, Jeffery GM: A retrospective examination of the patterns of recrudescence in patients infected with Plasmodium falciparum. Am J Trop Med Hyg. 1999, 61: 44-48.
Schneider P, Wolters L, Schoone G, Schallig H, Sillekens P, Hermsen R, Sauerwein R: Real-time nucleic acid sequence-based amplification is more convenient than real-time PCR for quantification of Plasmodium falciparum. J Clin Microbiol. 2005, 43: 402-405. 10.1128/JCM.43.1.402-405.2005.
Murphy JR, Baqar S, Davis JR, Herrington DA, Clyde DF: Evidence for a 6.5-day minimum exoerythrocytic cycle for Plasmodium falciparum in humans and confirmation that immunization with a synthetic peptide representative of a region of the circumsporozoite protein retards infection. J Clin Microbiol. 1989, 27: 1434-1437.
Jeffery GM, Young MD, Burgess RW, Eyles DE: Early activity in sporozoite-induced Plasmodium falciparum infections. Ann Trop Med Parasitol. 1959, 53: 51-58.
Eichner M, Diebner HH, Molineaux L, Collins WE, Jeffery GM, Dietz K: Genesis, sequestration and survival of Plasmodium falciparum gametocytes: parameter estimates from fitting a model to malariatherapy data. Trans R Soc Trop Med Hyg. 2001, 95: 497-501. 10.1016/S0035-9203(01)90016-1.
Shute PG, Maryon M: A study of gametocytes in a West African strain of Plasmodium falciparum. Trans R Soc Trop Med Hyg. 1951, 44: 421-438. 10.1016/S0035-9203(51)80020-8.
Miller MJ: Observations on the natural history of malaria in the semi-resistant West African. Trans R Soc Trop Med Hyg. 1958, 52: 152-168. 10.1016/0035-9203(58)90036-1.
Hawking F, Wilson ME, Gammage K: Evidence for cyclic development and short-lived maturity in the gametocytes of Plasmodium falciparum. Trans R Soc Trop Med Hyg. 1971, 65: 549-555. 10.1016/0035-9203(71)90036-8.
Day KP, Hayward RE, Dyer M: The biology of Plasmodium falciparum transmission stages. Parasitology. 1998, 116 (Suppl): S95-S109.
Diebner HH, Eichner M, Molineaux L, Collins WE, Jeffery GM, Dietz K: Modelling the transition of asexual blood stages of Plasmodium falciparum to gametocytes. J Theor Biol. 2000, 202: 113-127. 10.1006/jtbi.1999.1041.
Sinden R: Sexual development of malarial parasites. Adv Parasitol. 1983, 22: 153-216. full_text.
Nedelman J: Gametoctaemia and infectiousness in falciparum malaria: observations and models. Advances in Disease Vector Research. 1989, 6: 59-89.
Molineaux L, Gramiccia G: The Garki project, research on the epidemiology and control of malaria in the Sudan Savanna of West Africa. 1980, Geneva, Switzerland: WHO
Macdonald G, Göckel GW: The malaria parasite rate and interruption of transmission. Bull World Health Org. 1964, 31: 365-377.
Macdonald G, Cuellar CB, Foll CV: The dynamics of malaria. Bull World Health Org. 1968, 38: 743-755.
Drakeley C, Sutherland C, Bousema JT, Sauerwein RW, Targett GA: The epidemiology of Plasmodium falciparum gametocytes: weapons of mass dispersion. Trends Parasitol. 2006, 22: 424-430. 10.1016/j.pt.2006.07.001.
Ali E, Mackinnon MJ, Abdel-Muhsin AA, Ahmed S, Walliker D, Babiker HA: Increased density but not prevalence of gametocytes following drug treatment of Plasmodium falciparum. Trans R Soc Trop Med Hyg. 2006, 100: 176-183. 10.1016/j.trstmh.2005.04.021.
Ouédraogo AL, Schneider P, de Kruijf M, Nébié I, Verhave JP, Cuzin-Ouattara N, Sauerwein RW: Age-dependent distribution of Plasmodium falciparum gametocytes quantified by Pfs25 real-time QT-NASBA in a cross-sectional study in Burkina Faso. Am J Trop Med Hyg. 2007, 76: 626-630.
Bousema JT, Gouagna LC, Drakeley CJ, Meutstege AM, Okech BA, Akim INJ, Beier JC, Githure JI, Sauerwein RW: Plasmodium falciparum gametocyte carriage in asymptomatic children in western Kenya. Malar J. 2004, 3: 18-10.1186/1475-2875-3-18.
Nedelman J: Some new thoughts about some old malaria models. Math Biosci. 1985, 73: 159-182. 10.1016/0025-5564(85)90010-0.
Boudin C, Diop A, Gaye A, Gadiaga L, Gouagna C, Safeukui I, Bonnet S: Plasmodium falciparum transmission blocking immunity in three areas with perennial or seasonal endemicity and different levels of transmission. Am J Trop Med Hyg. 2005, 73: 1090-1095.
Bonnet S, Paul RE, Gouagna C, Safeukui I, Meunier JY, Gounoue R, Boudin C: Level and dynamics of malaria transmission and morbidity in an equatorial area of South Cameroon. Trop Med Int Health. 2002, 7: 249-256. 10.1046/j.1365-3156.2002.00861.x.
Boudin C, Robert V, Carnevale P, Ambroise TP: Epidemiology of Plasmodium falciparum in a rice field and a savanna area in Burkina Faso: seasonal fluctuations of gametocytaemia and malaria infectivity. Ann Trop Med Parasitol. 1991, 85: 377-385.
Muirhead-Thomson RC: Factors determining the true reservoir of infection of Plasmodium falciparum and Wuchereria bancrofti in a West African village. Trans R Soc Trop Med Hyg. 1954, 48: 208-225. 10.1016/0035-9203(54)90067-X.
Ross A, Killeen G, Smith T: Relationships between host infectivity to mosquitoes and asexual parasite density in Plasmodium falciparum. Am J Trop Med Hyg. 2006, 75 (Suppl 2): 32-37.
Carnevale P, Frézil JL, Bosseno MF, le Pont F, Lancien J: Etude de l'agressivité d'Anopheles gambiae a en fonction de l'âge et du sexe des sujets humains. Bull World Health Org. 1978, 56: 147-154.
Bayoh MN, Lindsay SW: Effect of temperature on the development of the aquatic stages of Anopheles gambiae sensu stricto (Diptera: Culicidae). Bull Entomol Res. 2003, 93: 375-381. 10.1079/BER2003259.
Colwell RR, Patz JA: Climate, infectious disease and health: an interdisciplinary perspective. Tech. rep., American Academy of Microbiology, Washington, USA. 1998
Jepson WF, Moutia A, Courtois C: The malaria problem in Mauritius: the binomics of Mauritian anophelines. Bull Entomol Res. 1947, 38: 177-208. 10.1017/S0007485300030273.
Nikolaev BP: On the influence of temperature on the development of malaria plasmodia in the mosquito. Leningrad Pasteur Institute of Epidemiology and Bacteriology. 1935, 2: 108-109.
Acknowledgements
We are grateful to numerous people who kindly provided useful data, literature references, or special knowledge. These are: Dr. A. Bomblies from the College of Engineering and Mathematical Sciences(CEMS)/University of Vermont (Anopheles gambiae s.l. larvae and female photos; malaria literature), Dr. M. Craig from the Medical Research Council/Durban (p d literature), Dr. J.-B. Duchemin from the 'Centre de Recherche Médicale et Sanitaire (CERMES)'/Niamey (construction of Figure 1), Dr. C. Drakeley from the London School of Hygiene and Tropical Medicine (gametocytogenesis and c), Prof. Dr. M. Eichner from the Department of Medical Biometry/Tübingen (maturation of gametocytes), Dr. C. Favier from the 'Laboratoire d'Océanographie' et du Climat: Expérimentations et Approches Numériques (LOCEAN)'/Paris (p d discussion), Dr. C. Guerra from the Malaria Atlas Project (PR information), Dr. A. Kiszewski form the Department of Immunology and Infectious Diseases/Harvard University (p d data and pd↓discussion), Dr. S. Louvet from the 'Centre de Recherches de Climatologie (CRC)'/Dijon (malaria literature), as well as Prof. Dr. R. Steffen and M. Funk-Baumann from the Institute of Social and Preventive Medicine/Zürich (references).
This study was part of the IMPETUS West Africa project and was supported by the Federal German Ministry of Education and Research (BMBF) under grant No. 01 LW 06001A in the GLOWA programme and by the Ministry of Innovation, Science, Research, and Technology (MIWFT) of the federal state of North Rhine-Westphalia under grant No. 313-21200200. The support by the EU project AMMA (African Monsoon Multidisciplinary Analysis; funded by the European Commission's Sixth Framework Research Programme through project No. 004089) and the NERC (Natural Environment Research Council) AMMA is gratefully acknowledged by AEJ and APM. Based on a French initiative, AMMA was built by an international scientific group and was funded by a large number of agencies, especially from France, United Kingdom, United States, and Africa. Detailed information on scientific coordination and funding is available on the AMMA international website http://www.amma-international.org. Finally, we wish to thank one anonymous reviewer whose comments helped to greatly improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
VE designed the study, undertook the literature review and proposed changes of the mathematical formulation of the LMM, as well as wrote the manuscript. AHF and APM contributed to the concept of the study. AHF supervised the PhD study of VE whose results formed the basis of the manuscript. APM was furthermore originally involved in the formulation of the LMM. AEJ contributed to the new design of LMM and provided the new model code. All authors read, suggested changes and approved the final manuscript.
Electronic supplementary material
12936_2010_1618_MOESM1_ESM.PDF
Additional file 1: Number of produced eggs per Anopheles female. Data with regard to the number of produced eggs per Anopheles female. (PDF 17 KB)
12936_2010_1618_MOESM2_ESM.PDF
Additional file 2: Data in terms of the development of immature mosquitoes from vertical life tables. Data in terms of the development immature mosquitoes taken from vertical life tables as derived under field conditions. (PDF 17 KB)
12936_2010_1618_MOESM3_ESM.PDF
Additional file 3: Data regarding the development of immature mosquitoes from horizontal life tables. Data regarding the development of immature mosquitoes taken from horizontal life tables as derived under controlled conditions. (PDF 22 KB)
12936_2010_1618_MOESM4_ESM.PDF
Additional file 4: Mosquito survival probabilities. Data with regard to the daily survival probability of adult mosquitoes (p d ) as derived from entomological field studies. (PDF 41 KB)
12936_2010_1618_MOESM5_ESM.PDF
Additional file 5: Mosquito-to-human transmission efficiencies. Data regarding the mosquito-to-human transmission efficiency (b). (PDF 21 KB)
12936_2010_1618_MOESM6_ESM.PDF
Additional file 6: Sexual parasite ratios. Data with regard to the sexual parasite ratio (sPR), that is the percentage of humans with gametocytes in their blood as well as the ratio between sexual and asexual parasite ratio (SAR), which is the proportion of malaria parasite positive humans that are gametocytaemic. (PDF 51 KB)
12936_2010_1618_MOESM7_ESM.PDF
Additional file 7: Human-to-mosquito transmission efficiencies. Data with regard to the human-to-mosquito transmission efficiency (c), i.e. the proportion of mosquito bites on infectious humans which infect susceptible mosquitoes. (PDF 27 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ermert, V., Fink, A.H., Jones, A.E. et al. Development of a new version of the Liverpool Malaria Model. I. Refining the parameter settings and mathematical formulation of basic processes based on a literature review. Malar J 10, 35 (2011). https://doi.org/10.1186/1475-2875-10-35
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1475-2875-10-35