Abstract
Background
Previously, we reported effects of the cryb mutation on circadian rhythms in period and timeless gene expression within isolated peripheral Drosophila tissues. We relied on luciferase activity driven by the respective regulatory genomic elements to provide real-time reporting of cycling gene expression. Subsequently, we developed a tool kit for the analysis of behavioral and molecular cycles. Here, we use these tools to analyze our earlier results as well as additional data obtained using the same experimental designs.
Results
Isolated antennal pairs, heads, bodies, wings and forelegs were evaluated under light-dark cycles. In these conditions, the cryb mutation significantly decreases the number of rhythmic specimens in each case except the wing. Moreover, among those specimens with detectable rhythmicity, mutant rhythms are significantly weaker than cry+ controls. In addition, cryb alters the phase of period gene expression in these tissues. Furthermore, peak phase of luciferase-reported period and timeless expression within cry+ samples is indistinguishable in some tissues, yet significantly different in others. We also analyze rhythms produced by antennal pairs in constant conditions.
Conclusions
These analyses further show that circadian clock mechanisms in Drosophila may vary in a tissue-specific manner, including how the cry gene regulates circadian gene expression.
Similar content being viewed by others
Background
Circadian clocks located within metazoan brains have been a focus of investigation for decades [1–4]. Such clocks are compelling in part because they influence timing across many levels of analysis; they are driven by molecular elements whose concerted output, in the form of neuronal signaling, controls physiology and behavior [5]. Recently, the presence of circadian clocks in peripheral tissues has been established in the fruitfly as well as in lower vertebrates and mammals [6–9]. For example, in Drosophila such clock functions have been demonstrated in antennae, wings, legs, a neuro-humoral gland, and internal excretory structures [6, 10, 11]. But it is unknown whether time-keeping mechanisms are identical wherever clocks are found within an animal. While it appears that the same molecules previously identified as clock components in the brain give rise to clock function in the periphery, it is not yet known whether clock genes and their encoded proteins act and interact in the same manner wherever they are expressed. Similarly, although circadian pacemaker cells in the Drosophila brain have been characterized anatomically as discrete clusters of cells called the Lateral Neurons [12, 13], the identity of clock cells in the tissues we studied is unknown. The same can be said about the function of these clocks: while circadian clock cells in the brain control behavioral rhythms, the biological functions of clocks in peripheral tissues are minimally understood, except perhaps in the case of the antenna [14].
Analysis of genetic and molecular mechanisms underlying circadian clocks in whole animals or isolated tissues is facilitated by the use of molecular reporters, such as firefly luciferase (luc). The use of firefly-luciferase (luc) as a real-time molecular reporter of gene expression has been illustrated in a variety of model systems including cyanobacteria, plants, Drosophila, and mammals [15–18]. This method has proved especially valuable in studies about molecular rhythms because real-time expression of clock genes and other chronobiological factors may be monitored over many daily cycles in vivo [17, 6, 19–21]. Applications of this technique are varied. For example, luc reporters have been employed to identify previously unappreciated genes that are involved in circadian timing [21, 22] as well as to demonstrate the presence of circadian clocks in isolated Drosophila tissues.
We previously employed luc reporting to study the effects of a cryptochrome mutation (cryb), concentrating on clock gene expression in isolated antennal pairs from Drosophila [23]. Earlier studies established that cry encodes a 'deep-brain' element of the photoreceptive pathway to the circadian clock [24–26]. But our study suggested a different role for cry in the periphery, because antennal rhythmicity in mutant specimens was dramatically reduced in constant darkness [23], an effect that is not consistent with the idea that the encoded protein (CRY) functions solely as a photoreceptor for the circadian system [24, 25].
While carrying out those studies, we became aware that there are interesting features of these peripheral rhythms, like the phase of peak expression, for example, that we were unable to compare rigorously amongst body parts. Such concerns motivated us to develop a set of tools for the analysis of circadian rhythms [27]. Here we apply two key features of this analytic package that were unavailable for our earlier report on the effects of cryb in the periphery [23]. First is a method to eliminate nonlinear trends in the data, a potential source of artifact that could affect whether luciferase activity is scored as rhythmic or arrhythmic. Figure 1 illustrates how rhythmicity generated by one antennal pair is extracted from rather weak output by the application of appropriate analytic tools. In addition, the normalization procedure facilitates comparisons between rhythms from different tissues by reducing the scale of the output to a mean of one for each case (see Results). Second, we were not previously able to examine effects of a given variable (genotype, body part) on circadian phase. The application of circular statistics to these data allows us to evaluate such effects.
Effect of detrending and normalization on the analysis of luciferase-reported rhythms. This example is taken from an antennal pair isolated from a BG-luc; cry+ adult. luc activity was recorded for 8 days in constant darkness and at a constant temperature of 27°C. a) The upper panel in this column shows a plot of the raw data given in counts per second of bioluminescence plotted on the ordinate. Samples were recorded hourly as indicated on the abcissa. The dashed line illustrates a trend line defined by the application of a 72 hour low pass filter (see [27] for more detail about this use of filters). The lower panel shows the autocorrelation function for the raw data plotted immediately above. We use the autocorrelation function to detect rhythmicity[23, 27]. Correlation coefficients with range from -1 to 1 appear on the ordinate and the lag is plotted on the abscissa. The shaded area centered around 0 defines a 95% confidence interval. In this case, the shape of the function indicates one rhythmic cycle followed by a decrease, a pattern that suggests the signal is not rhythmic, b) The upper panel in this column shows the detrended and normalized signal obtained from the raw data shown in a). The signal was obtained by dividing each data value by the corresponding value on the trend line for a given time point. The values on the ordinate are given in arbitrary units and vary around a mean of 1 (as described in [27]). The lower panel shows the autocorrelation function for the detrended and normalized signal shown immediately above it. The application of these procedures reveals the presence of significant rhythmicity within the data set shown in a) above. The RI value is the value of the autocorrelation function at the third peak (marked by the asterisk); it indicates the strength of rhythmicity (see Table 1, Materials and Methods and [27] for more detail). The RS value is obtained from the ratio of the RI value to the 95% confidence line. Thus when RS is ≥ 1, the rhythm is statistically significant (see Materials and Methods for more detail). The absence of an asterisk in the lower panel of a) indicates the absence of a third peak in the autocorrelation function for the raw data set.
Our earlier conclusions [23] have been substantially buttressed by the new features of these time-series analyses: With respect to its effects on clock-gene cyclings, the cryb mutation significantly reduces the number of rhythmic antennal pairs, heads, bodies and forelegs (but not wings) compared with cry+ controls. Moreover, we have intensified the analysis of the rhythmic specimens and thus observed that parameters of rhythmicity are altered in the subset of rhythmic mutant specimens. Among the new findings that have emerged from the current analyses, the most salient are that (1) cryb has a significant effect on the phase of clock gene expression in rhythmic peripheral tissues; and (2) in isolated cry+ tissues, the relationship between the peak phase time of luc-reported expression from per and tim genes (respectively) varies such that the peaks are indistinguishable in antennae and they differ significantly in wings or forelegs, for example. The findings reported here strengthen the hypothesis that clock mechanisms in the periphery differ from each other as well as from those operating in the central nervous system of Drosophila [23].
Results
We chose Drosophila strains in which luc was either fused downstream from the 5'-flanking sequence of the clock gene timeless (tim-luc), or downstream from a genomic sequence that spans the 5'-flanking region of the period gene and extends through the N-terminal 2/3 of its coding sequence (BG-luc) [20, 21]. These luc fusion constructs were introduced into the D. melanogaster genome by germ-line transformation and shown to mediate daily cycles of LUC activity over the course of several days' worth of monitoring live (whole) flies fed on luciferin-containing medium [20]. We were able to assess the effects of the cryptochrome mutation on clock-gene expression after carrying out genetic crosses that placed chromosomes bearing the reporter constructs into a homozygous cryb background and comparing the effects of this mutation on LUC temporal patterns to those influenced by the normal cry+ allele [23]. In addition, these controls allowed comparisons of tim-luc to BG-luc expression. Isolated heads, forelegs, bodies, wings and antennal pairs were assayed, although data from the latter tissue-type were essentially the only ones reported [23].
Effects of crybon rhythms in isolated clock tissues under light-dark cycles
We evaluated these various isolated tissues under a series of successive 12-hr-light12-hr-dark cycles (LD 12:12). These environmental conditions are the least likely to reveal deficits in the pattern of clock gene expression because the light-dark cycle provides a dominant stimulus to the clock (clock time is normally synchronized to this environmental cue) and is thought to increase the amplitude of clock gene cycling [20, 28, 29]. Rhythmicity was assessed for each specimen by autocorrelation analysis [30, 27]. This analysis provides a quantitative estimate of rhythmicity with statistical confidence; whereas the confidence interval is based solely on the number of data points used in the analysis without relying on the variability in the data set or any other feature of the measured values, the criterion for statistical confidence is the same for all individual or group analyses within an experiment (see [27] for more detail). In addition, the autocorrelation read-outs may be used in a less stringent (and more subjective) manner to evaluate rhythmicity, based on the shape of a given plot – even when statistical significance is not achieved (see [27] for discussion of this feature of applying autocorrelation). This qualitative criterion is conservative from at least one perspective: If we imagine that cryb's effect might be an elimination of per-luc and tim-luc cyclings (given the mutant's isolation phenotype [21]), elementary scrutiny of correlogram plots increases the chance that data from a given specimen could be judged rhythmic, thereby decreasing the likelihood that we would go overboard in evaluating mutationally induced damage to the clock system. Figure 2 provides an example of why we use a system of qualitative criteria to assess rhythmicity; while the correlogram of a pair of forelegs shown on the top row indicates a statistically significant rhythm, the foreleg pair shown on the bottom row is tabulated as rhythmic even though the correlogram does not achieve statistical significance. In an effort to include any specimen that could be judiciously apprehended as rhythmic, we applied this conservative criterion to obtain the data shown in Tables 1 and 2. We also show our analysis in graphic form for data averaged from each tissue of a given type to illustrate effects of cryb in cases for which only the rhythmic specimens were included (Figures 3 and 4; also see Materials and Methods).
Comparison of tim-luc; cry+ foreleg specimens illustrates rhythmicity with or without statistical significance. From left to right: the first column shows raw data on the ordinate plotted over time on the abcissa, the second column shows detrended and normalized data plotted over time and the third column shows autocorrelation with p = 0.05 confidence interval depicted by a gray area centered at 0. The top row shows the analysis of a pair of forelegs with robust rhythmicity. The autocorrelation function is significantly rhythmic as indicated by the asterisk and the strength of rhythmicity (RI) is 0.52 (see [27]). The bottom row shows a signal with weaker rhythmicity. While the shape of the data plots and the autocorrelation function is consistent with a rhythmic signal, the height of the third peak (with asterisk) fails to achieve statistical confidence. At 0.05, the RI is an order of magnitude weaker than the signal shown in the top row. Nevertheless, this signal is tabulated as rhythmic (see text and [27] for further detail).
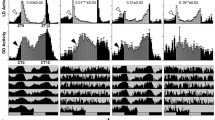
cryb vs. cry+: average BG-luc reported activity in rhythmic isolated body parts. The data shown here were collected under a light-dark cycle (LD 12:12) at a constant temperature of 25°C. The column labeled 'raw data' shows the average plots of luciferase activity for the rhythmic subset of samples as given in Table 1 or Table 2, respectively. Counts-per-second of bioluminescence are plotted on the vertical axis with time in hours given on the horizontal axis. The shaded region around the mean activity line indicates standard error of the mean (SEM). The column labeled 'normalized data' shows plots of the averaged detrended and normalized data as described under Figure 1 (also see Materials and Methods and [27]). The shaded region represents the SEM. Units on the ordinate are arbitrary and the plot is centered around a mean of 1. Time (in hours) is represented on the abcissa. The column labeled 'autocorrelation' shows correlograms for the normalized data. Correlation coefficients are plotted on the ordinate with a range of values from -1 to 1. The gray region centered around 0 describes a 95% confidence interval. The lag of the autocorrelation function is plotted on the abcissa. An asterisk is placed above the third peak of the autocorrelation function. The value at that point defines the Rhythmicity Index (RI), an estimate of the strength of rhythmicity [27, 31]. When the asterisk is not present, the autocorrelation function indicates a lack of rhythmicity. Values for the RI appear in the lower left corner of these plots along with a related number called the Rhythmicity Statistic (RS). The RS value is the ratio of the RI to the absolute value of the confidence line. This metric indicates that the rhythmicity described by the correlogram is statistically significant when the value is ≥ 1 (see Materials and Methods for more detail). The column labeled 'mesa' shows a spectral analysis of the data that provides an estimate of the period [37, 27]. Spectral density is given in arbitrary units on the ordinate and the range of periods we assess is shown on the abcissa. Asterisks are placed over the highest peak shown in a range between 18–30 hours. Although we take this value as the estimate of circadian period, there may be other periodicities present within the horizontal range (the width) of the peak or elsewhere on the plot and these additional rhythmic components are also present in the data. Absence of an asterisk indicates either the absence of a peak or that any peak within the plot occurs outside the circadian range. Note that the autocorrelation plot is used to determine rhythmicity and mesa is used to provide an estimate of the period only when warranted by correlogram (for more details see Materials and Methods and [27]). a.) averaged data for cry+ or cryb antennal pairs. These are assessed for rhythmicity on a specimen by specimen basis as tabulated in Table 2. b.) same as a.) for isolated heads as tabulated in Table 1. c.) same as b.) for isolated bodies. This analysis is continued in Figure 4.
cryb vs. cry+:average BG-luc reported activity in rhythmic isolated body parts continued. All of the details and definitions of the panels in this figure are the same as in Figure 3. d) Averaged data for cry+ or cryb wings. These are assessed for rhythmicity on a specimen by specimen basis as tabulated in Table 1. e)same as d) for isolated forelegs.
The cryb mutation significantly reduced the number of rhythmic specimens for each of the body parts we assayed as measured by both reporters in LD 12:12, with the exception of the wing (see Table 1 and Table 2). Moreover, whereas, on average, all of the luc-reported cycles were significantly rhythmic in a cry+ background, the minor fraction of cryb specimens that appeared rhythmic (based on the shape of the correlogram) were not always significantly rhythmic on average. Mutant rhythmicity that passed muster in that manner was evident for both reporters only in the wing and antennal pairs. In addition, BG-luc; cryb (but not tim-luc; cryb) cycles were significantly rhythmic in the forelegs. Otherwise, the mutation eliminated significant rhythmicity.
We were interested in whether the mutant specimens that retained rhythmicity appeared normal. In this regard, a potentially more informative indication of the cryb effect was provided by the Rhythmicity Index (RI), an estimate of a rhythm's strength that draws on the autocorrelation read-outs (see Tables 1 and 2; see Materials and Methods as well as [27, 31] for further discussion of this parameter). RI values indicated that the strengths of rhythmicity from the LD 12:12 monitorings were significantly lowered by cryb for both reporters and in all of the body parts (Table 1 and Table 2). Thus, the cryb mutation reduces the strength of cycling in these body parts; in other words, these rhythms are less robust than in the cry+ controls.
In Figures 3,4,5,6, plots of average counts for each tissue are presented, based on the rhythmic subset of specimens tabulated in Tables 1 and 2 for LD 12:12. These average signals indicate once again that cryb impinges on clock-gene cyclings. For example, with the exception of the BG-luc-reported wing data shown in Figure 4d, simple inspection of the raw data column suggests that cryb reduces or eliminates such cyclings under LD 12:12 (compare the raw data for cry+ v cryb for example, in Figure 3a, 3b, or 3c). The appearance of rhythmicity in the cryb specimens is mostly revealed after detrending and normalization (see Figures 3,4,5,6 the second column labeled normalized). However, in the case of heads and bodies – for which there were very few rhythmic cryb samples (Table 1) – no rhythmicity is evident in the averaged plots. One explanation for this could be that the separate rhythms are not in phase with one another or are noisy; thus the average may not appear to be rhythmic. Nevertheless, applying autocorrelation to the averaged time-courses revealed daily cyclings to have occurred in all cases except for the average taken from the rhythmic subset of BG-luc; cryb bodies. These results show that rhythmicity is evident in the mean signal as well as when it was initially tabulated on a specimen by specimen basis (see Materials and Methods). Nevertheless, there might not have been agreement between these two views of rhythmicity for any of the tissues (or between different approaches to the analysis of phase as described below). Although it is unlikely that arrhythmic specimens would give rise to a mean rhythm, it is conceivable that rhythmic specimens might give rise to an arrhythmic mean.
cryb vs. cry+: average tim-luc-reported activity in rhythmic isolated body parts. Details and definitions of the panels in the figure are the same as in Figure 3. Experimental conditions are the same as in Figure 3 with the exception that the reporter is tim-luc. The order of presentation is the same as in Figure 3,4: a.) averaged data for cry+ or cryb antennal pairs assessed as rhythmic on a specimen by specimen basis as tabulated in Table 2. b.) and c.) show rhythmic specimens from averaged rhythmic cry+ isolated heads and bodies respectively. Note that there are no rhythmic cryb heads or bodies to analyze because none were found as shown in Table 1. d.) isolated wings as tabulated in Table 1. This analysis is continued in Figure 6.
Output from phase analysis
We measured the time of peak luciferase activity for each of the five daily cycles included in the monitoring and analysis of a given specimen (see Materials and Methods). A mean peak time (per day) was thereby calculated for each specimen, with such a value taken as the representative phase for that specimen. One goal of quantifying the molecular phases was to compare the normal tim-luc time-course values to the BG-luc ones for each tissue in a cry+ genetic background. For this, we used circular statistics [27, 32]. Briefly, the phase of each specimen is plotted as a time point (Figures 7,8). An average vector is calculated based on the distribution of phase points around the unit circle. The angle of the vector corresponds to the mean phase for the group of points, and the magnitude of the vector represents the variability in the phase estimates [32]. The Watson-Williams-Stevens statistic was applied to evaluate whether two such vectors are significantly different from one another [32]. Significant differences were evident in the phase of these two clock genes' cyclical expression under a light-dark cycle, for all tissues except isolated antennal pairs and the heads (see Figure 7) and 8.
Circular phase analysis of luciferase expression in isolated body parts. The left column shows phase comparisons for BG-luc; cry+ (plotted with asterisk) vs tim-luc; cry+ (plotted with open circles). The right column shows BG-luc; cry+ (plotted as asterisk) vs. BG-luc; cryb (plotted as open circles). All of the data shown here were collected in a light-dark cycle (LD 12:12). The time of lights on is indicated as 0 h on the circle. On these plots time moves forward in a counter-clockwise direction. Phase estimates for each rhythmic specimen are plotted just outside the unit circle and a mean vector summarizes the phase of the group with the mean direction indicating the time and the magnitude of the vector indicating the dispersion (variability) of the individual estimates (see Materials and Methods and [27, 32]). The Watson-Williams-Stevens test returns an F-statistic that is used to evaluate whether the vectors are significantly different from one another[32]. Rayleigh's test [27, 32] shows each vector is significantly different (p < 0.05) from the null vector (random distribution) with the exception of the BG-luc; cryb vectors shown on the right for heads and bodies in b and c respectively. Beneath each circular plot the difference in hours is given, followed by the mean time for each vector with the number of specimens, n, in brackets, and a p-value for the comparison, a.) comparisons for isolated antennal pairs, b.) isolated heads, c.) isolated bodies. Number of rhythmic samples for each group are given in Table 1 and Table 2. This analysis is continued in Figure 8.
From similar analyses performed on the BG-luc data in a cry+ vs a cryb background, the mutation was revealed to affect the phase of BG-luc-reported cycling in all tissues except bodies (see Figure 7, and note that there were only 4 or 5 rhythmic BG-luc; cryb samples for analysis of heads and bodies, respectively; and that neither one of the mean vectors representing these samples is significant by Rayleigh's test). Thus cryb 's effect on the phase of these molecular rhythms is as potent as the effect on cycling as such.
The analysis of phase presented in Figure 7 and Figure 8 relies on an average estimate of phase for each specimen and it neglects any variability in the occurrence of peaktime associated with the daily rhythm in bioluminescence. As noted above, the mean vectors depicted within each panel of Figures 7,8 represent a vector average of the individual phase estimates with the direction of the vector indicating the mean time and the length of the vector indicating the variability (dispersion) of the estimates. An alternative analysis, presented in Figures 9,10, preserves the intraspecimen variability. This analysis, called a bivariate analysis [32], represents an individual specimen as a vector in the x-y plane. The position of each point (plotted as an asterisk or an open circle) is determined by the variability of the occurrence of the peak for that individual record. Thus, the points that fall on the diameter of the circle are precisely consistent from day to day, while those falling closer to the origin indicate greater variability. The position of the point within the circle describes the mean peak time for each specimen. In this way, each point indicates the head of a vector that summarizes the phase for a particular specimen. The tail of the vector would connect the point to the origin but we do not plot the vectors this way because the figure would be difficult to interpret. A statistical comparison between the two groups (in this case per-luc v tim-luc or per-luc; cry+ v per-luc; cryb) is obtained by first calculating a mean vector that connects the origin to the center of the cloud of points defined by the respective group and then testing whether or not these representative vectors are different from one another.
Bivariate phase analysis of isolated body parts. These data are the same as shown in Figure 4. The left column shows phase comparisons for BG-luc; cry+ (plotted with asterisk) vs tim-luc; cry+ (plotted with open circles). The right column shows BG-luc; cry+ (plotted as asterisk) vs. BG-luc; cryb (plotted as open circles). The axes for each plot describe an x-y plane with the origin occurring at the center of the unit circle plotted within the plane for reference. The point (0,1) defines the beginning of the subjective day, or time 0. Time moves in a counter clock-wise direction on this circle. Each point denotes the head of a vector that summarizes the phase of an individual specimen. The tail of this vector would extend from the origin to the plotted point, with the direction indicating the mean peak time across cycles and the magnitude (distance from the origin) describing the variability of the peaks for each specimen. However, these tails are not plotted to simplify the appearance of the figure. A mean vector is calculated and fully plotted to show the mean phase time for each group of points as well as the mean variability (indicated by its length). Below each plot: the length of each mean vector is given by r; the mean time of each vector is given by phi and the p-value used to assess whether the phase differs between groups is obtained by Hotelling's two-sample test (for more detail see [32]). This analysis is continued in Figure 10.
Bivariate phase analysis of isolated body parts. See Figure 9 legend for details.
The results shown in Figures 9 and 10 are consistent with those in Figure 7 and 8, but the interpretation of the figures is different. For example, Figure 8e (on the right) shows that the cryb mutation affects the mean peak phase significantly; this difference is evident in the distribution of the mean phase estimates estimates plotted outside the circle on the right in Figures 7,8. When these same luc records are plotted using the bivariate method as shown in Figures 9,10, both the temporal distribution and the intraspecimen variability determine the placement of individual points within the circle (on the right in Figure 10e). The plot in Figure 10e shows much more detail about the rhythmic output generated by each specimen; it is clear that the cry+ forelegs produced a stable rhythm in nearly all of the 33 cases as indicated by the presence of the asterisks on or near the edge of the circle. On the other hand, it is readily apparent from this plot that the 11 rhythmic cryb specimens are more variable in the daily timing of peak phase because more than half of the points representing this group are plotted within the circle, relatively closer to the origin than the cry+ points. Nevertheless, the statistical test that corresponds to the treatment of data depicted in Figures 9,10 only tells us that the phases are different; it is not possible to determine whether this difference comes from the temporal distribution or the variability or a combination of the two. Therefore, the interpretation of these two different phase analyses is that there is a significant effect of cryb on the peak phase of the clock in the foreleg (Figures 7,8) and that there is also an effect of this variant on the mean occurrence of peak phase (Figures 9 and 10).
Effects of crybon antennal rhythms in constant darkness and constant temperature
Temporally varying LUC activity was examined for antennal pairs in constant darkness (DD) to assess whether cryb affects free-running rhythmicity. As noted above, these rhythms may appear to be weaker in constant conditions than under LD 12:12 (see Table 2). Earlier studies have shown that the amplitude of rhythms in DD is reduced compared to LD [20]. These observations could reflect a weakening of synchrony between, for example, the two antennae within a well, or between multiple clock cells within a specimen. But the method for monitoring luc activity can also contribute to the appearance of damping within a record.
Linear as well as nonlinear trends in the data come into play in experiments using luciferase reporter technology [19, 20]. Such artifacts were shown (in one substrate replenishment experiment) to be the result of inevitable depletion of luciferin from the medium surrounding the tissues over time [19]. Removal of these trends quantitatively clarifies the record of bioluminescent activity with regard to any rhythmicity that might be present [27]. The normalization procedure we use (see Figure 1 and [27] for more detail) exposes the rhythm (if one is present) in a manner that is quantifiable without reference to the type of measurement that has been employed (for example, counts-per-second metric on the ordinate of the relevant plots becomes dimensionless). One salutary consequence is that comparisons between groups – differing, for example, by body part-are based on the nature of the rhythmicity per se (independent of tissue-dependent levels of overall reporter expression). Therefore, the use of computational techniques to detrend and normalize the signals permitted us to extract and characterize rhythms for comparative analysis – clearing out other features that were deemed relatively unimportant in terms of the manner by which tissue-type, background genotype, or transgene type would influence the appreciation of these clock-gene cyclings.
As indicated in Table 2, the effects of cryb in DD are consistent with its effects in LD 12:12. In constant conditions, the mutation significantly reduced the number of rhythmic antennal pairs for both reporters. However, degrees of rhythmicity were also impinged on by the conditions alone, in that only the BG-luc; cry+ cycles were significantly rhythmic on average.
From a more quantitative perspective, the mean RI value resulting from the DD monitorings was decreased by an order of magnitude in the cryb mutation compared to cry+ for tim-luc as well as BG-luc activity (see Table 2). This effect of cryb is further underscored by an analogous effect on rhythm amplitude. The measures of mean amplitudes given in Tables 1 and 2 stem from computing the distances (as graphed) from the peak (or trough) to the "mean line" running through plots of the detrended and normalized signals, cryb caused amplitude decrements for the time-courses mediated by expression of both luc-fusion transgene types (Table 2).
This cryptochrome mutation produced dramatic effects on the phase of both reporters in DD: The mean-phase values were estimated to occur more than 7 hours earlier for cryb antennae compared to the cry+ appendages. This effect of cryb indicates that the gene may contribute to regulation of the endogenous phase for the antennal clock. Alternatively, the extreme difference in phase could indicate the loss of synchrony between multiple clock cells within the antennae consistent with the large decrease seen in the RI value. These results suggest that cry may normally play a role in the determination of clock time or, alternatively, that it may act to synchronize clock time between individual clock cells.
Previous studies of cryptochrome's chronobiological role in Drosophila emphasized that CRY may function as a deep brain photoreceptor involved in mediating resetting of the clock by light [26]. Support for this hypothesis came from the observation that locomotor-activity rhythms in cryb flies are unaffected in constant darkness and also maintain rhythmicity under constant light, a condition that causes behavioral arrhythmicity in the wild type [33]. While antennal rhythms of gene expression and of odor sensitivity in DD are significantly attenuated in cryb tissues ([23], unlike locomotor rhythmicity [21]), it remained possible that such effects are due to an altered role of light on the developing clock. To address this possibility, we reared experimental subjects and prepared antennal samples in a temperature cycle (27°C:18°C) in DD and then tested the antennal samples in constant darkness at a constant warm temperature 27° (here called HH – for constant high temperature – to distinguish this experiment from the standard LD rearing->DD tests described above).
As shown in Table 2, the effects of cryb on molecular rhythmicity in HH are similar to what was observed in the LD and (standard) DD monitorings. The number of rhythmic specimens was significantly reduced by the mutation for both BG-luc- and tim-luc-reported rhythms. However, very few of the rhythmic specimens, among either cry+ or cryb antennal pairs, was significantly periodic (see Table 2). Further, unlike what was found in the other conditions, the RI values stemming from the HH test were similar across genotypes and reporters. Similiarly, there was no effect of the cryb mutant on the amplitude of the normalized rhythmic output of our reporters in these experiments (Table 2).
A combined effect of the temperature regimen together with that of cryb was detected on the phase of molecular cycling: A mutationally induced difference of 2.5 hours was observed in HH as opposed to 7 hours in DD. The direction of the cryb-induced phase modification was the same as that observed in DD at a lower temperature. More generally (and aside from the genotypic effect), high:low entrainment, followed by subjecting these isolated appendages to a constant high temperature, caused a phase effect: Peak times of LUC-reported cyclings were shifted 4 or 6 hours earlier in the HH tests – respectively, for BG-luc; cry+ and tim-luc; cry+ antennae – compared with the results of LD rearing and DD monitoring.
Discussion
We have developed a tool kit for the analysis of cyclical data [27] and here have applied it to molecular data involving circadian clocks in isolated tissues of Drosophila. Two features of this approach: the evaluation of rhythmicity and the evaluation of phase, have been emphasized.
The first prominent feature is the application of filters for normalizing and detrending the raw time-course data. Such a preparation may indicate whether or not a rhythmic signal is present, as shown in Figure 1. Subsequent criteria are evaluated by means of the autocorrelation function to determine whether a rhythm is present in the data and, if so, whether it is statistically significant. However, we do not rely on statistical significance as an absolute test of rhythmicity. On the one hand, statistical confidence provides a quantitative standard that removes investigator bias; on the other hand, biological signals can fail this test while still displaying the features of rhythmicity. We have adopted a strategy for addressing this complexity based on several criteria as discussed in the companion paper [27]. The overall approach is somewhat subjective, yet it is systematic and does not rely on an arbitrary decision about periodicity in the data. We evaluate each record – blind to treatment or genotype – as raw data or normalized/detrended data. If the shape of the autocorrelation function displays periodicity (a sinusoidal pattern) in the circadian range, we accept the presence of rhythmicity and quantify the strength of the rhythm using the RI value. In addition, we keep track of which samples are significantly rhythmic and which samples are not with the RS metric (see Tables 1 and 2 for examples). Although we go into this matter more thoroughly in the companion paper, we reiterate here that this subjective use of the autocorrelation function to establish rhythmicity is not unprecedented; in fact, it has been recommended as a valid approach to situations like our experiments where the number of data points is relatively small [30]. In general, it must be noted that the use of both tabulated and averaged data also supports this approach. For example, the average of the RI values given for the rhythmic per-luc antennal samples in LD as indicated in Table 2 is lower than the RI values shown for the mean signal presented in Figure 3a. This difference occurs because the rhythmicity expressed by individual samples within the respective groups is similar and the averaging process (portrayed in the plotted data shown in Figure 3a) tends to strengthen the rhythms in question and to eliminate idiosyncracies within a given record.
Thus, we have quantified how the cryb mutation affects molecular rhythmicity in two ways. First, it reduces the number of rhythmic peripheral-tissue specimens in all cases, except – and most intriguing – for the wing. Second, even when only the rhythmic cryb versus cry+ specimens are considered, the former genotype causes a significant reduction of RI values, with the exception of antennal pairs whose molecular time-courses were monitored at constant temperature.
A variety of claims have been made about the phase of clock gene expression in various tissues and cell types. While immunohistochemical studies have suggested that the course of wild-type per cycling may differ between photoreceptors and neurons in the central brain [34], molecular studies have suggested that there is no difference between the phase of per mRNA cycling in photoreceptors vs. the rest of the head (35). The interpretation of such studies is complicated by the inability to assess phase over several cycles within a specimen. However, even when such measurements have been facilitated by the use of real-time monitoring of luc-reporters, there has been an assertion that phase is essentially the same amongst isolated tissues [19]. Nevertheless, given our observation that the effects of the cryb variant may be tissue-specific, as well as the use of both per-luc and tim-luc reporters, we re-examined this question quantitatively.
Thus, the second analytic feature we emphasize is the analysis of phase. We have applied two complementary approaches. The first approach uses circular statistics to evaluate the distribution of peak phase estimates. The second approach uses a bivariate analysis that reveals intraspecimen variability as well as mean peak time to test differences in phase. Specifically, we applied these methods to ask whether the two luc reporters (BG-luc and tim-luc) peak at the same time in a cry+ (and otherwise clock-normal genetic background) and also whether the cryb mutation influences peak phase of the BG-luc reporter.
The observation of tissue-specific phase relationships between per-luc and tim-luc, along with the apparent difference in the absolute timing of phase is not surprising. Such differences could be explained both on the basis of differences in cell types and differences in function. Whereas peripheral clocks are not necessarily neuronal [36], it is conceivable that tissue specific differences in the intracellular environment would force different peak times on the clock mechanism. Further, based on the tissue specific effects of cryb it is possible that the configuration of a clock mechanism may vary between different cell types. For example, the full ensemble of clock factors present within these various tissues is not yet known.
Conclusions
Following our previous development of a collection of analytical tools for the study of molecular and behavioral cycles [27], we now provide intensively performed examples of the analysis of molecular rhythms in isolated tissues from Drosophila. In the main, but by no means exclusively, the current analyses were applied to published data revolving round effects of the cryptochrome gene as it functions in Drosophila's circadian system [23]. The results of the present study show that procedures for detrending and normalizing the data clarify the presence versus absence of rhythmicity – which tend strongly to be associated with cry+ functioning versus that putatively remaining in the cryb mutant – as well as permitting a more detailed understanding of the features accompanying a given molecular time-course. Our conclusions from extended and deepened analyses of these clock-gene cyclings are consistent with those in the earlier report [23], including the matter of peripheral-tissue rhythms being dependent in part on CRY-mediated functions. Moreover, current applications of our phase analysis uncovered new phenomena. These components of the tool-kit reveal that cryb alters the phase of period and timeless gene expressions, suggesting further that – at least in the periphery – CRY plays a quasi-central role in molecular timekeeping. More broadly, in peripheral tissues whose genotype was clock-normal, phase differences that were evident among the different body parts strengthen the notion that overall features of the timekeeping mechanisms vary according to the local molecular milieu. This is perhaps as it should be – because why would a structure such as the antenna necessarily wish to exhibit a maximum or mininim value for a given piece of clock-output that might be the same as those elaborated within the fly's legs?
The development of analytical strategies for analyzing biological time-series will continue to be important as new real-time methods (potentially including images of tissues) provide greater access to molecular and physiological cycles. Such strategies add depth as well as detail to the study of biological time-keeping mechanisms.
Materials and Methods
Peripheral tissues were dissected from D. melanogaster adults as described in Krishnan et al [23]. The per-luc (BG-luc) and tim-luc transgenic strains were originally described elsewhere [20, 21]. Automated monitorings of luciferase (LUC) activity were the same previously described [20, 23]. All of the data from light-dark cycles (LD 12:12) and from constant darkness (DD) were from the LUC monitorings reported in Krishnan et al [23], although most of the pertinent data were not separated as to per-luc versus tim-luc expressions, and many of the results were included as supplementary material. Additional cry+ specimens in Table 1, which did not appear in the earlier report, have been included here, substantially to augment the appreciation of normal clock-gene cycling in isolated tissues. We also include data from additional experiments collected under constant high temperature (27°C) [23]. These data were collected after the submission of the earlier report.
In these new experiments flies were reared in DD and in temperature cycles (12-hr 27°C: 12-hr 18°C). One-to-three day-old ether-anesthetized males were collected and housed for 2 days in these same conditions before the antennal pairs were dissected. The antennal pairs were placed immediately in luciferin-containing medium in 96-well plates and transferred to the luminometer (as described in [23]), where they were exposed to 2 additional days of the temperature-cycle in DD before being maintained at a constant temperature of 27°C for the duration of the LUC-monitoring runs.
The basic flow-chart for handling data from a given specimen and from an ensemble of like ones was as follows: Each record was evaluated for an adequate level of expression above 'no-specimen' background to insure that the tissue had survived and was producing valid data [cf. [23]]. If expression levels were adequate, the specimen was assessed for rhythmicity. Temporally varying LUC activity was detrended and normalized as described in Figure 1. Next, autocorrelation analysis [30] was performed to look for a rhythmic pattern of activity. The correlogram is a plot that reports correlation-coefficient values on the vertical axis versus time-lags plotted on the horizontal axis. Zero lag always provides a value of 1, because the correlation is perfect between the activity record and a copy of itself at each point. However, as one copy of the activity record is shifted along the time axis (in either direction) by one point (in other words, a lag of 1 hour), the correlation falls off. This process is repeated, and a correlation coefficient is calculated for the activity record against itself for each lag shown in the correlogram (see bottom row of Figure 1 for an example). If the correlation coefficients fall and rise in a periodic fashion, resembling a sinusoidal curve, the record of LUC activity is "rhythmic." As to whether such periodicity is significant, a 95% confidence interval is calculated based on the number of observations in the experiment. Rhythmic activity is statistically significant if the peaks and troughs of the autocorrelation function cross the boundary set by the confidence interval centered at 0 on the correlogram (for further detail see [27] and references therein). As noted above in Results text, we do not require statistical significance to score a record as rhythmic. The appearance of rhythmicity in the correlogram is applied as a qualitative criterion so that we do not treat weakly rhythmic data as arrhythmic data. The justification for this strategy is given in Levine et al [27]. In addition, we keep track of the number of specimens that generated statistically significant rhythms as indicated in Table 1 and Table 2.
We quantify the strength of a rhythm with the aforementioned Rhythmicity Index. RI is the height of the third peak of the correlogram [27, 31]. Whereas the confidence interval for the correlogram is based solely on the number of observations, the RI value is based on the robustness of any regular fluctuations in the data. For example, we record LUC activity every hour. If we increased the sampling frequency from once every 60 minutes to once every 30 or 15 minutes, the confidence interval would become smaller while the shape and amplitude of the correlogram would presumably remain unchanged from the curve obtained by 60 minute sampling. The RI value, however, would not vary, while the estimates of statistical significance would vary according to the sampling frequency.
It is nevertheless informative to monitor the statistical significance of periodicities; for this we devised a ratio that allows us to track whether or not a specimen is significantly rhythmic, the so-called Rhythmicity Statistic (RS). An RS value is a ratio of the RI value to the absolute value of the 95% confidence line. If RI is equal to or greater than the numerical height of the confidence line, then the rhythm is significant (by definition, the height of the peak is ≥ the height of the confidence interval used to determine statistical significance). Alternatively, if RI is less than the confidence line, the rhythm is not statistically significant. Thus, RS provides a numerical accounting of significance for an individual specimen or an average signal.
We define the amplitude of a rhythmic LUC time-course as the (plotted) distance (in arbitrary units) from the mean peak or mean trough of the normalized activity record to 1 (the latter is always the mean value of detrended and normalized data, as exemplified in Figure 1). The complete range of the rhythm is twice the amplitude.
Most of the analyses applied in the current study were described in detail in the companion paper [27]. We augmented such treatments of the data by developing two additional parameters, the Rhythmicity Statistic (RS) and a metric that allows specification of cycling amplitude. Analyses leading to the rhythmic parameters were applied to individual samples; their averages appear in Tables 1 and 2. In addition, averages of the LUC data computed across all records within a given group (which varied as to body part, luc reporter type, and cry allele) were obtained; and such averaged time-courses were formally analyzed, as shown in Figures 3,4 and Figures 5,6. Consequently, there are differences between the Tables and Figures in values of parameters such as the Rhythmicity Index (RI, see below), because the tables specify the means determined from individual-specimen analyses, while the figures provide parameters determined after computing the average time-courses.
Maximum Entropy Spectral Analysis (MESA) was employed to estimate the period of a rhythm, i.e., for a given time-course previously determined to be significantly periodic by correlogram. This method is presented in detail elsewhere [37, 27].
We have discussed the analysis of phase using circular statistics in the companion paper [27]. Briefly, an average estimate of peak phase, obtained for each specimen, is plotted as a point on a unit circle. A mean vector, extending from the center of the unit circle towards the diameter is calculated for each group of points; the direction of the vector indicates mean peak phase for the group and the length of the vector represents the variability or dispersion between the points (phase estimates for each specimen). The Watson-Williams-Stevens test returns an F-statistic for the comparison of vectors between two groups to determine whether they represent significantly different estimates of phase (see Figures 5,6 and [27, 32] for further detail).
One disadvantage of this phase analysis is the loss of information about the variability of phase across cycles for each specimen. Therefore, we have also introduced another approach using bivariate statistics to represent the molecular cycles more completely [32]. In this approach, the record of each specimen is represented as the tip of a vector whose direction indicates the mean phase estimate (as above) and whose distance from the origin in the x-y plane represents intraspecimen variability (see Figures 7,8). Each group appears as a distribution of points. A mean vector extending from the origin to the center of the distribution is calculated to describe the overall mean peak phase and variability of the group of points (see Figures 7,8, for example). Finally, the two groups are compared using Hotelling's two-sample test to determine whether the respective vectors are different. If a significant difference between vectors is obtained, this method does not specify whether the difference is due to the variability, the peak phase estimate or some combination of the two.
All of the analyses described above as well as the subsequent output (the figures) come from programs written for the current study and the just-previous one [27] using Matlab6 (Mathworks). This software is available on request.
References
Hall JC: Genetics of biological rhythms in Drosophila. Adv Genet. 1998, 38: 135-84.
Young MW: The molecular control of circadian behavioral rhythms and their entrainment in Drosophila. Annu Rev Biochem. 1998, 67: 135-52. 10.1146/annurev.biochem.67.1.135.
Moore-Ede M, Sulzman F, Czeisler C: The Clocks That Time Us. Cambridge, MA: Harvard University Press. 1982
Saunders DS: Insect Clocks. New York: Pergamon Press. 1982
Moore R, Reppert S, Klein DF, Ed: Suprachiasmatic Nucleus: The Mind's Clock. Oxford University Press. 1991
Plautz JD, Kaneko M, Hall JC, Kay SA: Independent photoreceptive circadian clocks throughout Drosophila. Science. 1997, 278: 1632-1635. 10.1126/science.278.5343.1632.
Whitmore D, Foulkes NS, Sassone-Corsi P: Light acts directly on organs and cells in culture to reset the vertebrate circadian clock. Nature. 2000, 404: 87-91. 10.1016/S0014-5793(97)00099-9.
Stokkan KA, Yamazaki S, Tei H, Sakaki Y, Menaker M: Entrainment of the circadian clock in the liver by feeding. Science. 2001, 291: 490-3. 10.1126/science.291.5503.490.
Damiola F, Le Minh N, Preitner N, Kornmann B, Fleury-Olela F, Schibler U: Restricted feeding uncouples circadian oscillators in peripheral tissues from the central pacemaker in the suprachiasmatic nucleus. Genes Dev. 2000, 14: 2950-61. 10.1101/gad.183500.
Giebultowicz JM, Stanewsky R, Hall JC, Hege DM: Transplanted Drosophila excretory tubules maintain circadian clock cycling out of phase with the host. Curr Biol. 2000, 10 (2): 107-10. 10.1016/S0960-9822(00)00299-2.
Emery IF, Noveral JM, Jamison CF, Siwicki KK: Rhythms of Drosophila period gene expression in culture. PNAS. 1997, 94: 4092-4096. 10.1073/pnas.94.8.4092.
Helfrich-Forster C, Stengl M, Homberg U: Organization of the circadian system in insects. Chronobiol Int. 1998, 15: 567-94.
Kaneko M: Neural substrates of Drosophila rhythms revealed by mutants and molecular manipulations. Curr Opin Neurobiol. 1998, 8 (5): 652-8. 10.1016/S0959-4388(98)80095-0.
Krishnan B, Dryer SE, Hardin PE: Circadian rhythms in olfactory responses of Drosophila melanogaster. Nature. 1999, 400: 375-8. 10.1038/22566.
Kondo T, Strayer CA, Kulkarni RD, Taylor W, Ishiura M, Golden SS, Johnson CH: Circadian rhythms in prokaryotes: luciferase as a reporter of circadian gene expression in cyanobacteria. Proc. Nat. Acad. Sci. USA. 1993, 90: 5672-5676.
Hicks KA, Millar AJ, Carre IA, Somers DE, Straume M, Meeks-Wagner DR, Kay SA: Conditional circadian dysfunction of the Arabidopsis early-flowering 3 mutant. Science. 1996, 274: 790-92. 10.1126/science.274.5288.790.
Brandes C, Plautz JD, Stanewsky R, Jamison CF, Straume M, Wood KV, Kay SA, Hall JC: Novel features of drosophila period Transcription revealed by real-time luciferase reporting. Neuron. 1996, 16: 687-92. 10.1016/S0896-6273(00)80088-4.
Yamaguchi S, Kobayashi M, Mitsui S, Ishida Y, van der Horst GT, Suzuki M, Shibata S, Okamura H: View of a mouse clock gene ticking. Nature. 2001, 409: 684-10.1038/35055628.
Plautz J, Straume M, Stanewsky R, Jamison C, Brandes C, Dowse HB, Hall JC, Kay S: Quantitative analysis of Drosophila period gene transcription in living animals. J. Biol. Rhythms. 1997, 12: 204-217.
Stanewsky R, Jamison CF, Plautz JD, Kay SA, Hall JC: Multiple circadian-regulated elements contribute to cycling period gene expression in Drosophila. EMBO J. 1997, 16 (16): 5006-18. 10.1093/emboj/16.16.5006.
Stanewsky R, Kaneko M, Emery P, Beretta B, Wager-Smith K, Kay SA, Rosbash M, Hall JC: The cryb mutation identifies cryptochrome as a circadian photoreceptor in Drosophila. Cell. 1998, 95 (5): 681-92. 10.1016/S0092-8674(00)81638-4.
Stempfl T, Vogel M, Szabo G, Wulbeck C, Liub J, Hall JC, Stanewsky R: Identification of circadian-clock regulated enhancers and genes of Drosophila melanogaster by transposon mobilization and luciferase reporting of cyclical gene expression. Genetics,. 2002, 160: 571-593.
Krishnan B, Levine J, Sisson K, Dowse HB, Funes P, Hall JC, Hardin PE, Dryer SE: A new role for cryptochrome in a Drosophila circadian oscillator. Nature. 2001, 411: 313-317. 10.1016/S0014-5793(97)00747-3.
Emery P, et al: Drosophila CRY is a deep brain circadian photoreceptor. Neuron. 2000, 26: 493-504.
Emery P, Stanewsky R, Hall JC, Rosbash M: A unique circadian rhythm photoreceptor. Nature. 2000, 404: 456-457. 10.1038/35006558.
Hall JC: Cryptochromes: sensory reception, transduction, and clock functions subserving circadian systems. Curr Opin Neurobiol. 2000, 4: 456-66. 10.1016/S0959-4388(00)00117-3.
Levine JD, Funes P, Dowse HB, Hall JC: Signal Analysis of Behavioral and Molecular Cycles. BMC Neuroscience. 2002, 3: 1-10.1186/1471-2202-3-1.
Hardin PE, Hall JC, Rosbash M: Feedback of the Drosophila period gene product on circadian cycling of its messenger RNA levels. Nature. 1990, 343: 536-540. 10.1038/343536a0.
Hardin PE: Analysis of period mRNA in Drosophila head and body tissues indicates that body oscillators behave differently from head oscillators. Mol. Cell. Biol.,. 1994, 14: 7211-7218.
Chatfield C: The analysis of time series. London, Chapman and Hall. 1980
Johnson E, Bray N, Ringo J, Dowse HB: Genetic and pharmacological identification of ion channels central to the Drosophila cardiac pacemaker. J Neurogenet. 1998, 12: 1-24.
Batschelet E: Statistical methods for the analysis of problems in animal orientation and certain biological rhythms. Washington DC, AIBS Monograph. 1965
Konopka RJ, Pittendrigh C, Orr D: Reciprocal behaviour associated with altered homeostasis and photosensitivity of Drosophila clock mutants. J. Neurogenet. 1989, 6: 1-10.
Zerr DM, Hall JC, Rosbash M, Siwicki KK: Circadian fluctuations of period protein immunoreactivity in the CNS and the visual system of Drosophila. J. Neurosci. 1990, 10: 2749-62.
Zeng H, Hardin PE, Rosbash M: Constitutive overexpression of the Drosophila period protein inhibits period mRNA cycling. EMBO J. 1994, 13: 3590-8.
Giebultowicz JM, Hege DM: Circadian clock in Malpighian tubules. Nature. 1997, 386: 664-10.1038/386664a0.
Dowse HB, Ringo JM: The search for hidden periodicities in biological time series revisited. J. Theor. Biol. 1989, 139: 487-515.
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Levine, J.D., Funes, P., Dowse, H.B. et al. Advanced analysis of a cryptochrome mutation's effects on the robustness and phase of molecular cycles in isolated peripheral tissues of Drosophila. BMC Neurosci 3, 5 (2002). https://doi.org/10.1186/1471-2202-3-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2202-3-5